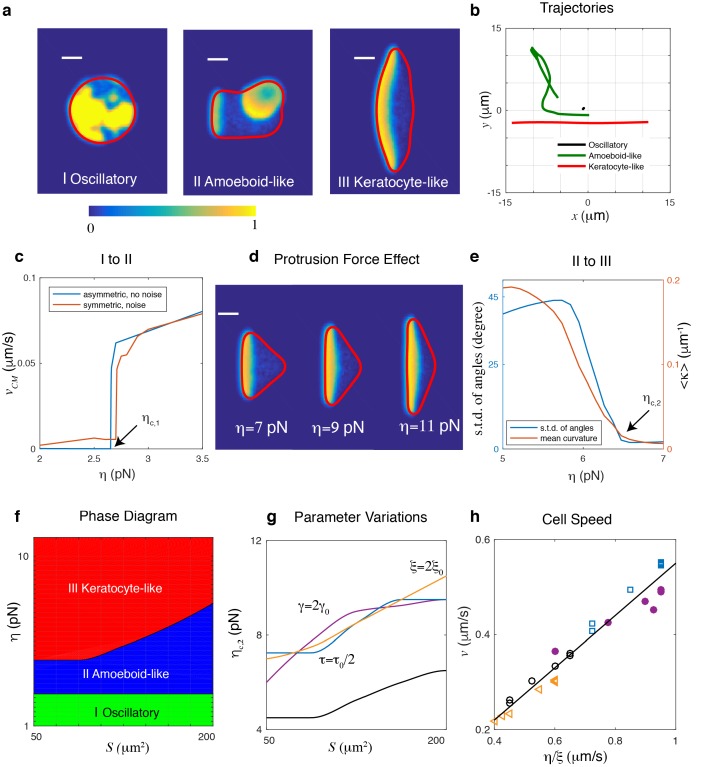
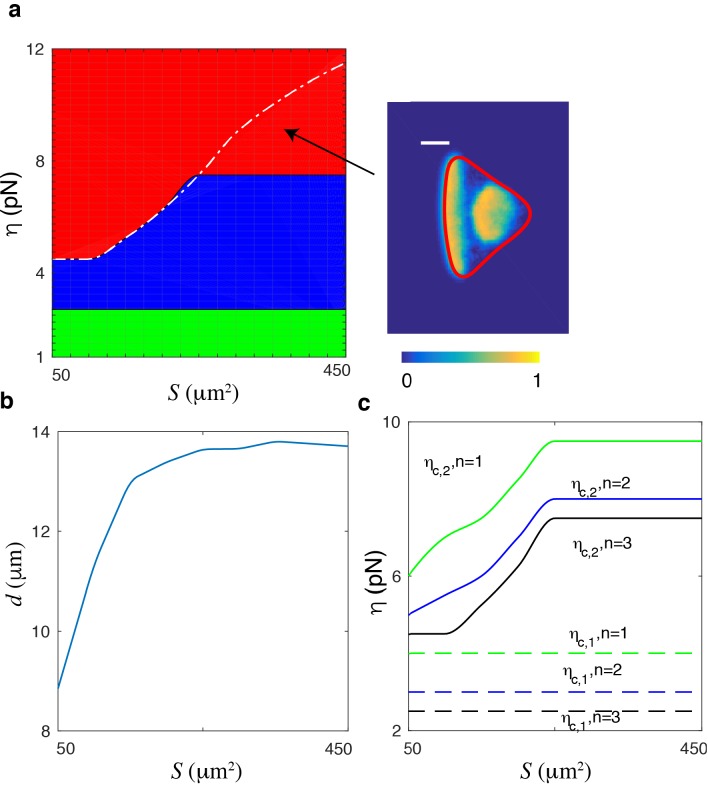
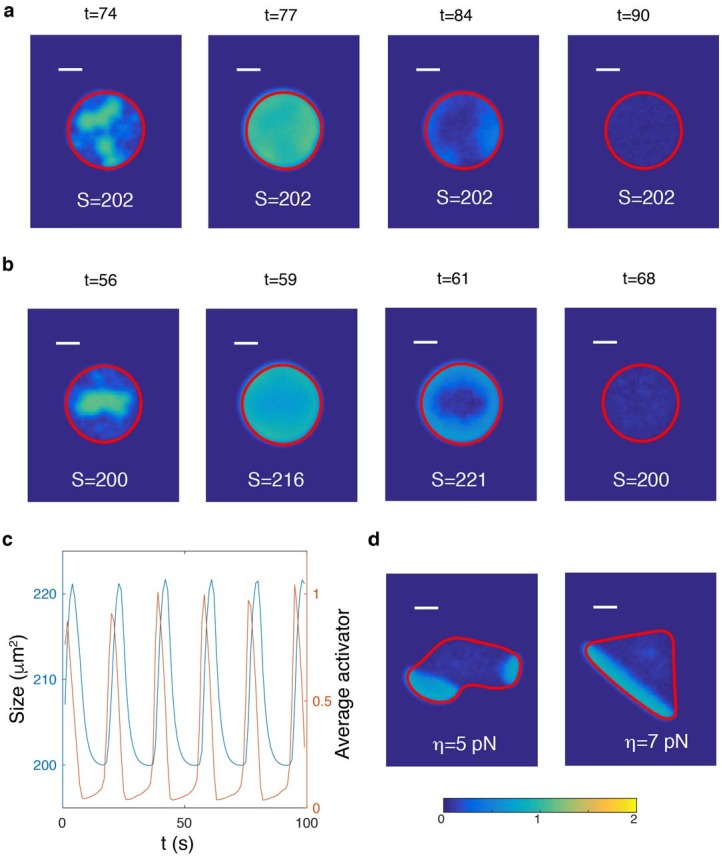
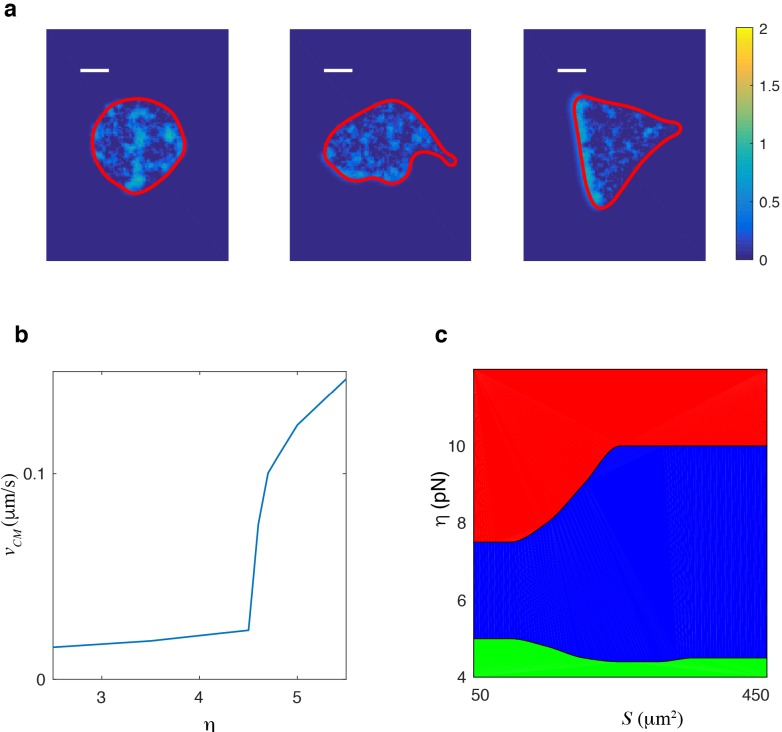
Figure 2. Different cell migration modes can be captured in the model by varying the protrusive strength $\eta$.

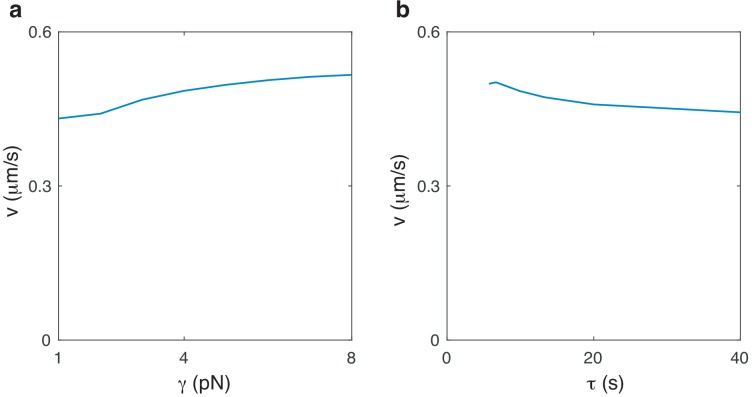
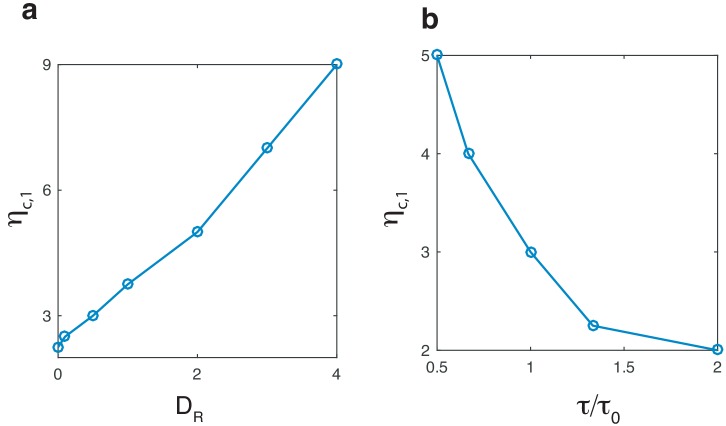
(a) Snapshots of a simulated cell showing (I) an oscillatory cell (${\displaystyle \eta =2\mathrm{p}\mathrm{N}}$), (II) an amoeboid-like cell (${\displaystyle \eta =4\mathrm{p}\mathrm{N}}$), and (III) a keratocyte-like cell (${\displaystyle \eta =11\mathrm{p}\mathrm{N}}$). All other parameters were assigned the default values and r = 8µm. Here, the activator concentration is shown using the color scale and the cell membrane is plotted as a red line (scale bar µm). (b) The trajectories of the three cells in (a). (c) The transition from oscillatory cell to amoeboid-like cell, with speed of the center of mass of a cell as a function of protrusion strength $\eta$ for r = 8µm. The red curve represents results from initial conditions where noise is added to a homogeneous $A$ and $R$ field while the blue curve corresponds to simulations in which the initial activator is asymmetric. Cells become non-motile at a critical value of protrusion strength, ${\eta }_{c,1}$. (d) Increasing the protrusive force $\eta$ will result in flatter fronts in keratocyte-like cells and a decreased front-back distance. The simulations are carried out for fixed cell area $S$. (e) The transition from amoeboid-like cell to keratocyte-like cell quantified by either the average curvature along a trajectory or the standard deviation of the angles of trajectory points as a function of protrusion strength $\eta$ (r = 8µm). Cell moves unidirectionally when the protrusion strength $\eta >{\eta }_{c,2}$. (f) Phase diagram determined by systematically varying $\eta$ and the initial radius of the cell, $r$. Due to strong area conservation, cell area is determined through $S=\pi r^2$. (g) The transition line of amoeboid-like cell to keratocyte-like cell for different parameter values. (h) The speed of the keratocyte-like cell as a function of $\eta /\xi$. The black line is the predicted cell speed with $v_b=\alpha \eta /\xi$, where $\alpha \approx 0.55$. Symbols represent simulations using different parameter variations: empty circles, default parameters; triangles, $\xi =2{\xi }_0$; filled circles, $\gamma =2{\gamma }_0$; squares, $\tau ={\tau }_0/2$.

Figure 2—figure supplement 1. Speed of keratocyte-like cells as a function of the surface tension and timescale of the inhibitor.

Speed of keratocyte-like cells as a function of the surface tension (a) and the timescale of the inhibitor (b). Parameters are as in Table 1 with r = 8µm.

Figure 2—figure supplement 2. Critical protrustion strength ${\eta }_{c,1}$ as a function of the inhibitor’s diffusion constant and time scale.

(a) The critical value ${\eta }_{c,1}$ of protrusion strength as a function of inhibitor’s diffusion constant $D_R$, and (b), the timescale of the inhibitor $\tau$, rescaled by the default value ${\displaystyle {\tau }_0=10s}$. Remaining parameters are as in Table 1 with r = 8µm.

Figure 2—figure supplement 3. Effects of tension.

Snapshot (bottom) and corresponding trajectory (top) of a cell that undergoes a turning instability. (a) Upon the reduction of surface tension from $\gamma$=2pN/µm to $\gamma$=1pN/µm. Parameters are taken from Table 1 with r = 6µm. (b) As in (a), but now after an increase in $D_A$ and $D_R$ to $D_A=D_R$=2 µm²/s and r = 8µm.

Figure 2—figure supplement 4. Parameter variations in the model.

Parameter variations in the model. (a) Phase space extended to maximum cell area ~ 450 µm², corresponding to r = 12µm. Green: oscillatory cell; blue: amoeboid-like cell; red: keratocyte-like cell. The dashed white line corresponding to the separation line $d=\lambda$ above which the keratocyte-like cells exhibit a single wave and below which keratocyte-like cells move unidirectional but with small waves repeatedly appearing at the back of the cell. (b) The keratocyte-like cell’s front-back distance $d$ along the white dashed line. The saturation value is the wavelength ${\displaystyle \lambda \approx 13\mu m}$. (c) Lines corresponding to ${\eta }_{c,1}$ and ${\eta }_{c,2}$ in the $(\eta ,S)$ phase space for different values of the Hill coefficient $n$. For all values of $n$ used in the simulations, ${\eta }_{c,1}$ is independent of the cell radius $r$ while ${\eta }_{c,2}$ increases with $r$, and thus $S$, and eventually saturates.

Figure 2—figure supplement 5. Oscillatory cells for strong and weak area conservation.

Oscillatory cells for strong (a, $B_S=10$) and weak (b, $B_S=0.1$) area conservation. Parameters are as in Table 1 with $\eta =2.5$ and r = 8µm. (c) Cell size (blue) and average activator concentration (red) as a function of time for the oscillatory cell in panel b. (d) Left, example of amoeboid-like cell for weak area conservation ($B_S=0.1$); right, example of keratocyte-like cell for weak area conservation ($B_S=0.1$). The colors represent the activator concentration, as indicated by the color bar. Scalebar = 5 µm.

Figure 2—figure supplement 6. Excitable dynamics can reproduce identical qualitative results.

Excitable dynamics can reproduce identical qualitative results. (a) Snapshots of the three different migration modes for an excitable version of the model. Left panel shows an nonmotile cell ($\eta =2$), middle panel shows an amoeboid-like cell ($\eta =4$), and the right panel displays a keratocyte-like cell ($\eta =10$). (b) Speed of the center of mass as a function of critical protrusion strength. As for the relaxation oscillator model (Figure 2c), the bifurcation is subcritical. (c) Phase diagram $(\eta ,S)$ space with green corresponding to nonmotile cells, blue representing amoeboid-like cells, and red corresponding to keratocyte-like cells. Scalebar = 5 µm.