Water mobility spectral imaging of the spinal cord: parametrization of model-free Laplace MRI

Abstract

Diffusion magnetic resonance imaging (dMRI) of biological systems most often results in non-monoexponential signal, due to their complexity and heterogeneity. One approach to interpreting dMRI data without imposing tissue microstructural models is to fit the signal to a multiexponential function, which is sometimes referred to as an inverse Laplace transformation, and to display the coefficients as a distribution of the diffusivities, or water mobility spectra. Until recently, this method has not been used in a voxelwise manner, mainly because of heavy data requirements. With recent advancements in processing and experimental design, voxelwise Laplace MRI approaches are becoming feasible and attractive. The rich spectral information, combined with a three-dimensional image, presents a challenge because it tremendously increases the dimensionality of the data and requires a robust method for interpretation and analysis. In this work, we suggest parameterizing the empirically measured water mobility spectra using a bimodal lognormal function. This approach allows for a compact representation of the spectrum, and it also resolves overlapping spectral peaks, which allows for a robust extraction of their signal fraction. We apply the method on a fixed spinal cord sample and use it to generate robust intensity images of slow- and fast-diffusion components. Using the parametric variables, we create novel image contrasts, among them the information entropy of the water mobility spectrum, which pack unique features of the individual diffusion regimes in the investigated system.

1. Introduction

Diffusion magnetic resonance imaging (dMRI) delivers a signal that is proportional to the local water mobility and, therefore, can be used to probe biological tissue at different length scales [1–7]. Water mobility in biological tissue cannot be described by a single, simple process such as Gaussian diffusion because of the complexity and heterogeneity of the system’s microstructure. In particular, the existence of a range of physical barriers at different scales and permeabilities, multiple exchanging water pools with different viscosities, and even active processes in live tissue, results in a non-monoexponential diffusion-weighted signal attenuation [8, 9]. Further complicating the interpretation and modeling of dMRI data is tissue anisotropy (e.g., axonal fibers), which creates a directional dependence of the acquired signal [1, 10].

An approach similar to the one used to investigate porous media with nuclear magnetic resonance (NMR) relaxation-based methods [11–13], multiexponential modeling of the diffusion signal can be used to characterize heterogenous biological systems [14–17]. Finding the coefficients of a multiexponential function is, in theory (for the practical case, please refer to the Theory section), equivalent to performing an inverse Laplace transformation (ILT), and, therefore, these methods are often termed Laplace NMR or MRI.

Treating the diffusion signal decay as a multiexponent provides a spectrum of diffusivities, which leads to a model-free description of the water mobility. Because of the heavy data requirements, diffusion-weighted Laplace approaches have most often been limited to NMR. As methods that make Laplace MRI more feasible and accessible emerge [18–20] and are applied [21–25], there is a concomitant growing need for dimensionality reduction. Whereas traditional Laplace NMR results in one- to three-dimensional spectral data, three additional spatial dimensions are added when this approach is combined with imaging. The increased dimensionality, along with the requirement to visualize the data in a summarized manner, creates a need for a more compact representation of the spectral information. In addition, a very important quantity that is usually derived from Laplace spectra is the signal fraction of the different spectral peaks (calculated by means of numerical integration), which is indicative of their associated water volume fraction. In many instances the spectral peaks are overlapping or somewhat indistinguishable, making it hard to robustly determine their limits and consequently making it impossible to reliably compute their signal fraction [26, 27].

In this work, we present a method to reduce the dimensionality of the nonparametric Laplace-based diffusivity spectrum by fitting it to a bimodal parametric function. This approach allows for a compact representation of the spectrum. Importantly, this method also resolves overlapping spectral peaks and allows for a robust extraction of their signal fraction.

2. Theory

2.1. Water mobility spectra

In the case of diffusion-weighted data, the signal attenuation, A, can be described by the following discrete sum [28]:

$$A\left(b_i\right)=\sum _{n=1}^{N}P\left(D_n\right)K\left(b_i,D_n\right)+ϵ\left(b\right),$$ (1)

where ϵ(b) is the experimental noise, which is assumed to be Gaussian. The parameter b is defined as $b={\gamma }^2{\delta }^2{G}^2\left(\mathrm{\Delta }-\delta /3\right)$, which is composed of a pair of magnetic pulsed gradients [29] of duration δ, separation ∆, and amplitude G, with γ being the gyromagnetic ratio. The measured diffusion parameter, D, is distributed according to P(D) with N discrete components, and K(b, D) relates b and D and is called the kernel. In this particular case, the kernel can be expressed as

$$K_D\left(b,D\right)=\text{exp}\left(-bD\right).$$ (2)

Encoding is done by sampling the diffusion weighting parameter space N_b times. In this case, Eq. 1 can be written in matrix form as

$$A=\mathbf{K}P+ϵ,$$ (3)

where A and ϵ are N_b × 1 vectors, P is an N × 1 vector, and K is an N_b × N matrix. Eq. 3 is the matrix form of the Fredholm integral of the first kind, which is a classic ill-conditioned problem [30]. The main implication is that the data inversion is inherently non-unique [11, 31]. A standard approach to solving ill-conditioned problems is to regularize them. When the spectrum is expected to be smooth, ℓ₂ regularization is appropriate [13]. While slightly distorted, a regularized problem has (by definition) a unique solution that depends on the data [13]. Therefore, the regularized problem considered in this study was

$$P^{\left(\alpha \right)}=\underset{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}P\ge 0}{\arg \min }\left({\Vert \mathbf{K}P-A\Vert }^2+\alpha {\Vert P\Vert }^2\right),$$ (4)

where $\Vert \cdots \Vert$ is the ℓ₂ norm. The regularization term is a measure of the desired smoothness in P(D). Choosing the suitable value of α is still an open research question, with several approaches having been proposed (for a comprehensive review, please refer to [32]). The regularization parameter in this study was chosen by means of the L-curve method [33]. Note that since P(D) is a probability density function, nonnegativity constraints were imposed.

Data processing was performed with in-house code written in MATLAB (The Mathworks, Natick, MA). To estimate the water mobility spectra in a voxelwise manner we used CVX, a package for specifying and solving convex problems [34, 35].

2.2. Parametrization using a bimodal lognormal function

Reports of two dominant diffusivity regimes in nerve tissue are very common in the dMRI and dNMR literature. As a result, a widely used model for water diffusion signal in nerve tissue has been a biexponential model, which assumes it is a sum of two components with distinct diffusion coefficients [8, 9, 36]. While our work here is not intended to debate or to question the validity of the biexponential model, it is important to understand that its use is rooted in the observation of the apparent slow and fast diffusion coefficients in nerve tissue. Later Laplace NMR and MRI studies have also reported bimodal water mobility spectra in different types of brain tissue [14–17, 24]. These studies have led Ronen et al. to use a bimodal lognormal function to describe the estimated diffusivity distributions in their investigation of the usefulness of Laplace MRI in the characterization of diffusion in the brain [17]. Here we are using the same parametric function to reduce the dimensionality of the nonparametric Laplace-based diffusivity spectrum and to achieve a robust separation of overlapping spectral peaks.

A lognormal distribution as a function of the diffusivity is given by

$$P_{log}\left(D\right)=\frac{1}{S\hspace{0.17em}\sqrt{2\pi }D}{e}^{-{\left(\ln D-M\right)}^2/\left(2S^2\right)},$$ (5)

and a bimodal lognormal distribution is given by

$$\begin{gathered} P_{bilog}\left(D\right)=\frac{f_{slow}}{S_{slow}\sqrt{2\pi }D}{e}^{-{\left(\ln D-M_{slow}\right)}^2/\left(2S_{slow}^2\right)} \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+\frac{f_{fast}}{S_{fast}\sqrt{2\pi }D}{e}^{-{\left(\ln D-M_{fast}\right)}^2/\left(2S_{fast}^2\right)}, \end{gathered}$$ (6)

where the volume fractions, f, and the lognormal distribution variables, S and M, of the slow and fast components are used.

Once (the nonparametric) P(D) was estimated by solving Eq. 4, it was fed into a subsequent optimization procedure that fit it to Eq. 6. A global minimum for this constrained optimization over the six variables was found by using MATLAB’s GlobalSearch procedure, with an fmincon solver and an objective function specified as the Jensen difference, which is a well-established method of measuring distance between two probability distributions [37].

3. Materials and Methods

3.1. Specimen preparation

The animal used in this study was housed and treated at the Uniformed Services University of the Health Sciences (USUHS) according to national guidelines and institutional oversight. As part of standard necropsy for an unrelated study, a healthy adult male ferret was euthanized and underwent transcardial perfusion with ice-cold 0.1M phosphate buffered saline (PBS, pH 7.4, Quality Biological) followed by 4% paraformaldehyde (PFA, Santa Cruz Biotechnology, in PBS 0.1M pH 7.4) at USUHS, according to standard methods. For the present study, the spinal cord tissue was extracted by careful surgical dissection. A cervical portion of the spinal cord was then transferred to a PBS-filled container for 7 days to ensure any residual PFA was removed from the tissue. The sample was then immersed in perfluoropolyether (Fomblin LC/8, Solvay Solexis, Italy) and inserted into a 5 mm Shigemi tube (Shigemi Inc., Japan) with a glass plunger matched to the susceptibility of water. The tube was oriented along the direction of the main magnetic field in a 5 mm birdcage radio frequency (RF) coil.

3.2. MRI data acquisition

MRI data were collected on a 7 T Bruker wide-bore vertical magnet with an AVANCE III MRI spectrometer equipped with a Micro2.5 microimaging probe and three GREAT60 gradient amplifiers, which have a nominal peak current of 60 A per channel. This configuration can produce a maximum nominal gradient strength of 24.65 mT/m/A along each of the three orthogonal directions. MRI data were acquired with a spin-echo diffusion-weighted sequence. The sample temperature was set at 16.8°C.

Diffusion-weighted data were collected in two sets, with diffusion gradients oriented perpendicular and parallel to the spinal cord axis of symmetry. In both cases, 20 diffusion gradient steps, G, were applied in linear increments from 0 to 852 mT/m, with duration δ = 3 ms and separation ∆ = 15 ms, resulting in a maximal b-value of 7290 s/mm².

Signal-to-noise ratio (SNR) was defined as the ratio between the average signal intensity within a tissue region of interest (ROI), and the standard deviation of the signal intensity within a background (i.e., no sample) ROI. SNR was similar in both perpendicular- and parallel-oriented diffusion gradient encoding. The highest SNR image (i.e., with b = 0) had an SNR of 60, and the lowest SNR image had an SNR of 54.

For all types of acquisitions, repetition time was TR = 3 s, and echo time was TE = 7.6 ms. A single 4 mm axial slice with a matrix size of 128 × 128 that led to in-plane resolution of 35 × 35 µm², was acquired with four averages.

4. Results and Discussion

4.1. Regularization and its effects

Although the focus of this paper is not the regularization process and its robustness, it is important to consider its influence on the mobility spectrum. The issue of balancing between the stability of the inversion and the over-smoothing effect of the regularization process is still an open question. When the diffusion signal source is comprised of relatively narrow spectral components, as might be the case with non-biological materials, ℓ₂ regularization is not suitable, and instead the ℓ₁ norm should be used [20]. However, the diffusion signal from biological tissue contains information from multiple length scales that include membranes acting as local barriers, intracellular organelles, extracellular matrix and macromolecules; as such, the diffusivity spectrum should span continuously, which is enforced by the ℓ₂ regularization.

Even though other methods for choosing the regularization parameter, α, such as Butler-Reeds-Dawson (BRD) [38] and generalized cross-validation (GCV) [38] are regularly used, we chose here the L-curve method, which is also well-established in the literature. We do not attempt to advocate for the use of the L-curve method; in fact, for the purpose of this work, the choice of α has little importance. Our approach for parametrization of the spectra is specifically designed to address, among other issue, ambiguities arising from under- and over-regularization.

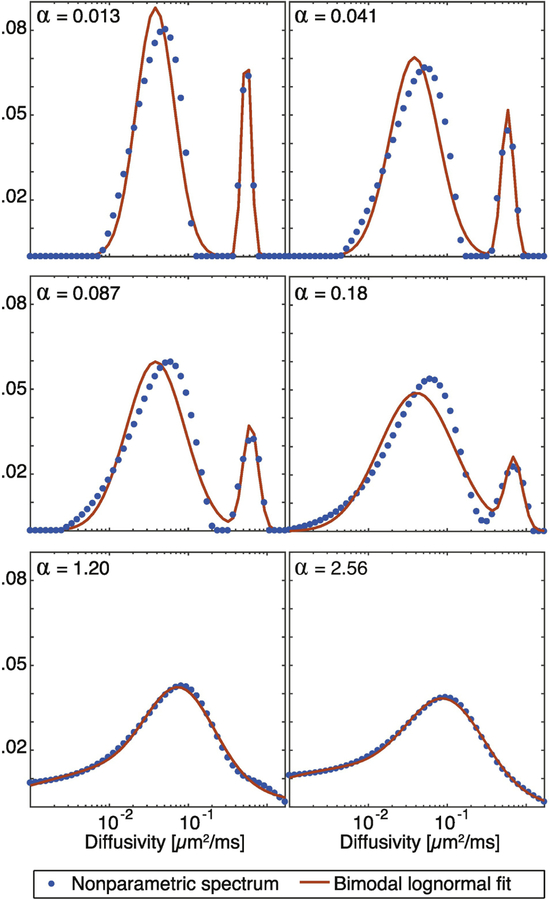
To illustrate, the signal from a representative white matter (WM) voxel was processed with several degrees of regularization (α), and resulted in the nonparametric spectra shown in Fig. 1 (dots). Each of these curves was then fitted to the bimodal lognormal distribution function, and was plotted as well (solid red line). Two well-separated peaks are evident when very small α values were used. As the regularization coefficient is increased, the peaks are starting to merge and become less distinguishable. Regardless of this fact, the fitting of the spectra to the bimodal lognormal function in Eq. 6 was not affected, and two spectral components were reliably identified at each of the regularization degrees. In this particular WM voxel, the L-curve method determined that α = 1.20 provides the optimal solution. While this result might appear to be over-regularized, two well-separated peaks are unlikely because of the vast microstructural heterogeneity in nerve tissue, which would be expected to yield a continuous water mobility spectrum. Whether or not this regularization coefficient is the optimal one is outside the current scope, but note that a smoother spectrum provides less spectral separation, and hence a greater challenge for our parametric fitting approach.

Figure 1:

Water mobility spectra perpendicular to the fibers from a representative white matter (WM) voxel. The effect of increasing the degree of regularization (α) is shown, along with the parametric fit to the spectra.

4.2. Resolving diffusion spectral peaks

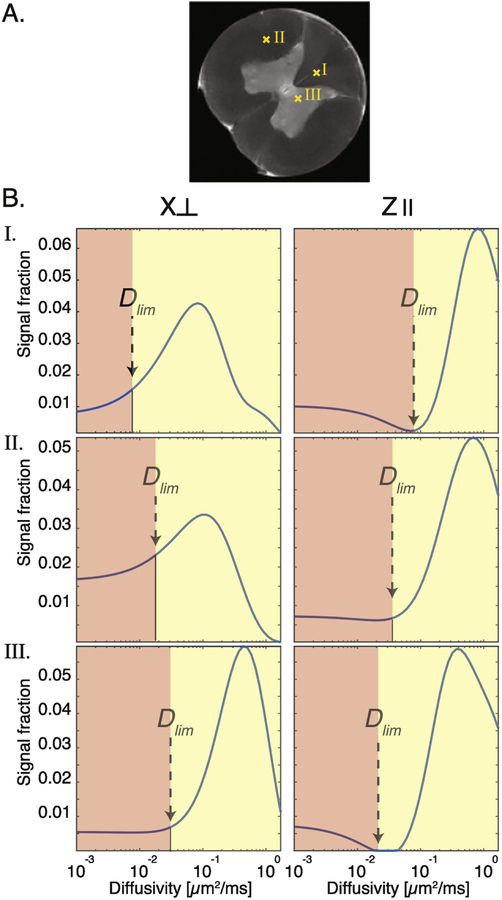
Examples of characteristic diffusivity spectra from different nerve tissue regions, types, and orientations are shown in Fig. 2. The spectra in Fig. 2B, whose locations are marked on the spinal cord proton density image in Fig. 2A, all exhibit non-monomodal characteristics. However, whether the orientation is perpendicular $\left(\text{X}\perp \right)$ or parallel $\left(\text{Z}\parallel \right)$, or whether the tissue type is gray or white matter, dramatically changes the distribution. Without parametrization of the spectra, the approach to obtaining the signal fraction is to judiciously determine the diffusivity limit, D_lim, where the contribution of the slow diffusivity component ends and the fast diffusivity component begins (Fig. 2B). In the case of diffusion in nerve tissue, in which two main components are assumed to exist, one would divide the spectrum into two parts, separated by D_lim, integrate over them, and obtain the signal fractions of the slow and fast components. The limitation of this method is clear: how does one choose D_lim? The arrows in Fig. 2B point to potential D_lim values, which change and move as a function of tissue type and orientation. Thus, a global D_lim value does not exist, and the choice of such value would significantly bias the resulting signal fraction.

Figure 2:

Variability of diffusivity spectra as a function of tissue type and orientation. (A) A proton density image of the spinal cord, on which the locations of spectra in (B) are indicated. (B) Diffusivity spectra from single voxels at different locations and gradient orientations. D_lim is a subjective, manually selected value according to which the spectrum is divided into two diffusivity components, slow and fast.

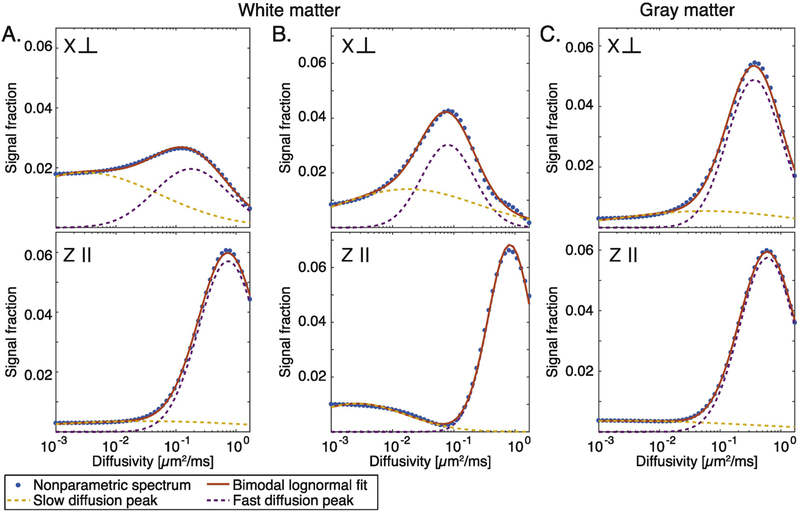
Although the nonparametric distribution (i.e., the one obtained directly from solving Eq. 4) contains the richest information compared with a parametric model, it may be challenging to interpret. Specifically, the overlapping spectral components are often hard to resolve, and the fact that their location on the spectrum is not constant, make it very difficult to automatically determine where one peak ends and the other begins. Fitting the diffusion spectrum in each voxel to the bimodal lognormal function in Eq. 6 allowed for a more robust interpretation of the data. Examples from white and gray matter, and from parallel and perpendicular orientations are shown in Fig. 3. Regardless of the tissue type or orientation, the parametrization captured most of the information contained within the nonparametric distributions.

Figure 3:

The nonparametric distributions and their fitted parametric models. Spectra from three representative voxels: two in white matter (A and B) and one in gray matter (C), with diffusion encoding perpendicular and parallel to spinal cord.

Using a bimodal function to fit the data involves the underlying assumption that regardless of the nerve tissue type and its orientation, the diffusivity spectrum should not contain more than two resolvable peaks. At first glance, this assumption sounds very limiting; however, two important arguments for using a bimodal model function should be kept in mind: (1) a continuously growing body of research demonstrates that dMRI or dNMR signal from nerve tissue contains two observable diffusion regimes, usually referred to as restricted and hindered [6, 8, 9, 17, 24, 36, 39], and (2) numerically inverting a Fredholm integral of one-dimensional data with ℓ₂ regularization very rarely results in more than two distinct spectral peaks [40].

4.3. Water mobility spectral imaging

In the case of NMR, automation of the process of identifying and resolving the water mobility spectral peaks is not necessary; instead, each spectrum can be examined and analyzed manually. Conversely, in conjunction with imaging and, specifically, when voxelwise analysis is desired, the large number of voxels requires a completely automated and robust method to identify the peaks and their point of separation and to resolve them. The most common and useful quantity one can derive from such spectra is the relative signal fraction of each of the spectral components, which is generally assumed to be proportional to the proton’s volume fraction, thus giving the spectral content physical meaning.

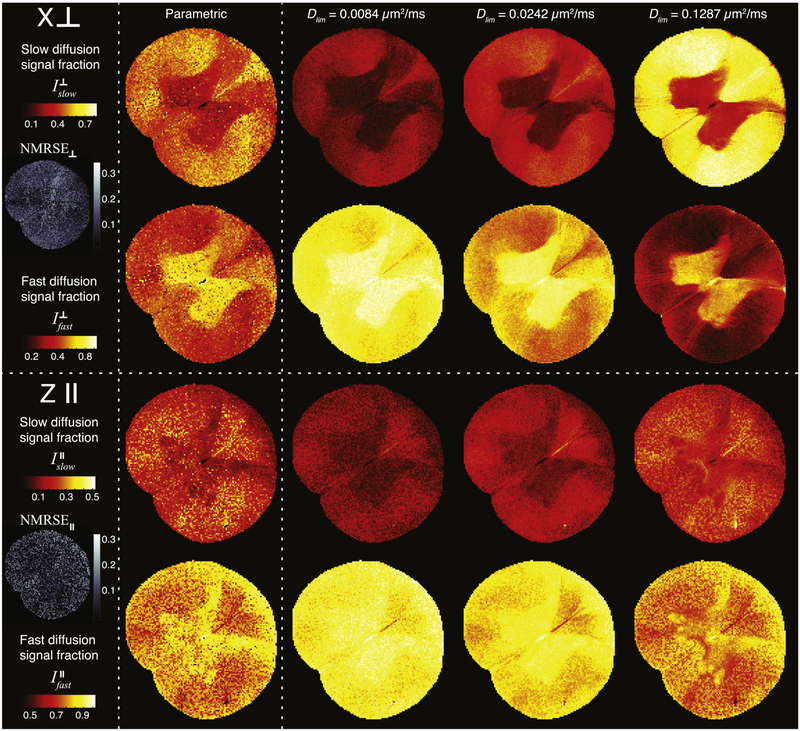
Knowing the parametric form of the slow and the fast diffusion spectral components allows for a simple integration over their entire range, which results in their respective signal fractions. Fig. 4 shows the slow and fast diffusion signal fraction images in the cases where the diffusion encoding gradients are oriented perpendicular ($\text{X}\perp$, top panel) and parallel ($\text{Z}\parallel$, bottom panel) to the spinal cord. At each orientation, the voxelwise signal fractions derived from the parametric model, and from using the conventional method with three different D_lim values, are shown (left to right). Maps of the average normalized root mean square error (NRMSE), which was defined as the RMSE divided by the mean of the measured data, are also shown in Fig. 4. The relatively low NRMSE values and their uniform spatial distribution indicate the good agreement and small bias of the fit. The parametric $\text{X}\perp$ diffusion images demonstrated a typical white–gray matter contrast: high $I_{slow}^{\perp }$ and $I_{fast}^{\perp }$ intensities in white and gray matter, respectively. This contrast is attributed to the higher density and content of barriers perpendicular to the spine’s axis of symmetry in white matter, compared with gray matter [24].

Figure 4:

Slow and fast diffusion signal fraction images with diffusion encoding perpendicular ($\text{X}\perp$, top panel) and parallel ($\text{Z}\parallel$, bottom panel). The images were obtained by using bimodal parametrization, and three different D_lim values, and subsequent integration, which resulted in quantitative images of $I_{slow}^{\perp }$, $I_{fast}^{\perp }$, $I_{slow}^{\parallel }$, and $I_{fast}^{\parallel }$. Average NRMSE maps at each gradient orientation are also presented, indicating high confidence of the fit and uniform spatial distribution.

Although clear from the examples in Fig. 2, we can now see how the subjective selection of D_lim is critical and how it significantly changes the image contrast of the signal fraction. As opposed to relaxation data, diffusion attenuation is highly dependent on the tissue orientation, or equivalently, on the diffusion gradients direction. While the fibers orientation arrangement in the spinal cord is mostly known a priori, each voxel in the brain could contain a population of anisotropic “pores” with different orientations. In the absence of an automated method of distinguishing and identifying the diffusion spectral peaks, one would necessarily have to simply select a global D_lim and apply it to all voxels, which should be expected to perform very poorly. To illustrate, the image contrast in $\text{Z}\parallel$ obtained by using D_lim = 0.1287 µm²/ms seems to be qualitatively similar to that of the parametric images. However, if we look at the same D_lim value images in $\text{X}\perp$, we see that the nonparametric images are completely saturated and are definitely different from the parametric ones and the expected image contrast.

An alternative to fitting the spectra to a bimodal lognormal function, Stanisz and Henkelman suggested to fit the signal directly to a two-component model [26], stating, similarly to our case, that “the T₂ spectra for white matter estimated using nonnegative least squares method results in overlapping components, making the estimation of the relative T₂ component amplitudes prone to a priori defined thresholds”. A comparison between their method to the approach we suggested here can be found in the Supplementary Material.

4.4. Dimensionality reduction

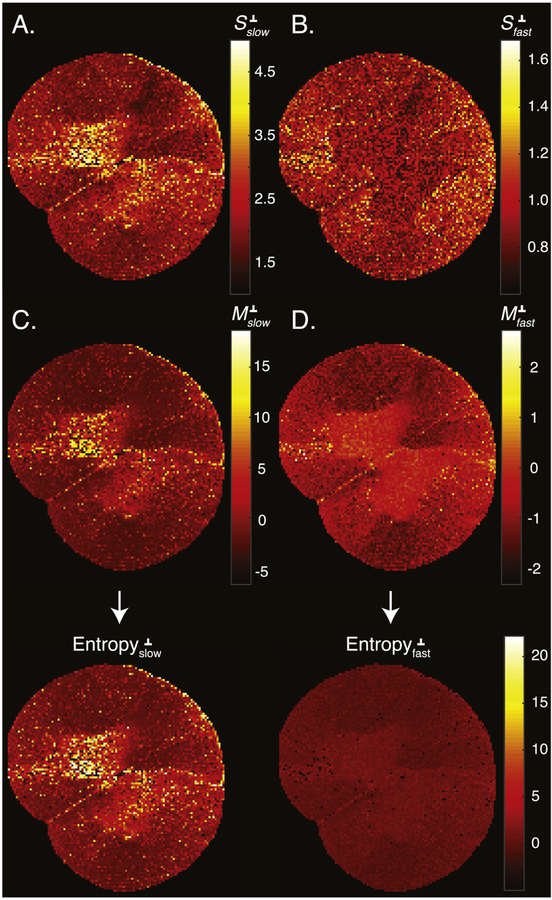
In this work, we discretized the spectra into N = 50 diffusivities values. With the current imaging matrix size of 128 × 128 our spatially resolved spectral data became a 128 × 128 × 50 matrix. A concise examination, study, and interpretation of the spectral information within the context of the image require the processed data be more compactly represented. After voxelwise parametrization of the diffusion spectra, the number of parameters in each voxel was reduced from 50 to 6. The six bimodal lognormal distribution parameters, f_slow, S _slow, M_slow, f _fast, S _fast, and M_fast, may be used to visualize specific aspects and properties of the parametrized distributions they represent.

The usefulness of such dimensionality reduction is reflected in the images of $S_{slow}^{\perp }$, $M_{slow}^{\perp }$, $S_{fast}^{\perp }$, and $M_{fast}^{\perp }$ shown in Fig. 5. These can be further developed into a family of statistical characteristics of the lognormal probability density function; among them are the mean, variance, skewness, etc. Images of the moments of the slow and fast diffusion components could then be analyzed and interpreted in the biological context of the investigated sample, which is beyond the scope of this work.

Figure 5:

Quantitative images of the lognormal probability density function parameters. Images of (A) $S_{slow}^{\perp }$, (B) $S_{fast}^{\perp }$, (C) $M_{slow}^{\perp }$, and (D) $M_{slow}^{\perp }$. Each pair of S and M parameters was then used to compute the entropy images of the slow- and fast-diffusion spectral components, which are shown at the bottom.

We suggest using a useful quantity, the information entropy of the lognormal distribution, by computing the expression $\ln \left(S\hspace{0.17em}{e}^{M+\frac{1}{2}}\sqrt{2\pi }\right)$. Generally, entropy refers to disorder or uncertainty, and in our context lower probability increases the uncertainty and thus increases the entropy. In that sense, a diffusivity value with low probability carries more information than when the same diffusivity value has a higher probability value. By using $S_{slow}^{\perp }$, $M_{slow}^{\perp }$, $S_{fast}^{\perp }$, and $M_{fast}^{\perp }$, the entropy of the slow and fast diffusion components perpendicular to the spinal cord were calculated; they are shown in the bottom panel of Fig. 5. We can see that the fast diffusion component has a relatively low entropy (i.e., carries less information), which is due to its relatively narrow peak. Conversely, the slow diffusion components have a much higher information content, which can be attributed to the shape of their associated spectral peaks. In particular, the slow diffusion components in gray matter were characterized by the widest spectral peaks (as can be seen in Fig. 3), which is concisely reflected in the entropy image.

5. Conclusions

In this paper we suggested parameterizing the empirically measured diffusivity spectra obtained from Laplace dMRI spinal cord data. The advantage is twofold: (1) the parametric form has a compact representation of the spectra, which can be used to infer useful statistical quantities, and (2) it provides a robust method to resolve overlapping spectral peaks. Based on previous studies (e.g., [17]) we chose a bimodal lognormal probability density function to model the nerve tissue–derived diffusivity spectra. We demonstrated the benefits of this parametrization on a fixed spinal cord sample and showed how it generates robust intensity images of slow- and fast-diffusion components. We suggested a novel image contrast, the information entropy of the water mobility spectrum, which packs unique features of the individual diffusion regimes in the investigated system. Finally, we note that this parametrization approach is not limited to diffusion-based Laplace applications but can also be used to process relaxation spectra (e.g., T₁ and T₂ distributions), and to characterize and reduce the dimensionality of multidimensional Laplace MRI data, such as D-T₁ [24]. In particular, one proposed method of myelin imaging is based on multiexponential analysis of multiecho data, where the myelin water fraction (MWF) is defined as the percentage of the total signal associated with the short T₂ peak [28, 41, 42]. MWF calculations use a predefined T₂ range cut-off (i.e., $T_2^{lim}$), which is inconsistent across different studies, mainly due to acquisition protocol, hardware, and inversion method, e.g., [27, 43, 44]. Our method can be applied to robustly and automatically assign the short T₂ peak in a consistent and reliable manner regardless of the experimental conditions, which may improve the reproducibility of MWF imaging.