Orphan spin polarization: A catalyst for high-throughput solid-state NMR spectroscopy of proteins

Abstract

Magic angle spinning solid-state NMR (MAS ssNMR) spectroscopy is a powerful method for structure determination of biomacromolecules that are recalcitrant to crystallization (membrane proteins and fibrils). Conventional multidimensional ssNMR methods acquire one experiment at a time. This approach is time consuming and discards orphan (unused) spin operators. Relatively low sensitivity and poor resolution of protein samples require long acquisition times for multidimensional ssNMR experiments. Here, we describe our recent progress in the development of multiple acquisition solid-state NMR methods for protein structure determination. A family of experiments called Polarization Optimized Experiments (POE) were designed, in which we utilized the orphan spin operators that are discarded in classical multidimensional NMR experiments, recovering them to allow simultaneous acquisition of multiple 2D and 3D experiments, all while using conventional probes with spectrometers equipped with one receiver. Three strategies namely, DUMAS, MEIOSIS, and MAeSTOSO were used for the concatenation of various 2D and 3D experiments. These methods open up new avenues for reducing the acquisition times of multidimensional experiments for biomolecular ssNMR spectroscopy.

(1). Introduction

Magic angle spinning solid-state NMR (MAS ssNMR) spectroscopy is becoming a central technique for chemical, biochemical, and biophysical research, spurring the need for a deeper understanding of theory and its applications to structure, dynamics, and ligand binding of proteins at atomic resolution^1–4. Higher magnetic field strengths and multidimensional NMR experiments have provided powerful new tools for investigating larger biomacromolecules^5–7. Unfortunately this comes at the cost of dramatically prolonged measurement times. In the past few years, several instrumental and methodological developments have increased the scope of ssNMR applications in biomedical research^8–12. These include the developments of low-E and E-free probes that increase the sensitivity of the RF coil and avoid RF heating caused by high power decoupling pulses^13–15. The use of dynamic nuclear polarization (DNP) at ultra-low temperatures ^16,17, paramagnetic relaxation enhancement (PRE)¹⁸, and ¹H detection using ultra-fast MAS probes has dramatically improved the scope of ssNMR for larger biomacromolecules^19,20. However, all these methods rely on acquiring one experiment at a time leading to longer experimental times.

In spite of tremendous progress in pulse sequence methodology, the ssNMR structure determination is still a time consuming process due to low-throughput multidimensional data acquisition. The conventional ssNMR experiments rely on the detection of single polarization transfer pathway and utilizes only about 5 to 10 % of total experimental time for pulse execution and acquisition of the signal, while 95% time the spectrometer is idle with recycle delay, waiting for completion of longitudinal T₁ relaxation and/or probe duty cycle. To best utilize the NMR polarization we have developed new strategies namely polarization optimized experiments (POE) that concatenates multidimensional experiments by utilizing multiple polarization pathways^21–26. The first example is DUMAS method that doubles the capability of ssNMR spectrometers via two acquisition periods without repeating the recycle delay. Several pairs of 2D and 3D experiments are concatenated via DUMAS for sequential assignment of proteins^21,22. DUMAS method is based on simultaneous cross polarization (SIM-CP) that creates two polarization transfer pathways for ¹³C and ¹⁵N, which are then used for recording two multidimensional experiments. This is enabled by long T₁ re-laxation of ¹⁵N nuclei which is the fundamental property of all biological solid or semi-solid proteins^27,28.

The poor sensitivity of conventional ssNMR experiments also results from the incomplete polarization transfer leading to residual spin polarization that is been discarded in conventional experiments. Although it is well known that the existence of residual polarization is a common phenomenon in a cross polarization experiments²⁹, it has not been fully exploited in biomolecular ssNMR experiments. In this direction we developed a MEIOSIS and MAeSTOSO methods that utilize the principles of DUMAS, and also uses the residual ¹³C and ¹⁵N polarization. Depending on the choice of experiments one can use DUMAS, MEIOSIS, and MAeSTOSO strategies for simultaneous acquisition of multidimensional experiments. We have demonstrated these approaches for simultaneous acquisition of several 2D and 3D experiments thereby representing a universal approach to high-throughput ssNMR spectroscopy of proteins. These methods are applied for structure determination various membrane proteins which are often Challenging to current solid-state NMR methods.

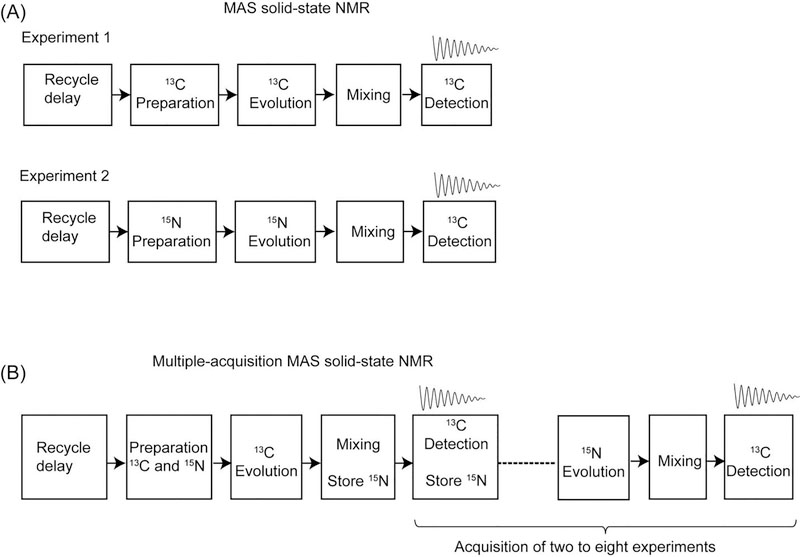
(2). Overview of single and multiple acquisition MAS solid-state NMR

Recent developments in homonuclear and heteronuclear recoupling schemes enabled efficient polarization transfer thereby facilitating protein sequential assignment of uniformly ¹³C and ¹⁵N labeled proteins^26,30–34. However ssNMR spectroscopy of proteins mainly relies on the detection of heavy atom resonances (¹³C and ¹⁵N) with experiments that are intrinsically less sensitive than ¹H detected experiments. Generally, a series of 2D and 3D spectra are necessary to assess the feasibility of structure determination. A schematic of pulse sequence events for conventional (or single acquisition) two-dimensional MAS experiments is shown in Figure 1A. The recycle delay occupies up to 95% of total experimental time while only a fraction of time is used for pulse execution and signal acquisition. Typically, the preparation period consists of ¹H-¹³C or ¹H-¹⁵N double resonance CP followed by t₁ evolution of ¹³C or ¹⁵N coherences. After the t₁ frequency labeling homonulear and/or heteronuclear mixing periods enable the polarization transfer followed by t₂ acquisition. Similarly a 3D experiment starts with ¹³C or ¹⁵N CP followed by multiple evolutions and mixing periods followed by ¹³C detection. The main drawback of these single acquisition methods is that a given 2D or 3D pulse sequence can only map any one of the coherence transfer pathways of protein backbone and side chain atoms. For example in a 2D or 3D NCACO and CANCO experiments the polarization pathways for an i^th residue are given by ¹⁵Nⁱ → ¹³Cαⁱ → ¹³COⁱ, and ¹³Cαⁱ → ¹⁵Nⁱ → ¹³COⁱ⁻¹ respectively, and this requires two separate experiments.

Figure 1:

Schematic of pulse sequence events for (A) conventional and (B) multiple acquisition 2D MAS ssNMR using single receiver. In the multiple-acquisition approach two to eight 2D experiments are simultaneously acquired in a single experiment.

Inspired by the previous work of Pines and Waugh²⁹, we asked ourselves: how to create multiple polarization pathways and detect them in a single experiment?. In fact, Waugh and coworkers have utilized the rich ¹H bath for multiple ¹³C CP acquisitions while holding the proton polarization in the transverse plane under continuous wave decoupling. Although the application of this method on current biological systems is limited due to shorter relaxation (T_1ρ and T₂) times, it however demonstrated the source of hidden polarization in the ¹H spin bath of solid samples. Another unique property in ssNMR is the long T₁ relaxation of low-abundant nuclei, in particular ¹⁵N nuclei of solid proteins can have few hundred milliseconds of T₁ relaxation²⁸. Based on these two unique features of solid systems we have pioneered Multiple acquisition solid-state NMR of proteins that follows the philosophy of multiple ¹³C acquisitions using single receiver while simultaneously storing the other spin operators in the form of ¹⁵N longitudinal polarization that will then be transferred to ¹³C and detected in the following acquisitions. A schematic of multiple acquisition MAS ssNMR is shown in Figure 1B, where a single recycle delay is used for acquiring two to eight experiments resulting from different polarization pathways. The novel feature of multiple acquisition schemes is that it not only records the conventional or parent experiment in the first acquisition but also stores the orphan (unused) spin polarization which will then be used in the subsequent acquisitions.

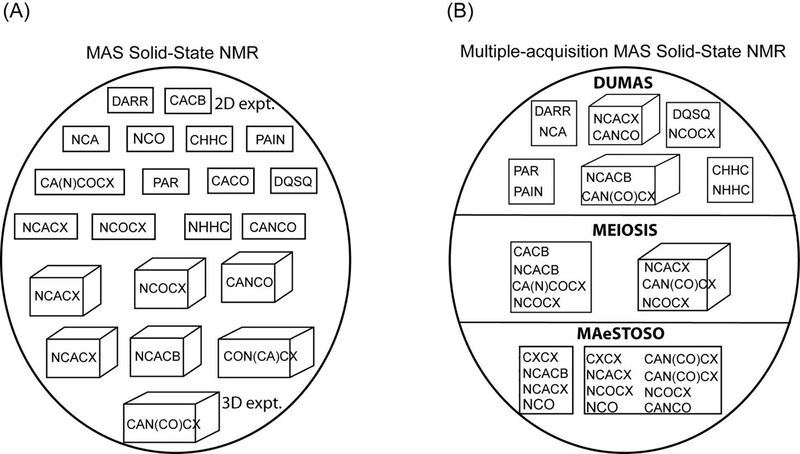
To this end we have designed three different strategies namely, DUMAS, MEIOSIS, and MAeSTOSO for concatenation of multi-dimensional experiments into a single pulse sequence^21–23,25. For example a 2D or 3D DUMAS-NCACO-CANCO experiment acquires ¹⁵Nⁱ → ¹³Cαⁱ → ¹³COⁱ, and ¹³Cαⁱ → ¹⁵Nⁱ → ¹³COⁱ⁻¹ polarization pathways in a single experiment. Figure 2A shows the various two and three-dimensional experiments that are respectively represented in rectangles and cubes. Few examples of concatenation of two and three dimensional experiments using DUMAS, MEIOSIS, and MAeSTOSO are shown in Figure 2B. While DUMAS approach records two spectra from dual polarization pathways (section 3), MEIOSIS and MAeSTOSO can record four to eight multi-dimensional spectra using transferred and residual polarization pathways (sections 4 and 5).

Figure 2:

(A) Various 2D (represented in square) and 3D (represented in cube) experiments that are used for protein ssNMR. (B) Few examples of DUMAS, MEIOSIS, and MAeSTOSO approaches that combine multiple experiments into a single 2D or 3D experiment represented in rectangle and cube respectively.

(3). Creation of dual polarization pathways and simultaneous acquisition of multidimensional experiments

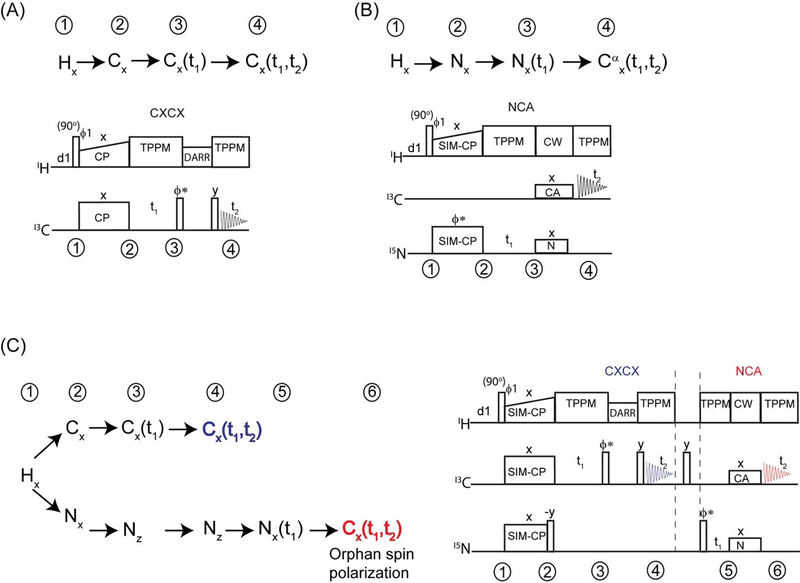
In ssNMR, the evolution of spin operators is dictated by dipolar couplings. Unlike in liquid-state NMR, the ¹³C and ¹⁵N edited experiments start with a single spin operator of ¹³C or ¹⁵N magnetization generated from the abundant spin (¹H) via Hartmann-Hahn (HH) cross-polarization. The CP transfer efficiency is affected by the overall dipolar coupling network of homo- and heteronuclear spins of the system under consideration^32,35. Figure 3A shows ¹³C and ¹⁵N edited CXCX and NCA correlation experiments and evolution of corresponding spin operators during the course of the pulse sequence. In both cases, the preparation period uses a double resonance CP to create initial ¹³C or ¹⁵N polarization followed by t₁ chemical shift evolution, mixing and ¹³C detection during t₂ period. CXCX and NC correlations are respectively obtained from homo and hetero nuclear mixing periods such as DARR and Specific-CP^30,31.

Figure 3:

Pulse sequences and corresponding polarization pathways for conventional (A) CXCX and (B) NCA experiments. (C) Dual polarization pathways that are used for simultaneous acquisition of CXCX and NCA using DUMAS ssNMR.

The rich proton spin bath can be used to create two polarization pathways (¹³C and ¹⁵N) using simultaneous cross polarization (SIM-CP). In this this approach (Figure 3B), namely DUMAS, SIM-CP represents the preparation period that creates initial ¹³C and ¹⁵N polarization which will then be used for acquiring ¹³C and ¹⁵N edited experiments in first and second acquisitions respectively. Figure 3B shows pulse sequence for simultaneous acquisition of CXCX and NCA experiments, dual polarization pathways at various stages of pulse sequence are also shown. During SIM-CP the RF amplitudes of both the ¹³C and ¹⁵N channels simultaneously satisfy the Hartmann-Hahn matching condition with respect to ¹H RF amplitude and MAS rate. It was found that the sensitivity of CP and SIM-CP are similar for ¹³C, whereas only a marginal loss (less than 10 %) of sensitivity was observed for ¹⁵N using SIM-CP²⁴. It is to be noted that the SIM-CP performance is benefited from strong ¹H-¹H dipolar coupling network that enables efficient spin diffusion thereby providing almost similar sensitivity for ¹³C and ¹⁵N with respect to double resonance CP. Following SIM-CP, CXCX experiment is acquired in the first acquisition while storing the ¹⁵N polarization along z-direction. The ¹⁵N polarization is then utilized for acquiring NC correlation experiment during second acquisition.

Successful application of DUMAS requires a rough estimation of relative sensitivity of independent experiments. For example, ¹³C-¹³C polarization transfer under PDSD or DARR is affected by several factors including short and long range dipolar couplings, orientation and scaling of anisotropic interactions of a given protein sample, and rate of magic angle spinning. Thus a given DARR mixing time provides ¹³C-¹³C transfer for broad range of distances. To achieve reasonable sensitivity for intra-residue backbone and side chain correlations it is often necessary to use multiple short mixing times ranging from 10 to 40 ms. Aromatic intra-residue correlations can sometimes require up to 100 ms mixing time due to extensive dynamics. On the other hand medium and long range inter-residue or inter protomer correlations are obtained from longer mixing times of 100 to 500 ms. Similarly one may have to use multiple DARR mixing times for NCACX and NCOCX 2D correlation experiments. However longer DARR mixing times dramatically reduce the sensitivity of the experiments due to multiple correlations as well as T₁ relaxation.

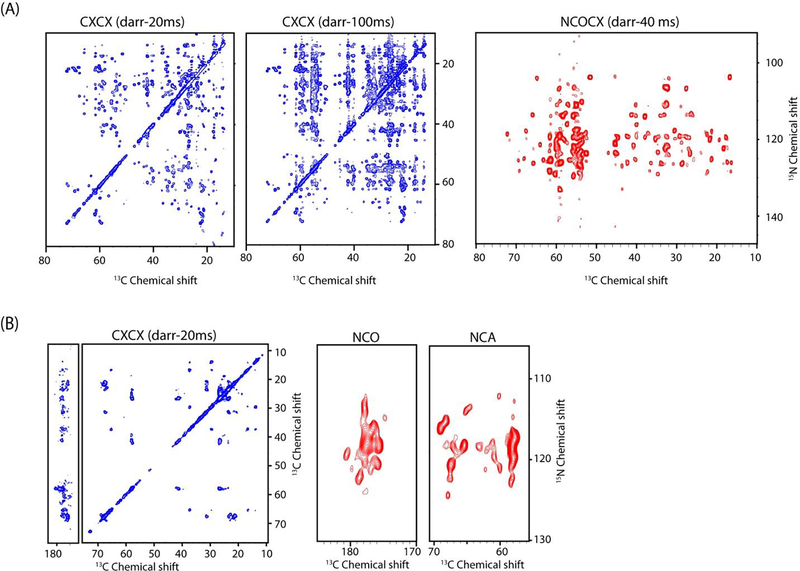
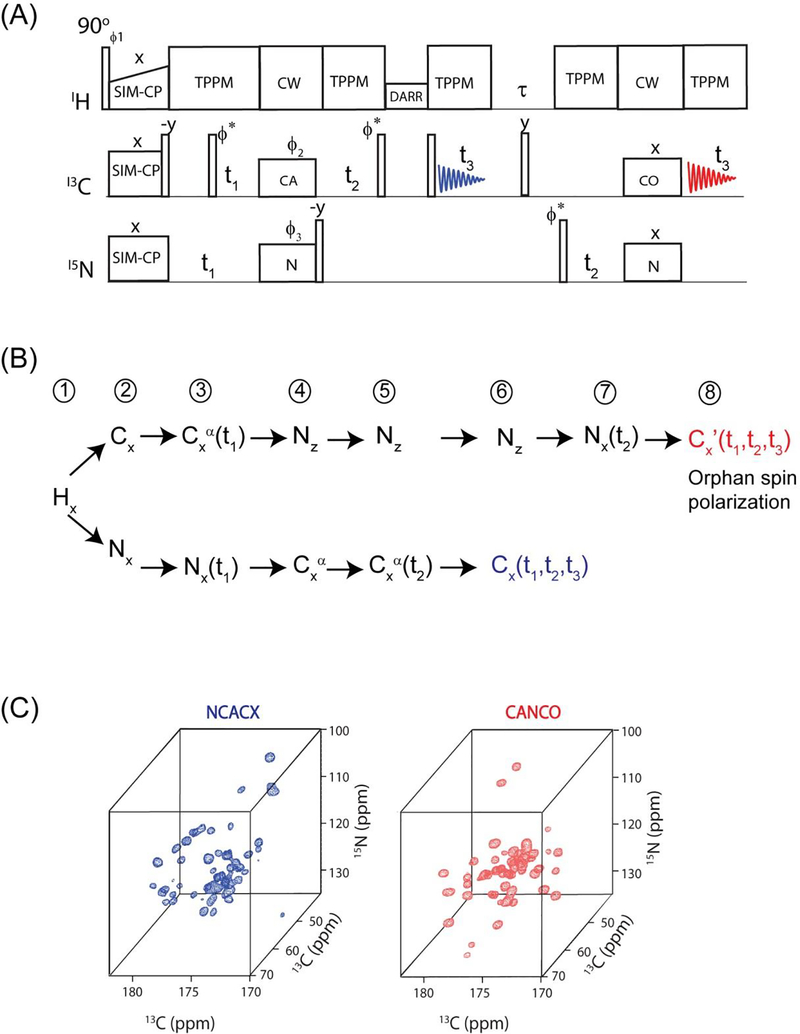
The 2D DUMAS experimental scheme is well suited for optimizing the sensitivity for multiple DARR mixing times for ¹³C and ¹⁵N edited experiments. A novel aspect of DUMAS experiments is that the ¹³C evolution followed by mixing period does not affect the ¹⁵N polarization which is stored along z-direction (Figure 3). Therefore, multiple CXCX experiments with different mixing times can be obtained during first acquisition without disturbing the second acquisition NC experimental parameters, and vice versa. Figure 4 shows two examples of 2D DUMAS experiments on ubiquitin and sarcolipin membrane protein. In Figure 4A both CXCX-20ms and CXCX-100ms experiments were acquired during the first acquisition with an experimental time of 12 and 24 hours respectively, while the NCACX in the second acquisition utilizes all 36 hours of signal averaging. From technical point of view this is done by creating two data acquisition files, where the CXCX mixing was set to 20 and 100 ms in first and second files respectively and second acquisition parameters are identical in both the files. After the completion of two experiments the CXCX data is processed separately whereas the second acquisition NCACX data was added from two files. Similarly one can also switch the second acquisition experiments without effecting the first acquisition, as shown in Figure 4B for sarcolipin membrane protein. In this case CXCX-20 ms experiment was acquired in the first acquisition, whereas second acquisition acquires both NCA and NCO. The DUMAS approach can be used for the concatenation of several pairs two and three dimensional experiments. An example of 3D DUMAS experiment for simultaneous acquisition of NCACX and CANCO is shown in Figure 5.

Figure 4:

CXCX and NC correlation spectra of (A) ubiquitin and (B) sarcolipin membrane protein obtained from 2D DUMAS experiments.

Figure 5:

(A) An example of 3D DUMAS pulse sequence for simultaneous acquisition of NCACX and CANCO, (B) Evolution of two polarization pathways are acquired in first and second acquisitions. (C) NCACX and CANCO 3D spectra of ubiquitin obtained from the above pulse sequence.

(4). Deconvolution of transferred and residual polarization pathways enables the acquisition of multiple two and three-dimensional experiments

In the quest of multiple polarization pathways, we examined the cross polarization density matrix operators. In fact, during the CP between two spin baths I and S (I, S = 1H, 13C, 15N), there is always a residual magnetization that remains on I spin³⁵. This phenomenon can be understood by the characterization the CP dynamics in DQ (double quantum) and ZQ (zero quantum) sub-spaces. In fact only a part of I-spin polarization, namely ZQ operator, is perpendicular to ZQ dipolar Hamiltonian and evolves during CP, the combination of ¹H-¹H spin diffusion and T_1ρ relaxation leads to incomplete polarization transfer. In the conventional methods the residual magnetization is often cancelled out by a z-filter or phase cycling to suppress the artifacts that may interfere with the desired polarization pathway of interest. Here we focus on recovering the residual polarization pathways of NC and CN selective cross polarization obtained from Specific-CP which is basic building block of almost all triple resonance ssNMR experiments. In particular, we demonstrate that in a single pulse sequence, the combination of SIM-CP and Specific-CP creates four polarization pathways that can be used for recording four different experiments utilizing two acquisitions per scan. This method, called MEIOSIS (Multiple ExperIments via Orphan SpIn operatorS), can be used for both 2D and 3D experiments²³.

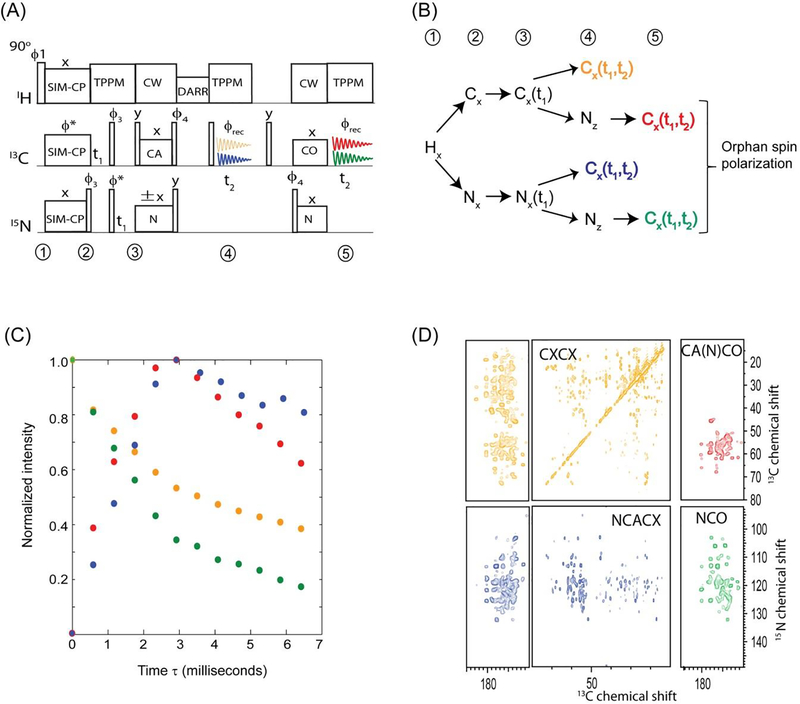
Figure 6A shows an example of 2D MEIOSIS pulse sequence, the spin operators of ¹H, ¹³C and ¹⁵N nuclei at various steps of the pulse sequence are shown in Figure 6B. The pulse sequence starts with simultaneous cross polarization of ¹³C and ¹⁵N followed by parallel evolutions represented by t1’ and t1” respectively. An NCA/CAN specific-CP is then used to create four magnetization pathways: NCA, NN, CAN, and CC. The NCA and CAN refers to polarization transferred from N to Cα and vice versa, while NN and CC result from the residual magnetization remaining on ¹⁵N and ¹³C nuclei that is not transferred to ¹³C and ¹⁵N during NCA specific-CP. A DARR mixing period sandwiched between two 90° pulses is applied to NCA and CC pathways followed by t₂’ acquisition, while the magnetization arising from the other two pathways (CAN and NN) is stored as ¹⁵N z-magnetization. After the first acquisition, the ¹⁵N magnetization is transferred to the ¹³CO group followed by a second FID, which gives the ¹³C spectrum resulting from the CAN and NN path-ways. The first acquisition gives sum of two 2D spectra CXCX and NCACX resulting from CC and NCA pathways respectively. While the second FID is the sum of NCO and CA(N)CO 2D spectra resulting from NN and CAN pathways respectively. In order to decode the two pathways in each acquisition, we alternate the phase of the specificCP ¹⁵N spin-lock between +x and −x. The resultant spectra for +x and −x phases are stored in separate memory allocations. Since the NCA and CAN transfer occur in a doubly tilted rotating frame, the phase switching of ¹⁵N spin-lock during specific-CP will invert the sign of the NCA and CAN transfer, whereas the residual CC and NN magnetization will not be effected by the phase alternation. Thus the addition and subtraction of two data sets with phases +x and −x respectively gives DARR and NCACX in first acquisition, and NCO and CANCO in the second acquisition.

Figure 6:

(A) Two-dimensional MEIOSIS pulse sequence for simultaneous acquisition of CXCX, NCACX, CA(N)CO and NCO experiments. (B) Evolution of spin operators during the pulse sequence. (C) Amplitudes of four pathways that are respectively color coded, residual pathways are represented in orange and green colors. (D) MEIOSIS spectra of ubiquitin obtained simultaneously using the pulse sequence shown in (A).

Figure 6C shows the amplitudes of four pathways as a function of NCA/CAN specific-CP contact time. The maximum of the NCA (or CAN) transfer occurs at approximately at 3 ms contact time, whereas the residual magnetization corresponds to, ~35 % for ¹⁵N, ~43% for the ¹³CO, and ~52% ¹³C aliphatic resonances. Figure 6D shows application of MEIOSIS approach for simultaneous acquisition of CXCX, NCACX, CANCO, and NCO experiments on U-¹³C-¹⁵N ubiquitin sample. Remarkably, the total experimental time for four experiments acquired simultaneously with the MEIOSIS sequence was ~29 hours, whereas the total experimental time for conventional single acquisition experiments was ~62hours, with CXCX and NCACX experiments acquired in 7 and 22 hrs, respectively, and NCO and CA(N)CO experiments took 3.5 and 28 hours, respectively. Similarly other combinations of CC, NCC, CNC, and NC correlation experiments can be concatenated using MEIOSIS approach²⁴.

The MEIOSIS approach is another example of polarization optimized experiments (POE) that recover the residual magnetization to speed-up the data acquisition. The two-dimensional MEIOSIS experiments can be used to assess the resolution and sensitivity of the spectra and make an educated decision on which dimension of the multidimensional spectra need to be acquired with higher resolution for more efficient resonance assignment. The MEIOSIS method can also extended to 3D experiments by incorporating an additional ¹³C evolution period prior to the first and second acquisitions. For example, three 3D experiments NCACX, NCOCX and CA(N)COCX were obtained from NCA, NN, and CAN pathways, respectively²³.

(5). How far can we push the residual polarization?

The current progress in biological solid-state NMR is greatly benefited from the advancements in NMR hardware including the developments of low-E or E-free probes that avoid RF heating caused by high power decoupling pulses. In fact these technological developments were crucial for successful of implementation of DUMAS and MEIOSIS dual acquisition experiments. Here, in order to fully utilize the residual polarization, we incorporate four acquisitions, namely MAeSTOSO approach that is a direct extension of 2D DUMAS and MEIOSIS. MAeSTOSO-4 and MAeSTOSO-8 simultaneously acquires four and eight two-dimensional experiments respectively utilizing four acquisition per scan²⁵. The first two acquisitions of MAeSTOSO-4 and MAeSTOSO-8 resembles DUMAS and MEIOSIS respectively. The main idea behind MAeSTOSO experiments is to use the residual polarization resulting from multiple NC periods, for acquiring additional experiments by incorporating two more acquisitions. In a single experiment MAeSTOSO-4 acquires a CC and NC experiments in the first and second acquisitions, and two more NC experiments are recorded in third and fourth acquisitions by utilizing ~30% and ~10% residual polarization respectively. Similarly, MEIOSIS can be extended to MAeSTOSO-8 to record eight experiments using four acquisitions per scan.

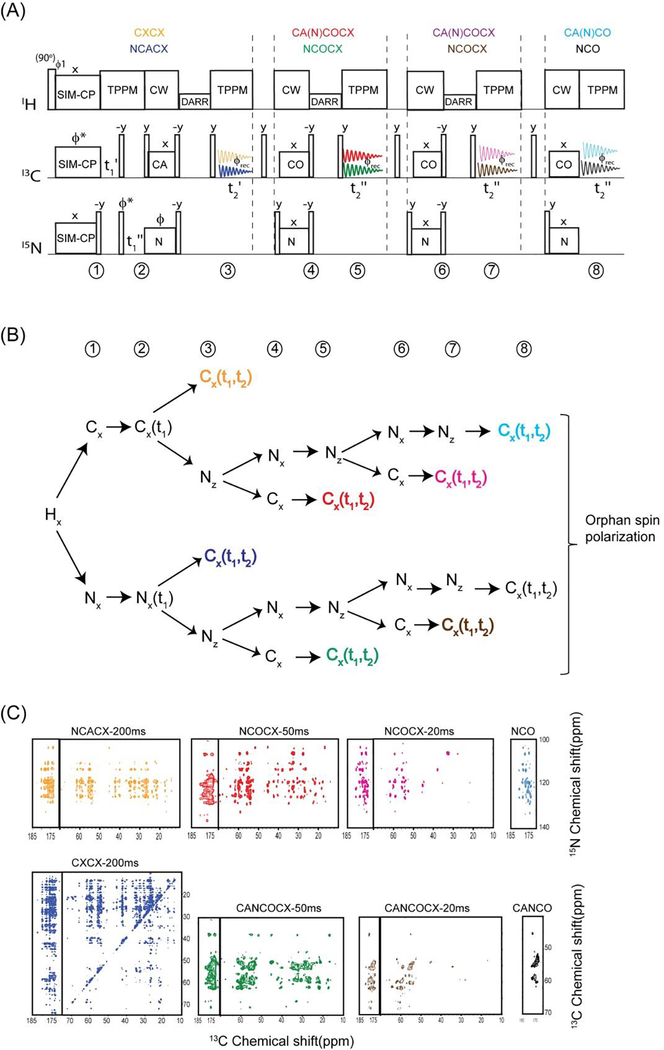
An example of MAeSTOSO-8 on U-¹³C-¹⁵N ubiquitin is shown in figure 7 for simultaneous acquisition of eight experiments, CXCX and NCACX in the first acquisition, a pair of CA(N)COCX and NCOCX with CC mixing times of 20 and 40 ms acquired in second and third acquisitions respectively, and the fourth acquisition records CA(N)CO and NCO. The two pathways in each acquisition were deconvoluted by addition and subtraction of two data sets obtained by switching the phase of ¹⁵N spin lock of NCA period. Schematic of polarization pathways at various stages of pulse sequence is shown in figure 7B. Because of polarization sharing at each NC step, the magnitude of residual polarization decreases with number of NC periods, leading to only 1% of polarization available for the fourth acquisition. Out of eight experiments NCACX-200ms and CA(N)CACX-40ms utilize the initial polarization from SIM-CP, and hence the sensitivity is similar to conventional experiments that are acquired via single acquisition methods. Whereas the remaining six experiments utilize either ¹³C or ¹⁵N residual polarization resulting in a lower sensitivity with respect to corresponding 2D experiments acquired separately using same number of scans. Using same number of t₁ increments as of 2D MAeSTOSO-8, conventional single acquisition 2D NCOCX and CO(N)CACX 2D spectra will require 10 days each, whereas CXCX, NCACB, CO(N)CACB, NCACX, CO(N)CACX, CO(N)CA, and NCA will need 5, 5, 5, 6, 6, and 1 days respectively. In total, the eight 2D experiments will require about 25 days if acquired separately using conventional methods in comparison to 10 days of total experimental time using MAeSTOSO-8, demonstrating a time saving of 70%. Similarly, MAeSTOSO can be used for other combinations of CC, CNCC, NCC experiments. To optimize the sensitivity of MAeSTOSO experiments one should acquire insensitive experiments in first two acquisitions that require larger number of scans thereby accumulating sufficient residual polarization to drive third and fourth acquisitions. As shown in figure 7C, the spectra acquired in first two acquisitions require more number of scans due to longer DARR mixing periods; this enables sufficient residual polarization for third and fourth acquisitions.

Figure 7:

(A) MAeSTOSO-8 pulse sequence for simultaneous acquisition on eight 2D experiments. (B) Evolution of spin operators during the course of the pulse sequence. (C) Simultaneous acquisition of eight 2D spectra of U¹³C-¹⁵N ubiquitin.

(6). Choosing DUMAS, MEIOSIS and MAeSTOSO startegies for simultaneous acquisition of ssNMR experiments

The inefficiency of the polarization transfer schemes together with undetected (orphan) spin operators contribute to the intrinsic insensitivity of the ssNMR experiments. DUMAS, MEIOSIS, and MAeSTOSOS represent a class of polarization optimized experiments (POE) that optimize the sensitivity by recovering the orphan spin operators to obtain multiple NMR experiments. A key feature of these experiments is that the amplitudes of these spin operators are different for each path way. Therefore, depending on the sensitivity of the experiments, one can chose one of these strategies for multiple data acquisitions. In general, protein sequential assignment begins with the acquisition of 2D CXCX, NC, CNC and NCC correlation experiments using shorter CC mixing times of 10 to 30 ms. These experiments can be simultaneously acquired by 2D DUMAS and MEIOSIS. Note that MEIOSIS can be used only if one of the experiments is CNC or CNCC. The finger prints obtained from these 2D spectra demonstrate the quality of spectral resolution as well as the sensitivity of a given protein sample. Robust backbone assignment can then be obtained by 3D-DUMAS-NCACX-CANCO or 3D-MEIOSIS NCACX-NCOCX-CA(N)COCX. Depending on the complexity of spectral overlap one may have to repeat these experiments with multiple mixing times, as we as the use of residue specific isotope labeling schemes. Recent studies on membrane proteins have shown that the spectral resolution can be improved by using water-edited experiments as well as the use of reverse unlabeling of hydrophobic residues^36,37. In fact these methodologies can be further improved by using multiple acquisition methods.

While DUMAS and MEIOSIS strategies are preferable for shorter CC mixing times, MAeSTOSO is more suitable for acquiring low sensitivity experiments, e.g., 2D CXCX (100–200 ms mixing time) or NCOCX (100–200 ms mixing times) that require a significantly higher number of scans. In this case the MAeSTOSO strategy is preferable as the accumulation of residual polarization is such that one can acquire simultaneously a greater number of experiments and optimize the total experimental time. Typically, longer mixing times are necessary to obtain long range distance restraints for protein structure determination^38–40. These experiments require several days of signal averaging for insensitive samples such as those of membrane proteins. One may also use selective or differential labeling schemes for obtaining unambiguous long-range correlations³⁹. In this case the bonus experiments obtained from MAeSTOSO can be compared with other data for cross checking the assignment. Thus MAeSTOSO can represent a cost-effective solution to acquire multiple experiments.

(7). Conclusions and outlook

The polarization optimized experiments (POE) presented in this chapter will bring a new dimension in ssNMR methodology by integrating various NMR pulse sequences using state-of-art NMR probe technology. More importantly this approach doesn’t overwrite the existing experiments, but rather provides a clever strategy to concatenate multiple experiments into a single pulse sequence. Using classical setup of ssNMR spectrometers multiple 2D and 3D experiments can be acquired, reducing by half the experimental time. The overall philosophy of the POE approach is to make the best out of the polarization generated. In fact the existence of unused polarization (orphan spin operators) was first pointed out by Pines et al. in the implementation of ¹H enhanced experiments via multiple cross polarization acquisitions²⁹. Historically, the solution NMR community has been the most attentive to detect multiple spin operators for simultaneous acquisition of 2D experiments such as COSY–NOESY and COCONOSY and/or enhance the signal⁴¹. Takegoshi and co-workers have implemented the equivalent of COCONOSY for solids as well as the double acquisition using discarded coherences in 2D spectra with the States method^42,43, paving the way for multiple acquisitions in biological solids. More recently, the afterglow phenomenon exploited by Kay and co-workers opened up the possibility for the acquisition of multidimensional NMR spectra of proteins in parallel^44,45. The latter approach has been implemented with either one or multiple receivers. While all these methods combine only a specific type of experiments, the POE experiments presented here represent a universal approach for multiple acquisitions of almost all types of double and triple resonance ¹³C detected experiments. Finally, when applied in concert with other fast acquisition and sensitivity enhancement techniques (e.g., Dynamic Nuclear Polarization, Paramagnetic Relaxation Enhancements, etc.) this approach can further push the boundaries of ssNMR applications to structural biology.