Abstract
Molecular dynamics simulations contain detailed kinetic information related to the functional states of proteins and macromolecules, but this information is obscured by the high dimensionality of configurational space. Markov state models and transition network models are widely applied to extract kinetic descriptors from equilibrium molecular dynamics simulations. In this study, we developed the Directed Kinetic Transition Network (DKTN)—a graph representation of a master equation which is appropriate for describing nonequilibrium kinetics. DKTN models the transition rate matrix among different states under detailed balance. Adopting the mixing time from the Markov chain, we use the half mixing time as the criterion to identify critical state transition regarding the protein conformational change. The similarity between the master equation and the Kolmogorov equation suggests that the DKTN model can be reformulated into the continuous-time Markov chain model, which is a general case of the Markov chain without a specific lag time. We selected a photo-sensitive protein, vivid, as a model system to illustrate the usage of the DKTN model. Overall, the DKTN model provides a graph representation of the master equation based on chemical kinetics to model the protein conformational change without the underlying assumption of the Markovian property.
I. INTRODUCTION
Conformational changes are essential to the function of many biomolecules. 1,2 The atomic details and mechanisms of these conformational changes cannot be directly probed using conventional experimental methods and are well beyond the scale of the quantum calculations. Molecular dynamics (MD) simulations have widely been used to investigate the dynamics and conformational distributions of biomolecules. 3–5 However, MD simulations on experimentally relevant time scales are often prohibitively expensive for physiologically relevant phenomena, such as protein folding. 4,6,7 Many enhanced sampling techniques have been developed to study processes beyond the reach of conventional MD simulations. 8–10 In these methods, biased sampling of conformational states is combined with a subsequent reweighting of the samples to achieve a Boltzmann distribution. However, to enhance the sampling efficiency, most biased sampling methods require a priori potentials, which may not be readily available in many complex processes. Recently, with the significant improvement of computational powers provided by graphical processing units (GPUs), the time scale accessible to direct MD simulations has improved from nanoseconds to milliseconds, reaching the folding time scales of some proteins. 11,12 These studies demonstrate that the underlying mechanism for protein conformational switches can be unraveled through extensive simulations. However, to deal with an enormous amount of data generated in these simulations, quantitative models are needed to distill the simulated conformational dynamics into thermodynamic and kinetic parameters. Many methods have been established to meet this need. 13–17 Among them, Markov state models (MSMs) 18 and transition network (TN) 15 are two popular approaches that use master equations 19–22 to compute thermodynamics and kinetic quantities from MD simulations.
MSMs characterize the underlying complex kinetics features of molecular simulations, including identifying metastable states and kinetically favorable pathways. To apply MSMs, one needs to partition the conformational space into discrete states. 23 The transition probability among those discrete states is estimated based on transitions observed in MD trajectories. 23 MSMs assume that the protein dynamics are Markovian, meaning that a jump between two states (x → y) after a time interval named the “lag time,” τ, does not depend on the trajectory prior to entering state x. Because only conditional transition probabilities are required, MSMs do not need a single long trajectory to sample the conformational space. Alternatively, ensembles of short trajectories are sufficient to establish an appropriate MSM. Due to the simplicity and efficiency, MSMs have been successfully and widely applied in many studies related to protein dynamics including folding and allostery. 24,25
The challenge for MSMs is ensuring that the Markovian approximation holds for the selected discrete states and lag time. Although some theoretical studies demonstrated that a Markovian discretization of state-space exists, 26,27 producing an appropriate discretization is still challenging in many cases. In some cases, different dimensionality reduction methods could lead to dramatically different MSMs based on the same simulations results. 26,28–30 Another important factor is the lag time τ. Because the transition probability needs to be estimated based on a given lag time, the selection of a proper lag time is critical to the quality of MSMs. Unfortunately, the selection of lag time may not be asymptotic, which makes the determination of lag time to maximize Markovian property of system a challenging task.
Besides MSMs, kinetic rate laws have also been used to model the conformational changes in MD simulations. Transition network (TN) models were established based on rate theory to model equilibrium properties. 14,15 TN is a discrete representation of conformational space and represents conformational changes through a network of subtransitions. 15 Each subtransition represents a conformational change between two relatively similar structures. In general, TN models are applied to equilibrium properties by calculating the free energy difference between two states instead of transition probabilities. 15 The free energy for each state is usually estimated within a harmonic approximation. 15 Because the free energy represents the distribution of states in equilibrium, and the edges represent equilibrium flux between adjacent states, a TN model represents the equilibrium kinetic and thermodynamic properties. Further studies demonstrated that the TN model could be reformulated within the framework of MSM based on Bayesian probabilities. 14,26
Here, we further improve the TN method by introducing the directed kinetic transition network (DKTN) which, unlike MSMs, is capable of reproducing nonequilibrium population dynamics. DKTNs, like MSMs, use the general master equation framework but allow for time-varying population fluxes. The building blocks for this model include the estimation of distribution and the “mean transition time (MTT)” between different states. Both can be estimated directly from the simulation. A simple four-state model system of the DKTN model and the connections between the DKTN model and the MSMs are illustrated in the supplementary material.
We use a model system vivid (VVD) protein to demonstrate the DKTN model. VVD is a photo-sensitive protein, which undergoes significant conformational changes from dark conformation to light conformation upon blue light excitation. Many computational and experimental studies have been conducted on the VVD protein. 10,31–34 The important residues and some potential conformational change mechanisms have been proposed. 10,31 However, most computational studies focus on the equilibrium property of VVD, without investigating the nonequilibrium conformational changes. The DKTN model simulates the time dependent evolution of the distributions for VVD from the dark or the light conformation as different starting conditions. Using the DKTN model, we demonstrated that VVD starting from the light state could reach the same equilibrium faster than VVD starting from the dark states.
II. THEORY
A. Describing the evolution of state populations using master equation
Assuming that the transitions among different states follow first order chemical kinetics, the time-evolving probability distribution of state occupation (i.e., the “population”) can be described using the following generalized master equation: 19
| (1) |
where P i(t) describes the population of the state i at time t and k ij and k ji are the rate of transitions from state j to state i and state i to state j, respectively. is the derivative of population with respect to time. In the matrix notation, Eq. (1) can be written as
| (2) |
where P(t) represents the population of different states at time t. K is the N * N rate matrix describing the transition rates among different states and is the key matrix in the DKTN model. An off-diagonal term k ij represents the transition rate from state j to state i, and the diagonal terms are .
For a specific initial condition P(0) = P 0, Eq. (2) can be solved using the matrix exponential of K as 35
| (3) |
where e Kt is given by the following power series:
| (4) |
By using spectral decomposition, the time dependent population can be solved as
| (5) |
Equivalently, the time dependent population can be expressed based on the left eigenvector and right eigenvector as
| (6) |
where and are the left eigenvector and right eigenvector of rate matrix K, respectively. λ i is an eigenvalue of rate matrix K. From Eq. (6), it is clear that the time-dependent population for any states is the combination of multiple exponential decay with the relaxation time as −1/λ i. The projection of initial population P 0 on the left eigenvector determines the amplitude of the exponential decay phase, and the right eigenvector determines the weights of the current decay phase. 19
Constructing the rate matrix K is essential for establishing the DKTN model. Accordingly, we use the information from the equilibrium distribution and the state transitions based on the detailed balance to construct the rate matrix K and model how a system approaches the equilibrium distribution.
B. Directed kinetic transition network (DKTN) model
The DKTN model can be constructed using microstates based on detailed balance. 36 We followed the same procedures as with the widely applied TN model and MSM. 15 First, the structures are grouped into different states based on the structure similarity. Unlike MSMs or TN models, the DKTN model uses a master equation to describe the chemical kinetics. In general, the TN model represents the system in the equilibrium, in which the fluxes between two states are equal to each other. The DKTN model simulates the reactions from both sides based on the detailed balanced constraint. Therefore, the TN model is a special case of the DKTN model as it evolves in the equilibrium state.
The DKTN model is a weighted and directed graph representation of a master equation, which includes nodes representing each state and directed edges representing reaction constants between two nodes. The nodes in the DKTN model are treated as the microstates similar to the microstates in the MSMs. 26 These microstates are clustered based on the structure similarity. The structure similarity in each microstate leads to the kinetic similarity. The equilibrium Boltzmann distribution of each microstate π s is estimated as the percentage of the number of snapshots in state S vs the total number of snapshots,
| (7) |
The free energy of each microstate could be estimated as
| (8) |
For a directed edge connecting two microstates , the combination of detailed balance and microscopic reversibility yields the following relationships:
| (9) |
where π μ and π v are the Boltzmann distributions of microstates μ and v, respectively, and and are the reaction rate constants for the transitions and , respectively. The terms f νμ and f μν are equilibrium fluxes for the transitions and , respectively. 15 The reaction rate represents how fast a transition between two microstates occurs and is the inverse of the mean transition time between them. Therefore, in the equilibrium, the mean transition time between two states is given by the inverse of the flux. 15 Obviously, the mean transition time from and are identical in the equilibrium and defined as τ νμ
| (10) |
In the current study, the “mean transition time” (MTT) or τ νμ is estimated through the collection of transitions in the equilibrium simulation as the average value of the transition time between two adjacent microstates in the simulations.
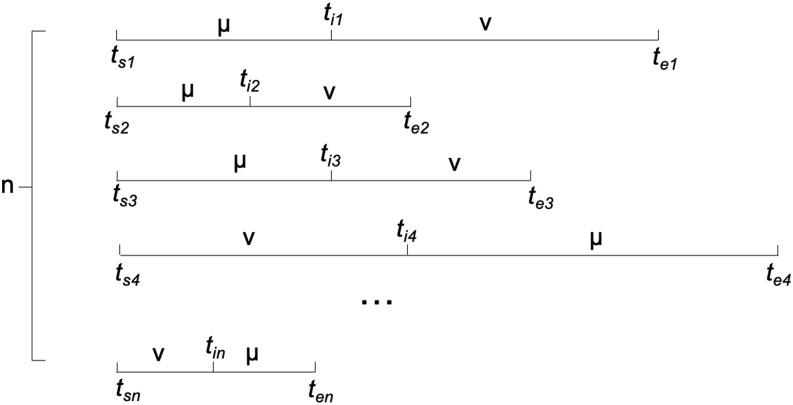
As shown in Fig. 1, all the adjacent transitions as or should be collected in the given simulations. For each transition, it is assumed that the starting timestamp for state μ or ν is t s, and the ending timestamp for the other state ν or μ is t e. In general, the transition time between μ and ν defined as (te − ts)/2 should be sufficient for the current analysis. Collecting all instances of or transitions, τ νμ or MTT between μ and ν is estimated as
| (11) |
FIG. 1.
The demonstration of the estimation of τ νμ for the microstate μ and ν.
After the estimation of τ νμ, the reaction rate constants for transitions and can be rewritten using Eqs. (9) and (10) as
| (12) |
Overall, the basic building blocks of the DKTN model include microstates (nodes V), transitions among microstates (edges E), and the reaction rate constants for the transitions (edge weights W). The reaction rate constants and are used as the directed edge constant E νμ and E μν that connect two microstates in the DKTN model. The reaction rate constants are the rate matrix K in the master equation, which is the key to solve the evolution of the population. Unlike the undirected TN models, which are static networks representing the equilibrium flux only, the DKTN model represents the kinetic property of system as chemical kinetic models. Other properties of the DKTN model and the relation to the MSMs are demonstrated in Sec. II C.
C. Equilibrium distribution for the DKTN model
The estimated equilibrium distribution is used to construct the rate matrix between different microstates using Eq. (12). For the master equation [Eq. (1)], the populations for different states will converge to a unique, stationary distribution P eq, which is the same as the estimated equilibrium distribution . P eq can be solved through Eq. (1), when the populations of different states converge to stationary distribution as the following:
| (13) |
The equations above are linear 37 and can be solved analytically. Given the conditions of and , the above linear equations have one unique solution as . Therefore, given the condition that the rate matrix K satisfies both the equilibrium distribution and detailed balanced constraint, the stationary distribution of the DKTN model is guaranteed to be the equilibrium distribution.
Although the rate matrix can be constructed using the estimated equilibrium distribution π s and MTT based on Eq. (12), the rate matrix can also be constructed based on the experimental rate constants if the data are available. It should be noted that even when the time-dependent state’s population is solvable using Eq. (6), the master equation [Eq. (1)] or the DKTN model does not necessary converge to a unique, stationary distribution. The stationary distribution could be obtained from the DKTN model if and only if the linear equations shown in Eq. (13) have a unique solution.
D. Relation to the Markov State Models (MSMs) and continuous time Markov Chain (CTMC) model
The DKTN model is also equivalent to the continuous time Markov chain (CTMC) model. The CTMC model is a more general case of MSMs, in which the key difference is the presence of time-varying fluxes. The transition probability matrix in CTMC could evolve over time through the transition rate matrix based on the Kolmogorov equation, 38,39
| (14) |
The above equation is the same representation to the master equation [Eq. (2)] with different notations, where P t represents the time dependent transition probability matrix among Markov states of CTMC model in time t, Q is the transition rate matrix, and is the first order derivative of the time dependent transition probability matrix with respect to time t. Because of the similarity of the Kolmogorov equation with the master equation, the DKTN model can be treated as a CTMC model, which can be further formulated as MSMs.
Comparing with MSMs, the CTMC model is an integral-differential Markov state model without the specific lag time. The transition probability matrix is constant in the MSMs and variable in the CTMC model. For a specific time t, the transition probability matrix among different states for the CTMC follows the following equation: 39
| (15) |
The current DKTN model can be translated into the MSMs following Eq. (15) to calculate the transition probability between different states at a particular time. A simple example containing four states to illustrate DKTN model is represented in the supplementary material.
E. Half-mixing time and effective reaction rate constant
The DKTN model could be used to model the dynamical properties among a large number of states. In most applications, only a few states carry chemical significance, such as “reactant” and “product” states. Most other states could be referred to as intermediate states. From the experimental point of view, it is informative to obtain an effective reaction rate constant between the “reactant” state and “product” state to describe the overall effective rate of the transitions between them. This transition is not an elementary reaction, however, but a combination of reaction rate constants in the system, which is named as “effective reaction rate constant.”
In chemical kinetics, the half-life is widely used to describe the rate for a decay process. 40,41 For a typical decay process, half-life is defined as the time required for the population halve. Clearly, for a simple decay phase as with decay constant λ, the half-life is ln 2/λ. However, in the DKTN model, the decay of each state follows Eq. (6), which is a combination of multiple decay processes. Therefore, we cannot use a single decay constant or a single half-life value to describe the time required to reach equilibrium. Adopting the mixing time concept in the Markov chain model, 42 we define the half-mixing time to describe the speed at which any particular state reaches equilibrium.
More specifically, the half-mixing time is defined as the smallest time t required for a particular state A to reach halfway to the equilibrium from the starting distribution, given by
| (16) |
where P(X t ∈ A) is the population of state A at time t and P eq(A) and P 0(A) are the equilibrium and the starting distribution for state A, respectively. Although the half-mixing time is difficult to calculate analytically, it is possible to calculate numerically from Eq. (6). It should be noted that for a “product” state which has starting population of 0, the half mixing time is the smallest time for the distribution to reach ½P eq(Product). Because this half-mixing time describes the transition from the reactant to the product states, we can further define an effective rate constant as
| (17) |
where is the equilibrium distribution and is the half mixing time for the product state.
Due to the detailed balance constraint, the DKTN model is also a reversible CTMC model which satisfies the following equation: 39
| (18) |
where and represent the equilibrium distribution for states j and i, respectively. The term represents the percentage of the equilibrium distribution for microstate j at time t starting with microstate i at time t = 0, and vice versa for . The equivalence of these two expressions in Eq. (18) indicates that at any given time t, the percentage of the equilibrium for state j in transition is identical to the percentage of the equilibrium for state i in transition. In other words, the half-mixing time (50% to equilibrium) for the state i in transition and state j in transition would be identical. Therefore, the reversible reaction from a “reaction” state to a “product” state has the exact same half-mixing time with the “product” state to a “reaction” state.
It is interesting to identify which conformational change is the most important to the overall transition from a “reactant” to a “product” state. After defining the half-mixing time and effective reaction rate to represent the rate of transition between “reactant” and “product” states, the importance of each edge (conformational transformation) can be calculated by the decrease in the effective reaction rate after removing the edge using
| (19) |
where is the effective reaction rate from the “reactant” state to the “product” state with all edges present and is the effective reaction rate from the “reactant” state to the “product” state with one edge removed. The decrease in such an effective reaction rate indicates the importance of that edge (conformational change) in the DKTN model. The calculation of edge importance is also demonstrated in the simple model presented in the supplementary material.
III. COMPUTATIONAL METHODS
A. Molecular dynamics simulation
The structures of dark and light states of VVD were obtained from the Protein Data Bank (PDB) 43 with the IDs as 2PD7 and 3RH8, respectively. Both structures include a flavin adenine dinucleotide (FAD) as a cofactor. Following a previous study, 10 the adenosine monophosphate (AMP) moiety was removed from the FAD to form the flavin mononucleotide (FMN) because they carry similar biological roles. The FMN force field from a previous study was applied. 44 Hydrogen atoms were added to the VVD and its cofactor to construct the simulation system, which was further solvated using an explicit water model (TIP3P) 45 and neutralized with a sodium cation and chloride anion. A total of 20 production simulations were carried out, including 10 simulations starting from the crystal dark state conformation (2PD7) with different random seeds and 10 simulations starting from the crystal light state conformation (3RH8) with different random seeds. Each simulation is a 1.05 μs canonical ensemble (NVT) Langevin MD trajectory at 300 K. For each simulation, the first 50 ns simulation was discarded as the equilibration, and the subsequent 1 µs simulation was used for analysis. For all simulations, the SHAKE method was used to constrain all bonds associated with hydrogen atoms. A step size of 2 fs was used, and simulation trajectories were saved every 10 ps. The cubic simulation box and periodic boundary condition were applied for all MD simulations. Electrostatic interactions were calculated using the particle mesh Ewald (PME) method. 46 The setup for all simulations was carried out using the CHARMM 47 simulation package version 41b1, and the subsequent simulations were conducted using OpenMM with the GPU support. 48
B. t-Distributed stochastic neighbor embedding (t-SNE) projection
The t-SNE method has widely been applied as a nonlinear dimensionality reduction method to project high dimensional data onto the low dimensional surface based on the location of each data point. To analyze MD simulations of biomacromolecules such as proteins, the simulation data in high-dimensional Cartesian space need to be projected onto low-dimensional distribution to abstract key functional or mechanistic information. In the t-SNE method, Gaussian functions are used to represent probability distribution of the high-dimensional data. For example, the probability distribution for two data points x i and x j in high-dimensional space as neighbors is calculated as
| (20) |
where σ is the width of the Gaussian distribution. Correspondingly, a Student’s t-distribution could be constructed to represent the probability in a low dimensional space for data points y i and y j as neighbors,
| (21) |
The gradient descent method is used to minimize the Kullback-Leibler (KL) divergence between the low-dimensional Student’s t-distribution and the high-dimensional Gaussian distribution until the convergence criterion is reached,
| (22) |
The t-SNE method is guaranteed to perform no worse than the principal component analysis (PCA) method. 49
A previous study in our group shows that in MD simulations, t-SNE could represent minima on the high dimensional free energy surface correctly. 50 In this study, the t-SNE method was applied for dimensionality reduction of the Cartesian structure and visualization of the DKTN model. The t-SNE implementation in the scikit-learn package 51 was used in this study.
C. Gaussian mixture mode
For good visualization analysis and functional insight, several metastable states were clustered using the Gaussian Mixture Model (GMM) before generating microstates. Each metastable state is an intermediate state representing a stable low energy basin on the free energy surface. The GMM can characterize different metastable conformational states by fitting the sample population to Gaussian distributions. 52 If a conformational basin distribution has non-Gaussian tail, more than one component of the mixture is required to represent it. 52 In this case, careful tuning is necessary to determine the number of components in the GMM so that each conformational basin distribution satisfies a Gaussian distribution. The number of components corresponds to the number of metastable states in the simulation.
The parameters of the GMM were estimated using the Expectation Maximization (EM) algorithm. 53 The EM algorithm contains two steps, named the expectation step (E) and maximization step (M). First, the parameters of each Gaussian component are randomly initialized as
| (23) |
where G k represents the kth Gaussian distribution and π k, μ k, and Σk represent the weights, the mean, and the covariance matrix of the kth distribution, respectively.
For the expectation step, the probability for x i assigned to kth Gaussian distribution as p ik could be computed as
| (24) |
where represents all Gaussian distributions, π k is the weights or prior probability for x i structure belonging to kth Gaussian distribution, and N(x i|μ k, Σk) represents the probability of finding x i in the Gaussian distribution with parameter μ k and Σk. This step is also named as “soft assignment.” In GMM, the probability belonging to each Gaussian distribution is assigned to each data point.
After obtaining the soft assignment for each structure belonging to each Gaussian distribution, the parameters for each distribution can be reevaluated using these soft assignment results. This step is named as the maximization step because the parameters are maximum likelihood estimations. Specifically, knowing the probability of each structure in each distribution as p ik, the parameters for kth Gaussian distribution is recalculated as
| (25) |
where γki is the normalized value of kth Gaussian distribution evaluated at state x i.
As a summary, after recalculating the parameters for each Gaussian distribution in the maximization step, the soft assignment of each structure for those distributions with new parameters can be recalculated in the expectation step. The expectation and maximization steps are performed iteratively until reaching convergence.
D. k-means clustering
After clustering the trajectories into the metastable states using GMM, a more fine-grained structural model referred to as microstates was determined using k-means clustering. Each microstate identified through k-means clustering method unambiguously belongs to one metastable state. k-means is widely applied in many areas for clustering, including for MD simulations. 10,54,55 Basically, k-means clustering method can be referred to as a special case of GMM, where the probability for each structure assigned to each cluster is either 0 or 1. The covariance matrix for each Gaussian distribution is zero, which represents an infinitesimal distribution to a single structure. The k-means clustering method also contains two steps, named the assignment step and update step. During the assignment step, based on the previous clustering center for each cluster, each structure is assigned to the nearest cluster. In the update step, based on the assignment result, the cluster center is updated as the average of all structures in the same cluster. These two steps are iteratively conducted until reaching convergence.
E. Root mean square deviation (RMSD)
The conformational difference is measured by root mean square deviation (RMSD) regarding a reference structure. For a molecular structure represented by the Cartesian coordinate, the RMSD is defined as the following:
| (26) |
The Cartesian coordinate vector is the ith atom in the reference structure. N is the number of all atoms. U is the rotation matrix to align the reference structure with the current structure.
IV. RESULTS
A. Construction DKTN model
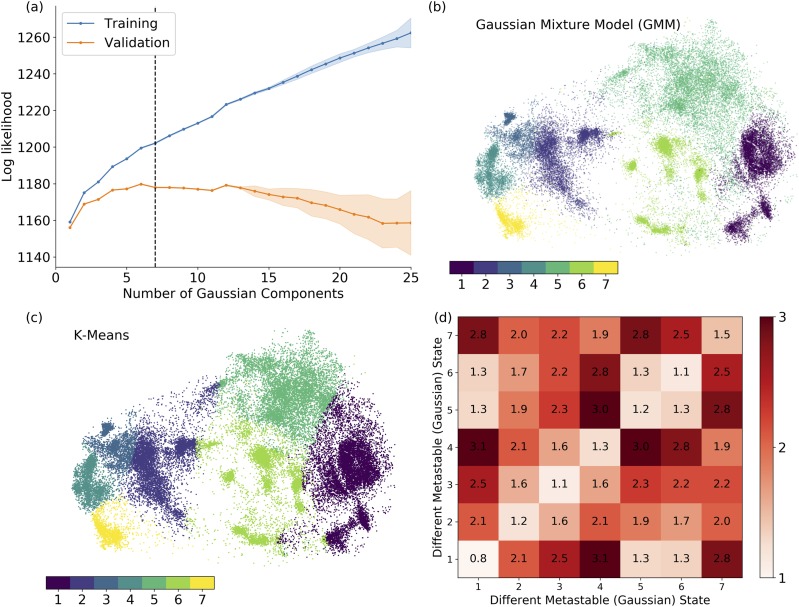
The metastable states are clustered using GMM on 20 µs of VVD trajectories, including 10 simulations with 1 µs length starting from the dark conformation and 10 simulations with 1 µs length starting from the light conformation, respectively. A previous study suggests that GMM could correctly model the dynamical properties of the system based on the assumption that the fluctuations around a particular metastable state satisfy a Gaussian distribution. 52 The number of metastable states required to adequately describe conformational statistics within a GMM was determined using cross-validation. 56 The overall quality of the Gaussian mixture model can be measured as the total probability of structures in the training or validation sets. As shown in Fig. 2(a), the total probability of the validation sets in GMM increases followed by a steady decrease. The number of Gaussian components was selected as seven to be well-separated on the t-SNE projection surface [Fig. 2(b)] while avoiding both underfitting and overfitting. k-Means clustering was conducted with seven clusters [Fig. 2(c)]. It is worth pointing out that GMM leads to a soft and smooth clustering, and k-means method leads to hard cutoff between each of the cluster pairs. To check the structural similarity among metastable states or within each metastable state, the pair-wised RMSDs between each of the state pairs are plotted in Fig. 2(d). The high RMSDs in off-diagonal terms suggest that each metastable state is well-distinguished from other metastable states. The low RMSDs shown in diagonal terms suggest that the structures within each metastable state are similar to each other. Overall, the results suggest that these metastable states are well-classified.
FIG. 2.
Metastable state classification of VVD simulations. (a) Cross-validation using Gaussian mixture model (GMM); (b) clustering results using GMM; (c) clustering results k-means method; and (d) averaged pair-wised RMSD values of each metastable state pair.
To establish an adequate DKTN model, the basic building blocks are the microstates which compose the metastable states clustered using k-means clustering. Because the distribution can be diverse, even within the same metastable state, the structures can be significantly different. For example, as shown in Fig. 2(d), the averaged RMSD in metastable state 7 is 1.5 Å, which suggests higher structure diversity in this state than other states. To address this issue, the metastable states are further refined into a collection of microstates. The number of microstates for each metastable state is selected to ensure that (1) the averaged RMSD for pair-wised structures belonging to the same microstate is less than 1.0 Å, (2) the microstates are well-distinguished on the t-SNE projection surface (not overlapping with each other), and (3) further clustering does not decrease the averaged RMSD in those microstates. After further clustering using the k-means clustering method, seven metastable states are clustered into 34 microstates, which serve as the basic building blocks of the DKTN model to construct the transition rate matrix K. The microstates and the averaged pair-wised RMSDs value in the same microstates belonging to the metastable states are listed in Table I.
TABLE I.
List of microstates and the averaged pair-wised RMSD value for structures belonging to the same microstate from each metastable state.
| Metastable state | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| List of microstates | 1–4 | 5–8 | 9–12 | 13–16 | 17–22 | 23–28 | 29–34 |
| Averaged pair-wised RMSD value | |||||||
| for structure in the same microstate | 0.681 | 0.951 | 0.881 | 0.983 | 0.995 | 0.767 | 0.981 |
| from each metastable state (Å) |
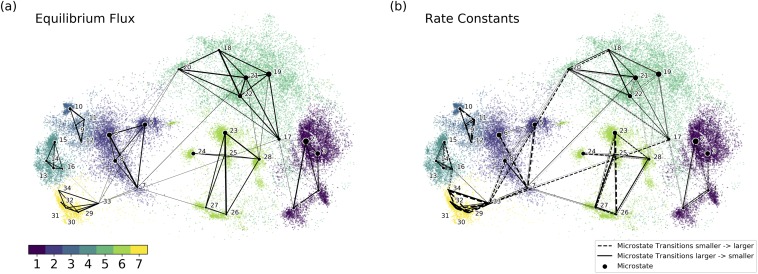
As described in the theory section, the MTT (mean transition time) between different microstates can be estimated from the simulation, and the rate constants between different microstates can be calculated based on the equilibrium distribution and MTT value. As shown in Fig. 3(a), the equilibrium flux is the product of the rate constant and the equilibrium distribution of each microstate and is equivalent to the inverse of the MTT. 15 It is clear that the equilibrium flux between different metastable states is much smaller than the flux inside each metastable state [Fig. 3(a)], verifying the stability of each metastable state in the equilibrium. The rate constants within different metastable states pairs are illustrated in Fig. 3(b). It should be noted that the rate constant from microstate a to b is different from the rate constant from b to a. In the following figures (Figs. 3–5), the point size of each microstate represents the current population of the microstate. The dashed and solid lines represent the transitions from a microstate with a smaller ID number to a microstate with a larger ID number and from a microstate with a larger ID number to a microstate with a smaller ID number, respectively. The width of the line represents the magnitude of the reaction rate constant.
FIG. 3.
Established DKTN model based on microstates: (a) the equilibrium flux between microstates in the equilibrium; (b) the rate constants between microstates. A dashed line represents the transitions from a microstate with a smaller ID number to a microstate with a larger ID number. A solid line represents opposite transition comparing to the dashed line. The width of the line represents the magnitude of the reaction rate constant (the bolder and the larger).
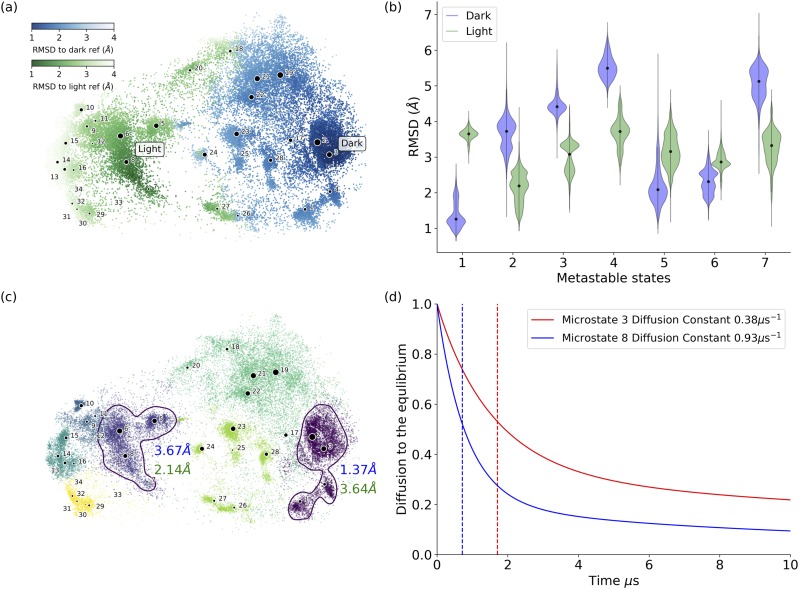
FIG. 4.
Distributions of RMSD values with reference to VVD dark and light structures for microstates and metastable states. (a) The RMSD value distribution on the t-SNE projection surface. The darker color indicates the smaller RMSD values. (b) Violin plots of the averaged RMSD values of each metastable state with reference to VVD crystal dark and light structures, respectively. Among all metastable states, state 1 (comprising microstates 1, 2, 3, and 4) has the lowest averaged RMSD value with reference to the crystal dark structure as 1.37 Å, and state 2 (comprising microstates 5, 6, 7, and 8) has the lowest averaged RMSD value with reference to the crystal light structure as 2.14 Å. (c) Distribution of metastable states illustrated in different colors. The nearest metastable states closest to either the dark or the light structures are highlighted by circles. Metastable state 1 circled at the right-hand side (comprising microstates 1, 2, 3, and 4) is the closest to the crystal dark structure. Metastable state 2 circled at the right-hand side (comprising microstates 5, 6, 7, and 8) is the closest to the crystal light structure. The averaged RMSD values of metastable states 1 and 2 with reference to the crystal dark and light structures are also labeled in color (blue: RMSD to crystal dark structure, green: RMSD to crystal light structure). (d) Diffusion time to equilibrium for simulations starting from microstate 3 (as VVD dark state) and microstate 8 (as VVD light state), respectively. The plot shows that the system could reach equilibrium faster when starting from the light state than starting from the dark state.
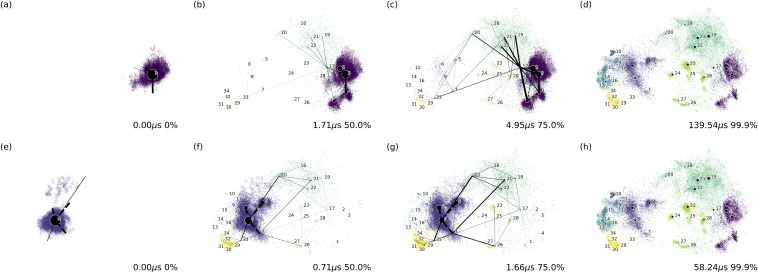
FIG. 5.
The time and distribution of the system starting from microstate 3 (VVD dark state) when evolving to (a) 0%, (b) 50%, (c) 75.0%, and (d) 99.9% of the equilibrium. The time and distribution of the system starting from microstate 8 (VVD light state) when evolving to (e) 0%, (f) 50%, (g) 75.0%, and (h) 99.9% of the equilibrium.
The RMSD values with reference to the crystal dark and light structures were calculated for each structure from the samplings. These values are represented as the darkness of the color on the t-SNE projection surface to illustrate the deviation for each microstate from either the dark or light structures of the VVD protein [Fig. 4(a)]. Specifically, the darker color indicates the smaller RMSD values. The blue color in Fig. 4(a) represents that the structure is close to the dark state, and the green color represents that the structure is close to the light state. The darker color indicates that a structure is closer to the specific structure, as shown in the color bar. Overall, microstate 3 has the lowest averaged RMSD to the crystal dark state structure as 1.08 Å, and microstate 8 has the lowest averaged RMSD to the crystal light state structure as 1.67 Å. The distributions for RMSD values of each metastable state regarding the VVD reference dark and light structure are illustrated as violin plots in Fig. 4(b). Metastable state 1 (comprising microstates 1, 2, 3, and 4) has the lowest averaged RMSD value with reference to the crystal dark structure as 1.37 Å, and metastable state 2 (comprising microstates 5, 6, 7, and 8) has the lowest averaged RMSD value with reference to the crystal light structure as 2.14 Å. Metastable states 1 and 2 with their labeled microstates are plotted and circled in Fig. 4(c) with their averaged RMSDs to the VVD light structure (shown in green) and to the VVD dark structure (shown in blue).
One advantage of the DKTN model is the ability to model the time evolution of system as it approaches equilibrium. To obtain this information from the VVD simulations, the ordinary differential equation of the DKTN model was solved with two different initial conditions, starting at microstate 3 (VVD dark state) and starting at microstate 8 (VVD light state), respectively. Throughout the simulations, the concentration of main components steadily decreases until reaching the equilibrium distributions [Fig. 4(d)]. Because the concentration of the initial structure is constantly decreasing, the concentration of other components will constantly increase until reaching equilibrium. Therefore, the decrease in the initial microstate concentration can be regarded as the speed for the whole system to reach equilibrium. To compare the speed to reach equilibrium for systems with different initial conditions, the half-mixing time and the diffusion rate constant were calculated using the effective reaction rate constant shown in the theory section. The result in Fig. 4(d) suggests that the system starting from the light conformation can reach equilibrium earlier than the system starting from the dark conformation. The diffusion half-mixing time and effective diffusion reaction rate for the simulation starting in microstate 3 are 1.71 µs and 0.38 µs−1, respectively. In comparison, the diffusion half mixing time and effective diffusion reaction rate for the simulation starting in microstate 8 are 0.71 µs and 0.93 µs−1, respectively.
After solving the ordinary differential equations for the DKTN model with different initial conditions (starting from microstate 3 or microstate 8, respectively), the time evolution of each system can be calculated analytically. The system evolution toward the equilibrium starting from microstate 3 (VVD dark state) is illustrated in Figs. 5(a)–5(d), representing 0%, 50%, 75.0%, and 99.9% of the equilibrium, respectively. Similarly, the system evolving to the equilibrium starting from microstate 8 (VVD light state) is illustrated in Figs. 5(e)–5(h), representing 0%, 50%, 75.0%, and 99.9% of the equilibrium, respectively. Starting from the dark state, it takes 139.54 µs for the system to reach equilibrium, while starting from the light state, it takes much less time, as 58.24 µs, for the system to reach the equilibrium. This demonstrates that the light state takes less time than the dark state to undergo conformational switching. Videos illustrating the time evolution of systems are provided in the supplementary material.
B. Characterization of key conformational changes
The importance of individual edges in the DKTN model can be quantified through the decrease in effective reaction rate constant upon removing certain transitions. Because an individual edge represents different conformational changes, key conformational changes for certain transitions could be identified based on the effective reaction rate constant associated with the corresponding edge. Table II lists the importance of the top 10 conformational changes for different transitions.
TABLE II.
Top 10 important microstate state conformational changes for transition between microstates 3 and 8, as well as between metastable states 1 and 2. a
| Transition from | Transition from | |||
|---|---|---|---|---|
| Top 10 conformational | metastable state 1 | metastable state 2 | ||
| changes decreased | Transition from | Transition from | (dark state) to | (light state) to |
| effective reaction rate | microstate 3 to | microstate 8 to | metastable state 2 | metastable state 1 |
| for certain transition | microstate 8 | microstate 3 | (light state) | (dark state) |
| 1 | 1:17 b (23.042%) c | 1:17 (23.042%) | 1:17 (22.226%) | 1:17 (26.302%) |
| 2 | 3:17 (17.747%) | 3:17 (17.747%) | 7:21 (19.179%) | 2:17 (18.477%) |
| 3 | 7:21 (17.656%) | 7:21 (17.656%) | 3:17 (17.013%) | 7:21 (18.201%) |
| 4 | 8:20 (16.792%) | 8:20 (16.792%) | 2:17 (15.437%) | 8:20 (17.305%) |
| 5 | 2:17 (16.054%) | 2:17 (16.054%) | 8:20 (12.665%) | 3:17 (13.752%) |
| 6 | 4:17 (9.309%) | 4:17 (9.309%) | 4:17 (8.912%) | 4:17 (9.619%) |
| 7 | 17:33 (8.740%) | 17:33 (8.740%) | 17:33 (7.757%) | 17:33 (9.035%) |
| 8 | 3:4 (5.440%) | 3:4 (5.440%) | 3:4 (5.138%) | 8:33 (5.289%) |
| 9 | 8:33 (5.108%) | 8:33 (5.108%) | 6:7 (4.319%) | 17:21 (4.186%) |
| 10 | 17:21 (4.044%) | 17:21 (4.044%) | 17:21 (4.178%) | 17:20 (3.966%) |
Numbers in bold indicate the edges with importance higher than 10%.
The edge representing microstate transition between microstates A and B (A:B).
The importance of a target edge as the decrease in effective reaction rate constant in the DKTN model after removing that edge comparing with the original DKTN model.
In Table II, the importance of individual conformational changes was investigated in two different scenarios: for the transitions between microstates 3 and 8 and for the transitions between metastable states 1 and 2. As demonstrated in the earlier part of this study, the closest microstate and metastable state to the crystal dark structure are microstate 3 (1.08 Å) and metastable state 1 (1.37 Å), respectively. Likewise, the closest microstate and metastable state to the crystal light structure are microstate 8 (1.67 Å) and metastable state 2 (2.14 Å), respectively. Because of the reversibility of the DKTN model which leads to the identical half-mixing time for the transition from microstates 3 to 8 and the transition from microstates 8 to 3, the importance of each edge will also be the same in both cases, as shown in Table II (columns 2 and 3). However, for the transitions between metastable states, the importance of edge will not be the same in reverse directions, as shown in Table II (columns 4 and 5). For example, removing the edge microstate 1:17 will decrease the effective reaction rate constant from metastable 1 to 2 by 22.2% and from metastable 2 to 1 by 26.3%. The difference suggests that the conformational change between microstates 1–17 is more important for the conformational switch from the light to dark structure than for the conformational switch from the dark to light structure. The top five edges are selected for the following analyses because they are shared by both microstate 3 and 8 transitions and metastable state 1 and 2 transitions (Table II), and all have more than 10% importance.
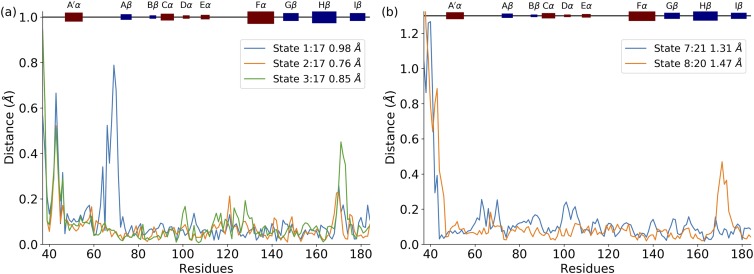
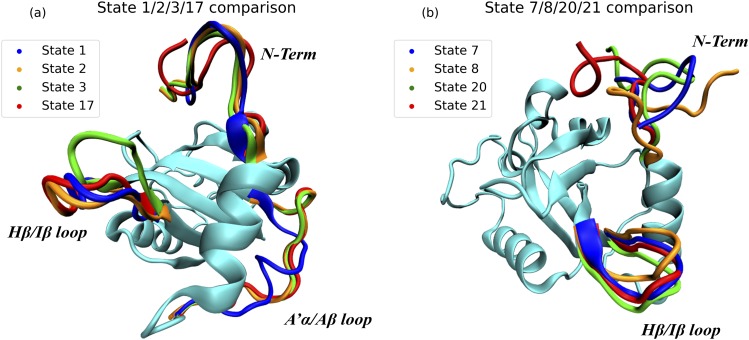
The top five edges include the conformational changes among microstates between 1 and 17, 2 and 17, 3 and 17, 7 and 21, and 8 and 20. The structural differences between each microstate pair associated with each edge are plotted in Fig. 6. Microstate 17 is critical to the conformational changes because the conformational switches from metastable state 1 (dark structure) have to pass through microstate 17 in order to reach other metastable states. In other words, without conformational switching into microstate 17, the crystal dark conformation will be trapped in metastable state 1. A detailed structural comparison revealed that the structural differences among the key structural changes are in the N-terminal, Hβ/Iβ loop, and A′α/Αβ loop, highlighting the importance of those secondary structures.
FIG. 6.
Structural comparison between microstate pairs associated with top five edges. (a) Structural comparison between microstate 17 and microstates 1, 2, and 3, respectively; (b) structural comparison between microstates 7 and 21 and between microstates 8 and 20. All structure pairs are superimposed, and the residue distance is measured by alpha carbon distance.
The structural comparisons of microstates 1, 2, 3, and 17 as well as 7, 8, 20, and 21 are illustrated in Fig. 6. Microstates 2, 3, and 17 have a similar A′α/Αβ loop structure, which is significantly different in microstate 1. Microstates 1, 2, and 17 share similar Hβ/Iβ loop conformations, which are significantly different from the one in microstate 3. Microstates 2 and 3 have similar conformations of the N-terminal, which are different from the N-terminal conformations shared by microstates 1 and 17. Based on the reaction rate constants among microstates 1, 2, 3, and 17 (Table III), it is revealed that the most probable pathway starting with microstate 3 (dark state) to reach microstate 17 is 3 → 2 → 1 → 17. The direct conformational changes from microstates 3 to 17 and from 2 to 17 have rather low reaction constants than the one from 1 to 17. According to the structural comparison in Fig. 7, in the most probable pathway 3 → 2 → 1 → 17, the first step (3 → 2) is that the Hβ/Iβ loop shifts without conformational changes in the A′α/Αβ loop or the N-terminal. In the second step (2 → 1), it is mainly that the A′α/Αβ loop forms a helixlike structure, which is coupled with the conformational change in the N-terminal. In the last step (1 → 17), the A′α/Αβ loop rearranges back to the normal conformation, and N-terminal changes into a new conformation, finishing the switch into the light state. Meanwhile, in the light conformational switch between microstates 8:20 and microstates 7:21, the Hβ/Iβ loop is also highlighted, which suggests the importance of this secondary structure.
TABLE III.
Rate constants among microstates 1, 2, 3, and 17.
| Reaction constant (μs−1) | 1 | 2 | 3 | 17 |
|---|---|---|---|---|
| 1 a | 0 | 0.882 | 0 | 0.184 b |
| 2 | 0.227 | 0 | 0.142 | 0.031 |
| 3 | 0 | 0.206 | 0 | 0.033 |
| 17 | 0.126 | 0.084 | 0.060 | 0 |
Each rate constant corresponds to the edge starting from the state in the first column and ending in the state in the top row.
Numbers in bold indicate the direction with highest reaction constant.
FIG. 7.
Comparison of key microstate structures: (a) microstates 1, 2, 3, and 17; (b) microstates 7, 8, 20, and 21.
V. DISCUSSION
A. Advantages and limitations of the DKTN model
The DKTN model goes one step further than a transition network model 15 to describe nonequilibrium time dependent population evolution. Although the TN model also models the system based on rate theory, it only describes the equilibrium properties such as equilibrium flux. 14 The DKTN model is a more general case of the TN model. Constructing the DKTN model does not require any prior knowledge about the reaction rate among states, or the free energy of each conformational state, for these could be estimated from the simulations. Different from MSMs, a large number of short trajectories are not needed to build the DKTN model. Instead, a long simulation leading to Boltzmann distribution is preferred. Specifically, the advantages of the DKTN model can be categorized into the following two parts.
1. Fully utilizing the long-time distribution and short-time transitions
In the TN model, 15 the free energy of each state is estimated based on its distribution in the simulation. The information about the transitions among microstates in the simulation is not used in the TN model. MSMs, on the contrary, do not take advantage of the distribution information from the long-time samplings. Instead, the transition probability among microstates is extracted from simulations using a short-time interval referred to as the lag time in MSMs. It is worth noting that the transition probability matrix in the MSMs does not always lead to the distribution in the equilibrium with the Boltzmann distribution estimated from the simulation. 27,29 One explanation accounting for this could be that the Markovian properties do not hold precisely for MSMs after discretizing the phase space into microstates. 29 Although the theoretical studies have demonstrated that the MSM approximation can be precise if the coordinates relevant to the slow transitions are fully discretized, 26,29 due to high-dimensionality of biomolecular systems and limitation of the clustering algorithms, the discretization of microstates is normally imperfect in practice. Therefore, the transition probability matrix estimated at the lag time cannot be used to predict the long-time behavior. 29
As a combination of the advantages between the TN model and MSM, the DKTN model combines both long-time Boltzmann distributions and short-time transitions. The underlying master equation provides the basic theoretical framework of the DKTN model for describing the evolution of the system using chemical kinetics without assuming equilibrium dynamics. It is more reliable to use the DKTN model to predict the long-time behavior from different starting conditions. Due to the detailed balance constraint, the DKTN model is guaranteed to converge to the Boltzmann distribution determined by the simulated trajectories.
2. The continuous propagation of dynamical system without specific lag time
The TN model has been used to describe macromolecular system properties in the equilibrium. 15 MSM is a dynamical model describing the propagation of a macromolecular system with the specific lag time interval within a Markovian approximation. The propagation of a simulation system is discretized via a specific lag time. With a longer lag time, transitions among states will be more likely and the Markovian properties of microstates will be more reliable, but this requires longer samplings. 23 The MSMs were widely used to investigate protein dynamical processes including folding 24 and allostery. 25 To establish an appropriate MSM, an adequate lag time must be adapted to fulfill the Markovian properties. 13,27 However, the validation of lag time cannot rely on the variational principle of MSMs, 57,58 which makes the selection of proper lag time challenging. This issue could be addressed in the DKTN model. As the underlying theoretical framework of the DKTN model, the master equation describes the evolution of the system based on chemical kinetics without assuming a constant transition probability matrix. Therefore, the DKTN model is different from the MSM in two aspects: the transition probability matrix and the lag time. The transition probability matrix, treated as constant in MSM, could change over time through the transition rate matrix in the DKTN model. The system propagation is discretized in MSM using a lag time, but is considered as continuous in the DKTN model. In some sense, the master equation based DKTN model could also be viewed as a continuous-time MSM, in which the lag time is no longer needed to describe system propagation.
Some limitations do exist in the DKTN model but could be addressed. One is related to the distribution estimated from the simulation. Because the construction of the DKTN model relies on the Boltzmann distribution estimated from the simulation, an adequate estimation of distribution is necessary. One way to obtain more accurate Boltzmann distribution is carrying out independent long simulations. Other options include advanced sampling techniques to obtain the accurate distribution. For example, replica exchange molecular dynamics (REMD) is an efficient approach to obtain Boltzmann distribution for different conformational states than normal MD simulations. 59 Other enhanced sampling techniques can also be combined with the DKTN model to obtain accurate distribution. 60,61
Another limitation arises for estimating the transition time among different microstates. If a simulation is trapped in some states, the estimation of transition time associated with states being less frequently visited may carry less statistical significance. Although estimation from the trajectories could be used, for more accurate estimation, the transition path sampling (TPS) method may be applied to estimate the transition time between any two microstates. Using TPS to estimate the transition time among microstates should work well when the number of microstates is small.
In summary, the DKTN model relies on accurate estimation of Boltzmann distribution and transition time among microstates. These two properties were estimated from the simulations of the model system in this study and can be estimated independently to establish a DKTN model in other cases. This independence of the estimations for transition time and Boltzmann distribution provides flexibility for the application of the DKTN model.
B. Conformational changes identified for VVD protein
In the current study, the DKTN model was applied on the VVD protein as the model system to investigate the kinetics of conformational changes and identify key allosteric structural changes. Specifically, local structural changes among microstates 1, 2, 3, and 17, and 7, 8, 20, and 21 are characterized. These local structural changes could be determining factors for the rate of light-to-dark state interconversion. Microstate 17 was identified as a “hub” for the VVD conformational change network. A detailed structure comparison highlights the difference in N-terminal and two loop regions (A′α/Aβ and Hβ/Iβ) among these microstates. Combining with the reaction rate constants among these states, a potential transition pathway from microstates 3 to 17 was proposed as the mechanism responsible for switching between VVD dark and light states. From the kinetic point of view, sequential transitions from microstates 3 to 17 through microstates 3, 2, 1, and 17 are more likely than other possible transition pathways. This dominant pathway reveals the roles of the A′α/Aβ and Hβ/Iβ loops related to key conformational changes between the dark and light states. The important role of the A′α/Aβ loop related to the protein function has been revealed by many experimental studies. For example, in the A′α/Aβ loop, the hydrogen bond between Asp68 and Cys71 could be crucial for conformational changes. Also, Pro66 behaves significantly differently in the light state vs dark state. 34 Recent studies also highlight this region as a hot spot related to evolutionary adaptation, where the residues can facilitate integration of an oxidative stress sensing mechanism into VVD-like proteins 62,63 or differentiate the signaling mechanism by regulating the evolutionarily selected residues in the adjacent β-strand. 64 The important role of the A′α/Aβ region has also been identified in recent computational studies. The rearrangement of the A′α/Aβ loop can be the initial step of conformational switches based on the machine learning results. 31 Perturbation on residue Met55 in the A′α/Aβ loop could lead to significant conformational changes according to our precious study of VVD using the rigid residue scan (RRS) method. 10 The detailed mechanistic function of the A′α/Aβ loop is finally characterized through the DKTN model in this study. The importance of Hβ/Iβ loop has also been revealed. There is one study emphasizing the residue Glu171 in the Hβ/Iβ loop. 65 The Glu171Cys mutation could enhance the cross-link of the light structure to form a dimer. 62 A previous computational study also suggests that removing the internal dynamics of Glu171 could significantly affect the light state simulation. 10 The detailed mechanistic function of the Hβ/Iβ loop revealed in the DKTN model provides unprecedented insight into the signal transduction of VVD protein.
VI. CONCLUSION
Adopting the advantage of MSMs, the DKTN model was developed in the current study as a graph representation of a master equation to study kinetics based on molecular dynamics simulations. Because the master equation is a powerful theoretical framework to describe the time dependent evolution of the state population, the DKTN model can simulate the nonequilibrium evolution of a dynamical system starting from any initial conditions. The rate constant for any transition observed in the simulation can be estimated using this method, providing critical kinetic information regarding individual states. In addition, the DKTN model can also be used to identify dominant transition pathways between any state pairs and to provide potential targets for kinetic regulations of the system. The application of the DKTN model on a photo-sensitive protein, vivid (VVD), demonstrated the advantage of this method in unraveling the subtle conformational changes among protein functional states and providing unprecedented mechanistic insight into key local conformational changes in VVD related to its functional states. Meanwhile, because of the similarity between the master equation and the Kolmogorov equation, the DKTN model also represents the Continuous Time Markov Chain (CTMC) model as a general MSM model without the lag time or constant transition probability matrix. In addition, the DKTN model is a more general model than the TN model, which can be considered as a special case of the DKTN model for the systems in equilibrium. Both advantages and limitations of the DKTN model are discussed in detail. Overall, the DKTN model could be an effective computational tool to model complex dynamical processes related to macromolecules such as protein folding and allostery.
SUPPLEMENTARY MATERIAL
See the supplementary material for a simple four-state dynamical system modeled by DKTN method and the videos illustrating the time evolution of systems starting from microstates 3 and 8, respectively.
ACKNOWLEDGMENTS
Research reported in this paper was supported by the National Institute of General Medical Sciences of the National Institutes of Health under Award No. R15GM122013. H.Z. is thankful for the financial support through the Southern Methodist University Dissertation Fellowship. Computational time was generously provided by the Southern Methodist University’s Center for Scientific Computation.
Contributor Information
Hongyu Zhou, Email: .
Peng Tao, Email: .
REFERENCES
- 1. Onufriev A., Bashford D., and Case D. A., “Exploring protein native states and large-scale conformational changes with a modified generalized born model,” Proteins: Struct., Funct., Bioinf. 55, 383–394 (2004). 10.1002/prot.20033 [DOI] [PubMed] [Google Scholar]
- 2. Motlagh H. N., Wrabl J. O., Li J., and Hilser V. J., “The ensemble nature of allostery,” Nature 508, 331–339 (2014). 10.1038/nature13001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Karplus M. and Kuriyan J., “Molecular dynamics and protein function,” Proc. Natl. Acad. Sci. U. S. A. 102, 6679–6685 (2005). 10.1073/pnas.0408930102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Klepeis J. L., Lindorff-Larsen K., Dror R. O., and Shaw D. E., “Long-timescale molecular dynamics simulations of protein structure and function,” Curr. Opin. Struct. Biol. 19, 120–127 (2009). 10.1016/j.sbi.2009.03.004 [DOI] [PubMed] [Google Scholar]
- 5. Amadei A., Linssen A. B., and Berendsen H. J., “Essential dynamics of proteins,” Proteins: Struct., Funct., Bioinf. 17, 412–425 (1993). 10.1002/prot.340170408 [DOI] [PubMed] [Google Scholar]
- 6. Daggett V., “Molecular dynamics simulations of the protein unfolding/folding reaction,” Acc. Chem. Res. 35, 422–429 (2002). 10.1021/ar0100834 [DOI] [PubMed] [Google Scholar]
- 7. Snow C. D., Nguyen H., Pande V. S., and Gruebele M., “Absolute comparison of simulated and experimental protein-folding dynamics,” Nature 420, 102 (2002). 10.1038/nature01160 [DOI] [PubMed] [Google Scholar]
- 8. Elber R. and Karplus M., “Enhanced sampling in molecular dynamics: Use of the time-dependent Hartree approximation for a simulation of carbon monoxide diffusion through myoglobin,” J. Am. Chem. Soc. 112, 9161–9175 (1990). 10.1021/ja00181a020 [DOI] [Google Scholar]
- 9. Huang X., Bowman G. R., and Pande V. S., “Convergence of folding free energy landscapes via application of enhanced sampling methods in a distributed computing environment,” J. Chem. Phys. 128, 205106 (2008). 10.1063/1.2908251 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Zhou H., Zoltowski B. D., and Tao P., “Revealing hidden conformational space of LOV protein Vivid through rigid residue scan simulations,” Sci. Rep. 7, 46626 (2017). 10.1038/srep46626 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Lane T. J., Shukla D., Beauchamp K. A., and Pande V. S., “To milliseconds and beyond: Challenges in the simulation of protein folding,” Curr. Opin. Struct. Biol. 23, 58–65 (2013). 10.1016/j.sbi.2012.11.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Voelz V. A., Bowman G. R., Beauchamp K., and Pande V. S., “Molecular simulation of ab initio protein folding for a millisecond folder NTL9 (1–39),” J. Am. Chem. Soc. 132, 1526–1528 (2010). 10.1021/ja9090353 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Bowman G. R., Huang X., and Pande V. S., “Using generalized ensemble simulations and Markov state models to identify conformational states,” Methods 49, 197–201 (2009). 10.1016/j.ymeth.2009.04.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Noé F. and Fischer S., “Transition networks for modeling the kinetics of conformational change in macromolecules,” Curr. Opin. Struct. Biol. 18, 154–162 (2008). 10.1016/j.sbi.2008.01.008 [DOI] [PubMed] [Google Scholar]
- 15. Noé F., Krachtus D., Smith J. C., and Fischer S., “Transition networks for the comprehensive characterization of complex conformational change in proteins,” J. Chem. Theory Comput. 2, 840–857 (2006). 10.1021/ct050162r [DOI] [PubMed] [Google Scholar]
- 16. Prinz J.-H., Keller B., and Noé F., “Probing molecular kinetics with Markov models: Metastable states, transition pathways and spectroscopic observables,” Phys. Chem. Chem. Phys. 13, 16912–16927 (2011). 10.1039/c1cp21258c [DOI] [PubMed] [Google Scholar]
- 17. Zhou H. and Tao P., “REDAN: Relative entropy-based dynamical allosteric network model,” Mol. Phys. 117, 1334–1343 (2018). 10.1080/00268976.2018.1543904 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Bowman G. R., Beauchamp K. A., Boxer G., and Pande V. S., “Progress and challenges in the automated construction of Markov state models for full protein systems,” J. Chem. Phys. 131, 124101 (2009). 10.1063/1.3216567 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Buchete N.-V. and Hummer G., “Coarse master equations for peptide folding dynamics,” J. Phys. Chem. B 112, 6057–6069 (2008). 10.1021/jp0761665 [DOI] [PubMed] [Google Scholar]
- 20. Cao S. and Chen S.-J., “Biphasic folding kinetics of RNA pseudoknots and telomerase RNA activity,” J. Mol. Biol. 367, 909–924 (2007). 10.1016/j.jmb.2007.01.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Swope W. C., Pitera J. W., Suits F., Pitman M., Eleftheriou M., Fitch B. G., Germain R. S., Rayshubski A., Ward T. C., and Zhestkov Y., “Describing protein folding kinetics by molecular dynamics simulations. 2. Example applications to alanine dipeptide and a Β-hairpin peptide,” J. Phys. Chem. B 108, 6582–6594 (2004). 10.1021/jp037422q [DOI] [Google Scholar]
- 22. Levy Y., Jortner J., and Berry R. S., “Eigenvalue spectrum of the master equation for hierarchical dynamics of complex systems,” Phys. Chem. Chem. Phys. 4, 5052–5058 (2002). 10.1039/b203534k [DOI] [Google Scholar]
- 23. Pande V. S., Beauchamp K., and Bowman G. R., “Everything you wanted to know about Markov state models but were afraid to ask,” Methods 52, 99–105 (2010). 10.1016/j.ymeth.2010.06.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Lane T. J., Bowman G. R., Beauchamp K., Voelz V. A., and Pande V. S., “Markov state model reveals folding and functional dynamics in ultra-long MD trajectories,” J. Am. Chem. Soc. 133, 18413–18419 (2011). 10.1021/ja207470h [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Bowman G. R., Bolin E. R., Hart K. M., Maguire B. C., and Marqusee S., “Discovery of multiple hidden allosteric sites by combining Markov state models and experiments,” Proc. Natl. Acad. Sci. U. S. A. 112, 2734 (2015). 10.1073/pnas.1417811112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Prinz J.-H., Wu H., Sarich M., Keller B., Senne M., Held M., Chodera J. D., Schütte C., and Noé F., “Markov models of molecular kinetics: Generation and validation,” J. Chem. Phys. 134, 174105 (2011). 10.1063/1.3565032 [DOI] [PubMed] [Google Scholar]
- 27. Sarich M., Noé F., and Schütte C., “On the approximation quality of Markov state models,” Multiscale Model. Simul. 8, 1154–1177 (2010). 10.1137/090764049 [DOI] [Google Scholar]
- 28. Pérez-Hernández G., Paul F., Giorgino T., De Fabritiis G., and Noé F., “Identification of slow molecular order parameters for Markov model construction,” J. Chem. Phys. 139, 015102 (2013). 10.1063/1.4811489 [DOI] [PubMed] [Google Scholar]
- 29. Noé F., Wu H., Prinz J.-H., and Plattner N., “Projected and hidden Markov models for calculating kinetics and metastable states of complex molecules,” J. Chem. Phys. 139, 184114 (2013). 10.1063/1.4828816 [DOI] [PubMed] [Google Scholar]
- 30. Liu H., Li M., Fan J., and Huo S., “Inherent structure versus geometric metric for state space discretization,” J. Comput. Chem. 37, 1251–1258 (2016). 10.1002/jcc.24315 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Zhou H., Dong Z., Verkhivker G., Zoltowski B. D., and Tao P., “Allosteric mechanism of the circadian protein Vivid resolved through Markov state model and machine learning analysis,” PLoS Comput. Biol. 15, e1006801 (2019). 10.1371/journal.pcbi.1006801 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Foley B. J., Stutts H., Schmitt S. L., Lokhandwala J., Nagar A., and Zoltowski B. D., “Characterization of a Vivid homolog in Botrytis cinerea,” Photochem. Photobiol. 94, 985–993 (2018). 10.1111/php.12927 [DOI] [PubMed] [Google Scholar]
- 33. Zoltowski B. D., Vaccaro B., and Crane B. R., “Mechanism-based tuning of a LOV domain photoreceptor,” Nat. Chem. Biol. 5, 827–834 (2009). 10.1038/nchembio.210 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Zoltowski B. D., Schwerdtfeger C., Widom J., Loros J. J., Bilwes A. M., Dunlap J. C., and Crane B. R., “Conformational switching in the fungal light sensor Vivid,” Science 316, 1054–1057 (2007). 10.1126/science.1137128 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Moler C. and Van Loan C., “Nineteen dubious ways to compute the exponential of a matrix, twenty-five years later,” SIAM Rev. 45, 3–49 (2003). 10.1137/s00361445024180 [DOI] [Google Scholar]
- 36. Schuster S. and Schuster R., “Detecting strictly detailed balanced subnetworks in open chemical reaction networks,” J. Math. Chem. 6, 17–40 (1991). 10.1007/bf01192571 [DOI] [Google Scholar]
- 37. Dongarra J. J., “Performance of various computers using standard linear equations software,” ACM SIGARCH Comput. Archit. News 20, 22–44 (1992). 10.1145/141868.141871 [DOI] [Google Scholar]
- 38. Anderson W. J., Continuous-Time Markov Chains: An Applications-Oriented Approach (Springer Science & Business Media, 2012). [Google Scholar]
- 39. Whitt W., Continuous-Time Markov Chains (Columbia University, New York, 2006), p. 65. [Google Scholar]
- 40. Connors K. A., Chemical Kinetics: The Study of Reaction Rates in Solution (John Wiley & Sons, 1990). [Google Scholar]
- 41. Ott E., Chaos in Dynamical Systems (Cambridge University Press, 2002). [Google Scholar]
- 42. Boyd S., Diaconis P., and Xiao L., “Fastest mixing Markov chain on a graph,” SIAM Rev. 46, 667–689 (2004). 10.1137/s0036144503423264 [DOI] [Google Scholar]
- 43. Berman H. M., Bhat T. N., Bourne P. E., Feng Z., Gilliland G., Weissig H., and Westbrook J., “The protein data bank and the challenge of structural genomics,” Nat. Struct. Mol. Biol. 7, 957–959 (2000). 10.1038/80734 [DOI] [PubMed] [Google Scholar]
- 44. Freddolino P. L., Gardner K. H., and Schulten K., “Signaling mechanisms of LOV domains: New insights from molecular dynamics studies,” Photochem. Photobiol. Sci. 12, 1158–1170 (2013). 10.1039/c3pp25400c [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Jorgensen W. L., Chandrasekhar J., Madura J. D., Impey R. W., and Klein M. L., “Comparison of simple potential functions for simulating liquid water,” J. Chem. Phys. 79, 926 (1983). 10.1063/1.445869 [DOI] [Google Scholar]
- 46. Essmann U., Perera L., Berkowitz M. L., Darden T., Lee H., and Pedersen L. G., “A smooth particle mesh Ewald method,” J. Chem. Phys. 103, 8577–8593 (1995). 10.1063/1.470117 [DOI] [Google Scholar]
- 47. Brooks B. R., Brooks C. L., MacKerell A. D., Nilsson L., Petrella R. J., Roux B., Won Y., Archontis G., Bartels C., and Boresch S., “CHARMM: The biomolecular simulation program,” J. Comput. Chem. 30, 1545–1614 (2009). 10.1002/jcc.21287 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Eastman P. and Pande V., “OpenMM: A hardware-independent framework for molecular simulations,” Comput. Sci. Eng. 12, 34–39 (2010). 10.1109/mcse.2010.27 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. van der Maaten L. and Hinton G., “Visualizing data using t-SNE,” J. Mach. Learn. Res. 9, 2579–2605 (2008). [Google Scholar]
- 50. Zhou H., Wang F., and Tao P., “t-Distributed stochastic neighbor embedding (t-SNE) method with the least information loss for macromolecular simulations,” J. Chem. Theory Comput. 14, 5499 (2018). 10.1021/acs.jctc.8b00652 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Pedregosa F., Varoquaux G., Gramfort A., Michel V., Thirion B., Grisel O., Blondel M., Prettenhofer P., Weiss R., and Dubourg V., “Scikit-learn: Machine learning in python,” J. Mach. Learn. Res. 12, 2825–2830 (2011). [Google Scholar]
- 52. Pisani P., Piro P., Decherchi S., Bottegoni G., Sona D., Murino V., Rocchia W., and Cavalli A., “Describing the conformational landscape of small organic molecules through Gaussian mixtures in dihedral space,” J. Chem. Theory Comput. 10, 2557–2568 (2014). 10.1021/ct400947t [DOI] [PubMed] [Google Scholar]
- 53. Bailey T. L. and Elkan C., “Fitting a mixture model by expectation maximization to discover motifs in bipolymers,” Proc. Int. Conf. Intell. Syst. Mol. Biol. 2, 28–36 (1994). [PubMed] [Google Scholar]
- 54. Zhou H., Dong Z., and Tao P., “Recognition of protein allosteric states and residues: Machine learning approaches,” J. Comput. Chem. 39, 1481–1490 (2018). 10.1002/jcc.25218 [DOI] [PubMed] [Google Scholar]
- 55. Kalescky R., Zhou H., Liu J., and Tao P., “Rigid residue scan simulations systematically reveal residue entropic roles in protein allostery,” PLoS Comput. Biol. 12, e1004893 (2016). 10.1371/journal.pcbi.1004893 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Kohavi R. A., “Study of cross-validation and bootstrap for accuracy estimation and model selection,” in IJCAI 1995, Montreal, Canada (Morgan Kaufmann Publishers Inc., 1995), Vol. 14, pp. 1137–1145. [Google Scholar]
- 57. Husic B. E. and Pande V. S., “Note: MSM lag time cannot be used for variational model selection,” J. Chem. Phys. 147, 176101 (2017). 10.1063/1.5002086 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. Noé F. and Nuske F., “A variational approach to modeling slow processes in stochastic dynamical systems,” Multiscale Model. Simul. 11, 635–655 (2013). 10.1137/110858616 [DOI] [Google Scholar]
- 59. Sugita Y. and Okamoto Y., “Replica-exchange molecular dynamics method for protein folding,” Chem. Phys. Lett. 314, 141–151 (1999). 10.1016/s0009-2614(99)01123-9 [DOI] [Google Scholar]
- 60. Zhou H. and Tao P., “Dynamics sampling in transition pathway space,” J. Chem. Theory Comput. 14, 14–29 (2018). 10.1021/acs.jctc.7b00606 [DOI] [PubMed] [Google Scholar]
- 61. Bernardi R. C., Melo M. C., and Schulten K., “Enhanced sampling techniques in molecular dynamics simulations of biological systems,” Biochim. Biophys. Acta, Gen. Subj. 1850, 872–877 (2015). 10.1016/j.bbagen.2014.10.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62. Zoltowski B. D. and Crane B. R., “Light activation of the LOV protein Vivid generates a rapidly exchanging dimer,” Biochemistry 47, 7012–7019 (2008). 10.1021/bi8007017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63. Lokhandwala J., Hopkins H. C., Rodriguez-Iglesias A., Dattenböck C., Schmoll M., and Zoltowski B. D., “Structural biochemistry of a fungal LOV domain photoreceptor reveals an evolutionarily conserved pathway integrating light and oxidative stress,” Structure 23, 116–125 (2015). 10.1016/j.str.2014.10.020 [DOI] [PubMed] [Google Scholar]
- 64. Pudasaini A., Shim J. S., Song Y. H., Shi H., Kiba T., Somers D. E., Imaizumi T., and Zoltowski B. D., “Kinetics of the LOV domain of ZEITLUPE determine its circadian function in Arabidopsis,” Elife 6, e21646 (2017). 10.7554/elife.21646 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65. Lamb J. S., Zoltowski B. D., Pabit S. A., Li L., Crane B. R., and Pollack L., “Illuminating solution responses of a LOV domain protein with photocoupled small-angle X-ray scattering,” J. Mol. Biol. 393, 909–919 (2009). 10.1016/j.jmb.2009.08.045 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
See the supplementary material for a simple four-state dynamical system modeled by DKTN method and the videos illustrating the time evolution of systems starting from microstates 3 and 8, respectively.