Significance
In evolutionary biology, it is generally assumed that evolution occurs in the weak mutation limit, that is, the frequency of multiple mutations simultaneously occurring in the same genome and the same generation is negligible. We employ mathematical modeling to show that, although under the typical parameter values of the evolutionary process the probability of multimutational leaps is indeed low, they might become substantially more likely under stress, when the mutation rate is dramatically elevated. We hypothesize that stress-induced mutagenesis in microbes is an evolvable adaptive strategy. Multimutational leaps might matter also in other cases of substantially increased mutation rate, such as growing tumors or evolution of primordial replicators.
Keywords: fitness landscape, stress-induced mutagenesis, epistasis, purifying selection, positive selection
Abstract
Is evolution always gradual or can it make leaps? We examine a mathematical model of an evolutionary process on a fitness landscape and obtain analytic solutions for the probability of multimutation leaps, that is, several mutations occurring simultaneously, within a single generation in 1 genome, and being fixed all together in the evolving population. The results indicate that, for typical, empirically observed combinations of the parameters of the evolutionary process, namely, effective population size, mutation rate, and distribution of selection coefficients of mutations, the probability of a multimutation leap is low, and accordingly the contribution of such leaps is minor at best. However, we show that, taking sign epistasis into account, leaps could become an important factor of evolution in cases of substantially elevated mutation rates, such as stress-induced mutagenesis in microbes. We hypothesize that stress-induced mutagenesis is an evolvable adaptive strategy.
A venerable principle of natural philosophy, most consistently propounded by Leibnitz (1) and later embraced by prominent biologists, in particular Linnaeus (2), is “natura non facit saltus” (“nature does not make leaps”). This principle then became one of the key tenets of Darwin’s theory that was inherited by the modern synthesis of evolutionary biology. In evolutionary biology, the rejection of saltation takes the form of gradualism, that is, the notion that evolution proceeds gradually, via accumulation of “infinitesimally small” heritable changes (3, 4). However, some of the most consequential evolutionary changes, such as, for example, the emergence of major taxa, seem to occur abruptly rather than gradually, prompting hypotheses on the importance of saltational evolution, for example by Goldschmidt (“hopeful monsters”) and Simpson (“quantum evolution”). Subsequently, these ideas have received a more systematic, even if qualitative, treatment in the concepts of punctuated equilibrium (5, 6) and evolutionary transitions (7, 8).
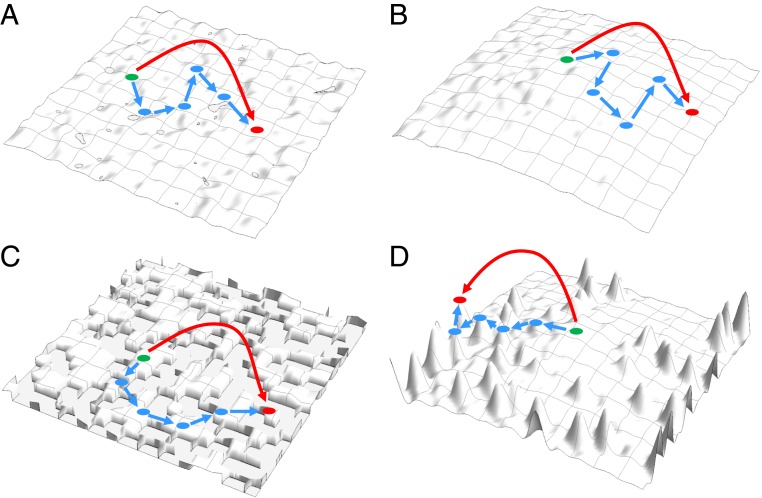
Within the framework of modern evolutionary biology, gradualism corresponds to the weak-mutation limit, that is, an evolutionary regime in which mutations occur one by one, consecutively, such that the first mutation is assessed by selection and either fixed or purged from the population, before the second mutation occurs (9). A radically different, saltational mode of evolution (10, 11) is conceivable under the strong-mutation limit (9) whereby multiple mutations occurring within a single generation and in the same genome potentially could be fixed all together. Under the fitness landscape concept (12, 13), gradual or more abrupt evolutionary processes can be depicted as distinct types of trajectories on fitness landscapes (Fig. 1). The typical evolutionary paths on such landscapes are thought to be 1 step at a time, uphill mutational walks (12). In small populations, where genetic drift becomes an important evolutionary factor, the likelihood of downhill movements becomes nonnegligible (14). In principle, however, a different type of moves on fitness landscapes could occur, namely, leaps (or “flights”) across valleys when a population can move to a different area in the landscape, for example to the slope of a different, higher peak, via simultaneous fixation of multiple mutations (Fig. 1).
Fig. 1.
Walks and leaps on different types of fitness landscapes. Dots show genome states; blue (shirt straight) arrows indicate consecutive moves via fixation of single mutations; red (long curved) arrows indicate multimutation leaps. (A) Nearly neutral landscape. (B) Landscape dominated by slightly deleterious mutations. (C) Kimura’s model landscape (a fraction of mutations is neutral; the rest are lethal). (D) Landscape combining beneficial and deleterious mutations.
We sought to obtain analytically, within the population genetics framework, the conditions under which multimutational leaps might be feasible. The results suggest that, under most typical parameters of the evolutionary process, leaps cannot be fixed. However, taking sign epistasis into account, we show that saltational evolution could become relevant under conditions of elevated mutation rate under stress so that stress-induced mutagenesis could be considered an evolvable adaptation strategy.
Results
Multimutation Leaps in the Equilibrium Regime.
Let us assume (binary) genomes of length L (in the context of this analysis, L should be construed as the number of evolutionarily relevant sites, such as codons in protein-coding genes, rather than the total number of sites), the probability of single mutation μ << 1 per site per round of replication (generation), and constant effective population size Ne >> 1. Then, the transition probability from sequence i to sequence j is (equation 3.11 in ref. 15)
| [1] |
where is the Hamming distance (number of different sites between the 2 sequences). The number of sequences separated by the distance h is equal to the number of ways h sites can be selected from L, that is,
| [2] |
where the last, approximate expression is valid under the assumption that L >> 1 and L >> h (h can be of the order of 1).
Assuming also µ << 1, we obtain a typical combinatorial probability of leaps over the distance h:
| [3] |
which is a Poisson distribution with the expectation Lμ.
In steady state, the probability of fixation of the state i is proportional to where
| [4] |
and where is the fitness of the genotype i [ is analogous to energy in the Boltzmann distribution within the analogy between population genetics and statistical physics (16)]. For other demographic structures and assumptions on the mutation process, the relationship between fixation probability can quantitatively differ while retaining the same form. In particular, for a population that produces offspring by binary division (fission), (17, 18).
Then, the rate of the occurrence and fixation of the transition is (15)
| [5] |
The distribution function of the fitness differential has to be specified (hereafter, we refer to x as fitness, omitting logarithm for brevity). We analyze first the case without epistasis, that is, with additive fitness effects of individual mutations:
| [6] |
where are independent random variables with the distribution functions . Then, the distribution function of the fitness difference is
| [7] |
which is obtained by using the standard Fourier transformation of the delta function.
Now, let us specify the distribution of the fitness effects of mutations , assuming an exponential dependency of the probability of a mutation on its fitness effect, separately for beneficial and deleterious mutations:
| [8] |
where is the normalization factor, is the ratio of the probabilities of beneficial and deleterious mutations, and is the inverse of the characteristic fitness difference for a single mutation (discussed below). For simplicity, we assume here the same decay rates for the probability density of the fitness effects of beneficial and deleterious mutations. Empirical data on the distributions of fitness effects of mutations (19, 20) clearly indicate that . From the normalization condition,
| [9] |
Note that the mean of the fitness difference (selection coefficient) when the distribution of the fitness effects is given by 8 is
| [10] |
For simplicity, we start with an assumption that the values of and are independent of i. For the model 8
| [11] |
Then, from Eq. 5, the fixation rate of an h-mutation leap is equal to
| [12] |
Substituting 11 into 7, we obtain
| [13] |
Consider first the case r = 0 (all mutations are deleterious). Then, . For Δ > 0, that is, decrease of the fitness, we have
| [14] |
Then, the fixation rate 12 of an h-mutation leap is equal to
| [15] |
where and is the Hurwitz zeta function . Therefore, the rate of fixation for leaps of the length h is equal to .
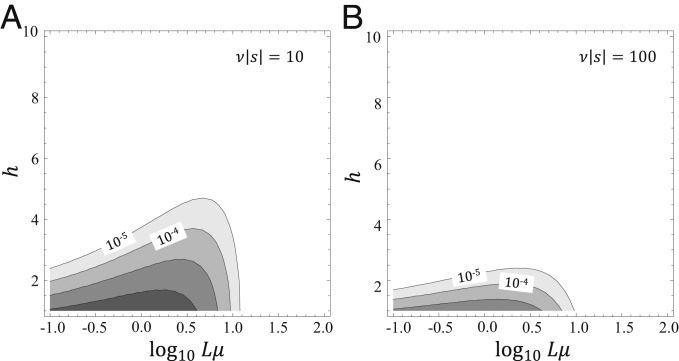
In one extreme, if (, neutral landscape), and mutations are fixed at the rate they occur. In the opposite extreme case of strong negative selection , where is the Riemann zeta function. For a rough estimate, can be replaced by 1, and then, . In this case, the maximum of W(h) is reached at , which gives a nonnegligible fraction of multimutation leaps among the fixed mutations only for . However, in this case, the value of at this maximum is exponentially small because . Therefore, in the regime of strong selection against deleterious mutations and at high mutations rates , multiple mutations actually dominate the mutational landscape, but their fixation rate is extremely low. Qualitatively, this conclusion seems obvious, but we now obtain the quantitative criteria for what constitutes “strong selection.” We find that, even for the rate of multimutation leaps can be nonnegligible (>10−4 per generation; Fig. 2A) at the optimal values, whereas for , any leaps with >1 are unfeasible (Fig. 2B).
Fig. 2.
Rates of leaps on a landscape dominated by deleterious mutations. Rates of transitions are plotted against the per-genome mutation rate (Lμ) and the leap length for different strengths of selection (A: ν|s| = 10 and B: ν|s| = 100). Contour lines indicate orders of magnitude and start from the rate of 10−5 leaps per generation.
Under a more realistic model, all values of (the inverse of the fitness effect of a mutation) are different. For and (no beneficial mutations), using Eq. 13, we get
| [16] |
For example, in Kimura’s neutral evolution model (21), is a binary random variable that takes a value of (, neutral mutation), with the probability , and a value of 0 (, lethal mutation), with the probability . Then, , and is replaced with in Eq. 3, a trivial replacement of the total genome length with the length of the part of the genome where mutations are allowed, . Accordingly, , and multimutation leaps become relevant for .
Let us now estimate the probability of leaps with beneficial mutations . Assuming (rare beneficial mutations), Eq. 13 takes the form
| [17] |
and the fixation rate of a leap including beneficial mutations is
| [18] |
If (weak positive selection), , so that the role of beneficial mutations is negligible. If (strong positive selection),
| [19] |
Comparing Eq. 19 with the result for (Eq. 18), one can see that, in this case, beneficial mutations are predominant among the fixed mutations if
| [20] |
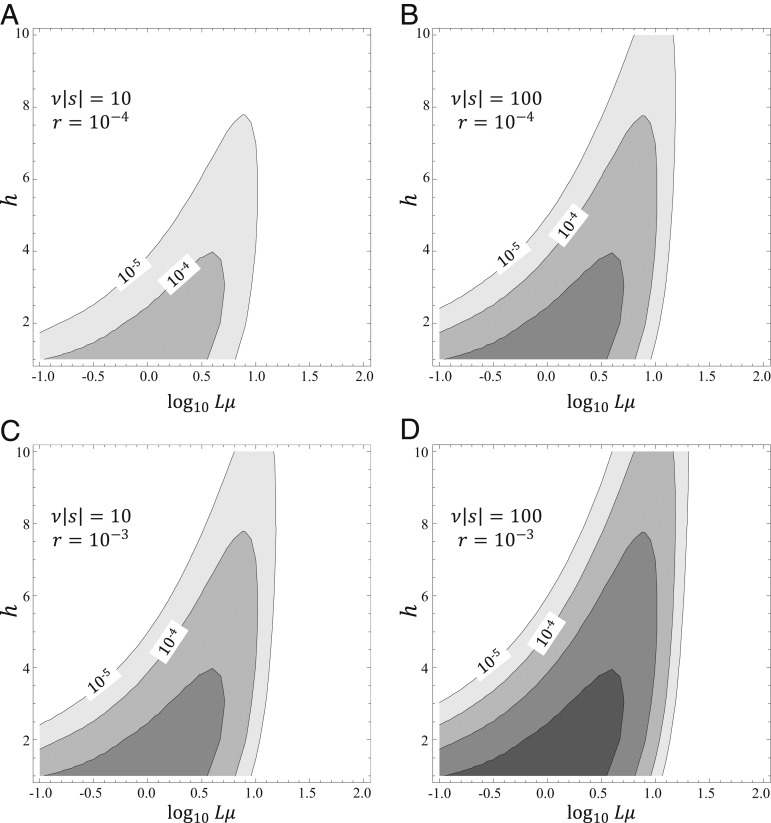
In this regime, multimutation leaps occur at nonnegligible rates under sufficiently high (but not excessive) mutation rates (Fig. 3).
Fig. 3.
Rates of leaps on a landscape combining beneficial and deleterious mutations. Rates of leaps are plotted against the per-genome mutation rate (Lμ) and the leap length for different strengths of selection (A and C: ν|s| = 10; B and D: ν|s| = 100) and for different frequencies of beneficial mutations (A and B: r = 10−4; C and D: r = 10−3). Contour lines indicate orders of magnitude and start from the rate of 10−5 leaps per generation.
The model considered above assumes independent effects of different mutations (no epistasis, “ideal gas of mutations” model). Now, let us take into account epistasis. In the case of strong epistasis, effects of combinations of different mutations are increasingly strong, diverse, and, effectively, unpredictable, resulting in a rugged fitness landscape (22). In the limit of epistasis strength and unpredictability, epistasis creates numerous highly beneficial combinations that, once they occur, are highly likely to be fixed, and a far greater number of highly deleterious combinations that are immediately lethal. Due to the effective randomness of genetic interactions, we consider the resulting landscape as essentially random for , with the frequency of the beneficial combinations independent of . In this case, the effective number of fixed leaps with is simply
| [21] |
If all single mutations are deleterious , their rate of fixation (Eq. 15) can be approximated by , whereas for all leaps of the length , effective number of fixed leaps is . Therefore, the condition for is
| [22] |
In the high-mutation regime , multiple mutations occur orders of magnitude more frequently than single mutations, overwhelming the difference of scale between and , and making multimutation leaps much more likely. In the low-mutation regime , the balance between single and multiple mutations tends to and the condition for the dominance of multimutation leaps becomes . Around the Eigen threshold (23), the condition corresponds to , that is, the frequency of beneficial multimutation combinations should be unrealistically high to sustain evolution by multimutation leaps.
A Nonequilibrium Model of Stress-Induced Mutagenesis.
The analysis presented above suggests that the necessary condition for fixation of multimutational leaps is the high-mutation regime. At low mutation rates , multimutation events occur too rarely to be fixed in realistic settings even if the frequency of beneficial combinations among them is reasonably high. However, in the high-mutation regime , the above analysis is problematic for 2 reasons. First, the expression for the fixation rate (Eq. 5) is technically valid only for the case when the new mutation is either fixed or lost before the emergence of the next one, which implies . Second, under any realistic model of the fitness landscape, most mutations should be deleterious. Thus, implies that most of the progeny carries 1 or more mutations, and therefore suffers from these deleterious effects. Under these conditions, the assumption of constant Ne is unrealistic, because the size of such a population will decrease under the mutational load, down to an eventual crash.
The complete analysis of the behavior of a variable-size population under the high-mutation regime and strong mutational effects is currently beyond the state of the art. Therefore, here we analyze a simplified model of the short-term behavior of a (microbial) population after the onset of stress-induced mutagenesis .
Consider a microbial population consisting of individuals. Under typical conditions, the population is in an equilibrium, so that approximately individuals survive the average generation span and produce progeny by division (here we consider simple asexual division as the progeny-generating process whereby each surviving individual produces 2 offspring; other demographic models can be accommodated without loss of generality). The typical mutation rate is low (, according to refs. 24 and 25), so the population can be considered homogeneous. Upon the onset of unfavorable conditions, the survival rate of the wild-type individuals drops to and the mutation rate in the stressed individuals increases such that .
If is not too small , the immediate wild-type survivors produce first-generation progeny. With the expected number of mutations per descendant being , the distribution of the number of mutations in the progeny is given by the Poisson distribution with the expected number of mutants with mutations of .
Let us consider a mutation landscape that is dominated by deleterious mutations with strong sign epistasis. All single mutations are deleterious, so the survival of their carriers over the generation time is . An overwhelming majority of multimutation combinations have even stronger negative effects, so for . Some small fraction of these combinations, however, is strongly beneficial in the new conditions, conferring to their carriers the survival rate of .
What would the function look like? Intuitively, should decay to 0 at large , or at least not grow, as it is overwhelmingly likely that a sufficiently large set of mutations would contain a subset that it unconditionally lethal. Here, for simplicity, we consider a general form of that equals 0 for and monotonically decays with from at an arbitrary rate.
If the deleterious effect of mutations is strong enough , then the only plausible source of beneficial mutants is the population of wild-type individuals (neither single mutants nor multiple mutants that do not carry the beneficial combinations survive to the next generation). The population of the wild-type individuals decays exponentially through both the diminished survival and through mutations, reaching at the -th generation after the onset of the unfavorable conditions. Ignoring stochastic fluctuations, the total number of wild-type individuals that survive until the population collapse can be estimated as
| [23] |
which is approximately equal to if .
Over the combined lifetimes of the surviving wild-type individuals, the expected number of beneficial mutants is
| [24] |
which depends on the genome-wide mutation rate and the shape of the function.
Let us first consider the 2 extreme cases of . In the limit of a completely flat function ( for all ), Eq. 23 gives . This function asymptotically reaches the value of with . In the other extreme of a rapidly decaying , that is, for , Eq. 23 gives . This function reaches its maximum at with .
It can be shown that the estimates for all other monotonically decaying functions reach their maxima at finite values of with
| [25] |
Indeed, let us consider first the simplest model . Then, Eq. 24 takes the form
| [26] |
As a function of , the quantity
| [27] |
reaches the maximum at , where is the solution of the equation
| [28] |
with the value at the maximum
| [29] |
For (rapid decay of , and . In the opposite limit of slowly decaying , , and .
For a general slowly decaying function , one can find that
| [30] |
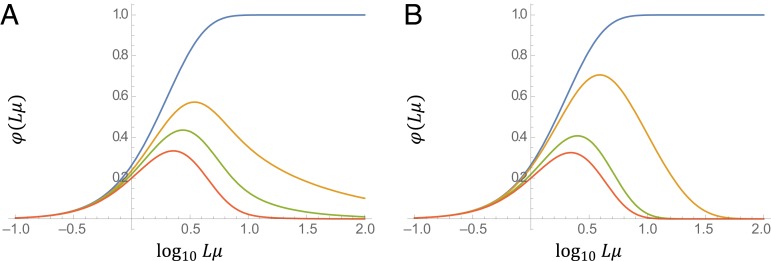
Importantly, even in this case, the optimal mutation rate increases only logarithmically with the decay rate; furthermore, the optimum value is notably robust to changes in (Fig. 4).
Fig. 4.
Abundance of beneficial multimutation combinations depending on the mutation rate. Abundance of beneficial multimutation combinations, , given by Eq. 24, relative to . (A) with (blue), (orange), (green), and (red). (B) de with (blue), (orange), (green), and (red).
The approximate condition for population survival, , can be derived from Eqs. 23 and 25 and is bounded from below by
| [31] |
at the optimal value of .
Discussion
Here, we obtained analytic expressions for the probability of the fixation of multimutation leaps for deleterious and beneficial mutations depending on the parameters of the evolutionary process, namely, effective genome size (L), mutation rate (μ), effective population size , and distribution of selection coefficients of mutations (s). Leaps in random fitness landscapes in the context of punctuated equilibrium have been previously considered for infinite (26, 27) or finite (28) populations. However, unlike the present work, these studies have focused on the analysis of the dynamics of the leaps rather than on the equilibrium distribution of their lengths. We further address the plausibility of beneficial multimutation leaps under epistasis and outside of equilibrium, for example in a microbial population under stress.
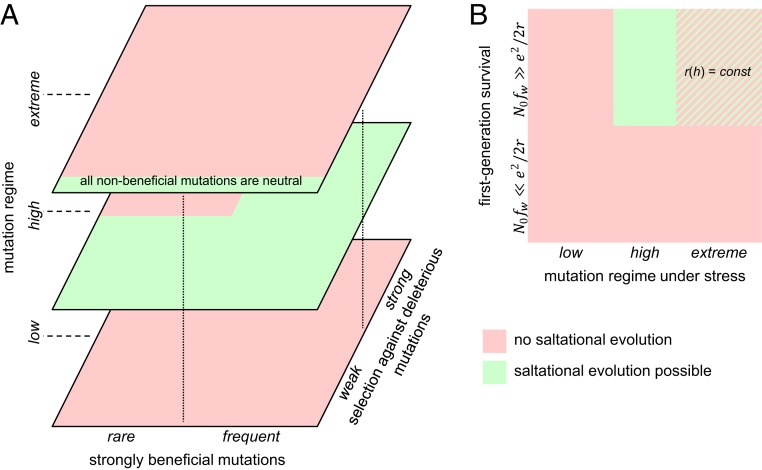
The principal outcomes of the present analysis are the conditions under which multimutation leaps are fixed at a nonnegligible rate in different evolutionary regimes (Fig. 5A). If the landscape is completely flat (strict neutrality, ), the leap length is distributed around that is , simply, the expected number of mutations per genome per generation. If , leaps are effectively impossible, and evolution can proceed only step by step (12). A considerable body of data exists on the values of each of the relevant parameters that define the probability of leaps. Generally, in the long term, the total expected number of mutations per genome per generation has to be of the order of 1 or lower (Eigen threshold) because, if , the population ultimately spirals into error catastrophe (it should be emphasized that error catastrophe, i.e., the loss of high-fitness genotypes through accumulation of deleterious mutations, is distinct from extinction catastrophe, i.e., loss of the entire population caused by deleterious mutation) (15, 23, 29–32). The selection for lower mutation rates is thought to be limited by the drift barrier and, accordingly, the genomic mutation rate appears to be inversely proportional to the effective population size, that is, (24, 25). Thus, , which appears to be an important universal in evolution.
Fig. 5.
Summary of the modeling results: evolution by multimutation leaps depending on the evolutionary regime and fitness landscape. (A) Multimutation leaps in the equilibrium regime. (B) First-generation multimutation leaps under stress-induced mutagenesis. The hatched area denotes the domain of the parameter space in which saltational evolution may or may not be possible depending on the r(h) value.
To estimate the leap probability, we can use Eq. 15 and the characteristic values of the relevant parameters, for example those for human populations. As a crude approximation, Lμ = 1, v = 104, |s| = 10−2 which, in the absence of beneficial mutations, translates into the probability of a multimutation leap of about 4 × 10−5. Thus, such a leap would, on average, require over 23,000 generations, which is not a relevant value for the evolution of mammals (given that ∼140 single mutations are expected to be fixed during that time as calculated using the same formula). However, short leaps including beneficial mutations can occur with reasonable rates, such as 5 × 10−4 for h = 3, and the frequency of beneficial mutations r = 10−4, so such leaps are only 8 times less frequent than single-mutation fixations. Conceivably, such leaps of beneficial mutations could be a minor but nonnegligible evolutionary factor. For organisms with Lμ < 1 and larger v, the probability of leaps is substantially lower than the above estimates, so that under “normal” evolutionary regimes (at equilibrium) the contribution of leaps is negligible.
However, in some biologically relevant and common situations, such as stress-induced mutagenesis, which occurs in microbes in response to double-stranded DNA breaks, the effective mutation rate can locally and temporarily increase by orders of magnitude (33, 34) while the population is going through a severe bottleneck (Fig. 5B). If the fraction of beneficial combinations of mutations satisfies the condition (31), even in the extreme case when the rest of the mutations are lethal, the population has a chance to survive when its mutation rate (Lμ) assumes a value close to the optimum value given by Eq. 30. This value depends on the rate of the decay of the fraction of beneficial combinations of mutations with the number of mutations. Specifically, the optimal value of Lμ equals 2 for the steepest decay of r(h) and increases logarithmically slowly for more shallow functions. Under an extremely severe stress (N0 = 109, fw = 10−3), the survival threshold [r(h)] corresponds to the fraction of beneficial pairs of mutations of about 3 × 10−6. This means that, in the case of a typical bacterial genome of 3 × 106 base pairs, for each (deleterious) mutation, there is, on average, 1 other mutation that yields a beneficial combination. This estimate pertains to the extreme case when all individual mutations are highly deleterious. Under more realistic conditions, when many mutations are effectively neutral, and a small fraction is beneficial, the threshold fraction of beneficial combinations will be considerably lower. These estimates indicate that multimutation leaps are likely to be an important factor of adaptive evolution under stress. An implication of these findings is that stress-induced mutagenesis could be a selectable adaptive mechanism, however controversial an issue the evolution of evolvability might be (35–39). It should be further noted that, in this situation, large populations will have a higher innovation potential than small populations because the former produce a greater diversity of multimutation combinations. In other terms, large populations have a greater chance to cross the entropy barrier to higher fitness genotypes (40). Thus, the stress-induced innovation regime is an alternative to innovation by drift that occurs, primarily, in small populations (during population bottlenecks) (14, 25). This conclusion complements the previous findings that large populations can readily cross fitness valleys through a series of consecutive mutations when the intermediate states are close to neutrality (41).
Remarkably, experiments on adaptive evolution of bacterial populations revealed repeated emergence of hypermutators (i.e., mutations in repair genes that greatly increase the mutation rate in the respective clones) (42–44) resulting, in some case, in simultaneous fixation of “cohorts” of beneficial mutations (45). Furthermore, subsequent analyses have shown that mutator genotypes exist only transiently but exert long-lasting effects on the population evolution (46). These findings seem to provide direct experimental validation of the multimutational leaps predicted by our model.
A different context in which multimutation leaps potentially might play a role is evolution of cancers. In most tumor types, mutation rate is dramatically, orders of magnitude elevated compared to normal tissues (47, 48). The effective population size in tumors is difficult to estimate, and therefore there is not enough information to use the condition (31) to assess the plausibility of multimutation leaps. Nevertheless, given the extremely high values of Lμ, it cannot be ruled out that the frequency of leaps is nonnegligible. Most of the mutations in tumors are passengers that have no effect on cancer progression or exert a deleterious effect (49, 50). Traditionally, tumorigenesis is thought to depend on several driver mutations that occur consecutively (51, 52). This is indeed likely to be the case in many tumors because the age of onset strongly and positively correlates with the number of drivers (53, 54). However, for a substantial fraction of tumors, no drivers are readily identifiable suggestive of the possibility that, in these cases, tumor progression is driven by “epistatic drivers” (53), that is, combinations of mutations that might occur by leaps.
Another, completely different area where multimutation leaps could be important could be evolution of primordial replicators, in particular those in the hypothetical RNA world, that are thought to have had an extremely low replication fidelity, barely above the error catastrophe threshold (23, 55, 56). Furthermore, because the primordial replicators are likely to have been incompletely optimized, the fraction of beneficial mutational combinations could be relatively high. Under these conditions, multimutational leaps could have been an important route of evolutionary acceleration and thus might have contributed substantially to the most challenging evolutionary transition of all, that from precellular to cellular life forms.
An important caveat of the above conclusions on the biological relevance of multimutational leaps is that the present analysis disregards clonal interference, that is, competition between clades in an evolving population, that plays a substantial role in the evolution of large populations under the high-mutation regime as indicated by both theory (17, 57, 58) and experiment (45, 59). Clearly, clonal interference has the potential to dampen the effect of multiple mutations. Nevertheless, it appears likely that a clone with multiple mutations would be a strong competitor under strong selection pressure, for example in the case of stress-induced mutagenesis.
Taken together, all these biological considerations suggest that multimutation leaps with a beneficial effect, the probability of which we show to be nonnegligible under conditions of elevated mutagenesis, could be an important mechanism of evolution that so far has been largely overlooked. Given that elevated mutation rate caused by stress is pervasive in nature, saltational evolution, after all, might substantially contribute to the history of life, in direct defiance of “Natura non facit saltus.”
Acknowledgments
M.I.K. acknowledges financial support from the Dutch Research Council via the Spinoza Prize. Y.I.W. and E.V.K. are funded through the Intramural Research Program of the National Institutes of Health.
Footnotes
The authors declare no competing interest.
References
- 1.Leibniz G. W., New Essays on Human Understanding (Cambridge University Press, New York, 1981). [Google Scholar]
- 2.Linnaeus C., Philosophia Botanica (Uppsala, 1751). [Google Scholar]
- 3.Darwin C., On the Origin of Species (John Murray, London, 1859). [Google Scholar]
- 4.Huxley J., Evolution: The Modern Synthesis: The Definitive Edition (MIT Press, Cambridge, 2010). [Google Scholar]
- 5.Gould S. J., Eldredge N., Punctuated equilibrium comes of age. Nature 366, 223–227 (1993). [DOI] [PubMed] [Google Scholar]
- 6.Eldredge N., Gould S. J., On punctuated equilibria. Science 276, 338–341 (1997). [DOI] [PubMed] [Google Scholar]
- 7.Szathmáry E., Smith J. M., The major evolutionary transitions. Nature 374, 227–232 (1995). [DOI] [PubMed] [Google Scholar]
- 8.Szathmáry E., Toward major evolutionary transitions theory 2.0. Proc. Natl. Acad. Sci. U.S.A. 112, 10104–10111 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Gillespie J. H., The Causes of Molecular Evolution (Oxford University Press, Oxford, 1994). [Google Scholar]
- 10.Theissen G., Saltational evolution: hopeful monsters are here to stay. Theory Biosci. 128, 43–51 (2009). [DOI] [PubMed] [Google Scholar]
- 11.Lynch M., Abegg A., The rate of establishment of complex adaptations. Mol. Biol. Evol. 27, 1404–1414 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Gavrilets S., Fitness Landscapes and the Origin of Species (Princeton University Press, Princeton, 2004). [Google Scholar]
- 13.Wright S., Adaptation and Selection. Genetics, Paleontology and Evolution (Princeton Univ. Press, Princeton, NJ, 1949). [Google Scholar]
- 14.Lynch M., The Origins of Genome Architecture (Sinauer Associates, Sunderland, MA, 2007). [Google Scholar]
- 15.Nowak M. A., Evolutionary Dynamics: Exploring the Equations of Life (Belknap Press, Cambridge, MA, 2006). [Google Scholar]
- 16.Sella G., Hirsh A. E., The application of statistical physics to evolutionary biology. Proc. Natl. Acad. Sci. U.S.A. 102, 9541–9546 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Gerrish P. J., Lenski R. E., The fate of competing beneficial mutations in an asexual population. Genetica 102-103, 127–144 (1998). [PubMed] [Google Scholar]
- 18.Johnson T., Gerrish P. J., The fixation probability of a beneficial allele in a population dividing by binary fission. Genetica 115, 283–287 (2002). [DOI] [PubMed] [Google Scholar]
- 19.Yampolsky L. Y., Kondrashov F. A., Kondrashov A. S., Distribution of the strength of selection against amino acid replacements in human proteins. Hum. Mol. Genet. 14, 3191–3201 (2005). [DOI] [PubMed] [Google Scholar]
- 20.Gorlov I. P., Kimmel M., Amos C. I., Strength of the purifying selection against different categories of the point mutations in the coding regions of the human genome. Hum. Mol. Genet. 15, 1143–1150 (2006). [DOI] [PubMed] [Google Scholar]
- 21.Kimura M., The Neutral Theory of Molecular Evolution (Cambridge University Press, Cambridge, UK, 1983). [Google Scholar]
- 22.Poelwijk F. J., Tănase-Nicola S., Kiviet D. J., Tans S. J., Reciprocal sign epistasis is a necessary condition for multi-peaked fitness landscapes. J. Theor. Biol. 272, 141–144 (2011). [DOI] [PubMed] [Google Scholar]
- 23.Eigen M., Selforganization of matter and the evolution of biological macromolecules. Naturwissenschaften 58, 465–523 (1971). [DOI] [PubMed] [Google Scholar]
- 24.Sung W., Ackerman M. S., Miller S. F., Doak T. G., Lynch M., Drift-barrier hypothesis and mutation-rate evolution. Proc. Natl. Acad. Sci. U.S.A. 109, 18488–18492 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Lynch M., et al. , Genetic drift, selection and the evolution of the mutation rate. Nat. Rev. Genet. 17, 704–714 (2016). [DOI] [PubMed] [Google Scholar]
- 26.Krug J., Karl C., Punctuated evolution for the quasispecies model. Physica A 318, 137–143 (2003). [Google Scholar]
- 27.Jain K., Krug J., Evolutionary trajectories in rugged fitness landscapes. J. Stat. Phys. 2005, P04008 (2005). [Google Scholar]
- 28.Zhang Y.-C., Quasispecies evolution of finite populations. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics 55, R381 (1997). [Google Scholar]
- 29.Lynch M., Bürger R., Butcher D., Gabriel W., The mutational meltdown in asexual populations. J. Hered. 84, 339–344 (1993). [DOI] [PubMed] [Google Scholar]
- 30.Bull J. J., Meyers L. A., Lachmann M., Quasispecies made simple. PLOS Comput. Biol. 1, e61 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Bull J. J., Sanjuán R., Wilke C. O., Theory of lethal mutagenesis for viruses. J. Virol. 81, 2930–2939 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Wilke C. O., Quasispecies theory in the context of population genetics. BMC Evol. Biol. 5, 44 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Ram Y., Hadany L., Stress-induced mutagenesis and complex adaptation. Proc. Biol. Sci. 281, 20141025 (2014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.MacLean R. C., Torres-Barceló C., Moxon R., Evaluating evolutionary models of stress-induced mutagenesis in bacteria. Nat. Rev. Genet. 14, 221–227 (2013). [DOI] [PubMed] [Google Scholar]
- 35.Kirschner M., Gerhart J., Evolvability. Proc. Natl. Acad. Sci. U.S.A. 95, 8420–8427 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Koonin E. V., The Logic of Chance: The Nature and Origin of Biological Evolution (FT Press, Upper Saddle River, NJ, 2011). [Google Scholar]
- 37.Lehman J., Stanley K. O., Evolvability is inevitable: Increasing evolvability without the pressure to adapt. PLoS One 8, e62186 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Cuypers T. D., Rutten J. P., Hogeweg P., Evolution of evolvability and phenotypic plasticity in virtual cells. BMC Evol. Biol. 17, 60 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Crother B. I., Murray C. M., Early usage and meaning of evolvability. Ecol. Evol. 9, 3784–3793 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.van Nimwegen E., Crutchfield J. P., Metastable evolutionary dynamics: Crossing fitness barriers or escaping via neutral paths? Bull. Math. Biol. 62, 799–848 (2000). [DOI] [PubMed] [Google Scholar]
- 41.Weissman D. B., Desai M. M., Fisher D. S., Feldman M. W., The rate at which asexual populations cross fitness valleys. Theor. Popul. Biol. 75, 286–300 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Sniegowski P. D., Gerrish P. J., Lenski R. E., Evolution of high mutation rates in experimental populations of E. coli. Nature 387, 703–705 (1997). [DOI] [PubMed] [Google Scholar]
- 43.Elena S. F., Lenski R. E., Evolution experiments with microorganisms: The dynamics and genetic bases of adaptation. Nat. Rev. Genet. 4, 457–469 (2003). [DOI] [PubMed] [Google Scholar]
- 44.Wielgoss S., et al. , Mutation rate dynamics in a bacterial population reflect tension between adaptation and genetic load. Proc. Natl. Acad. Sci. U.S.A. 110, 222–227 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Wiser M. J., Ribeck N., Lenski R. E., Long-term dynamics of adaptation in asexual populations. Science 342, 1364–1367 (2013). [DOI] [PubMed] [Google Scholar]
- 46.Couce A., et al. , Mutator genomes decay, despite sustained fitness gains, in a long-term experiment with bacteria. Proc. Natl. Acad. Sci. U.S.A. 114, E9026–E9035 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Stratton M. R., Campbell P. J., Futreal P. A., The cancer genome. Nature 458, 719–724 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Vogelstein B., et al. , Cancer genome landscapes. Science 339, 1546–1558 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.McFarland C. D., Korolev K. S., Kryukov G. V., Sunyaev S. R., Mirny L. A., Impact of deleterious passenger mutations on cancer progression. Proc. Natl. Acad. Sci. U.S.A. 110, 2910–2915 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.McFarland C. D., Mirny L. A., Korolev K. S., Tug-of-war between driver and passenger mutations in cancer and other adaptive processes. Proc. Natl. Acad. Sci. U.S.A. 111, 15138–15143 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Farber E., The multistep nature of cancer development. Cancer Res. 44, 4217–4223 (1984). [PubMed] [Google Scholar]
- 52.Vogelstein B., Kinzler K. W., The multistep nature of cancer. Trends Genet. 9, 138–141 (1993). [DOI] [PubMed] [Google Scholar]
- 53.Nordling C. O., A new theory on cancer-inducing mechanism. Br. J. Cancer 7, 68–72 (1953). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Armitage P., Doll R., The age distribution of cancer and a multi-stage theory of carcinogenesis. Br. J. Cancer 8, 1–12 (1954). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Szabó P., Scheuring I., Czárán T., Szathmáry E., In silico simulations reveal that replicators with limited dispersal evolve towards higher efficiency and fidelity. Nature 420, 340–343 (2002). [DOI] [PubMed] [Google Scholar]
- 56.Kun A., Santos M., Szathmáry E., Real ribozymes suggest a relaxed error threshold. Nat. Genet. 37, 1008–1011 (2005). [DOI] [PubMed] [Google Scholar]
- 57.Good B. H., Rouzine I. M., Balick D. J., Hallatschek O., Desai M. M., Distribution of fixed beneficial mutations and the rate of adaptation in asexual populations. Proc. Natl. Acad. Sci. U.S.A. 109, 4950–4955 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Neher R. A., Hallatschek O., Genealogies of rapidly adapting populations. Proc. Natl. Acad. Sci. U.S.A. 110, 437–442 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Maddamsetti R., Lenski R. E., Barrick J. E., Adaptation, clonal interference, and frequency-dependent interactions in a long-term evolution experiment with Escherichia coli. Genetics 200, 619–631 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]