Declining CO₂ price paths

Significance

Risk and uncertainty are important in pricing climate damages. Despite a burgeoning literature, attempts to marry insights from asset pricing with climate economics have largely failed to supplement—let alone supplant—decades-old climate–economy models, largely due to their analytic and computational complexity. Here, we introduce a simple, modular framework that identifies core trade-offs, highlights the sensitivity of results to key inputs, and helps pinpoint areas for further work.

Abstract

Pricing greenhouse-gas (GHG) emissions involves making trade-offs between consumption today and unknown damages in the (distant) future. While decision making under risk and uncertainty is the forte of financial economics, important insights from pricing financial assets do not typically inform standard climate–economy models. Here, we introduce EZ-Climate, a simple recursive dynamic asset pricing model that allows for a calibration of the carbon dioxide (${\mathrm{C}\mathrm{O}}_2$) price path based on probabilistic assumptions around climate damages. Atmospheric ${\mathrm{C}\mathrm{O}}_2$ is the “asset” with a negative expected return. The economic model focuses on society’s willingness to substitute consumption across time and across uncertain states of nature, enabled by an Epstein–Zin (EZ) specification that delinks preferences over risk from intertemporal substitution. In contrast to most modeled ${\mathrm{C}\mathrm{O}}_2$ price paths, EZ-Climate suggests a high price today that is expected to decline over time as the “insurance” value of mitigation declines and technological change makes emissions cuts cheaper. Second, higher risk aversion increases both the ${\mathrm{C}\mathrm{O}}_2$ price and the risk premium relative to expected damages. Lastly, our model suggests large costs associated with delays in pricing ${\mathrm{C}\mathrm{O}}_2$ emissions. In our base case, delaying implementation by 1 y leads to annual consumption losses of over 2%, a cost that roughly increases with the square of time per additional year of delay. The model also makes clear how sensitive results are to key inputs.

For over 25 y, the dynamic integrated climate–economy (DICE) model (1–3) has been the standard tool for analyzing CO₂ emissions-reductions pathways, and for good reason. One attraction is its simplicity, turning a “market failure on the greatest scale the world has seen” (4) and “the mother of all externalities” (5) into a model involving fewer than 20 main equations, 3 representing the climate system (6). DICE has spawned many variants (7). It has also helped set the tone for what many consider “optimal” CO₂ price paths. The core trade-off between economic consumption and climate damages leads to relatively low CO₂ prices today rising over time.

DICE and models like it have well-known limitations, including how they represent climate risk and uncertainty (7–15). DICE, for example, is not an optimal-control model, as commonly understood by economists employing modern dynamic economic analysis, even though it lends itself to those extensions (9–12). The underlying structure all but prescribes a rising CO₂ price path over time.

One important limitation is the form of the utility function. Constant relative risk aversion (CRRA) preferences, standard in most climate–economy models (1, 7, 16), assume that economic agents have an equal aversion to variation in consumption across states of nature and over time. Evidence from financial markets suggests that this is not the case (17). The risk premium (RP) of equities over bonds points to a fundamental difference in how much society is willing to pay to substitute consumption risk across states of nature compared to over time (18, 19). Some have explained the discrepancy by allowing for extreme events (20–22), and others have looked to more flexible preferences (23–26) or both (27). Our own preference specification follows Epstein and Zin (EZ) (24, 25).

EZ Preferences

Here, we use EZ preferences and focus on climate uncertainties. We approach climate change as an asset pricing problem with atmospheric CO₂ as the “asset.” The value of an investment in reducing CO₂ emissions depends on the state of nature, represented by its fragility ${\theta }_t$. That, in turn, helps determine the discount rate applied to the damages that would have occurred without the investment.

Our representative agent maximizes a recursive utility $U_t$ based on consumption $c_t$ and expectations $E_t$ over future utility for times $t\in \left\{\mathrm{0,1,2},\dots ,T-1\right\}$ :

$$U_t={\left[\left(1-\beta \right)c_t^{\rho }+\beta {\left(E_t\left[U_{t+1}^{\alpha }\right]\right)}^{\frac{\rho }{\alpha }}\right]}^{\frac{1}{\rho }}.$$ [1]

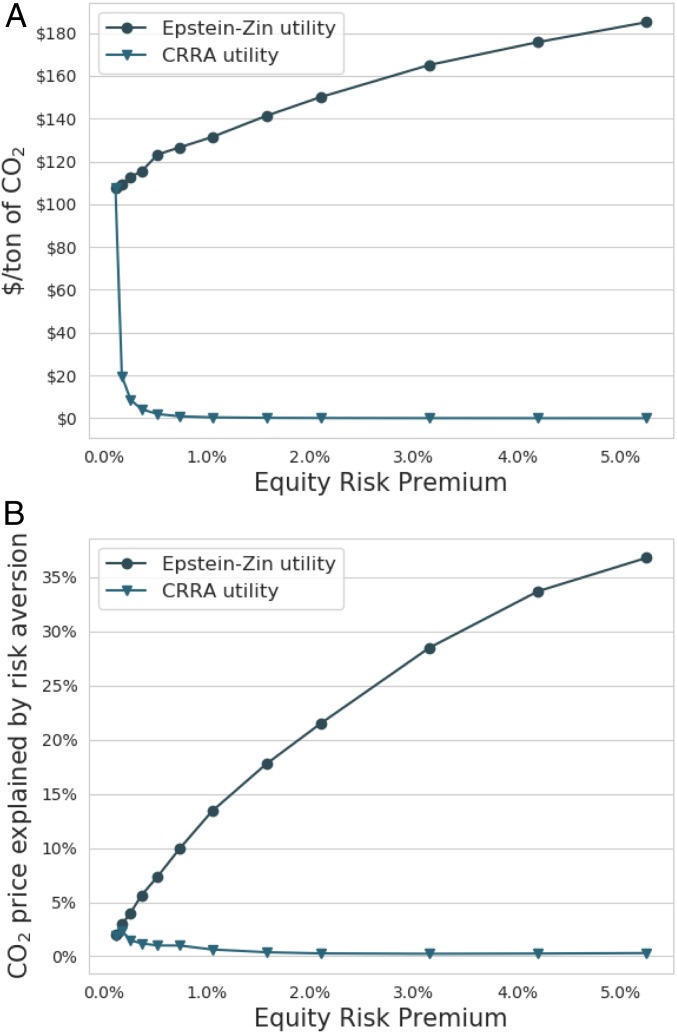
Parameters $\alpha$ and $\rho$ measure the agent’s willingness to substitute consumption across states of nature and across time, respectively. (See Methods for the final-period utility $U_T$ and further derivations.) CRRA preferences are a special case, with $\alpha =\rho$. Unlike with CRRA, Eq. 1 implies that CO₂ prices no longer collapse to zero with increasing risk aversion (RA) and equity risk premia (Fig. 1A). The same goes for the portion of CO₂ prices explained by RA (Fig. 1B).

Fig. 1.

Risk calibration. A shows how using EZ preferences, unlike CRRA, results in increasing 2015 CO₂ prices, in 2015 US$, with increasing RA, translated into the implied equity RP using Weil’s conversion (19), while holding implied market interest rates stable at 3.11%. B shows how the percentage of the 2015 CO₂ price explained by RA, as opposed to expected damages (EDs), increases with equity RP for EZ utility, while decreasing for CRRA (Risk Decomposition).

EZ preferences have since found their way into the climate–economic literature (9–12, 28–35). Some have embedded EZ into DICE (28, 35), and others employ supercomputers to solve (9–12). The complexity typically does not allow for analytic solutions (34). We here follow a simple binomial-tree model with a long history in financial modeling application (36). It is precisely this modeling choice—standard in financial economics but novel to climate–economic applications—that leads to our fundamentally differing CO₂ price paths. Mitigating climate risk provides a hedge, leading to high CO₂ prices early on. As uncertainties decline over time, so do CO₂ prices.

Model

The setting for EZ-Climate is a standard endowment economy (37). In each period, the agent is endowed with a certain amount of the consumption good ${\overline{c}}_t$. However, she is not able to consume the full ${\overline{c}}_t$ for 2 reasons: climate change and climate policy. In periods $t\in \left\{\mathrm{1,2},\dots ,T\right\}$, a portion of ${\overline{c}}_t$ may be lost due to climate-change damages, which are, in turn, a function of cumulative radiative forcing ($CR{F}_t$) up to time $t$ and of fragility ${\theta }_t$: $D_t\left({\text{CRF}}_t,{\theta }_t\right)$. Up to period $T-1$, the agent may elect to spend some of ${\overline{c}}_t$ to reduce her impact on the future climate, ${\kappa }_t$, which, in turn, depends on mitigation $x_t$. The resulting consumption $c_t$, after $D_t$ and ${\kappa }_t$ are taken into account, is given by:

$$c_0={\overline{c}}_0\left(1-{\kappa }_0\left(x_0\right)\right),$$ [2]

$$\begin{array}{l}\hfill c_t={\overline{c}}_t\left(1-{\kappa }_t\left(x_t\right)\right)\left(1-D_t\left(CR{F}_t,{\theta }_t\right)\right),\\ \hfill \text{for}t\in \left\{\mathrm{1,2},\dots ,T-1\right\},\text{and}\end{array}$$ [3]

$$c_T={\overline{c}}_T\left({1-D}_T\left(CR{F}_T,{\theta }_T\right)\right).$$ [4]

$CR{F}_t$ is a function of mitigation, $x_s$, in each period from 0 to $t$, calibrated to a combination of Representative Concentration Pathway (RCP) scenarios (Climate Damages).

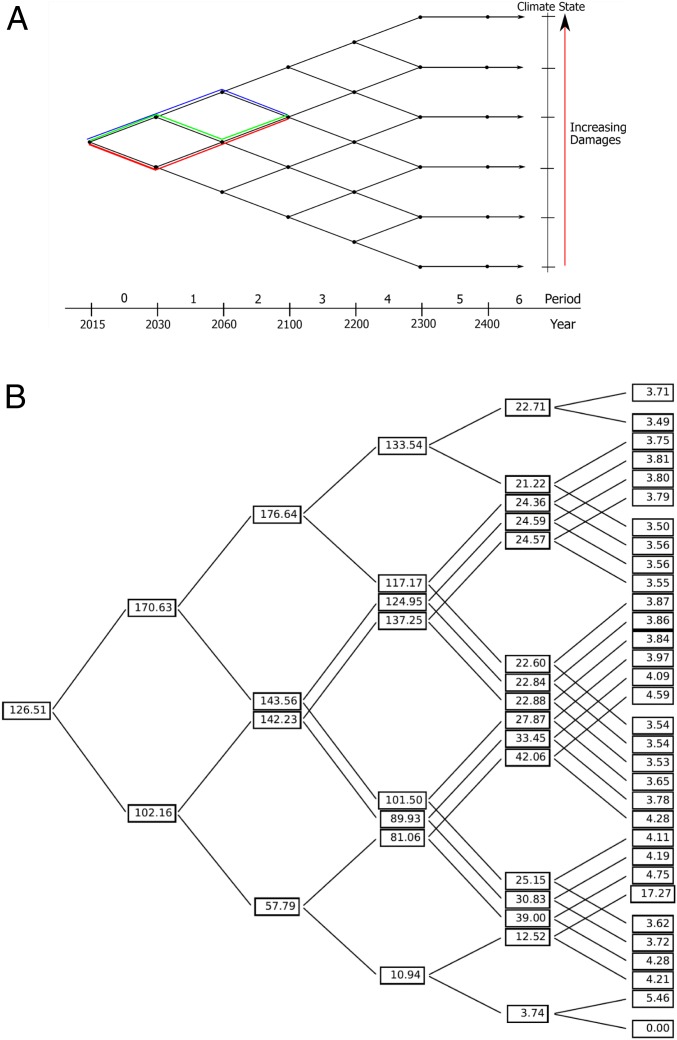
The agent maximizes utility given by Eq. 1 in each of $T$ periods by selecting, at each time and in each state, a level of mitigation $x_t$, creating in essence a “$2^{T+1}-1$”-dimensional optimization problem. Fig. 2A shows our base case, which uses a 7-period tree with decision nodes from 2015 through 2300. At each node, more information about ${\theta }_t$ and the resulting climate damages is revealed, before uncertainty is resolved at the beginning of the penultimate period in 2300. In the “easy” spirit of EZ-Climate, the limited number of decision points makes the solution both tractable and quickly solvable.

Fig. 2.

Model tree structure. A shows a diagram of the binomial tree structure (with probability $p=\frac{1}{2}$) used in solving the model for each state of nature ${\theta }_t$ across time $t\in \left\{\mathrm{1,2},\dots ,T\right\}$ , corresponding to years 2015, 2030, 2060, 2100, 2200, 2300, and final period 2400. Note the “recombining” tree structure, highlighted in the first 2 periods: Damage functions in any particular state are independent of the path taken, but $x_t$ and the resulting $U_t$ are path-dependent. B shows the CO₂ price in the base case ($peakT=6$, $disaster\hspace{0.17em}tail=18$, and $EIS=0.9$).

EZ-Climate provides an accessible, modular framework (7) that is dependent on key economic inputs—chiefly, RA and the elasticity of intertemporal substitution (EIS)—and 2 main climate-related ones: mitigation costs and climate damages. Costs depend primarily on assumptions around backstop technologies (38) and technological change. Damages depend on the full climate–economic chain from economic output to CO₂ emissions, from emissions to concentrations, from concentrations to $CRF$, and from $CRF$ to climate damages lowering economic consumption. While all of these calibrations are important, and uncertainties abound, a key addition is allowing for potentially catastrophic risk in form of climatic tipping points (TPs) (39, 40) (Climate Damages).

Results and Discussion

Fig. 2B shows CO₂ prices for each node of the tree in our base case. The 2015 CO₂ price comes from a single node in the tree. In each subsequent period, the price is set in expectation over all possible states of nature ${\theta }_t$ in that given period. All grouped nodes at a given time have the same ${\theta }_t$ and, thus, the same damage for a given amount of $CRF$. The price itself is path-dependent. Fig. 2B also shows the costs associated with bad ${\theta }_t$ draws in latter periods. Bad news is costly. Bad news late, when it is more difficult to counteract with more active policy, is worse. It is precisely the inability to know upfront when good or bad news arrives that accounts for the insurance value of early mitigation and, thus, the role that the resolution of risk over time plays in the declining CO₂ price.

Declining CO₂ Price.

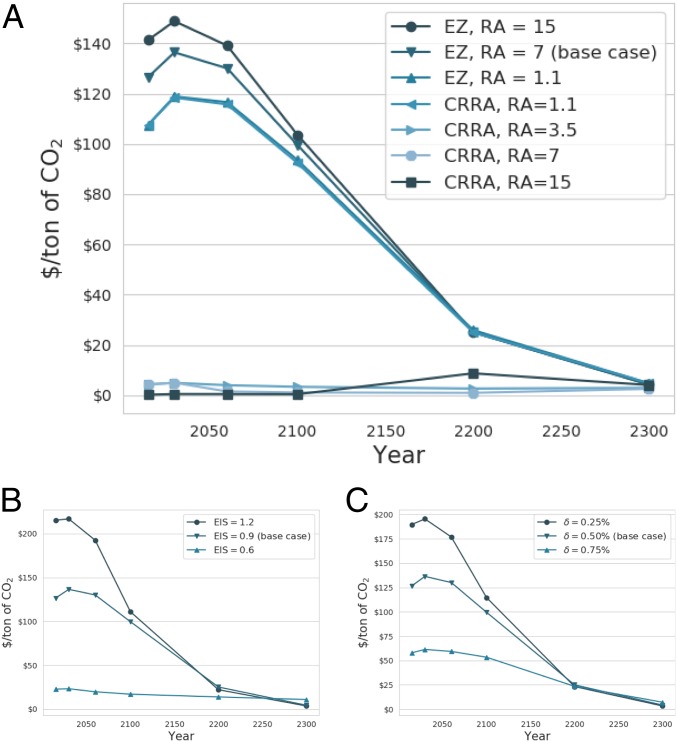
Unlike most modeled CO₂ price paths, ours typically rise briefly before declining over time. One partial explanation is the move from CRRA to EZ preferences. CRRA preferences duplicate the decline only with a $\text{RA}=\frac{10}{9}\sim 1.1$, when EZ collapses to CRRA. For higher RA, consistent with those estimated from models calibrated to financial-market data, early CRRA prices collapse to near zero (Fig. 3A). But going from CRRA to EZ preferences is not the only explanation, implied by the fact that CRRA price paths stay flat over time.

Fig. 3.

Declining CO₂ price paths. A shows how EZ utility here leads to CO₂ prices that start high and decline over time, regardless of assumed RA, a feature mimicked only by unrealistically low $\text{RA}=\frac{10}{9}\sim 1.1$, when EZ and CRRA utilities coincide (Economic Parameters). B and C show the importance of EIS and the rate of pure time preference ($\delta$), respectively. B varies real interest rates from 2.74% (EIS = 1.2) to 3.77% (EIS = 0.6) to keep $\overline{c}=1.5\%$. C fixes EIS at 0.9, while $\delta$ varies from 0.25% to 0.75% (SI Appendix, Figs. S5 and S6).

Others have pointed to reasons for declining CO₂ price paths including producer behavior (41), the need for directed technological change from “dirty” to “clean” sectors (42), or inertia (43). We here find 2 factors driving the declining CO₂ price paths: the resolution of uncertainty, combined with technological progress that makes mitigation significantly cheaper over time.

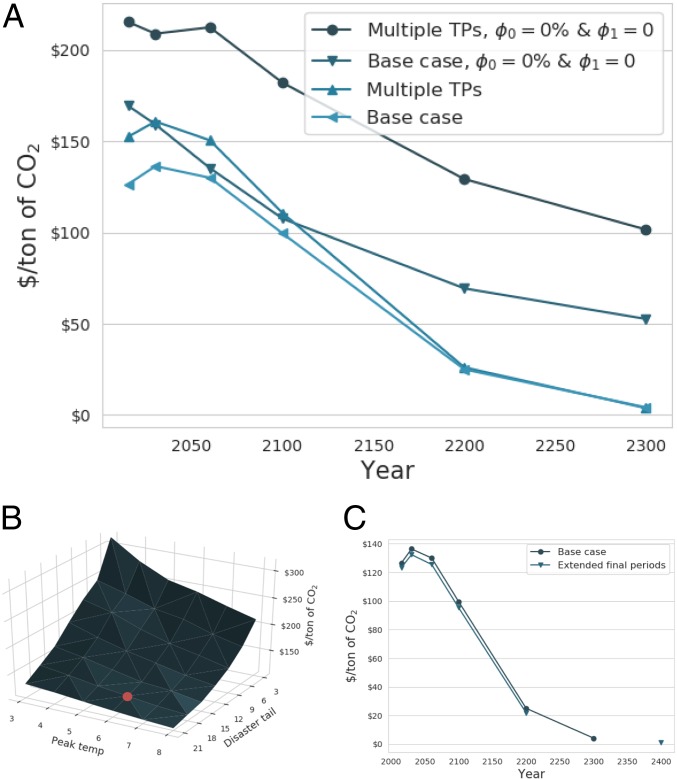
Our base case assumes exogenous technological progress ${\phi }_0=1.5\%$ and endogenous progress ${\phi }_1=0.015$ per year, linked to average mitigation efforts to date (Eq. 19). The combination makes mitigation costs diminishingly small hundreds of years out, helping to drive the declining price paths (Fig. 4A and SI Appendix, Fig. S3).

Fig. 4.

CO₂ price sensitivities. A shows the implications of technological change and TP assumptions. Setting ${\phi }_0=0\%\hspace{0.17em}{\phi }_1=0$ increases early-year and final-period prices, flattening the price path. Multiple TPs act akin to fattening the tail of the damage function, steepening the price path. They also interact with the no-technological-change assumption, increasing final-period prices. B shows that 2015 CO₂ prices depend crucially on “catastrophic” climate risk assumptions, set to $peakT=6^{○}$C and $disaster\hspace{0.17em}tail=18$ in the base case (Climate Damages). C, by contrast, shows the minimal implications of extending the final period from 2300 to 2400 for $t=6$ and 7, respectively, in the base case to 2400 and 2700.

Another reason for declining price paths is the assumed nature of TPs in the base case. Each node has a certain probability of hitting a TP, given by Eq. 22. Once hit, there is no reversing the resulting damages. That structure increases prices in early years, decreasing them later, as it introduces a nonconcavity into the damage function (37). Allowing for multiple TPs exacerbates that result in the base case, as it fattens the tail of the damage function (Fig. 4A). Assuming no technological change, meanwhile, increases final-period prices, more so with multiple TPs.

While the declining CO₂ price path is a persistent feature across model specifications (SI Appendix, Figs. S3, S5, and S6), the absolute CO₂ price in early years depends crucially on a number of calibration choices. Fig. 3 shows the importance of economic parameters, chiefly, EIS and the pure rate of time preference ($\delta$). Fig. 4B shows the sensitivity of the initial CO₂ price to assumptions around “catastrophic” climate risk. Our base case assumes 6 °C for the “peak temperature” ($peakT$) and 18 for the $disaster\hspace{0.17em}tail$ calibrations. While there is seeming convergence around 6 °C as an upper bound for what could conceivably be quantified (see, for example, https://helixclimate.eu/), declaring it equivalent to a “global TP” is at best unduly conservative (11, 15, 40), at worst arbitrary. Much more work is needed to justify any one particular parameter value and, thus, any one CO₂ price (7). Our goal with EZ-Climate is to provide a simple, modular framework to think about climate risks, uncertainties, TPs, and their implications for CO₂ prices.

Social Cost of Delay.

The optimal-control nature of EZ-Climate also allows for a calculation of the social cost of delay in implementing CO₂ prices. Unlike prior efforts (2, 7), we do not look to the CO₂ price for estimating that cost. In fact, doing so can be positively misleading. After constraining the price to $0 in the first period, the price in the second period is lower than in the unconstrained case. The price reflects the marginal benefits of additional emissions reductions, which are now lower. We here instead quantify the cost of delay by constraining mitigation to zero in the first period and asking how much additional consumption would be required during that period in order to bring the utility of the representative agent to the level of the unconstrained solution.

Table 1 shows the annual consumption loss during the constrained first period. For a 10-y delay, the equivalent annual consumption loss over the first constrained period is ∼23%: Each year of delay increases the annual consumption loss over the entire constrained period by ∼2.3%. It also increases the time interval of the loss, thus leading to a slightly more than quadratic rate of increase in the deadweight loss of utility over time. In rough monetary terms, delaying implementation by only 1 y costs society approximately $1 trillion. A 5-y delay creates the equivalent loss of approximately $24 trillion, comparable to a severe global depression. A 10-y delay causes an equivalent loss in the order of $10 trillion per year, approximately $100 trillion in total.

Table 1.

Social cost of delay by first-period length

First-period	Annual consumption impact
length, y	during first period, %
5	11
10	23
15	36

Absolute annual household consumption numbers are around $40 trillion per year.

Conclusion

Our conclusion could mimic that of DICE, introduced over 25 y ago (1), with one crucial difference: Like with DICE, and despite crucial recent advances (7, 35), “it should be emphasized that this analysis has a number of important qualifications,” especially, ironically, “the economic impact of climate change” (1). Unlike DICE, EZ-Climate does not “[abstract] from issues of uncertainty” (1). It embraces them, following a simple binomial-tree framework long used in the finance literature (36). The simple, modular framework also highlights the sensitivity of CO₂ prices to key inputs. There is no single, correct, “optimal” price path. One persistent feature, however, is declining price paths. That puts the focus on near-term action and on the large costs of delay.

Methods

Utility Specification.

Eq. 1 represents a special case of Kreps–Porteus preferences (23), following EZ (24, 25) for $t\in \left\{\mathrm{0,1,2},\dots ,T-1\right\}\hspace{0.17em}$, with $c_t$ given by Eqs. 2–4. In $t=T$ (=2400, in our base-case calibration), the representative agent receives utility from all present discounted consumption from $T$ onward. Consumption grows at a constant rate $r$ for $t\ge T$:

$$c_t=c_T{\left(1+r\right)}^{t-T},$$ [5]

with $c_T$ given by Eq. 4. The resulting final-period utility is:

$$U_T={\left[\frac{1-\beta }{1-\beta {\left(1+r\right)}^{\rho }}\right]}^{\frac{1}{\rho }}{c}_T.$$ [6]

Risk Decomposition.

Fig. 1B shows the split between EDs and the RP in explaining 2015 CO₂ prices (44). To calculate the cost of an additional ton of CO₂ emissions, we sum over all consumption damages, in every state of nature $s$ at every future time $t$, multiplied by the value of an additional unit of consumption for each $s$ and $t$. The 2015 CO₂ price, thus, is:

$${\mathrm{\sum }}_{t=1}^T{\mathrm{\sum }}_{s=1}^{S\left(t\right)}{\pi }_{s,t}{m_{s,t}D}_{s,t}={\mathrm{\sum }}_{t=1}^T{E}_0\left[{\tilde{m}}_t{\tilde{D}}_t\right],$$ [7]

where $S\left(t\right)$ denotes the number of states at time $t$, ${\pi }_{s,t}$ the probability of state $s$ at time $t$, and pricing kernel $m_{s,t}=\left(\frac{\partial U}{\partial c_{s,t}}\right)/\left(\frac{\partial U}{\partial c_0}\right)$. Eq. 7 can be further decomposed into ED and RP:

$$\underset{\text{ED}}{\underbrace{{\mathrm{\sum }}_{t=1}^T{E}_0\left[{\tilde{m}}_t\right]E_0\left[{\tilde{D}}_t\right]}}+\underset{\text{RP}}{\underbrace{{\mathrm{\sum }}_{t=1}^{T}co{v}_0\left[{\tilde{m}}_t,{\tilde{D}}_t\right]}}.$$ [8]

Note that $E_o\left[{\tilde{m}}_t\right]=1/R^f\left(0,t\right)$, where $R^f\left(0,t\right)$ is the payoff, at time $t$, to a $1 investment in a risk-free bond at $t_0$. Alternatively, $E_0\left[{\tilde{m}}_t\right]$ is the risk-free discount factor between today and $t$. ED, thus, is the sum of marginal climate damages, discounted back to the present at the risk-free rate:

$$\text{ED}={\mathrm{\sum }}_{t=1}^T{E}_0\left[{\tilde{D}}_t\right]/R^f\left(0,t\right).$$ [9]

RP then is the difference between the CO₂ price and ED.

Mitigation Costs.

Calibrating the mitigation cost requires specifying a relationship between the marginal cost of emissions reductions, equal to the per-ton tax rate $\tau$, the resulting flow of emissions per year $g\left(\tau \right)$, and the fraction of emissions reduced $x\left(\tau \right)$ .

Many modeling efforts have attempted to estimate the marginal abatement costs (MACs), often as part of integrated assessment models. See, for example, Stanford’s Energy Modeling Forum (https://emf.stanford.edu/). Perhaps the most influential, independent effort comes from McKinsey & Company in an attempt to estimate a bottom-up MAC curve (MACC) (45). McKinsey’s MACCs are, to a large extent, based on bottom-up “engineering” estimates. That makes them an easy target for critique by economists, who often focus on the large abatement opportunities with “negative” costs or the “energy-efficiency gap” (46, 47). We calibrate $\tau$, $g\left(\tau \right)$, and $\left(x\left(\tau \right)\right.$ based on McKinsey’s global MACC effort (48), with one crucial modification: We set $x\left(\tau \right)=0$ for $\tau \le 0$; i.e., we assume no net-negative cost mitigation. SI Appendix, Table S1 shows the resulting modified point estimates, which we fit to a power function for $x\left(\tau \right)$, yielding:

$$x\left(\tau \right)=0.0923{\tau }^{0.414}.$$ [10]

The corresponding inverse function, solving for $\tau$ to achieve $x$, yields the marginal cost of abatement:

$$\tau \left(x\right)=314.32x^{2.413}.$$ [11]

Ultimately, we are interested in the total cost to society $\kappa \left(\tau \right)$ for each particular tax $\tau$. We calculate $\kappa \left(\tau \right)$ using the envelope theorem, assuming the representative agent chooses $g\left(\tau \right)$ so as to maximize consumption $c$ given $\tau$: $\frac{dc\left(\tau \right)}{d\tau }=-g\left(\tau \right)$. Consumption $x$ associated with a particular $\tau$, thus, equals:

$$c\left(\tau \right)=\overline{c}-{\int }_0^{\tau }g\left(s\right)\hspace{0.17em}\text{ds}.$$ [12]

However, Eq. 12 is only correct if the government were to collect $\tau$ and then waste 100% of the proceeds $g\left(\tau \right)\tau$. Here, we assume instead that the proceeds are refunded in lump sum (49). Refunding $g\left(\tau \right)\tau$ and rewriting Eq. 12 yields total mitigation costs of:

$$K\left(\tau \right)={\int }_0^{\tau }g\left(s\right)\hspace{0.17em}ds-g\left(\tau \right)\tau .$$ [13]

The lump-sum refund does not allow for CO₂ tax proceeds to be used to decrease other distortionary taxes, which would make the total costs smaller still (50, 51). Rewriting $g\left(\tau \right)=g_0\left(1-x\left(\tau \right)\right)$, where $g_0$ is the emissions baseline, we can rewrite Eq. 13 as:

$$K\left(\tau \right)=g_0\left[\tau x\left(\tau \right)-{\int }_0^{\tau }x\left(s\right)ds\right].$$ [14]

Substituting Eqs. 10 and 11 into Eq. 14 and dividing by current aggregate consumption yields the societal cost of a given level of mitigation as a percentage of initial consumption $c_0$:

$$\kappa \left(x\right)=\left(g_{0}92.08/C_0\right)x^{3.413}.$$ [15]

Our base-case calibration assumes $g_0=$ 52 billion tons of CO₂-equivalent emissions and $c_0=$ $31 trillion/year representing current 2015 global consumption in 2015 US$. Eq. 15 assumes no technological progress and no backstop technology.

Backstop Technology.

We also allow for a backstop technology in form of CO₂ removal (38, 52) to become available at cost ${\tau }^{*}$ at $x_0$ and to be used exclusively for MACs $\ge \tilde{\tau }$. The MACC including a backstop follows:

$$B\left(x\right)=\tilde{\tau }-{\left(\frac{k}{x}\right)}^{\frac{1}{b}}.$$ [16]

We calibrate Eq. 16 to set $B\left(x_0\right)={\tau }^{*}$, and we impose a smooth-pasting condition at $x_0$, resulting in:

$$k=x_0{\left(\tilde{\tau }-{\tau }^{*}\right)}^{\frac{\tilde{\tau }-{\tau }^{*}}{\left(\alpha -1\right){\tau }^{*}}}.$$ [17]

Our base case assumes ${\tau }^{*}=\$\mathrm{2,000}$ and $\tilde{\tau }=\$\mathrm{2,500}$ in 2015 dollars. Under the most aggressive backstop scenario presented in Results and Discussion, we assume ${\tau }^{*}=\$300$ and $\tilde{\tau }=\$350$. SI Appendix, Fig. S1 shows the resulting 2015 $\tau \left(x\right)$.

Technological Progress.

SI Appendix, Fig. S1 is calibrated to $t=0$. In subsequent periods, we allow the MACC to decrease at a rate determined by a set of technological change parameters: a constant component ${\phi }_0$ and an endogenous component linked to mitigation efforts to date ${\phi }_1{X}_t$, where $X_t$ is the average mitigation up to time $t$ defined by:

$$X_t={\mathrm{\sum }}_{s=0}^t{g}_s{x}_s/{\mathrm{\sum }}_{s=0}^t{g}_s.$$ [18]

Mitigation costs at time $t$ are:

$${\kappa }_t\left(x\right)=\kappa \left(x\right){\left[1-{\phi }_0-{\phi }_1{X}_t\right]}^t.$$ [19]

This functional form allows for easy calibration. For example, if ${\phi }_0=0.005$ and ${\phi }_1=0.01$, and with average mitigation $X_t=50\%$, ${\kappa }_t\left(x\right)$ decreases at a rate of 1% per year.

SI Appendix, Fig. S3 shows the implications of both backstop technology and technological progress on the CO₂ price.

Climate Damages.

We derive $D_t\left(CR{F}_t,{\theta }_t\right)$ in 2 steps. Damages are a function of temperature changes $\mathrm{\Delta }T$, which, in turn, are a function of $CRF$. We calibrate $\mathrm{\Delta }T$ over time based on the International Energy Agency’s (IEA’s) projections for $\mathrm{\Delta }{T}_{100}$ using its “new policies scenario” (53), equating the values with $t=100$. We fit a displaced gamma distribution (54) around the IEA’s 2100 greenhouse gas (GHG) concentration projections for 450, 650, and 1,000 ppm. SI Appendix, Table S2 shows the calibration results. We translate $\mathrm{\Delta }{T}_{100}$ into $\mathrm{\Delta }{T}_t$ for $t=0$ (year 2015) through $t=385$ (year 2400) using:

$$\mathrm{\Delta }{T}_t=2\hspace{0.17em}\mathrm{\Delta }{T}_{100}\left[1-{0.5}^{\frac{t}{100}}\right].$$ [20]

SI Appendix, Fig. S2 shows the results for $\mathrm{\Delta }{T}_t$ based on $\mathrm{\Delta }{T}_{100}$ values. We then fit a log-normal distribution for equilibrium climate sensitivity (15, 55) around $\mathrm{\Delta }{T}_{100}$ to generate distributions for $\mathrm{\Delta }{T}_t$ based on emissions-reduction pathways $x_t$. One important possible extension is around timing, further probing our assumption of equating effects at $\mathrm{\Delta }{T}_{100}$ with climate sensitivity (56).

We calibrate damages $D_t$ based on $\mathrm{\Delta }T$ considering 2 multiplicative components: a noncatastrophic loss function and a catastrophic hazard function (32). The noncatastrophic component is in the form of a displaced gamma distribution (54), resulting in the loss function:

$$L\left(\mathrm{\Delta }{T}_t\right)=e^{-13.97\gamma {\mathrm{\Delta }{T}_t}^2}.$$ [21]

Parameter $\gamma$ is drawn from a displaced gamma distribution with its 3 parameters $a=4.5$, d = 21,341, and $p=-0.0000746$. That calibration, much like other econometrically based estimates extrapolating from past experience (57), all but rules out “catastrophic” damages and so-called climatic TPs or “tipping elements” (39, 40).

We augment this calibration with a “catastrophic” component, assuming a particular probability of hitting a climatic TP, $\text{Prob}\left(TP\right)$, in any given period, if temperature changes cross a $peakT$ threshold:

$$Prob\left(TP\right)={1-\left(1-{\left[\frac{\mathrm{\Delta }T\left(t\right)}{max\left[\mathrm{\Delta }T\left(t\right),peakT\right]}\right]}^2\right)}^{\frac{period}{30}}.$$ [22]

In the base-case calibration, we set $peakT=6^{○}C$ (Fig. 3B). While ad hoc, the number is, if anything, unduly conservative (15, 39, 40, 55). SI Appendix, Fig. S4A shows the resulting probabilities for a 30-y period. Conditional on hitting a TP at time $t^{*}$, the level of consumption for each subsequent $t\ge t^{*}$ is reduced by the factor $e^{-TPdamage}$, where $TPdamage$ is drawn from a gamma distribution with parameters $\alpha =1$ and $\beta =disaster\hspace{0.17em}tail$. SI Appendix, Fig. S4B shows the resulting probability of economic damages exceeding a particular percentage of total output.

We then generate distributions for $D_t\left(CR{F}_t,{\theta }_t\right)$ for each period for each of 3 maximum GHG concentration levels—450, 650, and 1,000 ppm—based on 6 million draws each. These 3 scenarios correspond roughly to constant mitigation of slightly over 90% for 450 ppm, almost 60% for 650 ppm, and the IEA’s “new policies scenario” (53) for 1,000 ppm. The mapping happens via $CRF$, interpolating and extrapolating across RCP scenarios (58). We fit a log-function, estimating radiative forcing based on GHG emissions in any 10-y interval as: $5.351\hspace{0.17em}\left[\log \left(\text{GHG}\right)-log\left(278\right)\right]$. Carbon absorption in any 10-y interval is given by $0.94835{|GHG-\left(285.6268+0.88414\mathrm{\sum }absorption\right)|}^{0.741547}$. We then interpolate between the 3 GHG levels to find a smooth damage function for any particular level of $CR{F}_t$. We assume a linear interpolation of damages between 650 and 1,000 ppm and a quadratic interpolation between 450 and 650 ppm, including a smooth pasting condition at 650 ppm. Below 450 ppm, we assume that climate damages exponentially decay toward zero, setting $S=dp/\left(l\ln \left(0.5\right)\right)$, where $d$ is the derivative of the quadratic damage interpolation function at 450 ppm and $p=0.91667$ is the average mitigation in the 450 ppm simulation, with $l$ as damage levels (SI Appendix, Fig. S4C).

The representative agent knows the distribution of possible final states ${\theta }_T$. She does not know ${\theta }_t$ for $t<T$. In line with the recombining tree structure (36), climate damages are the probability-weighted average of the interpolated damage function over all final climate states reachable from any one node:

$$D_t\left({\text{CRF}}_{t,}{\theta }_t\right)=\mathrm{\sum }_{{\theta }_T}Pr\left({\theta }_T|{\theta }_t\right)D_t\left({\text{CRF}}_{t,}{\theta }_T\right).$$ [23]

Introducing CO₂ removal (38, 52) (Backstop Technology), combined with stochastic climate states ${\theta }_t$, creates the possibility of GHG concentrations falling below preindustrial levels of 280 ppm. While we know of no analysis that estimates economic damages below 280 ppm, there clearly are costs, much like going (well) above 280 ppm. We introduce a penalty function of the form:

$$f\left(x\right)\hspace{0.17em}={\left[1+e^{\text{k}\left(x-m\right)}\right]}^{-1}.$$ [24]

We arbitrarily set $m=200$ as the GHG level resulting in half the total penalty. Scalar $k=0.05$ ensures a smooth penalty function. The combination ensures that $f\left(280\right)$ is almost zero, while still achieving a smooth surface. We further restrict $D_t\ge 0$ and $x_t\ge 0$.

Economic Parameters.

Fig. 3A shows the CO₂ price sensitivity to RA. With EZ, the CO₂ declines regardless of RA. We choose RA = 7 in our base-case calibration, a value roughly in line with attitudes toward large income risk across wealthy countries (59): RA in the United States alone is often higher ($>8$), while RA in European welfare states can be as low as 3. Similar patterns as those displayed in Fig. 3A (and in Fig. 4B for climate damage parameters) hold for mitigation cost parameters (SI Appendix, Fig. S3) and an exhaustive list of other economic parameters. The most important of these parameters appear to be the EIS (Fig. 3B and SI Appendix, Fig. S5) and the pure rate of time preference $\delta =\left(1-\beta \right)/\beta$ from Eq. 1 (Fig. 3C and SI Appendix, Fig. S6).

Our base case assumes an economic growth rate $\overline{c}=1.5$ with the rate itself unaffected by climate change, an important assumption to probe in future work (60, 61). SI Appendix, Fig. S5A shows that varying it, while keeping EIS = 0.9, has little influence on prices. SI Appendix, Fig. S5 B and C, however, shows the large influence of EIS, regardless of assumed $\overline{c}$. Note that EIS calibrations have changed widely over time, dependent on the type of risk modeled (62, 63). Modern comparable estimates range as high as 1.5 in a model with EZ preferences and consumption shocks (64), with significant implications for CO₂ prices in early years. We choose a lower EIS = 0.9 for our base case, in part because the only shocks to consumption in our model stem from climate risk. Crucially, our model only captures societal risk. Epstein himself, writing with 2 coauthors, has since offered a potent critique of EZ preferences as applied to individual preferences (65).