Abstract
Purpose:
Accurate tumor segmentation is a requirement for magnetic resonance (MR)-based radiotherapy. Lack of large expert annotated MR datasets makes training deep learning models difficult. Therefore, a cross-modality (MR-CT) deep learning segmentation approach that augments training data using pseudo MR images produced by transforming expert-segmented CT images was developed.
Methods:
Eighty one T2-weighted MRI scans from 28 patients with non-small cell lung cancers (9 with pre-treatment and weekly MRI and the remainder with pre-treatment MRI scans) were analyzed. Cross-modality prior encoding the transformation of CT to pseudo MR images resembling T2w MRI was learned as a generative adversarial deep learning model. This model augmented training data arising from 6 expert-segmented T2w MR patient scans with 377 pseudo MRI from non-small cell lung cancer CT patient scans with obtained from the Cancer Imaging Archive. This method was benchmarked against shallow learning using random forest, standard data augmentation and three state-of-the art adversarial learning-based cross-modality data (pseudo MR) augmentation methods. Segmentation accuracy was computed using Dice similarity coefficient (DSC), Hausdorff distance metrics, and volume ratio.
Results:
The proposed approach produced the lowest statistical variability in the intensity distribution between pseudo and T2w MR images measured as Kullback-Leibler divergence of 0.069. This method produced the highest segmentation accuracy with a DSC of (0.75 ± 0.12) and the lowest Hausdorff distance of (9.36 mm ± 6.00mm) on the test dataset using a U-Net structure. This approach produced highly similar estimations of tumor growth as an expert (P = 0.37).
Conclusions:
A novel deep learning MR segmentation was developed that overcomes the limitation of learning robust models from small datasets by leveraging learned cross-modality information using a model that explicitly incorporates knowledge of tumors in modality translation to augment segmentation training. The results show the feasibility of the approach and the corresponding improvement over the state-of-the-art methods.
Keywords: Generative adversarial networks, data augmentation, cross-modality learning, tumor segmentation, magnetic resonance imaging
1. INTRODUCTION
High-dose radiation therapy that is delivered over a few fractions is now a standard of care for lung tumors. The ability to accurately target tumors will enable clinicians to escalate the dose delivered to tumors while minimizing the dose delivered to normal structures. Tumor delineation remains the weakest link in achieving highly accurate precision radiation treatments using computed tomography (CT) as a treatment planning modality [1, 2]. The superior soft tissue contrast of magnetic resonance (MR) images facilitates better visualization of tumor and adjacent normal tissues, especially for those cancers located close to the mediastinum. Such improved visualization makes MR an attractive modality for radiation therapy [3]. Therefore, fast and accurate tumor segmentation on magnetic resonance imaging (MRI) could help to deliver high-dose radiation while reducing treatment complications to normal structures.
Deep convolutional network-based learning methods are the best-known techniques for segmentation and have been expected to achieve human expert-level performance in image analysis applications in radiation oncology [4]. However, such methods require a tremendous amount of data to train models that are composed of a very large number of parameters. Because MRI is not the standard of care for thoracic imaging, it is difficult to obtain enough MR image sets with expert delineations to train a deep learning method. Deep learning with a large number of MRI for segmenting lung tumors is difficult due to (i) lack of sufficient number of training data as MRI is not standard of care for lung imaging, and (ii) lack of sufficient number of expert delineated contours required for training.
The goal of this work is to compute a robust deep learning model for segmenting tumors from MRI despite lacking sufficiently large expert-segmented MRIs (N > 100 cases) for training.
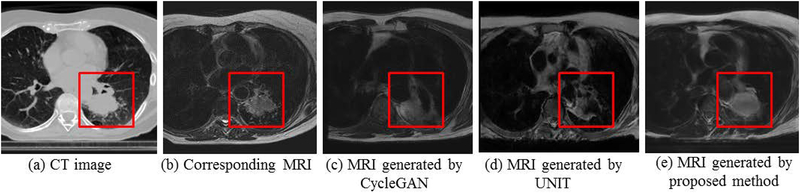
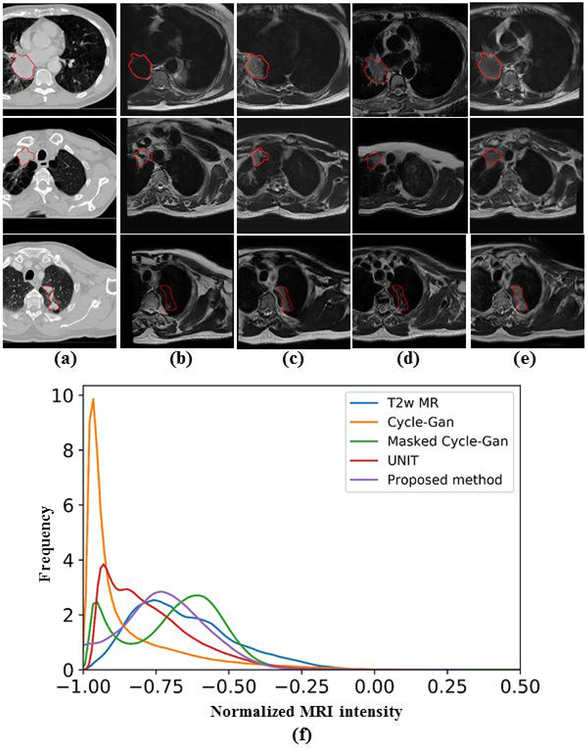
This work addresses the challenge of learning from small expert-segmented MR datasets by developing and testing a novel cross-modality deep domain adaptation approach for data augmentation. Our approach employs a cross-modality adaptation model encoding the transformation of CT into an image resembling MRI (called pseudo MR) to augment training a deep learning segmentation network with few expert-segmented T2w MR datasets. This cross-modality adaptation model is learned as a deep generative adversarial network (GAN) [5, 6] and transforms expert-segmented CT into pseudo MR images with expert segmentations. The pseudo MR images resemble real MR by mimicking the statistical intensity variations. To overcome the issues of the existing methods, which cannot accurately model the anatomical characteristics of atypical structures, including tumors [7], a tumor-attention loss that regularizes the GAN model and produces pseudo MR with well-preserved tumor structures is introduced. Figure 1 shows example pseudo MR images generated from a CT image using the most recent cross-modality adaptation method called the UNsupervised Image-to-Image Translation (UNIT)[8], the CycleGAN[9], and the proposed approach. The corresponding T2w MRI for the CT image acquired within a week is also shown alongside for comparison.
Figure 1.
Pseudo MR image synthesized from a representative (a) CT image using (c) CycleGAN [9] (d) UNIT[8] and (e) proposed method. The corresponding T2w MRI scan for (A) is shown in (b).
This paper is a significant extension of our work in [10] that introduced the tumor-aware loss to use pseudo MRI from CT for MRI segmentation. Extensions include, (a) application of the proposed approach on two additional segmentation networks, the residual fully convolutional networks (Residual-FCN) [11] and dense fully convolutional networks (Dense-FCN) [12], (b) comparison to the more recent image translation approach, called, the unsupervised image to image translation (UNIT) [8], (c) evaluation of longitudinal tumor response monitoring on a subset of patients who had serial weekly imaging during treatment, and finally, (d) benchmarking experiment against a shallow random forest classifier with fully connected random field based tumor segmentation on MRI for assessing performance when learning from a small dataset.
2. MATERIALS AND METHODS
2.1. Patient and image characteristics
A total of 81 T2-weighted (T2W) MRIs from 28 patients enrolled in a prospective IRB-approved study with non-small lung cancer (NSCLC) scanned on a 3T Philips Ingenia scanner (Medical Systems, Best, Netherlands) before and every week during conventional fractionated external beam radiotherapy of 60 Gy were analyzed. Nine out of the 28 patients underwent weekly MRI scans during treatment for up to seven MRI scans. The tumor sizes ranged from 0.28cc to 264.37 cc with average of 50.87 ±55.89 cc. Respiratory triggered two-dimensional (WD) axial T2W turbo spin-echo sequence MRIs were acquired using a 16-element phased array anterior coil and a 44-element posterior coil and the following scan parameters: TR/TE = 3000–6000/120 ms, slice thickness = 2.5 mm and in-plane resolution of 1.1 × 0.97 mm2 flip angle = 90°, number of slices = 43, number of signal averages = 2, and field of view = 300 × 222 × 150 mm3. Radiation oncologist delineated tumor contours served as ground truth. In addition, CT images with expert delineated contours from an unrelated cohort of 377 patients with NSCLC [13] available from The Cancer Imaging Archive (TCIA) [14] were used for training.
2.2. Approach overview
The notations used in this work are described in Table 1.
Table 1:
List of notations
| Notation | Description |
|---|---|
| {XCT,yCT} | CT images and expert segmentations |
| {XMR,yMR} | MR images and expert segmentations |
| pMR | pseudo MR image |
| pCT | pseudo CT image |
| GCT→MR | Generator for producing pMR images |
| GMR->CT | Generator for producing pCT images |
| DCT→MR | Discriminator to distinguish pMR from real T2w MR images |
| DMR→CT | Discriminator to distinguish pCT from real CT images |
| Total adversarial loss, adversarial loss for pMRI and for pCT | |
| Total cycle loss, cycle loss for pMR and pCT images | |
| Tumor shape loss | |
| Tumor location loss |
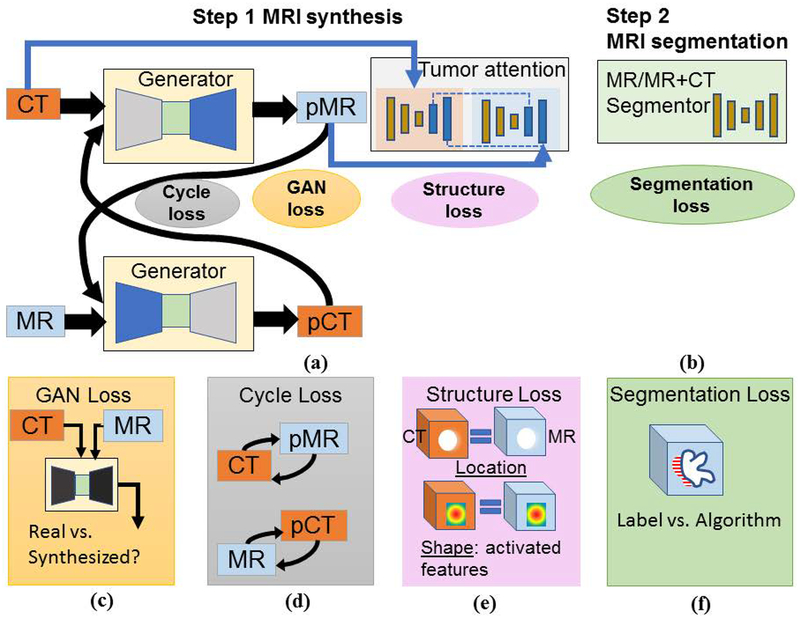
A two-step approach, as shown in Figure 2, consisting of (a) Step 1: CT to pseudo MR expert-segmented dataset transformation, and (b) Step 2: MR segmentation combining expert-segmented T2W MRI with pseudo MRI produced from Step 1 was employed. Pseudo MR image synthesis from CT was accomplished through cross-modality domain adaption (Figure 1a) using expert-segmented CTs with unrelated T2w MR images without any expert annotation. Pseudo MR generation is constrained by using two simultaneously trained GANs (transforming CT into MR, and MR into CT). The MR segmentation network in Step 2 uses the translated pseudo MRI with few real T2w MRI for training. Figure 1(c–e) depicts the losses used for pseudo MR synthesis whereas Figure 1f corresponds to the segmentation loss.
Figure 2.
Approach overview. (a) Pseudo MR synthesis, (b) MR segmentation training using pseudo MR with T2w MR. Visual description of losses used in training the networks in (a) and (b), namely, (c) GAN or adversarial loss, (d) cycle or cycle consistency loss, (e) tumor-attention loss enforced using structure and shape loss, and (f) segmentation loss computed using Dice overlap coefficient.
2.3. Cross-modality augmented deep learning segmentation:
2.3.1. Image pre-processing:
Prior to analysis using the deep networks, all T2W MR images were standardized to remove patient-dependent signal intensity variations using the method in [15]. The CT HU and MRI intensity values were clipped to (−1000, 500) and (0,667), respectively to force the networks to model the intensity range encompassing thoracic anatomy. The resulting clipped images were normalized to the range [−1,1] to ensure numerical stability in the deep networks that employ tanh functions[6].
2.3.2. Step 1: Unsupervised Cross-modality prior (MR-CT) for image translation learning and pseudo MR generation:
The first step in the approach is to learn a cross-modality prior to produce pseudo MR from CT scans in unsupervised way. Unsupervised here refers to learning from CT and MR scans that were acquired from unrelated set of patients, where corresponding images from the two modalities are unavailable. The cross-modality prior is learned as a generational adversarial network (GAN) model [5], which extracts a model of the anatomical characteristics of tissues in MR and CT using unlabeled MRI and expert-segmented CT scans.
Two GAN networks are trained simultaneously to generate pseudo MRI and pseudo CT from CT and MRI, respectively. Each GAN is composed of a generator and a discriminator that work together in a minmax fashion, whereby the generator learns to produce images that confound the discriminator’s classification. The discriminator trains to correctly distinguish between real and synthesized images. This loss is called the adversarial loss Ladv (Figure 1[c]) and is computed as a sum of losses for generating pseudo MRI and pseudo CT as: , shown in (eq 1) and (2).
| (1) |
| (2) |
Cycle loss, Lcyc introduced in [9] was used to soften the requirement for corresponding (e.g. patients) and perfectly aligned source (e.g. CT) and target (e.g. MRI) modalities for training, thereby, allowing unsupervised cross-modality adaptation learning. The cycle consistency loss also prevents the mode collapse endemic to generational adversarial networks[9]. Lcyc forces the networks to preserve spatial correspondences between the pseudo and original modalities (see Figure 1 (d)) and is computed as, for synthesizing pseudo MR and pseudo CT images, as shown in (eq 3).
| (3) |
Where and are the generated pseudo CT and pseudo MRI from generator GMRI→CT and GCT→MRI, respectively. Note that pseudo CTs are simply a by-product of generating the pseudo MR and are generated to add additional regularization in synthesizing pseudo MR images. The network used for implementing the adversarial and the cycle loss uses a standard CycleGAN architecture and consists of a pair of networks with encoders (implemented as a series of stride-2 convolutions for sub-sampling) and decoders (two fractionally strided convolutions) followed by tanh activation for synthesizing the images (see Figure 3).
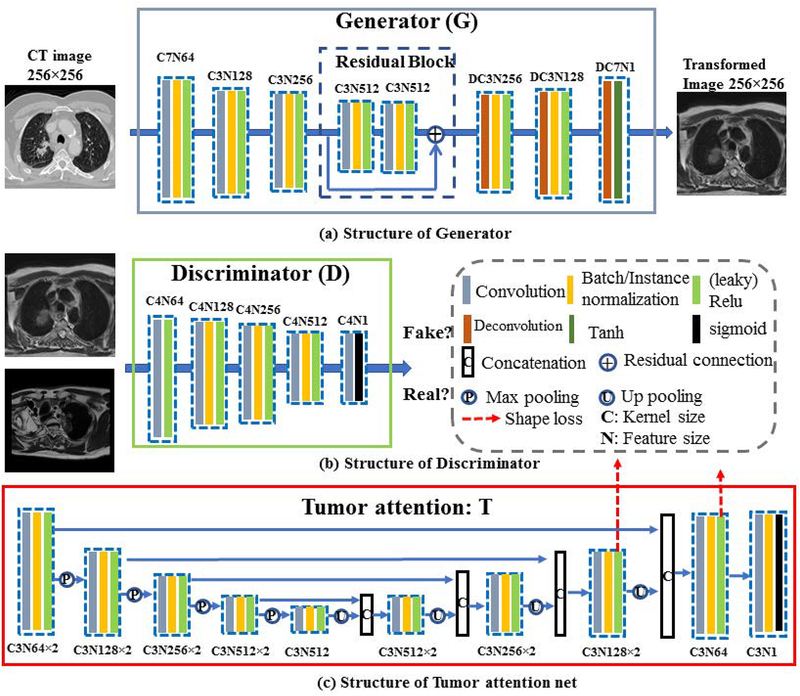
Figure 3.
Network structure of the generator, discriminator and tumor attention net. The convolution the kernels size, the number of features are indicated as C and N. For instance, C3N512 denotes a convolution with kernel size of 3×3 and feature size of 512.
2.3.2. Image translation networks - Generator structure
The generator architectures were adopted from DCGAN [6], which has been proven to result in stable and faster training of the GANs and avoids issues of mode collapse. Specifically, the generators consist of two stride-2 convolutions[6], 9 residual blocks[11] and two fractionally strided convolutions with half strides. As done in DCGAN[6], we used Rectified Linear Units (ReLU) to stabilize the generator network training. Also following the CycleGAN[9], instance normalization[16] was used in all except the last layer, which has a tanh activation for image generation. The instance normalization was used to yield stable training performance and faster convergence as shown in the CycleGAN method. Details of the structure is shown in Figure 3 (a).
2.3.3. Image translation networks - Discriminator structure
The discriminator was implemented using the 70×70 patchGAN, as proposed in pix2pix method[17]. PatchGAN has the benefit that several overlapping 70×70 image patches can be analyzed to compute the synthesis error instead of using a single image. This in turn improves training performance by allowing to back propagate larger errors than is possible when computed by averaging over an entire image. We used leaky ReLU instead of ReLU as proposed in DCGAN[6], and batch normalization [18] in all except the first and last layer to stabilize discriminator network training. Details of the structure is shown in Figure 3 (b).
2.3.4. Image translation networks - Tumor attention loss and network
Adversarial and cycle consistency losses enable a network to only learn transformation of global characteristics as a result of which structures with lots of inter-patient variations such as tumors are lost upon transformation from CT to pseudo MR images. This problem is addressed by introducing a structure-specific, tumor attention loss, Ltumor.
The tumor attention loss was implemented using a pair of 2D U-Nets that were composed of 4 convolutional and 4 deconvolutional layers with skip connections. Batch normalization was added after each convolution to speed up convergence. The two U-Nets were trained to produce a coarse tumor segmentation using the pseudo MR and the corresponding real CT images. The features from the two networks were aligned (or matched) in the last two layers (indicated by the dotted-red arrow in Figure 3(C)). The features from the last two layers were chosen as they contain the most information related to the segmentation of the tumor, such that those features that are most predictive of the tumor will be activated in these layers. Feature alignment is used to force the networks to produce highly similar segmentations. Hence, this loss is called the shape loss (Figure 3c). Feature alignment then induces an indirect loss in to the cross-modality network when the tumors differ in location and shape in the pseudo MR from the original CT images. The details of this network structure and the feature alignment is shown in Figure 3 (c).
The tumor attention loss is composed of tumor shape loss, (eq (4)) and tumor location loss, (eq (5)). The tumor shape loss minimizes the differences in the feature map activations (through Euclidean distances) from the penultimate network layer whereas the tumor location loss forces the two networks to produce identical tumor segmentations (through DSC).
| (4) |
| (5) |
where C, W and H are the feature channel, width and height of the feature.
The total loss is computed as:
| (6) |
where λcyc, λshape and λloc are the weighting coefficients for each loss. The computed losses are back-propagated to update the weights of the networks to produce a pseudo MRI and pseudo CT from the two networks. The algorithm for pseudo MR generation is shown in Algorithm 1.

2.4. Step 2: MRI tumor segmentation
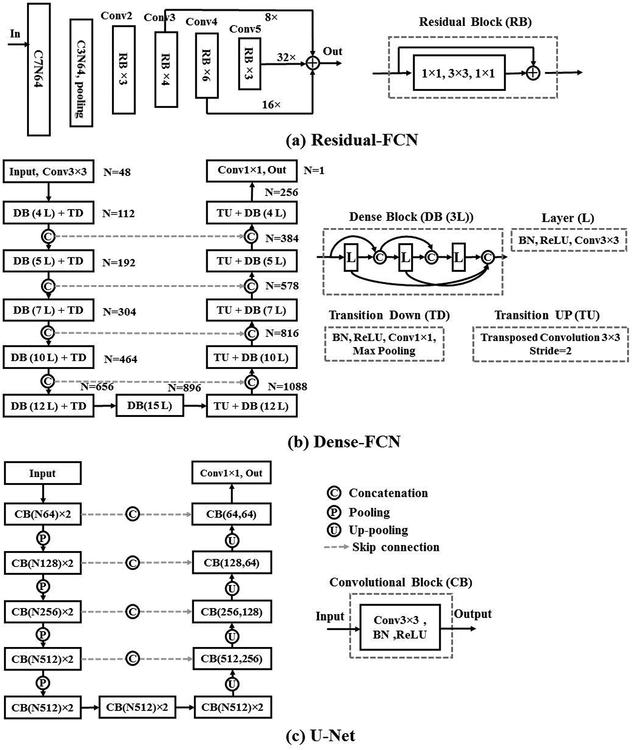
The pseudo MRI dataset, produced from Step 1, is combined with the few available expert-segmented T2W MRI scans (N = 6) to train a MRI tumor segmentation network. We evaluated the data augmentation strategy for training three different segmentation networks, Residual-FCN[11, 19], Dense-FCN[12] and U-Net[20] to assess whether the proposed data augmentation method improves performance across multiple networks (Figure 4). The networks are described below.
Figure 4.
The schematic of segmentation architectures, consisting of (A) Residual FCN, (B) Dense-FCN and (c) U-Net. The convolutional kernel size and the number of features are indicated as C and N.
Residual-FCN
Our implementation of Residual-FCN, differs from the original implementation[19] in that used the ResNet-50[11] as a backbone structure instead of the FCN-8s structure[19] for faster training. A schematic of the network structure is shown in Figure 4 (a). The input image was first processed by 7×7 and then 3×3 convolution filters. The resulting number of features are reduced through subsampling through max pooling. These features are then processed by conv2_3 conv3_4, conv4_6 and conv5_3 convolutional layers with residual blocks. The features from the second (conv3_4), third (conv4_6), and fourth (conv5_3) blocks are up-sampled by a scale fact of 8, 16 and 32, similar to the FCN-8s implementation. Those features are summed and passed on to the final output layer that uses sigmoid activation. All convolutional layers are followed by batch normalization. This network has 23.5M parameters.
Dense-FCN
The Dense-FCN[12] is composed of Dense Blocks (DB)[21], which successively concatenates feature maps computed from previous layers, thereby increasing the size of the feature maps. A dense block is produced by iterative concatenation of previous layer feature maps within that block, where a layer is composed of a Batch Normalization, ReLU and 3×3 convolution operation, shown in Figure 4 (b). Such a connection also enables the network to implement an implicit dense supervision to better train the features required for the analysis. Transition Down (TD) and Transition UP (TU) are used for down-sampling and up-sampling the feature size, respectively, where TD is composed of Batch Normalization, ReLU, 1×1 convolution, 2×2 max-pooling while TU is composed of 3×3 transposed convolution. We use the Dense103 layer structure[12], that uses dense blocks with 4,5,7,10 and 12 layers for feature concatenation and 5 TD for feature down-sampling and 5 TU for feature up-sampling, as shown in Figure 4 (b), and resulting in 9.3M parameters. The last layer feature with a size of 256 is converted to the size of 1 by a convolution 1×1 followed by a sigmoid function.
U-Net
The U-Net[20] is composed of series of convolutional blocks, with each block consisting of convolution, batch normalization and ReLU activation. Skip connections are implemented to concatenate high-level and lower level features. Max-pooling layers and up-pooling layers are used to down-sample and up-sample feature resolution size. We use 4 max-pooling and 4 up-pooling in the implemented U-Net structure, as shown in Figure 4 (c), which results in 17.2M parameters. The last layer of U-Net contains 64 channels and is converted to 1 channel for prediction by convolution kernel size of 1×1.
2.5. Implementation and training
All networks were trained using 2D image patches of size 256 × 256 pixels computed from image regions enclosing the tumors. Cross-modality synthesis networks, including the CycleGAN[9], masked CycleGAN[22], the UNIT networks[8], and tumor-aware CycleGAN (our proposed method) were all trained using 32000 CT image patches from 377 patients (scans), and 9696 unlabeled T2W MR image patches from 42 longitudinal scans of 6 patients, obtained by standard data augmentation techniques[23], including rotation, stretching, and using different regions of interests containing tumors and normal structures. Segmentation training was performed using 1536 MR images obtained from pre-treatment MRI from 6 consecutive patients and 32000 synthesized MR images from the CT images. The best segmentation model was selected from a validation set consisting of image slices from 36 weekly MRI scans not used for model training. Additional testing was performed on a total of 39 MRI scans obtained from 22 patients who were not used in training or validation. Three of those patients contained longitudinal MRI scans (7,7,6). Table II contains details of the numbers of analyzed scans, patients and ROIs (256×256) used in training and testing.
Table II.
data for MRI lung image translation and tumor segmentation training
| Unsupervised Image Translation | Data Number | |||
|---|---|---|---|---|
| CT | Scans | Label | 377 | |
| Patients | 377 | |||
| Images | 32000 | |||
| Real MRI | Scans | No Label | 42 | |
| Patients | 6 | |||
| Images | 9696 | |||
| Segmentation | ||||
| Training | Translated MRI | Scans | Label | 377 |
| Patients | 377 | |||
| Images | 32000 | |||
| Real MRI | Scans | Label | 6 | |
| Patients | 6 | |||
| Images | 1536 | |||
| Validation | Real MRI | Scans | -- | 36 |
| Patients | 6 | |||
| Test | Real MRI | Scans | -- | 39 |
| Patients | 22 | |||
The Adam optimizer with a batch size of 1 and a learning rate of 0.0001 as used to train the modality translation for all the methods. The learning rate was kept constant for the first 50 epochs and then linearly decayed to zero during the next 50 training epochs. The generator and discriminator is updated during each iteration as similar as in CycleGAN[9].
In addition to the network structure implementation as described previously, the GAN training was stabilized as proposed in the CycleGAN method. First, least-square loss was used in place of the typically used negative log likelihood. Next, model oscillation was reduced by updating the discriminator using a history of generated images (N=50) as in CycleGAN and proposed in Shrivastava et al[24]. All compared translation networks used these same implementation optimizations and were trained with same number of training epochs and training conditions including the datasets for equitable comparison.
For segmentation training, the U-Net was trained with batch size of 10, Residual-FCN was trained with batch size of 10 and Dense-FCN was trained with batch size of 6 and initial learning rate of 0.0001. We employed early stopping with a maximum epoch number of 100 to prevent overfitting. We also use Dice loss[25] for the segmentation loss, which shows the ability to reduce the impact of data imbalance.
All the networks were trained on Nvidia GTX 1080Ti of 11 GB memory. The ADAM algorithm[26] was used during training with preset parameters λcyc=10, λshape=5 and λloc=1.
2.6. Benchmarking segmentation performance
We benchmarked our method’s performance against a random forest with fully connected random field[27, 28] for segmentation when learning from small dataset, evaluated the segmentation networks (U-Net, Residual-FCN, Dense-FCN) training when augmented with pseudo MRI produced using three different cross-modality synthesis networks including (a) the CycleGAN[9], (b) masked CycleGAN [22], and (c) UNsupervised Image-to-image Translation Networks (UNIT) methods[8].
Random forest classifier baseline:
We implemented a random forest (RF) segmentation with fully connected conditional random field[27] approach for the MRI lung tumor segmentation. The feature set was chosen based on the features that have shown to be useful for MRI segmentation applied to brain tumor segmentation [29] [28]. These features included mean intensity, local maximum MRI intensity, local minimum MRI intensity, local mean minimum MRI intensity, mean gradient, std gradient, entropy, context sensitivity features with local patches of size (5×5, 11×11, 17×17, 23×23). We also used Gabor edge features computed at angles (ɵ=0, π/4, π/2, 3π/4) and at bandwidth of (γ = 0.1, 0.2, 0.3, 0.4) to further improve the accuracy. The RF classifier was trained using 50 trees and maximum depth of 50. Then the voxel-wise RF classifications were further refined by the fully connected conditional random field [28].
CycleGAN:
CycleGAN[9] implementation consisted of the standard CycleGAN method as described before, forming an unsupervised image translation.
Masked CycleGAN:
The main difference between masked CycleGAN[22] and CycleGAN is that it uses expert-segmentations on both CT and MRI modalities as an additional input channel to specifically focus training on the regions containing tumors. This method requires expert segmented datasets from both imaging modalities for image translation.
UNIT:
Similar to CycleGAN and proposed method, UNIT[8] performs unsupervised image translation, wherein corresponding source and target images or expert segmentation on both modalities are not required. The primary difference of this approach is in its encoder structure in the generator that uses a variational autoencoder (VAE)[30] with cycle consistency loss[9]. The encoder models the modality transformation as a latent code that is then used to generate images through a generator. We used the default implementation as described in UNIT[8], where the last layer of the encoder and first layer of the generator for both CT to MRI translation and MRI to CT translation networks are shared. The discriminator uses six convolutional layers as used in the original implementation.
2.7. Evaluation Metrics
The similarity of pseudo MRI to the T2w MRI was evaluated using Kullback–Leibler divergence[31] (K-L divergence), that quantifies the average statistical differences in the intensity distributions. The K-L divergence was computed using the intensity values within the tumor regions by comparing the intensity histogram for all the generated pseudo MR images and the intensity histogram computed from the training T2w MR images. The KL divergence measure quantifies the similarity in the overall intensity variations between the pseudo MR and the real MR images within the structure of interest, namely, tumors. The K-L divergence is calculated by eq. 7.
| (7) |
where PsMRI and QrMRI indicate the tumor distribution in pseudo MR and T2w MR images and the summation is computed over a fixed number of discretized intensity levels (N = 1000).
The segmentation accuracy was computed using DSC and Hausdorff distance. The DSC is calculated between the algorithm and expert segmentation as:
| (8) |
where, TP is the number of true positives, FP is the number of false positives, and FN is the number of false negatives.
The Hausdorff distance is defined as:
| (9) |
where, P and T are expert and segmented volumes, and p and t are points on P and T, respectively. Sp and St correspond to the surface of P and T, respectively. To remove the influence of noise during evaluation, Hausdorff Distance (95%) was used, as recommended by Menze[32]. We also calculated the relative volume ratio, computed as , where Vas is the volume calculated by algorithm while Vgs is the volume calculated by manually segmentation.
Finally, for those patients who had longitudinal follow ups, the tumor growth trends were computed using the Theil-Sen estimator[33], which measures the median of slope (or tumor growth) computed from consecutive time points as:
| (10) |
where vk, vi are the tumor volumes at times k and i for a lesion l.
The difference in growth rate between algorithm and the expert delineation was computed using the Student’s T-test.
3. RESULTS
3.1. Impact of the proposed tumor-attention loss in CT to MRI transformation
Figure 5 shows MRI produced using the proposed (Figure 5e), CycleGAN (Figure 5b), masked CycleGAN (Figure 5c) and UNIT (Figure 5d) for three representative examples. The expert-segmented tumor contour placed on the CT (Figure 5a) is shown at the corresponding locations on the pseudo MRI. As shown, this method produced the best preservation of tumors on the pseudo MR images.
Figure 5:
CT to pseudo MRI transformation using the analyzed methods. (a) Original CT; pseudo MR image produced using (b) CycleGAN[9]; (c) masked CycleGAN[22]; (d) UNIT[8] and (e) proposed method. In (f), the abscissa (x- axis) shows the normalized MRI intensity and the ordinate (y-axis) shows the frequency of the accumulated pixel numbers at that intensity for each method in the tumor region. The T2w MR intensity distribution within the tumor regions from the validation patients is also shown for comparison.
As shown, our method most closely approximated the distribution of MR single intensities as the T2w MRI. The algorithm generated tumor distribution was computed within the tumors of the 377 pseudo MRI produced from CT, while the T2w MR distribution was obtained from tumor regions from expert-segmented T2w MR used in validation (N=36). This was confirmed on quantitative evaluation wherein, our method resulted in the lowest KL divergence of 0.069 between the pseudo MRI and T2w MRI compared with the CycleGAN (1.69), the masked CycleGAN (0.32) and UNIT (0.28) with 1000 bins to obtain a sufficiently large discretized distribution of intensities, as shown in figure 5 (f).
3.2. Impact of data augmentation using transformed MRI on training U-net-based MRI tumor segmentation
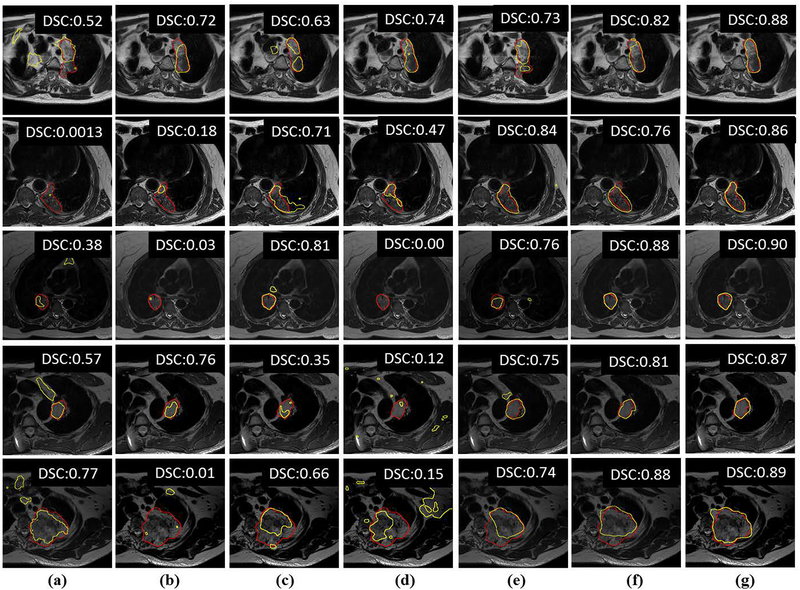
Figure 6 shows segmentation results from five randomly chosen patients computed using random forest classifier (RF+fCRF) (Figure 6a) and with a U-Net trained with only few T2w MRI (Figure 6b), and U-Nets trained T2w MRI and augmented data or pseudo MRI, corresponding to semi-supervised training and produced through cross-modality augmentation produced using cycle-GAN (Figure 6c), masked CycleGAN (Figure 6d), UNIT (Figure 6e) and the proposed approach (Figure 6g). Figure 6f shows the results of training with only pseudo MRI produced using proposed method in order to assess this method’s performance when using only augmented pseudo MR data. This mode setting corresponds to unsupervised domain adaptation. As shown, the both the semi-supervised and unsupervised modes of the proposed method’s generated contours (yellow) closely approximate expert-segmentation (red) (Figure 6g, Figure 6f). The UNIT method also led to performance improvements compared with the CycleGAN and masked CycleGAN methods, but was less accurate than our method. The overall segmentation accuracy using DSC and Hausdorff distances for these methods, including the RF+CRF methods are shown in Table III. As shown, our method resulted in the highest DSC and lowest Hausdorff distances on test sets that were not used either in training or model selection.
Figure 6:
Segmentations from representative examples from five different patients using different data augmentation methods. (a) RF+fCRF segmentation[28]; (b) segmentation using only few T2W MRI; training combining expert-segmented T2w MRI with pseudo MRI produced using (c) CycleGAN[9]; (d) masked CycleGAN[22]; (e) UNIT[8]; (g) proposed method. (f) shows segmentation results from training using only the pseudo MRI produced using proposed method. The red contour corresponds to the expert delineation while the yellow contour corresponds to algorithm generated segmentation.
Table III.
Segmentation accuracies computed using the U-Net for the different data augmentation strategies. Segmentation accuracies are shown using Dice similarity coefficient (DSC), 95th percentile Hausdorff distance (HD95) and volume ratio (VR) metrics.
| U-Net | ||||||
|---|---|---|---|---|---|---|
| Validation | Test | |||||
| Method | DSC | HD95 mm | VR | DSC | HD95 mm | VR |
| RF+fCRF[28] | 0.51±0.16 | 12.88±10.66 | 0.56±0.61 | 0.55±0.19 | 14.58±10.26 | 0.57±0.47 |
| Standard augmentation of T2w MRI | 0.63±0.27 | 7.22±7.19 | 0.34±0.31 | 0.50±0.26 | 18.42±13.02 | 0.54±0.27 |
| CycleGAN [9] pseudo MRI and T2w MRI | 0.57±0.24 | 11.41±5.57 | 0.50±0.53 | 0.62±0.18 | 15.63±10.23 | 0.54±1.27 |
| masked CycleGAN [22] pseudo and T2w MR | 0.67±0.21 | 7.78±4.40 | 0.84±0.30 | 0.56±0.26 | 20.77±18.18 | 0.37±0.57 |
| UNIT[8] | 0.63±0.29 | 7.74±4.80 | 0.45±0.27 | 0.63±0.22 | 17.00±14.80 | 0.47±0.28 |
| Tumor-aware pseudo MR and T2w MR | 0.70±0.19 | 5.88±2.88 | 0.23±0.15 | 0.75±0.12 | 9.36±6.00 | 0.19±0.15 |
| Tumor-aware pseudo MR | 0.62+0.26 | 7.47+4.66 | 0.35±0.29 | 0.72±0.15 | 12.45±10.87 | 0.25±0.19 |
3.3. Impact of network architecture on tumor segmentation accuracy
We evaluated the segmentation accuracy on two additional segmentation networks, Residual-FCN and Dense-FCN, to assess whether the data augmentation using the proposed method improved segmentation accuracy in those networks. Table IV summarizes the segmentation accuracy achieved when using the different data augmentation strategies. We also show the performance of the networks trained with no T2w MR but using only the pseudo MR images produced using proposed tumor-aware augmentation. As seen (Table III, IV), the proposed tumor-aware data augmentation resulted in most accurate segmentations in both networks, including when using the unsupervised training mode (with pseudo MR only training) in the test set. UNIT’s accuracy was consistently higher than the masked cycle GAN in all three networks in the test set.
Table IV.
segmentation accuracy comparison of Residual-FCN (RFCN) and Dense-FCN (DFCN). Segmentation accuracies are shown using Dice similarity coefficient (DSC), 95th percentile Hausdorff distance (HD95) and volume ratio (VR) metrics.
| Method | Networks | Validation | Test | ||||
|---|---|---|---|---|---|---|---|
| DSC | HD95 mm | VR | DSC | HD95 mm | VR | ||
| Standard augmentation of T2w MRI | RFCN DFCN |
0.62±0.24 0.68±0.28 |
9.31±5.30 8.06±4.89 |
0.33±0.29 0.29±0.25 |
0.50±0.19 0.57±0.23 |
23.96±17.00 24.98±16.51 |
0.48±0.23 0.51±0.99 |
| CycleGAN [9] pseudo MRI and T2w MRI | RFCN DFCN |
0.47±0.27 0.60±0.27 |
11.71±5.99 10.29±6.22 |
0.41±0.30 0.34±0.26 |
0.52±0.20 0.60±0.19 |
17.82±12.11 23.77±17.61 |
0.54±0.89 0.35±0.55 |
| masked CycleGAN [22] pseudo and T2w MR | RFCN DFCN |
0.42±0.28 0.60±0.23 |
16.01±7.65 9.85±6.85 |
0.44±0.31 0.48±0.35 |
0.54±0.25 0.55±0.24 |
20.36±12.02 25.11±20.89 |
0.54±1.46 0.47±0.33 |
| UNIT[8] pseudo and T2w MR | RFCN DFCN |
0.65±0.24 0.66±0.20 |
9.03±5.03 7.43±4.28 |
0.36±0.40 0.43±0.42 |
0.59±0.22 0.58±0.24 |
17.49±19.48 28.37±22.94 |
0.38±0.26 0.47±0.30 |
| Tumor-aware pseudo MR and T2w MR | RFCN DFCN |
0.70±0.21 0.68±0.20 |
7.56±4.85 7.37±5.49 |
0.22±0.16 0.27±0.28 |
0.72±0.15 0.73±0.14 |
16.64±5.85 13.04±6.06 |
0.25±0.22 0.21±0.19 |
| Tumor-aware pseudo MR | RFCN DFCN |
0.59±0.23 0.62±0.21 |
10.09±5.88 11.09±5.02 |
0.36±0.32 0.42±0.29 |
0.69±0.17 0.67±0.16 |
18.03±12.91 20.70±10.57 |
0.27±0.25 0.22±0.19 |
3.4. Comparison of longitudinal segmentations produced using algorithm and expert
We assessed the ability of these methods to longitudinally segment and measure tumor response to radiation therapy. Figure 7 shows the estimate of tumor growth computed using the proposed method used to train a U-Net from three patients with weekly MR scans who were not used for training. This method produced a highly similar estimate of tumor growth as an expert as indicated by the differences in tumor growth computed between algorithm and expert segmentation (week one only: 0.067 ± 0.012; CycleGAN [9]: 0.038 ± 0.028; masked Cycle-GAN[22]: 0.042 ± 0.041; UNIT[8]: 0.034 ± 0.031; proposed: 0.020 ± 0.011).
Figure 7:
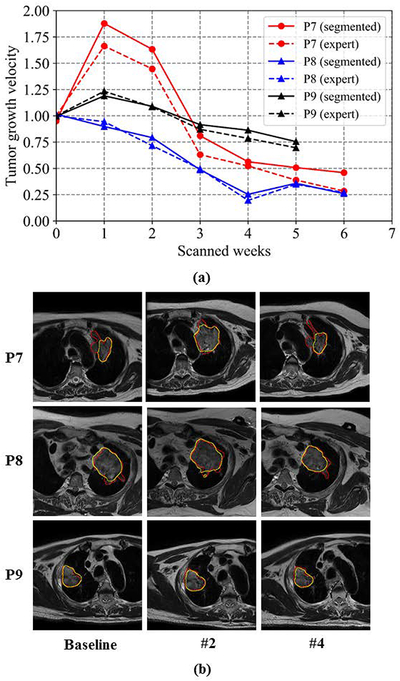
Longitudinal tumor volumes computed from three example patients using proposed method. (a) Volume growth velocity calculated by proposed versus expert delineation (b) Segmentation results from patient 7 and patient 8. The red contour corresponds to the expert delineation while the yellow contour corresponds to algorithm generated segmentation.
IV. DISCUSSION
A novel approach for augmenting the training of deep neural networks for segmenting lung tumors from MRI with limited expert-segmented training sets was developed. Our approach uses the structure of interest, namely tumor to constrain the CT to MR translation such that the generated pseudo MR preserve the location and shape of the tumors. Global distribution matching methods such as the CycleGAN cannot accurately model the transformation of less frequent structures like tumors and result in loss of the tumors in the transformed pseudo MRI. Our method also outperformed the more recent UNIT method that uses variational autoencoders that specifically learn a parametric function (typically a Gaussian) controlling the transformation between modalities. Results show that data augmentation obtained using our method improves segmentation accuracy and produced the most accurate segmentation of the compared methods regardless of the chosen segmentation architecture (U-Net, Residual-FCN, and Dense-FCN).
We also benchmarked the performance of our method against a shallow-learning based random forest classifier, when training with standard data augmentation, and when using only the pseudo MR data produced using our method. We found that the random forest classifier produced much lower accuracies due to large number of false positives when compared with all other deep learning methods, confirming prior results that deep learning methods are indeed capable of learning more accurate representation of the underlying data and lead to better classification/segmentation[28].
The proposed method improved the segmentation performance of other domain adaptation methods despite using only few MRI datasets for training. In fact, we found that adding any cross-modality augmentation is better than standard augmentation strategies. This is because, our method like in [38, 39], leverages labeled information from other imaging modalities to boost the performance in the target imaging modality. Solutions include using networks pre-trained on the same modality but a different task as in [39] or training a cross-modality model to synthesize images resembling the target distribution [22, 39] and as done in our work. However, for such methods to work, it’s crucial that the approximated model closely matches the target distribution. As shown in the results, the pseudo MRI produced using our method resulted in the closest match to the T2-w MRI tumor distribution measured by the K-L divergence. Therefore, this led to improved performance as the information from the unrelated, yet relatively large expert-segmented CT modality (N=377 cases) could be better leveraged to improve the performance despite having a small MRI training set. This is further underscored by the result that segmentation networks trained using only the pseudo MRI produced using our method yielded more accurate segmentations (on test) compared with other cross-modality augmentation methods that included some of the T2w MRI for training.
Prior works have used cycle loss [34, 35] to learn the cross-modality prior to transform modalities, where the network learns the transformation by minimizing global statistical intensity differences between the original and a transformed modality (e.g., CT vs. pseudo CT) produced through circular synthesis (e.g., CT to pseudo MR, and pseudo MR to pseudo CT). Although cycle loss eliminates the need for using perfectly aligned CT and MRI acquired from the same patient for training, it cannot model anatomical characteristics of atypical structures, including tumors. In fact, cycle-GAN based methods have been shown to be limited in their ability to transform images even from one MR to a different MR sequence [7]. This approach overcomes the limitations of the prior approaches by incorporating structure-specific losses that constrain the cross-modality transformations to preserve atypical structures including tumors. We note however that all of these methods produce pseudo MR representations that do not create synthetic MR images modeling the same tissue specific intensities as the original MRI. This is intentional as our goal is simply to create an image representation that resembles an MRI and models the global and local (structure of interest) statistical variations that will enable an algorithm to detect and segment tumors. The fact that the pseudo MR images are unlike T2w MRI is demonstrated by the lower accuracy particularly on test sets when excluding any T2w MRI from training. However, it is notable that the pseudo MR images produced by our method still lead to more accurate segmentations compared with other approaches.
We speculate that the higher DSC accuracy in the test sets resulted from the larger tumor volumes in the test 70.86±59.80 cc when compared with validation set of 31.49±42.67 cc. It is known that larger tumors can lead to higher DSC accuracies [7] and can lead to more optimistic bias in the accuracy. The reason for the differences in tumor volumes arose since the validation set used patients (N=6) with both pre-treatment (larger tumors) and during treatment (acquired during weekly treatment) MRI where there the tumors shrunk as they responded to treatment. On the other hand resulting in a total of 36 scans, the test set used only 3 patients with pre- and during-treatment MRIs (N=20), and the remaining (N=19) were all comprised of pre-treatment MRI. The reason for this set up is primarily because additional pre-treatment MRIs were included for testing only after the training models were finalized for blinded evaluation on new samples.
Unlike most prior works that employ transfer learning to fine tune features learned on other tasks, such as natural images [35–38], we chose a data augmentation approach using cross-modality priors. The reason for this is transfer learning performance on networks trained on completely unrelated datasets is easily surpassed even when training from scratch using sparse datasets [38]. This is because features of deeper layers may be too specific for the previously trained task and not easily transferable to a new task. The approach overcomes the issue of learning from small datasets by augmenting training with relevant datasets from a different modality.
This work has a few limitations. First, the approach is limited by the number of test datasets, particularly for longitudinal analysis due to the lack of additional recruitment of patients. Second, due to lack of corresponding patients with CT and MRI, it is not possible to evaluate the patient level correspondences of the pseudo and T2w MR images. Nevertheless, the focus of this work was not to synthesize MR images that are identical to true MRI as is the focus of works using generational adversarial networks to synthesize CT from MR [40]. Instead our goal was to augment the ability of deep learning to learn despite limited training sets by leveraging datasets mimicking intensity variations as the real MR images. Our approach improves on the prior GAN-based data augmentation approaches [41, 42], by explicitly modeling the appearance of structures of interest, namely, the tumors for generating fully automatic and longitudinal segmentation of lung tumors from MRI with access to only a few expert-segmented MRI datasets.
V. CONCLUSIONS
A novel deep learning approach using cross-modality prior was developed to train robust models for MR lung tumor segmentation from small expert-labeled MR datasets. This method overcomes the limitation of learning robust models from small datasets by leveraging information from expert-segmented CT datasets through a cross-modality prior model. This method surpasses state-of-the-art methods in segmentation accuracy and demonstrates initial feasibility in auto-segmentation of lung tumors from MRI.
ACKNOWLEDGEMENTS
This work was supported in part by Varian Medical Systems, and partially by the MSK Cancer Center support grant/core grant P30 CA008748, and by NIH R01 CA198121–03. We also thank Dr. Mageras for his insightful suggestions for improving the clarity of the manuscript.
REFERENCRES
- 1.Nieh CF. Tumor delineation: the weakest link in the search for accuracy in radiotherapy, Medical Physics 2008; 33(4): 136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Eisenhauer E, Therasse P, Bogaerts J et al. , New response evaluation criteria in solid tumours: revised RECIST guideline (version 1.1), European journal of cancer, 2009, 45: 228–247. [DOI] [PubMed] [Google Scholar]
- 3.Pollard JM, Wen Z, Sadagopan R, Wang J, Ibbott GS. The future of image-guided radiotherapy will be MR guided. The British journal of radiology 2017; 90(1073): 20160667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Thompson RF, Valdes G, Fuller CD, Carpenter CM, Morin O, Aneja S, et al. The Future of Artificial Intelligence in Radiation Oncology. International Journal of Radiation Oncology• Biology• Physics 2018; 102(2): 247–248. [DOI] [PubMed] [Google Scholar]
- 5.Goodfellow I, Pouget-Abadie J, Mirza M, et al. Generative adversarial nets, in: Advances in Neural Information Processing Systems (NIPS) 2014; p. 2672–2680. [Google Scholar]
- 6.Radford A, Metz L, Chintala S. Unsupervised representation learning with deep convolutional generative adversarial networks In: International conference in Learning Representations 2016. [Google Scholar]
- 7.Cohen JP, Luck M, and Honari S, “Distribution Matching Losses Can Hallucinate Features in Medical Image Translation,” in: International Conference on Medical Image Computing and Computer-Assisted Intervention (MICCAI), Springer, 2018. p. 529–537. [Google Scholar]
- 8.Liu M-Y, Breuel T, and Kautz J, “Unsupervised image-to-image translation networks,” in Advances in Neural Information Processing Systems, 2017, pp. 700–708. [Google Scholar]
- 9.Zhu JY, Park T, Isola P, Efros A. Unpaired image-to-image translation using cycle-consistent adversarial networks, in: Intl. Conf. Computer Vision (ICCV) 2017: p. 2223–2232. [Google Scholar]
- 10.Jiang J, Hu Y-C, Tyagi N et al. , Tumor-Aware, Adversarial Domain Adaptation from CT to MRI for Lung Cancer Segmentation, in: International Conference on Medical Image Computing and Computer-Assisted Intervention (MICCAI), 2018, pp. 777–785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.He K, Zhang X, Ren S, Sun J, Deep residual learning for image recognition, In Proceedings of the IEEE conference on computer vision and pattern recognition (CVPR), 2016. p. 770–778. [Google Scholar]
- 12.Jégou S, Drozdzal M, Vazquez D, Romero A, Bengio Y, The one hundred layers tiramisu: Fully convolutional densenets for semantic segmentation, in: Computer Vision and Pattern Recognition Workshops (CVPRW), 2017. p 1175–1183. [Google Scholar]
- 13.Aerts HJ, Rios Velazquez E, Leijenaar RT, Parmar C, et al. Data from NSCLC-radiomics The Cancer Imaging Archive, 2015. [Google Scholar]
- 14.Clark K, Vendt B, Smith K, Freymann J, et al. The cancer imaging archive (TCIA): maintaining and operating a public information repository, Journal of digital imaging 2013. 26 (6):1045–1057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Nyúl LG, Udupa JK. On standardizing the MR image intensity scale, Magnetic Resonance in Medicine. 1999. December; 42(6): p. 1072–1081. [DOI] [PubMed] [Google Scholar]
- 16.Ulyanov D, Vedaldi A, and Lempitsky V, “Improved texture networks: Maximizing quality and diversity in feed-forward stylization and texture synthesis,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2017, pp. 6924–6932. [Google Scholar]
- 17.Isola P, Zhu J-Y, Zhou T, and Efros AA, “Image-to-image translation with conditional adversarial networks,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 2017, pp. 1125–1134. [Google Scholar]
- 18.Ioffe S and Szegedy C, “Batch normalization: Accelerating deep network training by reducing internal covariate shift,” Proceedings of the 32nd International Conference on International Conference on Machine Learning, 37, 2015, pp. 448–456 [Google Scholar]
- 19.Long J, Shelhamer E, and Darrell T, “Fully convolutional networks for semantic segmentation,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2015, pp. 3431–3440. [DOI] [PubMed] [Google Scholar]
- 20.Ronneberger O, Fischer P, and Brox T, “U-net: Convolutional networks for biomedical image segmentation,” in International Conference on Medical Image Computing and Computer-Assisted Intervention, 2015, pp. 234–241. [Google Scholar]
- 21.Huang G, Liu Z, Weinberger KQ, and van der Maaten L, “Densely connected convolutional networks,” Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2017, pp. 4700–4708. [Google Scholar]
- 22.Chartsias A, Joyce T, Dharmakumar R, and Tsaftaris SA, “Adversarial image synthesis for unpaired multi-modal cardiac data,” in International Workshop on Simulation and Synthesis in Medical Imaging, 2017, pp. 3–13. [Google Scholar]
- 23.Roth HR, Lee CT, Shin H-C, Seff A, Kim L, Yao J, et al. , “Anatomy-specific classification of medical images using deep convolutional nets,” IEEE International Symposium on Biomedical Imaging (ISBI), 2015. [Google Scholar]
- 24.Shrivastava A, Pfister T, Tuzel O, Susskind J, Wang W, and Webb R, “Learning from simulated and unsupervised images through adversarial training,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2017, pp. 2107–2116. [Google Scholar]
- 25.Milletari F, Navab N, and Ahmadi S-A, “V-net: Fully convolutional neural networks for volumetric medical image segmentation,” in 3D Vision (3DV), 2016 Fourth International Conference on, 2016, pp. 565–571. [Google Scholar]
- 26.Kingma DP, Ba J. Adam: A method for stochastic optimization In: International conference in Learning Representations 2014. December 22. [Google Scholar]
- 27.Krähenbühl P and Koltun V, “Efficient inference in fully connected crfs with gaussian edge potentials,” in Advances in neural information processing systems, 2011, pp. 109–117. [Google Scholar]
- 28.Kamnitsas K, Ledig C, Newcombe VF, Simpson JP, Kane AD, Menon DK, et al. , “Efficient multi-scale 3D CNN with fully connected CRF for accurate brain lesion segmentation,” Medical image analysis, vol. 36, pp. 61–78, 2017. [DOI] [PubMed] [Google Scholar]
- 29.Hu Y.-c., Grossberg M, and Mageras G, “Semiautomatic tumor segmentation with multimodal images in a conditional random field framework,” Journal of Medical Imaging, vol. 3, p. 024503, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kingma DP and Welling M, “Auto-encoding variational bayes,” International Conference on Learning Representations, 2014. [Google Scholar]
- 31.Duda RO and Hart PE, “Pattern recognition and scene analysis,” ed: Wiley, New York, 1973. [Google Scholar]
- 32.Menze BH, Jakab A, Bauer S, Kalpathy-Cramer J, Farahani K, Kirby J, et al. , “The multimodal brain tumor image segmentation benchmark (BRATS),” IEEE transactions on medical imaging, vol. 34, pp. 1993–2024, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Lavagnini I, Badocco D, Pastore P, Magno F. Theil_sen nonparametric regression technique on univariate calibration, inverse regression and detection limits, Talanta 2011. 87:180–188. [DOI] [PubMed] [Google Scholar]
- 34.Wolterink JM, Dinkla AM, Savenije MH, Seevinck PR, et al. Deep MR to CT synthesis using unpaired data, in: Intl Workshop on Simulation and Synthesis in Medical Imaging, Springer, 2017: p. 14–23. [Google Scholar]
- 35.Zhang Z, Yang L, Zheng Y. Translating and segmenting multimodal medical volumes with cycle- and shape consistency generative adversarial network, in: IEEE Conf. on Computer Vision and Pattern Recognition (CVPR), 2018. P. 9242–9251. [Google Scholar]
- 36.Long M, Cao Y, Wang J, Jordan MI, Learning transferable features with deep adaptation networks, in: Intl Conf. Machine Learning (ICML), 2015. p. 97–105. [Google Scholar]
- 37.Van OA, Ikram MA, Vernooij MW, De Bruijne M. Transfer learning improves supervised image segmentation across imaging protocols, IEEE Transactions on Medical Imaging 2015. 34(5):1018–1030. [DOI] [PubMed] [Google Scholar]
- 38.Wong KCL, Syeda-Mahmood T, Moradi M. Building medical image classifiers with very limited data using segmentation networks. Med Image Analysis, 2018. 49: p. 105–116. [DOI] [PubMed] [Google Scholar]
- 39.Huo Y, Xu Z, Bao S, Assad A, Abramson RG, and Landman BA. Adversarial synthesis learning enables segmentation without target modality ground truth in: 15th International Symposium on Biomedical Imaging (ISBI), 2018, p. 1217–1220. [Google Scholar]
- 40.Emami H, Dong M, Nejad-Davarani SP, and Glide-Hurst C, Generating Synthetic CT s from Magnetic Resonance Images using Generative Adversarial Networks, Medical physics, 2018,p.3627–3636 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Springenberg JT, “Unsupervised and semi-supervised learning with categorical generative adversarial networks,” International Conference on Learning Representations, 2016. [Google Scholar]
- 42.Souly N, Spampinato C, and Shah M, “Semi and weakly supervised semantic segmentation using generative adversarial network,” IEEE International Conference on Computer Vision (ICCV), 2017. [Google Scholar]