Log-layer mismatch and modeling of the fluctuating wall stress in wall-modeled large-eddy simulations

Abstract

Log-layer mismatch refers to a chronic problem found in wall-modeled large-eddy simulation (WMLES) or detached-eddy simulation, where the modeled wall-shear stress deviates from the true one by approximately 15%. Many efforts have been made to resolve this mismatch. The often-usedfixes, which are generally ad hoc, include modifying subgridscale stress models, adding a stochastic forcing, and moving the LES–wall-model matching location away from the wall. An analysis motivated by the integral wall-model formalism suggests that log-layer mismatch is resolved by the built-in physics-based temporal filtering. In this work we investigate in detail the effects of local filtering on log-layer mismatch. We show that both local temporal filtering and local wall-parallel filtering resolve log-layer mismatch without moving the LES–wall-model matching location away from the wall. Additionally, we look into the momentum balance in the near-wall region to provide an alternative explanation of how LLM occurs, which does not necessarily rely on the numerical-error argument. While filtering resolves log-layer mismatch, the quality of the wall-shear stress fluctuations predicted by WMLES does not improve with our remedy. The wall-shear stress fluctuations are highly underpredicted due to the implied use of LES filtering. However, good agreement can be found when the WMLES data are compared to the direct numerical simulation data filtered at the corresponding WMLES resolutions.

I. INTRODUCTION

Turbulence is comprised of fluid motions of many scales. Resolving all such scales leads to direct numerical simulation (DNS). Direct numerical simulation provides the highest-fidelity solution to fluid problems, but its cost quickly goes beyond the capacity of the current supercomputers when deployed for practical high-Reynolds-number applications. Large-eddy simulation (LES) has been considered as a predictive and affordable alternative to DNS, as it resolves the flow-dependent large-scale motions directly, but models the small, less-energetic eddies that are more amenable to universal and calibration-free parametrization [1–3]. In wall turbulence, however, the requirement that LES must resolve the energy-containing motions everywhere makes LES only a little cheaper than DNS [4,5], because the size of the energy-containing eddies in the near-wall region becomes progressively comparable to the smallest dissipative eddies toward the wall [6]. The problem is more exacerbated by the fact that the currently available subgrid-scale (SGS) models underperform on coarse near-wall grids [7–9]. For application of LES to technologically relevant problems, one therefore requires an additional way of compensating for the lack of modeled stresses on coarse grids. This leads to wall-modeled LES (WMLES), where the grid spacing is chosen to scale with the local boundary-layer thickness [10,11], and an auxiliary way of augmenting the turbulent stress in the near-wall region is introduced. Following the taxonomy given in Ref. [12], WMLES is further categorized into two different types of approaches: wall-stress modeling and a hybrid of Reynolds-averaged Navier-Stokes (RANS) and LES. In the former, a formal LES framework is maintained everywhere in the LES domain, while the momentum transport in the unresolved near-wall region is modeled through the modified wall-boundary condition. In the latter, the turbulence model switches from a RANS parametrization within the entire boundary layer to a LES-like one in the outer region [7]. The two approaches, at first glance, may look similar. However, the key difference is in how LES is coupled to the low-dimensional representation of the near-wall turbulence, and this difference leads to near-wall flow patterns and modeling challenges unique to each approach. References [11,12] provide detailed discussions on this subtle but important distinction between the two approaches. Despite such difference, a chronic problem has been found commonly in the two approaches, which is log-layer mismatch [13–15].

The discussion from this point on focuses solely on wall-stress modeling and henceforth we use the terms WMLES and wall-stress modeling interchangeably. In a typical WMLES, the grid spacing (especially in the wall-normal direction) is chosen to be a fraction of the local boundary-layer thickness δ, typically at δ/Δ ≈ 20–[16–20]. The lack of turbulent stress in this coarse near-wall grid is compensated for by the modeled wall-stress boundary condition, which augments the total stress in the innermost region of boundary layers. Modeling the wall stress based on the nearest neighboring LES velocity has often led to underpredicted [21,22] or overpredicted [23,24] stresses and this mismatch between the modeled and the real skin friction leads to the so-called log-layer mismatch (LLM). Many efforts have been made to resolve this mismatch. Earlier works have focused on modifying the SGS stress models [25–30]. Later investigations suggest that LLM is not solely due to an inaccurate SGS stress model. Kawai and Larsson [21] argued that the flow in the near-wall region of WMLES is inevitably underresolved, making the input to the wall model (traditionally from the wall-adjacent LES data) contaminated by the truncation and SGS modeling errors. They then proposed that in order to resolve LLM, one needs to abandon the practice of using the first off-wall grid point for wall modeling and instead use the LES information slightly away from the wall.

This remedy by Kawai and Larsson has been useful for its robustness. However, its nonlocal nature appears to render this method impractical for flows involving complex wall geometry, by incurring significant user overhead in LES mesh preparation and wall-model implementation. First, ensuring the existence of a proper matching location (with a prescribed wall distance or number of elements below it) at the meshing stage is almost always impossible when complex geometries are meshed with unstructured elements. This situation was encountered in the recent applications of WMLES to a three-dimensional (3D) aircraft configuration involving multiple wall junctures [31] and an industry-scale gas-turbine combustor [32]. Second, data exchange between the wall faces and their proper matching locations in parallel, unstructured-grid flow solvers requires nonlocal search and message passing at each time step, which degrades parallel performance of the flow solver. Finally, this method unphysically detaches the wall stress from the closest LES velocity, failing to properly account for sharp turning angles or skewed velocity profiles commonly found in external aerodynamics applications [31]. Therefore, it is imperative that a local wall-modeling approach using the wall-adjacent LES data has to be developed, while resolving LLM appropriately. In addition to such practical concerns, the interpretations of how LLM is caused and subsequently resolved by the traditional remedy have been unclear, as it is based largely on a qualitative length-scale argument [21]. Although it is well demonstrated and understood that the near-wall solution in WMLES is underresolved, how this further develops into LLM has not been explored systematically.

This study aims at developing an alternative remedy for LLM that is better suited for complex-geometry applications and also providing a more comprehensive explanation of how LLM is caused and can be resolved through a quantitative analysis. The starting point of this work is the recent work of Yang et al. [33], where it was observed that the physics-based time filtering of the wall-model input (taken from the wall-adjacent LES solution) effectively resolves LLM in their integral wall-model framework, without using the LES information away from the wall for wall modeling. The paper is organized as follows. In Sec. II, flow configuration, wall models, and computational method are described briefly. Log-layer mismatch and its resolution with a prevailing remedy are reproduced in Sec. III and a method for resolving LLM is proposed and tested in Sec. IV. Section V provides an alternative explanation of how LLM is caused and resolved by the remedies. Section VI discusses briefly the prediction of wall-shear stress fluctuations in WMLES with respect to the filtered DNS. A summary is given in Sec. VII.

II. COMPUTATIONAL DETAILS

We use the open-source code LESGO to investigate the LLM problem. The code solves the filtered Navier-Stokes equations in a half channel with a staggered grid. The size of the computational domain is 2πδ × δ × 2πδ in the streamwise (x), wall-normal (y), and spanwise (z) directions, respectively, where δ is the half channel height. The code uses a pseudospectral approach in the wall-parallel directions, with a second-order accurate central finite-difference scheme used in the wall-normal direction. Details of this code can be found in Ref. [34] and the references cited therein. A symmetric condition is used at the top boundary. Periodic boundary conditions are applied in the homogeneous directions (x and z). The channel is driven by a constant pressure gradient. The scale-dependent Lagrangian-dynamic Smagorinsky model [34] is used for subgrid-scale stress modeling. While not reported here, no significant difference in computed flow statistics was found when employing different dynamic SGS models (at least for the statistics of interest here).

In WMLES, the no-slip wall boundary condition is replaced with the shear-stress boundary condition and the eddy viscosity is zero at the wall. For the channel configuration investigated in the present study, a simple logarithmic-law-like equilibrium wall model is employed,

$${\tau }_x=\rho {\left[\frac{\kappa u_{\Vert }}{\text{ln}\left(h_{wm}/y_0\right)}\right]}^2\frac{u_{wm}}{u_{\Vert }},{\tau }_z=\rho {\left[\frac{\kappa u_{\Vert }}{\text{ln}\left(h_{wm}/y_0\right)}\right]}^2\frac{w_{wm}}{u_{\Vert }},$$ (1)

where τ is the wall-shear stress, u_wm and w_wm are the LES velocities at the matching location (a distance y = h_wm away from the wall) in the x and z directions, respectively, $u_{\Vert }=\sqrt{u_{wm}^2+w_{wm}^2}$ is the modulus of the LES velocity at the matching location projected on the wall-parallel plane, and κ = 0.4 is the von Kármán constant. In addition, $y_0\equiv v/{\overline{u}}_{\tau }{e}^{\kappa B}$ is the effective roughness length and is kept constant at 1 × 10⁻⁴δ and 6.77 × 10⁻⁵δ depending on the cases, corresponding to the friction Reynolds numbers Re_τ ≈ 1400 and Re_τ ≈ 2000, respectively. Here B = 5.0 is the intercept in the logarithmic velocity profile and ${\overline{u}}_{\tau }$ is the mean friction velocity in the channel flow, which is known a priori in the present study. With the wall boundary condition provided by Eq. (1), the LES equations in the bulk region are integrated. At the next time step, the updated u_wm and w_wm are used in Eq. (1) again to supply the wall boundary condition for LES. Unless noted otherwise, lengths and velocities are normalized by the half channel height and the friction velocity.

III. THE LLM AND PREVAILING REMEDY FOR ITS RESOLUTION

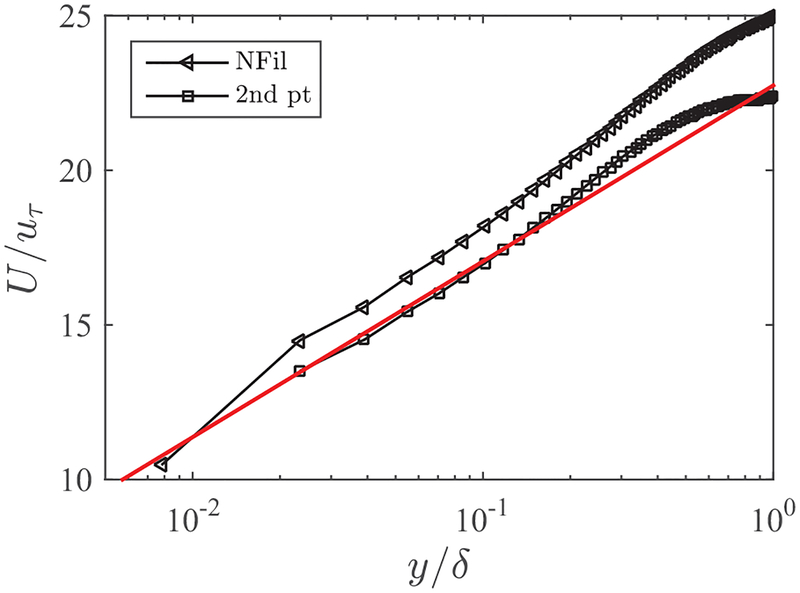
We first reproduce the LLM problem in a turbulent channel flow and show its resolution using a commonly used method. It has long been known that wall models operating on the raw LES velocity at the first off-wall grid point give rise to the so-called log-layer mismatch problem, leading to up to 15% deviation of the modeled wall-shear stress from the correct value, independent of the spatial discretization used, the SGS model employed, and the flow configuration of interest [21,35]. This LLM is reproduced in the present half channel calculation in Fig. 1 (the NFil case). The two cases in Fig. 1 use a grid of size 64³, with the grid spacing being uniform in each direction. As the present channel flow is driven by a fixed pressure gradient, the mean wall-shear stress is always correct and LLM here manifests itself as an erroneous upward shift of the mean-velocity profile (positive LLM). Note that LLM is not a problem specific to the simple wall model deployed in the present study. It is known to persist in WMLES using more comprehensive wall models as reported in Refs. [19,21]. A prevailing remedy for LLM is to use the LES information slightly away from the wall (e.g., u_wm equals u_LES at the second, third, or fourth off-wall grid point). The hypothesis is that the LES solution at the first off-wall point is likely contaminated by the numerical and SGS modeling error. Based on this reasoning, Kawai and Larsson [21] showed that LLM is resolved when providing the LES data at the nth off-wall point to the wall model (n ≥ 2). We reproduce the same result in Fig. 1 (the 2nd pt case) as well. Using the LES data from the third or fourth off-wall points produces essentially the same result, consistent with the findings in Ref. [21]. It should be noted that the shape of the mean-velocity profiles in the bulk region is a function of the wall boundary condition, and changes in the wall condition can lead to changes in the mean profile in the wake region.

FIG. 1.

Mean velocity profiles. The expected logarithmic law U/u_τ = 1/κ ln(y/y₀) is indicated by a solid red line. For the no-filtering cases (NFil), the first LES grid point from the wall is used as the wall-model input. For the second off-wall point case (2nd pt), the instantaneous LES velocity at the second LES grid from the wall is used as the wall-model input, with no filtering. For the cases shown here, y₀ = 0.0001δ, which corresponds to Re_τ = 1400.

Porté-Agel et al. [28] also reported that LLM can be resolved through a proper modification of the SGS model in the near-wall region. They argued that because the flow field is underresolved, the momentum flux through the top face of the first LES computational cell should be based on the imposed law of the wall du/dy = (u_τ/κy)(u_wm/u_∥) and dw/dy = (u_τ/κy)(w_wm/u_∥), instead of evaluating velocity derivatives directly with a finite-difference–finite-volume scheme. Because the velocity derivatives enter the SGS stress model and also the filtered Navier-Stokes equations, evaluating derivatives according to the imposed logarithmic law essentially reformulates the SGS model [36]. However, our numerical experiments show that this reformulation has limited impact on LLM (not shown).

IV. REMEDY FOR LLM

In this section we propose a simpler remedy for LLM, in which the wall model operates with the filtered LES data at the first off-wall grid point. This is motivated by an observation in Ref. [33], where LLM is avoided by providing the time-filtered LES signal at the first off-wall grid point to a wall model, according to

$$u_{wm}^n=(1-ϵ)u_{wm}^{n-1}+ϵu_{\text{LES}}^n.$$ (2)

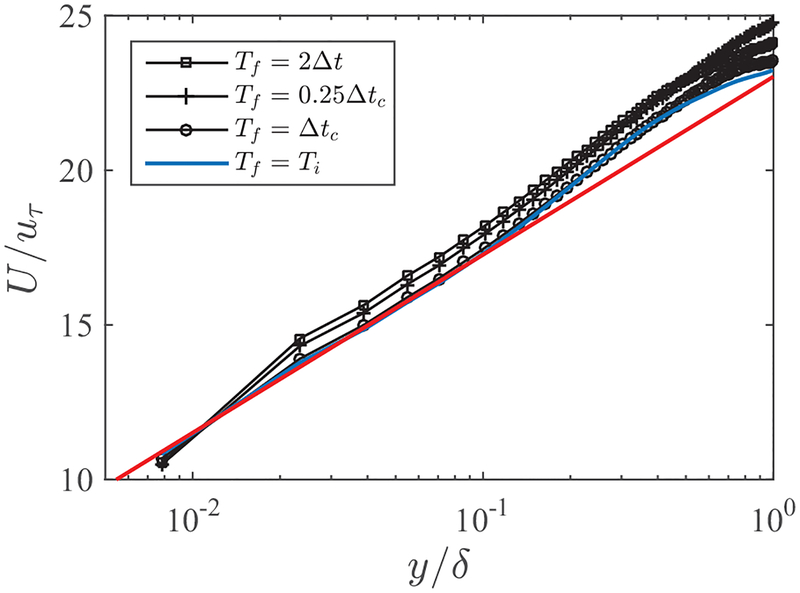
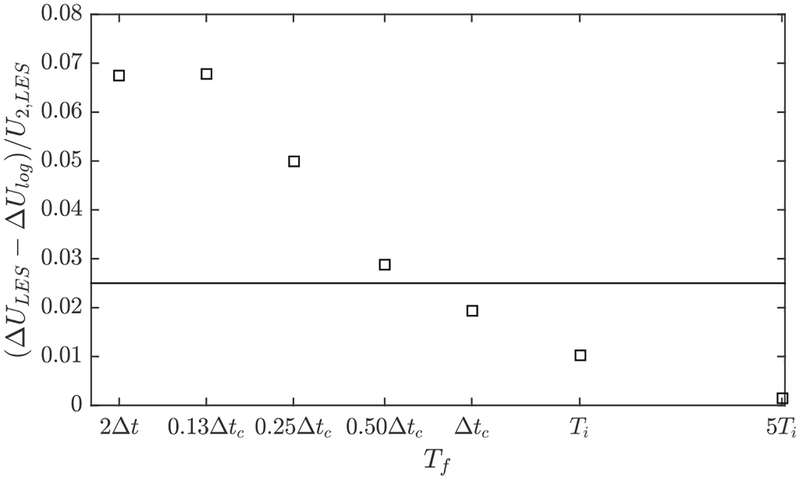
The w_wm is obtained similarly by filtering the spanwise LES velocity. Here u_wm is the velocity used in the wall model, the superscript n is the LES time step index, and u_LES is the instantaneous streamwise LES velocity at the first off-wall grid point (y = h_wm = Δy/2). The weight of time averaging is defined as ϵ = Δt/T_f, where Δt is the LES computational time step and T_f is a filtering time scale to be specified. We examine the effect of the filtering time scale on the WMLES prediction by considering the computational time step (T_f = 2Δt), a convective time scale at the matching location [T_f = Δt_c ≡ Δx/〈u(y = Δy/2)〉], and the characteristic time scale for the wall-normal turbulent transport at the matching location (T_f = T_i ≡ h_wm/κu_τ). As can be seen in Fig. 2, increasing the filtering time scale reduces the strength of LLM and the mismatch is essentially resolved (becomes sufficiently weak) with the filtering time scales T_f > Δt_c. Figure 3 quantifies the strength of LLM as a function of the filtering time scale. The strength of LLM is quantified here as (ΔU_LES – ΔU_log)/U_{2, log}, where ΔU_LES = 〈u(y = 1.5Δy)〉 – 〈u(y = 0.5Δy)〉 is the velocity difference between the first and second LES grid points,) ΔU_log/u_τ = 1/κ ln(1.5Δy/y₀) – 1/κ ln(0.5Δy/y₀) is the velocity increment expected from the log law, and U_{2, log}/u_τ = 1/κ ln(1.5Δy/y₀) is the expected velocity at the second LES grid point. A few observations can be made. Log-layer mismatch persists when using a raw LES signal (T_f = Δt, no time filtering). The strength of LLM drops to ≈2% with T_f = Δt_c and to about 1% with T_f = T_i. Because the uncertainty in the von Kármán constant is about 2.5% [37], taking T_f = Δt_c already resolves LLM. It was also verified that LLM remains negligibly small with very large filtering time scales (T_f ≫ T_i).

FIG. 2.

Mean velocity profiles obtained with the temporally filtered wall-model input at the first off-wall LES point. All cases use a grid of size 64³ and a roughness length scale y₀ = 0.0001δ. The logarithmic law is indicated by a solid red line.

FIG. 3.

Strength of LLM plotted against the filtering time scale. Here Δt is the LES time step size, Δt_c = Δx/〈u(y = 0.5Δy)〉, and T_i = h_wm/κu_τ. The line at 0.025 indicates the expected uncertainty in evaluating the strength of LLM owing to the variation in the von Kármán constant. For the cases shown here, y₀ = 0.0001δ, which corresponds to Re_τ = 1400.

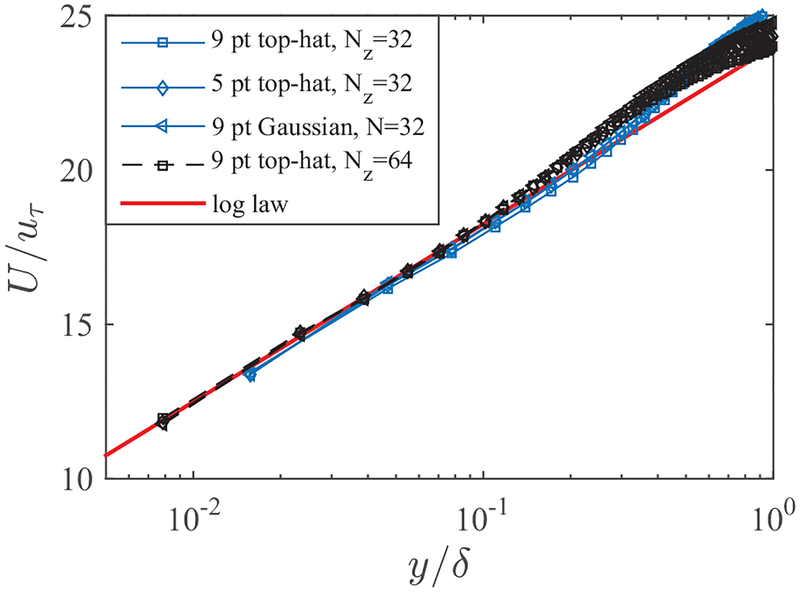
A temporal filtering with T_f = Δt_c is expected to have a similar effect as a 2Δx wall-parallel filtering. It is of interest here to know whether the wall-parallel spatial filtering is an equally useful remedy for LLM. Three types of spatial filters are tested (the nine-point top-hat filter, the nine-point Gaussian filter, and the five-point top-hat filter; all spatial filtrations are performed within the wall-parallel plane located at y = h_wm) in half channel WMLES calculations with 32³ and 64³ grid points. As shown in Fig. 4, the filter type has no noticeable impact on the resolution of LLM. Grid convergence is found, suggesting that the filter width only needs to be a few times the grid spacings (Δx and Δz). Similarly to the finding in the temporally filtered cases, it is found that LLM remains weak with much larger filter widths. The test cases in this section have used a fixed grid aspect ratio Δx = Δz = 2πΔy. Although not shown, we conducted several numerical experiments where the grid aspect ratio is varied (Δx = Δz = CΔy with C ranging from 1 to 10). Log-layer mismatch was again observed, but it was removed with the same filtering strategy.

FIG. 4.

Mean velocity profiles obtained with the spatially filtered wall-model input at the first off-wall LES point. The effective roughness height is y₀ = 6.8 × 10⁻⁵δ, which corresponds to a Re_τ = 2000 channel flow. The expected logarithmic law U/u_τ = 1/κ ln(y/y₀) is indicated using a solid red line. Solid blue lines are for a 32³ grid and dashed black lines are for a 64³ grid. Squares are for nine-point top-hat filters, diamonds are for five-point top-hat filters, and left-pointing triangles are for nine-point Gaussian filters.

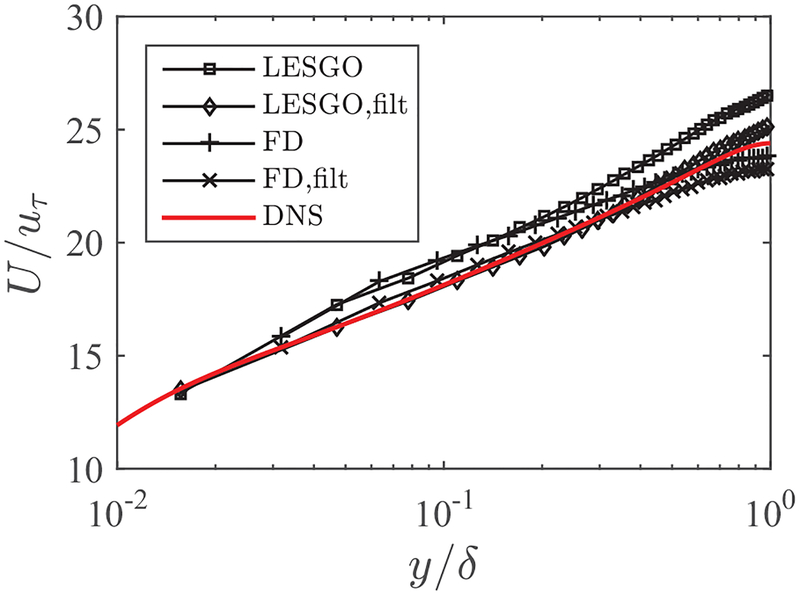
As the low resolving power of a less accurate numerical scheme can act as an effective filter, it is of interest to examine whether LLM can be removed by deploying lower-order numerical methods for the discretization of the LES equations. To this end, we carried out the same set of numerical experiments using a finite-difference channel flow code to investigate the effects of numerical methodology. In this code, the second-order finite-difference scheme is used for spatial discretization and the subgrid stress is modeled using the recently developed minimum dissipation model [38]. A grid of size 32 × 64 × 32 is used for a channel of size 2πδ × 2δ × 2πδ (note that this is a full channel and the grid aspect ratio is kept the same as in other cases). Figure 5 shows the mean-velocity profiles as functions of the wall-normal distance. With the finite-difference code (case FD), LLM occurs when the equilibrium model is applied directly to the first off-wall LES grid point, and we resolve LLM by applying a five-grid-point spatial filtering (case FD, filt). The LESGO results are included for comparison. Log-layer mismatch of similar magnitude is found. Employing a less-accurate spatial discretization does not seem to affect LLM in the near-wall region or the effectiveness of the proposed remedy. However, the flow in the bulk region is affected by the numerical methodology, where the law of wake is not captured at this particular resolution by the finite-difference code.

FIG. 5.

Mean velocity profiles. Here y₀ = 6.8 × 10⁻⁵δ. The lesgo and FD data are obtained with the spectral and second-order finite-difference codes, respectively, without filtering the wall-model input; “filt” means that the results are obtained with the five-grid-point spatial filtering. The red line is the DNS results of Hoyas and Jiménez [39].

Both the temporal filtering and wall-parallel spatial filtering allow a local wall-modeling procedure using the LES information right above the wall. We anticipate that the temporal filtering would be of greater utility for practical applications. This is because the wall-parallel filtering can be inappropriate in highly accelerating or decelerating flows and also due to the difficulty of constructing a discrete wall-parallel filter operating on unstructured mesh elements.

V. REVISITING THE CAUSE OF LLM

At this point, it is important to realize that the remedy suggested in the preceding section, as opposed to the prevailing remedy, neither introduces additional grid resolution near the wall nor uses the LES information away from the wall. This is in direct contradiction to the common perception that LLM is caused by the near-wall LES solution contaminated by the numerical and SGS modeling errors due to the too-large grid spacing [21]. With our remedy, LLM is resolved even when the near-wall LES solution remains significantly underresolved. This implies that potentially a distinctly different mechanism beyond the naive numerical-error argument may be at work in producing LLM. Identifying the correct cause of LLM is of great importance in wall-stress modeling, because this would have significant implication on developing alternative wall-modeling strategies, as in the progress made in the hybrid RANS-LES community over the past decades for model developments [7]. In this section we propose an alternative explanation of how LLM is caused in WMLES based on detailed analysis of flow statistics near the wall.

We first consider the validity of the argument made by Bou-Zeid et al. [34]. They argued that wall models can overpredict the wall stress even in the absence of the numerical and SGS modeling errors in LES. Based on the commonly found scaling τ_{w, wm} ~ ρu² between the wall-model input and output, they deduced that the mean wall stress modeled by a wall model can be overpredicted due to the fluctuations inherent in the LES velocity, even if the LES velocity is correct in the mean sense: 〈τ_{w, wm}〉 ~ ρ〈u〉² + ρ〈u′²〉 > ρ〈u〉² ~ 〈τ_w〉. Here 〈·〉 indicates ensemble averaging, τ_w is the true wall stress, τ_{w, wm} is the modeled wall stress, u′ is the instantaneous velocity fluctuation, and u is the instantaneous velocity. This argument may explain a negative LLM (downward shift of the mean-velocity profile due to the overpredicted wall stress), but the positive LLM is clearly not explained by this mechanism. In fact, close scrutiny of the near-wall flow statistics given in Table I shows that this scaling argument does not explain the negative LLM either. The mean velocity (〈u〉²) and the level of velocity fluctuations (〈u′²〉/〈u〉²) show no appreciable change in the cases with and without LLM. Instead, comparing the case with LLM (NFil) with the cases without LLM (Fil and 2nd pt), a notable difference is found in the resolved Reynolds shear stress at the first off-wall grid point. We notice the Reynolds shear stress −〈u′ v′〉 is significantly smaller when LLM persists, suggesting that turbulence near the wall is less energetic. Considering a momentum balance at the first off-wall LES grid point, the total shear stress −〈u′ v′〉 + 〈(u + v_t)〉∂u/∂y〉 is balanced by the imposed mean pressure gradient [(1/ρ)(dp/dx)]. Therefore, a smaller −〈u′ v′〉 necessarily leads to an increased 〈(u + v_t)〉∂u/∂y〉. The increased 〈(u + v_t)〉∂u/∂y〉 may be due to a corresponding increase in either the LES eddy viscosity ν_t or the velocity gradient, d〈u〉/dy, or both. However, because $\langle u(y)\rangle \equiv 0+{\int }_0^y\langle du/d{y}^{\prime }\rangle d{y}^{\prime }$, LLM is associated much more likely with the increased d〈u〉/dy. This was confirmed from the WMLES solution, where the LES eddy viscosity at the first off-wall grid point is almost identical in the cases considered in Table I. We therefore conclude that the positive LLM is a result of underpredicted Reynolds shear stress. Because −〈u′ v′〉 is not sufficiently large, the velocity gradient d〈u〉/dy increases to compensate for the deficit, leading to a positive LLM.

TABLE I.

List of the relevant quantities near the wall. The nomenclature for the cases is the same as in Fig. 1. Here u is the instantaneous streamwise LES velocity at y = h_wm and u′ is the instantaneous streamwise velocity fluctuation. In addition, 〈u′ v′〉 is the resolved Reynolds shear stress evaluated at the first LES grid point for all cases. All quantities are in wall units. For all the cases shown here, y₀ = 0.0001δ, which corresponds to Re_τ = 1400.

Cases	hwm	${\langle u\rangle }_{y=h_{wn}}^2$	${\langle u{\prime }^2\rangle }_{y=h_{wn}}$	〈u′2〉/〈u〉2	−〈u′v′〉y=Δy/2	LLM strength
NFil	Δy/2	1.1 × 102	4.7	4.2%	0.22	7%
Fil	Δy/2	1.1 × 102	5.7	5.2%	0.28	2%
2nd pt	3Δy/2	1.8 × 102	7.4	4.1%	0.27	2%

A more fundamental question is then why the Reynolds shear stress is underpredicted when using the raw LES data at the first off-wall grid point as the wall-model input (as in the case NFil). We consider how the modeled wall-shear stress and the input LES velocity is related at the instantaneous level,

$${\tau }_{wm}=\rho {\left[\frac{\kappa }{\text{ln}\left(h_{wm}/y_0\right)}\right]}^2{u}^2=\rho {\left[\frac{\kappa }{\text{ln}\left(h_{wm}/y_0\right)}\right]}^2\left({\langle u\rangle }^2+2\langle u\rangle u^{\prime }+u^2\right)\approx \langle {\tau }_w\rangle +2\rho \left[\frac{\kappa }{\text{ln}\left(h_{wm}/y_0\right)}\right]u_{\tau }{u}^{\prime }=\langle {\tau }_w\rangle +C\rho u_{\tau }{u}^{\prime }.$$ (3)

Here it is assumed that the term that is second order in fluctuations (u′²) is negligibly small compared to others. Equation (3) suggests that the instantaneous fluctuations in the wall stress ${\tau }_w^{\prime }$ are proportional to the instantaneous fluctuations in the input LES velocity (i.e., ${\tau }_w^{\prime }~\rho u_{\tau }{u}^{\prime }$). When u is taken from the first LES off-wall grid point, this implies that the wall model responds immediately to the change in u, instantaneously draining more momentum when u′ > 0 and less momentum when u′ < 0. This effectively “locks” the wall-adjacent LES velocity, damping the near-wall fluctuations. Consequently, the Reynolds shear stress −〈u′ v′〉 becomes less energetic. Overall, this problem is the direct consequence of the unphysical high correlation between the LES velocity at the first off-wall point (likely located at y⁺ ≫ 100 for high-Reynolds-number flows) and the wall-shear stress (defined at y⁺ = 0). The correlation coefficient C in the present WMLES calculations (N = 64³) can be estimated from Eq. (3) to be 0.2. Note that C, in the framework of the recent inner-outer interaction model [40], can be interpreted as the superposition effect of the velocity signal in the log-layer region on the wall-shear stress [41–43]. The coefficient C in the high-Reynolds-number experiment or DNS is found to be less than 0.1 at wall distances comparable to the matching locations in the present study [40].

This analysis suggests that LLM can be mitigated by disrupting the unphysical correlation between ${\tau }_{wm}^{\prime }$ and u′ in coarse WMLES. This hypothesis can be confirmed by a numerical experiment, where the imposed shear stress at the wall is constructed by a superposition of the known mean wall-shear stress with the fluctuations having a controllable correlation with the LES velocity at the first off-wall grid point. Note that the channel flow driven with the known pressure gradient allows the construction of such simple wall models, as the mean wall-shear stress is known a priori. For this purpose, we model the wall stress according to

$${\tau }_{wm}=\langle {\tau }_w\rangle +C\rho u_{\tau }{[u-\langle u\rangle ]}_{y=\Delta y/2},$$ (4)

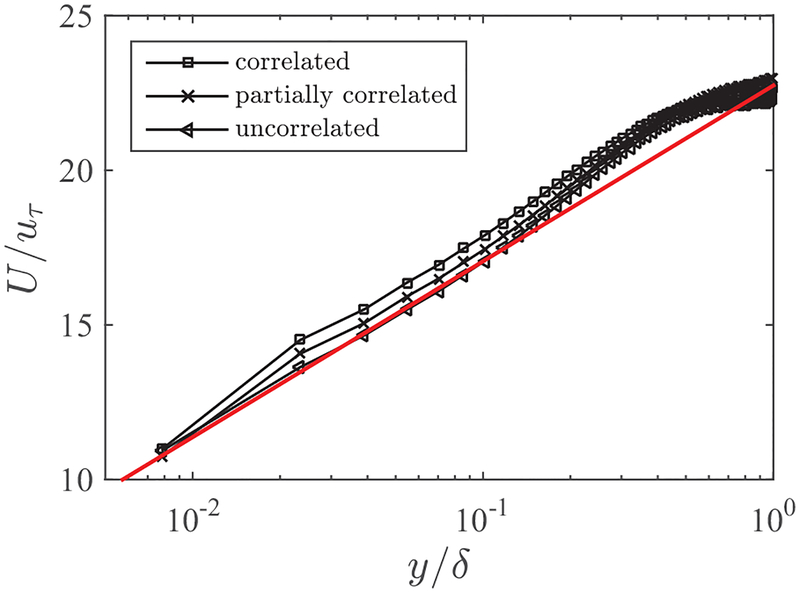
with C = 0.2, 0.1, and 0. As can be seen in Fig. 6, a 7% LLM is found with C = 0.2. The LLM reduces with C = 0.1 and LLM is essentially resolved with C = 0.

FIG. 6.

Semilogarithmic plot of the mean-velocity profiles as functions of the wall-normal distance. The wall stresses are specified according to Eq. (4). Here C = 0.2 for the correlated case, C = 0.1 for the partially correlated case, and C = 0 for the uncorrelated case. For the cases shown here, y₀ = 0.0001δ, which corresponds to Re_τ = 1400.

To summarize, the proposed mechanism of LLM is as follows. When a wall model operates with the LES velocity at the first off-wall grid point, the modeled stress fluctuations are instantaneously (and unphysically) correlated to the LES velocity, causing damping of turbulence adjacent to the wall. Then, to satisfy the momentum balance, the reduced Reynolds shear stress −〈u′ v′〉 gives rise to an increased 〈du/dy〉, leading to LLM.

It becomes more clear now how filtering the LES signal provided to the wall model resolves LLM. Filtering disrupts the unphysical direct coupling between ${\tau }_w^{\prime }$ and u′ by removing the velocity fluctuations u′ in Eq. (3) and subsequently leading to a more energetic 〈u′ v′〉 and eventually to a reduction of LLM. The same argument can be used to explain how the traditional remedy of using the LES information away from the wall, as advocated by Kawai and Larsson [21], helps resolve LLM. In this case, the wall-shear stress is correlated with the LES velocity far away from the wall, which effectively removes the damping or locking cycle between the wall-shear stress and the wall-adjacent LES velocity. This argument could also be used to explain how the control-based wall model developed in Ref. [35] resolves LLM, where the wall-shear stress is modified such that the near-wall RANS solution matches as closely as possible the near-wall LES solution. As reported in Ref. [35], the control strategy essentially decorrelates the modified stress from the first off-wall LES velocity, but correlates it with the second off-wall LES velocity.

VI. WALL STRESS FLUCTUATIONS

The discussion in the previous sections has focused on the first-order quantities. High-order quantities including the wall-stress fluctuations are of interest in a few applications [44,45]. When compared to DNS, WMLES inevitably underpredicts the fluctuations in the wall-shear stress [46] owning to the implied use of LES filters. A fair comparison is between WMLES and the filtered DNS at the corresponding LES resolution.

Table II reports the root-mean-square (rms) values of the wall-stress fluctuations from WMLES and the filtered DNS. The grid sizes of the WMLES are 32³, 64³ and 128³ and the DNS is filtered at the corresponding LES resolutions. The input LES velocities to the equilibrium wall model is filtered with a nine-point top-hat filter. The DNS is a channel flow at Re_τ ≈ 2000. The DNS resolution is $\Delta x^{+}=12.3,\Delta y_{\text{min}}^{+}=0.22,\Delta y_{\text{min}}^{+}=6.1$, and Δz⁺ = 6.1. Details of this DNS data set can be found in Ref. [39]. Based on the data in Table II, we reconfirm that WMLES underpredicts the fluctuations in the wall stress; meanwhile, we find that the rms wall-stress fluctuations from WMLES agree well with those from the DNS filtered at the corresponding LES resolution.

Table II.

Root mean square of the streamwise wall-stress fluctuations. We test three wall models: the equilibrium model used at the first off-wall LES grid point, with a nine-point top-hat filtering of the wall-model input; the equilibrium wall model used at the second off-wall LES grid point (no filtering); and the integral wall model in its original form [33] (with a temporal filtering of the first off-wall LES data). For each wall model, WMLESs at three grid sizes are conducted. The rms of the DNS stress fluctuations is 0.42. The last three rows are for the filtered DNS data. All numbers are in wall units.

LES grid	Corresponding LES grid size	Wall model	rms of the streamwise wall stress
323		Equilibrium model first grid	0.16
643		Equilibrium model first grid	0.21
1283		Equilibrium model first grid	0.25
323		Equilibrium model second grid	0.13
643		Equilibrium model second grid	0.19
1283		Equilibrium model second grid	0.24
323		Integral model	0.15
643		Integral model	0.20
1283		Integral model	0.26
	323		0.14
	643		0.19
	1283		0.25

VII. CONCLUSION

Log-layer mismatch in WMLES refers to the erroneous shift of the mean-velocity profile below or above the logarithmic layer, when wall-stress models are operated with the LES velocity at the wall-adjacent control volumes. In boundary layers, LLM leads to the skin friction error up to 15%, not admissible in application of WMLES for practical engineering applications. A prevailing remedy for resolving LLM in WMLES is based on a hypothesis that the near-wall LES solution is contaminated by the inherent truncation and SGS modeling errors owing to the use of too-large grid spacings near the wall, especially in the wall-normal direction. This remedy suggests providing the wall model the LES data at least two to three cells away from the wall. This method has proven to be robust, resolving LLM with little effort when using structured grids. However, this remedy was recently found to be not only impractical in terms of the LES mesh preparation for complex geometries (with corners and junctures) and implementation in the unstructured parallel flow solvers, but also inaccurate in accounting for the complex velocity profiles found in external aerodynamics (e.g., skewed 3D mean-velocity profile).

In this paper we proposed a simple remedy for LLM that is well suited for application to complex flows. This method resolves LLM by simply providing the wall model the filtered LES data in the wall-adjacent control volumes. It is shown that both spatial and temporal filtering work.

The perception of LLM being attributable simply to the numerical error [21] does not explain how our method resolves LLM, as our remedy still uses the LES data right above the wall. We proposed a mechanism explaining the cause of LLM based on quantitative analysis of the near-wall flow statistics in WMLES of turbulent channel flow, summarized as follows. Log-layer mismatch is thought to be a consequence of the underpredicted Reynolds shear stress \〈u′ v′〉\ near the wall. This is compensated for by the increase in the velocity gradient ($\frac{\partial \langle u\rangle }{\partial y}$) near the wall, eventually leading to the erroneous shift of the mean-velocity profile (that is, LLM). The reason why the Reynolds shear stress is underpredicted when wall models are given the wall-adjacent LES data is first explained based on how the wall stress from the wall model is coupled to the wall-adjacent LES velocity at the instantaneous level. It is proposed that the unphysically strong coupling between the wall-adjacent LES velocity [defined likely at y⁺ ≫ O(100) in WMLES] and the wall stress (defined at y⁺ = 0) makes the wall-stress fluctuations an effective damper of the near-wall turbulence. According to this analysis, resolving LLM requires decorrelating the wall stress and the wall-adjacent LES velocity, and numerical experiments further carried out (Fig. 6) provide support to this argument. Theproposed mechanism can also explain how both the traditional remedy and our method proposed here help removing LLM. The LES flow field in the near-wall region is admittedly underresolved, but we conclude that this is not necessarily the culprit of LLM.

We reconfirm that WMLES does not predict the wall-shear stress fluctuations well. However, it is found that WMLES captures the rms of the filtered DNS wall stress. A better description of the fluctuating wall stress requires adequate modeling of the unresolved SGS wall-stress fluctuations. Although a direct path to such SGS modeling is not known, the insights and understanding gained from the superposition-modulation model [47–53] might be a promising starting point for the finer-scale stress modeling.