Abstract
Large-eddy simulation (LES) has proven to be a computationally tractable approach to simulate unsteady turbulent flows. However, prohibitive resolution requirements induced by near-wall eddies in high–Reynolds number boundary layers necessitate the use of wall models or approximate wall boundary conditions. We review recent investigations in wall-modeled LES, including the development of novel approximate boundary conditions and the application of wall models to complex flows (e.g., boundary-layer separation, shock/boundary-layer interactions, transition). We also assess the validity of underlying assumptions in wall-model derivations to elucidate the accuracy of these investigations, and offer suggestions for future studies.
Keywords: large-eddy simulation, turbulence, wall modeling
1. INTRODUCTION
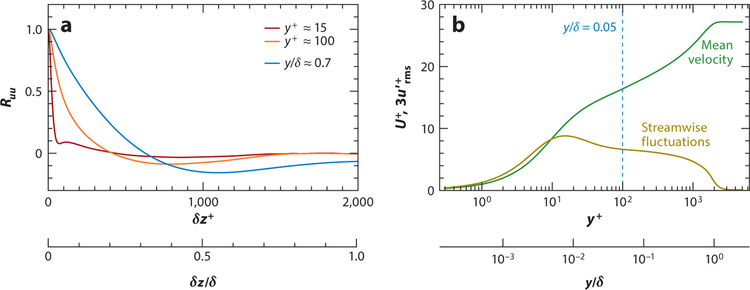
Large-eddy simulation (LES) has become an indispensable engineering tool in the prediction and analysis of unsteady, multiscale, and multiphysics turbulent flows over the past several decades. The accuracy of the LES approaches is primarily due to the fact that the dynamics of the energy-dominant and flow-dependent large eddies are directly resolved on a computational mesh rather than being modeled (as their interactions would be in a steady, Reynolds-averaged context). One notable exception is the flow near solid boundaries and walls, where quasi-streamwise vortices that dominate the near-wall flow field scale with the viscous length, δν = ν/uτ, instead of the local boundary-layer thickness, δ. In this case, ν is the fluid kinematic viscosity, and denotes the friction velocity defined with the wall-shear stress and fluid density. Specifically, these near-wall eddies are approximately l+ ~ O(102) in size along the span near the edge of the buffer layer and grow linearly with increasing distance from the wall (Jiménez 2012). The superscript + denotes the quantities nondimensionalized with ν and uτ (i.e., wall unit). As the friction-based Reynolds number Reτ = δ/δν increases, these near-wall vortices decrease in size relative to the boundary-layer thickness and therefore introduce resolution requirements that are potentially prohibitive. These resolution arguments can be drawn from structural considerations. Figure 1a shows the spanwise correlations of the streamwise velocity fluctuations at varying distances from the wall, which have small correlation length scales near the wall but scale with the boundary-layer thickness near the edge of the boundary layer (l/δ ~ 0.5 at y/δ = 0.7).
Figure 1.
(a) Spanwise two-point autocorrelations of the streamwise velocity at y+ ≈ 15, y+ ≈ 100, and y/δ ≈ 0.7. (b) Mean velocity profile and streamwise fluctuations for a Reθ = 6,500 zero–pressure gradient boundary layer. Data from Sillero et al. (2014).
LES can be either wall-resolved or wall-modeled depending on whether these near-wall eddies are resolved on the computational grid or modeled, respectively. Although much is known about the dynamics and structure of high–Reynolds number, near-wall turbulence (for a review, see Smits et al. 2011), this knowledge has not directly translated into computationally accurate and robust wall models for LES. Instead, existing phenomenological models are built largely on equilibrium assumptions (either directly, by assuming an equilibrium stress or velocity distribution in the inner layer, or indirectly, through the eddy viscosity characterizing the inner-layer Reynolds stress).
In his pioneering work, Chapman (1979) estimated and contrasted the number of computational grid points necessary for direct numerical simulation (DNS), wall-resolved LES (WRLES), and wall-modeled LES (WMLES), which have been recently revisited by Choi & Moin (2012), whose results are briefly outlined in this review. Consider the local resolution requirements of a differential volume scaled by the local boundary-layer thickness, dV = δ dxdz. Throughout this review, x, y, and z denote the streamwise, wall-normal, and spanwise directions, respectively. The number of grid points, dN, in this differential volume can then be characterized by
| 1. |
| 2. |
for WRLES and WMLES, respectively. In these equations, ni denotes the number of grid points used to resolve a length of δ in the xi direction, and and denote, respectively, the streamwise and spanwise grid spacings in wall units necessary to resolve the near-wall eddies in a WRLES. The total number of grid points, N, can then be obtained by integrating Equations 1 and 2 along the streamwise and spanwise directions, which results in scalings of , , and Nwm ~ ReL for DNS, WRLES, and WMLES, respectively (Choi & Moin 2012), where ReL is based on the streamwise length. Although WRLES has a more favorable scaling than DNS, the near-quadratic Reynolds number dependence of the number of grid points renders such an approach infeasible for realistic configurations. Thus, a strategy where only the outer-layer eddies are resolved and the near-wall eddies scaling in size with viscous units (lν) are modeled is required (see Figure 2). If the resolution is chosen, for instance, as Δ/δ ~ 0.05, the velocity gradient at the wall and, thus, the wall stress cannot be accurately computed by simply differencing the near-wall solution because the near-wall velocity profile is not resolved, nor is the inner-layer velocity fluctuation peak captured by the LES (profiles in Figure 1b at y/δ ≤ 0.05 are subgrid). As the near-wall cells increase in size, computational cost savings are realized also by reducing the temporal stiffness induced by the viscous sublayer (particularly beneficial for explicitly time-stepped, compressible flow solvers).
Figure 2.
Schematic illustrating a typical wall-modeled grid resolution, chosen to resolve the energetic eddies in the outer portion of the boundary layer, whose size scales with δ. Contours visualized represent the instantaneous streamwise velocity in a turbulent channel flow (Reτ = 4,200). The contours range from U + = 6 (blue) to 18 (white). Data taken from the direct numerical simulation of Lozano-Durán & Jiménez (2014); reproduced with permission, courtesy of A. Lozano-Durán.
Wall-modeled approaches can be broadly characterized into two categories: a hybrid Reynolds-averaged Navier–Stokes (RANS)/LES formulation, where RANS equations are solved near the wall and interface to an LES away from the solid boundary, or formulations where the LES governing equations are solved in the entirety of the domain. In the former category, the delineation of the RANS and LES domains is either explicit, as in zonal approaches, or implicitly described by the closure model, as in detached-eddy simulation (DES). The theoretical foundations of hybrid RANS/LES and DES approaches have been detailed in previous reviews (Piomelli & Balaras 2002, Fröhlich & von Terzi 2008, Piomelli 2008, Spalart 2009, Mockett et al. 2012) and are not reiterated in this article. This review instead focuses on the latter approach, where LES governing equations deploying formal subgrid models are valid everywhere in the domain, whereas wall (or virtual wall) boundary conditions are augmented to account for the effect of the unresolved inner layer of the boundary layer. It should also be noted that several reviews describe recent progress in WMLES (Larsson et al. 2016, Moin et al. 2016).
This review is organized as follows: Section 2 reviews the construction and assumptions for different wall models, with particular emphasis on recent advances and novel methodologies that have been developed in the past decade, including wall-modeled approaches that do not rely on thin boundary-layer (or RANS) approximations. As the wall models are now being generalized to complex flows, a critical assessment of the underlying assumptions is presented. Section 3 revisits the actual costs of WMLES to date compared to the past projections of the necessary computational complexity. Section 4 surveys the results of wall-modeled simulations in complex flow environments including laminar–turbulent transition, flow separation, realistic engineering geometries, shock/boundary-layer interactions, and the interaction of wall models with other physics (e.g., combustion, aeroacoustics); finally, Section 5 describes future directions and offers concluding remarks.
2. WALL MODELING METHODOLOGIES
2.1. Wall-Stress Modeling
If we consider the boundary closure necessary for the application of momentum conservation in the first cell near the wall, then the wall stress must be provided from the boundary condition whether the simulations are wall resolved or wall modeled. In a wall-resolved calculation, the wall-shear stress can be approximated by reconstructing the wall-normal gradient using a Dirichlet no-slip condition at the wall. If the inner layer is unresolved, then the wall-shear stress must be computed in some alternative manner. The simplest approximation for the wall-shear stress is algebraically related to the velocity at some distance from the wall y*. In the absence of pressure gradient effects on the boundary layer, the velocity profile can be assumed to satisfy a logarithmic law (Deardorff 1970, Schumann 1975, Grötzbach 1987):
| 3. |
where κ denotes the von Kármán constant and B is an intercept coefficient. Equation 3 is a nonlinear equation that can be solved for the wall friction velocity uτ. Other algebraic closures of the wall stress rely on different assumptions on the shape of the velocity profile, potentially accounting for the viscous sublayer and buffer layer (Spalding 1961, Werner & Wengle 1993) or the influence of the pressure gradient (Manhart et al. 2008). The more general Monin-Obukhov similarity theory (see Yaglom 1979), which incorporates the effects of non-neutral stratification in the atmospheric boundary layer, continues to be used frequently in geophysical LES (Moeng 1984, Porté-Agel et al. 2000, Brasseur 2010). In these algebraic closures, it is typically assumed that the law of the wall is valid locally and instantaneously, and a no-penetration condition is enforced for the wall-normal velocity.
The strict assumptions on the velocity profile (and, potentially, its parametric coefficients) can be relaxed by considering the thin boundary-layer equations (TBLE). The TBLE solve for the suitably averaged wall-parallel velocity components ũi (Balaras & Benocci 1994, Cabot & Moin 2000, Wang & Moin 2002) (written here for an incompressible flow):
| 4. |
| 5. |
where ṽt represents an eddy viscosity closure of the unresolved Reynolds stress in the inner layer. A no-slip boundary condition is applied at the wall, and the wall-parallel velocities (u1 and u3) are matched to the LES solution at some distance from the wall (y*). The pressure is assumed to be wall-normal independent, and the wall-normal velocity (u2) is determined through the direct integration of the divergence-free constraint. The wall stress is computed from , evaluated at the wall. Extension of the TBLE to compressible flows in general requires solving the full compressible Navier–Stokes equations in the wall-model domain (Kawai & Larsson 2013, Park & Moin 2014) because the satisfaction of mass and energy conservation is no longer trivial.
If the left-hand side of Equation 4 (responsible for unsteadiness, convection, and pressure gradient effects) is neglected, then Equation 4 reduces to the equilibrium stress balance model, and the velocity field,ũi, obtained is regarded as a steady RANS solution for the velocity profile in the inner layer of the boundary layer. This is a statistical interpretation of the solution for y ≤ y*, which can be thought of as an ensemble of many eddies when the LES grid size is much larger than the inner viscous unit and the LES time step is much larger than the timescale of these near-wall eddies (Piomelli & Balaras 2002). This interpretation is valid as the near-wall cells become larger compared to the inner viscous scale; an autonomous minimal channel (Jiménez & Moin 1991) would require a cell size (or filter width) of Δx+ ≳300, Δz+ ≳100, and experimental evidence suggests that this is achieved for Δ+ ≳ 1,800 (Nakayama et al. 2004). In this limit, the wall-model eddy viscosity, μt, can be closed using a mixing-length argument:
| 6. |
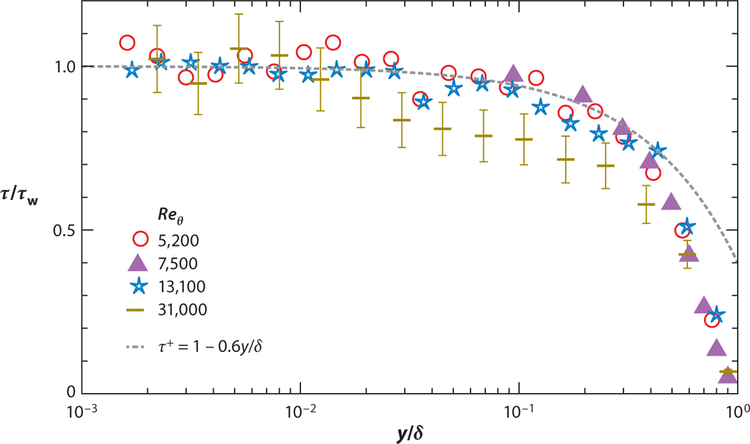
where D(y) is a damping function (e.g., van Driest damping) to ensure the eddy viscosity vanishes at the wall at a desired rate, and a constant value for the von Kármán constant is presumed (κ ≈ 0.41 for zero–pressure gradient boundary layers). It can be verified analytically that this choice of the eddy viscosity yields a velocity profile that satisfies the linear sublayer and the logarithmic law of the wall (Wang & Moin 2002). This simplification to the TBLE will lead to a constant total stress (viscous and Reynolds stresses) layer in the inner layer, which can easily be verified by integrating the right-hand side of Equation 4 from the wall to the matching location (dτ/dy = 0). For high–Reynolds number turbulent boundary layers in the absence of pressure gradients, there is experimental and numerical evidence that a constant stress layer exists for y+ ≲100 and then departs linearly with respect to y/δ (see Figure 3). These data (given the uncertainty and scatter in Figure 3) suggest that 0.95 <τ/τw < 1 can be achieved for y/δ ≲ 0.03 for sufficiently high Reynolds numbers.
Figure 3.
Total stress (sum of viscous and Reynolds stress) versus wall-normal distance for Reθ = 5,200 (red open circles) (DeGraaff & Eaton 2000), 7,500 (purple triangles) (Klebanoff 1955), 13,100 (blue stars) (DeGraaff & Eaton 2000), 31,000 (dark yellow lines) (DeGraaff & Eaton 2000), and τ+ = 1 − 0.6y/δ (dashed gray line) (Spalart 1988). An estimate of the uncertainty is shown for the Reθ = 31,000 data.
Several recent studies have attempted to assess the accuracy of the equilibrium approximation to the TBLE (discussed in Section 4). Alternatively, the validity of this approximation can be analyzed using a modified von Kármán integral analysis. Assuming that the wall-normal pressure gradient is negligible across the boundary layer and using the inviscid streamwise momentum equation outside the boundary layer , one can simplify Equation 4 to yield
| 7. |
which is similar to the equation derived by Hoffmann & Benocci (1995). The limit of y* → δ(x) in Equation 7 would yield the classical von Kármán momentum integral formula, where the first and last terms on the right-hand side will vanish. The three surviving terms can be seen to be functions of either the displacement thickness (δ*) or the momentum thickness (θ). Thus, with the assumption that the boundary-layer profile u(y) ≤ U∞, the second surviving term on the right-hand side (nondimensionalized by the local wall stress) can be bounded as
| 8. |
where Π is the Clauser parameter (Clauser 1954, Townsend 1956). There are two implications of this scaling, provided that is bounded (note that we are not insisting that Π be constant). First, the contribution of the pressure gradient term to the modeled wall stress as it appears in Equation 7 can be made negligibly small by controlling , which is a function of the LES resolution in the outer-layer units. This is the mathematical manifestation of the often-made statement that the pressure gradient effects are captured in equilibrium wall models because the majority of the boundary layer is resolved by the outer LES. Second, the resolution of the outer-layer LES (or the value of the matching location y*) necessary for the equilibrium assumption to be valid [τw ≈ τ(y*)] may be a function of the pressure gradient, Π; that is, the value of y* may need to be reduced in the presence of strong pressure gradients (although estimates of Π and δ* are not necessarily available a priori). This is a subtle but important distinction from recommendations that the wall-model height (y*) be a fixed fraction of the boundary-layer thickness [e.g., y* ≈ 0.1–0.2δ (Larsson et al. 2016)], which are not qualified with the magnitude of the local pressure gradient. Similar arguments can be made to scale the term more closely related to the momentum thickness in Equation 7. However, these arguments do not apply in the vicinity of the separation point where τw → 0.
Nonequilibrium wall models that retain some or all of the terms on the left-hand side of the TBLE are potentially more accurate than the equilibrium models because they adequately treat the additional terms arising in Equation 7 related to the outer layer. Wang & Moin (2002) performed a systematic investigation of the accuracy of the different TBLE formulations using an equilibrium approximation, an equilibrium assumption retaining the pressure gradient term, or all of the terms in Equation 4. Their key insight is that, if the convective terms are retained, then the (unsteady) inner-layer RANS solution will resolve some of the Reynolds stress, and the eddy viscosity in Equation 6 must be reduced accordingly to avoid the skin friction overprediction. Wang & Moin argued that, because the velocity fields between the inner-layer TBLE and the outer-layer LES are equal, matching the Reynolds stress at y = y* is equivalent to matching the unresolved Reynolds stress. This can be achieved by modifying the von Kármán constant across the inner layer as
| 9. |
where νSGS is the LES eddy viscosity. More recent investigations by Kawai & Larsson (2013) and Park & Moin (2014) suggest improvements to the calculation of κwm. Kawai & Larsson (2013) noted that the modeled κwm does not need to be independent of the wall-normal distance in the inner-layer solution. They observed that, as the Reynolds number increases, the embedded grid in the inner layer is unlikely to be able to support significant Reynolds stress (as Δx+ and Δz+ become large), so the computation of κ should asymptotically approach its nominal, constant value toward the wall independent of the value of νSGS from the LES. The approach of Wang & Moin (2002) (Equation 9), which does not account for this wall-normal variation of the resolved Reynolds stress, is shown by Kawai & Larsson (2013) to be potentially inaccurate in high–Reynolds number boundary layers. The modification proposed by Kawai & Larsson (2013) is to introduce a linear blending of the nominal von Kármán constant with Equation 9 based on the resolution of the embedded inner-layer grid; this blending is parameterized by an O(1) scaling coefficient that must be prescribed. Park & Moin (2014) subsequently found that the optimal value of this scaling coefficient is flow and mesh dependent, and they instead suggested an approach where κ is adjusted dynamically without the need for the ansatz regarding its particular linear variation:
| 10. |
where is the magnitude of the strain-rate tensor, is the resolved Reynolds stress in the inner-layer solution, and denotes the deviatoric component of the mean strain-rate tensor. The last term in Equation 10 is the negative of the eddy viscosity associated with the resolved turbulence in the wall-model solution. This correction therefore naturally excludes the portion already resolved from the stress being modeled.
Recent studies have also examined the influence of the pressure gradient in the absence of the convective or unsteady terms in Equation 4 (Manhart et al. 2008, Duprat et al. 2011, Maheu et al. 2012). These approaches are based on defining a mixed scaling for the normalized wall distance ŷ = yuτ p/ν, where the velocity scale is built from the friction velocity and a velocity scale that includes the pressure gradient effects, up (following Simpson 1983):
| 11. |
Similar to the results of Wang & Moin (2002), these investigations find more accurate predictions of the flow field when the pressure gradient effects are modeled versus when the equilibrium form of the wall model is used. However, Hickel et al. (2012) suggested that inclusion of the pressure gradient effects without the convective (and unsteady) terms is inconsistent with the momentum equations outside of the boundary layer (Bernoulli limit). Although this reasoning would suggest that the consideration of the pressure gradient alone by Wang & Moin (2002) and Catalano et al. (2003) is inconsistent, the turbulent eddy viscosity form suggested by Duprat et al. (2011), which utilizes a mixed velocity scaling, may still improve the wall-stress accuracy.
It is also possible to account for the nonequilibrium effects through the presumed shape of the near-wall velocity profile. Yang et al. (2015) suggested a velocity profile that is linear inside of the viscous sublayer or of the following form in the overlap region:
| 12. |
where the full approximation consists of 11 undetermined coefficients. These undetermined coefficients are solved from the application of boundary conditions, continuity, and the von Kármán momentum integral equation. This approach accounts for many nonequilibrium effects while maintaining the algebraic computational complexity so long as Equation 12 is valid.
Separation points, uτ → 0, are not necessarily treated accurately by many of the presumed velocity profiles or eddy viscosity closures. Massive separation of the boundary layer (due to an abrupt change in geometry, for instance) may produce vanishing eddy viscosities (e.g., μt,eq → 0 as uτ → 0 in Equation 6), effectively causing the simulations to revert to wall-stress closures that are dominated by the molecular viscosity μ. There is, however, no a priori estimate of the rate at which uτ → 0 toward the separation point in flows with mild, adverse pressure gradients. This has resulted in ad hoc treatment of separation in previous studies where a no-slip boundary condition is applied in regions where either the boundary layer is known to separate (Bodart et al. 2013) or solution inaccuracies and artifacts appear at corners (Cabot 1996). Section 4 reviews the accuracy of WMLES in separated regimes, but the treatment of separation points in wall-stress models remains a theoretical challenge.
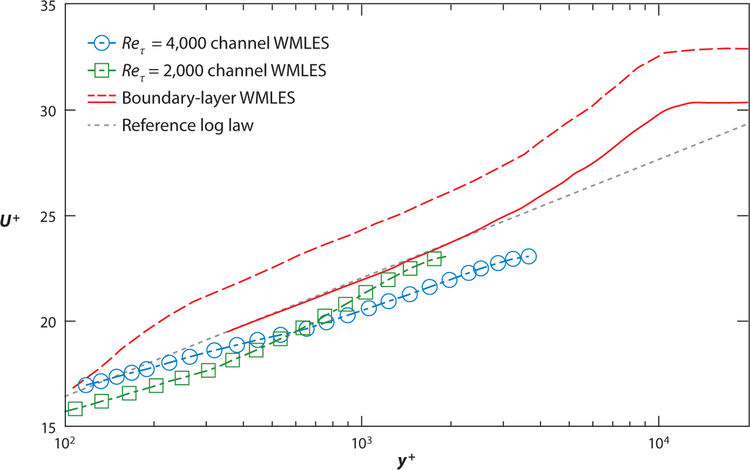
The location of the off-wall matching location, where the LES provides the outer boundary condition on the wall-model equations, has thus far been left unspecified. The precise choice of y* has been the subject of recent attention. This location must be at least the size of the first grid cell near the wall but sufficiently close to the wall such that a constant stress-layer approximation is valid if equilibrium approximations of the TBLE are made. The most natural choice is to use the velocity (or temperature) in the first grid cell as the matching condition. However, this choice has led to difficulties where the predicted velocity profiles appear shifted with respect to the actual law of the wall in both hybrid RANS/LES formulations (Nikitin et al. 2000) and WMLES solutions (Cabot & Moin 2000, Nicoud et al. 2001, Lee et al. 2013), referred to as the log-layer mismatch (see Figure 4). Both Kawai & Larsson (2012) and Wu & Meyers (2013) observed that these errors are largest in the first cell, where the stress-carrying eddies that scale with distance from the wall must be underresolved. In fact, for a logarithmic velocity profile (see Equation 3), the leading error for the discrete approximation of the mean shear at a distance y = d Δy from the wall is given by (Wu & Meyers 2013)
| 13. |
for an nth order accurate discretization. The first grid cell would correspond to a value of d = 1/2 or d = 1 (depending on the centering of the solution variables), and the Taylor series remainder can be large and does not vanish with increasing n at these locations. Kawai & Larsson (2012) suggested that the matching location be placed m grid points inside the domain, where m is determined based on the details of the numerical scheme and considerations of the boundarylayer thickness. For their choice of numerical method, the mean Reynolds shear stress appears to converge for Δy/y* ≲0.3, which has been referred to colloquially as the third grid point solution, although they ultimately advocated that this off-wall location be a specified fraction of the boundary-layer thickness. Note that, in complex geometries with concave wall junctures (such as those of a realistic aircraft), it is difficult or perhaps impossible to provide an off-wall location that maintains a specified y/δ fraction and has m − 1 grid points below it in the wall-normal directions (Park & Moin 2016c). Wu & Meyers (2013) also augmented the boundary treatment for the calculation of the wall-normal derivative, and suggest that the eddy viscosity coefficient in the LES subgrid scale (SGS) model [e.g., dynamic Smagorinsky model (Germano et al. 1991, Lilly 1992)] can be adjusted to prevent the log-layer mismatch by a proper consideration of the turbulent kinetic energy budget. A solution to the log-layer mismatch problem has also been proposed by Bou-Zeid et al. (2004). The mean wall stress in an algebraic formulation is related to the velocity at the matching location by 〈τw〉 ∝ 〈u(y*)2〉, but the law of the wall satisfies 〈τw〉 ∝ 〈u(y*)2〉. Because 〈u(y*)2〉 > 〈u(y*) 2〉, the modeled wall stress in the LES will be larger than expected. As a remedy, they propose using a spatially filtered version of the velocity at the first cell to compute the wall stress from an algebraic closure, which also relieves the log-layer mismatch.
Figure 4.
Compilation of the log-layer mismatch data from various wall-modeled large-eddy simulation (WMLES) calculations. Red dashed and solid lines are from the boundary layer WMLES of Kawai & Larsson (2012) with the first and third point matching, respectively (Ma = 1.7, Reθ = 5 × 104). The blue line with circular symbols is the Reτ = 4,000 channel WMLES with the first point matching (Templeton et al. 2006); the green line with square symbols is the Reτ = 2,000 channel WMLES with the first point matching (Lee et al. 2013); the gray dotted line is the reference log law.
A recent investigation (Yang et al. 2017) suggests that the mismatch is instead caused by unphysically high correlation between the wall stress and the LES data at the first off-wall cell, which leads to damping of the near-wall Reynolds shear stress and, in turn, an overestimation of the velocity gradient. This mechanism may provide a unified explanation for different remedies; the artificial correlation can be inhibited either by filtering the wall-model input (Bou-Zeid et al. 2004) or using the LES data away from the wall as the TBLE boundary conditions (Kawai & Larsson 2012). This mechanism deviates from the common perception that the near-wall numerical or SGS modeling errors are responsible for the mismatch, but it currently does not provide a clear explanation of some reported mismatches involving the velocity deficits in the log layer (negative log-layer mismatch).
2.2. Virtual Wall Boundary Conditions
If the solution cannot be accurately computed near the wall due to the presence of steep wall-normal gradients, then one approach is to terminate the LES domain at some finite distance above the wall and to provide boundary conditions at this virtual boundary (Chung & Pullin 2009, Inoue & Pullin 2011). An equation for the wall stress is derived by integrating the TBLE to some distance from the wall h and assuming a local inner scaling based on ν and uτ:
| 14. |
where denotes a wall-parallel filtration, and is the wall-normal gradient of the streamwise velocity at the wall. From the solution of η0, the slip velocity at a lifted virtual wall height (h0), which corresponds to the location of the bottom boundary in the LES, can be determined by assuming that a constant stress layer exists at 0 ≤ y ≤ h0 and that the streamwise velocity satisfies a logarithmic profile. Chung & Pullin (2009) determined the local, Kármán-like constant in the logarithmic velocity profile by considering the near-wall eddies to be described by the streamwise-aligned stretched vortices (Lundgren 1982, Misra & Pullin 1997). The original Chung & Pullin (2009) model assumes that there is no transpiration or spanwise velocities at the virtual lifted wall, but they are accounted for in later work by Cheng et al. (2015) to better represent flow in the vicinity of separation and reattachment. The identification of a lifted surface in the presence of complex geometries, however, may pose challenges in the simulation of practical engineering configurations.
2.3. Dynamic Slip Wall Modeling
An alternative approach to wall modeling has been introduced in which one derives boundary conditions for the filtered Navier–Stokes equations instead of relying on thin boundary-layer approximations (as in Equation 4). Recall that the governing equations for LES can be derived from the application of a spatial filter to the Navier–Stokes equations, but the wall-stress models described above have not connected themselves formally to the boundary conditions associated with the spatial filtration. Specification of the true wall stress is phenomenologically consistent with the hypothesis that the outer (large-scale) structures are related to the inner layer through the wall stress (Townsend 1980). However, the use of the true (unfiltered) boundary conditions for the filtered fields is valid only when the near-wall filter width is small compared to the velocity (or temperature) gradient (Ghosal & Moin 1995), which is certainly violated in WMLES. Bose & Moin (2014) derived the formal filtered boundary conditions from a modified Germano differential filter of the form (Germano 1986, Bose 2012)
| 15. |
where and ϕ denote the filtered and unfiltered variables, respectively, and lp denotes a length-scale regularization parameter. The regularization parameter is proportional to Δ2 away from boundaries (where Δ denotes an approximate filter width) and lp = 0 at the boundary. Given the singularity constraint that lp vanishes at all boundaries, Equation 15 yields the following Robin boundary condition for the velocity field when evaluated at a no-slip wall:
| 16. |
where the slip length CΔw is a measure of an isotropic near-wall filter width. This slip length can be computed from a Germano-like dynamic procedure (Bose & Moin 2014). It can be verified by inspection that this slip boundary condition smoothly reverts to a no-slip condition if CΔw/lv ≪ 1 or at a separation point where . In the limit when CΔw/lv ≫ 1, the wall will produce a finite Reynolds stress as the wall admits both local slip and transpiration in order to maintain the proper total shear stress at the wall. The admission of local transpiration has been shown to reduce the overprediction of near-wall streamwise turbulence intensities; a potential explanation for this is that unresolved eddies incident on the wall (splatting) are not forced to immediately transfer their momentum into the wall-parallel velocity components due to a no-penetration condition at the wall, as is typically applied. This interpretation of a non-zero Reynolds stress at the wall is potentially also consistent with the analysis of the inner wall layer in the limit of asymptotically large Reynolds numbers (Pullin et al. 2013). Although this approach to wall modeling may appear rather different, Yang et al. (2016) showed that the stress generated by this model can be equivalent to an equilibrium wall-stress model and is functionally similar to the boundary conditions imposed in a virtual wall approach.
The slip wall model differs from the formulation of traditional wall models in two distinct ways. First, the derivation of the boundary condition in Equation 16 did not require any assumption on the near-wall velocity profile, alignment of the wall stress with a predominant flow direction, the equilibrium state of the boundary layer, or the introduction of inner-layer eddy viscosities. Instead, the form of the wall boundary condition follows from constraining the form of the spatial filter applied to the Navier–Stokes equations (lp = 0 at the wall). Second, there are no empirically specified coefficients when the slip length is computed dynamically. However, the accuracy of the slip wall model is limited by the robustness of the dynamic procedure to compute the slip length, which was recently found to be sensitive to the SGS models and numerical methods used. Addressing this robustness issue and the inclusion of other physical effects (compressibility and heat transfer) are currently under active research at the Center for Turbulence Research at Stanford University (Bae et al. 2016, Lozáno-Duran et al. 2017).
2.4. Control-Based Strategies for Approximate Wall Boundary Conditions
A final class of wall models that have been introduced during the past two decades is based on control theory. The wall-parallel shear stresses can be computed to produce a given target velocity profile (either presumed or obtained from a near-wall RANS solution) (Nicoud et al. 2001; Templeton et al. 2006, 2008). Construction of the adjoint Navier–Stokes equations with respect to the prescribed wall stress allows the wall stress to adjust based on the particular SGS model and near-wall discretization errors to produce the desired near-wall solution. Although the control-based approaches have not proliferated in their use (likely due to the complexity of their implementation), these studies have elucidated the structural aspects of the near-wall LES field as a function of the computed wall stress. Templeton et al. (2008) found that the streamwise stress computed from a control-based wall model (which accurately reproduces the channel solution up to Reτ = 20,000) has the highest correlation with the LES streamwise velocity fluctuations at the second wall-normal grid point before rapidly falling off at larger distances. This is consistent with the mechanism of the log-layer mismatch in Section 2.1 and the remedy of coupling the wall model to interior grid cells where the correlation is weaker. The control-based wall models also offer insight into the performance of an ideal equilibrium wall model where the deviation of the LES mean velocity profile for y < y* from the target RANS profiles is minimized. When y* is taken to be the size of the wall-adjacent cell, Templeton et al. (2008) found that this minimization necessarily leads to the overpredicted intensities near the wall. This may provide an explanation for the excessively large near-wall velocity fluctuations observed in some wall-model formulations. The adjoint formalism also offered a rigorous method to evaluate sensitivities of wall-model formulations with respect to a priori specified model coefficients or the location of coupling (y*). These approaches provide useful tools that may help analyze and guide the development of wall models, even if the final resultant model does not invoke control theory.
It is also possible to obtain a target (mean) velocity profile using control theory by augmenting the LES SGS closure rather than the boundary condition. This alternative approach has been used in the prediction of channel flows, albeit at relatively low Reτ (less than 103) (Langford & Moser 1999, Völker et al. 2002, Bhattacharya et al. 2008). The motivating idea of augmenting the SGS closure rather than the boundary condition does not necessarily require the control-based methodology and could be pursued as another approach to the near-wall modeling problem.
2.5. Thermal Wall Boundary Conditions and High-Speed Flows
We now turn our attention to the closure of approximate boundary conditions for an unresolved thermal boundary layer (which necessitates the modeling of the wall heat flux) and other associated modeling challenges in high-speed boundary layers. The formulations of thermal boundary conditions for WMLES are based largely around thin boundary-layer approximations made to the total energy equation. Following the equilibrium assumptions discussed in Section 2.1 and assuming constant fluid properties, the total energy equation simplifies to
| 17. |
where, using statistical arguments discussed above that the cells contain an ensemble of eddies, and represent the averaged velocity and temperature in the inner layer, respectively; λ is the thermal conductivity; is the modeled Reynolds stress; and qturb is the turbulent heat flux. In an equilibrium boundary layer, it is assumed that the turbulent heat flux is dominated by transport of heat (enthalpy) by the near-wall eddies such that , where λt is a turbulent thermal conductivity (Rannie 1956). Similar reasoning suggests that turbulent thermal conductivity can be related to the eddy viscosity through a turbulent Prandtl number ; prescribing an eddy viscosity and Prt then closes the equilibrium total energy equation in Equation 17. In the absence of strong viscous heating, these approximations lead to the well-known strong Reynolds analogy, which states that the local skin friction and heat transfer are proportional (St = Cf/2, where St is the Stanton number). The strong Reynolds analogy has been shown experimentally to be robust with departures of the constant skin friction–Stanton number proportionality less than 30% for high-speed boundary layers with freestream Ma < 10, and weakly dependent on the Reynolds number (Reθ = 103–105) (Deissler & Loeffler 1959, Hill 1959), which has also been confirmed in DNS of zero–pressure gradient turbulent boundary layers in the presence of wall heating (Wu & Moin 2010). Additionally, the presence of the terms accounts for viscous heating in the inner layer such that the wall model can capture the near-wall temperature peaks even if this local extremum is not captured in the outer-layer LES. In simulations of high-speed boundary layers where this viscous heating becomes significant, care must be taken to ensure that the term (where ũi is the Favre-averaged LES velocity) that arises from the viscous work done by the SGS model is present in the total energy equation, so that the outer-layer LES provides an accurate thermal boundary condition to the wall model. This term is sometimes neglected in compressible LES formulations (Nagarajan et al. 2003, Chai & Mahesh 2012).
There are still few WMLES calculations focused on heat transfer, but some caution is warranted following previous experimental investigation into the law of the wall for heat transfer in flows with substantial pressure gradients. The obvious limitation in the use of assumptions that lead to a strong Reynolds analogy is near a separation point or in a separation bubble, where the skin friction vanishes but the heat transfer does not. Additionally, whereas the use of the law of the wall seems to lead to modest errors in the prediction of mean velocity profiles for flows with modest pressure gradients, these errors appear to be significantly amplified in the prediction of the inner-layer temperature profiles and wall heat transfer (Bradshaw & Huang 1995, Huang & Bradshaw 1995).
3. REVISITING PROJECTIONS OF COMPUTATIONAL COST AND COMPLEXITY
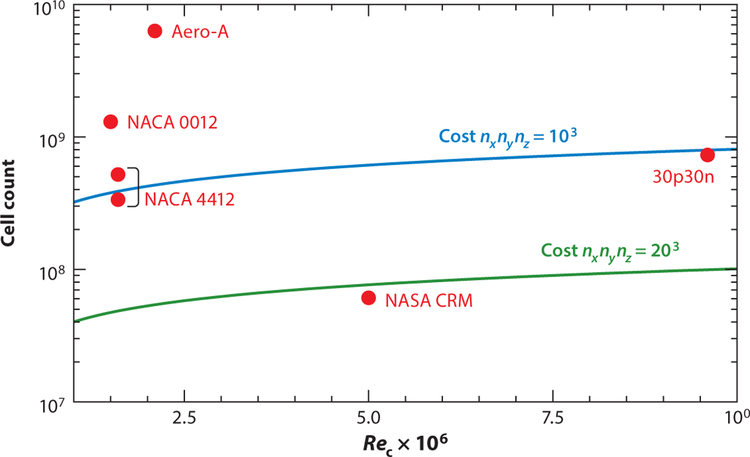
There have been several estimates of the cost of WMLES over the past several decades (Chapman 1979, Spalart et al. 1997, Choi & Moin 2012, Larsson et al. 2016), as well as recent prognostication on the utility of WMLES in specific application areas (Gourdain et al. 2014, Slotnick et al. 2014, Tyacke & Tucker 2015). These estimates differ in their methods of estimating the wall-shear stress or boundary-layer thickness (either with experimental correlations or RANS simulations) and in the requisite resolution of the outer-layer scales (ni in Equations 1 and 2). We can now compare the actual cost of wall-modeled calculations from recent simulations to these estimates, both in terms of absolute cost and in terms of their Re scaling over a limited range. Figure 5 shows computational cell counts associated with various airfoil simulations (discussed in Section 4) scaled to an airfoil section with an aspect ratio (span to mean chord) of 4. Strong conclusions cannot be drawn due to a limited number of data points and the narrow chord Reynolds number (Rec) range. However, the majority of calculations performed seem to require outer-layer resolution of nxnynz ≳ 203 for accuracy; this will increase the cost prefactor, assumed by Choi & Moin (2012), by a factor of three to five. Additionally, the scatter in the resolution required even at equivalent Reynolds numbers may be partially explained by the difficulty in generating optimal grids [where δ3/(ΔxΔyΔz) is fixed] when δ = δ(x). In practice, computational grids for increasingly complex geometries are more likely generated by setting resolutions based on a nominal or average boundary-layer thickness (as was assumed in Chapman’s cell estimates shown in Figure 5). This challenge underscores the need for concurrent development of mesh generation technologies for engineering applications in conjunction with further research on near-wall modeling.
Figure 5.
Cell count versus chord Reynolds number for spanwise-periodic airfoil simulations with an aspect ratio of 4; symbols denote the (scaled) cost of actual wall-modeled large-eddy simulation (WMLES) calculations of varying airfoils (NACA 0012, NACA 4412, Aerospatiale-A, NASA Common Research Model (CRM), and the MD 30P/30N), and lines denote Chapman’s cost estimates using nxnynz = 103 (green) and 203 (blue).
The numerical implementation of the wall model and its corresponding impact on the efficiency are indeed important, but they are not discussed in this review. Detailed discussions regarding the implementation of wall models can be found for two-layer zonal wall models on unstructured grids (Jaegle et al. 2010, Larsson et al. 2016, Park & Moin 2016a), slip wall models on unstructured grids (Bose 2012), wall modeling using immersed-boundary techniques (Yang et al. 2015, Dhamankar et al. 2016), wall modeling using finite element or spectral differencing schemes (Lodato et al. 2014), and wall modeling using a lattice Boltzmann approach (Malaspinas & Sagaut 2014). Studies have reported that the cost of wall modeling is often small compared to the rest of the flow solution. The more computationally intensive, full, nonequilibrium TBLE formulation has required approximately a factor of two cost increase over the baseline cost of non-wall-modeled LES. It is important to note that increases in cost of factors of two or three can be small compared to the orders of magnitude of savings afforded by wall modeling at high Reynolds numbers. However, if the wall-stress calculation is costly compared to computations at internal cells, then load imbalance at large processor counts may be a more pertinent concern.
For examples where significant fractions of the boundary layer are laminar (including airfoil design, vehicular aerodynamics, and turbomachinery), the computational cost can be dominated by the resolution of the laminar boundary layer rather than the turbulent region (Spalart et al. 1997, Slotnick et al. 2014). This result can be deduced by inspection of Equation 2, where the number of grid points is inversely related to the boundary-layer thickness . The laminar boundary-layer thickness, particularly near the leading edge, is small compared to the thickness in the turbulent region and thus contributes significantly to the overall cost. The large surface curvature often found in the laminar region close to the leading edge may pose additional resolution requirements in the wall-tangential direction. Although the increased cost associated with the laminar regions has undoubtedly been observed in simulations to date, there are two reasons that this analysis leads to overly pessimistic conclusions. First, this scaling presumes that an isotropic resolution is used in the laminar regions. The assumption of isotropic resolution in Equation 2 is based on structural considerations of turbulence in the outer layer (y/δ > 0.1), but this may not be necessary in a laminar region where the solutions may not be rapidly changing in the stream- or spanwise directions. Admitting modest cell aspect ratios [e.g., AR = O(10)] would then reduce the scaling prefactor by orders of magnitude, making the cost of the turbulent regions dominant again. Second, based on isotropic cell resolution in the laminar boundary layer, Slotnick et al. (2014) concluded that petascale resources would be required to compute airfoils with Lz/c = 1 and Rec ~ 106. This is, however, inconsistent with the cost incurred by the recent wall-modeled simulations carried out in this Re regime, as discussed in Section 4. Although laminar boundary layers are not fully resolved in these calculations, they compare favorably with experimental measurements quantitatively. However, as Slotnick et al. (2014) correctly pointed out, the relaxation of the requirements in the laminar region is predicated upon the ability of the LES to accurately capture the laminar–turbulent transition.
4. APPLICATION OF WALL-MODELED LARGE-EDDY SIMULATION TO COMPLEX FLOWS
4.1. High–Reynolds Number, Rough-Wall, and Transitional Boundary Layers
The refinements in the implementations of the equilibrium and algebraic wall models have enabled the simulation of higher–Reynolds number boundary layers. Reτ on the order of 106–108 have been studied in channel flows (Chung & Pullin 2009, Lee et al. 2013), and 104 ≲ Reθ≲ 1012 have been considered in boundary layers (Inoue & Pullin 2011, Kawai & Larsson 2013). Although it is expected that the obtained mean profiles compare well with measurements and the law of the wall theory, as the underlying wall-model assumptions are strictly valid in these flows, the predictions of outer-layer velocity defect and turbulent fluctuations also show favorable agreement with experimental measurements. However, it remains unclear if the wall-modeled calculations will capture the appearance of the outer-layer peak in the streamwise turbulent fluctuations, the locations of which scale with (Hultmark 2012, Marusic et al. 2013). The inner peak at y+ ≈ 15 is almost certainly unresolved by WMLES, but at high Reynolds numbers, the outer-layer peak is likely also unresolved when the grid-resolution estimate of Choi & Moin (2012) is used (δ/Δxi ~ 10). Rough-wall boundary layers have also been simulated by modifying the inner-layer law of the wall using empirical correlations for the downward shift of the velocity profile as a function of the roughness height [ΔU + = f (k+)] in a virtual wall–based approach (Saito et al. 2012) or by admitting roughness drag coefficients into an integral wall model (Yang et al. 2015). These approaches appear to recover Reynolds number insensitivities in fully rough boundary layers.
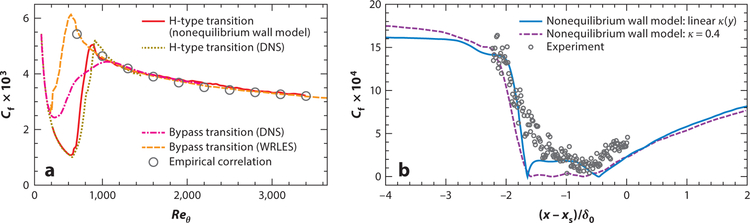
The resolution of unsteady, hydrodynamic instabilities coupled with dynamic procedures to automatically deactivate SGS models in laminar boundary layers has enabled WRLES to properly capture the location of the laminar–turbulent transition (Sayadi & Moin 2012). The wall stress supplied by wall models that presume turbulent Reynolds shear stress (see Equation 6) needs to be suppressed and replaced with a laminar closure upstream of the transition point. Bodart & Larsson (2012) used a sensor-based approach where the wall model is suppressed whenever the fluctuating velocity at the edge of the wall-model layer relative to the friction velocity falls below a specified threshold . This approach successfully allows the development of linear instabilities in flat-plate boundary layers, and the transition locations are well predicted (Bodart & Larsson 2012, Park & Moin 2014) (Figure 6a). Approaches using a slip wall model rely on the Germano-like dynamic procedure to produce vanishing slip lengths (CΔw → 0) in laminar regions.
Figure 6.
(a) Skin friction coefficient predictions for an H-type transitional boundary layer. The red solid line represents a nonequilibrium wall model (Park & Moin 2014), the dark yellow dashed line represents a DNS of H-type transition (Sayadi et al. 2013), the magenta dashed line with dots represents a DNS of bypass transition (Wu & Moin 2009), the orange line with long dashes represents a WRLES (Schlatter et al. 2010), and the gray circles represent the empirical correlation (Fernholz & Finley 1996). Adapted from Park & Moin (2014). (b) Skin friction coefficient predictions for an oblique shock/boundary-layer interaction at Ma = 1.7, β = 6°. The blue solid line represents a nonequilibrium wall model with linear κ(y) (Kawai & Larsson 2013), the purple dashed line represents a nonequilibrium wall model with constant κ = 0.4 (Balaras et al. 1996), and the gray circles represent the experiment (Souverein et al. 2010). Adapted from Kawai & Larsson (2013). Abbreviations: DNS, direct numerical simulation; WRLES, wall-resolved large-eddy simulation.
4.2. Estimation of Near-Wall Fluctuations
Capturing unsteady, turbulent fluctuations is one of the motivations for performing LES despite its increased cost over lower-fidelity approaches. In the context of WMLES, fluctuations at the surface (e.g., pressure and shear stress fluctuations) and in the unresolved inner layer are important quantities of interest. Park & Moin (2016b) assessed the ability of WMLES to predict wall pressure and wall-shear stress fluctuations; at wall-parallel resolutions of Δxt/δ ≲0.05, the pressure fluctuations are recovered within a few percent of the DNS, whereas the skin friction fluctuations remain underpredicted. This is consistent with the high–Reynolds number approximation of the wall-normal momentum equation, , which would suggest that the pressure fluctuations are imposed from the outer layer. Wall-shear stress fluctuations and the inner-layer fluctuation peak, however, are connected to the near-wall eddies, which are unresolved and must be explicitly reconstructed in wall-modeled calculations.
Empirical models to reconstruct the inner-layer streamwise turbulence intensities (Marusic et al. 2010, Mathis et al. 2011) and shear-stress fluctuations (Mathis et al. 2013) in zero– or weak–pressure gradient boundary layers (0 ≤ |Π| ≲ 2) have been formulated. If the effect of the outer-layer scales is to modulate the amplitude of the near-wall velocity signal (Hutchins & Marusic 2007, Mathis et al. 2009), then the near-wall velocity signal can be synthesized from the statistically universal signal at the same wall-normal location u* and the large-scale velocity signal in the log region according to
| 18. |
where α and β are calibration coefficients to describe the large-scale superposition and amplitude modulation on the small scales, respectively. This model has been successfully used to reconstruct the streamwise turbulence statistics in the inner layer given a time-resolved velocity signal from the outer layer in a variety of equilibrium boundary layers (channels, flat plates, pipes). This model has been subsequently used to reconstruct the inner-layer statistics from a WMLES that compared favorably with experimental measurements (Inoue et al. 2012). It has also served as the basis for providing a fluctuating wall-shear stress component with an algebraic wall-stress model (Sidebottom et al. 2014); unsurprisingly, its inclusion does not augment mean statistics but does enhance the spectral content of the flow near the wall.
4.3. Pressure Gradients and Wall-Modeled Large-Eddy Simulation in Complex Geometries
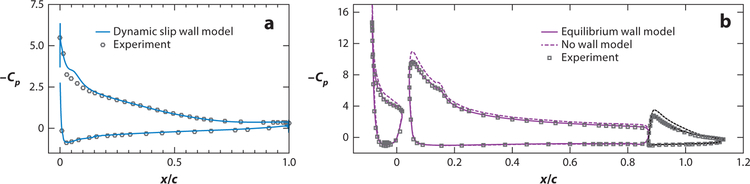
Practical engineering applications often consist of complex geometries, which engender the imposition of pressure gradients onto the boundary layers. There have been several recent investigations of the onset of stall on airfoils due to either trailing-edge separation [in the case of the NACA 4412 at Rec = 1.6 × 106 (Bose & Moin 2014, Park & Moin 2014, Iyer et al. 2016)] or leading- and trailing-edge separations [in the case of the Aerospatiale-A airfoil at Rec = 2.1 × 106 (Davidson et al. 2003, Kawai & Asada 2013)]. The proper resolution of the separated shear layer above the separation bubble is regarded as critical in all of these studies. In the case of the NACA 4412, predictions of the surface pressure coefficient and the velocity profiles in the separation region near the trailing edge compare favorably with the experimental measurements using equilibrium and fully nonequilibrium wall models, as well as the dynamic slip wall model. Specifically, these studies properly capture the flattening of the pressure coefficient on the suction side near the trailing edge, where the flow is separated; the dynamic slip wall modeling result is shown in Figure 7a, where the overprediction of the pressure coefficient near the leading edge is a result of an artificially induced transition. Predictions of the laminar separation and turbulent reattachment on the Aerospatiale-A airfoil agree well with the experimental measurements, but notable discrepancies in the separated region at the trailing edge can be found using algebraic and equilibrium wall models, as well as the nonequilibrium wall model of Kawai & Larsson (2013). These discrepancies near the trailing edge underscore the sensitivity of separated boundary layers in mild adverse pressure gradients to subtle differences in wall-model assumptions, implementations, and LES resolution of the outer layer, considering that wall-resolved calculations (at reduced spanwise extents) do capture the size of the separation bubble (Mary & Sagaut 2001). The periodic hill configuration of Almeida et al. (1993) has also been used to validate the wall-model accuracy in separating and reattaching flow configurations. Balakumar et al. (2014) found favorable agreement with DNS results using the slip, equilibrium, and nonequilibrium wall models, with the nonequilibrium wall model providing slightly more accurate predictions near the separation point. However, simulations were conducted at a relatively low Reynolds number (Reh = 10,595), and the differences may be more attributable to differences in the numerical methods in the outer-layer LES than the different wall models employed. The wall-mounted hump configuration of Greenblatt et al. (2006a,b) involving a moderately high–Reynolds number turbulent inflow (Reτ ≈ 2,000) has also been considered by Avdis et al. (2009) and Park (2017), who found that the full nonequilibrium TBLE model outperforms simpler equilibrium wall models in the separation bubble and recovery regions. Where available, turbulence intensities are moderately well predicted, although underpredicted away from the wall.
Figure 7.
(a) Surface pressure coefficients for a NACA 4412 airfoil at angle of attack (AoA) 13.8°. The dark blue line represents a dynamic slip wall model (Bose & Moin 2014); the gray hexagons represent the experiment (Wadcock 1978). (b) Surface pressure coefficients for the MD 30P/30N multi-element airfoil at AoA = 19°. The purple dashed and solid lines represent no wall model and an equilibrium wall model, respectively (Bodart & Larsson 2011); the light blue squares represent the experiment (Chin et al. 1993). Panel a reproduced from Bose & Moin (2014). Panel b reproduced from Bodart & Larsson (2011).
Wall-modeled calculations have also been performed with more geometrically realistic configurations, including high-lift devices and airfoils with finite span. Bodart et al. (2013) performed LES using an equilibrium wall model of a multi-element McDonnell-Douglas 30P/30N airfoil (Rec = 9×106) at increasing angles of attack (AoA) through the onset of stall; Figure 7b shows the predicted pressure coefficient at AoA = 19°. The predicted lift polar appears qualitatively similar to the experimental measurements and the maximal lift is well captured, although the stall angle is predicted at a higher AoA in the LES (≈23°) than in the experiment (≈21°). This discrepancy is potentially attributed to the blockage corrections applied to the experimental data, limited spanwise domain lengths, or difficulties in statistically converging the LES calculations, particularly in the presence of low-frequency unsteadiness in the separated regions. Lehmkuhl et al. (2016) have also simulated the NASA common research model (Rec = 5 × 106, AR = 9, Ma = 0.85) using an algebraic wall-stress closure (Werner & Wengle 1993) at AoA = 4°. Predictions of the shock location, surface-pressure coefficients, and total lift and drag compare well with the experimental measurements, despite the relatively coarse grid (δ/Δ ~ 10) and complex flow topologies that are not considered in the algebraic wall-stress closure (e.g., shock/boundary-layer interactions). Ambo et al. (2017) have used the slip wall model to simulate a commercial automobile (ReL ~ 7×106) and showed good agreement with the measured pressure coefficient on the side-view mirrors, which experiences both laminar separation and an attached turbulent boundary layer near its trailing edge as a consequence of a three-dimensional laminar–turbulent transition. Similarly, favorable predictions of pressure coefficients and the velocity profiles have also been obtained by Alin et al. (2010) using an equilibrium wall model (Fureby et al. 2004) to simulate a simplified submarine (ReL = 12×106 on the DARPA SUBOFF model). Although there are not many studies of complex geometries, initial experience has been encouraging, suggesting that resolving the nonuniversal outer scales can lead to accurate predictions of complex flow phenomena, such as transition or the onset of separation.
4.4. High-Speed and Compressible Turbulent Boundary Layers
High-speed and compressible boundary layers introduce the additional complexity of modeling non-negligible viscous heating near the wall and shock/boundary-layer interactions, which are both of importance for aeronautical applications. Kawai & Larsson (2013) applied the nonequilibrium wall model with a modified κ calculation to the simulation of an Ma∞ = 1.7 oblique shock interacting with a turbulent boundary layer. Overall prediction of the wall skin friction (see Figure 6b) and the mean streamwise velocity profiles agree well with the experimental measurements. Although the boundary layer does not undergo massive separation, the probability of the appearance of reverse flow is also well captured by the WMLES. Predicting the low-frequency unsteadiness potentially requires resolving large coherent streaks in the boundary layer that scale with the boundary-layer thickness (Dolling 2001, Ganapathisubramani et al. 2007), which should be resolved by a WMLES. Bermejo-Moreno et al. (2014) considered a similar oblique shock/boundary-layer interaction (Ma ≈ 2, Reθ ≈ 1.4 × 104) using an equilibrium wall model, but the flow is confined inside a rectangular cross-sectioned duct. The agreement of the vertical velocity components with the experimental measurements near the duct side walls suggests that the secondary corner flows present in the WMLES are well predicted. However, simulations of a shock-free, supersonic duct by Vane et al. (2014) using the same equilibrium wall model show a much stronger secondary corner flow compared to the experimental measurements and elevated shear stress predictions in the duct corners, suggesting that the locally one-dimensional approximations introduced in the equilibrium wall model may be inadequate for the prediction of secondary flows. Similar conclusions are reached in studies of supersonic flows over a compression ramp where the rate of the wall-pressure rise is well predicted downstream of the corner but is initially delayed (Dawson et al. 2013).
The relative success of WMLES in predicting the momentum boundary layer in high-speed configurations is consistent with experience in SGS modeling in compressible flows, that is, scaling incompressible closure models to account for variable inertia (rather than true compressibility). The scaling of the incompressible closure models for the unresolved Reynolds stresses holds when the turbulent fluctuation Mach number is sufficiently small (Mt ≲ 0.2) (Lele 1994). In addition, in the modeled inner layer, the convective Mach number is greatly reduced as the velocity approaches that of a no-slip surface. Difficulties, however, may be encountered in the prediction of the thermal boundary layers (or wall heat transfer) if the strong Reynolds analogy is invalid. Following Morkovin (1962), this will be encountered if there are significant stagnation temperature variations across the boundary layer, which is true for strongly heated or cooled walls.
4.5. Wall Modeling in Multiphysics Large-Eddy Simulation
The discussion thus far has focused on the accuracy of wall models to provide an accurate wall stress or a prediction of near-wall or surface quantities of interest (e.g., skin friction or the mean or fluctuating surface pressure). In multiphysics simulations, the effect of the wall model may nonlinearly couple with additional physics to affect the macroscopic flow. One example has been WMLES of supersonic combustion in scramjet engines (Larsson et al. 2015, Saghafian et al. 2015): Inlet air is heated and compressed by an oblique shock train in a long isolator duct, and the subsequent combustion occurs at supersonic Mach numbers. Heating near the walls due to the viscous dissipation is substantial and is likely unresolved, as the location of the peak temperature scales with the inner viscous units. Modeling of the viscous heating and heat loss at the walls and prediction of the near-wall temperature is crucially important, as reaction rates of the subsequent combustion are exponentially dependent on the near-wall temperature. Simulations by Saghafian et al. (2015), for instance, demonstrate that the inclusion of wall modeling is necessary to predict the boundary-layer viscous heating necessary to stabilize the reaction upstream of the combustor cavity in the HIFiRE (Hypersonic International Flight Research and Experimentation) rig, which is consistent with experimental measurements (Hass et al. 2011). Similarly, Zhang et al. (2013) extended equilibrium wall models to account for radiative heat fluxes in the inner layer due to the presence of the wall, which results in particularly improved predictions of the mean temperature profiles in turbulent channel flows with heated walls.
Wall modeling is also crucial to the prediction of far-field noise radiated from flows at subsonic Mach numbers. Brès et al. (2015) performed LES of an isothermal, subsonic jet exhausting from a straight nozzle (Ma = 0.9, Rej = 106 quasi-laminar. Modeling of the experiment’s roughness patch used to trip the boundary layer was also vital in properly matching the boundary-layer thickness at the nozzle exit. The effect of wall modeling is even more pronounced at lower Mach numbers, where the prediction of the radiated sound is dependent largely on the surface pressure fluctuations. Kocheemoolayil & Lele (2014) computed the far-field noise from a NACA 0012 airfoil section (Rec = 1.5 × 106, near the wall) and found that the surface pressure fluctuations predicted by the LES lead to the far-field noise prediction agreeing with experimental measurements within <3 dB. However, this calculation required the rather fine wall-normal grid spacing (Δy+ ≲ 10), which may have reduced the relative impact of the applied wall model.
WMLES has also been applied to predicting distortions of optical signals by turbulent flows, which is important in airborne and ground laser systems for target detection and communication. Resolving optically relevant scales in high Re number flows does not significantly alter the cost of typical WRLES (Mani et al. 2008). However, in wall-modeled calculations, proper resolution of density fluctuations within boundary layers (which are directly responsible for optical distortion) requires a grid resolution beyond what is typically needed for obtaining accurate mean flow statistics. This is consistent with the finding of Park & Moin (2016b) that accurate prediction of the wall-pressure fluctuations in WMLES requires grid resolutions more stringent than that required for the mean velocity. With this consideration, Kamel et al. (2016) successfully carried out aero-optical LES computations of supersonic turbulent boundary layers (up to Reθ = 6.9 × 104) and subsonic separated flows over a cylindrical turret at ReR = 5.6 × 105 (based on the turret radius) using an equilibrium wall model.
5. CONCLUDING REMARKS AND FUTURE DIRECTIONS
Given the current and projected growth in computational power, the intractable Reynolds number scaling of the computational cost of DNS or WRLES necessitates wall-modeled approaches to LES. Advances made in the past decade are based on analysis of wall-stress models obtained from the thin boundary-layer approximation and novel derivations of new approximate wall boundary conditions. These have facilitated the simulation of high–Reynolds number flows with complex physics including but not limited to laminar–turbulent transition, flow separation, heat transfer, high-speed boundary layers, and multiphysics environments. Validation studies have shown favorable agreement with experimental measurements overall. In certain flow regimes where the wall-model assumptions are violated, the level of favorable agreement has been surprisingly encouraging. The derivation of the slip wall model does not invoke any inner-layer phenomenology, and it has also shown encouraging results. Continued WMLES calculations will likely elucidate the limits of the accuracy of existing models and their necessary resolution requirements. There are, however, some remaining challenges.
First, adequate resolution of the boundary-layer thickness that is presumed in wall-modeled approaches may not be tenable in many circumstances, including in thin, laminar boundary layers. The development of models that can adequately describe the growth of boundary-layer instabilities, their receptivity to external perturbations, and their subsequent coupling to the downstream turbulent field will be necessary. Some initial attempts, based on the use of parabolized stability equations, to describe the laminar boundary layer coupled to a downstream simulation have been made (Lozano-Durán et al. 2016).
Second, the off-wall location, y*, where the LES is coupled to the wall model (with the exception of the slip wall model, which does not have this requirement) has been prescribed as a fraction of the local boundary-layer thickness. In flows around complex geometries, the boundary-layer thickness is not known a priori, and it would be difficult to smoothly map the off-wall location y* = y*(x) such that y*/δ remained at a constant fraction of the spatially developing boundary layer. Therefore, it will be necessary to construct wall models that behave robustly with respect to the placement of y* or do not require knowledge of δ. Similarly, most of the wall models presented in this review assume that the wall stress is aligned with the predominant streamwise direction identified at y = y*. This orientation can be difficult to identify in boundary layers with mean three-dimensionality (e.g., swept wings), and the assumption about the alignment of the wall stress with the LES velocity at y* may be invalid in a swirled or separated flow.
Third, additional validation of wall-model accuracy in flows with pressure gradients (especially boundary-layer separations due to mild, adverse pressure gradients) is still needed. Many of the investigations of separated flows that have been performed to date involve conditions that will robustly result in separation bubbles (e.g., bluff bodies or shock-induced separation) or Re numbers that have not been sufficiently high upstream of the recirculation regions to warrant scale separation between the inner and outer layers. These additional validation cases will help clarify the need for, benefits of, and necessary improvements to nonequilibrium wall-model formulations.
Fourth, multiphysics applications will require a more detailed description of the flow near the boundaries, beyond the mean shear stress. Several applications presented in this review have demonstrated how the fluctuations in the inner layer or the presence of local extrema that are unresolved by the outer-layer LES nonlinearly affects the quantities of interest, such as far-field noise, heat release in reacting flows, or wall heat transfer. The prediction of the wall-normal velocity fluctuations is also of interest in the transport of inertial particles that may settle near a wall, as well as in the deposition of liquid films on walls. The selection of validation cases for wall models should more readily consider these cases, as the accuracy of wall models may very well dominate the overall accuracy of the solutions to multiphysics problems.
Lastly, establishing confidence in wall-modeled calculations in the absence of validation data is not straightforward. To treat complex flows, many of the newly developed wall models have introduced additional complexity with accompanying empiricism (e.g., model coefficients, parameters, or other simplifying assumptions regarding the state of the boundary layer). This additional empiricism will, at best, introduce unquantified sensitivities into LES predictions and, at worst, limit the predictive capability in increasingly complex flows. Thus, additional efforts to develop fully dynamic wall models and to quantify the effect of wall modeling errors are needed.
ACKNOWLEDGMENTS
The authors thank Dr. Xiang Yang, Dr. Jeremy Templeton, Dr. Daniel Chung, Dr. Adrian Lozano-Durán, and Prof. Parviz Moin for feedback and comments on early versions of this manuscript. G.I.P. acknowledges the support of NASA (grant NNX15AU93A), and S.T.B. acknowledges the support of Navair (SBIR Topic N132–102) during the preparation of this manuscript.
Footnotes
DISCLOSURE STATEMENT
The authors are not aware of any biases that might be perceived as affecting the objectivity of this review.
LITERATURE CITED
- Alin N, Bensow RE, Fureby C, Huuva T, Svennberg U. 2010. Current capabilities of DES and LES for submarines at straight course. J. Ship Res. 54:184–96 [Google Scholar]
- Almeida GP, Duro DFG, Heitor MV. 1993. Wake flows behind two-dimensional model hills. Exp. Therm. Fluid Sci. 7:87–101 [Google Scholar]
- Ambo K, Yoshino T, Kawamura T, Teramura M, Philips DA, et al. 2017. Comparison between wall-modeled and wall-resolved large eddy simulations for the prediction of boundary-layer separation around the side mirror of a full-scale vehicle. Presented at 55th AIAA Aerosp. Sci. Meet., Jan. 9–13, Grapevine, TX, AIAA Pap 2017–1661 [Google Scholar]
- Avdis A, Lardeau S, Leschziner M. 2009. Large eddy simulation of separated flow over a two-dimensional hump with and without control by means of a synthetic slot-jet. Flow Turbul. Combust 83:343–70 [Google Scholar]
- Bae H, Lozano-Durán A, Moin P. 2016. Investigation of the slip boundary condition in wall-modeled LES In Annual Research Briefs 2016, pp. 75–86. Stanford, CA: Cent. Turbul. Res. [PMC free article] [PubMed] [Google Scholar]
- Balakumar P, Park G, Pierce B. 2014. DNS, LES, and wall-modeled LES of separating flow over periodic hills Proc. Cent. Turbul. Res. Summer Progr., July 6–Aug. 1, pp. 407–15. Stanford, CA: Cent. Turbul. Res. [Google Scholar]
- Balaras E, Benocci C. 1994. Subgrid-scale models in finite-difference simulations of complex wall bounded flows In Application of Direct and Large Eddy Simulation to Transition and Turbulence, pp. 2-1–2-6. Neuilly-Sur-Seine, Fr: Advis. Group Aerosp. Res. [Google Scholar]
- Balaras E, Benocci C, Piomelli P. 1996. Two-layer approximate boundary conditions for large-eddy simulations. AIAA J. 34:1111–19 [Google Scholar]
- Bermejo-Moreno I, Campo L, Larsson J, Bodart J, Helmer D, Eaton JK. 2014. Confinement effects in shock wave/turbulent boundary layer interactions through wall-modelled large-eddy simulations. J. Fluid Mech. 758:5–62 [Google Scholar]
- Bhattacharya A, Das A, Moser RD. 2008. A filtered-wall formulation for large-eddy simulation of wall-bounded turbulence. Phys. Fluids 20:115104 [Google Scholar]
- Bodart J, Larsson J. 2011. Wall-modeled large eddy simulation in complex geometries with application to high-lift devices In Annual Research Briefs 2011, pp. 37–48. Stanford, CA: Cent. Turbul. Res. [Google Scholar]
- Bodart J, Larsson J. 2012. Sensor-based computation of transitional flows using wall-modeled large eddy simulation In Annual Research Briefs 2012, pp. 229–40. Stanford, CA: Cent. Turbul. Res. [Google Scholar]
- Bodart J, Larsson J, Moin P. 2013. Large eddy simulation of high-lift devices. Presented at 21st AIAA Comput. Fluid Dyn. Conf., June 24–27, San Diego, CA, AIAA Pap 2013–2724 [Google Scholar]
- Bose S 2012. Explicitly filtered large-eddy simulation: with application to grid adaptation and wall modeling PhD Thesis, Stanford Univ., Stanford, CA [Google Scholar]
- Bose ST, Moin P. 2014. A dynamic slip boundary condition for wall-modeled large-eddy simulation. Phys. Fluids 26:015104 [Google Scholar]
- Bou-Zeid E, Meneveau C, Parlange MB. 2004. Large-eddy simulation of neutral atmospheric boundary layer flow over heterogeneous surfaces: blending height and effective surface roughness. Water Resour. Res 40:W02505 [Google Scholar]
- Bradshaw P, Huang GP. 1995. The law of the wall in turbulent flow. Proc. R. Soc. Lond. A 451:165–88 [Google Scholar]
- Brasseur JG. 2010. Designing large-eddy simulation of the turbulent boundary layer to capture law-of-the-wall scaling. Phys. Fluids 22:021303 [Google Scholar]
- Brès GA, Jaunet V, Le Rallic M, Jordan P, Colonius T, Lele SK. 2015. Large eddy simulation for jet noise: the importance of getting the boundary layer right. Presented at 21st AIAA/CEAS Aeroacoust. Conf., June 22–26, Dallas, TX, AIAA Pap 2015–2535 [Google Scholar]
- Cabot W 1996. Near-wall models in large eddy simulations of flow behind a backward-facing step In Annual Research Briefs 1996, pp. 199–209. Stanford, CA: Cent. Turbul. Res. [Google Scholar]
- Cabot W, Moin P. 2000. Approximate wall boundary conditions in the large-eddy simulation of high Reynolds number flow. Flow Turbul. Combust 63:269–91 [Google Scholar]
- Catalano P, Wang M, Iaccarino G, Moin P. 2003. Numerical simulation of the flow around a circular cylinder at high Reynolds numbers. Int. J. Heat Fluid Flow 24:463–69 [Google Scholar]
- Chai X, Mahesh K. 2012. Dynamic k-equation model for large-eddy simulation of compressible flows. J. Fluid Mech. 699:385–413 [Google Scholar]
- Chapman DR. 1979. Computational aerodynamics development and outlook. AIAA J. 17:1293–313 [Google Scholar]
- Cheng W, Pullin DI, Samtaney R. 2015. Large-eddy simulation of separation and reattachment of a flat plate turbulent boundary layer. J. Fluid Mech. 785:78–108 [Google Scholar]
- Chin V, Peters D, Spaid F, McGhee R. 1993. Flowfield measurements about a multi-element airfoil at high Reynolds numbers. Presented at 23rd Fluid Dyn. Plasmadyn. Lasers Conf., July 6–9, Orlando, FL, AIAA Pap 1993–3137 [Google Scholar]
- Choi H, Moin P. 2012. Grid-point requirements for large eddy simulation: Chapman’s estimates revisited. Phys. Fluids 24:011702 [Google Scholar]
- Chung D, Pullin DI. 2009. Large-eddy simulation and wall modelling of turbulent channel flow. J. Fluid Mech. 631:281–309 [Google Scholar]
- Clauser F 1954. Turbulent boundary layers in adverse pressure gradients. J. Aeronaut. Sci 21:91–108 [Google Scholar]
- Davidson L, Cokljat D, Fröhlich J, Leschziner MA, Mellen C, Rodi W. 2003. Task 2: near-wall models In LESFOIL: Large Eddy Simulation of Flow Around a High Lift Airfoil, ed. Davidson L, Cokljat D, Fröhlich J, Leschziner MA, Mellen C, Rodi W, pp. 22–57. Berlin: Springer [Google Scholar]
- Dawson DM, Lele SK, Bodart J. 2013. Assessment of wall-modeled large eddy simulation for supersonic compression ramp flows. Presented at 49th AIAA/ASME/SAE/ASEE Joint Propuls. Conf., July 14–17, San Jose, CA, AIAA Pap 2013–3638 [Google Scholar]
- Deardorff JW. 1970. A numerical study of three-dimensional turbulent channel flow at large Reynolds numbers. J. Fluid Mech. 41:453–80 [Google Scholar]
- DeGraaff DB, Eaton JK. 2000. Reynolds-number scaling of the flat-plate turbulent boundary layer. J. Fluid Mech. 422:319–46 [Google Scholar]
- Deissler RG, Loeffler AL. 1959. Analysis of turbulent flow and heat transfer on a flat plate at high Mach numbers with variable fluid properties Tech. Rep. TR-R-17, Natl. Aeronaut. Space Admin., Washington, DC [Google Scholar]
- Dhamankar NS, Blaisdell GA, Lyrintzis AS. 2016. Implementation of a wall-modeled sharp immersed boundary method in a high-order large eddy simulation tool for jet aeroacoustics. Presented at 54th AIAA Aerosp. Sci. Meet., Jan. 4–8, San Diego, CA, AIAA Pap 2016–0257 [Google Scholar]
- Dolling DS. 2001. Fifty years of shock-wave/boundary-layer interaction research: What next? AIAA J. 39:1517–31 [Google Scholar]
- Duprat C, Balarac G, Mtais O, Congedo PM, Brugire O. 2011. A wall-layer model for large-eddy simulations of turbulent flows with/out pressure gradient. Phys. Fluids 23:015101 [Google Scholar]
- Fernholz H, Finley P. 1996. The incompressible zero-pressure-gradient turbulent boundary layer: an assessment of the data. Prog. Aerosp. Sci 32:245–311 [Google Scholar]
- Fröhlich J, von Terzi D. 2008. Hybrid LES/RANS methods for the simulation of turbulent flows. Prog. Aerosp. Sci 44:349–77 [Google Scholar]
- Fureby C, Alin N, Wikström N, Menon S, Svanstedt N, Persson L. 2004. Large eddy simulation of high- Reynolds-number wall bounded flows. AIAA J. 42:457–68 [Google Scholar]
- Ganapathisubramani B, Clemens NT, Dolling DS. 2007. Effects of upstream boundary layer on the unsteadiness of shock-induced separation. J. Fluid Mech. 585:369–94 [Google Scholar]
- Germano M 1986. Differential filters of elliptic type. Phys. Fluids 29:1757–58 [Google Scholar]
- Germano M, Piomelli U, Moin P, Cabot WH. 1991. A dynamic subgrid-scale eddy viscosity model. Phys. Fluids A 3:1760–65 [Google Scholar]
- Ghosal S, Moin P. 1995. The basic equations for the large eddy simulation of turbulent flows in complex geometry. J. Comput. Phys 118:24–37 [Google Scholar]
- Gourdain N, Sicot F, Duchaine F, Gicquel L. 2014. Large eddy simulation of flows in industrial compressors: a path from 2015 to 2035. Philos. Trans. R. Soc. Lond. A 372:20130323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greenblatt D, Paschal KB, Chung-Sheng Y, Harris J. 2006a. Experimental investigation of separation control part 2: zero mass-flux oscillatory blowing. AIAA J. 44:2831–45 [Google Scholar]
- Greenblatt D, Paschal KB, Yao CS, Harris J, Schaeffler NW, Washburn AE. 2006b. Experimental investigation of separation control part 1: baseline and steady suction. AIAA J. 44:2820–30 [Google Scholar]
- Grötzbach G 1987. Direct numerical and large eddy simulation of turbulent channel flows In Encyclopedia of Fluid Mechanics, Vol. 6, pp. 1337–91. Houston: Gulf [Google Scholar]
- Hass N, Cabell K, Storch A, Gruber M. 2011. HIFiRE direct-connect rig (HDCR) phase I scramjet test results from the NASA Langley Arc-Heated Scramjet Test Facility. Presented at 17th AIAA Int. Space Planes Hypersonic Syst. Technol. Conf., April 11–14, San Francisco, AIAA Pap 2011–2248 [Google Scholar]
- Hickel S, Touber E, Bodart J, Larsson J. 2012. A parametrized non-equilibrium wall-model for large-eddy simulations Proc. Cent. Turbul. Res. Summer Prog., June 24–July 20, pp. 127–36. Stanford, CA: Cent. Turbul. Res. [Google Scholar]
- Hill FK. 1959. Turbulent boundary layer measurements at Mach numbers from 8 to 10. Phys. Fluids 2:668–80 [Google Scholar]
- Hoffmann G, Benocci C. 1995. Approximate wall boundary conditions for large eddy simulations In Advances in Turbulence V, ed. Benzi R, pp. 222–28. Berlin: Springer [Google Scholar]
- Huang P, Bradshaw P. 1995. Law of the wall for turbulent flows in pressure gradients. AIAA J. 33:624–32 [Google Scholar]
- Hultmark M 2012. A theory for the streamwise turbulent fluctuations in high Reynolds number pipe flow. J. Fluid Mech. 707:575–84 [Google Scholar]
- Hutchins N, Marusic I. 2007. Large-scale influences in near-wall turbulence. Philos. Trans. R. Soc. Lond. A 365:647–64 [DOI] [PubMed] [Google Scholar]
- Inoue M, Mathis R, Marusic I, Pullin DI. 2012. Inner-layer intensities for the flat-plate turbulent boundary layer combining a predictive wall-model with large-eddy simulations. Phys. Fluids 24:075102 [Google Scholar]
- Inoue M, Pullin DI. 2011. Large-eddy simulation of the zero-pressure-gradient turbulent boundary layer up to Reθ = O(1012). J. Fluid Mech. 686:507–33 [Google Scholar]
- Iyer P, Park G, Malik M. 2016. A comparative study of wall models for LES of turbulent separated flow Proc. Cent. Turbul. Res. Summer Prog., June 26–July 22, pp. 325–34. Stanford, CA: Cent. Turbul. Res. [Google Scholar]
- Jaegle F, Cabrit O, Mendez S, Poinsot T. 2010. Implementation methods of wall functions in cell-vertex numerical solvers. Flow Turbul. Combust 85:245–72 [Google Scholar]
- Jiménez J 2012. Cascades in wall-bounded turbulence. Annu. Rev. Fluid Mech. 44:27–45 [Google Scholar]
- Jiménez J, Moin P. 1991. The minimal flow unit in near-wall turbulence. J. Fluid Mech. 225:213–40 [Google Scholar]
- Kamel MS, Wang K, Wang M. 2016. Predictions of aero-optical distortions using LES with wall modeling. Presented at 54th AIAA Aerosp. Sci. Meet., Jan. 4–8, San Diego, CA, AIAA Pap 2016–1462 [Google Scholar]
- Kawai S, Asada K. 2013. Wall-modeled large-eddy simulation of high Reynolds number flow around an airfoil near stall condition. Comput. Fluids 85:105–13 [Google Scholar]
- Kawai S, Larsson J. 2012. Wall-modeling in large eddy simulation: length scales, grid resolution, and accuracy. Phys. Fluids 24:015105 [Google Scholar]
- Kawai S, Larsson J. 2013. Dynamic non-equilibrium wall-modeling for large eddy simulation at high Reynolds numbers. Phys. Fluids 25:015105 [Google Scholar]
- Klebanoff PS. 1955. Characteristics of turbulence in boundary layer with zero pressure gradient Tech. Rep. TR-1247, Natl. Advis. Comm. Aeronaut., Washington, DC [Google Scholar]
- Kocheemoolayil JG, Lele SK. 2014. Wall modeled large eddy simulation of airfoil trailing edge noise. Presented at 20th AIAA/CEAS Aeroacoust. Conf., June 16–20, Atlanta, GA, AIAA Pap 2014–3304 [Google Scholar]
- Langford JA, Moser RD. 1999. Optimal LES formulations for isotropic turbulence. J. Fluid Mech. 398:321–46 [Google Scholar]
- Larsson J, Kawai S, Bodart J, Bermejo-Moreno I. 2016. Large eddy simulation with modeled wall-stress: recent progress and future directions. Mech. Eng. Rev 3:15–00418 [Google Scholar]
- Larsson J, Laurence S, Bermejo-Moreno I, Bodart J, Karl S, Vicquelin R. 2015. Incipient thermal choking and stable shock-train formation in the heat-release region of a scramjet combustor. Part II: large eddy simulations. Combust. Flame 162:907–20 [Google Scholar]
- Lee J, Cho M, Choi H. 2013. Large eddy simulations of turbulent channel and boundary layer flows at high Reynolds number with mean wall shear stress boundary condition. Phys. Fluids 25:110808 [Google Scholar]
- Lehmkuhl O, Park G, Moin P. 2016. LES of flow over the NASA Common Research Model with near-wall modeling Proc. Cent. Turbul. Res. Summer Prog., June 26–July 2 2, pp. 335–41. Stanford, CA: Cent. Turbul. Res. [Google Scholar]
- Lele SK. 1994. Compressibility effects on turbulence. Annu. Rev. Fluid Mech. 26:211–54 [Google Scholar]
- Lilly DK. 1992. A proposed modification of the Germano subgrid-scale closure method. Phys. Fluids A 4:633–35 [Google Scholar]
- Lodato G, Castonguay P, Jameson A. 2014. Structural wall-modeled LES using a high-order spectral difference scheme for unstructured meshes. Flow Turbul. Combust 92:579–606 [Google Scholar]
- Lozano-Durán A, Bae HJ, Bose ST, Moin P. 2017. Dynamic wall models for the slip boundary condition In Annual Research Briefs 2017. Stanford, CA: Cent. Turbul. Res. In press [PMC free article] [PubMed] [Google Scholar]
- Lozano-Durán A, Hack M, Park G, Moin P. 2016. Modeling boundary-layer transition in DNS and LES using parabolized stability equations In Annual Research Briefs 2016, pp. 29–37. Stanford, CA: Cent. Turbul. Res. [Google Scholar]
- Lozano-Durán A, Jiménez J. 2014. Effect of the computational domain on direct simulations of turbulent channels up to Reτ = 4200. Phys. Fluids 26:011702 [Google Scholar]
- Lundgren TS. 1982. Strained spiral vortex model for turbulent fine structure. Phys. Fluids 25:2193–203 [Google Scholar]
- Maheu N, Moureau V, Domingo P, Duchaine F, Balarac G. 2012. Large-eddy simulations of flow and heat transfer around a low-Mach number turbine blade Proc. Cent. Turbul. Res. Summer Prog., June 24–July 20, pp. 137–46. Stanford, CA: Cent. Turbul. Res. [Google Scholar]
- Malaspinas O, Sagaut P. 2014. Wall model for large-eddy simulation based on the lattice Boltzmann method. J. Comput. Phys 275:25–40 [Google Scholar]
- Manhart M, Peller N, Brun C. 2008. Near-wall scaling for turbulent boundary layers with adverse pressure gradient. Theor. Comput. Fluid Dyn. 22:243–60 [Google Scholar]
- Mani A, Wang M, Moin P. 2008. Resolution requirements for aero-optical simulations. J. Comput. Phys 227:9008–20 [Google Scholar]
- Marusic I, Mathis R, Hutchins N. 2010. Predictive model for wall-bounded turbulent flow. Science 329:193–96 [DOI] [PubMed] [Google Scholar]
- Marusic I, Monty JP, Hultmark M, Smits AJ. 2013. On the logarithmic region in wall turbulence. J. Fluid Mech. 716:R3 [Google Scholar]
- Mary I, Sagaut P. 2001. Large eddy simulation of flow around a high lift airfoil In Direct and Large-Eddy Simulation IV, ed. Geurts BJ, Friedrich R, Métais O, pp. 157–64. Berlin: Springer [Google Scholar]
- Mathis R, Hutchins N, Marusic I. 2009. Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628:311–37 [Google Scholar]
- Mathis R, Hutchins N, Marusic I. 2011. A predictive inner–outer model for streamwise turbulence statistics in wall-bounded flows. J. Fluid Mech. 681:537–66 [Google Scholar]
- Mathis R, Marusic I, Chernyshenko SI, Hutchins N. 2013. Estimating wall-shear-stress fluctuations given an outer region input. J. Fluid Mech. 715:163–80 [Google Scholar]
- Misra A, Pullin DI. 1997. A vortex-based subgrid stress model for large-eddy simulation. Phys. Fluids 9:2443–54 [Google Scholar]
- Mockett C, Fuchs M, Thiele F. 2012. Progress in DES for wall-modelled LES of complex internal flows. Comput. Fluids 65:44–55 [Google Scholar]
- Moeng CH. 1984. A large-eddy-simulation model for the study of planetary boundary-layer turbulence. J. Atmos. Sci 41:2052–62 [Google Scholar]
- Moin P, Bodart J, Bose S, Park GI. 2016. Wall-modeling in complex turbulent flows In Advances in Fluid-Structure Interaction, ed. Braza M, Bottaro A, Thompson M, pp. 207–19. Berlin: Springer [Google Scholar]
- Morkovin MV. 1962. Effects of compressibility on turbulent flows Colloq. Int. Mec. Turbul, pp. 367–80. Paris: Cent. Natl. Res. Sci. [Google Scholar]
- Nagarajan S, Lele SK, Ferziger JH. 2003. A robust high-order compact method for large eddy simulation. J. Comput. Phys 191:392–419 [Google Scholar]
- Nakayama A, Noda H, Maeda K. 2004. Similarity of instantaneous and filtered velocity fields in the near wall region of zero-pressure gradient boundary layer. Fluid Dyn. Res 35:299–321 [Google Scholar]
- Nicoud F, Baggett JS, Moin P, Cabot W. 2001. Large eddy simulation wall-modeling based on suboptimal control theory and linear stochastic estimation. Phys. Fluids 13:2968–84 [Google Scholar]
- Nikitin NV, Nicoud F, Wasistho B, Squires KD, Spalart PR. 2000. An approach to wall modeling in large-eddy simulations. Phys. Fluids 12:1629–32 [Google Scholar]
- Park GI. 2017. Wall-modeled large-eddy simulation of a high Reynolds number separating and reattaching flow. AIAA J. In press [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park GI, Moin P. 2014. An improved dynamic non-equilibrium wall-model for large eddy simulation. Phys. Fluids 26:015108 [Google Scholar]
- Park GI, Moin P. 2016a. Numerical aspects and implementation of a two-layer zonal wall model for LES of compressible turbulent flows on unstructured meshes. J. Comput. Phys 305:589–603 [Google Scholar]
- Park GI, Moin P. 2016b. Space-time characteristics of wall-pressure and wall shear-stress fluctuations in wall-modeled large eddy simulation. Phys. Rev. Fluids 1:024404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park GI, Moin P. 2016c. Wall-modeled LES: recent applications to complex flows In Annual Research Briefs 2016, pp. 39–50. Stanford, CA: Cent. Turbul. Res. [PMC free article] [PubMed] [Google Scholar]
- Piomelli U 2008. Wall-layer models for large-eddy simulations. Prog. Aerosp. Sci 44:437–46 [Google Scholar]
- Piomelli U, Balaras AE. 2002. Wall-layer models for large-eddy simulations. Annu. Rev. Fluid Mech. 34:349–74 [Google Scholar]
- Porté-Agel F, Meneveau C, Parlange MB. 2000. A scale-dependent dynamic model for large-eddy simulation: application to a neutral atmospheric boundary layer. J. Fluid Mech. 415:261–84 [Google Scholar]
- Pullin DI, Inoue M, Saito N. 2013. On the asymptotic state of high Reynolds number, smooth-wall turbulent flows. Phys. Fluids 25:015116 [Google Scholar]
- Rannie W 1956. Heat transfer in turbulent shear flow. J. Aeronaut. Sci 23:485–89 [Google Scholar]
- Saghafian A, Shunn L, Philips DA, Ham F. 2015. Large eddy simulations of the HIFiRE scramjet using a compressible flamelet/progress variable approach. Proc. Combust. Inst 35:2163–72 [Google Scholar]
- Saito N, Pullin DI, Inoue M. 2012. Large eddy simulation of smooth-wall, transitional and fully rough-wall channel flow. Phys. Fluids 24:075103 [Google Scholar]
- Sayadi T, Hamman CW, Moin P. 2013. Direct numerical simulation of complete H-type and K-type transitions with implications for the dynamics of turbulent boundary layers. J. Fluid Mech. 724:480–509 [Google Scholar]
- Sayadi T, Moin P. 2012. Large eddy simulation of controlled transition to turbulence. Phys. Fluids 24:114103 [Google Scholar]
- Schlatter P, Li Q, Brethouwer G, Johansson AV, Henningson DS. 2010. Simulations of spatially evolving turbulent boundary layers up to Reθ = 4300. Int. J. Heat Fluid Flow 31:251–61 [Google Scholar]
- Schumann U 1975. Subgrid scale model for finite difference simulations of turbulent flows in plane channels and annuli. J. Comput. Phys 18:376–404 [Google Scholar]
- Sidebottom W, Cabrit O, Marusic I, Meneveau C, Ooi A, Jones D. 2014. Modelling of wall shear-stress fluctuations for large-eddy simulation Proc. Australas. Fluid Mech. Conf., 19th, Dec. 8–11, Melbourne, Aust., Pap 224 Melbourne, Aust.: Australas. Fluid Mech. Soc. [Google Scholar]
- Sillero JA, Jiménez J, Moser RD. 2014. Two-point statistics for turbulent boundary layers and channels at Reynolds numbers up to δ+ ≈ 2000. Phys. Fluids 26:105109 [Google Scholar]
- Simpson RL. 1983. A model for the backflow mean velocity profile. AIAA J. 21:142–43 [Google Scholar]
- Slotnick J, Khodadoust A, Alonso J, Darmofal D, Gropp W, et al. 2014. CFD Vision 2030 Study: a path to revolutionary computational aerosciences Tech. Rep. CR-2014–21817, Natl. Aeronaut. Space Admin, Washington, DC [Google Scholar]
- Smits AJ, McKeon BJ, Marusic I. 2011. High Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43:353–75 [Google Scholar]
- Souverein LJ, Dupont P, Debiéve JF, Van Oudheusden BW, Scarano F. 2010. Effect of interaction strength on unsteadiness in shock-wave-induced separations. AIAA J. 48:1480–93 [Google Scholar]
- Spalart PR. 1988. Direct simulation of a turbulent boundary layer up to Reθ = 1410. J. Fluid Mech. 187:61–98 [Google Scholar]
- Spalart PR. 2009. Detached-eddy simulation. Annu. Rev. Fluid Mech. 41:181–202 [Google Scholar]
- Spalart PR, Jou W, Strelets M, Allmaras S. 1997. Comments on the feasibility of LES for wings, and on a hybrid RANS/LES approach Advances in DNS/LES: Proc. 1st AFOSR Int. Conf. DNS/LES, ed. Liu C, Liu Z, pp. 4–8. Columbus, OH: Greyden [Google Scholar]
- Spalding D 1961. A single formula for the law of the wall. J. Appl. Mech 28:455–58 [Google Scholar]
- Templeton JA, Wang M, Moin P. 2006. An efficient wall model for large-eddy simulation based on optimal control theory. Phys. Fluids 18:025101 [Google Scholar]
- Templeton JA, Wang M, Moin P. 2008. A predictive wall model for large-eddy simulation based on optimal control techniques. Phys. Fluids 20:065104 [Google Scholar]
- Townsend AA. 1956. The properties of equilibrium boundary layers. J. Fluid Mech. 1:561–73 [Google Scholar]
- Townsend AA. 1980. The Structure of Turbulent Shear Flow. Cambridge, UK: Cambridge Univ. Press [Google Scholar]
- Tyacke JC, Tucker PG. 2015. Future use of large eddy simulation in aero-engines. J. Turbomach 137:081005 [Google Scholar]
- Vane ZP, Bermejo-Moreno I, Lele SK. 2014. Wall-modeled large-eddy simulations of a supersonic turbulent flow in a square duct. Presented at 44th AIAA Fluid Dyn. Conf., June 16–20, Atlanta, GA, AIAA Pap 2014–2209 [Google Scholar]
- Völker S, Moser R, Venugopal P. 2002. Optimal large eddy simulation of turbulent channel flow based on direct numerical simulation statistical data. Phys. Fluids 14:3675–91 [Google Scholar]
- Wadcock AJ. 1978. Flying-hot-wire study of two-dimensional turbulent separation of an NACA 4412 airfoil at maximum lift PhD Thesis, Calif. Inst. Technol., Pasadena [Google Scholar]
- Wang M, Moin P. 2002. Dynamic wall modeling for large-eddy simulation of complex turbulent flows. Phys. Fluids 14:2043–51 [Google Scholar]
- Werner H, Wengle H. 1993. Large-eddy simulation of turbulent flow over and around a cube in a plate channel In Turbulent Shear Flows 8, ed. Durst F, Friedrich R, Launder BE, Schmidt FW, Schumann U, Whitelaw JH, pp. 155–68. Berlin: Springer [Google Scholar]
- Wu P, Meyers J. 2013. A constraint for the subgrid-scale stresses in the logarithmic region of high Reynolds number turbulent boundary layers: a solution to the log-layer mismatch problem. Phys. Fluids 25:015104 [Google Scholar]
- Wu X, Moin P. 2009. Direct numerical simulation of turbulence in a nominally zero-pressure-gradient flatplate boundary layer. J. Fluid Mech. 630:5–41 [Google Scholar]
- Wu X, Moin P. 2010. Transitional and turbulent boundary layer with heat transfer. Phys. Fluids 22:085105 [Google Scholar]
- Yaglom AM. 1979. Similarity laws for constant-pressure and pressure-gradient turbulent wall flows. Annu. Rev. Fluid Mech. 11:505–40 [Google Scholar]
- Yang XIA, Bose S, Moin P. 2016. A physics-based interpretation of the slip-wall LES model In Annual Research Briefs 2016, pp. 65–74. Stanford, CA: Cent. Turbul. Res. [Google Scholar]
- Yang XIA, Park GI, Moin P. 2017. Log-layer mismatch and modeling of the fluctuating wall stress in wall-modeled large-eddy simulations. Phys. Rev. Fluids 2:104601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang XIA, Sadique J, Mittal R, Meneveau C. 2015. Integral wall model for large eddy simulations of wall-bounded turbulent flows. Phys. Fluids 27:025112 [Google Scholar]
- Zhang YF, Vicquelin R, Gicquel O, Taine J. 2013. A wall model for LES accounting for radiation effects. Int. J. Heat Mass Transf. 67:712–23 [Google Scholar]