Dynamic wall models for the slip boundary condition

1. Motivation and objectives

The near-wall resolution requirements to accurately resolve the boundary layer in wall-bounded flows remains a pacing item in large-eddy simulation (LES) for high-Reynolds-number engineering applications. Chapman (1979) and Choi & Moin (2012) estimated that the number of grid points necessary for a wall-resolved LES scales as Re^1.9, where Re is the characteristic Reynolds number of the problem. The computational cost is still too high for many practical problems, especially for external aerodynamics, despite the favorable comparison to the Re^2.6 scaling required for direct numerical simulation (DNS) where all the relevant scales of motion are resolved.

By modeling the near-wall flow such that only the large-scale motions in the outer region of the boundary layer are resolved, the grid-point requirements for wall-modeled LES (WMLES) scale at most linearly with increasing Reynolds number. Therefore, wall-modeling stands as the most feasible approach compared to wall-resolved LES or DNS. Several strategies for modeling the near-wall region have been explored in the past, and most of them are effectively applied by replacing the no-slip boundary condition in the wall-parallel directions by a Neumann condition. This fact is motivated by the observation that, with the no-slip condition, most subgrid scale models do not provide the correct stress at the wall when the near-wall layer is not resolved by the grid (Jiménez & Moser 2000).

Examples of the most popular and well-known wall models are the traditional wall-stress models (or approximate boundary conditions), and detached eddy simulation (DES) and its variants. Approximate boundary condition models compute the wall stress using either the law of the wall (Deardorff 1970; Schumann 1975; Piomelli et al. 1989) or the solution obtained by solving a simplified version of the boundary-layer equations close to the wall or the Reynolds-averaged Navier-Stokes (RANS) equations (Balaras et al. 1996; Chung & Pullin 2009; Kawai & Larsson 2013; Park & Moin 2014). DES (Spalart et al. 1997) combines RANS equations close to the wall and LES in the outer layer, with the interface between RANS and LES domains enforced implicitly through the change in the turbulence model. The reader is referred to Piomelli & Balaras (2002), Cabot & Moin (2000), Spalart (2009), Larsson et al. (2016), and Bose & Park (2018) for a more comprehensive review of wall-modeled LES.

One of the most important limitations of the models above is that they depend on precomputed parameters and/or assume explicitly or implicitly a particular law for the mean velocity profile close to the wall. Only recently this has been challenged by Bose & Moin (2014) with a dynamic wall model based on the Germano’s identity that is free of any a-priori specified coefficients. In addition, the no-transpiration condition used in most wall models was replaced by a Robin boundary condition in the wall-normal direction. In the present study, we extend the work by Bose & Moin (2014) and propose a new methodology to build dynamic wall models for LES independent of any a-priori tunable parameters.

This report is organized as follows. A new approach for constructing dynamic wall models is formulated in Section 2. The models are derived and implemented as described in Section 3 and 4. The results for turbulent channel flow and three-dimensional transient channel flow are offered in Section 5. Finally, conclusions are given in Section 6.

2. Formulation of the problem

2.1. Previous dynamic models

Bose & Moin (2014) introduced a dynamic procedure for a wall model free of any a-priori parameters. The model was motivated from a specific form of the differential filter at the wall (Germano 1986; Bose & Moin 2014), and takes the form of a Robin boundary condition,

$${\overline{u}}_i=l\frac{\partial {\overline{u}}_i}{\partial n},$$ (2.1)

where u_i is the i-th velocity component, n is the wall-normal direction, and l is the slip length. The dynamic model computes l via a modified form of the Germano’s identity (Germano et al. 1991),

$$l^2\left({\text{Δ}}_R^2\frac{\partial {\widehat{\overline{u}}}_i}{\partial n}\frac{\partial {\widehat{\overline{u}}}_j}{\partial n}-\frac{\partial {\overline{u}}_i}{\partial n}\frac{\partial {\overline{u}}_j}{\partial n}\right)+T_{ij}^{SGS}-{\widehat{{\tau }_{ij}}}^{SGS}=\widehat{{\overline{u}}_i{\overline{u}}_j}-{\overline{u}}_i{\overline{u}}_j,$$ (2.2)

where $\left(\overline{\cdot }\right)$ is the grid filter, $\left(\widehat{\cdot }\right)$ is the test filter, Δ_R is the filter size ratio between the test and grid filters, ${\tau }_{ij}^{SGS}$ and $T_{ij}^{SGS}$ represent the grid and test filter subgrid stress (SGS) tensors, respectively. Eq. (2.2) is then solved for l by using a least-squares.

In Bose & Moin (2014), the model was tested for a series of turbulent channel flows and the NACA 4412 airfoil. We implemented the model and attempted to reproduce the channel flow results. However, the model did not perform as expected with our current implementation, which uses a different subgrid scale model and numerical discretization. This motivated the present study, and our results from model (2.2) are discussed at the end of Section 5.

2.2. Slip length based formulation

The problem of constructing a wall model consists of estimating the stress at the wall, τ_w, given the current and/or past states of the flow. The estimated stress is then imposed as a boundary condition for wall-modeled LES. An important observation is that the coupling of the wall model and the governing equations forms a dynamical system such that for a statistically steady flow, the equilibrium state must be stable and $\Vert {\tau }_w-{\tau }_w^{DNS}\Vert$ is below the acceptable tolerance in some norm ‖ ⋅ ‖. We will refer to this condition as the stable-dynamical-model requirement. The wall model should also encode information about the type of wall (smooth, rough, hydrophobic, etc.). For the slip boundary condition of the form Eq. (2.1), the problem can be reformulated as finding the value of l that provides the correct wall stress. The relationship between l and τ_w is shown in Section 4 for a channel flow.

The equilibrium wall model (EQWM) (Kawai & Larsson 2013) can be interpreted easily in the framework described above. The model computes the wall stress by solving the ordinary differential equation (ODE)

$$\frac{d}{dn}\left[\left(\mu +{\mu }_R\right)\frac{dU}{dn}\right]=0,$$ (2.3)

where U is the wall-parallel velocity component, and μ_R is a RANS-based eddy viscosity from the zero-pressure-gradient flat-plate turbulent boundary layer (ZPGFPBL), which contains information that the wall is smooth. The equation is integrated from the wall to a wall-normal distance of Δ_ref, where the external LES velocity field is used to supply the boundary condition for the ODE. Moreover, for a ZPGFPBL, if ${\overline{u}}_i$ is equal to $u_i^{DNS}$ at a wall-normal distance of Δ_ref, then the μ_R is tuned such that ${\tau }_w\approx {\tau }_w^{DNS}$. The implications are that when the LES grid resolution is fine enough to accurately resolve the outer flow, the equilibrium solution of the dynamical system is bound to provide good prediction of the wall stress. It is also easy to show (in the context of ZPGFPBL or similar flows) that the solution is stable and the flow will tend to the correct equilibrium when the stress is under- or overestimated.

We propose a procedure to build dynamic wall models based on a stable-dynamical-system requirement, where dynamic wall model refers to those models that do not depend on any RANS eddy viscosity or tunable parameters, although they may depend on the test filter form and width as in the dynamic SGS models (i.e., dynamic Smagorinsky and its variants). In addition, we will impose four more model requirements, namely, that (R1) the model only uses information of flow quantities at the wall, (R2) the wall stress is imposed through a slip boundary condition, (R3) the wall is impermeable on average, and (R4) the dynamic model should only use up to two test filter levels.

Condition (R1) has a practical implication since wall models using information far from the wall are difficult (and ambiguous) to implement in complex geometries (Yang et al. 2017). The use of condition (R2) is beneficial for generating extra wall stress by the means of nonzero Reynolds stress at the walls. (R3) is an important constraint to support mass conservation, and in the case of a channel flow, no special treatment is required given the symmetry of the set-up (see Section 3). Regarding (R4), in the limit of the grids required for WMLES, increasing the levels of test filtering adds little information since most of the fluctuating energy content is already lost.

Assuming the slip boundary condition holds for both grid- and test-filtered velocity fields, the starting point for formulating the model is given by the equation

$$l^2\frac{\partial {\overline{u}}_i}{\partial n}\frac{\partial {\overline{u}}_j}{\partial n}-{\widehat{l}}^2\frac{\partial {\widehat{\overline{u}}}_i}{\partial n}\frac{\partial {\widehat{\overline{u}}}_j}{\partial n}={\overline{u}}_i{\overline{u}}_j-{\widehat{\overline{u}}}_i{\widehat{\overline{u}}}_j,$$ (2.4)

where $\widehat{l}$ is the slip length at the test filter level. We will assume a linear functional dependence of the slip length with the filter size of the form $\widehat{l}={\text{Δ}}_{R}l$. The next step is to include a control term $\mathcal{F}$, a function of the flow, in order to meet the stable-dynamical-model requirement,

$$l^2\left(\frac{\partial {\overline{u}}_i}{\partial n}\frac{\partial {\overline{u}}_j}{\partial n}-{\text{Δ}}_R^2\frac{\partial {\widehat{\overline{u}}}_i}{\partial n}\frac{\partial {\widehat{\overline{u}}}_j}{\partial n}\right)={\overline{u}}_i{\overline{u}}_j-{\widehat{\overline{u}}}_i{\widehat{\overline{u}}}_j+\mathcal{F}.$$ (2.5)

To close the functional form of $\mathcal{F}$, we will assume that it is only a function of the wall stress at different filter levels. Taking into account restriction (R4), there are six possible definitions of wall stress under test filtering,

$${\mathcal{T}}_{ij}^1=-{\overline{u}}_i{\overline{u}}_j-{\tau }_{ij}^{SGS}(\overline{\mathbf{u}})+2\nu S_{ij}(\overline{\mathbf{u}})-p(\overline{\mathbf{u}}){\delta }_{ij},$$ (2.6)

$${\mathcal{T}}_{ij}^2=-{\widehat{{\overline{u}}_i\overline{u}}}_j-{\widehat{{\tau }_{ij}}}^{SGS}(\overline{u})+2\nu \widehat{S_{ij}}(\overline{u})-\widehat{p}(\overline{u}){\delta }_{ij},$$ (2.7)

$${\mathcal{T}}_{ij}^3=-{\widehat{\widehat{{\overline{u}}_i\overline{u}}}}_j-{\widehat{\widehat{{\tau }_{ij}}}}^{SGS}(\overline{u})+2\nu \widehat{\widehat{S_{ij}}}(\overline{u})-\widehat{\widehat{p}}(\overline{u}){\delta }_{ij},$$ (2.8)

$${\mathcal{T}}_{ij}^4=-{\widehat{\overline{u}}}_i{\widehat{\overline{u}}}_j-{\tau }_{ij}^{SGS}(\widehat{\overline{\mathbf{u}}})+2\nu S_{ij}(\widehat{\overline{\mathbf{u}}})-p(\widehat{\overline{\mathbf{u}}}){\delta }_{ij},$$ (2.9)

$${\mathcal{T}}_{ij}^5=-{\widehat{{\widehat{\overline{u}}}_i\widehat{\overline{u}}}}_j-{\widehat{{\tau }_{ij}}}^{SGS}(\widehat{\overline{\mathbf{u}}})+2\nu \widehat{S_{ij}}(\widehat{\overline{\mathbf{u}}})-\widehat{p}(\widehat{\overline{\mathbf{u}}}){\delta }_{ij},$$ (2.10)

$${\mathcal{T}}_{ij}^6=-{\widehat{\widehat{\overline{u}}}}_i{\widehat{\widehat{\overline{u}}}}_j-{\tau }_{ij}^{SGS}(\widehat{\widehat{\overline{\mathbf{u}}}})+2\nu S_{ij}(\widehat{\widehat{\overline{\mathbf{u}}}})-p(\widehat{\widehat{\overline{\mathbf{u}}}}){\delta }_{ij},$$ (2.11)

where ${\mathcal{T}}_{ij}^k$ is the wall stress tensor at different filter levels, and ${\tau }_{ij}^{SGS}$, S_ij and pδ_ij are the subgrid stress, the strain-rate and pressure tensors, respectively, computed from the specified (test- or grid-filtered) velocity field. In particular, we elect to compute $T_{ij}^{SGS}$ from Eq. (2.2) as ${\tau }_{ij}^{SGS}(\widehat{\overline{u}})$. Note that τ_w can be computed as the norm of the wall-parallel components of the projection of ${\mathcal{T}}_{ij}$ onto the wall-normal direction. The formulation above also allows accounting for different types of walls by adding the appropriate drag term into Eqs. (2.6)–(2.11).

Then, a family of dynamic wall model can be formulated as

$$l^2\left(\frac{\partial {\overline{u}}_i}{\partial n}\frac{\partial {\overline{u}}_j}{\partial n}-{\text{Δ}}_R^2\frac{\partial {\widehat{\overline{u}}}_i}{\partial n}\frac{\partial {\widehat{\overline{u}}}_j}{\partial n}\right)={\overline{u}}_i{\overline{u}}_j-{\widehat{\overline{u}}}_i{\widehat{\overline{u}}}_j+a_k{\mathcal{T}}_{ij}^k,$$ (2.12)

where a_k are constants that need to be specified. In order to limit the parameter space of a_k, we limit the constant a_k to have values equal to −1, 0 or 1.

Finally, the model from Eq. (2.12) needs to satisfy the stable-dynamical-model requirement in order to be usable. This condition can be formally expressed as

$$\{\begin{array}{l}\text{ a) If }{\tau }_w\approx {\tau }_w^{DNS},\text{ then }{a}_k{\mathcal{T}}_{ij}^k\approx 0,\hfill \\ \text{ b) If }{\tau }_w>{\tau }_w^{DNS},\text{ then }{a}_k{\mathcal{T}}_{ij}^k\langle 0\text{ for }t\rangle T_a,\hfill \\ \text{ c) If }{\tau }_w\langle {\tau }_w^{DNS},\text{ then }{a}_k{\mathcal{T}}_{ij}^k\rangle 0\text{ for }t>T_a,\hfill \end{array}$$ (2.13)

where t is time and T_a is a characteristic time scale of the flow to adapt to changes in the boundary condition. Condition a) implies that the change in the predicted l for the next step should be minimal when starting from a flow configuration where ${\tau }_w\approx {\tau }_w^{DNS}$. This is achieved by a ${\mathcal{T}}_{ij}^k\approx 0$. The physical response of the flow under changes in the slip length was studied in Bae et al. (2016), who reported that increasing l results in increasing τ_w, and vice versa. Hence, conditions b) and c) are related to the stability of the model and are necessary to guarantee that the predicted slip length drives the flow in the correct direction. For example, when ${\tau }_w>{\tau }_w^{DNS}$, l at the next step should decrease (that is, $a_k{\mathcal{T}}_{ij}^k<0$), and when ${\tau }_w<{\tau }_w^{DNS}$, l must increase $\left(a_k{\mathcal{T}}_{ij}^k>0\right)$.

In addition, we make the modeling choice of assuming the invariance of wall stress under test filtering when the flow is in the equilibrium state, that is, we assume $T_i{j}^k$ are equivalent when $a_k{\mathcal{T}}_{ij}^k\approx 0$. The physical rationale behind this assumption lies in the observation that, in LES, we aim to obtain the same wall stress regardless of the grid resolution (or filter). A similar approach was adopted by Anderson & Meneveau (2011) for modeling rough walls. This assumption is taken into account by imposing ∑_k a_k = 0. This assumption is also required in order to guarantee that the wall models revert to the no-slip boundary condition as the grid size Δ_g → 0.

The system in Eq. (2.12) is over-determined and l is computed via least-squares. For incompressible flows, the isotropic part ${\tau }_{ij}^{SGS}$ is usually not defined by the SGS models. Since the system is already over-determined, we will exclude the i = j components of Eq. (2.12).

2.3. Wall-stress based formulation

An alternative family of wall models can be directly formulated in terms of the wall stress, independent of the slip length. We propose to introduce a dynamic correction $\text{Δ}{\mathcal{T}}_{ij}$ such that

$${\mathcal{T}}_{ij}^{k*}={\mathcal{T}}_{ij}^k+\text{Δ}{\mathcal{T}}_{ij}^k$$ (2.14)

where ${\mathcal{T}}_{ij}^{1*}$ is intended to be an accurate estimation of the stress at the wall. If we assume that $\text{Δ}{\mathcal{T}}_{ij}^k$ is a function of the strain and rotation rate tensors (S_ij and R_ij), its most general form is given by (Lund & Novikov 1992)

$$\text{Δ}{\mathcal{T}}_{ij}^k={\text{Δ}}_g^2[B_1\left|S\right|S_{ij}+B_2{S}_{il}{S}_{lj}+B_3{R}_{il}{R}_{lj}+B_4\left(S_{il}{R}_{lj}-R_{il}{S}_{lj}\right)+B_5\left(S_{il}{S}_{lm}{R}_{mj}-R_{il}{S}_{lm}{S}_{mj}\right)],$$ (2.15)

where |S| = (S_ij S_ij)^1/2, Δ_g is the grid size based on the volume of the cell, and B_i are coefficients that depend on the invariants of S_ij and R_ij.

We further simplify the formulation by setting B_i = B ⋅ b_i, where b_i are fixed predetermined values that are either −1, 0, or 1. The different models in the family correspond to the various combinations of b_i. Our modeling choice is to dynamically compute the coefficient B by assuming

$${\mathcal{T}}_{ij}^{2*}={\mathcal{T}}_{ij}^{4*}.$$ (2.16)

The problem is solved by least squares, omitting the diagonal components. The more general formulations where all coefficients C_i are computed dynamically will be investigated in future works.

The stable-dynamical-model requirement is now formulated as

$$\{\begin{array}{l}\text{ a) If }{\tau }_w\approx {\tau }_w^{DNS},\text{ then Δ}{\mathcal{T}}_{ij}^1\approx 0,\hfill \\ \text{ b) If }{\tau }_w>{\tau }_w^{DNS},\text{ then Δ}{\mathcal{T}}_{ij}^1\langle 0\text{ for }t\rangle T_a,\hfill \\ \text{ c) If }{\tau }_w\langle {\tau }_w^{DNS},\text{ then Δ}{\mathcal{T}}_{ij}^1\rangle 0\text{ for }t>T_a.\hfill \end{array}$$ (2.17)

Compared to the family of models presented in Section 2.2, the formulation from Eq. (2.14) has the advantage of being independent of a particular choice of boundary condition and may be applied through either a Neumann or a slip (with or without transpiration) boundary condition. We choose to impose the resulting wall stress, ${\mathcal{T}}_{ij}^{1*}$, through a slip boundary condition with transpiration (see Eq. 4.2). An additional advantage is the use of only one test filter level.

3. Numerical experiments

We run a set of simulations divided into two groups. The first group consists of three WMLES of channel flow denoted by C1, C2 and C3, that will assist to build a-priori potential dynamic wall models in Section 4. The second group is intended to assess the performance of the new dynamic wall models in an actual LES implementation under different grid resolutions and Reynolds numbers. Two flow configurations are tested: a plane turbulent channel flow (2–D channel) and a three-dimensional transient channel flow (3–D channel). From now on, the streamwise, wall-normal and spanwise spatial directions are represented by the subindices 1, 2 and 3, respectively.

The simulations are computed by discretizing the Navier–Stokes equations in primitive variables with staggered second-order finite differences in space (Orlandi 2000), and a fractional-step method (Kim & Moin 1985) with a third-order Runge-Kutta time-advancing scheme (Wray 1990). The flow is driven by imposing a constant mean pressure gradient. The SGS model used is the dynamic Smagorinsky model (DSM) (Germano et al. 1991; Lilly 1992). The value of eddy viscosity for the ghost cells below the wall is set to be the same as the first interior grid point (except when explicitly mentioned otherwise). Periodic boundary conditions are applied in the streamwise and spanwise directions. For the top and bottom walls, we impose either a no-slip (NS), slip boundary condition (for dynamic wall models) or the Neuman boundary condition (for EQWM). The formulation for the EQWM is the one by Kawai & Larsson (2013) with a matching location at the third grid cell for the streamwise velocity.

The test filter operation on a variable f in a given spatial direction at point i is computed as 1/6f(i – 1) + 2/3f(i) + 1/6f(i + 1) (Simpson’s rule). The operation is repeated for all three directions in the interior of the domain. This corresponds to a discrete fourth-order quadrature over a cell of size 2Δ₁ × 2Δ₂ × 2Δ₃ centered at the variable that is being filtered, where Δ₁, Δ₂ and Δ₃ are the grid sizes in the three directions, respectively. At the wall, the same filtering operation is used in the horizontal directions while the wall-normal filter is one-sided and given by 2/3f(1) + 1/3f(2), with f(1) and f(2) denoting values at the first and second wall-normal grid points. This is an integration over a cell of size 2Δ₁× Δ₂×2Δ₃. We will denote the test filter above by TF1. A second test filter, TF2, is used to evaluate the effect of the filter shape, and it is given by 1/4f(i–1)+1/2f(i)+1/4f(i+1) in the interior of the domain and 1/2f(1)+1/2f(2) at the wall. This corresponds to a second-order quadrature. It is impotant to specify in detail the filter operation as dynamic wall models are particularly sensitive to this choice (see Section 5).

The size of the 2–D and 3–D channel domain is 8πδ × 2δ × 3πδ in the streamwise, wall-normal and spanwise directions, respectively, where δ is the channel half-height. For the 2–D channel calculations, the simulations are started from a random initial condition and run for at least 100δ/u_τ after transients, where u_τ is the friction velocity. In the case of the 3–D channel, the calculations were started from a 2–D fully developed plane channel flow at Re_τ ≈ 950. The subsequent calculations were performed with a transverse pressure gradient of $\frac{\partial P}{\partial x_3}=10{\tau }_w^{2D}/\delta$, where ${\tau }_w^{2D}$ is the mean wall shear stress in the unperturbed channel. The simulations were run for one u_τ/δ and averaged over six realizations.

Finally, 2–D channel results are compared with DNS data from Hoyas & Jiménez (2006) and Lozano-Durán & Jiménez (2014) for Re_τ ≈ 2000 and 4200, and with the law-of-the wall for Re_τ > 4200. The 3–D channel flow cases are compared with WMLES using EQWM and non-equilibrium wall model (NEQWM) from Park & Moin (2014), and DNS data from Giometto et al. (2017).

A detailed list of cases is shown in Table 1. The cases are labeled in the first column following the convention ([Wall model]-[Reynolds number]-[Grid resolution]). Additional cases with different values of Δ_R, test-filtering operations, or SGS model were run to study the sensitivity of the model on these choices, but are not included in the table. The second column lists the wall model applied (NS, EQWM, S-DWM, W-DWM). Note that for the cases with NS, the SGS model is responsible for providing the necessary wall stress and is known to be underpredicted for the DSM (Jiménez & Moser 2000). The dynamic models S-DWM and W-DWM are constructed using the procedure specified in Section 4, and the exact form of the model will be given there. The third column shows the value of Δ_R used for the model, and the fourth column is Re_τ. The final column of the table indicates three different grid resolutions, labeled as G0, G1, and G2, that correspond to 320 × 25 × 120 (Δ₁ = Δ₂ = Δ₃ = 0.080δ), 512 × 40 × 192 (Δ₁ = Δ₂ = Δ₃ = 0.050δ), and 1024 × 80 × 384 (Δ₁ = Δ₂ = Δ₃ = 0.025δ), respectively, in the streamwise, wall-normal, and spanwise directions.

Table 1.

Tabulated list of cases for channel flow simulations.

Case	Wall model	ΔR	Reτ	Grid
C1	l = lc1	N/A	4200	G1
C2	l = lc2	N/A	4200	G1
C3	l = lc3	N/A	4200	G1
EQ-2000-G1			2000	G1
EQ-4200-G0			4200	G0
EQ-4200-G1	EQWM	N/A	4200	G1
EQ-4200-G2			4200	G2
EQ-1E5-G1			105	G1
NS-2000-G1			2000	G1
NS-4200-G0			4200	G0
NS-4200-G1	NS	N/A	4200	G1
NS-4200-G2			4200	G2
NS-8000-G1			8000	G1
NS-1E5-G1			105	G1
S-DWM-2000-G1			2000	G1
S-DWM-4200-G0			4200	G0
S-DWM-4200-G1	S-DWM	1.8	4200	G1
S-DWM-4200-G2			4200	G2
S-DWM-8000-G1			8000	G1
S-DWM-1E5-G1			105	G1
W-DWM-4200-G1			4200	G1
W-DWM-4200-G2	W-DWM	N/A	4200	G2
W-DWM-1E5-G1			105	G1
S-DWM-3D950-G1	S-DWM	1.8	950	G1

3.1. Stability of the slip boundary condition

Although a systematic analysis of the stability of the slip boundary condition was not performed, all channel flow calculations included in this report were stable starting from a random initial condition for different grids and Reynolds numbers. However, this was not the case for some preliminary tests on LES of a flat-plate turbulent boundary layer not reported here. In those cases, a flow field generated from a previous coarse no-slip calculation was required as an initial condition for the simulation to be stable. Despite the limited literature involving the slip boundary condition with transpiration, Carton de Wiart & Murman (2017) reported that compressible channel flow calculations with the slip boundary condition became unstable at high Reynolds numbers.

4. Construction of filter-invariant wall-stress dynamic wall models

4.1. Slip length based dynamic wall models

Ideally, we would like to construct a dynamic wall model of the form (2.12) that satisfies condition (2.13), where the coefficients a_i are determined based only on first principles. However, the task is quite challenging due to the highly non-linear nature of the Navier-Stokes equations, and it is difficult to assess whether condition (2.13) will be satisfied a-priori once the wall model is coupled with the flow. Furthermore, this condition must hold for a broad range of equilibrium and non-equilibrium flow configurations of interest. Instead, to make the problem tractable, we will evaluate models in Eq. (2.12) a-posteriori by considering only three reference channel flow simulations at Re_τ = 4200 with DSM and grid G1. The first case, C1, is computed using the slip length, l_c1, that supplies the correct mean stress at the wall. In a channel flow with transpiration, the wall stress is given by

$$\langle {\tau }_w\rangle =\nu \langle \frac{\partial {\overline{u}}_1}{\partial x_2}\rangle {|}_w-\langle {\overline{u}}_1{\overline{u}}_2\rangle {|}_w-\langle {\tau }_{12}^{SGS}\rangle {|}_w,$$ (4.1)

where 〈·〉 denotes averaging in homogeneous directions and time. If ${\tau }_w^{DNS}$ is known, l_c1 is easily obtained by introducing the slip boundary condition (2.1) in the term $\langle {\overline{u}}_1{\overline{u}}_2\rangle |w$, and the resulting equation for l_c1 is〉

$$l_{c1}^2=\frac{\nu \langle \partial {\overline{u}}_1/\partial x_2\rangle {|}_w-\langle {\tau }_{12}^{SGS}\rangle {|}_w-{\tau }_w^{DNS}}{\langle \left(\partial {\overline{u}}_1/\partial x_2\right)\left(\partial {\overline{u}}_2/\partial x_2\right)\rangle }.$$ (4.2)

Note that Eq. (4.2) is not a wall model itself but rather a compatibility condition that links the stress at the wall with the slip length. The second and third cases, denoted by C2 and C3, are analogous to C1 but with l_c2 = 1.35〈l_c1〉 and l_c3 = 0.65〈l_c1〉, respectively.

We proceed to evaluate the performance of different dynamic wall models using condition (2.13) with T_a = 0. Starting from cases C1, C2 and C3, we compute the slip length at the next time step, $l_{c1}^m$, $l_{c2}^m$, and $l_{c3}^m$, evaluated from all possible models in the family (2.12). Condition (2.13a) can be quantified by ${ϵ}_{c1}=\left|l_{c1}^m-l_{c1}\right|/l_{c1}$. Conditions (2.13b) and (2.13c) can be similarly quantified by ${ϵ}_{c2}=\left(l_{c2}-l_{c2}^m\right)/l_{c2}$ and ${ϵ}_{c3}=\left(l_{c3}^m-l_{c3}\right)/l_{c3}$. For a model to be viable, it is necessary that ϵ_c1 ≪ 1 and ϵ_c2, ϵ_c3 > 0. We defined the “best” model as the one with ϵ_c1 < 0.05 and maximum ϵ_c2+ϵ_c3. Additionally, in order for the model to be less sensitive to the filter size ratio, the above requirements should hold for both Δ_R = 1.6 and 1.8. After a search over all possible models complying with our constraints, Table 2 shows the coefficients a_i corresponding to the best potential model, denoted by S-DWM.

Table 2.

Parameters for S-DWM (Eq. 2.12), and its errors associated with Eq. (2.13).

Model name	a1	a2	a3	a4	a5	a6	ΔR	ϵc1	ϵc2	ϵc3
S-DWM	1	0	0	−1	−1	1	1.6	0.033	0.203	0.340
							1.8	0.023	0.427	0.609

4.2. Wall stresses based dynamic wall models

We apply the same procedure described above for the family of models given in Section 2.3. We define τ_c1, τ_c2, and τ_c3 as the τ_w for the three test cases C1, C2, and C3, and the ${\tau }_{c1}^m$, ${\tau }_{c2}^m$, and ${\tau }_{c3}^m$ as the corresponding predictions given by the model. This condition was used to evaluate the requirement (2.17). Many viable models were identified, and one candidate is shown in Table 3 and denoted by W-DWM. One important remark is that in this case, the eddy viscosity at the wall was set to be zero, and the cases C1, C2 and C3 were rerun using this condition. A more exhaustive analysis of this family is deferred to future work.

Table 3.

Parameters for W-DWM (Eq. 2.15), and its errors associated with Eq. (2.17).

Model name	b1	b2	b3	b4	b5	$\frac{\left|{\tau }_{c1}^m-{\tau }_{c1}\right|}{{\tau }_{c1}}$	$\frac{{\tau }_{c2}-{\tau }_{c2}^m}{{\tau }_{c2}}$	$\frac{{\tau }_{c3}-{\tau }_{c3}^m}{{\tau }_{c3}}$
W-DWM	−1	−1	−1	1	1	0.055	0.070	0.24

5. Results

5.1. Channel flow

In this section, we assess the performance of S-DWM and W-DWM compared to EQWM and NS (coarse LES) calculations. The results are discussed in terms of the error in the streamwise mean velocity in the log region (x₂ = 0.1δ–0.4δ). This choice was necessary in order to include higher Reynolds number cases where the corresponding DNS was not available and the law of the wall is used instead. Restricting the error to be evaluated only in the log-layer is justified as wall models mainly impact the solution by vertically shifting the mean velocity profile and do not alter its shape for the range of grid resolutions tested (see Figure 2a). In particular, we measure error as

$$\mathcal{E}={\left[\frac{\underset{0.1\delta }{\overset{0.4\delta }{\int }}{\left(\langle {\overline{u}}_1\rangle -\langle u_1^{DNS}\rangle \right)}^{2}d{x}_2}{\underset{0.1\delta }{\overset{0.4\delta }{\int }}{\left(\langle u_1^{DNS}\rangle \right)}^{2}d{x}_2}\right]}^{1/2}.$$ (5.1)

In the case where a corresponding DNS does not exist, $\langle u_1^{DNS}\rangle$ is taken to be the law of the wall,

$$\langle u_1^{DNS}\rangle =\frac{1}{\kappa }\text{log}{x}_2^{+}+B,$$ (5.2)

with κ = 0.392 and B = 4.48 (Luchini 2017), where (·)⁺ denotes wall units given by u_τ and ν.

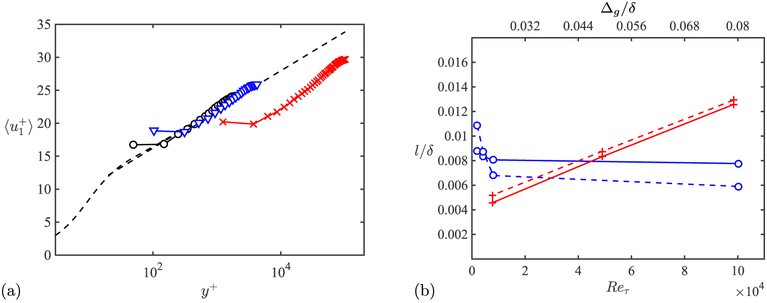
Figure 2.

(a) Mean velocity profiles for S-DWM for Re_τ = 2000 (○), 4200 (▽), and 10⁵ (×) for grid G1. DNS for Re_τ = 4200 and law-of-the-wall (dashed lines). (b) The slip lengths l/δ as a function of grid resolution for Re_τ = 4200 (top axis, +) and Reynolds number for grid G1 (bottom axis, ○) for S-DWM (solid lines) and optimal slip lengths (dashed lines).

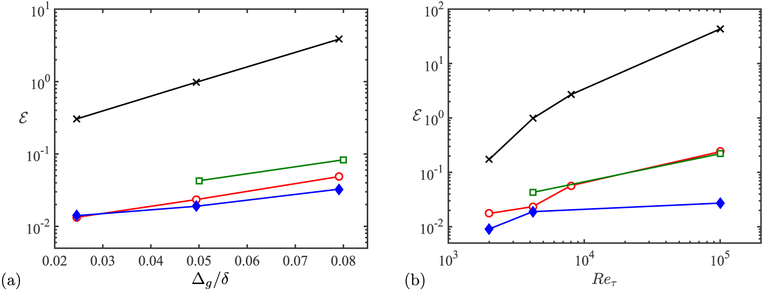
Figure 1 shows $\mathcal{E}$ as a function of grid resolution and Reynolds number. S-DWM and W-DWM perform better than the NS by an order of magnitude for all cases. At moderate Reynolds numbers (Re_τ < 8000) and all grid resolutions, the error for S-DWM is almost identical to that of the EQWM (~2–4%). The error for W-DWM is slightly larger, but still comparable to the EQWM (~5–10%). However, with increasing Reynolds number, the performance of both S-DWM and W-DWM deteriorates (~20%), while the EQWM does not. This is not surprising as the EQWM is calibrated to work well in channel flow settings. The mean velocity profiles for S-DWM at three Reynolds numbers are shown in Figure 2(a).

Figure 1.

Error in the streamwise mean velocity profile, $\mathcal{E}$, as a function of (a) grid size (for Re_τ = 4200) and (b) Reynolds number (for grid G1). NS (×); S-DWM (○); W-DWM (□); and EQWM (♦).

The slip lengths predicted by S-DWM are shown in Figure 2(b) as a function of Reynolds number and grid resolution and compared to the optimal slip lengths (Eq. 4.2). It is remarkable that S-DWM captures the overall behavior of the optimal slip lengths, that is, a strong dependence on grid resolution and a weak variation in Reynolds number.

Three additional cases were computed to analyze the sensitivity of the S-DWM to Δ_R, shape of the test filter, and choice of SGS model. The effect of Δ_R turned out to be negligible for the plausible range of values Δ_R = 1.4, 1.6, 1.8, and the difference in $\mathcal{E}$ was less than 1%. On the contrary, the test filter shape and SGS model highly impacted the prediction of the mean flow. Case S-DWM-4200-G1 was repeated using test filter TF2, and the error increased from 2.5% to 32%. When S-DWM-4200-G1 was run using the anisotropic minimum-dissipation (AMD) model (Rozema et al. 2015), the stress ${\tau }_{12}^{SGS}$ was already larger than $u_{\tau }^2$, and the slip length prediction by S-DWM was clipped to zero, reverting to the no-slip condition. Although this is consistent with the fact that ${\tau }_{12}^{SGS}>u_{\tau }^2$, it also implies that the correct stress at the wall can never be obtained through the slip boundary condition with a single slip length. Indeed, it was shown in Bae et al. (2016) that the slip lengths in the wall-normal direction must be larger than the wall-parallel ones in order to drain the excess of stress supplied by the SGS model. This suggests that the family of models (2.12) should be generalized to a two slip-length formulation to overcome this limitation.

Finally, we discuss the results for the model presented in Bose & Moin (2014). We tested three Reynolds numbers (Re_τ = 950, 2000, 4200), three grid resolutions (Δ_x,y,z/δ = Δ/δ = 0.04, 0.05, 0.10), two SGS models (AMD model and DSM), three different values for Δ_R (1.4, 1.6, 1.8), and test filters TF1 and TF2. $T_{ij}^{SGS}$ was computed as in Section 2. The ambiguity regarding the isotropic part of ${\tau }_{ij}^{SGS}$ mentioned in Section 2 was not discussed in Bose & Moin (2014), and this component is set to zero in our current implementation. All of the cases simulated yielded an imaginary slip length (clipped to zero) when solving Eq. (2.2), and hence, results from Bose & Moin (2014) could not be reproduced. One certain deviance from Bose & Moin (2014) is the numerical discretization (staggered second-order finite differences versus collocated second-order finite volumes). Other differences are the SGS model, test filter, and methodology to compute $T_{ij}^{SGS}$.

5.2. Three-dimensional transient channel flow

In order to assess the performance of S-DWM in non-equilibrium scenarios, we simulated a three-dimensional transient channel flow (Moin et al. 1990). A plane channel flow simulation was modified to incorporate a lateral (transverse) pressure gradient 10 times that of the streamwise pressure gradient. The resulting flow is one with strong transverse acceleration during the initial transient. Details of the simulations are given in Section 3.

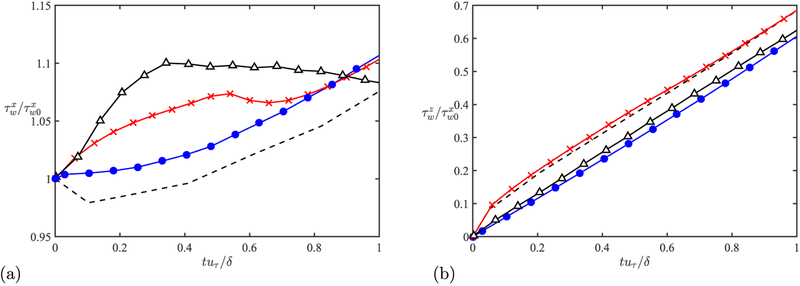
The evolution of streamwise and spanwise wall stress as a function of time is shown in Figure 3. The WMLES tested were S-DWM, EQWM, and NEQWM. The results show that the NEQWM provides the best prediction for the evolution of the spanwise wall stress, although the results from the other models are comparable.

Figure 3.

Wall stress in the (a) streamwise and (b) spanwise directions as a function of time for S-DWM (△), EQWM (●), and NEQWM (×). DNS (dashed line).

6. Conclusions

Most wall models for LES rely on a RANS eddy viscosity in order to estimate the stress at the wall. In the present study, we explore the construction of dynamic wall models that are free from a-priori tunable parameters and only depend on the flow configuration at the wall and, at most, on the test filter ratio Δ_R.

We have presented two families of dynamic models based on the invariance of the wall stress under test filtering. The models are effectively applied through a slip boundary condition with the associated slip length l. We have devised the coupling between wall models and LES as a stable dynamical system that must provide the correct wall stress at the statistically steady equilibrium. Based on this idea, the potential of different models has been evaluated for a turbulent channel flow using precomputed flow fields at three different states: one supplying the correct wall stress, and two whose wall stresses are above or below the correct value.

We have tested the performance of two dynamic wall models, S-DWM and W-DWM, in a plane turbulent channel flow at various Reynolds numbers and grid resolutions. The results have been compared with those from EQWM and no-slip boundary condition (no WM) on a coarse grid. In all cases, both S-DWM and W-DWM performed substantially better than the no-slip, and are comparable to the EQWM for Re_τ < 8000 and for all grid resolutions investigated. S-DWM have also been tested for a three-dimensional transient channel flow, where the performance was also similar to that of the EQWM.

Future efforts will be devoted to investigate the feasibility of dynamic models robust to different SGS models, numerical methods, and flow configurations.