Effect of Segmentation Variation on ECG Imaging

Abstract

ECG imaging (ECGI) is the process of calculating electrical cardiac activity from body surface recordings from the geometry and conductivity of the torso volume. A key first step to create geometric models for ECGI and a possible source of considerable variability is to segment the surface of the heart. We hypothesize that this variation in cardiac segmentation will produce variation in the computed ventricular surface potentials from ECGI. To evaluate this hypothesis, we leveraged the resources of the Consortium for ECG Imaging (CEI) to carry out a comparison of ECGI results from the same body surface potentials and multiple ventricular segmentations. We found that using the different segmentations produced variability in the computed ventricular surface potentials. Not surprisingly, locations of greater variance in the computed potential correlated to locations of greater variance in the segmentations, for example near the pulmonary artery and basal anterior left ventricular wall. Our results indicate that ECGI may be more sensitive to segmentation errors on the anterior epicardial surface than on other areas of the heart.

1. Introduction

Electrocardiographic imaging (ECGI) is a technique already used to noninvasively diagnose and guide treatment of cardiac arrhythmias. ECGI involves the numerical inversion of a forward model that predicts the cardiac electrical activity through the torso [1, 2]. Although many advancements have been made in ECGI techniques, the uncertainty of these pipelines to variations that inevitably occur in their clinical use is not well quantified.

Uncertainty in ECGI could arise in many of the stages performed in ECGI pipelines. A frequently overlooked source of uncertainty relates to the forward model generation within the ECGI pipelines, particularly the segmentation of the geometric model, which is typically customized for each patient. This segmentation step often requires manual input and user judgment, providing a potential origin of error and uncertainty. We have previously shown that segmentations of the same patient geometry, especially of the cardiac surface, can vary widely with each operator [3]. However, we do not evaluate how this variability might affect the end result of the ECGI pipeline.

In this study, we analyzed the effect of segmentation variability on the resulting ECGI solutions. Our hypothesis was that variation in cardiac segmentation will produce meaningful error in the computed ventricular surface potentials using ECGI. We used the collaborative framework of the Consortium on ECG Imaging (CEI) to perform multiple segmentations of the same patient to provide the data necessary to analyze the effect on the results of ECGI. We found that both the degree and location of variation in the ECGI solution corresponded to variation of the segmented cardiac surfaces.

2. Methods

To analyze the effect of cardiac segmentation variability on ECGI, we computed cardiac surface potentials using multiple segmented ventricular geometries in the ECGI pipeline. A single patient CT scan was segmented by five research groups within the CEI and collected using the COVALIC platform (https://challenge.kitware.com). From the five segmented myocardial volumes, an aggregate segmentation was created using the STAPLE algorithm [4]. Surface meshes were made from each of the segmentations, which were then registered to an existing torso surface mesh using a modified iterative closest point technique. Variations of the segmentations were computed compared to the aggregate segmentation using the DICE coefficient. Regional variation of the segmentation was further quantified by calculating the variance of the minimum distance from each point on the aggregate cardiac surface to each segmented cardiac surface.

ECGI was performed with the same body surface potential maps (BSPM) and each of geometries generated with the segmentations, including the aggregate segmentation. Epicardial and endocardial surface potentials were computed with the boundary element method (BEM) and Tikhonov regularization as implemented in the Forward/Inverse toolkit in SCIRun (scirun.org) [5–7]. A Laplacian matrix which accounts for volumetric distances was included as a regularizer to enable computed solutions also over the endocardial surfaces. Computed source potentials were mapped onto the aggregate heart geometry for point-wise comparison. We compared the computed potentials from each segmentations to the potentials from the aggregate segmentation using the correlation coefficient (ρ), relative root mean squared error (rRMSE), and relative error (RE). We also computed the variance at each point over the surface of the heart and through the recorded beats.

The patient data used in this study were collected by Sapp et al. [8] and is available for open use on the EDGAR database (http://edgar.sci.utah.edu) [9] a shared resource of the CEI.

3. Results

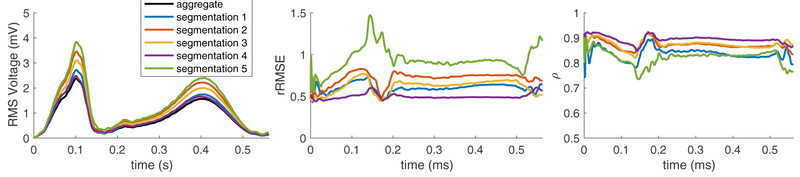
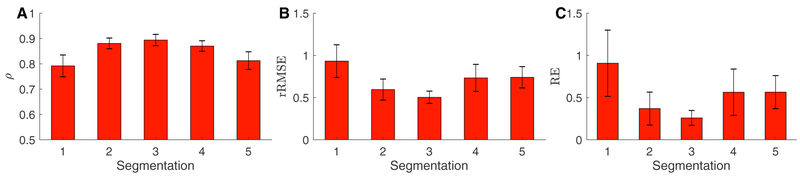
Comparing computed endocardial and epicardial potentials from each of the segmentations to the aggregate potentials showed variation in the computed solution. The variance of the computed solutions changed over the course of the cardiac cycle and was similar in morphology to the amplitude of the RMS voltage over the surface of the heart. Each metric also varied over time and with differing segmentations, as shown in Figure 1. The mean correlation of the computed potentials compared to the aggregate potentials is shown in Figure 2 and had mean values of ρ = 0.85, a rRMSE = 0.71, and RE = 0.54 for all segmentations. The mean error metrics of the cardiac potentials compared to the solution from the aggregate solution generally correlated to the accuracy of the segmentations, in that solutions that had a lower mean rRMSE and RE and higher ρ corresponded to segmentations that agreed more closely with the aggregate segmentation (Figure 3).

Figure 1.

Error over time of the ECGI potentials with various segmentations compared to the aggregate solution.

Figure 2.

Mean error of the ECGI potentials with various segmentations compared to the aggregate solution.

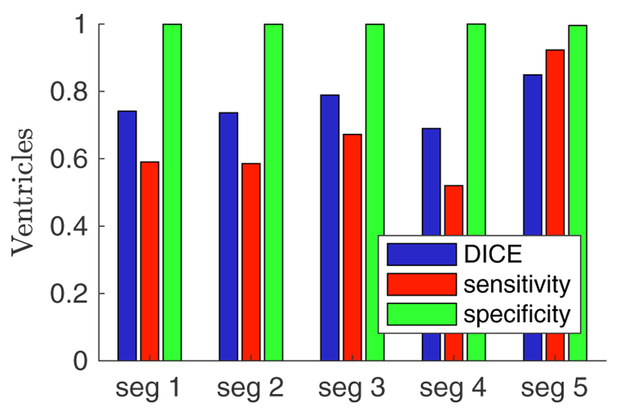
Figure 3.

Variation of the individual cardiac segmentations compared to the aggregate segmentation. Sensitivity and specificity were calculated using the STAPLE algorithm.

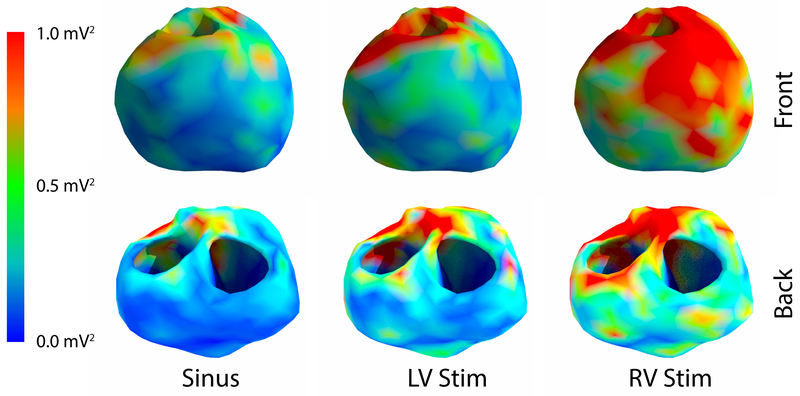
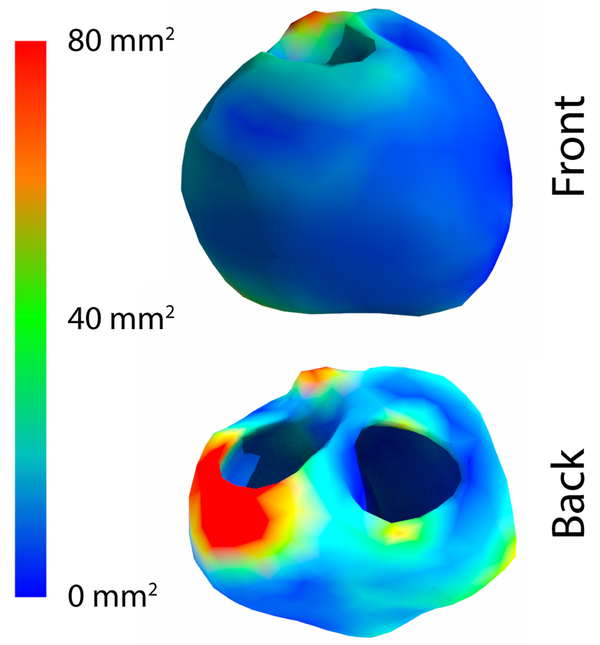
Comparing the variance of computed endocardial and epicardial potentials over the surface of the heart revealed consistent areas of higher variation. As shown in Figure 4, the anterior surface generally had higher mean variance in the computed potentials than did the posterior surface. The epicardial surface also generally had a higher variance than the endocardial surface, yet there were regions of high variance on the anterior endocardial surface which corresponded spatially to regions of high variance on the epicardial surface. Not surprisingly, locations of high variance in the potential corresponded to locations of greater variability of the segmentations (Figure 5), for example near the pulmonary valve and the basal, anterior, left ventricular wall. However, some locations, such as the basal, posterior wall and the endocardial, right ventricular apex, showed lower variance of the computed potentials despite showing high variation in the segmentation. Additionally, regions on the endocardial surface in the anterior region showed higher variance in the computed potentials, yet demonstrated low variance in the minimum distance to each geometry.

Figure 4.

Mean variance by location for example beats of the cardiac surface potential due to the differing segmentations.

Figure 5.

Variance of the minimum distance to the meshes generated from the various segmentations.

4. Discussion and Conclusions

Our results indicate that the cardiac potentials computed using ECGI may be sensitive to variability in the cardiac segmentations. However, some regions of the heart are more sensitive to perturbations in the cardiac segmentation than others, e.g. the anterior surface of the heart. These findings also suggest that more analysis of the model generation pipeline is needed to ensure that the inverted forward models, upon which ECGI is based, are as accurate and robust as possible and that unavoidable errors are quantified and characterized.

Errors in ECGI solutions due to segmentation variation were not uniformly distributed over the surface of the heart. The posterior regions of the heart were less sensitive to these changes than the anterior regions, likely because the distance between the heart and torso surfaces is much smaller on the anterior cardiac surface than on other locations in the heart. The anterior endocardial regions that showed high variance in the computed solution despite low variance in the distance to the mesh reveal a source of variance that were not capturing in our geometry variation metrics. Since the distance to each mesh to the aggregate was not correspondence based, the mesh variance on the endocardial may have included distances to the epicardial surfaces, masking the variance in the region.

These findings also support a growing concern regarding the need to quantify the uncertainty of simulations and, in this case, segmentation steps. More robust quantification of the segmentation variation could provide more insight into the relationship between better segmenations and more accurate ECGI solutions. For instance, correspondence-based shape statistics [10] would provide a more consistent comparison of the variation in each region. A more complete analysis of the uncertainty, such as with the generalize polynomial chaos theory [11], could also provide a more complete understanding of how such segmentation variation affects forward models of ECG and ECGI.

Although only the effect of segmentation variation was addressed in this study, other sources of variation in the model generation process should be expected to also cause variation in the computed cardiac activity. For example, the inclusion of the inhomogeneity of the torso and the segmentation of the various tissue regions are likely to affect the ECGI solutions. Mesh generation, quality, and resolution could provide some different ECGI solutions depending on the techniques of the various groups.