Intrinsic concentration cycles and high ion fluxes in self-assembled precipitate membranes

Abstract

Concentration cycles are important for bonding of basic molecular building components at the emergence of life. We demonstrate that oscillations occur intrinsically in precipitation reactions when coupled with fluid mechanics in self-assembled precipitate membranes, such as at submarine hydrothermal vents. We show that, moreover, the flow of ions across one pore in such a prebiotic membrane is larger than that across one ion channel in a modern biological cell membrane, suggesting that proto-biological processes could be sustained by osmotic flow in a less efficient prebiotic environment. Oscillations in nanoreactors at hydrothermal vents may be just right for these warm little pores to be the cradle of life.

1. Introduction

Where did life begin? Darwin famously speculated about a ‘warm little pond’ [1]. Indeed that is one theory today [2]. A rival theory holds that the oceans, rather than ponds, were the cradle of life [3]. Of course, Darwin knew nothing of hydrothermal vents on the ocean floors, discovered only in the late 1970s [4,5]. A particular class of vent emitting warm, rather than hot, mineral-laden water at alkaline pH [6] has been highlighted as of particular significance in terms of a possible birthplace of life [7–9]. We demonstrate here that hydrothermal vents can function just as well as, or better than warm little ponds in terms of providing an environment in which complex chemistry can occur via cycles of condensation reactions, and so-called wet–dry cycles of warm little ponds would not be necessary. Moreover, the ubiquity of suitable vents on the Hadean ocean floors, allied to the endogenous supply of the necessary raw materials to them, compared to the scarcity of suitable ponds and the need to postulate for ponds a supply of organic raw materials through the external agent of meteorite bombardment, argues in favour of the oceanic and against the lacustrine hypothesis.

1.1. The origin of life: ponds versus vents

The modern lacustrine hypothesis puts forward the idea of life emerging from hydrothermal ponds. The claim is that life evolved from organic compounds being dumped into these ponds from meteorite impacts, then being concentrated and reacting during wet and dry periods [2,10]. A key point for both ponds and vents is the need for a condensation mechanism [11] by which ester and peptide bonds could have been synthesized in the absence of enzymatic catalysis and the possibility, or not, for it to occur [12]. It has recently been argued that wet and dry cycles are necessary and are only available at ponds that dry out and not at vents under the sea [10]. But is that really the case? In fact not: cells today use molecular crowding and excluded volume effects to stabilize such reactions [13–18]. The thermodynamic challenge to bond formation is overcome in highly concentrated solutions [12,19] such as in a confined environment [20].

1.2. Chemical garden membranes at hydrothermal vents

The precipitation reactions that occur as mineral-laden water emerges at an alkaline vent into the ocean give rise to an extremely complex ever-growing and changing network of tiny compartments in the form of tubes and vesicles [6] separated by thin gel-like membranes semipermeable to some chemical species [21], providing an out-of-equilibrium, not-well-mixed environment with strong concentration gradients [22,23].

Hydrothermal vents are natural, geological versions of chemical gardens [24–27], studied since the seventeenth century. Modern work on chemical gardens has led to increased understanding of the complex interaction of fluid mechanics and chemistry called chemobrionics that produces these self-assembled membrane systems [28]. This body of work has more recently built upon knowledge of liquid-phase chemical hydrodynamics [29–32], with the added complexity of a growing solid interface. Chemical gardens refer to hollow structures that form when a metal salt seed is submerged into an alkaline solution, i.e. sodium silicate, which have been produced in three- [33–37], two- [38,39] and even one-dimensional [21,40] configurations. The two-dimensional systems mimic the confinement that may be found when the mineral-bearing fluid is trapped between delimiting structures. These numerous experimental studies have revealed a wide variety of spatial structures, depending on the chemical system, the ion concentrations and the forced or natural nature of the convective flow. However, this work has been either qualitative or specific to a given fluid flow regime. Most studies have focused on relatively fast convection, driven by either buoyancy forces resulting from concentration gradients ensuing during precipitation, or by an imposed external pressure. Despite the controlled flow conditions, specifically designed to neglect intrinsic osmotic forces across the solid membrane, developing theoretical models that explain the multitude of growth regimes of chemical gardens, and the transitions between them, has remained a challenge. In this work, we focus on the coupling of the slow osmosis-driven fluid dynamics and chemical precipitation during the growth of a semipermeable two-dimensional membrane. We show experimentally and theoretically that such a system can exhibit different dynamical regimes, ranging from stable, to oscillatory and explosive. We demonstrate the existence of temporal cycles of concentration and pressure in growing precipitate membranes and quantify these. We explore the implications of our findings for the micro- and nano-scale behaviour at alkaline submarine hydrothermal vents and the chemistry therein.

2. Experimental methods

The precipitation of minerals at hydrothermal vents involving, for example, iron with silicates and phosphates are relatively fast [41,42], so that the rate of the transport of ions to the reaction site determines the growth of the membrane. This transport of ions across the hydrothermal vent membrane is controlled by its osmotic properties and the pressure of the internal fluid. In the laboratory, we use an analogue chemical system to mimic the dynamics of ion transport and membrane growth in the hydrothermal vent. We have ensured the same mechanisms of transport are present as those in the real vent, so that the systems are dynamically similar. The experiments are performed in a Hele-Shaw cell, i.e. a two-dimensional geometry, which represents a horizontal cross-section through the porous vent structure and the transport of ions across it (figure 1b).

Figure 1.

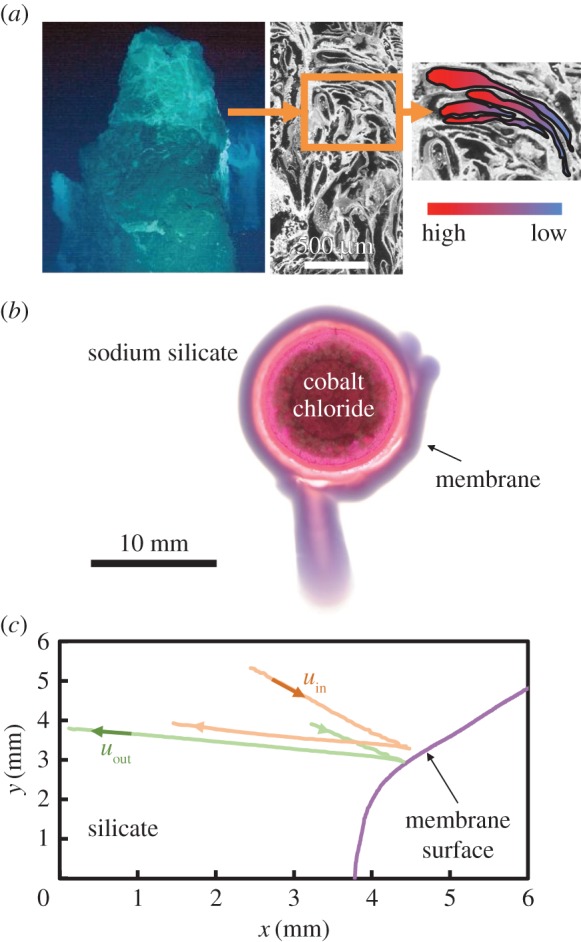
(a) Poseidon vent in the Lost City hydrothermal field (from Kelley et al. [43]), with typical porous structure (from Kelley et al. [6]) reprinted with permission from AAAS and an illustration of the concentration gradients within it. The laboratory analogue of a horizontal cross-section of a growing vent structure: (b) photograph of the cobalt chloride pellet surrounded by the precipitate membrane, and (c) measured trajectories of two seed particles near the membrane surface, at a silicate concentration of 0.28 M. The outside silicate solution flows towards the membrane with speed u_in driven by the osmotic pressure. Accumulation of water inside the cell builds up the internal pressure, which forces cobalt solution out of the membrane at speed u_out. (Online version in colour.)

Experiments were performed using cobalt (II) chloride hexahydrate (CoCl₂ · 6H₂O) as the metal salt to react with an aqueous solution of sodium silicate (Na₂SiO₃) with concentrations in the range 0.10–2.0 M. In order to achieve reproducibility and homogeneity, CoCl₂ · 6H₂O (Sigma-Aldrich) crystals were initially pressed into pellets with a diameter of 10 mm and thickness 1 mm by a KBR Port-A-Press^TM Kit (International Crystal Laboratories) under an equivalent pressure of 110 MPa. The experiments were conducted in a horizontal Hele-Shaw cell, consisting of two transparent acrylic plates (130 × 100 × 6 mm) separated by a gap of 1.0 mm. The cell was fitted to stainless steel back frames by a PTFE front frame with the dimension of 160 × 115 mm, with underlying uniform lighting from an LED lightbox. The experiment started by placing a pellet at the centre of the Hele-Shaw cell and injecting Na₂SiO₃ solution into cell using a syringe. The dynamics of each experiment was recorded by a Nikon D300s digital single-lens reflex (DSLR) camera (4288 × 2848 pixels) with a Hoya circular polarizing lens filter, located above the cell. The flow in the vicinity of the membrane formed by reaction of the two aqueous solutions is depicted in figure 1b.

In order to visualize the motion in the liquid surrounding the pellet, the silicate solution was seeded with 20 μm polyamide particles (Dantec Dynamics). The suspension was left to stand for 4 h to achieve neutral buoyancy at a low seeding density, to avoid both particle–particle and particle–plate interactions. An area of the cell of approximately 30 mm² was photographed at a frame rate of 1/3 Hz. The speed of the particles was calculated from the time derivative of the measured particle trajectories.

To follow the pressure dynamics inside the membrane, a hole of diameter 8 mm at the centre of the upper Hele-Shaw cell plate was connected to a relative pressure sensor (PS-2114, PASCO Scientific) by a silicone tube of inner diameter 3.0 mm. The pressure was measured at a sampling rate of 20 Hz and a resolution of 1 Pa. The pressure and speed measurements were used to estimate the membrane permeabilities in the inow and outow regions.

The osmotic pressure p_o across the semipermeable membrane was calculated based on the relation [44–46] p_o = ϕ_Co c_CoRT − ϕ_Si c_SiRT, where ϕ_Co and ϕ_Si are the activity coefficients for CoCl₂ and Na₂SiO₃ solutions, respectively [47,48], R is the ideal gas constant and T is the absolute temperature. A sample of the solution of cobalt within the pellet region was collected and its concentration was measured as 3.4 M using an Agilent Cary 60 ultraviolet–visible spectrophotometer.

3. Results

3.1. Osmotic advection and chemical precipitation

The precipitation of minerals at hydrothermal vents in the early ocean formed porous membranes with osmotic properties, such as those seen today in the Lost City field (figure 1a). Osmosis drives water with small ions inwards across the vent walls, while internal fluid pressure expels water with small and large ions through larger pores and channels. A balance of internal and osmotic pressures determines the in/out circulation and the vent membrane growth. In the laboratory and theoretical model, we consider a two-dimensional geometry, which represents a horizontal cross-section through the porous vent structure and the transport of ions across it (figure 1b).

The flow in the vicinity of the membrane formed by reaction of two aqueous solutions, an inner solution containing cation Co²⁺ and an outer solution of anion ${\mathrm{SiO}}_3^{2-}$ at concentration c_Si is depicted in figure 1b,c. The membrane is permeable to the cobalt ion but impermeable to the silicate one, so that an osmotic pressure p_o develops across it. The gradient of pressure p_o/L_m drives water from the exterior environment into the cell enclosed by the membrane, thereby increasing the internal pressure p; here, L_m is the membrane thickness. This increase in pressure, in turn, opens small cracks in the membrane and drives the saturated aqueous solution of cobalt outwards through these. A dual permeability membrane is therefore formed: the chemistry controls the low permeability of the inflow regions, while the internal pressure and solid mechanics of the membrane determine the higher permeability in the outflow regions. At the outer surface of the membrane, the reaction

$${\text{Co}}^{2+}(aq)+{\text{SiO}}_3^{2-}(aq)\to {\text{CoSiO}}_3(s)$$ 3.1

occurs at the interface between the two fluids, to form a precipitate layer of product, whose thickness grows with time. This nucleation and precipitation process is rapid [49,50], so that the formation of the product is limited by the supply of silicate ion when c_Co ≫ c_Si.

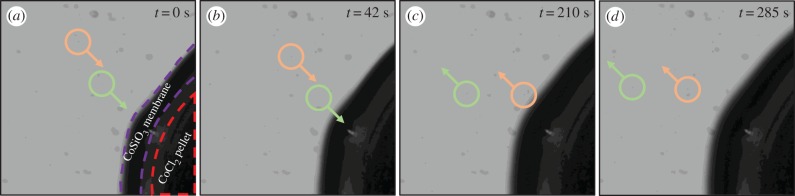
The growth of the cobalt chloride membrane is shown in figure 2. Three zones can be distinguished: a central zone with a dark pink colour is the cobalt chloride pellet, an intermediate liquid zone with colour gradient from pink to clear contains the dissolved cobalt ion, Co²⁺(aq); and the external zone with a purple colour is the membrane, which contains precipitated cobalt silicate, CoSiO₃(s). The motion of polyamide seed particles is tracked in figure 3. The particles are seen to first approach the membrane surface and then move outward.

Figure 2.

(a–d) Sequence of photographs showing the growth of the cobalt chloride membrane with 0.275 M Na₂SiO₃ and a saturated solution of CoCl₂. Field of view: 17 × 26 mm². (Online version in colour.)

Figure 3.

(a–d) Sequence of photographs showing the movement of two seed particles in the sodium silicate solution near to the membrane with 0.275 M Na₂SiO₃ and a saturated solution of CoCl₂. The particles are in the middle of the dashed circles. Field of view: 6.55 × 6.55 mm². (Online version in colour.)

Imaging and speed measurements show that the inflow and outflow regions of the membrane are distinct, and the permeability for the inflow is much smaller than that for the outflow, k_in ≪ k_out this complex structure enables the membrane to self-regulate both flows.

3.2. Pressure and concentration of solid: nonlinear evolution

In the laboratory, we have measured the pressure inside the pellet, but we cannot measure directly the concentration of solid at the reaction front on the outer surface of the membrane. We can, however, measure the surface area of the solid membrane S. We expect this surface area to grow following dS/dt ∼ dL_m/dt ∼ u_out c ∼ −dc/dt + u_in c_Si/L_r. The last term here is approximately constant, so that any temporal oscillations in c will be reflected as oscillations in S too [51]. Figure 4 depicts the evolution of the measured rate of change of the surface area of the solid membrane, as well as the pressure inside the pellet, for a range of concentrations of the silicate solution. The measurements show oscillations for both pressure and dS = dt, which are initially in anti-phase but gradually slip into phase at larger time. The oscillation period increases slowly with time.

Figure 4.

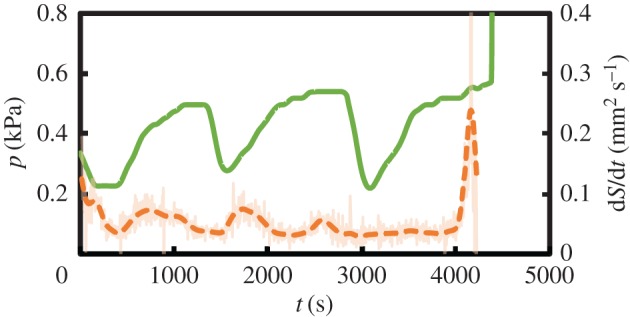
Measured pressure (solid line) and rate of increase of surface area of precipitate (dashed line) as a function of time with 0.275 M Na₂SiO₃ and a saturated solution of CoCl₂. (Online version in colour.)

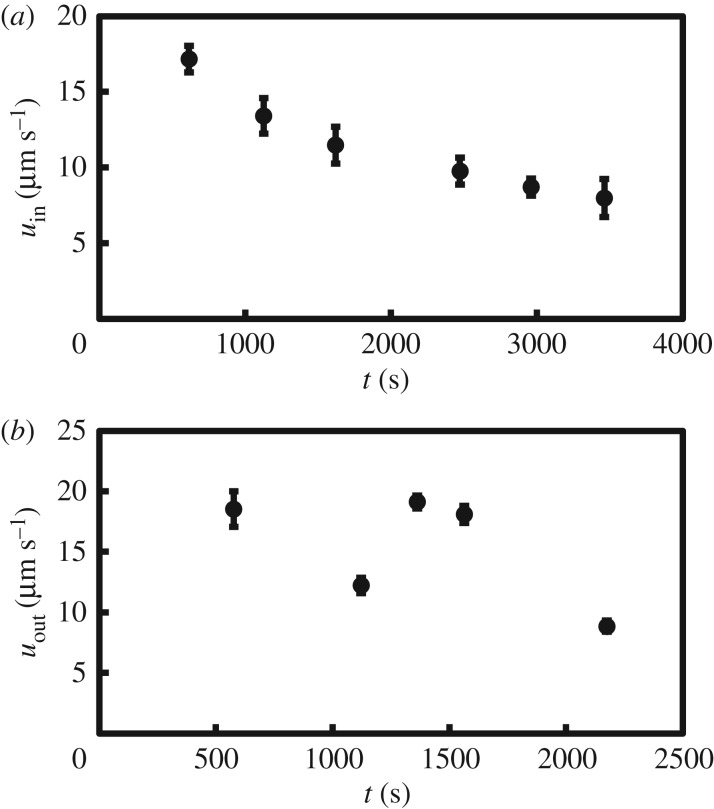
Figure 5 shows the measured inward and outward speeds of the tracked particles as a function of time. The inward velocity is approximately uniform in the azimuthal direction, over the inflow regions of the membrane. The outflow velocity is more localized in the azimuthal direction, with outward jet-like flows interspaced by regions of much slower flow.

Figure 5.

Measured inflow (a) and outflow (b) speeds near the membrane surface with 0.275 M Na₂SiO₃ and a saturated solution of CoCl₂.

4. Discussion

4.1. Ionic flux

We have demonstrated that the membrane has the ability to self-regulate the inward and outward flows, so that they are of similar magnitude. It does so by developing regions with two very distinct permeabilities: the low permeability drives osmotic flow of water inwards, while the larger permeability allows the outward flow of cobalt solution. This quasi-balance of flows enables the in/out circulation of ions through the membrane wall to be long-lived. In our experiments, the flux of ions flowing out through the porous membrane, driven by osmosis, can be readily estimated to be F = u_outc_Co ∼ 10²¹ ions m⁻² s⁻¹. Across one pore of radius R = 4.5 × 10⁻⁴ m [51], the flow is ∼10¹⁵ ions s⁻¹. For smaller solute concentrations, of the order of ∼10⁻³ M, as found in today’s cells [52], the flow in one pore would be ∼10⁹ ions s⁻¹. This flow then decreases to zero as the membrane becomes blocked. Our maximum pore flows are much larger than those measured in one ion channel in a living cell today, of ∼10⁷ ions s⁻¹ [52], thus suggesting that proto-biological processes could be sustained by osmotic flow in a less-efficient prebiotic cell. This is compatible with the necessity for ‘leakiness’ in bioenergetic terms in protocells before the last universal common ancestor, LUCA [21,53,54].

4.2. Warm little pores

The minimal physical model presented here is capable of describing the emergent dynamical regimes observed in our laboratory experiments. The focus has been on reducing the multitude of physical and chemical processes in the self-assembling precipitate to the interaction of osmotic flow and chemical reaction in the membrane. This is a beautiful example of active fluid dynamics, where the chemistry controls the flow, which in turn determines the membrane formation pattern. This fluid mechanics can now be applied to give us insight into the dynamics at hydrothermal vents, since any prebiotic chemistry involving the formation of such osmotic membranes would potentially have those regimes.

In a hydrothermal vent, similar processes are taking place, but in a less constrained, more complicated system. A glance at a microscopic slice through a Lost City vent (e.g. fig. 1b of [21]), one of the alkaline classes particularly highlighted in terms of origin-of-life studies, shows a series of tiny compartments linked together with membranes of different thicknesses. Across these membranes, there is exchange with the environment [55]. Each compartment delimited by membranes may be considered a natural version of our Hele-Shaw cell, a reactor within which new membranes may form, grow and explode, so giving a complex spatio-temporal dynamics.

Thus, within this series of compartments, one may find environments where, in a given place at a given time, as for Goldilocks [56], things are just right: the right temperature, pH, reactant concentrations and so on, for complex chemistry to begin and be sustained. (It is possibly this sort of Goldilocks idea of a warm little pond that is ‘just right’ that Darwin may have had in mind when he wrote his famous phrase.) Recent simulations likewise highlight the importance of a long series of interconnected porous structures in enabling synthesis of biopolymers [57].

Within such a compartment, chaotic advection [58] is necessarily acting [59], and such advective processes can drive the accumulation of reactants within a pore [60]. Such an environment offers the possibility of good mixing by advection and diffusion on the small scale, coupled with inflow of new reactants and outflow of intermediate products, this ranging from well-mixed to plug flow reactors [61]. Furthermore, as we have shown here, the dynamics of these natural reactors is astonishingly versatile. Once the gel-like membrane blocks at the surface, osmosis continues. This draws water from the pores to the central region, i.e. it reduces water in the pores, which may be replaced by a gas phase emanating from chemical reaction to maintain the pressure and the integrity of the solid structure. Given that the membrane is semipermeable, the solutes in some blocked pores can thus become concentrated. In other words, the blocking of the membrane causes a redistribution of the water within the semipermeable structure driven by osmosis, whereby localized large increases in solute concentration can develop within the blocked pores.

An important aspect of arguments on the origin of life, from either the lacustrine point of view, or from our oceanic vent viewpoint, is the repeated cycling or oscillation, where each cycle enables some reaction and over many cycles, one can obtain a significant yield of the product. In the explosive regime, we see only one explosion, but that is a result of our simple geometry with a single pellet. In a vent with a continuous flow of reactants, there would be multiple such events. Such multiple de- and re-hydration cycles favour the formation of long and biologically relevant peptides [62]. The lacustrine model evaporates ponds to concentrate material, but our alkaline hydrothermal vent vesicles are many orders of magnitude smaller, so giving them an advantage as nanoreactors.

We should note that the timescales of the oscillations and explosions in our experiments are of the order of 1–4 × 10³ s. This is clearly much shorter than the natural diurnal or seasonal rhythms proposed in the lacustrine model as the origin of the wet–dry cycles in early bioreactions [10]. A small pore size in a hydrothermal vent precipitate favours longer periods of concentration oscillations and explosion. Indeed the flow is slower in a small pore, so it takes longer to get material in and out by the osmotic flow. Nevertheless, provided the oscillatory timescale is larger than the reaction timescale, the reaction can take place when the medium becomes sufficiently dry and concentrated [63]. So a network of pores in the gel-like membrane can provide many oscillatory cycles and thus promote a more effective reaction site than a larger pond. In this view, life began from intrinsic cycles of concentration in chemical nanoreactors; we may call them warm little pores. In summary, we have demonstrated that the chemical energy associated with the concentration gradients across a growing membrane, such as a hydrothermal vent structure, can drive significant flows across it, and also lead to its explosion. Such flows can carry multiple ions across the membrane, particularly small ones, this favouring further reactions. We have noted in particular the concentration oscillations, which have been previously identified as a necessary condition for the formation of peptides. We have therefore demonstrated the use of one source of chemical energy, in particular gradients in concentration, to generate fluxes of kinetic and chemical energy across the porous structure of a hydrothermal vent, which in turn, could favour energetically the early biochemical reactions taking place within its pores.

The membrane develops with two very different permeabilities for the inflow and outflow. This is what makes in/out circulation possible. In bio-membranes, ion channels select chemically for the in/out flows. What biology seems to have done is to add more and different ways through the cell membrane. Some of these are very specific, not just to a single chemical species but also in a single direction. Here we have a self-assembled membrane demonstrating similar capabilities to an ion channel: what we see in this system is the very beginnings of such selectivity. Thus, this chemical garden is really working like a possible proto-cell: it is self-contained and controls the inflow and the outflow chemically and volumetrically. Perhaps proto-life could have learnt from this self-organized system by a take-over process as complex organic chemistry got started within it.

Data accessibility

This article has no additional data.

Competing interests

We declare we have no competing interests.

Funding

S.S.S.C. acknowledges the financial support of the UK Leverhulme Trust project RPG-2015-002. J.H.E.C. acknowledges the financial support of the Spanish MINECO project FIS2016-77692-C2-2PP. S.S.S.C. and J.H.E.C. acknowledge the European COST action CA17120.