Probing complexity: thermodynamics and computational mechanics approaches to origins studies

Abstract

This paper proposes new avenues for origins research that apply modern concepts from stochastic thermodynamics, information thermodynamics and complexity science. Most approaches to the emergence of life prioritize certain compounds, reaction pathways, environments or phenomena. What they all have in common is the objective of reaching a state that is recognizably alive, usually positing the need for an evolutionary process. As with life itself, this correlates with a growth in the complexity of the system over time. Complexity often takes the form of an intuition or a proxy for a phenomenon that defies complete understanding. However, recent progress in several theoretical fields allows the rigorous computation of complexity. We thus propose that measurement and control of the complexity and information content of origins-relevant systems can provide novel insights that are absent in other approaches. Since we have no guarantee that the earliest forms of life (or alien life) used the same materials and processes as extant life, an appeal to complexity and information processing provides a more objective and agnostic approach to the search for life's beginnings. This paper gives an accessible overview of the three relevant branches of modern thermodynamics. These frameworks are not commonly applied in origins studies, but are ideally suited to the analysis of such non-equilibrium systems. We present proposals for the application of these concepts in both theoretical and experimental origins settings.

1. Introduction and state of the art

There remains one a priori fallacy or natural prejudice, the most deeply-rooted, perhaps, of all which we have enumerated: one which not only reigned supreme in the ancient world, but still possesses almost undisputed dominion over many of the most cultivated minds: : : This is, that the conditions of a phenomenon must, or at least probably will, resemble the phenomenon itself.

John Stewart Mill [1]

1.1. Contemporary origins research

The most common approach to abiogenesis is to seek ways that aspects of life as we know it can be re-capitulated in abiotic systems, ideally within the ensembles that are ‘representative’ of the early Earth. This philosophy has yielded mixed results [2,3]. There are some who argue that synthesizing the most essential components of life may be understood in the coming years [4]. Critics would point out that such experiments require contrived, overly clean and unrealistic conditions (e.g. [5,6]). However, there is a deeper and potentially more pressing concern of driving forces: how and why might a system of biomolecular pieces come together to form a living whole? This grand challenge can be subdivided into a number of philosophical sticking points.

Firstly, the debate concerning what constitutes life is as contentious as at any point in the history of the field [7–12]. Secondly, there are equal volumes of debate concerning the sequential ordering of the appearance and integration of different facets of life. Some prioritize autocatalytic reaction cycles or primitive metabolisms as essential to drive any prebiological process [13–20]. Others argue that nothing life-like will arise in the absence of a bounding, membrane-like structure [21–24]. Still others contend that without any form of genetic system or primitive replicator, evolution and hence life cannot emerge [25–30]. Yet others are exploring alternative conceptual frameworks, including statistical chemistry approaches [31], and more recently, ‘Messy Chemistries’ [32,33], among others. Origins research has also highlighted several paradoxes related to initiating such a highly circular and functionally interdependent process as life.

Given these significant unknowns, we should remain open to the possibility that life did not take a linear, single, minimal and direct path from non-living to living. Indeed, there have been suggestions in this direction recently [34]. The glaring disadvantage of this approach is that it offers much fewer constraints and intermediate objectives than the traditional origins approaches. We therefore propose the concepts of increasing complexity and information processing as an alternative guiding principle for modelling or experimental studies of the emergence of life. Elaborating this proposal will be the focus of the present work.

1.2. Recent progress in thermodynamics and complexity science

Progress in stochastic thermodynamics, information thermodynamics and computational mechanics now allows the objective calculation of quantities that were all but intuitive ideas until recent decades. Information itself has been a well-defined quantity since the pioneering work of Shannon [35]. However, it has been repeatedly noted that context dependence, meaning and function are missing in Shannon's formalism, not to mention the fact that it essentially measures randomness (degree of surprise). This led to the formulation of other information metrics such as physical complexity and functional information [36–40]. These will be discussed further in the following section.

Although rigorous and universal definitions for function, utility and meaningfulness are still elusive, great progress has been made in unifying traditional thermodynamics with theories of information and complexity. Complexity often serves as a placeholder for ‘too difficult to comprehend’, and many have attempted to formalize it mathematically. One approach, borne out of nonlinear dynamical systems studies in the late 1970s and early 1980s, has been particularly successful at capturing the notion of complexity in a general way. This field, now known as computational mechanics, started with the objective of deriving state information about a dynamical system from limited observations (this problem is the essence of probabilistic inference and appears in most sciences, albeit under different guises). What eventually emerged, through the efforts of Professor James Crutchfield, his student at the time Cosma Shalizi and many other researchers over the intervening years, was a method known as epsilon machine reconstruction [41–45]. Once the epsilon machine for a given input has been constructed, it is straightforward to calculate a range of key metrics including the statistical complexity, entropy production rate and others. This will be discussed further in §2.

Another area that has experienced great strides in recent decades is stochastic thermodynamics, also known as the thermodynamics of small systems, or fluctuation theorems [46–50]. This theoretical framework was able to generalize concepts such as free energy to small systems arbitrarily far from equilibrium, which is all but impossible using classical thermodynamics. It is also now possible to calculate relative probabilities of phase space trajectories to their reverse counterparts, with the main finding that this quotient depends purely upon the difference in entropy production of the forward and reverse paths. This opened up a whole new realm of statistical physics with wide-ranging applications, in particular, the study of dynamic macromolecules such as genetic polymers and molecular machines [51–55].

Last but not least, researchers in the field of information thermodynamics have constructed formal frameworks that incorporate the role of information in the dynamics of physical systems. Although entropy has existed as a construct for over 100 years, and Shannon formalized the concept of information in the mid-twentieth century, there were still missing links regarding the mechanisms by which information and energy are related. This link now appears to have been largely forged by the bellows of theoretical insight, and the fires of experimental observation. Hence a comprehensive thermodynamic theory of information is now available [56–59]. With this new formalism, it is possible to place exact limits on the efficiency with which information can be exploited to convert disordered energy into ordered energy, or dissipate ordered energy to write information. The potential applications and insights from these achievements are profound and far-reaching.

Note that the aforementioned three areas of progress are deeply connected. Computational mechanics provides a means of constructing minimal prediction machines. Those prediction machines can be optimized to effectively interconvert between information and energy. Changes in information content in such systems can be quantified by analysing relative probabilities of phase space trajectories using fluctuation theorems.

1.3. Motivation for the application of thermodynamics and complexity to the emergence of life

As mentioned above, aspects of primitive metabolism and synthesis may be solved in the near future. But the larger enigma of turning a set of prebiotic molecules into an evolving ecosystem is not understood (note however the attempt that began with the pioneering work of [60]). In order to make further headway, we need to explore potential driving forces for the self-organization of a non-equilibrium system containing materials that could comprise prebiological systems. Note that these materials may not be immediately recognizable as biological. For example, they may be polymers other than peptides, nucleic acids, etc. Such an exploration should also be maximally free of preconceptions about the story of how life emerged. The natural world is not obliged to be readily comprehensible, nor align with human expectations.

In environments that experience variations (all environments of astrobiological focus), a prebiological system able to adapt to such variations, or in fact make use of them, would be more resilient than an equivalent system that only persists in a confined region of environmental phase space. The non-adaptive system would at some point be wiped out by fluctuations.

Fluctuations that are wholly stochastic cannot be mitigated except by shear robustness. However, fluctuations that have reproducible (learnable) features can be mitigated through some form of internal modelling, prediction or learning process. Modern life performs prediction by learning from past events, using a range of mechanisms and over a range of time scales (e.g. [61–65]). Humans, crows, elephants, octopi and other cognitive animals can learn to solve problems through play and training. Mammalian immune systems use an orchestrated form of evolution to search the space of antibodies and produce long-term records of successful searches [66,67]. Gene regulatory networks show associative learning capabilities [68,69], and even individual protein molecules behave akin to combinatorial logic gates [70]. Evolution can also be thought of as a learning process, as organisms, collectives and ecosystems encode information about both the abiotic and biotic components of their environments [71–73].

The importance of the use and encoding of information in the biosphere cannot be understated, and the journey from complex physico-chemical dynamics to biological dynamics had to involve a transition to adaptive encoding and control of information at some point (including non-genetic systems) [74,75].

A great deal of research has explored the emergence of information in biomolecular systems, in particular the genetic and catalytic polymers [76–84], and self-replicating systems [25,85,86]. These studies focus upon the quantitative relations between the information content of polymeric systems, and the disequilibria that drive the system. In the present work, we wish to go further and consider not just information itself, but the processing and exploitation of that information, up to and including learning.

Extant life is replete with information processing structures, mechanisms and systems. The first life would have had drastically more primitive information processing capacity. But for a proto-organism to be precarious [87], i.e. for it to exist in any environment beyond the ideal ‘incubation’ environment, it would have to begin to process information about the new environment, such that the perturbations away from the incubation environment could be managed. Any predictable phenomena in the new environment could potentially be encoded and modelled by the system. If the modelling ability were to feed back positively on the robustness or proliferation of the prebiological system, then it will be selected for (not in a strictly biological sense, but in a dynamical stability sense).

The extent to which a system undergoes some form of learning or computation can be quantified using the frameworks of information thermodynamics and computational mechanics. Roughly speaking, if a system's epsilon machine exhibits high entropy rate and statistical complexity, and if these metrics are growing with time, then the system is increasing its computational capacity and hence may also be exhibiting life-like characteristics. In general, theoretical and experimental studies of emergence seek systems that exhibit growing complexity (preferably perpetual complexity growth, or open-endedness). Measurements of statistical complexity would therefore be an invaluable guide as to which systems are becoming more life-like from a non-living initial condition. Complexity comparisons may be performed over time or between members of an ensemble that is spread over a given parameter space.

1.4. Executive summary

We propose that the strong correlation between life, complexity and information processing, combined with recent progress in quantifying complexity and information processing, can be wielded to construct guiding experimental and theoretical protocols for origins studies. Our thesis comprises the following points:

• (1)Complexity and information processing are fundamental and necessary conditions for life, and hence must feature in any hypothesis for life's beginnings.
• (2)Complexity and information processing are now rigorously defined, measurable and aligned with their intuitive meanings, thanks to advances in stochastic thermodynamics, information thermodynamics and computational mechanics.
• (3)New experimental and theoretical approaches that exploit this progress could bring great advances to origins studies, by guiding paths towards more complex and more life-like prebiological systems.

2. Foundations and recent advances of modern statistical physics

This section will present brief surveys of the pertinent aspects of stochastic thermodynamics, computational mechanics and information thermodynamics. We cannot present these fields in their entirety since they are vast and not all aspects are directly relevant. There are also other reviews available (e.g. [42,49,58]). Our objective is simply to give a high-level overview of the areas most relevant to the origins field. Those who are already well versed in any of the three subdisciplines should feel free to skip those sections.

Recent decades have seen significant progress in the ability to model and experimentally manipulate micro-to-nanoscale physical systems, including those upon which life depends to harness free energy from the environment, or process information [52,53,88–90]. Because of the peculiarities of very small energy and length scales, it was necessary to develop a new thermodynamic description of these systems called stochastic thermodynamics [46–49,91]. Much of this progress was motivated by a desire to derive quantitative descriptions of the sub-micrometre structural units of living cells and viruses, for which stochasticity and randomness dominate. The many degrees of freedom (approx. 10²³) and assumptions of reversibility and equilibrium upon which classical thermodynamics is built are problematic when describing the small systems and large gradients operative in cells. Though the laws of classical thermodynamics hold on average for infinitely sampled small systems, individual microscopic trajectories of small systems can drastically deviate from equilibrium values (e.g. [48,53,92]).

Proponents of the alkaline hydrothermal vent theory for life's emergence, including Michael Russell and Elbert Branscomb, have argued strongly that in order for life to emerge, significant geochemical gradients in the environment must have been available. They further argue that the emergence of prebiotic transduction mechanisms able to couple with these geochemical gradients in order to create other, downhill gradients was required [93–95]. They hypothesize such prebiotic transduction mechanisms would be akin to molecular motors and enzymes, but in contrast to modern biology, were comprised largely of the inorganic constituents of minerals found in vents [16]. These authors have also stressed the importance of accounting for the nanoscopic dimensions of these mineral systems in analogy with the stochastic behaviour of molecular motors and enzymes.

Despite this, much work remains to derive quantitative models and design experiments to probe the nanoscale processes taking place within alkaline vent systems (though note the important work of [96]). This may be due in part to a paucity of awareness of the great progress in stochastic thermodynamics. There is also an inherent difficulty in the experimental study of these small systems, especially when the non-equilibrium conditions characteristic of vents are simulated. Nonetheless, we contend that stochastic thermodynamics is a necessary tool to constrain and rationalize whether the nanoscopic minerals and organic molecules in vents would have evolved into ever more life-like systems. Our goal is to introduce some of the fundamental concepts of stochastic thermodynamics. Beyond this, we explain how the recent extension of stochastic thermodynamics to fundamental models of information processes may allow for the determination of energetic lower bounds necessary to acquire and process information in a submarine alkaline vent or other prebiotic environment.

2.1. Introduction to fluctuation theorems

An important concept in stochastic thermodynamics is the driving protocol Ω, defined as the time-dependent profile of a control parameter λ, used to do work, W, on a system. An example of such a parameter would be the extension by which an RNA molecule was stretched in the experiments of Collin et al. [53].

In what follows we first consider a system that starts at an equilibrium state A and is then driven out of equilibrium by the control parameter to some terminal state B, following a predetermined schedule (the driving protocol). Together with the first law of thermodynamics, the Clausius statement of the second law tells us that (for a single heat bath) the work required to vary λ must be equal to or greater than the free energy difference between the terminal states of the protocol [48]:

$$W[\mathit{\Omega }]\ge \mathrm{\Delta }F.$$ 2.1

For macroscopic systems, there is no expectation to observe a violation of this law. However, when one considers small, non-equilibrium systems where fluctuations and overdamped motion dominate, the inequality above can be violated. To interrogate small systems, a reinterpretation of the process described above is necessary.

Imagine a small molecule such as RNA that, in its natural course, folds and unfolds to function properly. If one were to perform an experiment where they repeatedly drive a single RNA molecule from a folded (state A) to unfolded state (state B), they would find the work required to unfold the RNA molecule can vary for each realization of the experiment [48,53]. Some realizations will require less work than the free energy difference of the folded and unfolded states, in violation of equation (2.1). This variation in work values is not due to the control parameter, since the same driving protocol is used for each unfolding process. Rather, it is due to the stochastic fluctuations of the heat bath which bombard the RNA molecule. From such an experiment, work distributions for this process can be obtained and the free energy difference between the folded and unfolded state of the RNA molecule can be determined from Jarzynski's relation:

$$⟨{\mathrm{e}}^{-\beta W}⟩={\mathrm{e}}^{-\beta \mathrm{\Delta }F}.$$ 2.2

Brackets 〈•〉 denote an average over many realizations of the process described above, β ≡ (k_BT)⁻¹ is inverse temperature, k_B is Boltzmann's constant, and T is the environmental (equilibrium) temperature at the start of the unfolding process. Note that the start and terminal states of the process are equilibrium states.

Jarzynski's relation was one of the first prominent results of stochastic thermodynamics and has been experimentally verified, including for the RNA (un)folding protocol by Collin et al. [53]. This relation enables the determination of equilibrium free energy states of individual biomolecules from non-equilibrium work processes, such as unfolding individual polymers. However, there can be significant errors in computing free energies of single molecules using Jarzynski's relation if the work distributions are undersampled [97].

Crooks fluctuation theorem (equation (2.3)) is a more general result that applies to systems that obey microscopic reversibility [91]. Before introducing Crooks fluctuation theorem, it is necessary to differentiate between the forward protocol, Ω_f and the reverse protocol, Ω_r. An example of a forward protocol is the process of unfolding RNA described above. The reverse protocol is simply the control parameter schedule for the forward protocol in reverse. So if for the forward protocol one drives the system from A to B, then for the reverse protocol one would drive the system from B to A. The general form of Crooks fluctuation theorem states that the ratio of the probability to observe a system trajectory X_f during the forward protocol, Ω_f, to the probability to observe the reverse trajectory X_r during the reverse protocol, Ω_r, is given by an exponential factor of the entropy production ΔS, in the system and environment, during the forward protocol [47,48,55,91]:

$$\frac{P[{\mathit{\Omega }}_{\mathrm{f}}\mathit{(}{\mathit{X}}_{\mathrm{f}}\mathit{)}]}{P[{\mathit{\Omega }}_{\mathrm{r}}\mathit{(}{\mathit{X}}_{\mathrm{r}}\mathit{)}]}=\exp \left(\frac{W_{\mathrm{f}}-\mathrm{\Delta }F}{k_{\mathrm{B}}T}\right).$$ 2.3

This equality holds for systems driven arbitrarily far from equilibrium and provides insight into irreversible processes by relating the degree of time asymmetry a system exhibits to entropy production. Stated more simply, if one were to record the system of interest driven during the forward protocol and then play the movie backwards, the distinguishability of the two movies depends upon the entropy produced during the forward protocol. Breaking time symmetry incurs a thermodynamic cost, which must be paid for by dissipation. It is this same cost which must be paid to drive directed behaviour of molecular machines to reliably complete work cycles in finite time. The Crooks fluctuation theorem has also been experimentally verified and does not suffer from the problem of under-sampling that the Jarzynski relation does [53,55].

Recent work by Crooks, Sivak, and others has begun to shed light on the impact that different driving protocols have on the efficiency of performing various types of work on driven nanoscale systems [55,98–100]. How does one optimize the driving protocol to perform work on a system with minimal dissipative cost? An elegant approach to the problem is currently under development and has been applied to both information processing systems and biological macromolecules [101,102]. There has also been recent interest in considering a stochastic driving protocol rather than a well-defined one as in the examples above [103]. The detailed mathematics of optimal driving protocols are beyond the scope of this article as they involve calculating geodesics along Riemann manifolds, geometry typically encountered in General Relativity. However, we encourage readers to review these papers, as the important role of the ‘driving protocol’ and its optimization is qualitatively discussed later.

2.2. Computational mechanics and information thermodynamics

Information theory and computer science are relatively young fields compared to classical thermodynamics. And yet their influence has been profound and rapid. They have taken us from an industrial age of power through liberating electrons from organic materials and donating them to an oxidized atmosphere, to a digital age where electrons instead encode and transfer information on a massive scale. This may become the most major of the major evolutionary transitions.

2.2.1. Shannon entropy

The foundations of computer science were laid by Turing, von Neumann and others. Although this paved the way for the digital age, the relationship between information, computation and energy would take somewhat longer to formulate. A rigorous treatment of information and communication was provided by Shannon [35]. This framework relates information content to probabilities of received signal content (the degree of surprise of receiving a certain signal). More generally, the Shannon entropy is a metric of probability distributions:

$$H[X]=-\sum _i{p}_i\mathrm{lo}{\mathrm{g}}_2{p}_i,$$ 2.4

where i indexes the possible states of a system, members of a signal alphabet, or outcomes of a measurement, etc., and p_i is the probability of observing state i. Equation (2.4) is maximized for uniform distributions (complete ignorance), and vanishes under complete knowledge (when one probability in the set is unity and all others vanish). This expression can also be seen as a generalization of Boltzmann's entropy formula (which applies to the special case of equally likely states in an ensemble), and is also equivalent to the expression due to Gibbs (whom was less explicitly concerned with information). Shannon's result and its link to the classical thermodynamics of Carnot, Boltzmann and Gibbs illustrated the deep connection between available or free energy, and the state of knowledge of the observer of a system. Knowledge clearly was power; however, there was still a missing piece. Carnot had shown how efficiently thermal gradients can be converted into work, but the restrictions of equilibrium thermodynamics did not permit a quantitative understanding of dynamic processes that interconvert between heat, work and information.

2.2.2. Maxwell's demon

Maxwell semi-whimsically introduced his demon in 1867, and it was still defying a thorough exorcism until the latter half of the twentieth century, when it was finally vanquished by the efforts of Szilard, Landauer and others (see [104] for an overview). It had been shown that many measurement protocols that the demon might use could be performed with negligible energy expenditure. However, it was Landauer [105] who demonstrated that erasing information carries an inevitable energetic and entropic cost. When a system such as a Szilard engine [104] is reset to its starting state (which it must be to be cyclic), information about its previous state is lost. This loss produces a net entropy contribution of $k_{\mathrm{B}}\log 2$, due to the two-to-one phase space map that arises from erasing the single bit of stored state information. Thus any entropy reduction from converting a quantity of heat into work by a demon system is offset by at least this ‘Landauer bound’ (in general more entropy than this limit is generated).

Hence the second law of thermodynamics was saved, and its safety has been reinforced by increasingly accurate nanoscale experiments [58,59,106–110]. It was then possible to calculate and verify bounds on the free energy that one could yield from a system given a source of information about that system (e.g. [59,110,111]).

More recently, a complete framework that includes the use of information (conventionally bits on a tape) as a resource has been presented [56,57,112–114]. This formalism allows the calculation of efficiency limits for the exploitation of information for the conversion of disordered energy into ordered energy, or the minimal cost of dissipating ordered energy to write information into a subsystem's state. In the limit of no information, this framework reduces to Carnot's theory. Garner et al. [56] concluded that the most efficient information processing devices are prediction machines that minimize the storage of superfluous or non-predictive information. The lower bound on the dissipative cost of pattern manipulation was found to be given by the crypticity of the pattern (see Crutchfield [42] and references therein for further details on the crypticity of a time series). In the field of computational mechanics, it has been proposed that the minimal and optimal predictor of a time series is the epsilon machine of Shalizi & Crutchfield [44]. The story of its development now follows.

2.2.3. Complexity metrics

The most well-known early attempts to quantify complexity were due to Kolmogorov & Chaitin [115,116]. Given an input sequence describing a system (e.g. a discrete time series of discretized measurements), the Kolmogorov–Chaitin complexity (KCC) measures the size of the minimal program that reproduces the time series when fed into a universal Turing machine. In other words, the KCC is a measure of minimum description length (greater degree of regularity allows a more compact description). Simple systems such as crystals at equilibrium have small KCC due to their high degree of symmetry. Less predictable systems have higher KCCs. However, herein lies the flaw in the KCC: it is maximized by random strings, for which the minimal program is simply a copy of the string itself. Clearly, a string of random bits is unpredictable, but not complex, since it exhibits precisely zero structure. In addition, there is no universal procedure for computing the KCC of arbitrary input strings.

In light of these issues, more recent efforts have extended thermodynamic and computational concepts to formalize complexity (note also the early work of [117]). Thirty years ago, Charles Bennett, known for his contributions to the thermodynamics of computation, surveyed various candidate measures of complexity, and did not conclude that any of them satisfied the necessary requirements [38]. Adami & Cerf [37] developed a metric that extended the KCC and prioritized meaning and context. Their ‘physical complexity’ measured regularities in strings in the context of given environments, inspired by analysis of genetic sequences. Such sequences can be highly meaningful or functional in one niche, but useless in others.

The nobel laureate Murray Gell-Mann also contributed to the development of complexity metrics [39]. He and Seth Lloyd noted that it is essential to capture reproducible, deterministic components of a system, and also the stochastic components (already captured by the Shannon entropy rate). Their metric, known as the total information, was a summation of the effective complexity (measuring the reproducible aspects of the system), and the Shannon entropy rate (measuring the stochastic aspects). This approach is conceptually similar to the epsilon machine approach of computational mechanics described below.

The contribution of Hazen et al. [40] prioritized the function of strings given the ensemble of all similar strings. In particular, their ‘functional information’ quantified the probability of the emergence of functional members of the ensemble. This was applied to digital organism genomes and biopolymer sequences, but did not achieve the generality of the framework discussed next.

2.2.4. Epsilon machine reconstruction

Computational mechanics began with the fundamental issue of deriving state information from partial measurements [118]. How can we objectively and optimally glean details about a system's phase space dynamics when we can only measure a small fraction of its degrees of freedom? It was discovered that simply projecting a subset of the degrees of freedom of a system can reveal structure in the larger phase space of that system. A striking example of this was simple timing measurements in the dripping faucet experiment [119,120]. These ideas of phase space projection from time series eventually led to the concept of causal state splitting reconstruction. This process characterizes all the possible causal states that could comprise a minimal model of a time series, and groups those that are ‘causally equivalent’ (see [42–44] for full details).

As was noted by Gell-Mann & Lloyd [39], any metric for complexity should include both stochastic and deterministic elements, and vanish for perfectly stochastic or perfectly ordered systems. The computational mechanics approach solves this issue. It includes a rigorous procedure for generating predictive models of a given input (causal state splitting reconstruction, as mentioned above). Those models are optimal and minimal by design, and can thus be used to quantify the complexity of the input.

In its simplest form, this modelling process takes as input a discrete time series. Through causal state splitting reconstruction, it computes the minimal effective causal states of a Markov model that can reproduce time series that are statistically equivalent to the input series (up to an accuracy quantified by the parameter epsilon). Once this Markov model is constructed, it is then straightforward to calculate the Shannon entropy rate (the degree of randomness of the time series), and the statistical complexity (the information content of the state space of the epsilon machine). The full mathematical details of these metrics can be found in [42–44]. For the present discussion, it is sufficient to be aware of the interpretation of these quantities: the entropy rate measures degree of randomness, and the statistical complexity measures regularities in the dynamics of the system, indeed its degree of self-organization [43]. Also crucial is the fact that there is a definite procedure for the computation of these metrics from a given time series.

Let us consider the meaning of these quantities with some simple examples. If a process has vanishing entropy rate, that implies it is completely deterministic. An example would be periodic bit flipping (0101010101…), or in the continuous realm, a noiseless periodic oscillation such as a sine wave. Conversely, processes with high entropy rate have a high degree of stochasticity. Predicting future values of such series is inherently difficult or impossible for a pure noise signal. However, it is simple to construct a Markovian representation of such processes. Coin-flipping could, for example, be represented with a single-state machine that has two transitions, each with probability 1/2 (see fig. 1b of [42]). Each equally likely transition produces a head or a tail. Deterministic processes can also be compactly represented by epsilon machines. Typically, they would comprise a small number of states with transition probabilities that have a highly non-uniform distribution.

Complex systems combine elements of both of these extremes: they exhibit both deterministic and stochastic elements, and both elements contribute to any emergent structures and the ability to perform computation. A prime biological example is genes and their replication. The familiar crystal structure of DNA shows a high degree of symmetry and predictability. Likewise, it can be replicated with astounding fidelity. But clearly, perfect replication would grind evolution to a halt. Mutations are the engine of novelty and evolutionary invention. Mutations are thus an information source that interact with selective forces to produce and stabilize new characteristics and variations. However, mutation rates that are too high (large entropy rate) produce offspring that are not viable and the system suffers an error catastrophe. Hence at the genetic level, the profound complexity of life stems from a combination of the highly reproducible structure and function of DNA, and the stochastic fluctuations from mutations. This characterization of complexity as the rich middle ground between order and chaos has been noted by many (e.g. [42,121,122]).

3. Conceptual and experimental proposals

In light of the previous sections, we will now present examples of how modern thermodynamics could provide novel insights and guidance in origins-related research. As previously proposed by Branscomb & Russell [93–95], molecular machines or engines that process information and convert free energy are essential to life. This suggests they should have become part of life's story at an early stage. Hence we can ask: at what point in Earth's history would emergent information processors appear, and in which physical systems would they manifest? Of particular relevance to this theme issue is whether assemblages of information processors can emerge and evolve in chemical gardens or alkaline vent systems comprised of catalytic, nano-to-meso phase mineral assemblages.

Several proposals have been put forward for how information is created and endures as a heritable trait in mineral systems. Perhaps one of the best-known examples is the clay mineral hypothesis [123,124]. Some have suggested that this system is an unlikely vehicle for information creation and transfer [125,126], but several newer proposals have been suggested [127–129]. We posit that such questions can be answered in a natural and intuitive way by viewing minerals as stochastic sensors with some capacity to learn, and invoke the ‘control parameter’ from stochastic thermodynamics of single-molecule manipulation experiments as a likely ‘stochastic signal’ that an emergent sensor, a mineral in our case, might learn about. More specifically, we interpret this control parameter as the environment from the perspective of nano-phase minerals such as green rust.

3.1. Pumping and stochastic sensing in iron layered double hydroxide minerals

The role of iron minerals in the origins of life has long been emphasized [130]. This is due to several properties including their catalytic abilities [131–136], the diverse spaces of structure and function of iron minerals [128,137], their ability to bind biomolecules [96,138], their role in biological enzymes and energetics [139–142] and their potential to store information [125].

The first practical application of stochastic thermodynamics to such minerals comes from the consideration that prebiotic chemistry involves small-scale systems which when viewed as individual entities, require the framework of fluctuation theorems to determine quantities such as free energy, dissipation and other thermodynamic properties. If one accepts the argument that analogues to functioning molecular machines are requisite structures at life's emergence, one cannot escape the need to use stochastic thermodynamics to characterize and engineer such molecular structures. For instance, Russell and colleagues have hypothesized that layered double hydroxide (LDH) minerals such as green rust can act as primitive molecular pumps. Their line of reasoning relies upon evidence that LDH compounds are capable of anionic exchange, and thus there is a degree of mobility for molecules within their interlayer cavities. Secondly, a publication by Wander et al. [143] determined the hole polaron hopping rates for three distinct pathways between iron lattice sites along the cationic sheets of green rust.

Polarons are ‘self-trapped’ charges, equivalent to electrons or holes which deform the crystal lattice within their local vicinity. Concerted charge hopping among the dominant hopping pathways in two adjacent cationic sheets would lead to laminar deformation, potentially capable of pumping and condensing interlayer molecules. How much energy is required to carry out this function though, and what is the dissipative cost? Can experiments be carried out on individual nanoparticles to determine this? Along with computational modelling, we suggest single particle experiments with iron minerals such as green rust are necessary to confront these questions. Single-nanoparticle electrochemistry is an emerging field which provides an attractive complement to current prebiotic chemistry studies [144]. In addition, a recent experimental approach developed by Ross et al. [145], called relaxation fluctuation spectroscopy, offers a method to study nanoscale systems which are not amenable to the traditional force spectroscopy experiments previously described for RNA hairpins.

The second compelling reason to employ stochastic thermodynamics in the study of prebiotic mineral systems is evidenced in its connection to information processing and learning [112,113,146–151]. To confront the question of if and how information manifested in prebiotic mineral systems, one must determine what the information was correlated with and what the requisite energetic budget is to store and process information.

Many authors have used fluctuation theorems to analyse information incorporation into polymer species [76–84]. Here, we propose a similar analysis for mineral and mineral-organic systems relevant to the origins of life. Put simply, we aim to measure whether mineral systems could build abstract internal representations of (structured) external signals (e.g. driving protocols). Calculating the entropy production for such signals is straightforward using the fluctuation theorems of §2. A key challenge, however, would be the appropriate choice of measurement apparatus and variables to quantify information uptake by the internal mineral system. This builds on an earlier proposal due to Greenwell & Coveney [125]. However, their model did not take into account progress in the field of information thermodynamics or computational mechanics, since it was proposed before many of the important developments in those fields.

Zenil et al. [152] observed that in evolutionary biology ‘…attention to the relationship between stochastic organisms and their stochastic environments has leaned towards the adaptability and learning capabilities of the organisms rather than toward the properties of the environment’. While we advocate the exploration of how prebiotic mineral systems learn and adapt, the structure and predictability of the environment must always be carefully considered. In general, we interpret the environment as the mechanisms by which external control parameters couple to an internal system, in our case a mineral. Hence the time-dependent ‘protocol’ discussed in previous sections is akin to the ‘algorithm’ concept invoked by Walker & Davies [74] and Zenil et al. [152]. It is important to stress that such stochastic, time-dependent driving protocols are a function of naturally varying parameters such as pH and chemical potentials, which for submarine, alkaline vent systems are dictated by processes such as serpentinization, local petrology, hydrodynamics and ocean chemistry [153–156]. Among the heterogeneous mixtures of mineral precipitates driven by variations in pH, Eh and chemical concentrations, we hypothesize that some fraction will emerge for which the interplay of the mineral system with a structured environment will lead to the acquisition and utilization of information, as seen in stochastic sensors and information engines.

3.2. Open-endedness and the role of information

We now turn from mineral experiments to theoretical concepts related to information and learning. All attempts thus far at modelling perpetually emergent complexity (open-endedness) reach some form of saturation, especially those with simple or equilibrium boundary conditions. But from a learning perspective, it is not surprising that systems with a simple problem to solve (e.g. finding a minimum in an energy landscape, or simply replicating faster than competitors) produce simple solutions to that problem. Clearly, the problem of surviving as an organism is vastly more complicated than just replicating faster, or dissipating an external gradient as rapidly as possible. We contend that a primary element in the survival problem is the encoding, processing and utilization of information [62,152,157]. And crucially, the process of learning itself creates more to learn about.

For example, when early photosynthesizers learned to channel photon energy into water-splitting such that water could be used as an electron donor, they solved the problem of finding readily available electron donors. However, they simultaneously created a huge new problem for the biosphere: oxidative stress. This new challenge pushed evolutionary innovation to new realms, as organisms struggled to survive in an oxidized atmosphere.

In the anthropic realm, when humanity learned to build automobiles as a means of transport, it then also had to find ways to construct smooth roads, safe traffic control systems and costly systems for protecting financial liability. Those systems then also gave rise to further optimization problems.

Hence, solving problems invariably creates more problems, and if the creation of new problems outstrips the rate of solution of existing problems, there is a potential engine for open-ended complexity. One could interpret niche construction in a similar way: when an organism alters its environment, the alteration normally creates additional challenges for other species, or even the organism itself (there are impending anthropic examples of this). Mature ecosystems show that this process seems to iterate perpetually, through competition and symbioses that may resolve existing survival challenges, while creating new ones for future inhabitants.

Despite the failure to simulate open-endedness, there have been results in recent years demonstrating how structured, non-equilibrium driving forces can promote emergent complexity in non-living systems. Jeremy England has published several works in this vein, showing, for example, that chemical systems will exhibit self-organization through resonant matching with time-varying external forcing [158,159].

Additionally, in the origins realm, there has been a surge of interest in wet–dry cycles for the promotion of polymerization in prebiotic systems [29,32,160–162]. Alongside the physical chemistry of this effect, one could also interpret these results as an internal self-organization due to the information content of the external driving force. Periodic cycling between wet and dry conditions makes a certain quantity of information available to the internal system. The effect of this informational driving (as compared to steady-state driving) is reflected in the enhanced disequilibrium state of the internal system (sustained existence of polypeptides or long genetic polymers). If one was to observe the system without prior knowledge of the driving protocol, the polymer size distribution would contain information about whether any wet–dry cycling had been performed (the system has a degree of memory). The emergence of longer polymers is known to be extremely difficult under simpler modes of external forcing, though one area of success has been thermophoresis [163].

We suggest that the England results and the wet–dry cycle results reflect a common underlying effect: systems that are beginning to primitively learn about their environment.

3.3. Requirements for emergent learning

To take this concept further, we suggest three necessary conditions for emergent learning:

• (1)The ability of a system to form a dynamic memory of its environmental perturbations. This could be as simple as a persistent, low entropy compositional distribution, or as sophisticated as a Hopfield network (perhaps comprised of a chemical reaction network, or redox states of a mineral structure).
• (2)The possibility of simple computational circuits and information transfer among the components of the system. These would allow it to carry out a learning process. An example would be a Hebbian-type process for associative learning.
• (3)A positive feedback or reinforcement mechanism between the process of learning and the lifetime or resilience of the learning system. In a Darwinian system, this would be natural selection.

Many systems of relevance to origins studies have shown the potential for information processing, including chemical reaction networks [164–169], genetic polymers [170–172] and mineral structures [125]. Hence the field is now poised to make significant strides by modelling such systems (numerically and experimentally), and using the tools of modern thermodynamics described above to quantitatively assess their information processing ability. Note the distinction between information processing discussed here, and information in prebiotic systems, for which there is already a large literature [76–84].

Assessments based upon information processing ability could be used to compare instantiations of similar systems that are spread through parameter space. This is particularly relevant to high-throughput, automated chemistry experiments where many combinations of reactants and conditions need to be compared as quickly as possible [33,173,174].

It is often difficult to objectively carry out this comparison, and researchers commonly seek recognizable life-like features such as self-reproduction or chemotaxis. An automated system that instead screens for complexity and information processing would be more agnostic, since it does not distinguish using familiar features of extant life. Systems could also be monitored in time to see whether their information processing abilities are growing. A cartoon example of a system set-up that uses this approach is presented in figure 1.

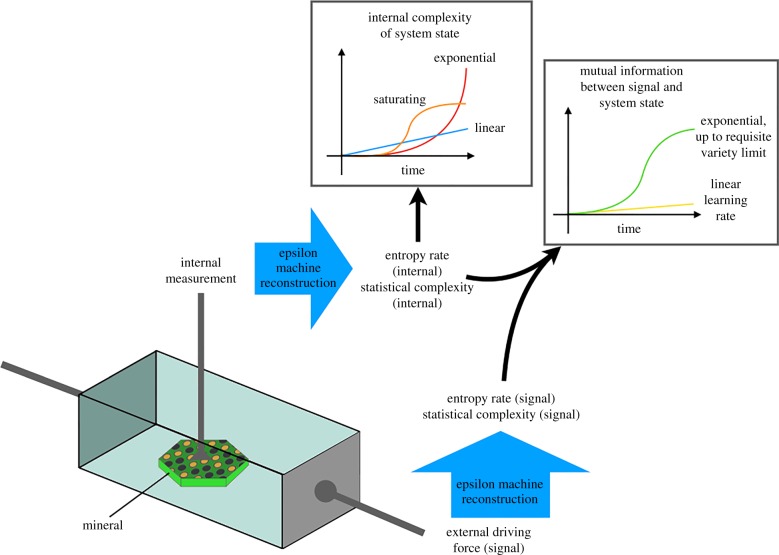
Figure 1.

Schematic of an example analytical set-up for measuring complexity in a driven system. There is a time-varying electron flow through this system via the anode and cathode plates. The entropy rate and statistical complexity of this signal can be calculated using the techniques described in §2. An internal measurement of the system could be a simple voltage sensor within a mineral structure or a more elaborate measurement. The measurement time series (labelled ‘internal measurement’) could also be analysed in terms of entropy and complexity. Increases in complexity over time are suggestive of information incorporation. In particular, if the system were to exhibit exponential complexity increase (red curve in upper inset graph), that might imply that the system is somehow learning and that the learning ability feeds back positively on the learning process. One could also calculate the mutual information between input signal and system response (top right inset), in order to estimate the rate at which the system is encoding information from the external signal. Image produced with help from Danyang Li. (Online version in colour.)

In this example, the external driving force is simply a time-varying voltage across two plates at either end of the system. The internal composition could include minerals and small organic molecules. The driving force can be thought of as a signal, and in general would include deterministic and stochastic elements. This signal could form the input of an epsilon machine reconstruction process, as outlined in §2. The result of this process would be complexity metrics including entropy rate and statistical complexity.

Internal measurements of the system would also be used as input for another process of epsilon machine reconstruction. The result would be two sets of complexity metrics, one for the system boundary conditions (signal), and a second for the internal response of the system. It would also be possible to measure the mutual information between the internal and external signals (see right-hand inset of figure 1). This would serve as a measure for the rate of information uptake by the internal system. Note the green curve on the right inset graph of figure 1. This mutual information measure increases exponentially as the system learns but then saturates, producing a sigmoidal profile. We have denoted this as the requisite variety limit, in reference to the concept of the same name introduced by the cyberneticist W Ross Ashby [175] (see also [112]). Simply put, this refers to the fact that every environment contains a quantity of discernable (and learnable) states. Any system that learns about its environment must ‘be aware of’ at least this number of external states, such that it can regulate itself against changes in those external states.

The computational mechanics approach can thus be used as a screening metric: quantify the complexity of the driving signal and then calculate complexities of system responses. One can compare the complexities of the responses and use that as a guide for which systems to explore further, under the assumption that the more complex systems (greater computational capacity) are more likely to evolve towards living systems. In general, we are seeking those systems that produce the largest internal complexity per unit complexity of the driving signal.

3.4. Associative learning in a prebiological setting

In addition to analyses of complexity in prebiological systems, we also present the following more explicit example of how learning might play a role in early chemical evolution. Let us imagine a system that is potentially prebiotically relevant (e.g. a non-enzymatic metabolic cycle). Under ideal conditions, the cycle proceeds to synthesize organic monomers that could comprise a proto-organism. When the system is perturbed away from that ideal window, the metabolic process diminishes. This would likely apply to recent examples of prebiotic metabolisms that have been experimentally demonstrated [133,136].

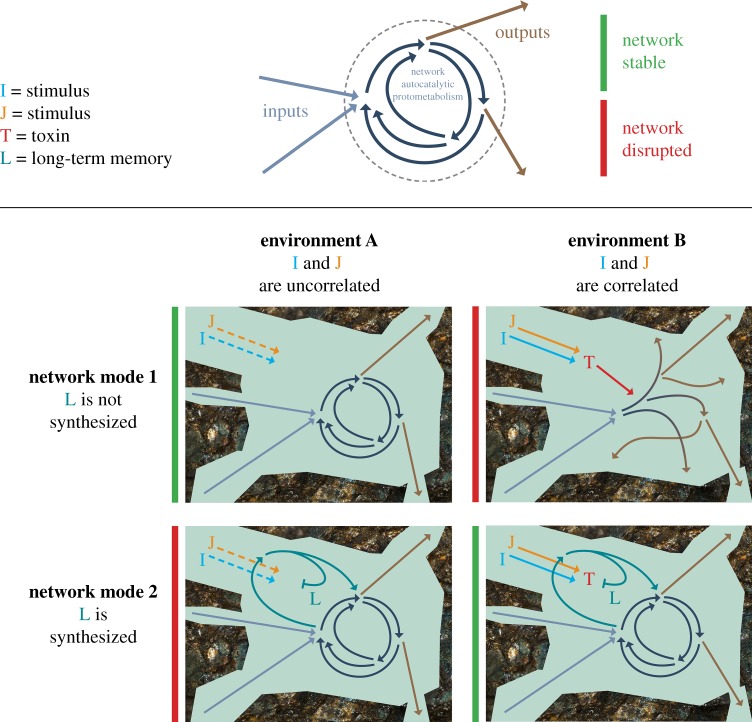
Let us now imagine an augmented version of the metabolism that has additional reactions and compounds, which permit sensitivity to the environment. This sensitivity allows environmental information to be encoded. The augmented version can also process that information in some way, and this processing then modulates the reactions and physical processes that the system undergoes. The set of all augmented metabolic systems is vast, and most will have a neutral or destructive effect on their own persistence. However, if a subset of those systems exhibits a positive feedback with regards to information processing capacity and the extra resilience that it confers, then that subset will be screened out, to the exclusion of others. A simplified example of this is shown in figure 2.

Figure 2.

Simple example of how associative learning could confer resilience in a prebiotic system. See text for full description. Image produced by Michael L. Wong. (Online version in colour.)

This network autocatalytic protometabolism functions under ideal conditions but is catastrophically damaged by a highly reactive compound T, that forms through the reaction of I and J (centre right panel of figure 2). In general, the concentrations of I and J will be time-varying, and under ‘environment B’ they are also temporally correlated (perhaps delivered by a common geophysical process). Thus, the metabolic system will be more resilient if that correlation can be learned, and used to trigger production of compound L, which can preferentially react with T and prevent the breakdown of the metabolism (lower right panel of figure 2). Synthesizing L in the absence of T wastes scarce free energy (lower left panel of figure 2). When I and J are not correlated, the system need not synthesize L (centre left panel of figure 2). Chemical associative learning was successfully simulated by McGregor et al. [176], and similar reaction networks could be used in this example system. Note that we have omitted other reactions and compounds that may be present, but do not play a role in the associative learning process.

The motivation of this example is to understand the conditions under which a learning ability could be physically selected for. It is well understood how learning networks encode and process information, but in the context of origins research, the learning behaviour and the architecture for performing the learning must both emerge spontaneously. Such a feat has not yet been achieved, but would be a watershed moment for complexity science.

4. Conclusion

Stochastic thermodynamics of information processes and computational mechanics provide a firm basis to evaluate any theory about the emergence of biological information from abiotic systems. The creation and manipulation of information is necessarily bounded by the energetics of a system and its environment. Thus, when researchers claim a gain in information or complexity of their system under study, evaluating the thermodynamics or epsilon machine of the system can act as verification for such claims, and provide a lower bound on how much information processing is possible for that system. If submarine alkaline, hydrothermal mounds were the site of life's emergence and evolution to the Last Universal Common Ancestral Set, this implies a large amount of information acquisition and processing had already occurred and could in principle be bounded using the tools introduced above. This task will require careful interpretation to map the relevant thermodynamic and information theoretic quantities to the geochemical systems and processes at play in submarine alkaline vents. Likewise, these concepts provide possible benchmarks for hypotheses concerning the emergence and evolution of information in any prebiotic system. This would provide the research community with standard definitions by which results can be compared.

Much origins research is guided by specific storylines or specific compounds. Here, we are advocating a complementary approach where one does not seek specific compounds, pathways or products. Instead the guide is marginal increases in key thermodynamic metrics that are demonstrably associated with biological activity. These metrics, stemming from recent progress in thermodynamic theory, include statistical complexity and entropy rate. This allows modellers or experimenters to screen their systems in terms of computational or learning capacity. Such abilities are absolutely fundamental to the operation of life as we know it, and hence must have become part of life's repertoire at an early stage of its emergence from the non-living world.

Data accessibility

This article has no additional data.

Competing interests

We declare we have no competing interests.

Funding

We received no funding for this study.