Natural selection based on coordination chemistry: computational assessment of [4Fe–4S]-maquettes with non-coded amino acids

Abstract

Cysteine is the only coded amino acid in biology that contains a thiol functional group. Deprotonated thiolate is essential for anchoring iron–sulfur ([Fe–S]) clusters, as prosthetic groups to the protein matrix. [Fe–S] metalloproteins and metalloenzymes are involved in biological electron transfer, radical chemistry, small molecule activation and signalling. These are key metabolic and regulatory processes that would likely have been present in the earliest organisms. In the context of emergence of life theories, the selection and evolution of the cysteine-specific R–CH₂–SH side chain is a fascinating question to confront. We undertook a computational [4Fe–4S]-maquette modelling approach to evaluate how side chain length can influence [Fe–S] cluster binding and stability in short 7-mer and long 16-mer peptides, which contained either thioglycine, cysteine or homocysteine. Force field-based molecular dynamics simulations for [4Fe–4S] cluster nest formation were supplemented with density functional theory calculations of a ligand-exchange reaction between a preassembled cluster and the peptide. Secondary structure analysis revealed that peptides with cysteine are found with greater frequency nested to bind preformed [4Fe–4S] clusters. Additionally, the presence of the single methylene group in cysteine ligands mitigates the steric bulk, maintains the H-bonding and dipole network, and provides covalent Fe–S(thiolate) bonds that together create the optimal electronic and geometric structural conditions for [4Fe–4S] cluster binding compared to thioglycine or homocysteine ligands. Our theoretical work forms an experimentally testable hypothesis of the natural selection of cysteine through coordination chemistry.

1. Introduction

In extant biology, [4Fe–4S] clusters are prosthetic groups with structural, electron transfer and catalytic roles [1–3]. In the cell, synthesis and delivery of iron–sulfur ([Fe–S]) clusters to apo proteins is a controlled process involving iron chaperones, cysteine desulfurases, electron transfer proteins and scaffold proteins [4–8]. Outside the cell, these protein cofactors are known to assemble spontaneously when cysteine containing peptides or proteins are presented with iron cations, sulfide/hydrogen sulfide anions, and excess thiol [9]. Furthermore, even without the presence of an anchoring peptide, [Fe–S] clusters are known to form spontaneously in solutions containing thiols in millimolar concentration [10–15]. Pioneering works [16–19] have demonstrated that peptides as short as seven amino acids with a CxxCxxC sequence can bind [4Fe–4S] clusters in aqueous, buffered solution. This CxxCxxC motif was designed on the basis of the cluster binding amino acid sequence of bacterial ferredoxins (Fd). Recently, the Fd-maquette (FdM) work [17] was expanded to 8-mer peptides with the CxxxCxxC motif [20], which is the canonical cluster binding sequence for the [4Fe–4S] cluster [21] in radical S-adenosylmethionine (SAM) metalloenzymes [22]. These peptide bound metal clusters, termed [4Fe–4S]-maquettes, are valuable biomimetic models for structure/function studies. They also provide an experimental handle to explore their significance as possible prebiotic catalysts and as proto-metalloenzymes in early evolution [23].

In the context of emergence of life theories, there is a persistent discontinuity between geochemical processes and extant biochemical transformations. It has been proposed that [4Fe–4S] cluster complexes and [4Fe–4S]-maquettes encompass part of the link between inorganic and organic worlds and thus, aid in the elimination of the discontinuity between non-living and living systems [24]. Spontaneously formed, peptide bound [4Fe–4S] clusters could have potentially facilitated the electron transfer, reductive cleavage of covalent bonds, and atom transfer reactions that are commonly carried out by redox active, extant metalloenzymes. The presence of short peptides, as chelating organic ligands, are generally considered to promote [4Fe–4S] cluster stabilization relative to free, terminal thiol ligands. Molecular [4Fe–4S] cluster complexes in the pores and capillaries of hydrothermal vent walls could take advantage of thermodynamically favourable conditions to facilitate catalytic processes involving the redox activation of small and inert molecules, such as CO₂, H₂, CH₄, and N₂ [25,26]. Unless present in the early Earth environment, these processes are obligatory for the chemical evolution of the building blocks of life. In the context of hydrothermal vent hypotheses, they were likely fuelled by a complex network of geochemical processes at hundreds of atmospheres and hundreds of degrees Celsius at the bottom of the ocean floor in the background of extreme proton (4–6 orders of magnitude) and considerable electron gradients (close to 0.5 V) [25–30].

The set of 22 genetically encoded amino acids are thought to have emerged as a result of natural selection for their physico-chemical properties [32]. Prior to establishment of genetic code-based protein expression, thioglycine (referred to as thioGly) and homocysteine (homoCys) are conservative analogues to cysteine (Cys), as their thiol side chain length varies by only a methylene group. In the prebiotic context, they could originate from radical coupling of glycyl/alanyl and sulfhydryl/methylthiolyl radicals to form thioGly/Cys/homoCys or the de-methylation of methionine via radical chemistry to give homoCys. [Fe–S] clusters coordinated with thioGly or homoCys could have displayed roles such as electron transfer, small molecule activating catalysts or templates through amino acid ligation similarly to extant biological [Fe–S] clusters with Cys coordination. Currently unexplored are the structure, stability and redox properties of [4Fe–4S]-maquettes coordinated by alternative thiol ligands.

To investigate the coordination chemistry of cysteine as a ligand in comparison to alternative thiol containing amino acids, we examined the tetrakis-thiolato [4Fe–4S] cluster structure and stability coordinated by homocysteine (homoCys, Hey, J), thioglycine (thioGly, Sly, U) and cysteine (Cys, C) using computational methodologies. By conducting empirical force field-based molecular dynamics and density functional theory-based stationary structural calculations, we examined the secondary structure of peptides containing at least three cysteine residues in comparison to the above alternative thiol amino acids. In addition, we investigated the energetics of cluster binding by these different peptides using spectroscopically validated density functional theory. Our results suggest that alternative amino acids have some, but not all properties of cysteine for [Fe-S] cluster binding, and highlight a previously unknown selection pressure for cysteine as biology's only genetically encoded thiol containing amino acid.

2. Methods

2.1. Peptides

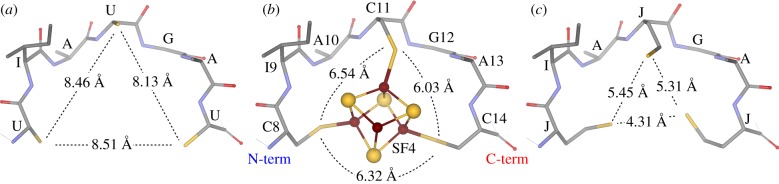
In the given study, we considered short (7-mer, yIAyGAy, where y = U, C or J) and long (16-mer, GGyGGGyGGyGGyGGW, where y = U, C or J) peptide sequences in which the Cys-containing peptides have already been investigated experimentally [18,19] and computationally [33]. The initial structures with expanded conformations were generated using the PROTEIN utility in the Tinker suite of modelling programs [34–37] and optimized using the AMBER99SB [38–41] force field parameters. The JIAJGAJ (referred to as homoCys-FdM-7 or FdM-7-J), GGJGGGJGGJGGJGGW (homoCys-FdM-16-G or FdM-16-G-J), UIAUGAU (thioGly-FdM-7 or FdM-7-U) and GGUGGGUGGUGGUGGW (thioGly-FdM-16-G or FdM-16-G-U) peptides were manually created by adding and removing a methylene group to the Cys residues of CIACGAC (FdM-7-C) and GGCGGGCGGCGGCGGW (FdM-16-G-C) peptides, respectively. These compositional changes required the extension of the force field parameters as summarized in electronic supplementary materials. All new parameters were generated based on existing parameters of analogous side chains. Figure 1 summarizes the initial structural differences with respect to cluster nest geometry for the protonated yIAyGAy peptides, when using the crystal structure of bacterial ferredoxin from Peptostreptococcus asaccharolyticus (Fd-Pa, PDB code: 1DUR [42–44]) with the N-terminal cluster binding motif of CIACGAC. Atomic positional coordinates for molecular structures described in the paper are provided in the electronic supplementary materials.

Figure 1.

Comparison of the [4Fe–4S] cluster nest geometry as a function of ligating thiolate residues using the crystal structure of the [4Fe–4S] cluster containing ferredoxin (Fd-Pa, PDB code: 1DUR [41–43]). (a) UIAUGAU, (b) CIACGAC (native cluster binding motif), (c) JIAJGAJ. (Online version in colour.)

2.2. Molecular dynamics calculations and secondary structure analysis

All force field-based (AMBER99SB [38–41]) molecular dynamics calculations were carried out using the Tinker suite of modelling programs [34–37]. Each peptide was soaked in an approximately 6 nm water bath of a periodic truncated octahedron geometry containing 3610 water molecules that are treated using the TIP3P model [45,46]. The sequence of MD simulation steps started with 5 ns constant pressure/temperature (NPT) equilibration before switching to 100 ns constant volume/temperature (NVT) production runs with frame sampling frequency of 1 ps. The temperature and pressure control was achieved by using Berendsen thermostat and barostat [47]. The NPT and NVT MD simulations used the Nose-Hoover [48] and Beeman [49] integrators, respectively. The cut off distances for van der Waals interactions was set to 12 Å. The Ewald cut-off parameter was set to 7 Å with a PME grid dimension of 72 × 72 × 72 that is slightly larger than the boundary box [50,51]. The peptide secondary structure analysis was completed by our toolkit (doi:10.5281/zenodo.1442864) that monitors S … S distances, [2Fe–2S] and [4Fe–4S] nest formation and lifetime, and peptide conformation characterized by various representations of Ramachandran plots [52–54]. Several scenarios for [2Fe–2S] nest formation were considered that included the possibility for multiple [2Fe–2S] cluster binding events. Two scenarios are discussed in the manuscript for the [4Fe–4S] nests. The ceiling for [4Fe–4S] nest formation, as an upper limit, is defined by MD frames when the peptide backbone does not transect the triangle formed by the S-centres of the three Cys residues regardless of whether side chain atoms block the [4Fe–4S] cluster coordination. Since the backbone atoms are expected to move slower than the flexible side chains due to their involvement in intramolecular network of weak interactions, these frames may accommodate a [4Fe–4S] cluster only upon considerable side chain rearrangement. In addition, we marked ‘nesting’ the MD frames displaying unobstructed [4Fe–4S] nests, where both the arrangement of the backbone and side chain atoms allow for a direct ligand-exchange reaction (peptide with three thiol versus three free thiols) with a preformed [4Fe–4S] cluster. The selection criteria for a nest site has been developed based on the crystal structure of bacterial [4Fe–4S] ferredoxins as detailed in [33]. Furthermore, short (1 ns) simulations were completed for three β-mercaptoethanol (βME) molecules, as free ligands in solution and complete [4Fe–4S]-maquettes with frozen S–CH₂-groups without the presence of the iron and sulfide ions in the above-mentioned water bath. These calculations were used to refine the estimated cluster binding enthalpy values.

2.3. Density functional calculations

Given the lack of validated and reliable force field parameters for Fe³⁺_(aq), Fe²⁺_(aq), SH^–_(aq), S²⁻_(aq) ions and aqueous [2Fe–2S]^2+/+, [4Fe–4S]^2+/+ clusters, in addition to the limitation of semi-empirical quantum chemical methods in treating accurately spin-polarized [Fe–S] clusters, we employed quantum chemical, hybrid density functionals. We only used exchange and correlation functionals as implemented in the Gaussian16 suite of programs [55] that have already been validated spectroscopically for [4Fe–4S] clusters [56]. The specific combination of hybrid exchange (Becke88 [57]+5% Hartree–Fock) and correlation (Perdew86 [58]) density functionals along with a saturated basis set (def2TZVP [59]) used throughout the study. This combination of functionals was developed by reproducing both ground state electronic and geometric structures of [4Fe–4S]²⁺ clusters from X-ray crystallography and X-ray absorption spectroscopy. In all calculations, we took into account three conceptually different magnetic coupling schemes within and between the two [2Fe–2S] rhombs of a [4Fe–4S] cluster. These were constructed by merging well-defined ionic fragments of Fe³⁺, Fe²⁺, S²⁻, deprotonated peptide³⁻ ligand and a deprotonated βME⁻ ligand. The spin-coupling representations of [αα] and [ββ] describe formally [2Fe^2.5+–2S²⁻]⁺ rhombs, where the iron ions are ferromagnetically coupled with m_s = ±9/2 ground state. The α and β labels indicate the majority spin-up and spin-down components, respectively. Distinct spin coupling of two rhombs can be achieved according to [ααββ], [αβαβ] and [αββα] patterns. These electron spin configurations correspond to open shell, singlet ground electronic states (S_t = 0) that contain antiferromagnetically coupled rhombs. All thermochemical results reported here are Boltzmann averages of electronic (SCF) energy of the three isomers. Dispersion corrections of Grimme's D3BJ method [60,61] were included in all calculations. The calculated translational entropy was corrected for the reduced free volume in condensed phase corresponding to 200 µM solution [62]. This correction, which can be as high as 30%, includes the calculation of an ‘effective solute concentration’ of the [4Fe–4S]–maquette in the free volume of the solution that is not excluded by the water molecules. The translational entropy of maquette complexes was then calculated using the equation S_trans,corr = 11.1 + 12.5 ln(molar mass of the maquette) + 12.5 ln(T) – 8.1 ln(maquette effective concentration). The numerical details of the translational entropy correction are summarized in the electronic supplementary materials. Solvation effects in quantum calculations were considered by employing the SMD polarizable continuum model [63] with water parameters. All stationary structures were confirmed to be equilibrium structures without imaginary normal modes.

3. Results and discussion

3.1. Secondary structure analysis of FdM-7 peptides

Previously, we have reported a detailed secondary structure analysis for the CGGCGGC (FdM-7-G-C) peptide [33], which revealed the omnipresence of [2Fe–2S] nests (25 ± 3%) along the NVT MD trajectories. The same analysis defined an upper limit of only 1.6% of the frames with peptide backbone conformation amenable to [4Fe–4S] cluster coordination. These peptide frames can be characterized by avoidance of the backbone atoms from the triangle formed by the S-centres of three Cys residues. In these [4Fe–4S] nesting ceiling conformations, the slower moving peptide backbone does not interfere with the presence of a [4Fe–4S] nest (figure 1) regardless of the side chains alignment. However, only at most 0.2% of the frames along a 100 ns trajectory have the preferred structure for cluster coordination through ligand-exchange processes, when the cluster nest is in avoidance of any side chain or either of the backbone atoms. Thus, even for the most flexible peptide with Gly as intervening amino acid, the [4Fe–4S] nest formation is possible, but as a rare event on the timescale of these simulations. Importantly, Ramachandran plot analysis [52–54] revealed non-biological ϕ/φ dihedral angle distributions, as the most favourable combinations were predicted to be located in the −60° to 0°/0° to +60° and 0° to +60°/0° to −60° regions, centred diagonally around the ϕ = 0 and φ = 0 origin.

Introduction of bulkier hydrophobic side chain groups (I and A versus G) in going from CGGCGGC (FdM-7-G-C) to the CIACGAC (FdM-7-C) sequence does not manifest in significantly different peptide secondary structure distribution. This is in contrast to the experimental reconstitution yields of 29% and 6% for the reduced [4Fe–4S]⁺(CIACGAC) and [4Fe–4S]⁺(CGGCGGC) maquettes, respectively, reported in earlier studies [18,19]. Our recent experimental work indicates that under optimal experimental conditions in the presence of excess βME, 90 ± 10% reconstitution yields can be achieved for oxidized ([4Fe–4S]²⁺) Fd- and radical SAM-maquettes, regardless of the amino acid sequence as long as three thiols are present in the vicinity of one another [20]. However, we observe similar lower yields (12 ± 5%) for the reduced ([4Fe–4S]¹⁺) Fd- and radical SAM-maquettes as reported in the literature [20].

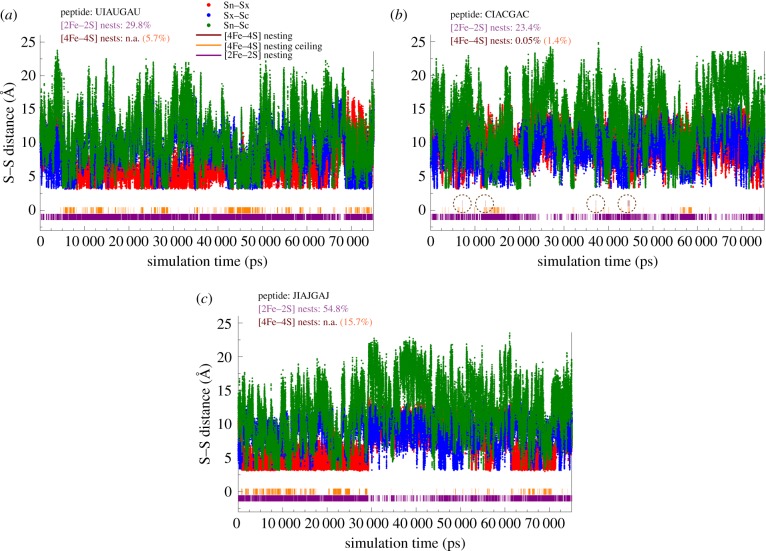
Figure 2 summarizes the most pertinent information of the secondary structure analyses, which are the S … S distances and cluster nesting events. The complete secondary analysis for each peptide is provided in the electronic supplementary materials. Throughout the simulations, the percentage of [2Fe–2S] cluster nests remains high (purple bars next to the abscissa, figure 2a–c) for all three peptides. More than 50% of the frames for homocysteine containing FdM-7-J are due to the frequent vicinity of the N-terminal (S_n) and central (S_x) S(Hey) centres (see the first 30 ns trajectory, red trace, figure 2c). The high [2Fe–2S] nest frequency also translates into a high percentage of favourable S(Hey) positions (orange bars, [4Fe–4S] nesting ceiling) in which the triangle formed by the S(Hey) centres is not transected by the peptide backbone. Depending on whether a stepwise cluster assembly (Scheme 1 in [33]) or ligand-exchange process takes place involving a preformed cluster [19], the former can lead to [4Fe–4S] cluster side chain rearrangement and thus cluster assembly, while the latter could take place during a single collision event that we considered here (vide infra).

Figure 2.

Comparison of S … S distances between N-terminal, central (X), and C-terminal (in Å) Cys residue, as a function of simulation time (in ps, up to 75 ns period is shown for the most representative events) for FdM-7-U (thioGly, (a)), FdM-7-C (Cys, (b)), and FdM-7-J (homoCys, (c)) with per cent probabilities of nest formation (graphically illustrated with purple, orange and brown bars at the bottom of the plot). The lack of brown marks at the bottom of each panel indicates absence of viable [4Fe–4S] nests for [4Fe–4S] cluster coordination, with the exception of (b) (FdM-7-C) at around 10 ns and 42 ns (circled). (Online version in colour.)

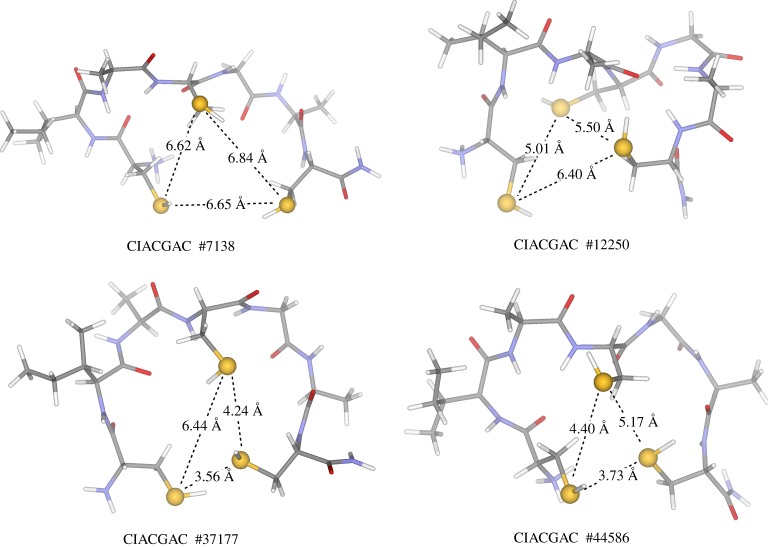
The only sequence where we observed actual [4Fe–4S] nest formation (slightly more than 50 individual frames) without any appreciable steric disturbance from a side chain or any backbone atoms with the cluster nest is the FdM-7-C, a Cys containing peptide. Representative examples for spontaneously formed [4Fe–4S] nests are shown in figure 3. In particular, the last frame shown in figure 3 is notable, since it is part of a block of conformations lasting for 270 ps, where [4Fe–4S] nests persist. The favourable backbone conformations are supported by a network of intramolecular H-bonding/dipole interactions. All the shown cluster nests in figure 3 are adequate to accommodate a preformed [4Fe–4S] cluster in a ligand-exchange reaction [19]. By contrast, the longer and shorter side chains in homoCys and thioGly do not show favourable conformations for [4Fe–4S] cluster coordination by a direct ligand-exchange process, despite that all of the Cys-, homoCys- and thioGly-based simulations were started from exactly the same initial peptide conformation (figure 1), and were run under identical simulation conditions (ceteris paribus). The most prevalent issue with the peptide conformation is the tendency of the flexible backbone to thread through the plane formed by the three S(Cys) centres. The interference between the backbone atoms and the thiol functional group is the most trivial. While the thiols form a triangle required for cluster binding, the nearby peptide backbone atoms enter into the space required for [4Fe–4S] cluster coordination. Contrarily, the three longer thiolate side chains in homoCys-containing peptide FdM-7-J become kinetically less favourable in forming a triangle with ca 6 Å S … S distances. These differences in peptide conformation among the coded Cys and non-coded homoCys and thioGly amino acids with respect to [4Fe–4S] cluster binding already draw the attention to the selective nature of Cys residue's coordination chemistry.

Figure 3.

Spontaneously formed [4Fe–4S] cluster nests with S … S distances (in Å) for the CIACGAC FdM-FdM-7-C peptide as indicated by brown vertical bars at the bottom of the secondary structure analysis plots in figure 2b. The nest lifetimes for frames #7138, #12250 and #37177 are 1 ps. However, #44586 is part of a block of frames that last for close to 270 ps (see also on page 9 of electronic supplementary material). (Online version in colour.)

3.2. Secondary structure analysis of FdM-16 peptides

The motivation to investigate the secondary structure of 16-mer peptides containing non-coded thioGly and homoCys residues originates from our previous observations of the formation of stable [4Fe–4S] cluster nests with circa 2 ns lifetime [33] involving the first three Cys residues of the GGCGGGCGGCGGCGGW (FdM-16-G-C) peptide. The spacing of the Cys residues is notable since the peptide encompasses both the radical SAM CxxxCxxC and the Fd CxxCxxC cluster binding motifs. The results of MD simulations reported in this study for all three FdM-16 variant peptides, ceteris paribus, are summarized in table 1. The simulation results in graphical representations are summarized on pages 11–22 of electronic supplementary materials. The results parallel the outcome of the CGGCGGC (FdM-7-C) simulations (vide infra). The [2Fe–2S] cluster nests in the 16-mer are omnipresent. From the cumulative numbers (70–112%) obtained for all possible events combined, we can anticipate that the conformation of the 16-mer peptide with three thiol containing residues will always allow for the coordination of a [2Fe–2S] cluster. The more than 100% value for FdM-16-G-U peptide represents that it is certain that the four thioGly residues will form a plant ferredoxin-type [2Fe–2S]-maquette. It is unexpected that the FdM-16-G-C peptide shows the lowest yield for [2Fe–2S] nests given that it displays the greatest tendency to form [4Fe–4S] nests. We can rationalize this with the expected coordination chemistry differences between a more compact [2Fe–2S] rhomb than an expanded [4Fe–4S] cluster and the intermediate flexibility of the –CH₂–SH moiety of cysteine. When the thiol group is directly attached to the peptide backbone as in FdM-16-G-U, the upper limit (ceiling) of [4Fe–4S] nests was calculated to be the highest (7.5%). This gradually drops to 1.4 and 0.4% for FdM-16-G-C and FdM-16-G-J, respectively, as the length of the thiol side chain grows and conformational flexibility increases. As a result, the peptide backbone detrimentally transects through the triangle formed by the three S-centres with respect to [4Fe–4S] cluster coordination in going from FdM-16-G-U to FdM-16-G-J. Although to a more modest degree than observed before (0.6%, [33]), only the FdM-16-G-C peptide shows an appreciable 0.1% probability for forming a [4Fe–4S] nest. As can be seen from the cumulative numbers in the last column of table 1, for a 100 ns trajectory this means that approximately 1000 nesting frames are ready for accepting a preformed [4Fe–4S] cluster via a direct ligand-exchange process, which corresponds to a rare-event, but with not zero probability.

Table 1.

Observed differences in nesting for different cluster binding motifs of 16-mer peptides. The percentage of frames showing three-thiol [2Fe–2S] and [4Fe–4S] nest formation along 100 ns of constant volume and temperature MD trajectories for GGyGGGyGGyGGyGGW (y = U for FdM-16-U thioGly, C for FdM-16-C Cys, and J for FdM-16-J homoCys) peptides are shown. The first value for [4Fe–4S] nest corresponds to the per cent of peptide conformations that can accept a preformed [4Fe–4S] cluster. The second value in parentheses is the per cent of conformations where the peptide backbone does not transect through the plane defined by the three S(thiol) centres, as a measure for the ceiling of cluster nest formation.

binding motif	CxxxCxxCa	CxxxCxxxxxC	CxxxxxxCxxC	CxxCxxCb	cumulative CxxxCxxCxxC
y = U or Sly
[2Fe–2S]	31.2	28.9	15.0	37.2	112.3c
[4Fe–4S]	n.a (2.9)	n.a (1.5)	n.a (2.0)	n.a (1.1)	n.a (7.5)
y = C or Cys
[2Fe–2S]	21.3	10.8	23.1	15.0	70.2
[4Fe–4S]	0.1 (0.7)	n.a (0.1)	n.a (0.3)	n.a (0.3)	0.1 (1.4)
y = J or Hey
[2Fe–2S]	6.9	36.6	26.4	14.6	84.5
[4Fe–4S]	n.a (0.1)	n.a (0.3)	n.a (0.03)	n.a (0.0)	n.a (0.4)

^aRadical SAM cluster binding motif.

^bBacterial ferredoxin cluster binding motif.

^cThe frame percentage greater than 100% is due to the presence of four thiol groups in these peptides.

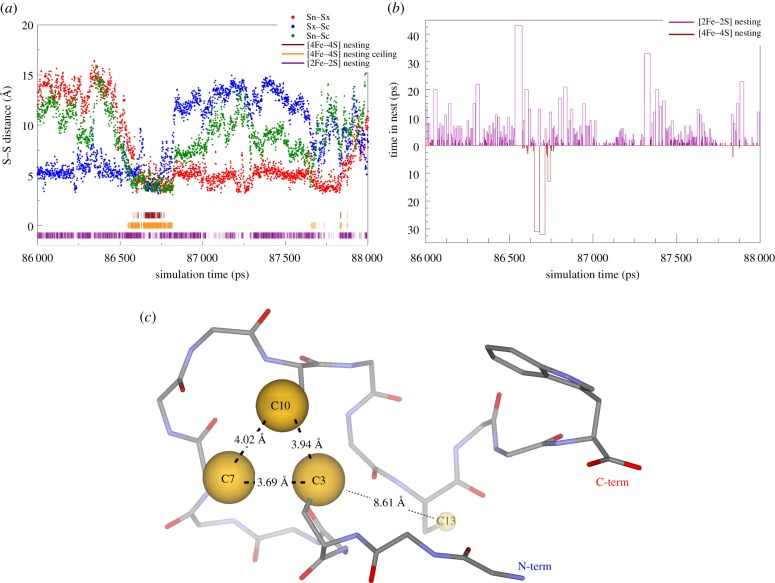
Figure 4 highlights the relevant periods of the trajectory that show the lifetime of the [4Fe–4S] cluster at the N-terminal end of the 16-mer peptide through the CxxxCxxC cluster binding motif. These nesting conformations of peptide with Cys occur despite that all calculations with Sly and Hey non-coded amino acids started from exactly the same structure as the Cys coded amino acid containing peptide. The thioGly-containing peptide shows the highest percentage for favourable backbone conformation without interfering with the space required for [4Fe–4S] cluster binding. However, due to the adjacent location of the thiol ligand to the backbone, the analysis tool finds backbone atoms within a sphere that would be reserved for an approaching [4Fe–4S] cluster.

Figure 4.

Zoomed in region to 86–88 ns range of the S … S distance (a) and nest lifetime (b) plots for the [4Fe–4S] cluster nesting events (marked with brown lines in (a) and brown bars pointing down in (b)) along the 100 ns NVT MD trajectories for GGCGGGCGGCGGCGGW (FdM-16-G-C) peptide. Purple lines in (a) and purple bars pointing up in (b) indicate [2Fe–2S] cluster nests and their lifetimes, respectively. Panel (c) shows the ‘kinked ribbon’ conformation of the peptide that allows for the existence of the [4Fe–4S] nest for ca 0.1 ns similar to that observed in our earlier MD simulations [33]. (Online version in colour.)

3.3. Structure and stability of [4Fe–4S]-FdM-7 maquette

In order to establish a reference for cluster stability calculations, we invoked a specific ligand-exchange reaction (equation (3.1)) between the protonated peptide and a preformed, homoleptic [4Fe–4S] cluster with βME ligands. The presence of the [Fe₄S₄(βME)₄]²⁻ cluster in physiologically relevant, buffered aqueous solution has been confirmed by us [20] and others [11,13,15]. In this entropically strongly favoured, isodesmic reaction, we assume that the neutral thiol groups of the peptide transfer their protons to the dissociating anionic βME ligands.

$$\begin{array}{r}[\mathrm{F}{\mathrm{e}}_4{\mathrm{S}}_4(\beta \mathrm{ME}{)}_4{]}^{2-}\hspace{0.17em}+\mathrm{peptide}{\mathrm{H}}_3\rightleftharpoons \\ [\mathrm{F}{\mathrm{e}}_4{\mathrm{S}}_4(\mathrm{peptide})(\beta \mathrm{ME}){]}^{2-}\hspace{0.17em}+3\hspace{0.17em}\beta \mathrm{MEH}\end{array}$$ 3.1

3.3.1. Solution structure of the reference cluster: [Fe₄S₄(βME)₄]²⁻

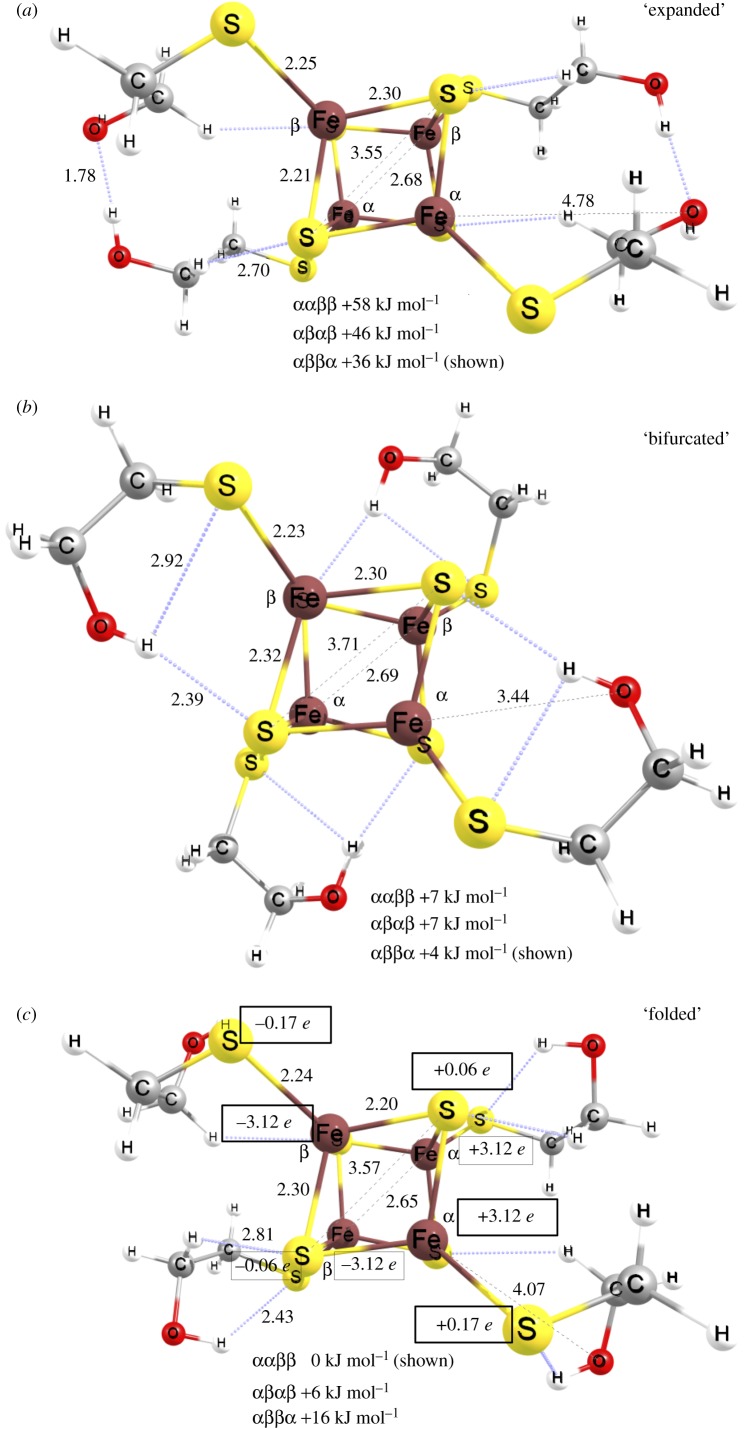
Crystallographic structures of the reference cluster (CCDB [64] codes: CESSEY [65] and HETSFE [66]) show the βME ligands in extended conformation as they weave in between unit cells and create an intricate H-bonding pattern. The H-bonds and the Coulomb interactions between the anionic cluster and its counter-ions (Ph₄N⁺ and Me₄N⁺) form the network of crystal packing interactions. However, in solution alternative, lower energy conformations are available for the βME ligands. We carried out an extensive conformational search and localized the lowest energy equilibrium structure, which is shown in figure 5 at a considerably lower energy than those in the crystallographic, extended conformation. Atomic coordinates for all optimized structures are shown in electronic supplementary material. We localized equilibrium structures for the hydroxyl groups folding in to form bifurcated H-bonding interactions with both thiolate S (S^t) and sulfide S (S^s) centres (figure 5b). Given the greater nucleophilicity of the S^t versus S^s (despite the formally lower negative charge of the former), a lower energy conformation was found when the H-bonding involved only the S^t centres. This is expected, since the sulfides are involved in covalent interactions with three Fe ions, while the thiolate is only bound to a single Fe centre in an overall −2 charged [4Fe–4S] cluster. The intramolecular H-bonds elongate the Fe–S^t(βME) bonds (figure 5b,c) relative to those in the extended βME arms (figure 5a). This is expected for priming the cubane for the ligand-exchange processes that accompany transfer into a peptide nest. It is also notable how well coordination geometry and spin-coupling schemes parallel each other. The lowest energy pattern of antiferromagnetically coupled S_t = 9/2 [2Fe–2S]⁺ rhombs of the cubane underscores the importance of the –O–H … S^t and the weaker –C–H … S^s interactions. The network of H-bonding interactions remains self-contained within the same rhomb of the cubane in which the Fe centres are ferromagnetically coupled to give rise to the m_s = ±9/2 spin states. See also the atomic spin densities with identical signs for the left- and right-hand side of the cubane in figure 5c.

Figure 5.

Equilibrium structures of [Fe₄S₄(βME)₄]²⁻ complex with expanded (a), bifurcated (b) and folded (c) βME ligand conformations. Pairs of labels αα (right-hand side) and ββ (left-hand side) indicate the ferromagnetically coupled m_s = +9/2 and m_s = −9/2 rhombs, respectively. These formally 2Fe^2.5+ centres at the top and bottom of cluster structures in (a,b) are antiferromagnetically coupled along the βα pairs of Fe ions. (c) The atomic spin density values from Mulliken population analysis of the converged electronic structure with a left-/right-hand side arrangement of the rhombs that are antiferromagnetically coupled. The three energy levels below the structures are the relative electronic (SCF) energies of the three spin-coupling schemes. (Online version in colour.)

3.3.2. Solution structures of [4Fe–4S]-maquettes: [Fe₄S₄(βME)(yIAyGAy)]²⁻, where y = U, C and J

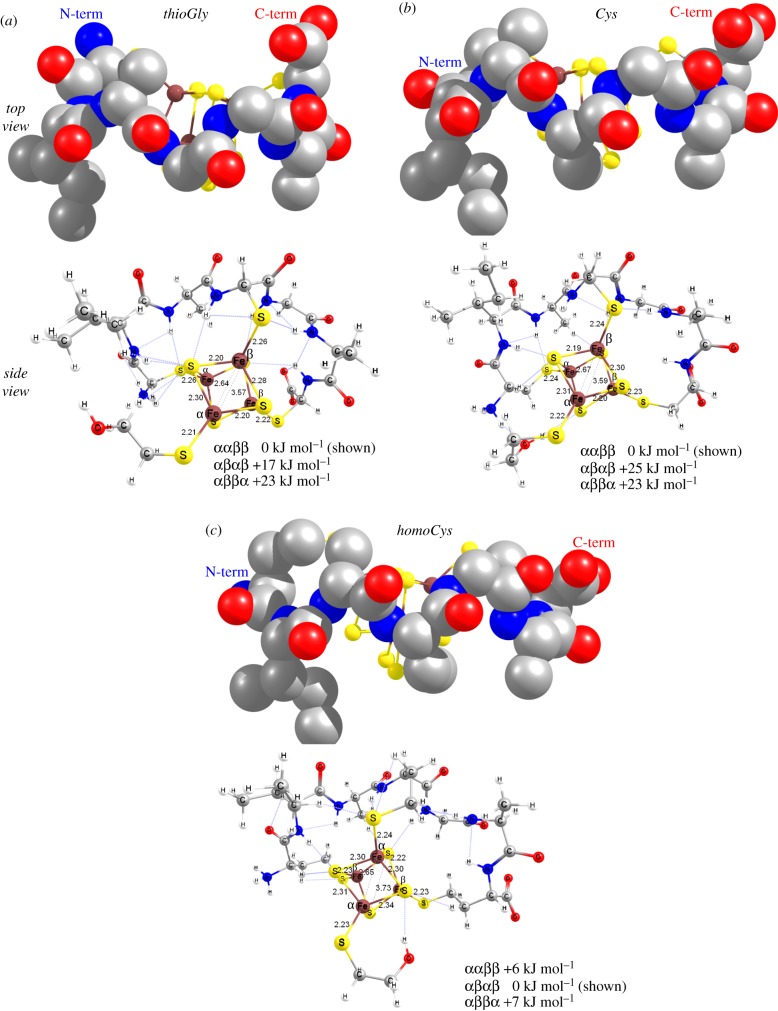
The right-hand side of equation (3.1) requires optimized, equilibrium structures of the [4Fe–4S]-maquettes, which manifest potential caveats in obtaining experimentally relevant thermochemical data due to conformational flexibility of the coordinated peptide. While we investigated the energetic consequence of this to a modest extent (vide infra), we can consider the coordinated peptide conformation, as seen experimentally in the crystal structure of Fd-Pa (PDB code: 1DUR [42–44]), as a reference state. Thus, the initial structures shown in figure 1 were used unchanged in all quantum chemical calculations with varied thiol ligand lengths. The [4Fe–4S] cluster with a single βME ligand and three dangling Fe–S^t bonds was superimposed with the S(Cys) centres of the Sly, Cys, and Hey containing peptide. The lowest energy, structurally optimized equilibrium structures in top and side views are shown in figure 6 as illustrations for the coordinated peptide conformation and the network of interactions between the peptide and the [Fe₄S₄(βME)]⁺ moiety.

Figure 6.

Optimized equilibrium structures of (a) [Fe₄S₄(UIAUGAU)(βME)]²⁻, (b) [Fe₄S₄(CIACGAC)(βME)]²⁻ and (c) [Fe₄S₄(JIAJGAJ)(βME)]²⁻ maquettes in top view (upper row, space filling model) showing the ‘kinked-ribbon’ peptide conformation (H atoms and βME ligand are not shown for clarity) and side view with selected distances for cluster geometry and ligand coordination (bottom row) that also illustrate the network of interactions between the peptide and the cluster. (Online version in colour.)

The CxxCxxC backbone conformations in the folded protein (figure 1) and in the optimized solvated peptide (figure 6) reveal only minor differences. While such similarities do not persist in the MD simulations among the folded protein conformation and the free, aqueous solution conformation of a peptide, this result underscores the purpose of quantum chemical calculations to mitigate differences due to conformational variability among the peptides. Both CxxC fragments of the CxxCxxC peptide display an S-shaped arrangement of the backbone atoms (see top views, figure 6) that are conjoined at the central thiol residue at an acute hinge angle. The alignment of the peptide C=O and N–H dipoles are very similar; however, their distances to the cluster vary greatly due to the differences in the length of the thiol anchoring ligands (see side views in figure 6). Furthermore, the different thiolate coordination scenarios generate significant variations among the coded and non-coded amino acids that are clearly manifested in the highlighted Fe–S^t, Fe–S^s, Fe … Fe and S^s … S^s distances, number and length of the H-bonding interactions between the backbone functional groups and the S centres, and also in the relative energies as a function of specific Fe … Fe spin-coupling schemes as shown in figure 6.

The calculated electronic (SCF) energy differences in the thioGly and Cys containing maquettes show a similar trend, but the homoCys is distinct. There is a clear energetic preference for a specific spin-coupling scheme where the left-hand side, m_s = +9/2 [2Fe–2S] rhomb of figure 6, panels (a) and (b) is antiferromagnetically coupled to the right-hand side, m_s = –9/2 rhomb. The homoCys coordinated cluster has considerably reduced energetic differences among the various spin-coupling schemes, which is highly similar to the reference [Fe₄S₄(βME)₄]²⁻ complex (figure 5c, an example for left-/right-hand side coupling). Figure 6c shows the lowest energy structures in which the top [2Fe–2S] rhomb (m_s = +9/2) is antiferromagnetically coupled to the rhomb in the back (m_s = –9/2), similar to those shown in figure 5a,b. The characteristically shorter Fe–S^s distances (2.2 Å) in between versus (2.3 Å) within the rhombs are the direct manifestation of the stronger covalent Fe–S^s interaction along the antiferromagnetic coupling path versus the weaker ones along the ferromagnetically coupled rhombs. This is compensated by slightly shorter Fe … Fe distances (2.65 versus 2.67 Å) and the considerably longer S^s … S^s distances (3.73 versus 3.59 Å). These differences are the result of the direct exchange interaction among the high spin, valence delocalized Fe centres within the m_s = ±9/2 [2Fe–2S]⁺ rhombs of a diamagnetic S_t = 0 [4Fe–4S]²⁺ cluster.

Similar to the homoleptic, βME coordinated reference cluster complex, variations in the Fe–S^t distances of the optimized [4Fe–4S]-maquette structures are also informative of the structural differences among the three studied peptides. The Fe–S^t(βME) bond lengths of 2.22 ± 0.01 Å can be taken as a reference value for the cluster thiolate interaction without steric strain or intramolecular H-bonding interactions to the coordinated thiolate S centre. Despite starting from the same thiolate conformation for the βME ligand as posed by the fourth, distal Cys coordination to the cluster binding motif in the crystal structure of Fd-Pa (PDB code: 1DUR [42–44]), the optimized maquette structures show variability whether the distal hydroxyl group of βME forms a H-bonding interaction or not. As shown in figure 5 (folded and bifurcated versus extended thiolate arms), the intramolecular H-bonding with the ligand is more favourable energetically than interaction with solvent water molecules. This is further compounded by additional H-bonding to one of the S^s centres. As discussed for the reference [Fe₄S₄(βME)₄]²⁻ cluster, this interaction with S^s can introduce up to 36 kJ mol⁻¹ variation in relative energies for the lowest energy spin-coupling states.

The peptide thiol S^t positions from the anchoring Fe ions are clear features of the strength of H-bonding interactions with the peptide backbone. The N-terminal and central Fe–S^t distances are consistently 0.04 Å longer than the C-terminal Fe–S^t distances for the thioGly-containing maquette. Given the lack of notable H-bonding interactions involving the C-terminal S^t centre, it behaves similarly to the S^t of the βME ligand. The lower strength of the peptide/thiol H-bonding in the Cys maquette versus the thioGly is shown by the reduced deviation of 0.02 Å between the Fe–S^t bond lengths. These differences practically disappear (at most 0.01 Å) for the homoCys maquette, which is a direct indication that homoCys thiol side chain behaves highly similarly to the free βME thiol with respect to cluster anchoring or coordination. This is also suggested by the similar H-bonding pattern and arrangement of the ‘spectator’ βME ligand in the homoCys maquette in comparison to the [Fe₄S₄(βME)₄]²⁻ reference cluster.

3.3.3. Ligand-exchange/cluster transfer thermodynamics

The thermochemical analysis of the equilibrium [4Fe–4S] cluster structures on both sides of the ligand-exchange reaction depicted by equation (3.1) supplemented with those of the fully protonated peptide and the protonated βME allows for the calculation of experimentally relevant Gibbs free energy and enthalpy values for the maquette formation reaction. The Gibbs free energy values were corrected with the translational entropy differences between the ideal gas phase and the condensed phase at 200 µM maquette concentration (see the electronic supplementary material). Furthermore, we also considered the conformational flexibility of the free peptide (ΔH^corr(peptide conformation), table 2) which affects the left-hand side of equation (3.1). Before coordination to the [4Fe–4S]²⁺ cluster, the free peptide in a water bath can adopt more stable conformations than when it is coordinated in the maquette complex. Thus, peptide coordination to the cluster may require 10–20 kJ mol⁻¹ reorganization energy. On the contrary, the dissociating three βME molecules treated in the same water bath model may interact with each other through H-bonding, Coulomb/dipole and van der Waals/dispersion interactions, which can lower the overall reaction enthalpy. From the quantum chemical section (vide infra), we established the energy range for the various spin-coupling schemes and thiolate ligand conformations, which is best exemplified by the relative energies in figure 5.

Table 2.

Summary of calculated Gibbs free energy and reaction enthalpy values (in kJ mol⁻¹) for the [4Fe–4S]-maquette ([Fe₄S₄(peptide)(βME)]²⁻) formation in ligand-exchange reaction from a preformed [Fe₄S₄(βME)₄]²⁻ complex as depicted in equation (3.1). The ΔH^corr. values were calculated from 1 ns NVT MD runs for the peptide and the three βME molecules in water bath, as well as the various spin-coupling schemes of the [4Fe–4S] clusters.

peptide	ΔHrxn	ΔGrxn	ΔHcorr.(peptide conformation)	ΔHcorr.(βME molecules)	ΔHcorr.(spin coupling)
thioGly - UIAUGAU	−64	−162	+10.2 ± 3.5	−5.0 ± 1.1	< +58
Cys - CIACGAC	−80	−169	+9.5 ± 3.1	−5.0 ± 1.1	< +58
homoCys - JIAJGAJ	−3	−123	+18.6 ± 9.1	−5.0 ± 1.1	< +58

The overall Gibbs free energy values in table 2 (ΔG^rxn) clearly indicate that the cluster formation by ligand-exchange is spontaneous for all peptides regardless of the length of the thiolate side chain. This is in support of our observations of similar maquette formation yields for a wide range of cysteine containing peptides [20] with a variety of coded amino acids at intervening positions of the Cx₂Cx₂C motif. However, there are also significant differences in table 2 that show clear thermodynamic preference for the formation of the [4Fe–4S]-maquette with the coded Cys containing peptide CIACGAC. When the various correction terms to enthalpy are considered, including the thiolate conformational and spin-coupling scheme energy, the overall exothermic reaction could switch to endothermic for the non-coded amino acids. The enthalpy values (ΔH^rxn), as a direct indication of cluster/peptide interaction energy, clearly show the thermodynamic preference of the coded amino acid coordination through three thiolates with −80 kJ mol⁻¹ stronger interaction than three of the coordinated βME ligands together. This can be rationalized by the ideal chelating geometry defined by the spacing of the amino acids and the length of the thiolate arms. In addition, the balanced steric repulsion between the peptide and the cluster and the network of H-bonding/dipole interactions between the backbone functional groups and the cluster S-centres further contribute to the added stability of Cys. The binding energy difference between the peptide and βME ligands diminishes for the homoCys as the longer side chain behaves highly similar to the non-chelating βME ligand. The shortest thiolate anchor in thioGly maquettes coordinates the cluster weaker than Cys, but maintains an extensive network of intramolecular interactions as expected from the optimized equilibrium structures of thioGly- (figure 6a, side view) and Cys-containing (figure 6b, side view) maquettes. The reduced cluster binding affinity of thioGly can be rationalized by the increased steric bulk repulsion between the cluster and the peptide despite the numerous H-bonding interactions relative to the Cys maquette.

4. Discussion

With respect to coded and non-coded thiolate side chain containing amino acids, our work highlights the significance of the length of peptide thiolate side chains in coordinating [4Fe–4S] clusters. While the short thiol in thioglycine directly connected to the peptide backbone shows a favourable network of interactions between the peptide and the cluster, the close proximity of the negatively charged cluster and the steric bulk moderates [4Fe–4S] cluster binding. The presence of a single methylene group between the backbone and the coordinating thiolate, as in cysteine, alleviates the steric bulk from the peptide, maintains the H-bonding and dipole network, and provides covalent Fe–S(thiolate) interactions that together create the optimal electronic and geometric structural conditions for [4Fe–4S] cluster binding. When transitioning from cysteine to homocysteine, the extension of the thiol side chain with an additional methylene group diminishes the benefit of peptide coordination to a modest chelating effect manifested by effectively creating a higher local thiolate concentration for [4Fe–4S] cluster binding in comparison to free thiol molecules in aqueous solution. Thus, homoCys is expected to behave similarly to the free thiol (βME) in a coordinated [4Fe–4S] cluster. It is also notable that neither thioGly nor homoCys are described in the Protein Databank [67] as part of a native protein matrix resulting from post-translational modifications of coded amino acids. However, derivatives of both non-coded amino acids considered here are known as GL3 [68–70] and HCS/KCY [71–75] in the Protein Databank as part of synthetic short peptides.

The thermodynamic preference for [4Fe–4S]-maquette formation in the presence of coded, cysteine containing peptides was established based on empirical force field-based molecular dynamics simulations and high level, quantum chemical calculations. These computational modelling results are currently being followed up by experimental studies in our laboratories. We predict that peptides harbouring the non-coded amino acids will exhibit lower yields for reconstitution of [4Fe–4S]²⁺ clusters in aqueous buffers. Furthermore, since our simulation results indicate that peptides can exist in a nest conformation suitable for receiving a fully formed cluster, they support a reconstitution mechanism wherein [4Fe–4S] cluster incorporation into a peptide nest does not proceed through [Fe–S] cluster decomposition and reassembly, but is more likely a thermodynamically favourable, direct ligand-exchange process.

Extant biology can couple electron transfer reactions to a build up of chemical potential. This chemical potential (often in the form of high ATP/ADP ratios, and the membrane spanning ion gradient) is then used to drive otherwise generally unfavourable reactions such as amino acid and nucleoside polymerization. In the context of emergence of life scenarios, spontaneous [Fe–S] cluster formation in aqueous solution can be a plausible way for facilitating electron transfer reactions by protocatalysts. Experimental reports [10,11,14,16,17,20] have expanded our awareness of which cysteine thiolate motifs can coordinate [Fe–S] clusters. Our work here highlights potential reasons for why cysteine, and not functional analogues of cysteine, may have been selected as the preferred [Fe–S] cluster ligands in nature.

5. Conclusion

Empirical force field-based molecular dynamics simulations and spectroscopically validated density functional calculations provided support for the thermodynamic preference of cysteine, an essential, genetically coded amino acid for the coordination of [4Fe–4S] clusters, in comparison to the non-coded analogues thioglycine and homocysteine that contain a shorter and longer thiolate, respectively. The coordination chemistry-based evolutionary selection in the case of [4Fe–4S] cubanes can be contrasted with [2Fe–2S] cluster nest formation, which was observed to be more prevalent for the non-coded amino acids for both short (7-mer) and long (16-mer) peptides. The length of the cysteine thiol side chain forms an ideal spacing between the peptide and the cubane that mitigates the steric bulk, facilitates the network of H-bonding and dipole interactions, and promotes covalent Fe–S(thiolate) bonding. These interactions are less favourable when considering peptides containing thioglycine. Peptides with homocysteine are predicted to behave as free thiolates (such as β-mercaptoethanol), with modest influence of the chelating nature on [Fe–S] cluster binding and stability. We can also confirm from the comparison of 7-mer and 16-mer peptides that sequence length likely influences the coordination, binding and stability of [Fe–S] cluster species, as the probability of [4Fe–4S] cluster nests ready for direct ligand-exchange with a preformed cubane cluster is doubled for the longer peptide. This is advantageous for the biomimetic aspects of this work, since we can thus use both the N-terminal and C-terminal flanking amino acids for designing substrate binding pockets in order to promote the functionalization of the unique, fourth Fe-site that is not involved in coordination to the peptide. In summary, we propose that peptides with cysteine are thermodynamically more favourable for [4Fe–4S] cluster coordination than alternative thiolate containing non-coded amino acids. These observations are based on well-established computational methodologies; thus, they generate an experimentally testable hypothesis of ‘natural selection’ through coordination chemistry. In proto-ferredoxins and [4Fe–4S] cluster containing proto-metalloenzymes, homoCys and thioGly coordinated clusters may have displayed lower stability and thus, may have had shorter half lives, while Cys containing peptides could have persisted as thermodynamically preferred nests for [4Fe–4S] cluster binding.

Data accessibility

Electronic supplementary materials are made available at the ZENODO OpenScience Repository under registered dataset as doi:10.5281/zenodo.3361945 (v. 1.0).

Authors' contributions

R.K.Sz., E.M.S., and S.E.M. participated in the design of the study, drafted and then critically revised the manuscript; R.H. carried out molecular dynamics simulations, participated in data analysis and provided support to the in-house secondary structure analysis toolkit; all authors gave final approval for publication and agree to be held accountable for the work performed herein.

Competing interests

We have no competing interests.

Funding

This work was supported by the National Science Foundation, Chemistry of Life Processes programme, grant no. 1609557 to R.K.S. and E.M.S. S.E.M. is partially supported by NSF grant no. 1724300 ‘Collaborative Research: Biochemical, Genetic, Metabolic, and Isotopic Constraints on an Ancient Thiobiosphere’.