Does the Processing of Sensory and Reward-Prediction Errors Involve Common Neural Resources? Evidence from a Frontocentral Negative Potential Modulated by Movement Execution Errors

Abstract

In humans, electrophysiological correlates of error processing have been extensively investigated in relation to decision-making theories. In particular, error-related ERPs have been most often studied using response selection tasks. In these tasks, involving very simple motor responses (e.g., button press), errors concern inappropriate action-selection only. However, EEG activity in relation to inaccurate movement-execution in more complex motor tasks has been much less examined. In the present study, we recorded EEG while volunteers performed reaching movements in a force-field created by a robotic device. Hand-path deviations were induced by interspersing catch trials in which the force condition was unpredictably altered. Our goal was twofold. First, we wanted to determine whether a frontocentral ERP was elicited by sensory-prediction errors, whose amplitude reflected the size of kinematic errors. Then, we explored whether common neural processes could be involved in the generation of this ERP and the feedback-related negativity (FRN), often assumed to reflect reward-prediction errors. We identified a frontocentral negativity whose amplitude was modulated by the size of the hand-path deviations induced by the unpredictable mechanical perturbations. This kinematic error-related ERP presented great similarities in terms of time course, topography, and potential source-location with the FRN recorded in the same experiment. These findings suggest that the processing of sensory-prediction errors and the processing of reward-prediction errors could involve a shared neural network.

Introduction

Decision-making theories and motor-control models have been developed as two separate fields of research. Although prediction error plays a central role in driving behavioral adaptation in both theoretical frameworks, its nature and the neural substrates involved in its processing are assumed to be different. On the one hand, reinforcement learning theory of decision-making stipulates that behavioral adaptation relies on the maximization of numerical reward signals (Sutton and Barto, 1998). The mesencephalic dopamine system carries reward-prediction error-signals used by the anterior cingulate cortex (ACC) as a training signal to adjust the behavior in subsequent trials (Schultz et al., 1997; Schultz, 1998). On the other hand, it is commonly assumed in motor-control theories that the nervous system predicts the sensory consequences of motor commands on the basis of internal models (Miall and Wolpert, 1996), and that adaptation is driven by sensory-prediction errors (Wolpert, 1997; Tseng et al., 2007; Berniker and Kording, 2008). The cerebellum and the parietal cortex would be central in the processing of sensory-encoded kinematic-errors (Bastian, 2006; Tanaka et al., 2009).

In humans, the electrophysiological correlates of error-processing have been extensively investigated in research on decision making. In particular, two evoked responses (ERP) have been thoroughly studied: the error-related negativity (Ne/ERN; Falkenstein et al., 1991; Gehring et al., 1993) and the feedback-related negativity (FRN; Miltner et al., 1997). Both are negative potentials characterized by a frontocentral topography, with common neural generators suggested to be located in the ACC (Dehaene et al., 1994; van Veen and Carter, 2002; Gentsch et al., 2009) and/or in the supplementary motor area (SMA; Dehaene et al., 1994; Vidal et al., 2000). However, these two ERPs critically differ in the internal or external nature of the processed error signal. Whereas the Ne/ERN is observed ∼90 ms after producing an erroneous response and would reflect an internal predictive error signal, the FRN peaks ∼250 ms after an external performance feedback, and is often assumed to reflect reward-prediction errors.

So far, error-related ERPs have been almost exclusively explored in cognitive tasks requiring elementary motor responses (e.g., button press). That is, in situations in which errors concern inappropriate action selection only, and the evaluation of the performance is discrete (e.g., failure or success). In contrast, ERP correlates of error processing have been studied less in more complex motor tasks in which inaccurate movement-execution produces kinematic errors that vary continuously in magnitude within a single movement and across trials (Krigolson et al., 2008; Anguera et al., 2009; Vocat et al., 2011).

In the present study, we compared an ERP elicited by externally produced kinematic errors with an FRN evoked by a discrete performance-feedback signal. In this purpose, we recorded EEG while volunteers performed reaching movements in a force-field created by a robotic device. Hand-path deviations of different sizes were induced by interspersing catch trials in which the force condition was unpredictably altered. In the same experiment, we provided our participants with a visual feedback about their movement-duration in all trials with unchanged force-field (in which no hand-path deviation was produced). Our goal was twofold. First, we tested whether an ERP could be observed that is parametrically modulated by the magnitude of the error itself. Then, we explored whether the processing of sensory- and reward-prediction errors could involve common neural resources.

Materials and Methods

Participants.

Fifteen male participants aged 21–35 years (mean, 24.6 years) volunteered for the experiment. Fourteen of them were right handed and one ambidextrous, as assessed by the Edinburgh Handedness Inventory (Oldfield, 1971). All participants had normal or corrected-to-normal vision and were free of neurological or psychiatric disorders, and gave informed consent according to a protocol approved by the Ethics Board of the Institut de Neurosciences de la Timone.

Experimental setup.

Participants performed reaching movements using a robotic exoskeleton (KINARM, BKIN Technologies) that permits flexion and extension of the elbow and shoulder in the horizontal plane, and can apply mechanical loads to each of these two joints. Participants were comfortably seated with their right arm supported against gravity by the robotic device (Fig. 1A). The height of the chair was adjusted so that the shoulder was abducted by ∼70°. The reaching movements always started from the same initial position with the elbow joint anteflexed 90° and the shoulder horizontally abducted 45°.

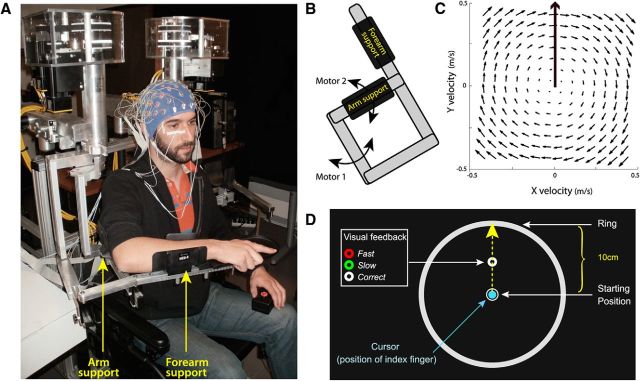
Figure 1.

Experimental setup. A, EEG was recorded while participants performed reaching movements in a force-field created by a robotic exoskeleton. B, The field was produced by applying mechanical loads to the shoulder and elbow joints through two torque-motors (M1 and M2). C, Using the transformation from joint torque to endpoint force, a clockwise curl-field was created in which the force applied to the hand was proportional and acted perpendicular to the velocity of the hand. D, The robotic device was coupled with a virtual 2D reality display (data not shown here) that permit to project visual stimuli in the same horizontal plane as the hand. Participants had to make “shooting” movements in the direction of the donut, and cross the outer ring within 375 ± 50 ms. At the time their index reached the ring, the donut changed color providing feedback about movement duration.

Throughout the task, participants maintained the right hand in a fist with the index extended in a pointing position. Using a semisilvered mirror, direct vision of the hand was prevented throughout the task, while a cursor representing the position of the index finger tip and the visual display were projected onto the same plane as the (not visible) hand. Head position was restrained using a chin rest.

Task.

To be able to relate EEG activity to error processing, independent of motor correction, we used a task in which participants experienced kinematic errors without having the opportunity to correct their movements. Participants performed a “shooting” task (Tseng et al., 2007) in which they were required to make reaching movements with no on-line corrections. The starting position was indicated by a 1.5 cm diameter white circle located at the center of a large outer ring (10 cm radius). A 0.5-cm-diameter donut was projected 5 cm away from the starting position, along the body midline (Fig. 1D). Participants were instructed to make “shooting” movements in its direction and to reach the outer ring. As detailed below (see Experimental protocol), catch trials (20%) were interspersed in which kinematic errors of different sizes were produced by changing the force environment unexpectedly, using a robotic device. The task of the participants was to reach the outer ring, within a given duration; specifically, their index finger-tip had to cross it within 375 ± 50 ms (ending their movement ∼3 cm beyond it). They were informed that they would not be penalized for not moving precisely through the donut, but that moving always in the same direction (that is, producing as much as possible the same movement throughout the trials) was very helpful to keep movement duration constant. Movement duration was computed on-line and corresponded to the duration between the time at which the speed of the hand exceeded 0.07 m/s and the time at which the fingertip cursor reached the outer ring. Throughout the task, participants had to keep their eyes fixed on the donut. At the time their index reached the ring, the participants received a visual feedback about the duration of their movement: the donut turned green, red, or remained white to indicate that the movement was too slow (duration > 375 + 50 ms), too fast (duration <375–50 ms) or performed at the correct speed (375–50 ms ≤ duration ≤ 375 + 50 ms), respectively.

To initiate a trial, participants had to maintain their index finger in the start circle for 500 ms before it disappeared to warn them to get ready (READY). Following a 1500 ms delay, the donut was filled in white to indicate that the movement could be initiated (GO). Participants were informed that they were not performing a reaction-time task and should take all the time they needed to plan their movement. To avoid on-line movement correction, the fingertip cursor was turned off when reaching the outer ring (Fig. 1D). Upon the end of movement, as the index fingertip was ∼3 cm beyond the ring, the robot brought their arm passively back to the start position. The fingertip cursor and the starting-position circle reappeared only when the hand was back in its initial position. Each trial lasted ∼5 s.

Experimental protocol.

To examine electrophysiological correlates of movement-execution error-processing, we applied mechanical perturbations to the movement using a clockwise curl-field in which the force was set to f = B × v, where f = (fx, fy) depends on the velocity of the hand v = (vx, vy), and B = (0, −α, α, 0) N·sec·m⁻¹, with α the force-amplitude parameter (Fig. 1C). Four different force-field amplitudes were used by setting α = 0, 3, 6, or 9. The field was produced by the torque-motors of the robotic exoskeleton, using the transformation from endpoint force to joint torque: t = J′ × f, where J = [l1 × sinθ1 + l2 × sin(θ1 + θ2), l2 × sin(θ1 + θ2); l1 × cosθ1+l2 × cos(θ1+θ2), l2 × cos(θ1+θ2)] is the configuration-dependent differential transformation matrix (Jacobian matrix).

In this experiment, we opted for an experimental design in which participants first adapted to the strongest force-field (α = 9; Fig. 2A) and then performed an experimental phase in which movement perturbations were obtained by unpredictably reducing the intensity of the field in a small number of trials (catch trials with α = 0, 3, 6; Fig. 2B). This design was chosen so as to maximize the amplitude of the small hand-path deviation typically observed in the “unperturbed” trial (n + 1) that follows a perturbed trial (n; Thoroughman and Shadmehr, 2000). Indeed, the small kinematic-error observed on trial n + 1 is expected to be larger when it is produced by an unlearning process (induced by removing a learned force-field in trial n) than when it reflects to a learning process (induced by introducing a new force-field in trial n; Kitago et al., 2013). These (n + 1) trials will be analyzed in a separate paper.

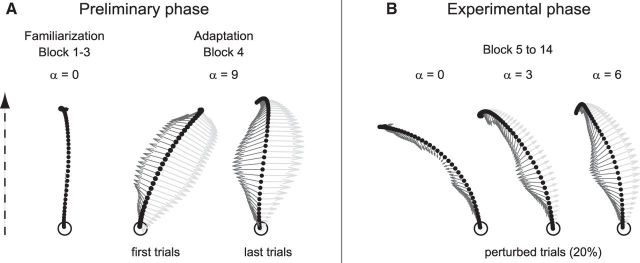
Figure 2.

Representative hand-paths along with vectors (arrows) with schematic representations of the forces applied by the robot (light gray) and the force applied by the participant's hand (dark gray). The dotted arrow indicates the direction of the movements. A, Preliminary familiarization and force-field adaptation phase. Before adaptation, movements performed in the null field (α = 0) were roughly straight. Upon initial exposure to the force-field (α = 9), hand paths were clearly deviated. However, participants quickly (within 10–15 trials) adapted to the new dynamic condition, and by the end of the adaptation block they moved straight ahead again. B, After adaptation, during the experimental phase, movements performed in the strongest force-field (α = 9) were not perturbed anymore and thus corresponded to unperturbed trials. In contrast, reducing the force-field amplitude in catch trials to α = 0, 3, or 6 produced usually large, medium, and small kinematics errors.

The experiment included two phases: (1) A preliminary phase, in which participants learned the task while the motors of the robot were turned off (α = 0), and then adapted to the force-field (α = 9). (2) An experimental phase, in which 80% of the movements were performed in the force-field (α = 9), whereas in 20% of catch trials the force was unexpectedly reduced (α = 0, 3, 6). EEG signals were recorded during the experimental session only and the total experiment lasted ∼3.5 h.

Preliminary phase (familiarization and force-field adaptation).

First, the participants sat in the KINARM for calibration and received verbal instructions about the task requirements. Then they learned the shooting task, performing three blocks of 30 reaching movements in the “null field” (Blocks 1–3, α = 0). During the first two blocks of trials, they had full vision of their limb, whereas it was occluded in the third block, in which only a cursor figured the position of their fingertip. During a fourth block of 30 trials, the strongest force-field (Block 4, α = 9) was applied. Although hand-paths were clearly deviated in the first trials (Fig. 2A), all participants quickly (within 10–15 trials) adapted to the new dynamic condition; by the end of the block they moved straight ahead again (Fig. 2A).

Experimental phase.

The experimental phase consisted of 10 blocks of 120 trials, including 96 trials (80%) performed in the strongest force-field (Block 5–14, α = 9), to which they previously adapted, interspersed with 3 × 8 catch trials (20%) in which the amplitude of the force-field was unpredictably reduced to α = 6, 3, or 0. Because participants had adapted to the strongest force-field (α = 9) during the previous phase, movements performed in this field were not perturbed and thus corresponded to unperturbed trials in which no systematic kinematic error was observed. In contrast, reduced force-field catch trials, with α = 6, 3, or 0, produced usually small, medium or large kinematics errors, respectively (see Figs. 2B, 3B,C). To maintain adaptation to the strong force-field (α = 9), two catch trials were always separated by at least three unperturbed (α = 9) trials. Each block lasted ∼10 min and breaks of ∼2 min were allocated between blocks. At the end of each block, participants were verbally informed about the percentages of too slow, too fast, and correct movement-duration trials they performed.

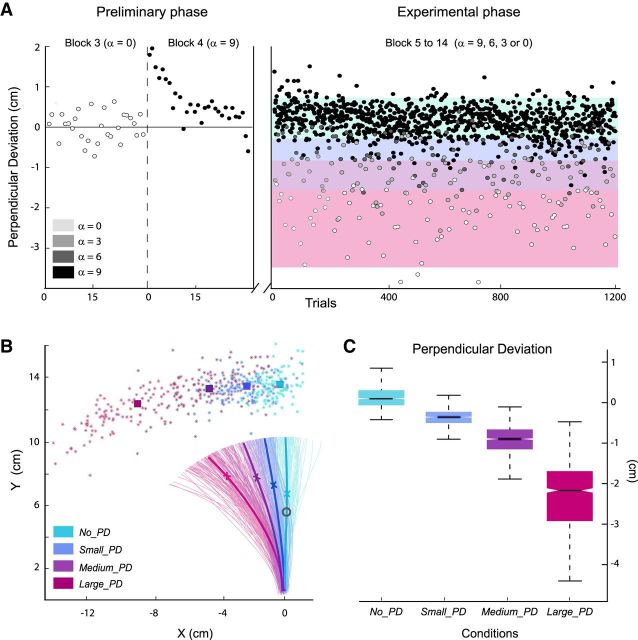
Figure 3.

Behavioral data. A, For a representative participant, PD of the last 60 trials of the familiarization phase (Blocks 3 and 4) and the 1200 trials of the experimental phase. Trials were binned into four categories according to their PD (color bands): No_PD, Small_PD, Medium_PD, and Large_PD. B, For the same participant, hand paths for all individual trials of the experimental phase; colored stars show hand positions at movement ends. The mean hand-paths for the different categories of trials are plotted in thick lines mean hand-positions at velocity-peak and movement-end are shown by crosses and squares, respectively. The eye-fixation donut (visual feedback) is also indicated in gray. C, Box plots indicating for each categories of trials, the 25^th, 50^th, and 75^th percentiles, as well as the extreme values of the mean PD of all trials.

Here, we have to emphasize that the trial sequence was specifically designed to avoid an overlap (within the same trial) of the FRN evoked by the movement-duration feedback and the ERP related to the kinematic error produced by the mechanical perturbation. The visual feedback on movement duration was provided only in the trials where no unexpected change in the force condition was applied (unperturbed trials); in trials where the hand-path was perturbed (by an unexpected diminution of the amplitude of the force-field), the donut remained white regardless of the duration of the movement. The visual feedback was used to induce a FRN, which will be used in the present study for comparison purposes. Therefore, for data analysis, the FRN was calculated using the EEG signal recorded during the unperturbed trials, whereas the ERP related to the kinematic error was computed from the perturbed trials.

Behavioral data recording and analysis.

The angular position and velocity data of the motor resolvers were collected at 1000 Hz. Off-line signals were resampled at 100 Hz then filtered with a second order, zero phase-shift Butterworth filter (cutoff frequency of 10 Hz). Finger position and velocity were calculated from these angular data. Kinematic data were analyzed using MATLAB (MathWorks). All the trials in which the maximum velocity was reached after crossing the outer ring were excluded from the analyses (∼5% of the trials).

To quantify kinematic errors, we computed the perpendicular deviation (PD) at maximum velocity; that is, the deviation from the straight line that connects the starting position to the donut, measured at peak velocity. To take into account “natural” hand-path curvatures that might characterize individual baseline-unperturbed reaching movements, we quantified the kinematic error in the catch-trial n as the difference: (PDn − PDn-1). As reaching movement, errors were reflected by increased hand-path lengths and durations also, we computed these measures. As shown in Figures 2B, 3A,B, different force amplitudes produced kinematic errors of different sizes. However, for a given level of perturbation, quite variable PDs were observed for the different trials and the PD distributions corresponding to the different force diminutions (α = 9, 6, 3, or 0) were partially overlapping (Fig. 3A, black, dark gray, light gray, and white dots). Because our primary focus was on the kinematic errors, we resorted trials into four equal-effective categories according to the observed PD: No_PD, Small_PD, Medium_PD, and Large_PD trials (Fig. 3A, different color bands). Only the unperturbed trials n-1 that preceded directly a catch trial n were retained. First, this ensured that unperturbed trials included only movements that could not have been influenced by a perturbation occurring on a preceding trial. Second, this allowed computing ERPs based on comparable numbers of trials for all conditions.

In addition to the amplitude of the deviation (PD), the duration of the movements as well as the lengths of the hand paths were calculated for the different types of trials (No_PD, Small_PD, Medium_PD, and Large_PD trials).

EEG recording.

EEG activity was recorded continuously at 1024 Hz using a 64-channel Biosemi ActiveTwo system (BioSemi) referenced to the Common Mode Sense-Driven Right Leg ground. Electrodes were embedded into an elastic cap and evenly distributed over the scalp according to the extended 10–20 EEG system. For each participant, electrode locations and nasion and preauricular points were recorded by an infrared camera (Rogue Research). EOG activity was recorded with surface electrodes placed near both outer canthi (saccades) as well as under and above the left orbit (blinks). Electrode impedance was kept <5 kΩ.

EEG preprocessing.

Data were cleaned from nonstereotyped artifacts (e.g., electrode drift or movement artifacts and spurious muscle activity) using the free software ELAN (http://elan.lyon.inserm.fr/; Aguera et al., 2011). The continuous EEG signals were re-referenced to the average of the mastoids and bandpass filtered between 0.1 Hz and 30 Hz (Butterworth order 2). First, changes in signal amplitude exceeding 100 μV/500 ms were automatically detected. Then data were visually inspected for remaining nonstereotyped artifacts; corresponding channels and signal segments were excluded from further analysis. Stereotyped eye-movement artifacts (e.g., blinks) were kept in the data to be removed in a later step by means of independent component analysis (ICA).

Data were further preprocessed using custom routines and functions from the free and open source EEGLAB toolbox (v9, http://sccn.ucsd.edu/eeglab/; Delorme and Makeig, 2004) written in MATLAB (MathWorks). Signals were cut into time-segments from −1000 to 2000 ms with respect to reaching-movement onset and then downsampled to 256 Hz to be submitted to a temporal ICA using the infomax algorithm (Bell and Sejnowski, 1995). The resulting 64 independent components (ICs) corresponding to the 64 input channels were visually screened to identify (based on their topographies and time courses) the ICs corresponding to eye-blinks. New EEG signals, exempt from these stereotyped artifacts, were obtained by backprojecting the ICs into the channel space removing the identified ICs; the latter data were used to compute the ERPs.

ERPs.

For each participant, two types of ERPs were computed: (1) deflections induced by the kinematic error (ERP-K), obtained by time locking EEG activity to the movement onset, and (2) waveforms related to the visual feedback about movement-duration time locked to the color change of the donut. The ERPs were analyzed in a time window from −500 to 1000 ms relative to the selected time locking point. ERP-Ks were computed for each trial category, No_PD, Small_PD, Medium_PD, and Large_PD, and feedback-related waveforms were obtained for too fast and correct duration trials, from which the FRN (difference wave between punishments and reward) was computed. Because eight participants produced very few too slow movements (<15 trials), we excluded this type of trials from the analyses. On average, to compute the individual ERP-Ks, 75 No_PD, 75 Small_PD, 73 Medium_PD, and 71 Large_PD trials were retained. The FRNs were obtained based on 132 fast and 145 correct trials on average. For both kinds of ERPs, the baseline value was computed from the 200 ms preceding the respective onset point. As a control, we also calculated the FRN using the 200 ms before movement onset as baseline. Because very similar results were obtained for both baseline windows, we present only the FRN computed using the 200 ms before the visual feedback (donut color change) as baseline.

As a control, we also computed the ERP-K using a different time locking procedure. Indeed, it seems reasonable to assume that the time at which a kinematic error signal is issued varies with the amplitude of the hand-path deviation; the larger the PD the earlier the hand-path deviation should be perceived. In addition, the time at which the hand is deviated to a given x-position and an error-signal is issued should be more variable for small than for large perturbations (Fig. 3B). To discard the possibility that this underlied the variation in amplitude of the ERP-K across conditions (a better signal-alignment achieved for the large perturbation conditions), we computed ERP-Ks locked to the time at which the hand was deviated to the x-position − mean PD of the unperturbed trials = 0.5 cm. The results were very similar to those obtained when time locking the EEG signals on movement onset, and therefore will not be presented here.

ERP analysis.

We tested whether the amplitudes of the ERP-K were modulated by the size of the kinematic error. Statistical ERP analyses were restricted to the activity recorded at electrode FCz, where the maximum of the negative component was recorded. For each perturbed condition (Small_PD, Medium_PD and Large_PD), in a time window from 200 to 350 ms after movement onset, we identified the time-point at which the associated ERP became significantly different from the waveform corresponding to the No_PD trials. Specifically, on the individual ERPs and for each condition Small_PD, Medium_PD, and Large_PD, a t test comparing the perturbed with the No_PD condition was computed at each time-point. The first time-point for which the p value was <0.05 for at least 20 consecutive sampling points (∼19.5 ms) was selected (Luck, 2005) as the start of a 30 ms window over which the signal-amplitude was averaged. In Figure 4A, the topographies are shown for the center of the averaging windows indicated by arrowheads. The mean amplitudes were submitted to a repeated-measures ANOVA with type of trials (Small_PD, Medium_PD, and Large_PD) as within-subject factor. Huyn–Feldt correction was applied whenever appropriate.

Figure 4.

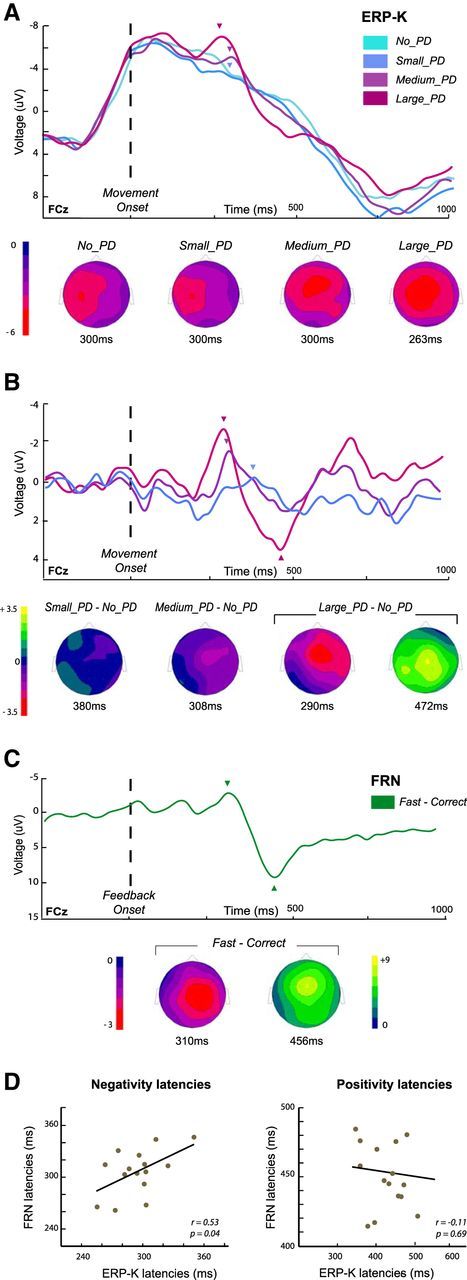
ERPs related to the kinematic errors (ERP-K) and to the movement-duration feedback (FRN). A, Grand average ERP-Ks for the four categories of trials, No_PD, Small_PD, Medium_PD, and Large_PD, at the FCz electrode. Topographies are shown at the center of the 30 ms signal-amplitude averaging-windows indicated by arrowheads (see Materials and Methods). B, Grand averages of the ERP-K difference-waveforms corresponding to the three categories of perturbed trials, Small_PD, Medium_PD, and Large_PD conditions. In each case, the topographies are shown at the peak of the negativity (arrowheads). For the Large_PD − No_PD difference curve, the topography at the positivity peak is also presented. C, Grand averaged of the FRN (fast − correct difference curves). Topographies are shown at the negativity- and positivity-peak latencies (arrowheads). D, Scatter plots showing the relation between the latencies of the negative and positive components of the two types of ERPs. Within-subject correlations have been calculated between the peak latencies identified on the difference waves Large_PD − No_PD (ERP-K) and fast − correct (FRN).

For each participant, difference waves were also obtained by subtracting the activity observed in the No_PD trials from the ERP-Ks observed for the perturbed trials. For these waveforms, mean amplitudes were computed in 30 ms windows centered on the negativity peak identified on the grand average curves (see Figs. 4B, 5B, arrowheads) and analyzed as previously described.

Figure 5.

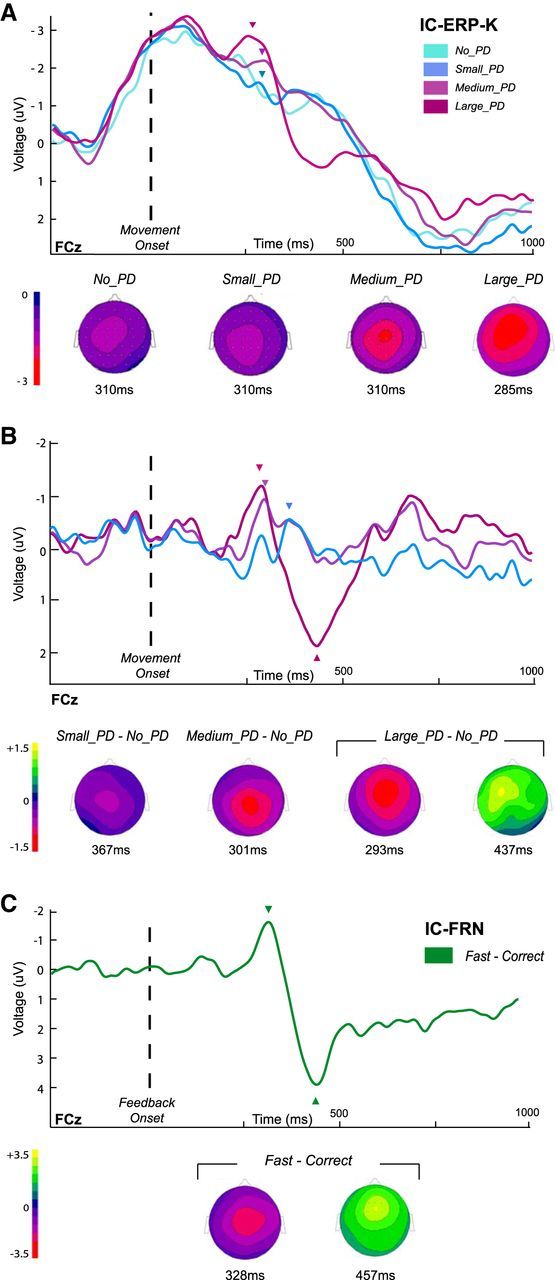
IC-ERPs obtained from the EEG signals reconstructed from the ICs related to the processing of the kinematic errors (see Materials and Methods). IC-ERP-Ks were calculated by time locking the new signals on the onset of movement and IC-FRNs were obtained by time locking on the presentation of the movement-duration feedback. A, Grand average IC-ERP-Ks for the four categories of trials, No_PD, Small_PD, Medium_PD, and Large_PD, at the FCz electrode. Topographies are shown at the center of the 30 ms signal amplitude averaging-windows indicated by arrowheads (see Materials and Methods). B, Grand averages of the 15 individual IC-ERP-K difference waveforms for the three categories of perturbed trials. Topographies are shown at the peak latencies (arrowheads). C, Grand averaged of the IC-FRN (fast − correct difference curves). Topographies are shown at the negativity- and positivity-peak latencies (arrowheads).

In addition, to investigate the relationship between the ERP-K and the FRN, we looked at the correlations between the latencies of the negative and positive components of the two types of ERPs across all 15 participants. In this purpose, we considered the difference waves Large_PD − No_PD and Fast − Correct obtained for each participant (Fig. 4D).

For all tests, significance threshold was set at 0.05; for post hoc t tests a Bonferroni correction was applied. The same analyses were applied to the independent component identification (IC-ERPs) computed as described below.

IC-ERPs.

ICA was used to perform a blind source separation of the signal (Makeig et al., 1997). Our aim was to first identify for each individual the IC(s) that would account for a substantial part of the ERP-K profiles, and then to quantify the proportion of the FRN that could be accounted for by the selected ICs. This procedure was intended to investigate the similarities between the ERP-K and the FRN (Makeig et al., 2004; Debener et al., 2005a,b; Onton et al., 2006; Gentsch et al., 2009; Roger et al., 2010; Wessel et al., 2012). In this purpose, we used the automated ICs selection procedure proposed by Wessel and Ullsperger (2011) and implemented as the free and open source MATLAB toolbox COMPASS (http://jrw.lima-city.de/e_compass.htm).

Before being submitted to the COMPASS algorithm, ICs (that were obtained from the EEG-preprocessing step) were screened as recommended by Wessel et al. (2012, 2013). Namely, in addition to ICs representing eye-blink artifacts already removed, components unlikely to represent meaningful event-related activity were excluded from the selection process. Using the DIPFIT2.2 plug-in for EEGLAB, all ICs with dipole solutions outside the brain, and with a residual variance larger than 15% for both one and two dipole solutions were identified. Further, ICs corresponding to electrode artifacts, characterized by maps with extremely focal activity, were identified using the Grubbs' iterative test for outliers implemented in COMPASS with a threshold set to p = 0.0001. The results of these automatic classification procedures were visually checked for inaccuracies (no manual rectification was needed). The remaining nonartifactual ICs were subjected to the COMPASS routine.

To identify the IC(s) driving substantial portion of the ERP-K profiles, we derived spatiotemporal templates from the difference wave obtained by subtracting the ERPs observed for the unperturbed (No_PD) trials from the ERPs for the most perturbed (Large_PD) trials (see Wessel and Ullsperger, 2011). Specifically, for each individual we input a 300-ms-wide time window centered about the peak of negativity. The ERP topographies observed at the window-center time-point was used to identify electrode sites of maximal activity, from which the relevant time courses were extracted (Wessel and Ullsperger, 2011). On average, 1.6 ICs (range, 1–3) were identified per participant. We also proceeded to the selection of the ICs using as template the ERP observed in the most perturbed (Large_PD) trials (centering the time-range about the same time-point as the windows used for the ERP-profile statistical analyses). In this case, 1.7 ICs per participants were selected. (63% of independent components were selected for both templates).

New individual EEG signals were obtained based on the activity accounted for by the selected ICs by backprojecting the IC(s) into channel space. From the reconstructed EEG, IC-ERP-K and IC-FRN were computed by proceeding in the same way as for the original ERPs.

Source reconstruction.

We used an imaging approach to reconstruct the sources of the evoked responses. We performed a distributed cortical source reconstruction for the ERP-K difference-waveforms and the FRN. Inversion was performed on the individual curves; for each participant, for the two types of ERPs and for both negative and positive components, a 300 ms time-window centered on the peak of activity was used. We used head meshes describing the boundaries of different head compartments (scalp, inner skull, and cortical sheet) based on the MNI template provided with SPM8 (Mattout et al., 2007). The EEG data and the MNI templates were coregistered using the nasion and preauricular fiducials, as well as the recorded electrode locations. Group inverse solutions were obtained using the empirical Bayesian approach implemented in SPM8 (Mattout et al., 2006), using the multiple sparse prior model (Friston et al., 2008). For the ERP-Ks, inversion for all three difference curves (corresponding to the different types of trials) was performed together; only the results for the Large_PD − No_PD curve will be presented here.

Following inversion, for each individual and each ERP type a 150-ms-wide time window (centered in the inversion window) was extracted. For each time sample, we identified the cortical points (cortical sheet vertices or dipolar sources) where activation exceeded some specified threshold, given the data, according to the posterior probability maps provided by the Bayesian inversion (Friston and Penny, 2003). This method that was originally defined for transepithelial potential and fMRI processing has been transposed to M/EEG only recently (Albouy et al., 2013). As the data were difference curves, we considered a zero-value threshold. This approach presents two main advantages: First, it provides inference at the 3D cortical surface of each individual, as a result of the Bayesian inversion; second, it is not submitted to the multiple-comparison problem because the probability that an activation has occurred, at any particular cortical vertex, is the same, irrespectively of whether only that vertex or the entire brain is analyzed (Friston and Penny, 2003). For each time sample of the time windows of interest, we used PPMs with a threshold of 5% of false positive at most, Bonferroni-corrected across participants.

This step provided for each participant and each time sample a list of cortical dipoles (vertices) significantly activated. For each participant, we identified the vertices with activity emerging for at least 26 consecutive sampling time-points (∼25.4 ms). We retained the vertices that showed significant activation in at least 10 of 15 participants. For visualization purposes, the individual meshes were then converted into 2 × 2 × 2 mm voxel images.

Results

In the present study, we wanted first to determine whether movement execution errors, induced by unpredictable changes in the force condition, were associated with a frontocentral activity whose amplitude was modulated by the size of the kinematic error. In addition, to investigate its properties, we compared this kinematic-error-related ERP with another frontocentral ERP well described in the literature: the FRN.

Behavioral performance

Data from a representative participant are plotted in Figure 3A. During the adaptation phase, upon initial exposure to the new force environment, movements were substantially perturbed. However, participants easily learned to compensate for the force-field, and rapidly (within 10–15 trials) their hand paths became straighter. During the experimental phase, all participants made kinematic errors of variable sizes when the force-field was unexpectedly reduced to α = 6, 3, or 0. No sign of movement on-line correction was observed, as illustrated by the individual hand paths plotted in Figure 3B. Amplitudes of the induced hand-path deviations observed at the group level for the different conditions (No_PD, Small_PD, Medium_PD, Large_PD) are presented in Figure 3C.

The trial categories differed as for hand-path length and duration, measures that also reflect kinematic error (F_(3,42) = 5.41, p = 0.003 and F_(3,42) = 11.2, p < 0.001, respectively). Large_PD trials presented longer hand paths than Medium_PD trials (t₍₁₄₎ = −3.74, p < 0.001), and Medium_PD longer hand-paths than Small_PD trials (t₍₁₄₎ = −2.9, p = 0.02). Increased durations were observed for Large_PD relative to Medium_PD trials (t₍₁₄₎ = −3.81, p < 0.001), and Medium_PD relative to Small_PD trials (14) = −3.11, p = 0.02).

ERP data

The analyses of the ERPs time locked to movement onset (ERP-Ks) revealed that kinematic errors elicited a frontocentral negative potential (Fig. 4A). This deflection was clearly visible in the Large_PD and Medium_PD trials, reaching its maximum at FCz ∼270 ms and 305 ms after movement onset, respectively. Note that to localize the negativity peaks, we considered a 150-ms-wide window from 200 ms to 350 ms after the movement onset (see Materials and Methods). For the Small_PD trials, however, activity was clearly lateralized between C1 and C3, as for the unperturbed movements (No_PD trials). The topographies shown in Figure 4A for the Large_PD and Medium_PD conditions correspond to the center of the 30 ms averaging time-windows defined for the comparison tests (see Materials and Methods). As there was no significant difference between the No_PD and the Small_PD trials, an averaging-window could not be defined in the same way; for this latter condition we chose to use the same time window as for the Medium_PD condition.

To test whether the amplitude of the ERP-K was modulated by the size of the kinematic error, we compared the mean amplitudes (averaged over the 30 ms windows) for the three levels of deviation; −6.9 μV (window = 263 ± 15 ms), −5.4 μV (300 ± 15 ms), and −3.8 μV (300 ± 15 ms) for the Large_PD, Medium_PD and Small_PD conditions, respectively. A repeated-measures ANOVA revealed a significant effect of error magnitude on the ERP-K amplitude (F_(2,28) = 8.14, p = 0.0016). Post hoc comparisons indicated that ERP-Ks were larger in the Large_PD than in the Small_PD condition (t₍₁₄₎ = −4.02, p < 0.001). The difference between Large_PD and Medium_PD was marginally significant (t₍₁₄₎ = −2.33, p = 0.051), while the amplitude of the ERP-K did not differ between Medium_PD and Small_PD (t₍₁₄₎ = −1.69, p = 0.2).

As can be seen in the grand average curves presented in Figure 4A, the ERP-K presented a large negative wave akin to a slow-moving negative potential that has been shown to be associated with the preparation and execution of a movement (movement-monitoring potential; Grünewald-Zuberbier and Grünewal, 1978). To remove this component, present in all trials regardless of kinematic error, we considered difference waves obtained by subtracting the activity observed in the No_PD trials from the ERP-Ks observed for the perturbed trials (Fig. 4B). The difference waves observed at FCz showed that movement-execution errors were associated with a negative deflection, followed by positivity. Comparing the topographies in Figure 4A,B, one sees how computing the difference waves resulted in recentering the scalp distributions. The two components were the most marked in the grand average Large_PD − No_PD difference curve, with a negative deflection peaking at FCz ∼290 ms (−3.0 μV) and a positivity maximum at Cz at 472 ms (peak amplitude = 3.5 μV). For the Medium_PD and Small_PD conditions, the difference curves presented a negativity peaking at 308 ms (−1.7 μV) and 380 ms (−0.3 μV), and a positive deflection ∼490 ms (1.6 μV) and 544 ms (1.7 μV), respectively. The amplitude of the negativity differed significantly across the three conditions (F_(2,28) = 4.711, p = 0.017), with a larger amplitude for the Large_PD condition than for the Small_PD condition (t₍₁₄₎ = −2.99, p = 0.008, other pairwise comparisons did not reach significance). For most participants, positivity peaks could not be identified for all conditions, and thus were not submitted to the same analysis. Figure 4C shows the profiles of the grand-average ERPs corresponding to the difference waveform fast–correct (see Materials and Methods). The latter presented a profile consistent with previous descriptions of the FRN, with a negativity peaking ∼310 ms (−2.7 μV) followed by a large positivity reaching its maximum ∼455 ms (9.8 μV) after the visual feedback. Both positive and negative components had central topographies peaking at Cz and FCz, respectively.

Comparing the ERP-K (Fig. 4B) with the FRN (Fig. 4C), one sees the similarity between the two types of waveforms; in both cases, a frontocentral negativity was followed by a positive deflection. Examining the topographies, one may notice however slight differences; the ERP-K presenting a slightly more anterior negativity (around FCz) than the FRN (around Cz), whereas the pattern was reversed for the positivity (more anterior for the FRN). In addition, whereas the time courses of the two ERPs were quite similar, the positivity was substantially larger for the FRN than the ERP-K. In addition, a second negative peak was visible in the ERP-K that was absent in the FRN waveform. Considering the two difference waveforms Large_PD − No_PD (Fig. 4B, violet curve) and fast–correct (Fig. 4C) for the 15 participants, a significant correlation between the negativity-peak latencies was observed (r = 0.53, p = 0.04; Fig. 4D, left), whereas the positivity latencies were not correlated (r = −0.11, p = 0.69; Fig. 4D, right).

In addition, as our aim was to compare two ERPs both elicited by an external error signal (the FRN evoked by a discrete performance feedback, and the ERP-K elicited by kinematic errors varying continuously in magnitude) it was important to ensure the external nature of the error signal driving the FRN. In this purpose, we computed additional ERPs. We regrouped the perturbed trials (in which movement-duration feedback was uninformative, kept constant), according to movement duration: perturbed–fast (duration < 375–50 ms), perturbed–correct (375–50 ms ≤ duration ≤ 375 + 50 ms) and movement-trials performed too slowly (duration > 375 + 50 ms) discarded here. We locked the corresponding EEG signals to the time at which the fingertip of the participant reaches the outer ring (corresponding to the time of the movement-duration feedback in the unperturbed trials), and computed the ERP-difference perturbed–fast- perturbed–correct. The resulting difference wave did not present any significant negative deflection (t₍₁₄₎ = 0.81, p = 0.43) in contrast to the FRN (t₍₁₄₎ = −6.16, p < 0.001). (The same 30 ms time-window was used for both tests, centered on the negativity peak present in the FRN). These results permit to rule out the possibility of the FRN to be driven by an internally generated error signal.

IC-ERP data

The profiles of the IC-ERP-K were highly similar to those of the ERP-Ks (compare Figs. 4A, 5A), accounting for 96.3, 97.4, 94.2, and 97.8% of the variance of the original ERPs for the No_PD, Small_PD, Medium_PD, and Large_PD condition, respectively; suggesting that the ICs were properly selected.

The error-related negative deflection was clearly visible for the Large_PD and the Medium_PD condition (Fig. 5A), reaching its maximum at FCz, 254 ms (−2.9 μV), and 297 ms (−2.3 μV) after the movement onset, respectively. In Figure 5A, the topographies of the IC-ERP-K are presented at the center of the averaging window (see Materials and Methods). Importantly, as for the original ERP-Ks, the amplitude of the IC-ERP-K frontocentral negativity was modulated by the size of the kinematic error; a repeated-measures ANOVA revealing a significant effect of kinematic-error magnitude on the amplitude of the negativity at FCz (F_(2,28) = 3.7, p = 0.03). Post hoc comparisons showed that Large_PD trials were associated with significantly larger negativity than Small_PD trials (t₍₁₄₎ = 2.81, p = 0.013; other pairwise comparisons did not reach significance).

One may notice that the large left-lateralized negativity starting before movement onset, that characterized the original ERP-Ks, was also partly reproduced. Indeed, as the ICA decomposes the raw EEG signal into a set of temporally maximally independent components, expectedly distinct ICs were not obtained accounting respectively for the negativity related to the kinematic-error and the negativity related to movement production (movement-monitoring potential). Indeed, these two events are here intrinsically temporally correlated. Thus, as for the original ERP-K, we computed difference waves, which again resulted in recentering the scalp distributions and highlighting a negative wave, peaking at 293 ms followed by a positive deflection, maximal at 437 ms, for the Large_PD condition (compare Fig. 4B and Fig. 5B). For the Medium_PD and the Small_PD conditions, the negative deflection was also observed, maximum at 301 ms and 367 ms, respectively, whereas the positive component could not be clearly identified (Fig. 5B).

To quantify the portion of the FRN that could be accounted for by the ICs related to the processing of the kinematic errors, we time locked the reconstructed EEG signals on the movement-duration visual feedback (donut color change) and computed new IC-FRNs. The grand-average of the difference curve fast–correct, obtained by subtracting for each participant the ERP related to the correct movement-duration trials from the wave associated with the too fast trials, is depicted in Figure 5C at the FCz electrode. A negative deflection peaks at 328 ms after the presentation of the feedback; followed by a positive deflection at 457 ms. Interestingly the IC-FRN is very similar to the original FRN, accounting for 91% of the variance of the original ERP. In addition, as for the original FRN, activity estimated over a 30 ms window centered on the negativity peak differed significantly from baseline (t₍₁₄₎ = −3.048, p = 0.008).

Localization

For each participant, we performed a distributed cortical source reconstruction for the difference-waveforms Large_PD − No_PD (ERP-K) and fast–correct (FRN). No spatial constraint or assumption was applied. Figure 6 shows, for each type of ERPs, the regions that showed increased activity for at least 10 of the 15 participants; the coordinates of the centroids of the clusters are listed in Table 1. Results suggest that common sources were involved in the generation of both ERPs; almost all consistent with previous literature reports about Ne/ERN and FRN generators (Walsh and Anderson, 2012; Hauser et al., 2014). Namely, shared sources might be located in the pre-SMA (Dehaene et al., 1994; Wessel et al., 2012), as well as in the IFG (Wessel et al., 2012; Hauser et al., 2014) in the right hemisphere. Also, activity in medial precentral regions (Wessel et al., 2012, Hauser et al., 2014) and areas located at the junction of the paracentral lobule and the precuneus (Hauser et al., 2014) might contribute to the generation of both ERPs. In addition to frontal structures, our findings also suggest the involvement of occipital regions (Roger et al., 2010). Given the clearly different nature of the error signals, differences in the source patterns were also expected. In particular, different patterns of activation of visual regions could be noticed. Activations that appear to be specific to each ERP are listed in Table 1(middle and bottom).

Figure 6.

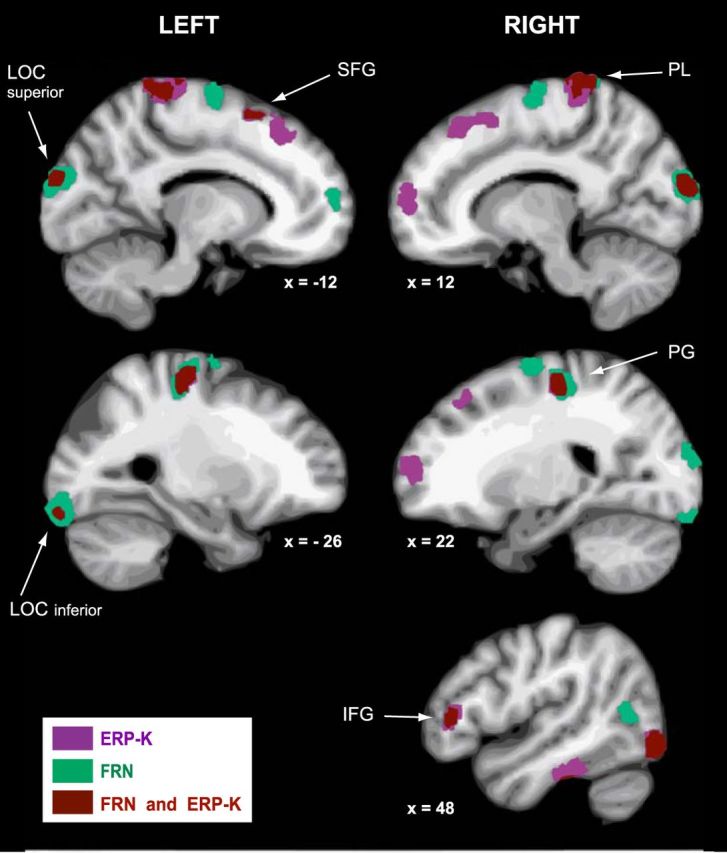
For the difference waves Large_PD − No_PD (ERP-K) and fast − correct (FRN), regions showing significant activation in at least 10 of the 15 participants (see Materials and Methods). Areas are indicated in violet for the ERP-K, in green for the FRN, and regions overlaps are indicated in brown. The coordinates of the centroids of the clusters are listed in Table 1. IFG, Inferior frontal gyrus; LOC, lateral occipital cortex; PG, precentral gyrus; PL, paracentral lobule; SFG, superior frontal gyrus.

Table 1.

Coordinates of the centroids of the clusters showing significant activation (see Materials and Methods) for at least 10 of 15 participants

Anatomical region	Hemisphere	X	Y	Z
Regions activated for the ERP-k and the FRN
Inferior frontal gyrus pars triangularis	R	45	36	6
Superior frontal gyrus (pre-SMA)	L	−15	16	59
Precentral gyrus	R	25	−22	58
Precentral gyrus	L	−31	−24	58
Paracentral lobule / precuneus	R	11	−36	73
Paracentral lobule / precuneus	L	−10	−36	73
Lateral occipital cortex inferior	R	41	−81	−10
Lateral occipital cortex inferior	L	−30	−93	−18
Lateral occipital cortex superior	R	14	−96	18
Lateral occipital cortex superior	L	−12	−96	22
Regions activated for the ERP-K only
Superior frontal gyrus (vmPFC)	R	19	61	10
Superior frontal gyrus (dmPFC)	R	16	32	50
Superior frontal gyrus (dmPFC)	L	−13	31	49
Superior frontal gyrus (pre-SMA)	R	16	18	54
Inferior frontal gyrus pars triangularis	L	−47	34	5
Inferior frontal gyrus pars opercularis	L	−55	4	6
Superior temporal gyrus	L	−59	−40	10
Inferior temporal gyrus	R	55	−29	−27
Inferior temporal gyrus	L	−52	−29	−30
Superior parietal lobule	R	28	−52	64
Regions activated for the FRN only
Superior frontal gyrus (vmPFC)	L	−16	60	10
Superior frontal gyrus (SMA)	R	16	9	69
Superior frontal gyrus (SMA)	L	−16	−7	68
Middle frontal gyrus (dlPFC)	R	36	9	54
Middle frontal gyrus (dlPFC)	L	−35	10	54
Prencentral gyrus	R	57	7	30
Superior temporal gyrus	R	60	−11	−5
Superior temporal gyrus	L	−56	−9	−5
Supramarginal gyrus	R	60	−26	35
Supramarginal gyrus	L	−58	−26	33

Top, For both the ERP difference waves. Middle, For the Large_PD − No_PD (ERP-K) wave only. Bottom, For the fast − correct (FRN) difference curve only. vmPFC, Ventro-medial prefrontal cortex; dmPFC, dorso-medial prefrontal cortex; pre-SMA, pre-supplementary motor area; SMA, supplementary motor area; dlPFC, dorso-lateral prefrontal cortex.

Discussion

We identified a frontocentral waveform (ERP-K) whose amplitude is modulated by the size of hand-path deviations induced by unpredictable mechanical perturbations. A strong similarity in timing and source-location between the ERP-K and the FRN elicited by the feedback about movement-duration points to common sources involved in the processing of sensory-prediction errors and in the processing of reward-prediction errors. Two different interpretations can be proposed. The first interpretation is that sensory-prediction errors constitute negative feedbacks for the nervous system (as defined in reinforcement learning theories). Another possibility is that sensory- and reward-prediction errors both constitute surprising events, independent of a valence dimension.

A frontocentral ERP modulated by the magnitude of kinematic errors

The spatial and temporal constraints of the reaching task ensured that participants experienced kinematic errors without having the opportunity to correct their movements (Tseng et al., 2007). This allowed us to demonstrate unambiguously that the amplitude of the ERP-K was related to the size of kinematic errors, and not to online movement-corrections (Anguera et al., 2009). Indeed, visual inspection of the hand trajectories revealed no corrective submovements, even in the late part of the reaches. Additionally, we precluded adaptation to develop over trials by using unpredictable, interspersed catch trials. Our purpose was to dissociate variation in the size of the kinematic errors from any adaptive error-reduction process, as this confound would have complicated the interpretation of the results (Vocat et al., 2011).

Our results are consistent with previous work, suggesting that the performance-monitoring system classically investigated in cognitive tasks does not function according to an all-or-nothing rule. In their seminal study, Gehring et al. (1993) already showed that the amplitude of the Ne/ERN was modulated by the speed-versus-accuracy emphasis. The influence of several other factors has since been demonstrated, among which are response-similarity (Gehring and Fencsik, 2001) and response-accuracy judgment (Scheffers and Coles, 2000). Parametric modulation has also been demonstrated for the FRN. According to the reinforcement learning theory, the amplitude of this potential changes as a function of the size of the reward-prediction errors; the difference between the values of actual and expected outcomes (Schultz, 2007). In agreement with this assumption, many studies have found that FRN amplitude is inversely related to outcome likelihood (Walsh and Anderson, 2012), but the relationship between reward magnitude and FRN amplitude has not been demonstrated yet. It has been suggested that separate brain systems represent reward probability and reward magnitude (Walsh and Anderson, 2012).

It is central to note that the response itself remained categorical in nature (e.g., success or failure) in these previous studies and the amplitude of the negative wave did not reflect the magnitude of the error (inaccuracy of the response) itself. In contrast, the amplitude of the ERP-K in the present study is directly modulated by the size of the sensory encoded kinematic-error.

Are sensory-prediction error signals processed as negative feedbacks?

The reinforcement learning theory accounts for the FRN in terms of reward-prediction error-signals that arise from the dopamine system and arrive at the anterior cingulate (Holroyd and Coles, 2002). In this framework, the similarities between the ERP-K and the FRN would indicate that discrepancies between intended and actual movements are processed as negative feedbacks by the nervous system. In our experiment, the explicit goal of the task was to execute movements with correct durations. Interestingly, a negative potential (ERP-K) akin to the FRN was evoked by the mismatches between the predicted and the observed sensory consequences produced by the mechanical perturbation, even though participants were not penalized for not moving straight ahead. It is therefore possible that the neural mechanisms involved in the processing of sensory-prediction errors and driving motor learning overlap with the mechanisms implicated in learning from reward-prediction errors.

Decision-making theories and motor-control models have long remained blind to each other. Only recently have theoretical frameworks been developed that integrate concepts issued from both fields (Trommershäuser et al., 2008; Friston et al., 2009, 2011; Rigoux and Guigon, 2012). In particular, until very recently most studies in motor learning have almost exclusively focused on adaptation driven by sensory-prediction errors and have been assumed to occur regardless of motivation factors (Shadmehr et al., 2010).

Recent work has started exploring different forms of motor learning (Huang et al., 2011; Izawa and Shadmehr, 2011). Izawa and Shadmehr (2011) showed that participants can adapt to a visuomotor perturbation based solely on a binary feedback (success or failure) without experiencing sensory-prediction errors (no visual feedback on hand trajectory). They also observed that binary error signals alone do not induce sensory remapping. From these findings, these authors concluded that distinct neural mechanisms are engaged in learning from sensory-prediction and reward-prediction errors. However, although their findings confirm that different types of error-signals induce different patterns of sensorimotor adaptation (that sensory mismatch is necessary to induce sensory remapping), they are not incompatible with the idea that a common neural network might be involved in the processing of sensory-prediction errors and reward-prediction errors. Indeed, their findings allow for the notion that discrepancies between intended and actual movement may in themselves be experienced as unpleasant events (may be related to a feeling of losing control), even if they are not directly related to the explicit goal of the task.

Do the kinematic-error related ERP and the FRN reflect a common surprising event detection system?

An alternative interpretation of the similarity between the ERP-K and the FRN is that both potentials reflect the effect of surprise evoked by all outcomes, positive or negative, violating expectations. In our task, this could be the case for the large FRN that follows negative feedbacks on movement duration, as well as for the ERP-K that could reflect the surprise evoked by the sudden introduction of a mechanical perturbation in a catch-trial.

This would fit with an increasing number of studies contradicting the assumption by Holroyd and Coles (2002) that the FRN amplitude reflects signed reward-prediction error (Oliveira et al., 2007; Alexander and Brown, 2011; Chase et al., 2011; Talmi et al., 2012). In a seminal study, Oliveira et al. (2007) showed that the FRN is elicited by unexpectedness rather than by negative feedback. Recently, Hauser et al. (2014) investigated localization of the FRN generators using concurrent EEG-fMRI recording. Their findings contradict earlier theories about the network organization of the FRN and are in line with a recent theory that dopamine neurons also encode surprise-like saliency signals (Matsumoto and Hikosaka, 2009; Bromberg-Martin et al., 2010a, 2010b), which are most probably also projected to the ACC (Bromberg-Martin et al., 2010b).

Alexander and Brown (2010, 2011) proposed a computational model that generalizes the standard reinforcement learning theory and successfully simulates the FRN deflection based on surprise-signals. These authors intend to offer a unifying framework robust enough to reconcile and account for the diversity of medial prefrontal cortex (mPFC) effects that have been observed with a broad range of methods. In their model, the mPFC, and especially dorsal regions, may be central to forming expectations about actions and detecting surprising outcomes.

In this framework, the ERP-K and the FRN that we observed could both arise from a similar network implicated in the generation of the frontocentral negativities commonly described as the Ne/ERN, correct-related negativity (Vidal et al., 2000), FRN, and N2. Recently, a parsimonious interpretation proposed that behind the specific spatio-temporal features of these ERPs, they all reflect a single frontal midline theta-rhythm sensitive to mismatch signals in the service of behavioral adaptation (Cavanagh et al., 2012).

Further research

A central issue still remains open: how do frontocentral negativities relate to learning? Concerning the FRN in particular, findings remain ambiguous. For instance, it has been shown that the size of the FRN following negative outcomes correlates with the probability that participants will not repeat the punished response in the next trial (Yasuda et al., 2004; Cohen and Ranganath, 2007; van der Helden et al., 2010). However, these results do not demonstrate a direct relation between the FRN and learning processes; the system that generates the FRN might be influenced by expectation, which shapes behavior. Also, not all studies report concomitant electrophysiological and behavioral variations; the FRN sometimes remains constant throughout learning as response accuracy increases (Holroyd and Coles, 2002; Eppinger et al., 2009; Bellebaum et al., 2010).

In the present study, the experimental design we used was intended to allow dissociating error-processing from motor-correction mechanisms. Based on our results we cannot determine whether the error-related ERP (ERP-K) reflects the coding of the importance of the action failure (the amount of the discrepancy between intended and actual movement) or if it rather corresponds to a content-free unspecific alert signal proportional to the degree of surprise. In particular, we found no significant difference between the ERP-K observed in the slightly perturbed trials (Small_PD trials) relative to the unperturbed trials. As it has been shown that sensory-motor adaptation occurs even if errors are too small to be consciously noticed (Malfait and Ostry, 2004), this raises the issue of the involvement of this ERP in motor learning processes. Further research is needed to establish whether this frontocentral negativity scales with the necessary motor-command adjustment; that is, whether it carries information used in the selection of muscle-activation patterns in forthcoming movements.

Consistent with previous research, unpredictable changes in the force-field amplitude, in addition to kinematic errors in the catch trials, induced adaptive responses observable in subsequent trials (data not shown) visible as slight hand-path deviations in the opposite direction (Thoroughman and Shadmehr, 2000). In future studies, we will need to dissociate the amplitude of the experienced kinematic-error (prediction-error) from the amplitude of the force-pattern adjustment (learning) observed in subsequent trials (Diedrichsen et al., 2005) to determine whether the ERP-K relates to motor adaptation processes or corresponds to an unspecific orienting response.