The Evolution of Statistical Methods in Speech, Language, and Hearing Sciences

Abstract

Purpose

Scientists in the speech, language, and hearing sciences rely on statistical analyses to help reveal complex relationships and patterns in the data collected from their research studies. However, data from studies in the fields of communication sciences and disorders rarely conform to the underlying assumptions of many traditional statistical methods. Fortunately, the field of statistics provides many mature statistical techniques that can be used to meet today's challenges involving complex studies of behavioral data from humans. In this review article, we highlight several techniques and general approaches with promising application to analyses in the speech and hearing sciences.

Method

The goal of this review article is to provide an overview of potentially underutilized statistical methods with promising application in the speech, language, and hearing sciences.

Results

We offer suggestions to identify when alternative statistical approaches might be advantageous when analyzing proportion data and repeated measures data. We also introduce the Bayesian paradigm and statistical learning and offer suggestions for when a scientist might consider those methods.

Conclusion

Modern statistical techniques provide more flexibility and enable scientists to ask more direct and informative research questions.

Data from the speech, language, and hearing research domains present a number of challenges for statistical analyses. Data are rarely normally distributed, sample sizes are often small, and experimental designs include repeated observations from the same subjects across conditions or over time. Furthermore, data are often missing, and the patterns of missing data may be related to key variables of interest. These characteristics are problematic for many widely used traditional statistical methods and analyses. Fortunately, the discipline of statistics has progressed to better accommodate the realities of study designs involving human subjects and problems with complete data availability. By relaxing problematic assumptions, modern statistical methods can help researchers to conduct robust and well-founded studies. Despite the availability of these newer statistical methods, they remain underutilized in the speech, language, and hearing sciences. In our companion article, we review basic statistical principles for scientists and clinicians in the speech, language, and hearing sciences. The goal of this work is to elaborate on advanced statistical methods that can be applied to common issues in these research fields.

As we note in the aforementioned companion work, there is very rarely a single optimal statistical procedure for a given analysis—each approach comes with benefits and drawbacks, and different statistical philosophies provide distinct but valid perspectives on analytical problems. As such, the goal of this work is to highlight promising methods with which applied researchers may be unfamiliar. We do not propose to provide a comprehensive description or mathematical derivation of these techniques, as this would be impractical and potentially unhelpful for a clinical and research-focused audience. Instead, we encourage researchers to consider further investigation of the most applicable methods for their own work.

We begin by examining data that are recorded and analyzed as proportions, then we address designs using repeated observations and longitudinal data. In addition to the ways in which standard, frequentist statistical practice may be improved through better procedure selection and appropriate interpretation, there are alternative perspectives on data analysis that may be useful to some practitioners. We highlight two domains for additional reading. First, we introduce Bayesian statistics: an alternative statistical philosophy that provides analogues of most common frequentist procedures, with some benefits particularly for small studies or complex longitudinal deigns. Second, we briefly discuss statistical learning, also called machine learning (among other things). Techniques in this area sacrifice many of the inferential abilities of traditional statistical models, but excel at prediction in settings with large sample sizes and substantial uncertainty about the relationship between explanatory factors and outcome variables.

Subject Data Recorded as a Proportion

Standard statistical practice can be improved by careful consideration of the data properties. We illustrate this idea through a scenario that arises regularly in this field: Study participants are often tested repeatedly on yes/no or correct/incorrect questions, and then those responses are summarized into a percent correct score for analysis. Scores on experimental tasks are reported as percent correct for common areas such as speech recognition (McCreery et al., 2015), word learning tasks (McGregor, Gordon, Eden, Arbisi-Kelm, & Oleson, 2017), and speech production accuracy in a specific condition (Dunn et al., 2014). In many cases, the goal is to perform a hypothesis test to compare the equality of proportions arising from two or more groups. A simple approach is to perform a two-sample Student's t test or regression analysis on untransformed data. When doing so, there are two primary assumptions to consider. The first is whether the proportions are normally distributed, and the second is whether there is homogeneity or equal variances across all of the proportions. Particularly when proportional speech recognition scores approach ceiling or floor levels of performance, these assumptions are both violated, and researchers frequently turn to transformations to analyze their proportion data.

Shown in Figure 1 are the two most popular transformations of proportion data: an arcsine unit (AU) square root transformation to approximate normality and equal variances and a logistic transformation, $log\left(\frac{\mathit{p}}{1-\mathit{p}}\right)$, described in more detail below. A rationalized AU (RAU) transformation ($\mathrm{RAU}=\left(\frac{146}{\mathit{\pi }}\right)\ast \mathit{AU}-23$) is also regularly used and has even more severe scaling. Before deciding which transformation to perform, the first question to ask is whether a transformation is required at all. We may be able to perform the analysis on raw proportion data, allowing for much more intuitive interpretations, and without violating statistical assumptions. We see from Figure 1 that both transformations are approximately linear (noncurved) between 0.3 < p < 0.7. Although it is not shown in this figure, the variances are relatively stable in this range as well. Therefore, some analyses of proportion data may not benefit from a transformation, because the proportions are approximately normal and the variances are approximately equal. In such cases, one can safely use a t test or regression analysis directly on the proportion data. When the proportion data fall near the boundaries of 0 or 1, however, alternative approaches become critical. Always evaluate the distribution of the residuals of the analysis to evaluate departures from normality and equality of variances. If the model residuals are irregularly distributed, it may be an indication that these statistical assumptions have been violated and that alternative analysis approaches or transformation of the proportional data may be needed.

Figure 1.

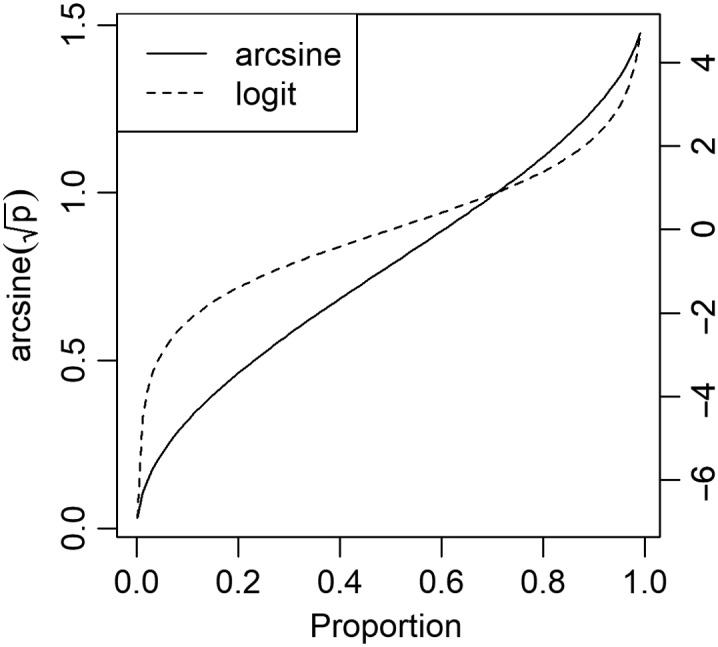
Comparison of how the arcsine transformation and logistic transformation relate to the raw proportion value.

One alternative approach is to alter the data collection mechanism to reduce the chance of scoring at floor or ceiling levels. Methodological approaches for measuring speech recognition adaptively, such as using procedures that adapt the level of the signal or masker or both (e.g. Leibold & Buss, 2016), have been developed to minimize the potential for floor and ceiling effects and problems with heterogeneity of variance that can result. This is an instance where changes in methodological approaches can help to simplify statistical analyses by reducing the likelihood of unequal variances across subjects or conditions that can occur because of floor and ceiling effects. When such methodological solutions are not possible, a common solution to attempt to normalize proportional data in the field has been to use an arcsine square root transformation to approximate normality and equal variances (Studebaker, 1985). Traditional statistical tests (t tests, regression, analysis of variance [ANOVA], etc.) are then performed on the transformed variable. Although the arcsine transform does often provide approximate normality and equal variances, the transformation also results in values that are uninterpretable in a practical sense, such as reports of speech recognition scores of –23% or 123% at the extremes. For example, see the solid line in Figure 1 that denotes the transformation performed by the arcsine procedure. Note that when a proportion is higher than 0.7, then the arcsine-transformed value is greater than 1.0. Transformations, by definition, change the data, and such changes can influence the practical interpretation of the data.

For example, consider a hypothetical study where the effects of a novel hearing aid noise reduction algorithm were compared across two signal-to-noise ratios (SNRs) for a group of adults with hearing loss. At a 5-dB SNR, the mean proportion correct without noise reduction is 80% and the mean proportion correct with noise reduction is 85%. At the 10-dB SNR, the mean proportion correct without noise reduction is 92% and the mean proportion correct with noise reduction is 97%. At both SNRs, the benefit of the SNR processing is 5% but because the variance in the higher SNR conditions is compressed, the scientists conducting this study decide to apply a transform to convert all of the scores to RAU. For the RAU, the difference in noise reduction benefit that was 5% is 7 RAU at the 5-dB SNR and 14-RAU at the 10-dB SNR. The RAU transform has addressed the problems related to inequality of variances across conditions but has distorted the reader's ability to interpret the practical or clinical significance of these findings.

Rather than an arcsine transformation, another option is to take a logit transformation on the proportions, $\mathit{v}=log\left(\frac{\mathit{p}}{1-\mathit{p}}\right)$, and analyze v. In this case, we are not analyzing the individual question level 0, 1 data such as would be done in logistic regression, but rather, we are taking a transformation on the proportion for each subject and analyzing the transformed data in the same way that one would use the arcsine transformation. The expression $\frac{\mathit{p}}{1-\mathit{p}}$ is known as the odds, making v the log-odds. Analyzing data on the log-odds scale assumes the data are linear in the log-odds (not in the proportion). A one-unit increase in the x variable relates to β unit change in the log-odds, where β is the regression coefficient associated with x. Testing and inference on v now relates to an odds ratio, which has a widely known and understood meaning. This is often interpreted on the odds ratio scale by exponentiating β. Warton and Hui (2011) showed that performing regression on logit-transformed data or using logistic regression, and random effects models involving the logit link function had higher power than arcsine-transformed linear models. Similar to the arcsine transformation, the primary goal of the logit transformation in this context is to approximate normality and stabilize the variance. The logit transformation maps proportions, which are between 0 and 1, to the whole real number line. The transformation also guarantees a reverse mapping back to the proportion scale, which guarantees that our predicted proportion will be between 0 and 1 no matter what. In Figure 1, the dashed line shows how the transformation compares to the arcsine transformation. We see more curvature near the boundaries of 0 and 1. Thus, the logit transform resolves the problems related to variance and mitigates the problems associated with interpretation of effects that can occur with arcsine or other transformation methods. Although interpretations of the odds ratio can be confusing to some when compared to interpreting differences of means and proportions, it offers far more practical value than the arcsine transformation.

Data transformations are an important and necessary component to meeting statistical assumptions for data analysis. When analyzing data on a transformed scale, be aware that the assumptions are met on that transformed scale. Therefore, interpretations must also be made on the transformed scale (reverse transforming the bounds of a confidence interval does not, in general, produce a confidence interval on the original scale). Data transformations should be reported in the statistical methods of manuscripts or research reports to promote transparency in the statistical methods and also allow consumers to assess the impact of any data transformations on the interpretation of the findings.

Repeated-Measures ANOVA

Perhaps, the most commonly used experimental design in speech, language, and hearing sciences involves testing the same subject under multiple conditions or across multiple time points. Historically, these repeated observations would be analyzed using repeated-measures analysis of variance (RM ANOVA) or multivariate analysis of variance (MANOVA) to test for differences between groups, across conditions, or growth over different points in time. Generally speaking, both RM ANOVA and MANOVA are used to create a statistical model where the means resulting from multiple conditions can be tested for equality while adjusting for correlation resulting from the same subject being measured under each of the conditions. From the user perspective, the biggest drawback of these methods is likely in how they treat missing values. The ANOVA-based methods assume the data are missing completely at random (MCAR; Little & Rubin, 2002). MCAR implies that any missing values are MCAR and not by any mechanism that is either observed or unobserved, or related to variables of interest in the study. For example, consider a study measuring speech understanding in quiet, in speech-spectrum noise, and in a noise composed of two talkers (e.g., Corbin, Bonino, Buss, & Leibold, 2016). Participants are to be measured in all three conditions, and we want to compare the mean speech perception scores in all three conditions against each other. Suppose participants cannot complete the two-talker condition because it is more difficult than the other masking conditions, and we base our analyses only on those that did well and could complete the two-talker masker condition. Because we do not observe the part of the population that would perform poorly, our estimate in that condition will be biased downward.

In the example above, subjects that are only able to complete one or two of the three conditions will be removed by statistical software for an RM ANOVA, often without an error message or prominent warning. Therefore, the results of the study analyzed with RM ANOVA will have a reduced sample size, degrees of freedom, and power to detect a statistically significant difference. Even if that MCAR assumption is met, then the study performing RM ANOVA will be unbiased but underpowered. On the other hand, if the MCAR assumption is not met, and there is some systematic mechanism related to missingness, then the results of the RM ANOVA will be biased because the subset of individuals on which the analysis is based can no longer be considered a random sample of the population. Suppose our study participants are missing a condition completely at random. Then, if they finish the speech understanding in quiet and in noise conditions, and perform above average on those two conditions, we could reasonably infer that the individual would also perform above average on the two-talker masker condition assuming that the results in conditions are positively correlated with one another. On the other hand, if only the best performing individuals finished all three conditions and the individuals who would have performed poorly in the two-talker masker dropped out, then we would not have accurate data on the population in that condition, and we would naively analyze only the individuals who do well, leading us to biased results. This scenario where the value of the missing observation depends on scores that we have observed but does not depend on any other unobserved factor is known as missing at random (MAR). In longitudinal studies, this means that an individual who dropped out of the study would remain along the same trajectory as that which was observed.

When a study has missing data, then the reason for missingness should be examined and presented in manuscripts or research reports. A justification should be reported to support the assumption being made. We can sometimes distinguish between MCAR and MAR by fitting a model to predict the observed probability of nonresponses from known covariates. If the coefficients in the logistic regression predicting missingness are significantly different from zero, then the missing data are likely not MCAR.

The practical drawbacks to RM ANOVA do not end in the treatment of missingness. For details, we refer readers to Long (2011) but enumerate several salient points here. First, in both RM ANOVA and MANOVA, the computer software generally fits orthogonal polynomials to the data. Thus, instead of using time variables (t, t ², t ³, etc.), which are highly correlated with each other, to represent curvilinear trends in the data, the software creates uncorrelated polynomials instead. See Hedeker and Gibbons (2006) for an example of how uncorrelated polynomials are constructed. Although the statistical fit to the data might be good, and orthogonal polynomials provide other statistical and computational benefits, the resulting parameter estimates are largely uninterpretable in a practical sense. Second, RM ANOVA is the most basic model, in terms of correlation structure, that we could fit. The primary driver of the RM ANOVA model is a subject-specific random effect. This random effect is meant to separate out the variance from within the subject, ${\mathrm{\sigma }}_e^2$, versus variation between subjects, ${\mathrm{\sigma }}_b^2$. Therefore, it accounts for the correlation that occurs when data are collected from the same person across conditions or over time. Intuitively, a subject is assumed to deviate from (either above or below) the population mean level of the effect by the same amount at every condition or time point. This constant effect may be unrealistic for many studies. For example, our speech perception participants often exhibit more variance between subjects in the noise and two-talker masker conditions than in the quiet condition (e.g. Corbin et al., 2016).

Another implication of constant rate of change is that the correlation between any repeated measures will all be the same, measured by the intraclass correlation $\rho =\frac{{\mathrm{\sigma }}_b^2}{{\mathrm{\sigma }}_b^2+{\mathrm{\sigma }}_e^2}$. This assumption is more broadly known as sphericity. Violation of the sphericity assumption results in the F test being too liberal. The sphericity assumption is most often assessed via Mauchly's Test of Sphericity (1940). Mauchly's test is criticized for failing to detect departures from sphericity in small samples and overdetecting them in large samples. Due to these criticisms, many argue that an adjustment should always be used (Howell, 2012). Because the F test in the RM ANOVA is too liberal when sphericity is determined to not be met, the correction is to reduce the degrees of freedom in the test, making the F statistics approximately follow an F distribution, and subsequently increasing the p value. The two most popular adjustments are the Geisser and Greenhouse (1958) adjustment and the Huynh and Feldt (1970) adjustment. They estimate the deviation from sphericity through a measure called ϵ and adjust the F distribution degrees of freedom based on the size of ϵ. With all of these concerns, the reduction in degrees of freedom and reduction in the F statistic in the resulting RM ANOVA will likely be underpowered.

Third, MANOVA, which is the application of ANOVA that allows for multivariate dependent variables, takes the correlation between conditions to the other extreme. MANOVA fits a unique correlation to every pairwise combination of conditions. For studies involving more than just a few conditions, MANOVA needs to estimate a large number of parameters, further reducing the degrees of freedom and the power of the test.

Fourth, RM ANOVA and MANOVA do not readily account for additional predictor variables. Research questions may involve adjusting for categorical covariates, continuous covariates, or time-varying covariates. Often, these covariates to adjust for may be age, degree of hearing loss, or socioeconomic status, and ANOVA methods force us to categorize these variables rather than treating them as continuous. This is the same argument for using regression-based techniques rather than analysis of covariance that was discussed in the companion paper (Oleson, Brown, & McCreery, 2019).

The linear mixed model (LMM) is an alternative that can overcome the deficiencies listed for both RM ANOVA and MANOVA. LMMs are called by other names including linear mixed effects regression, variance component models, multilevel models, hierarchical linear models, mixed models, or two-stage models. There is a great deal of literature on mixed models. See Hedeker and Gibbons (2006); Fitzmaurice, Laird, and Ware (2011); or Long (2012) for excellent overviews of longitudinal data analysis methods with mixed models. Although different disciplines refer to these models using different names, the same fundamental mechanics form the basis of these statistical approaches. These models better accommodate missing data, because they make a less restrictive assumption that the data are MAR rather than MCAR. In addition, these models allow individual growth curves, and distinct correlations among pairs of conditions, or different patterns of correlation (e.g., decay over time). Finally, LMMs readily allow for predictor variables of various numbers and types.

RM ANOVA has a long history in the fields of speech, language, and hearing sciences as an appropriate analytical technique. When there are only a few test conditions with no missing data and approximately equal correlations between the test conditions, then an RM ANOVA analysis is satisfactory. Our three-condition speech understanding example is an example of a situation where RM ANOVA is a valid analytical tool to use if all data are completely observed. Even so, the LMM will yield the same analysis but with greater versatility.

Saletta, Goffman, Ward, and Oleson (2018) used LMMs in a study where the data are set up in a standard repeated condition format to examine motor control in children with specific language impairment. Study participants were each measured under five different conditions, and the stated hypotheses were to compare the group means for the five conditions. The dependent variables were speech stability and duration, and they wished to relate each to the independent variables group (specific language impairment, typically developing) and task (five conditions). Each study participant was asked to respond to each of five separate conditions. Complicating this analysis was the fact that the variance for each task was different. They used a random-intercept LMM to account for within-subject correlation and allowed the variances under each task to differ. Relaxing assumptions about equality of variances across conditions can be very useful in studies with human subjects where these assumptions are rarely met.

Gantz, Dunn, Oleson, and Hansen (2018) demonstrated another example of the utility of mixed models. In this study, and many longitudinal studies in the field, participants with cochlear implants returned for follow-up appointments at varying time intervals over the course of the study. However, each participant may return a different number of times, and the measurement times differed from subject to subject. A continuous time model like this with continuous covariates cannot be analyzed by the RM ANOVA or MANOVA methods because these approaches are based on the rigid assumption that time points are fixed and identical for each subject. Such an analysis is relatively straightforward to perform as an LMM using modern statistical software, such as R or SAS. In this particular example, and in many studies of longitudinal growth, the longitudinal trend was nonlinear, exhibiting a sharp increase in speech understanding immediately postimplant of the cochlear implant, with the growth expected to ultimately reach some plateau. The authors used a piecewise regression model with a random intercept, random slope, and fixed effects for age at implant and duration of hearing loss. This approach allowed for variability in how time points were represented in the model and allowed the analysis to account for individual differences in the slope of longitudinal growth across participants, which is a trend that is often observed among people who receive cochlear implants.

Bayesian Statistics

Bayesian methods are not currently prevalent in the fields of speech, language, and hearing research, but they can provide a valuable alternative analysis tool to answer many research questions. There are many excellent textbooks describing Bayesian methods for interested investigators. These include, but are certainly not limited to, Gelman et al. (2013), Congdon (2006), Cowles (2013), and Kruschke (2014). In general, for any frequentist statistical analysis, a Bayesian alternative exists. Bayesian methods and their frequentist counterparts will very often lead to the same decisions/conclusions. In situations where the methods will lead to the same conclusions, the choice between the two paradigms is generally philosophical in nature. Most of the practical differences stem from the fact that Bayesian statistics uses a different interpretation of probability. Many practitioners find it more natural to think about the Bayesian paradigm's “probability” of something being true, rather than to consider the more traditional statistical inference defined as what one would expect to see given a specified null hypothesis under repeated sampling.

One area where Bayesian methods are becoming more popular is in statistical modeling of complex scientific phenomena. Indeed, the Bayesian paradigm is particularly effective in hierarchical designs when one can divide complex processes into smaller, well-defined components using conditional probability. In situations like this, it may be difficult to find and fit a corresponding frequentist model that can answer the same research questions that a Bayesian hierarchical model (BHM) can answer. In the remainder of this section, we introduce the fundamentals of how Bayesian statistics work and explore reasons why the Bayesian approach to probability can provide more intuitively interpretable results. We conclude by presenting an application that utilizes the hierarchical structure of Bayesian modeling.

Bayesian inference is based on what is known as the posterior distribution, p(θ | Y), where Y is the outcome variable and θ represents the parameters of interest (population means, differences, regression effects, etc.) The posterior distribution contains the information needed for statistical inference and summarizes our knowledge of the parameters of interest based on (a) what we assumed at the beginning of the study and (b) what we have learned about θ after observing all of the data, Y. What we assume at the beginning of the study is known as the prior distribution p(θ), and what we learn from the data is known as the likelihood, p(Y | θ). The prior summarizes our knowledge about θ before collecting data and can be either vague/uninformative or highly informative, depending on how much is known a priori. This distribution can be based on previous studies and should reflect scientific plausibility.

The likelihood, p(θ | Y), is the foundation of most frequentist techniques and gives the Bayesian model for the data. This probability distribution describes what kind of data, Y, we would expect to see for a given set of parameters, θ. For example, if we wanted to perform a Bayesian two-sample test, we would say that Y follows a normal distribution with unknown means for observations coming from each of two groups and an unknown common variance. A Bayesian regression analysis would assume that Y follows a normal distribution with unknown variance and that the mean is defined by a linear combination of covariates. For comparison, the p values in frequentist statistics are generated under the assumption that the values in θ are specified by the null hypothesis.

These three components (prior, likelihood, posterior) are the foundation for Bayesian inference. First, an investigator specifies the data model (form of the likelihood), as well as what is known about the parameters at the beginning of the study (prior). Next, data are observed and assumed to have come from the specified likelihood or data model. Finally, Bayes' rule is used to combine the prior and likelihood to obtain the posterior distribution: the summary of what the final state of knowledge is for those parameters after updating our prior knowledge with the observed data information. When this posterior distribution is obtained, the investigator may interpret the results; these are often presented as point estimates (posterior means) and credible intervals (intervals which contain the true value with some percent posterior probability). A key benefit of credible intervals is that we can interpret them in terms of the probability that many practitioners incorrectly ascribe to frequentist confidence intervals. For example, a 95% frequentist confidence interval for the difference in two group means might be (–1.25, –0.55). The frequentist interpretation is strictly in terms of the procedure: “confidence intervals constructed in this way can be expected to contain the true mean difference in 95% of studies.” We can make no statement about how likely the true difference is to lie between –1.25 and –0.55, because frequentist probability cannot define what it means for this event to be “likely” or “unlikely”—just because we do not know whether the confidence interval contains the true value does not make that event random, from a frequentist perspective. Bayesian procedures, on the other hand, use probabilities to describe uncertainty. It is therefore sensible, if we obtained the same values from a Bayesian credible interval, to interpret them as: “given the prior and model, we believe that the true mean difference lies between –1.25 and –0.55 with 95% probability.” The details of implementing these procedures are generally handled by software, but an understanding of the general pattern is nevertheless important for any application of Bayesian statistics.

One of the biggest hurdles for new practitioners of Bayesian statistics is learning how to quantify knowledge using probability distributions. For example, we might not know beforehand if the impact of socioeconomic status is going to have a positive or negative impact on our speech understanding measure. We might nevertheless be fairly certain it should not be very large in magnitude—say between –10 and 10. A distribution that satisfies these assumptions is a normal distribution with a mean of 0 and an SD of approximately 3. An even less informative distribution would be a normal distribution with a mean of 0 and an SD of 10. This kind of prior specification/elicitation requires careful reasoning and consultation with subject matter experts.

Although Bayesian statistics has been around longer than frequentist statistics, it did not gain widespread use until the last few decades, when advances in computing power and development of modern sampling algorithms vastly increased the range of problems to which the paradigm can be easily applied. Estimating a posterior distribution is a difficult computational problem in all but the simplest of cases. Modern Bayesian computing takes many forms, but the standard for applied research has long been to use algorithms to generate many samples from the posterior and use summary statistics of those samples to estimate parameters of interest. Bayesian methods are now readily implemented using SAS PROC MCMC, OpenBUGS, JAGS, Stan, and multiple packages in R, just to name a few.

Although switching to Bayesian methods can be an adjustment, they are becoming ever more popular and more widely accepted and are based on a sound philosophical foundation. The Bayesian approach lends itself to a common sense interpretation of probability, and the use of priors presents a formal means to incorporate scientific knowledge and expertise into statistical models. Mixed models and hierarchical linear models are particularly well adapted to the Bayesian paradigm, falling under the general umbrella of BHM.

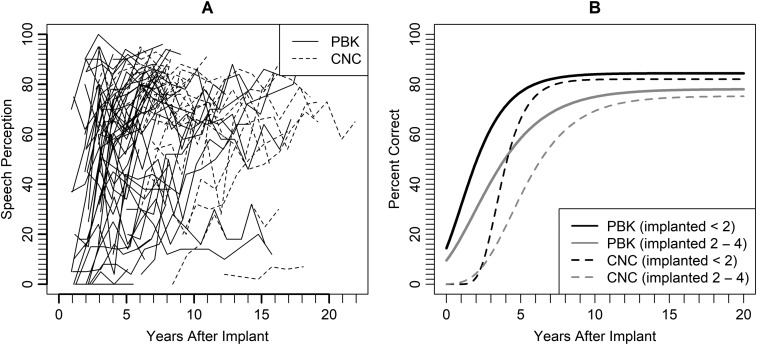
Consider the previous example of speech perception scores that are measured over time. These scores follow nonlinear trajectories, increasing over time and eventually reaching an asymptote. Rather than take various transformations of the dependent variable or the time variable to try and create a linear relationship, we can instead use a nonlinear function to directly measure the growth pattern. However, nonlinear models are likely to require multiple random effects to adequately model individual growth trajectories, and standard software will have a hard time fitting models with more than two random effects. Bayesian models, on the other hand, make it easier to fit such models. Oleson, Cavanaugh, Tomblin, Walker, and Dunn (2016) used a Gompertz growth function to evaluate how children who were born deaf but were implanted before the age of 2 years compared to children who were implanted between the ages of 2 and 4 years. The outcome variable was language as measured by the Phonetically Balanced Kindergarten score, which was used for children from approximately ages 1 to 5 years, and the Consonant–Nucleus–Consonant score, which was used for children from approximately ages 5 to 17 years. The nonlinear trajectory described above can be seen in the individual trends shown in Figure 2A. In order to fit a plausible nonlinear model to these data, the use of a random effect is typically required for each parameter in the nonlinear function. In this case, the random effects are also related between two different language measures. A corresponding frequentist model would require two outcome measures to accommodate separate but correlated trends that would share the same three random effects for the nonlinear growth function. In addition, we would need to be able to obtain approximate maximum likelihood estimates and to have a significance test for a group effect. Such a model is unlikely to be fit in standard software without many simplifying assumptions being made. On the other hand, we can devise a Bayesian hierarchical linear model to fit this situation by breaking the model down into simpler conditional pieces.

Figure 2.

Figure 2A shows the individual trends for participants who took the Phonetically Balanced Kindergarten (PBK) and Consonant–Nucleus–Consonant (CNC) tests repeatedly over time. Each line represents a single participant. Figure 2B demonstrates the Bayesian hierarchical model fitted lines for PBK and CNC with the black line denoting children implanted with a cochlear implant before the age of 2 years and the grey line denoting children implanted between the ages of 2 and 4 years.

Begin by defining the data model, which assumes that language score follows a normal distribution with some mean and some unknown variance. The process model follows and defines what form the mean of the normal distribution follows. The authors assume the mean follows a Gompertz growth curve, which specifies an intercept, a growth rate, and a maximum threshold. There was a random subject effect for each of those parameters that allowed for subject-specific growth patterns. The final step in a BHM is to specify appropriate prior distributions for each of the remaining parameters. The parameters in this model, after breaking the system down into smaller and more understandable conditional processes, are typically estimated through sampling algorithms, most commonly Markov Chain Monte Carlo. The results of the fitted model in this example, showing the estimated group level curves, can be seen in Figure 2B. Individual-specific growth curves can be viewed in Oleson et al. (2016). In addition to such visualizations, these models allow us to compare both the achieved asymptote and the growth rates between the two groups. The authors found significant effects in both maximum speech perception and the growth rate.

Although Bayesian statistical modeling has not been widely used in speech, language, and hearing sciences, there are numerous advantages of this modeling approach that can be useful for scientists in these fields compared to traditional frequentist statistical methods. For additional information about Bayesian statistical approaches, including examples of Bayesian applications, see the article by McMillan and Cannon (2019) in this research forum.

Statistical Learning

Another approach to data analysis that has become much more widely used in the last few years carries many names, and researchers from different backgrounds prefer different methods within it. Commonly invoked names include machine learning, statistical learning, deep learning, pattern recognition, data mining, informatics, data science, predictive modeling, artificial intelligence, and so forth. To be sure, each of these terms tends to include a different array of techniques on average, but the degree of common ground is substantial. Given our background as statisticians, it is perhaps unsurprising that we favor the high-level classification of Leo Breiman, who referred to many of these techniques as “algorithmic models,” in contrast to the “data models” of traditional statistics (Breiman, 2001). His division split statistical models into the former group, in which the data-generating mechanism is assumed to be complex and unknown—something to be estimated—and the latter, in which we make specific assumptions about the data-generating mechanism (likelihood) and then proceed to estimate parameters.

In statistical learning, and more specifically for “supervised” learning techniques, the focus is on the use of algorithms to determine good rules for predicting some outcome measure from a set of explanatory variables. The outcome may be categorical or continuous, depending on the technique, and the explanatory variables may take any number of forms. Although all the usual covariates are equally of interest in this paradigm (e.g., exposure variables, treatment indicators, demographic factors), some algorithms excel at using highly nontraditional data sources, such as images, video, or audio.

These techniques can be quite powerful, and products based on them have become ubiquitous in modern life. Accordingly, they have generated much interest among researchers. Nevertheless, to successfully apply statistical learning techniques, there are several prerequisites and costs as well as benefits. The principle drawback of these techniques is the lack of formal inference—quantifying evidence. Unlike the previously discussed techniques, one will generally be unable to produce p values or Bayesian- credible intervals when applying statistical learning models. A second and related drawback is the general lack of interpretability. Often called black box models, the predictive rules learned by these techniques may be the combination of the results of many decision trees, hundreds of nested linear combinations of input covariates, or many other ensembles of basic components—these techniques are good at prediction, not providing interpretable rules for clinicians or evaluating evidence for researchers. We therefore propose three criteria that should be met before these techniques are seriously considered for an analysis in the speech, language, and hearing sciences:

1. The goal of a study is to make predictions, or to make a tool to generate predictions.

2. The number of observations is large.

3. An appropriate algorithm can be found to match your data.

The first point is clear: Choose techniques that match your study goals. The second serves to highlight the point that the more observations you have available, the more likely a given algorithm will be to learn nuanced and robust prediction rules. The final point may be relatively straightforward, or very difficult, depending on your level of expertise and the problem at hand.

For analyses with one observation per subject, many “off-the-shelf” tools with robust and flexible software support will perform quite well: random forests, gradient boosted machines, and support vector machines, among others. For longitudinal analyses, more care is needed. For nontraditional data sources such as images, audio, or video, one may need to construct a custom neural network, or apply one of many available published neural network architectures. Further description of any of these options is beyond the scope of this work, but for the subset of practitioners with interest and sufficient data, hopefully this provides a starting point for further research.

We use data from Tomblin et al. (2015) to showcase the utility of a statistical learning model. In this longitudinal study, language outcomes of children with mild to severe hearing loss during preschool years were recorded. In our example analysis, we consider the problem of predicting whether or not a child will have a language score above the normed average (100) in the third year based on all available data recorded up to that time. The binary outcome was taken to be 1 for the above 100 group, and 0 otherwise, and we apply gradient boosted trees as implemented in the Xgboost software package (Chen et al., 2018). The variables used in the prediction are age at testing, age the hearing aid was fit, family income, mother's education level, father's education level, better ear pure-tone average, speech intelligibility index, residual speech intelligibility index (Tomblin, Oleson, Ambrose, Walker, & Moeller, 2014), hours per week of hearing aid use, and previous year's language scores.

Unlike traditional statistical analyses, we do not obtain coefficient estimates or p values. Instead, a probability is estimated for each observation under cross validation, allowing us to infer how well the model is expected to perform for predicting new observations. In this case, the accuracy was estimated to be 0.8512, with a sensitivity of 0.8506 and a specificity of 0.8519. In addition to predicting the outcome, we do obtain relative measures of variable importance. The top five variables driving the prediction were Year 2 language score, Year 2 pure-tone average score, biological father's education, biological mother's education, and the age at which the hearing aid was fitted. Such a summary does not describe the type of relationship between these predictors and the outcome; it simply indicates that one exists.

The sample size in this example analysis is on the small side for a machine learning problem (n = 168), but the algorithm works nonetheless. When compared to a traditional logistic regression model, additional advantages present themselves. The logistic model has decent performance with accuracy measured under cross-validation of 0.816, sensitivity of 0.8313, and specificity 0.8000. Nevertheless, five observations were automatically excluded due to missing Year 2 language scores, and many other less informative covariates had to be dropped from the model for the same reason. If prediction is truly the focus of a study, then the ability to apply robust machine learning models that handle missing data automatically is very convenient.

Discussion

In this work, we aimed to highlight important areas where research studies in the speech, language, and hearing sciences would benefit from greater use of more modern, general, or philosophically distinct statistical methods. There is no one-size-fits-all approach to data analysis, so it is important for researchers to be aware of ways in which even standard practice may be suboptimal and to be aware of promising alternative approaches.

Box (1979) argued that “all statistical models are wrong, but some are useful.” As we have alluded to throughout the review article, many statistical methods should ultimately lead the researcher to the same conclusion, as long as the signal that we are detecting is sound. We do not expect that all of the assumptions behind a chosen statistical method are perfectly met, but we do expect that the model and its assumptions are a close enough match to reality to be useful. Another statistical principle to follow is credited to Albert Einstein, “Everything should be made as simple as possible, but not simpler.” Good statistical practice indicates that we should choose the simplest statistical method to address the research question of interest. If the model is too simple, then we may miss an important signal, but if the model is too complex, then we may detect a signal that is not real. There are many opportunities to apply these principles in the speech, language, and hearing sciences, and it is our hope that this review article will help orient investigators to the problem of selecting appropriate and robust statistical models.

Funding Statement

This research was supported by National Institute of Deafness and Other Communication Disorders Grant R01 DC013591, awarded to Ryan McCreery.