Abstract
Afterload plays important roles during heart development and disease progression, however, studying these effects in a laboratory setting is challenging. Current techniques lack the ability to precisely and reversibly alter afterload over time. Here, we describe a magnetics-based approach for achieving this control and present results from experiments in which this device was employed to sequentially increase afterload applied to rat engineered heart tissues (rEHTs) over a 7-day period. The contractile properties of rEHTs grown on control posts marginally increased over the observation period. The average post deflection, fractional shortening, and twitch velocities measured for afterload-affected tissues initially followed this same trend, but fell below control tissue values at high magnitudes of afterload. However, the average force, force production rate, and force relaxation rate for these rEHTs were consistently up to 3-fold higher than in control tissues. Transcript levels of hypertrophic or fibrotic markers and cell size remained unaffected by afterload, suggesting that the increased force output was not accompanied by pathological remodeling. Accordingly, the increased force output was fully reversed to control levels during a stepwise decrease in afterload over 4 hours. Afterload application did not affect systolic or diastolic tissue lengths, indicating that the afterload system was likely not a source of changes in preload strain. In summary, the afterload system developed herein is capable of fine-tuning EHT afterload while simultaneously allowing optical force measurements. Using this system, we found that small daily alterations in afterload can enhance the contractile properties of rEHTs, while larger increases can have temporary undesirable effects. Overall, these findings demonstrate the significant role that afterload plays in cardiac force regulation. Future studies with this system may allow for novel insights into the mechanisms that underlie afterload-induced adaptations in cardiac force development.
Keywords: engineered heart tissues (EHTs), magnetics, afterload, maturation
1. Introduction
Cardiomyocytes within the human heart develop and mature in response to environmental cues. This maturation is largely driven by mechanical forces created by the cyclical loading and contraction of the heart. These forces can roughly be broken up into two different categories: forces experienced during heart filling (preload), and forces felt during heart ejection (afterload). In an in vitro setting, cardiac afterload can be thought of as the resistance of the culture environment to tissue contraction, while preload can be thought of as the loading applied to the tissue prior to the onset of contraction.
At early stages of cardiomyocyte development, increases in environmental stiffness can have a pro-maturation effect on the spread area, aspect ratio, sarcomere length, contractile force, contractile power, and work produced by immature cardiomyocytes.1,2 Similar effects on cytoskeletal alignment, sarcomeric content, passive tension, contraction frequency, and force production have been observed in human stem cell derived cardiomyocytes exposed to mechanical strain.3–11 Conversely, it has been shown that a lack of proper environmental forces during cardiac development can result in congenital defects12,13 or pathological remodeling.14 These results indicate that preload and afterload can significantly alter postnatal cardiomyocyte maturation and performance.
After cardiomyocytes reach their fully-matured state, additional physiological growth can occur in response to higher demands in blood flow caused by pregnancy or physical exercise. This beneficial response has been demonstrated in vitro with short-term applications of moderate increases in environmental load.14,15 However, sustained conditions such as increases in systemic vascular resistance, arterial hypertension, or loss of working myocardium due to myocardial infarction can result in pathological cardiomyocyte hypertrophy and a decline in cardiac function. This adaption has been shown in animal models exposed to prolonged or high levels of environmental loading.14,16,17
These studies exemplify the critical importance of the load magnitude and its exposure time when it comes to the regulation of cardiomyocyte function. That is, intermittent exposure to the physiological loads drives cardiomyocyte maturation and allows for necessary adaptations in their activity, while prolonged exposure to the pathophysiological loads can result in heart failure. Therefore, a platform that can accurately modulate the dose and duration of environmental load over prolonged periods would be beneficial for studying the development of immature cardiac tissues and for elucidating the mechanisms that lead to pathological remodeling of the adult heart.
Here, a technique for fine-tuning afterload in engineered heart tissues (EHTs) is presented. The motivation for focusing on afterload enhancement comes from data supporting the notion that afterload has a more significant effect on cellular hypertrophy than preload does.15,18 However, because preload and afterload are intimately linked, increases in preload are not completely avoidable. In this study, EHTs containing neonatal rat cardiomyocytes were exposed to increasing amounts of afterload over seven days. During this period, the contractile responses of the tissues were monitored to determine whether the loading regime resulted in the enhancement or decline of these properties.
2. Materials and methods
2.1. Afterload device fabrication
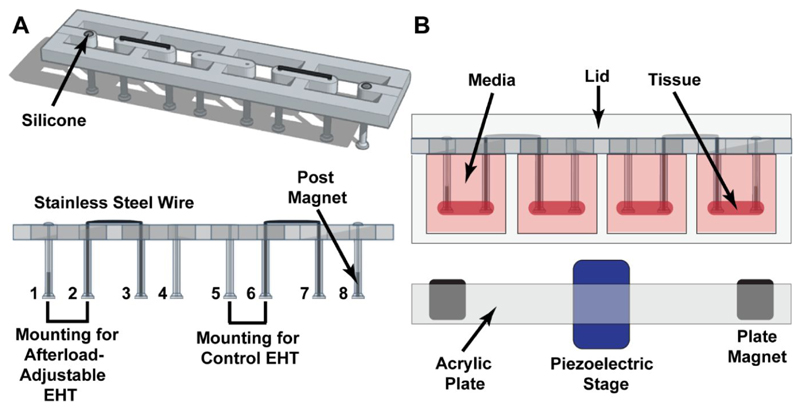
To enable afterload adjustment, magnetically responsive silicone posts were assembled by inserting cylindrical (0.5 mm in diameter, 2.0 mm in height) N40 Neodymium permanent magnets (HKCM Engineering, Eckernförde, Germany) into racks of hollow silicone posts. These magnets were positioned at the tips of the posts at the edges of the silicone rack (posts 1 and 8; Figure 1A). In this configuration, each rack contained two sets of afterload adjustable posts and two sets of control posts. The silicone posts used for these studies had a material stiffness of 0.6 mN/mm. Metal braces were manually cut and bent from straight 0.016 inches (~ 0.4 mm) diameter stainless steel archwire (Ormco, Orange, CA, USA) and were used to fix one post within each set. This fixation was done to ensure that alterations in afterload were directly translated to the rEHTs. Lastly, the open surfaces of the posts containing the magnets were sealed with Sylgard® 184 silicone elastomer (Dow Corning, Midland, Michigan, USA) to prevent magnet oxidation.
Figure 1. Tissue racks.
(A) Angled and side views of an EHT rack, showing the locations of the magnets, metal braces, and silicone seals. A single rack contains mountings for two afterload-affected EHTs (posts 1-2 and 7-8), and two mountings for control EHTs (posts 3-4 and 5-6). (B) Sectional view of EHT rack in testing environment.
Prior to experimentation, the posts were sterilized by placing them in 70% ethanol for 20 minutes and then washing them two times in sterile water (Braun, Kronburg, Germany) for 20 minutes under a tissue culture hood. The posts were air dried within the hood before tissue casting to maintain sterility and to ensure secure tissue attachment. Autoclaving the posts containing the magnets would irreversibly reduce their magnetic strength, as the autoclave reaches a maximum temperature (121 ºC) well above their operating temperature (80 ºC).
The magnet plate contained two rows of six cylindrical (13 mm in diameter, 14 mm in height) N52 Neodymium permanent magnets (HKCM Engineering, Eckernförde, Germany) with a residual induction of 1430-1480 mT. This plate was fabricated out of acrylic plastic (Abelco GmbH, Büchen, Germany) and designed such that, when placed directly below the tissue culture plate, the magnets were axially aligned with the smaller magnets within the posts (Figure 1B). Due to the strength of the magnets, they were press-fit into the holes to keep them in place. Otherwise, the attractive force between the magnets would cause them to dislodge from the acrylic housing plate and attach to one another.
The acrylic plate was perpendicularly mounted to a linear-travel PPS 20 precision piezoelectric stage (Micronix USA, Santa Ana, CA, USA) which has a travel range of 51 mm. Importantly, this piezoelectric stage is primarily made of aluminum and ceramic, so it does not interfere with the field produced by the magnets. The stage was fitted with an analog encoder with 10 nm resolution (Micronix USA, Santa Ana, CA, USA) and was always operated in the closed loop mode, which ensures that the stage moves to its prescribed location with a high degree of precision and self-corrected for any discrepancies in its positioning.
2.2. Magnet stability
To determine whether the plate and post magnets were susceptible to temperature- or humidity-induced losses in their magnetic strength, the baseline weight and strength of these magnets were measured in ambient conditions, and then again after being in the incubator for three weeks. During this period, the post magnets were removed and placed back in the incubator every few days, to simulate the temperature cycles that the posts would go through during routine culture. Magnet weight was assessed with a precision laboratory scale. Field strength measurements were taken every week using an SS495A Hall sensor (Honeywell, Morris Plains, NJ, USA). This sensor has an operating range of ± 670 mT, making it well-suited to measure the magnetic strength of the plate and post magnets (543 mT and 448 mT at the surface, respectively, according to the manufacturer). Additionally, the sensor is ratiometric, so the change in output voltage is proportional to the magnetic field strength, according to Faraday’s Law of Induction. For these measurements, a DC power source was used to supply the Hall sensor with 6 V, while a voltmeter was used to quantify changes in voltage when the Hall sensor was placed in direct contact with the magnets. At the end of the testing period, the magnets were also physically examined for the presence of crumbling, cracking, or rusting using an Axiovert 25 microscope (Zeiss, Oberkochen, Germany).
2.3. Quantification of magnetic post stiffness
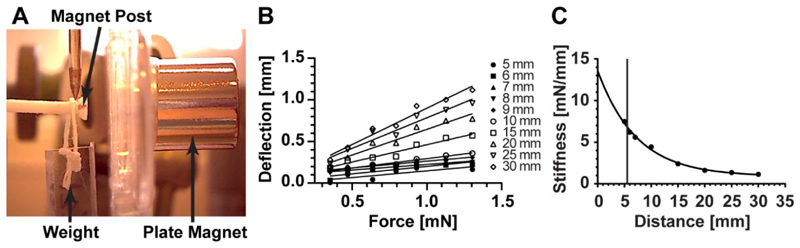
The relationship between magnet spacing and post stiffness was determined optically. A video camera was used to track the bending movement of a magnetic post under the influence of various weights, while a linear stage was used to translate the magnet plate towards and away from this post. To prevent these weights from interfering with the magnetic interaction between the plate and post magnets, they were made of acrylic plastic and were hung from the posts using string. The captured videos were analyzed in ImageJ using color thresholding techniques to determine post locations in the absence and presence of the plate magnet and weights. The difference in post location with and without the weights was defined as the post deflection. Upon plotting the gravitational force of the weights (Eqn. 1) against the post deflection under the influence of that force, we observed that the data followed a linear trend. Since the post material is homogeneous, isotropic, and elastic, post stiffness could be calculated according to Hooke’s Law (Eqn. 2) as the slope of a linear fit through this data (Eqn. 3):
| (1) |
| (2) |
| (3) |
Where F represents force, k is the post stiffness, x is the post deflection, m is the mass of the attached weight, and g is the acceleration due to gravity (9.8 m/s2). Post stiffness was calculated this way for magnet spacings ranging from 5 mm to 30 mm.
2.4. Formation and maintenance of rat EHTs
Rat engineered heart tissues (rEHTs) were produced as previously described.14 Briefly, polytetrafluoroethylene (PTFE) spacers (EHT Technologies, Hamburg, Germany) were used to create agarose (2% in phosphate buffer solution) (Invitrogen, Carlsbad, CA, USA) voids within a 24-well plate (Thermo Fisher Scientific, Waltham, MA USA). The silicone racks were then inverted and placed on top of these wells, such that the posts were facing downwards and centered within the agarose voids. Ventricular cells (containing approximately 25% non-cardiomyocytes)19 from newborn Wistar rats (postnatal day 0–3) were isolated by a fractionated DNAse and trypsin digestion. A mixture of ~ 500,000 cells, 5 mg/ml bovine fibrinogen (Sigma-Aldrich, St. Louis, MO, USA), 2x Dulbecco's Modified Eagle Medium (DMEM), and 3 U/ml thrombin (Merck Millipore, Burlington, MA, United States) was pipetted into the agarose casting molds (100 μL per rEHT) in the space surrounding the silicone posts. This created tissues with a volume of approximately 12 mm x 3 mm x 2.8 mm. Following tissue solidification (~ 2 hours), the silicone racks were transferred to new 24-well plates containing standard EHT medium (DMEM, 1% penicillin/streptomycin, 10% horse serum, 10 μg/ml insulin, and 33 μg/ml aprotinin, 0.5 ng/ml triiodothyronine and 50 ng/ml hydrocortisone) and maintained in a humidified temperature and gas-controlled incubator (37 ºC, 7% CO2, 40% O2). Culture medium was exchanged every second day. On day 20, the concentration of horse serum in the medium was reduced to 4%, and on day 22 it was omitted entirely. This serum-free medium was exchanged daily from day 22 onwards. The rEHTs were consistently housed within sterile 24-well plates, which maintained sterility and allowed for gas exchange throughout the duration of the experiment. Up until the initiation of the afterload regimen, the 24-well plates were cultured within the incubator and were only removed to perform contractility measurements within a temperature and gas-controlled analysis environment. On day 20, the 24-well plate containing rEHTs, along with the afterload device, was permanently transferred to this environment, where they remained for the duration of the experiment.
2.5. Afterload regimens
As an initial assessment of the afterload system, afterload-affected rEHTs were exposed to a stepwise increase in afterload from a basal value of 0.91 mN/mm to a maximal value of 6.85 mN/mm. Tissue contractile properties were assessed immediately following this intervention.
Using a separate set of tissues, a week-long afterload regimen was initiated 20 days following tissue casting, at the peak of force development. On day 20, afterload (post resistance) was increased by 0.09 mN/mm (from a baseline of 0.91 mN/mm to a starting value of 1.0 mN/mm). Thereafter, afterload was increased according to the average tissue response on the previous day. Afterload was initially increased by 0.5 mN/mm per day between days 21 and 23. Due to noted increases in tissue contractility e.g. post deflection, the magnitude of afterload was further increased by 1.0 mN/mm between days 23 and 24 and by 2.0 mN/mm between days 24 and 25.
Following a decrease in tissue contractility on day 25, the change in afterload magnitude was decreased to 1.35 mN/mm and the total magnitude of afterload was increased to its maximal value (6.85 mN/mm) on day 26. This was done to determine whether the observed negative response was primarily due to the magnitude of the load, or the large change in afterload. After noting tissue recovery under lower changes in load we chose to maintain afterload at this value until the end of the experiment, on day 27. Henceforth, changes in afterload will be referred to as ΔAL, while the magnitude of environmental afterload will be designated by |AL|.
Following a similar week-long afterload regimen, another set of rEHTs were sequentially exposed to smaller magnitudes of afterload every hour, starting from a value of 6.85 mN/mm, and then decreasing to 5.5 mN/mm, 3.5 mN/mm, 2 mN/mm, and lastly, 0.91 mN/mm. The contractile properties of these tissues were measured at each value of afterload.
2.6. Contractility analysis
Spontaneous rEHT contractile parameters were determined using automated video-optical recording hardware and analysis software (EHT Technologies, Hamburg, Germany) as previously described20,21 with a few modifications. This system houses EHTs within a temperature, humidity, and gas-controlled environment with a glass lid. Situated directly above this incubator-like environment is a camera, mounted on computer-controlled X, Y, and Z-axes. LEDs below the EHT plate illuminate individual tissues while the camera records their contractile movement. For this system to be compatible with the magnetic afterload device, the standard interior LED lighting system was removed and replaced with the afterload device.
During recording, custom software is used to automate camera movement and the optical recording parameters for the tissue analysis period. This software computes contractile properties including active contractile force, fractional shortening (FS), contractile velocity, relaxation velocity, and the diastolic tissue length (DL). The systolic length (SL) of the tissue (Eqn. 4) can be calculated from the fractional shortening of the tissue:
| (4) |
The contractile work (W) produced by an EHT was approximated as the change in the elastic potential energy required to deflect the silicone posts (Eqn. 5).
| (5) |
These contractile measurements were initiated 13 days following tissue casting (day 13), at which time the tissues started producing measurable forces. On days when tissue afterload was altered (days 20-27), tissue recordings were performed immediately following afterload adjustment.
2.7. Histological analysis
Following the afterload regimen, a portion of the rEHTs was fixed with formaldehyde and embedded in paraffin for immunohistochemistry. For this procedure, 3 μm sections were transversally cut at the center of the tissues. A mouse anti-dystrophin monoclonal antibody (Millipore, MAB1645) was used at a dilution of 1:200 with a 60 min antigen retrieval in EDTA-buffer, pH 8.0. This dystrophin antibody concentration was optimized using paraffin sections from adult rat hearts. Histological sections were visualized with an UltraView Universal DAB Detection Kit (Roche) and microscopic images were taken with a Hamamatsu NanoZoomer 2.0-HT slide scanner. Average cell cross-sectional areas were determined from dystrophin-positive cells by manually measuring 50 random cells per tissue section in ImageJ, using the freehand trace function.
2.8. RNA isolation and quantification of gene expression
Upon completion of the experiment on day 27, a portion of the control and afterload-affected tissues was frozen in liquid nitrogen for qPCR analysis. The rEHTs were homogenized with steel beads in a highly chaotropic isolation buffer. A phenol-chloroform based total RNA extraction was combined with a silica column purification step according to manufacturer’s instructions (Lexogen Split RNA Extraction Kit). For reverse transcription and qPCR, a High Capacity cDNA Reverse Transcription Kit (Applied Biosystems) and HOT FIREPol EvaGreen qPCR Mix Plus (Solis BioDyne) were used according to manufacturers’ instructions. Experiments were performed on an ABI PRISM 7900HT Sequence detection system (Applied Biosystems). Beta-glucuronidase (Gusb), beta-actin (Actb), and 18S ribosomal RNA served as internal control genes/RNAs to countervail variability.
2.9. Physiological context of afterload regimen
To determine the physiological context of the loads applied to the rEHTs during our experiments, post stiffness was compared to the circumferential systolic wall tension in the left ventricle of the human heart in vivo. This analysis was performed at the endocardial surface of the left ventricle during end-systole since this is the region of highest stress and the time point that most closely corresponds to peak aortic pressure. For this calculation, the left ventricle was represented by a pressure vessel with prolate spherical geometry e.g. a circular cross-section in the transverse plane and an ellipsoid-shaped cross-section in the longitudinal plane. Additionally, the left ventricular wall was defined to be homogenous, purely elastic, and of uniform thickness, and it was assumed that the stress within the wall was purely derived from its internal pressure.
Under these conditions, according to Mirsky,22 the circumferential stress (σθ) at the endocardial surface of the left ventricle (Eqn. 6) can be approximated by:
| (6) |
Where dl and dt are, respectively, the semi-major/longitudinal and semi-minor/transverse axes of the heart, Pi is the internal pressure, and t is the thickness of the heart wall. From this equation, gestational wall stresses were calculated at various time points using published values of left ventricular end-systolic diameters, posterior wall thickness, and pressure.23–27
Using this same equation, and physiological measurements of the left ventricle following birth, Colan et al.28 developed an equation for circumferential end-systolic wall stress in the human heart with respect to patient age. This equation was subsequently used to calculate values of circumferential wall stress from birth onwards (Eqn. 7):
| (7) |
As mentioned previously, our analysis assumes that the heart wall is composed of a homogeneous elastic material when it actually contains various types of cells and extracellular matrix proteins. For this calculation, we are interested in the stress normalized to cardiomyocyte area, since they are the primary force-producing unit within the heart wall and the major resistive unit to preload under physiological loading.29 Assuming that the wall tension is distributed evenly across a given section of tissue and that 80%30,31 of this area is occupied by cardiomyocytes, the normalized physiological cardiac stress (σc,p) is a factor of 1.25 times higher than the calculated stresses.
These values of systolic stress were then compared to stresses produced by rEHTs under the influence of magnetic afterload. To calculate EHT stress, tissue contractile forces were divided by the cross-sectional area of the tissue. Based on our previous works, the percentage of rEHT cross-sectional area that is occupied by cardiomyocytes is approximately 20% at peak force development. As such, the cardiac stress was calculated to be 5 times the calculated stresses for an individual rEHT (Eqn. 8):
| (8) |
Where F is the measured force (mN), and AEHT is the average cross-sectional area of the rEHT (mm2). To calculate tissue areas, rEHT diameters were measured from screenshots (produced by the image analysis software) of the tissues in end-systole, an average was taken from each measurement day, and this value was used to calculate the average tissue area, assuming a circular cross-section.
2.10. Statistical analysis
Quantitative PCR data analyses were carried out using the ΔΔ-Ct method. Statistical tests for contractile data were performed in GraphPad Prism. For repeated measures, differences between control and afterload-affected rEHTs were either assessed using a two-way ANOVA or mixed-effects model with repeated measures, and a Bonferroni correction for multiple comparisons. Statistical significance was assessed at p < 0.05, and p-values are graphically displayed as follows: * = p < 0.05, ** = p < 0.01, *** = p < 0.001, and **** = p < 0.0001. Error bars in graphs represent standard error of the mean.
3. Results
3.1. Afterload system
A device was designed and fabricated to have precise control over the environmental afterload experienced by EHTs. This system (top view: Figure 2A, front view: Figure 2B) has four primary components: a 24-well plate of EHTs grown on magnetic and control silicone posts (Figure 2C), a magnet plate (Figure 2D), a piezoelectric stage (Figure 2E), and an array of LEDs (Figure 2F). The piezoelectric stage is used to translate the magnet plate towards the magnetic silicone posts (Video S1). As the plate approaches the posts, the attractive force between the two sets of magnets becomes stronger. Therefore, the closer the magnet plate is to the posts, the larger the load (afterload) that the EHTs must contract against.
Figure 2. Afterload device and its individual components.
(A) Top view of the afterload device in its assembled form. (B) Close-up front view of the device. (C) The 24-well plate containing 6 racks of EHTs sits on top of an aluminum plate holder. (D) The magnet plate containing two rows of cylindrical permanent magnets is horizontally mounted to the (E) piezoelectric stage below the EHTs. (F) A plate with strips of LEDs sits at the base of the device to illuminate the tissues for imaging.
3.2. Magnet stability
To assess whether the magnets were experiencing losses in their magnetic strength over time, a custom-built Hall sensor was used to measure their magnetic field strength at room temperature and then again following one, two, and three weeks in an incubator at 37 ºC. To replicate the real-life magnet environment as closely as possible, the plate magnets were left in open air within the incubator, while the post magnets were placed inside of silicone posts, and partially submerged in phosphate buffer solution (PBS). Over this three-week period, no significant losses in magnetic strength were observed, nor were any appreciable changes in magnet weight found (Table 1). Additionally, upon examining the tested magnets under a microscope, we observed no visible changes in their microstructure, implying that the magnets did not experience any changes in their physical or magnetic properties following three weeks in an incubator environment.
Table 1. Magnet stability.
The magnets used in these experiments were assessed for changes in their physical and magnetic properties over a three-week period. Magnetism was assessed by recording changes in the Hall voltage (ΔV) generated by the magnets, while magnet weight was measured using standard laboratory scales. No significant changes in either parameter were found. The error reported in this table is the standard error of the mean, which was calculated from n = 3 post magnets and n = 3 plate magnets.
| Post Magnets | Plate Magnets | |||
|---|---|---|---|---|
| Week | ΔV | Weight (mg) | ΔV | Weight (mg) |
| 0 | 0.600 ± 0.110 | 67.433 ± 2.668 | 2.920 ± 0.000 | 14040 ± 10 |
| 1 | 0.630 ± 0.105 | 67.810 ± 2.725 | 2.920 ± 0.000 | 14048 ± 13 |
| 2 | 0.657 ± 0.116 | 67.733 ± 2.854 | 2.920 ± 0.000 | 14042 ± 6 |
| 3 | 0.600 ± 0.081 | 66.557 ± 2.131 | 2.920 ± 0.000 | 14066 ± 11 |
3.3. Magnet post characterization
In this device, afterload, or post resistance, increases as the acrylic magnet plate translates closer to the posts. The relationship between magnet separation distance (the distance between the edge of the magnet within the silicone rack and the edge of the magnet within the magnet plate) and post stiffness was determined optically. This was achieved by tracking the bending movement of a magnet post under the influence of the attractive magnetic force emanating from an axially aligned plate magnet and the gravitational force applied to it by a weight hanging from its end (Figure 3A). This bending movement was recorded for a range of weights at various magnet separation distances (Figure 3B). Upon compiling this data, the relationship between magnet spacing and post resistance was found to follow an inverse exponential trend (Figure 3C). According to these results, the afterload device allows for alterations in post resistance starting from the baseline stiffness of 0.91 mN/mm (in the absence of the plate magnet), to a maximal value of 6.85 mN/mm (at a spacing of 5.5 mm). Additionally, we found that there were no differences in afterload with respect to tissue location within the magnet plate (Figure S1), nor any negative effects of the magnetic field produced by these magnets on the contractile properties of the rEHTs (Figure S2).
Figure 3. Quantification of Post stiffness.
Post stiffness was determined optically, using a camera to track post displacement under the influence of differing weights and magnet separation distances. (A) An image showing the optical method for obtaining post stiffness. (B) Increasing the magnitude of the weight attached to the end of the post resulted in a linear increase in post bending, independent of the magnet separation distance. (C) The relationship between magnet plate distance x and post resistance k is given by the inverse exponential equation: k = 12.69e −0.138x +0.91. The vertical line indicates the closest possible distance between the bottom of the magnet post and magnet plate (5.5 mm).
3.4. Tissue contractile properties
In an initial test of the afterload system, the rEHTs were exposed to a rapid increase in afterload from 0.91 mN/mm to 6.85 mN/mm. Upon doing this, we found no significant changes in the systolic and diastolic tissue lengths or the spontaneous beating frequency of the afterload-affected tissues (Figure S3). However, values of tissue force, force production rate, and force relaxation rate significantly increased, while post deflection, fractional shortening, work production, contractile velocity, and relaxation velocity were all found to significantly decrease. Alternatively, there were no appreciable changes in any of these properties for control tissues.
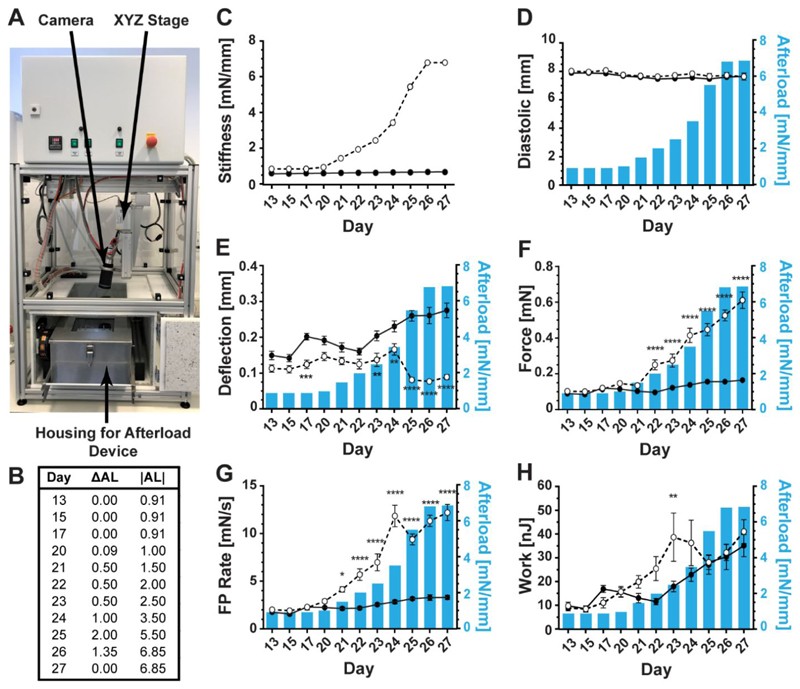
To explore the effects of slowly increasing afterload over time, the tissues and afterload device were permanently placed within the temperature, gas, and humidity-controlled contractile analysis environment (Figure 4A). From day 20 to 27 after casting, the magnet plate was moved in steps towards the bottom of the culture plate, exposing the rEHTs grown on magnetic posts to increasing afterload (Figure 4B). Between days 13-17, the magnitude of afterload experienced by the afterload-affected tissues was slightly higher than that of control tissues (due to the embedded magnets), and this difference became larger over the course of the week-long experiment (Figure 4C). We observed that there were no significant differences in the systolic or diastolic lengths between the control and afterload affected tissues over the testing period (Figure 4 and Figure S4).
Figure 4. Tissue measurements.
measured properties of control (solid line and closed circles) and afterload-affected (dashed line and open circles) tissues when increasing tissue load from a stiffness of 0.91 mN/mm to 6.85 mN/mm, over a one-week period. (A) Picture of afterload device in the assessment environment. (B) Tissue afterload regimen, where ΔAL indicates the change in environmental afterload from the previous day and |AL| is the magnitude of afterload on each day. (C) Environmental afterload experienced by control (solid line and closed circles) and afterload-affected (dashed line and open circles) tissues over the testing period. (D) The average diastolic length of the tissues remained relatively unchanged during the testing period for afterload-affected and control tissues. (E) Post deflection increased over time in both control and afterload-affected rEHTs, however, a sharp decline occurred in afterload-affected tissues on day 25, which was partially recovered by day 27. (F) The average contractile forces produced by the tissues during the testing period increased for both experimental groups, but to a much higher degree in afterload-affected tissues. (G) The rates of tissue contraction also continually increased for both groups of tissues, with the exception of a small decrease in afterload-affected tissues on day 24. (H) Tissue work production followed an increasing trend in control rEHTs. Contractile work in afterload-affected rEHTs also initially increased, but began to decline on day 24 and continued declining until day 26. However, by day 27, these tissues had surpassed their day 23 values. Error bars in graphs represent standard error of the mean. Statistical significance was assessed for n = 12 control tissues and n = 12 afterload-affected tissues at p < 0.05, and p-values are graphically displayed as follows: * = p < 0.05, ** = p < 0.01, *** = p < 0.001, **** = p < 0.0001.
During the observation period of day 13-27 after casting, rEHTs grown on control posts showed a fairly continuous increase in contractile activity, i.e. post deflection, fractional shortening, peak force, and velocity were all approximately 1.9-fold higher on day 27 when compared to day 13, while work production was 3.6-fold higher (Figure 4D and Figure S4). This is the usual behavior of rat EHTs and most likely reflects time-dependent contractile maturation.20
Between day 13 and 20, i.e. before the intervention started, the group of rEHTs grown on magnetic posts produced marginally smaller post deflections than the controls (a significant difference was reached on day 17), likely explained by the slightly stiffer magnet posts (0.91 vs. 0.60 mN/mm). The stepwise afterload regimen starting at day 20 did not induce a significant decrease in post deflection until day 24 (Figure 4E). At this point, afterload was ~ 4-fold higher in magnet tissues compared to controls. In fact, the post deflections measured for magnet tissues (absolute or relative) were 47% higher on day 24 than on day 13, akin to the development of rEHTs on control posts (+54%). Further increase in afterload on day 25 led to a >50% drop in deflection from day 24, which stabilized on day 26 despite an additional increase in environmental load. On day 27, deflection was ~ 4-fold lower for afterload-affected tissues when compared to control rEHTs. Fractional shortening, contraction velocity, and relaxation velocity demonstrated a similar dependence on changes in afterload magnitude (Figure S4).
Force, which is the product of post deflection (mm) and post stiffness (mN/mm), steadily increased over time in afterload-affected rEHTs and reached values 5.9-fold higher on day 27 compared to baseline values from day 13 (maximal force ~ 0.6 mN; Figure 4F). It is interesting to note that force increased between days 26 and 27 in the absence of additional afterload application, indicating a continuous adaptation of the rEHTs to the increasing environmental load. Force production rate (mN/s), i.e. the velocity of tension development, also increased with rising afterload, but with a transient drop between days 24 and 25, the time point when afterload was increased by a large step (ΔAL 2 mN/mm) (Figure 4G). However, this drop was almost fully recovered by day 26 and even surpassed by day 27. Again, showing an adaptation of the rEHTs to higher loads, as long as the change in load was kept low. A similar trend was found for the velocity of tension relaxation (Figure S4).
Work production, e.g. the product of force and displacement, by afterload-affected rEHTs increased over time and reached values 4.6-fold higher than baseline measurements (Figure 4H). During days 22 and 23, work production in these rEHTs was 2.2-fold higher than those measured for control tissues. On day 24, following a moderately large ΔAL of 1.0 mN/mm, these values began to decrease. An even larger drop in work was observed on day 25 when ΔAL = 2.0 mN/mm. However, following a smaller increase in afterload on day 26, the magnitude of work production again increased, and in the absence of further afterload application, surpassed earlier values.
This data demonstrates that post deflection, work production, fractional shortening, contraction velocity, and relaxation velocity are negatively influenced by large stepwise increases in afterload, while force production rate and relaxation rate are moderately affected by these changes and contractile force is positively affected. In fact, we observed a remarkable adaptation in rEHT force development to these stepwise increases in afterload.
Following a replicate week-long experiment, rEHTs were exposed to sequential step-wise decreases in afterload over 4 hours. During this period, the average post deflection and contractile force produced by control tissues remained steady (Figure S5). In contrast, the average post deflection increased upon each drop in afterload, and contractile forces decreased. In consequence, chronically afterload-enhanced rEHTs reached control deflection and force values after 4 hours.
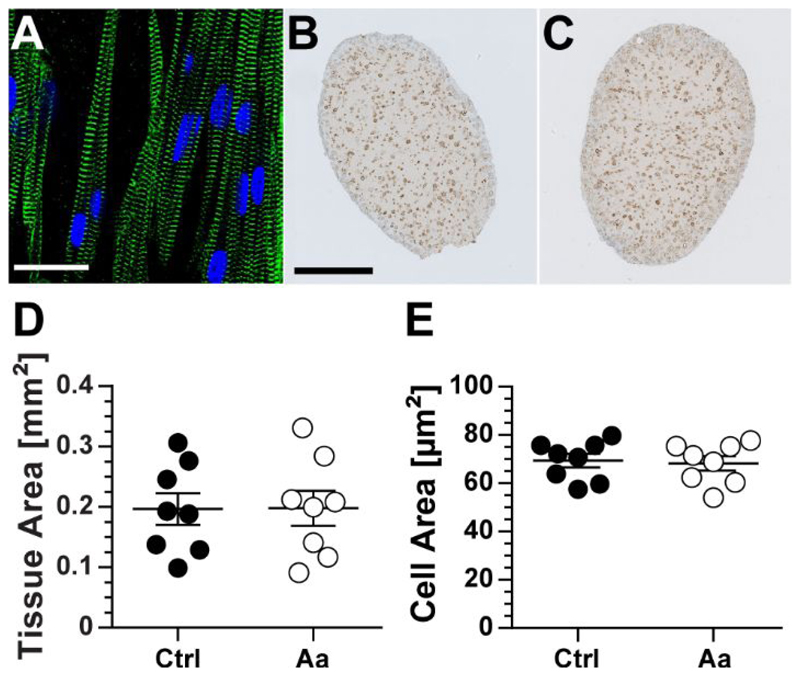
3.5. Tissue structure
In examining rEHT structure, we find that the surface region of these tissues contain a higher density of cardiomyocytes with well-defined and interconnected sarcomeric structures, which are oriented along the longitudinal direction of the tissue (Figure 5A). To determine whether there was an effect of the applied afterload regimen on the structural properties of the rEHTs, the tissues were fixed, embedded in paraffin, and immunohistochemically stained for dystrophin following the completion of the experiment (Figure 5B and 5C). Analysis of these images revealed no differences in the cross-sectional area of the tissues (Figure 5D) or individual cells (Figure 5E).
Figure 5. Tissue and cellular structure.
(A) Immunofluorescent image of a region close to the surface of a rat EHT stained with antibodies against α-actinin (green) and DRAQ5 (blue). Dystrophin stained cross-sections of (B) control (Ctrl) and (C) afterload-affected (Aa) tissues were analyzed for differences in (D) tissue and (E) cellular area. No significant differences in either parameter were found. Scale bar in immunofluorescent image is equivalent to 20 μm and that in dystrophin images equates to 200 μm. Error bars in graphs represent standard error of the mean. Statistical significance was assessed for n = 8 control tissues and n = 8 afterload-affected tissues at p < 0.05.
3.6. Quantitative PCR of hypertrophy and fibrosis markers
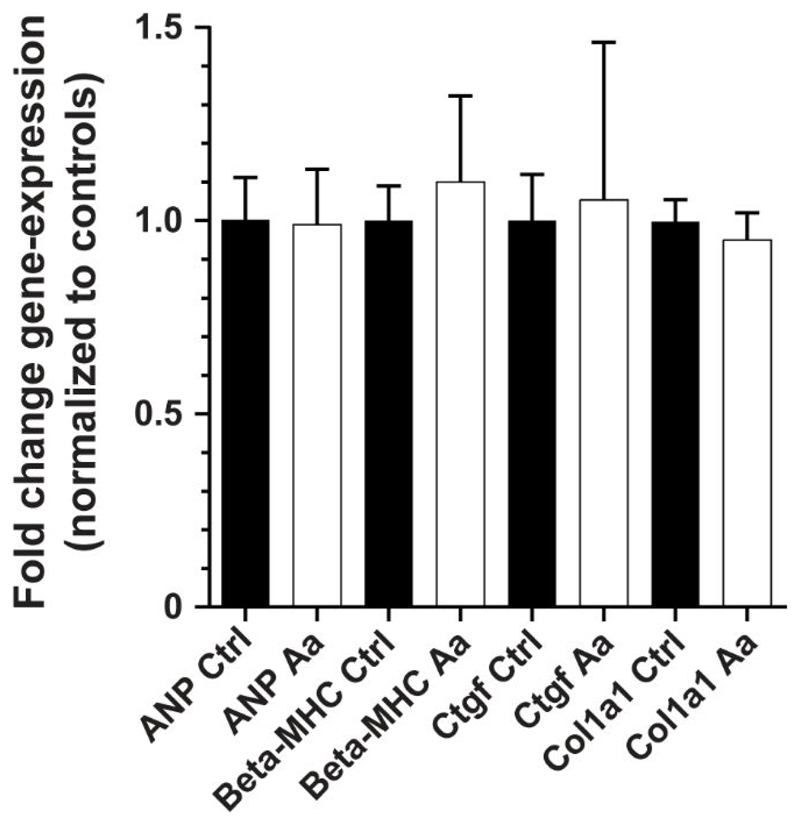
We have previously observed that strong (>12-fold) increases in environmental afterload can initiate pathological hypertrophy and fibrosis in EHTs.14 To assess whether these tissues experienced similar outcomes, qPCR analysis was performed on control and afterload-affected rEHTs following completion of the afterload regimen. This analysis tested for mRNA levels of atrial natriuretic peptide (ANP, Nppa), beta-myosin heavy chain (beta-MHC, Myh7), collagen-1 pro-alpha chain (Col1a1), and connective tissue growth factor (Ctgf). The results of this examination revealed no differences in transcript concentrations between control and afterload-affected tissues, suggesting that the loads applied during the afterload regimen neither induced pathological hypertrophy nor fibrosis (Figure 6).
Figure 6. Results of qPCR analysis.
An analysis of hypertrophic and fibrotic genes revealed no differences in the mRNA levels of atrial natriuretic peptide (ANP, Nppa), beta-myosin heavy chain (Beta-MHC, Myh7), collagen-1 pro-alpha chain (Col1a1), and connective tissue growth factor (Ctgf) between control (Ctrl) and afterload-affected (Aa) tissues. Error bars in graphs represent standard error of the mean. Statistical significance was assessed for n = 4 control tissues and n = 3 afterload-affected tissues at p < 0.05 using the ΔΔ-Ct method.
3.7. Physiological context of afterload regimen
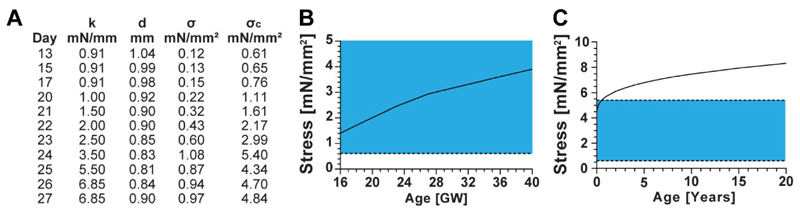
To have a physiological understanding of the loads applied to the rEHTs in our system, we compared these loads to those seen in the human heart during development. This analysis revealed that the afterload device is capable of applying loads in the range of 0.91 mN/mm to 6.85 mN/mm to rat-based EHTs. When these values are normalized to the rEHT cross-sectional area and adjusted for the area percentage of cardiomyocytes within an rEHT, the stress applied by the afterload device to the rat cardiomyocytes was found to range from 0.61 mN/mm2 (on day 13) to 5.40 mN/mm2 (on day 24) (Figure 7A). Interestingly, this applied stress decreased when afterload was further increased to a smaller degree, on days 25 and 26, This was a result of the tissue cross-sectional area initially decreasing on day 24, and then recovering on days 25 and 26.
Figure 7. Comparison between computed and experimental systolic wall stress.
Values of left ventricular end-systolic stress experienced by cardiomyocytes within the human heart were calculated by modeling the ventricle as a prolate spheroid-shaped pressure vessel. (A) Loads produced by our magnetic afterload device were calculated, assuming a circular tissue cross-section and that 20% of the EHT cross-sectional area was occupied by cardiomyocytes. Where, k is the post stiffness, d is the tissue diameter, σ is the calculated tissue stress, and σc is the cardiomyocyte-perceived stress. (B) Published values of left ventricular diameters, wall thickness, and pressure at end systole were used to estimate stress from 16 to 40 weeks of gestation. (C) A previously established equation was used to calculate stress from birth onwards28. (C) The blue regions in the graphs indicate the range of stresses applied by the afterload device, where the upper and lower bounds are indicated by dashed lines.
Modeling the gestational left ventricle as a prolate spheroid and using published values of cardiac dimensions and blood pressure (Table S2), we calculated that the wall tension perceived by cardiomyocytes in the human heart vivo increases from 1.12 mN/mm2 at 16 gestational weeks to 3.12 mN/mm2 at 40 gestational weeks (Figure 7B). Employing a previously established equation for systolic wall stress in the human heart, we estimated that this stress continues to increase after birth, from a value of around 4.06 mN/mm2 shortly after birth to 8.31 mN/mm2 in a full-grown adult (Figure 7C).
Using the calculated values of wall stress produced by the afterload device and employing the method proposed from Elzinga and Westerhof,32 it is possible to estimate maximum systolic pressure that could be achieved by an artificial human heart composed of rat engineered heart tissues. Systolic wall tension in 20-year-old human hearts was calculated to be 6.65 mN/mm2.
Alternatively, maximal wall tension in our rEHTs (with 20% of the cross-sections occupied by cardiomyocytes) was 1.08 mN/mm2. Assuming an average maximum systolic blood pressure of 120 mmHg, the pressure produced by the artificial heart would be ~ 20 mmHg (1.08 mN/mm2 / 6.65 mN/mm2 x 120 mmHg). This value is quite low when compared to 120 mmHg. Though, if we manage to increase the cardiomyocyte coverage in the rEHTs to match that in the human heart (~ 80%), the maximal systolic blood pressure would approach 80 mmHg. Maturing these tissues in culture to increase force production on a per-cell basis would further increase this value. Overall, these comparisons show that the afterload device can be used to apply human physiological loads to rEHTs, and that a heart made from these tissues could potentially produce 80 mmHg of systolic pressure, but that these outcomes are largely dependent on the contractile state and content of the tissues.
4. Discussion
Afterload plays an important role in the regulation of cardiac contractile function. However, experimentally studying this effect in a highly controlled manner over prolonged periods of time has proven to be technically difficult. Live models offer little control over afterload magnitude while excised hearts and muscle preparations have a very limited window of time in which they can be used before deteriorating. In addition, these models are low throughput, require time-consuming preparation and maintenance, and induce higher costs. Due to these limitations, some investigators have opted to study afterload in engineered heart tissue (EHT) systems.
In a previous study, we exposed EHTs composed of neonatal cardiomyocytes to a substantial (>10-fold) and instantaneous increase in afterload by inserting metal braces into hollow versions of the silicone posts (afterload enhancement).14 This increase in afterload resulted in pathological hypertrophy, i.e. lower force development, slower relaxation kinetics, an increase in fibrosis, a reactivation of fetal genes (hypertrophic gene program), and metabolic alterations consistent with a pathological cardiomyocyte state. In contrast, Leonard et al. recently demonstrated that a singular small-to-medium increase in afterload in human EHTs promotes force development and maturation.33 However, a means of fine-tuning tissue loads in EHTs is lacking. Moreover, these previous studies have only examined the effect of a single increase in afterload magnitude, which does not mimic what happens in the body during heart development nor during the progression of diseases such as aortic valve stenosis. The goal of this project was to design a device capable of applying distinct values of afterload – which can be precisely varied over time – to EHTs. This was achieved using a magnetics-based approach with three major elements: small permanent magnets in the tips of the EHT posts, an array of larger permanent magnets positioned below the 24-well culture plate, and a linear piezoelectric stage, which was used to translate the magnet plate towards the cultured tissues.
Piezoelectric stages have many advantages when compared to conventional stepping or servo motorized stages. First, the travel resolution for piezoelectric stages is in the nanometer range, while most motorized stages have resolutions in the micrometer or millimeter range. Also, piezoelectric motors are self-locking, i.e. the motor does not experience any slippage upon the cessation of movement. Unlike a standard mechanical motor, piezoelectric stages are lubricant free and have fewer moving parts, which translates into them requiring less maintenance and having a longer service life. Moreover, these stages are relatively compact, which is an important trait for our system, as we need the stage to be able to fit within the space-limited imaging and incubator environments. Lastly, piezoelectric stages can be built out of almost entirely non-magnetic materials. This is of particular importance for our device because a magnetic stage could disrupt the fields produced by the magnets used in our system.
The software used to control the piezoelectric stage (Micronix Motion Controller Platform) allows the user to easily adjust for multiple parameters. In addition to travel distance, this software can be used to define travel speed, acceleration, and spatial travel limits. To ensure a higher level of travel accuracy, the stage was fitted with an optical analog encoder. This encoder uses a sensor to transmit location information to the computer software. A feedback mechanism within the software ensures that the travel distance prescribed by the user is accurate and corrects this position if necessary. Therefore, even if the stage is bumped, the software will correct the position. These properties make this system very precise, reliable, and user-friendly.
The feasibility of this design depends on the stability of the magnets within the posts and those within the magnet plate. Several different environmental factors can cause permanent magnets to demagnetize, including high temperatures, physical damage, and oxidation.34 Depending on the duration and extremity of this event, the demagnetization can be reversible or irreversible. As a magnet is heated up, increased molecular movement causes the magnetic domains to misalign, and the overall strength of the magnet is reduced. In general, at temperatures below the maximum working temperature of the magnet, this reduction is completely reversible. Past this point, some percentage of the magnetic strength is irreversibly lost. In our system, the magnets are exposed to temperatures up to 37 ºC, which is well below their maximum working temperature (60 ºC for those in the magnet plate and 80 ºC for those in the posts, according to the product guide). As such, irreversible losses were improbable, but reversible losses were possible. However, after three consecutive weeks in the incubator, we found no measurable losses in magnet strength (Table 1).
Neodymium magnets are primarily composed of neodymium, iron, and boron. If left in a humid environment for prolonged periods of time, diffusion of oxygen, water vapor or hydrogen along grain boundaries inside the magnet can cause the iron to rust, which will partially demagnetize the magnet. To prevent this, neodymium magnets are often coated with a protective layer of nickel, which is resilient to humid environments but can deteriorate following prolonged exposure to high-humidity.35 Following three weeks in a humid biological incubator, no alterations to the physical microstructure of the magnets were found.
The effective implementation of this device as a means to alter afterload in engineered heart tissues is also dependent on the uniformity of the applied magnetic field. Compounding effects from adjacent magnets within the magnet plate could lead to differences in the magnetic field applied to the post magnets, based on the location of the tissue within that field. However, we found no measurable differences in post deflection with regard to tissue location (Figure S1), implying that the afterload felt by each tissue is equivalent, regardless of its position.
Additionally, there is some evidence that the presence of low level oscillatory magnetic fields can alter cardiovascular function.36,37 However, other studies have found no effect of either stagnant nor oscillating magnetic fields in the range of 400 mT to 9.4 T on cardiac force production, heart rate, heart rhythm, electrical activity, or heart pathology.38–41 Some studies have even found beneficial effects of culturing cardiomyocytes in the presence of a magnetic field.42–47 The largest fraction of the magnetic field present in our system is produced by the plate magnets. When the magnet plate is in its position closest to the rEHTs, the magnetic field strength imposed on the tissue is in the range of 220 mT (0.22 T). We found that culturing rEHTs in the presence of this field for six days did not result in altered contractile function of the tissues (Figure S2). Though it is not known whether there were other effects of this field on the cardiac tissues, these results suggest that any effect on the contractile function of these tissues was minimal.
Prior to initiating our experiments, the relationship between magnet spacing and post stiffness had to be established. This relationship was determined by attaching a large magnet to a linear track and translating it towards an axially-aligned magnet post under the influence of a defined weight. Concurrently, post deflection was optically tracked using a digital camera. Upon analyzing the post deflection for different magnet spacings, it was determined that this relationship followed an inverse exponential trend with a minimum stiffness of 0.91 mN/mm and a maximal stiffness of 6.85 mN/mm. The basal stiffness of the magnet post in the absence of an externally applied magnetic field (0.91 mN/mm) is noticeably higher than that of an empty post (0.6 mN/mm). This indicates that the presence of the magnet increases the resistance of the post. This difference may contribute to the smaller deflections measured for the rEHTs on the adjustable afterload posts compared to those on control posts in the absence of a magnetic field (Figure 4E, days 13-20). Despite this discrepancy, during this period, there were not any significant differences in the measured contractile properties for the two groups of tissues (albeit a decline in deflection on day 17). However, this is an acknowledged shortcoming of the current afterload device design.
In an initial study with this system, rEHTs were exposed to a quick step-wise increase in afterload. Upon measuring the contractile properties of these tissues, we found significant increases in force, force production rate, and force relaxation rate, but significant decreases in post deflection, tissue shortening, work production, contractile velocity, and relaxation velocity. Previously, we found that a step-wise increase in afterload from 0.95 to 11.5 mN/mm had a similar effect, with the exception that force production, force production rate, and force relaxation rate (which were measured at a delayed time point) also decreased.14 However, our current results are consistent with those found by a previous study that exposed human EHT to a step-wise increase in afterload from 0.09 to 9.2 mN/mm.33 These results suggest that force, force production rate, and force relaxation rate are less sensitive to alterations in afterload than the others such as fractional shortening, but will also decline in the presence of very large magnitudes of afterload.
To determine the effect of smaller magnitudes of afterload, racks of posts containing control and afterload affected rEHTs were exposed to increasing amounts of afterload application over a 7-day period. With the exception of day 24, the average diastolic and systolic lengths of the afterload-affected tissues were not significantly different from those measured for the control tissues, nor did these values significantly change with alterations in |AL| (Figure 4). This suggests that the tissues experienced little to no change in strain during the testing period. The afterload device was designed so that the permanent magnets within the magnet plate were axially aligned with the undeformed positions of the posts containing magnets. In general, the diastolic lengths of EHTs decrease over time in culture. Thus, to minimize an initial alteration in preload strain, afterload application was initiated before substantial tissue compaction had occurred. From here on, we believe that the resting tissue length remained unchanged due to a balance in the attractive magnetic force pulling the post into its undeformed position with the resistive force of the tissue to strain. Importantly, despite preload strain remaining unchanged, the preload tension experienced by EHTs in our system – which can be thought of as the force that brings the posts back into their undeformed positions during diastole – also increases with rising values of afterload. Though the independent effects of afterload and preload cannot be segregated in this system, the lack of tissue straining implies that any changes in EHT properties can be directly attributed to increases in afterload and preload tension, and not to tissue stretching i.e. the Frank Starling mechanism. This characteristic is a notable advantage of our system compared to others, which have reported increases in tissue diastolic length with the application of afterload.33,48
Imposing increasing afterload over time did not affect post deflection nor fractional shortening in afterload-affected rEHTs until environmental afterload reached values ~ 4 times that experienced by control tissues (Figures 4 and S4). In fact, both groups of tissues demonstrated a ~ 50% increase in deflection between days 13 and 24 (4 days after the start of intervention). This is in contrast to a recent study which found that even a small singular increase in load resulted in decreased tissue deflection.33 However, the contractile measurements reported in this study were conducted three weeks following the afterload intervention, whereas ours were performed immediately. Therefore, it is difficult to make direct comparisons between the two.
Given that more force is needed to deflect stiffer posts, the same deflection translated into higher force and work production, increasing with the magnitude of afterload application (Figure 4). Further increase in afterload (day 24 to day 25) resulted in a steep decrease in tissue shortening and work production, but force continued to increase. Other experiments which have examined the effect of a singular increase in afterload oneffect of a singular increase in afterload on the contractile properties of native heart tissues49–52 and EHTs33,53 have found that force and work production increase with moderate enhancements in afterload application and decrease past a certain threshold of afterload. In our study, work production in afterload-affected rEHTs declined on day 24 but recovered again by day 27. Alternatively, force production continuously increased during the testing period. These findings imply that work production is more sensitive to increases in afterload application than force.
Indices of contractile function such as fractional shortening, twitch velocity, and contraction and relaxation rates (mN/s) also showed a transient drop between day 24 and 25, indicating a limit of tissue adaptation to large changes in afterload. Afterload was moderately increased between day 20 and 24 (ΔAL = 0.09-1.35 mN/mm at a time) and was increased to a larger degree between days 24 and 25 (ΔAL = 2.0 mN/mm). Importantly, when the daily increase in afterload was lowered to 1.35 mN/mm between days 25 and 26, and to 0 mN/mm between days 26 and 27, these properties did not continue to decline, though the total amount of environmental afterload had increased to a higher value (6.85 mN/mm). It has been previously demonstrated that native heart tissue responds to increases in afterload with reduced contraction velocity.49,51,54–56 The same response has been observed in immature EHTs, 14,33 as well as a decrease in fractional shortening and post deflection. In our system, these properties were only shown to decrease when rEHTs were exposed to a 2.0 mN/mm change in environmental afterload and recovered in the presence of higher afterload when the ΔAL remained below 1.35 mN/mm. These results indicate that, in addition to (or more than) the absolute magnitude of afterload, the change in afterload has a strong effect on the resulting contractile state of the tissue.
It is well known from extensive studies on animals that pathological hypertrophy is accompanied by the upregulation of fetal cardiac genes, including atrial natriuretic peptide (ANP), brain natriuretic peptide (BNP), α-skeletal actin, and β-myosin heavy chain (β-MHC), as well as increased expression of collagen-1 and connective tissue growth factor.57 We previously found that rapidly increasing afterload from a baseline value of 0.95 mN/mm to 11.5 mN/mm (~ 12-fold increase) yielded cellular hypertrophy and significant increases in the expression of these genes.14 It was therefore somewhat unexpected that the afterload regimen employed in the present study had no effect on transcript levels of hypertrophy or fibrosis markers. The data initially suggested induction of a physiological form of hypertrophy. However, we didn´t observe altered EHT structure or cell size, similar to a former study applying small to moderate increases in afterload.33 These data, coupled with the observation that the force increase in afterload-enhanced rEHTs was fully reversible in 4 hours suggest that the loads applied in this study did not result in structural remodeling of the tissues, but rather, initiated a physiological force response to increased afterload.
More than 100 years ago, Gleb von Anrep observed a slow but powerful positive inotropic reaction of the heart to an increase in afterload.58 Anrep postulated this effect to be catecholamine mediated, however, this hypothesis was later disproved.59 In the 1970s, the slow Anrep-effect (together with the fast Frank-Starling-effect) were reproduced in vitro.60 We speculate that the increased, but reversible, forces observed in our experiments might be explained by the Anrep-effect, implying that an increase in afterload alone (without an increase in preload strain) is sufficient to induce this physiological adaptation.61 Additionally, in skeletal muscle, high loads have recently been shown to unlock additional myosin motors, resulting in higher forces (thick-filament regulation of force).62 The authors of this work concluded “As thick-filament structure and protein composition are essentially the same in heart and skeletal muscle, thick-filament mechanosensing may also be a fundamental component of the regulation of contractility in the heart.” Future work is necessary to determine which (if either) of these mechanisms resulted in the contractile behavior observed in our experiments. The new magnetic post system will serve an integral role in elucidating this effect.
Finally, to determine how the loads applied to the rEHTs during our experiments compare to those experienced by an intact human heart, we compared the environmental stresses produced by the afterload device to calculated values of end-systolic wall stress within the human heart (Figure 7). This analysis assumed that the left ventricle is of semi-spherical shape, and composed of an isotropic and homogenous elastic material with uniform, but not negligible, wall thickness. Despite these simplifications, similar approximations have been found to yield values of average circumferential stress that are not significantly different from geometrically accurate FEA models63,64 nor experimental measurements.65,66 It is important to note that the accuracy of these models is highly limited when estimating local stresses, especially those located further from the equatorial or surface regions of the model, as well as they are less precise when used to calculate stresses in the longitudinal or radial directions or at end diastole.64,67,68 To account for differences in cardiomyocyte coverage in an rEHT (~ 20%) compared to the human heart (~ 80%), calculated values of stress were multiplied by scaling factors to yield the proportion of cardiomyocyte stress. Upon completing this comparison, we found that stress within the human heart increases from approximately 1.12 mN/mm2 at 16 weeks gestation to 8.31 mN/mm2 in a full-grown adult. After scaling the measured rEHT forces based on their cross-sectional area and the area percentage of cardiomyocytes, the stress perceived by these cells ranges from 0.61 mN/mm2 to 5.40 mN/mm2.
Therefore, we demonstrated that this device can be used with rEHTs to produce physiological stresses that mimic those present during human gestation up to early adulthood. If the force-producing capability of the cardiomyocytes within the EHTs can be increased via environmental maturation, and the cardiomyocyte coverage within the EHTs can be improved (from ~ 20 % to ~ 80 %) by limiting hypoxic regions via perfusion strategies,69,70 we postulate that this system could be used to apply a full range of physiologically relevant stresses to EHTs composed of immature rat or human cardiac tissues. However, since rat and human hearts are physiologically different (e.g. distinct geometries and muscle isoforms) a similar analysis will have to be performed on human EHTs to prove the validity of this claim.
5. Conclusions
Here, a new device for altering afterload in engineered heart tissues was presented. The results of initial experiments demonstrate that the magnetic afterload device developed for this study is an effective means of fine-tuning physiological afterloads in EHTs with a minimal effect on tissue strain. In contrast to other systems, tissue contractility can be measured during the afterload intervention, as well as over extended periods of time. Using this device, we found that small daily increases in afterload are effective in enhancing the contractile properties of rEHTs, while moderate to large increases can temporarily reduce these endpoints. These findings suggest that both the magnitude and change in afterload application play important roles in the development of contraction in immature cardiomyocytes. Going forward, this system can be used to study the mechanisms that underlie adaptations in force development, maturation, and pathological remodeling in cardiac tissues exposed to various afterload regimens.
Supplementary Material
Supporting Information Available: The Supporting Information is available free of charge on the ACS Publications website
Acknowledgments
We thank Jutta Starbatty for her technical assistance, Bülent Aksehirlioglu for lending his manufacturing expertise, Kristin Hartmann of the HEXT Mouse Pathology Facility for assistance with histology, and Alice Casagrande Cesconetto for her contributions to the editing of this manuscript.
References
- (1).McCain ML, Yuan H, Pasqualini FS, Campbell PH, Parker KK. Matrix elasticity regulates the optimal cardiac myocyte shape for contractility. AJP Hear Circ Physiol. 2014;306:H1525–H1539. doi: 10.1152/ajpheart.00799.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (2).Jacot JG, McCulloch AD, Omens JH. Substrate stiffness affects the functional maturation of neonatal rat ventricular myocytes. Biophys J. 2008;95:3479–3487. doi: 10.1529/biophysj.107.124545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (3).Gwak S, Bhang S, Kim I, Kim S, Cho S, Jeon O, Yoo K, Putnam A, Kim B. The effect of cyclic strain on embryonic stem cell-derived cardiomyocytes. Biomaterials. 2008;29:844–856. doi: 10.1016/j.biomaterials.2007.10.050. [DOI] [PubMed] [Google Scholar]
- (4).Shimko VF, Claycomb WC. Effect of Mechanical Loading on Three-Dimensional Cultures of Embryonic Stem Cell-Derived Cardiomyocytes. Tissue Eng Part A. 2008;14:49–58. doi: 10.1089/ten.a.2007.0092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (5).Földes G, Mioulane M, Wright JS, Liu AQ, Novak P, Merkely B, Gorelik J, Schneider MD, Ali NN, Harding SE. Modulation of human embryonic stem cell-derived cardiomyocyte growth: A testbed for studying human cardiac hypertrophy? J Mol Cell Cardiol. 2011;50:367–376. doi: 10.1016/j.yjmcc.2010.10.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (6).Tulloch NL, Muskheli V, Razumova MV, Korte FS, Regnier M, Hauch KD, Pabon L, Reinecke H, Murry CE. Growth of engineered human myocardium with mechanical loading and vascular coculture. Circ Res. 2011;109:47–59. doi: 10.1161/CIRCRESAHA.110.237206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (7).Mihic A, Li J, Miyagi Y, Gagliardi M, Li SH, Zu J, Weisel RD, Keller G, Li RK. The effect of cyclic stretch on maturation and 3D tissue formation of human embryonic stem cell-derived cardiomyocytes. Biomaterials. 2014;35:2798–2808. doi: 10.1016/j.biomaterials.2013.12.052. [DOI] [PubMed] [Google Scholar]
- (8).Chun YW, Voyles DE, Rath R, Hofmeister LH, Boire TC, Wilcox H, Lee JH, Bellan LM, Hong CC, Sung H-J. Differential responses of induced pluripotent stem cell-derived cardiomyocytes to anisotropic strain depends on disease status. J Biomech. 2015 doi: 10.1016/j.jbiomech.2015.09.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (9).Ruan J, Tulloch NL, Saiget M, Paige SL, Razumova MV, Regnier M, Chan Tung K, Keller G, Pabon L, Reinecke H, Murry CE. Mechanical Stress Promotes Maturation of Human Myocardium From Pluripotent Stem Cell-Derived Progenitors. Stem Cells. 2015;33:2148–2157. doi: 10.1002/stem.2036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (10).Kroll K, Chabria M, Wang K, Häusermann F, Schuler F, Polonchuk L. Electro-mechanical conditioning of human iPSC-derived cardiomyocytes for translational research. Prog Biophys Mol Biol. 2017;130:212–222. doi: 10.1016/j.pbiomolbio.2017.07.003. [DOI] [PubMed] [Google Scholar]
- (11).Zhang W, Kong CW, Tong MH, Chooi WH, Huang N, Li RA, Chan BP. Maturation of human embryonic stem cell-derived cardiomyocytes (hESC-CMs) in 3D collagen matrix: Effects of niche cell supplementation and mechanical stimulation. Acta Biomater. 2017;49:204–217. doi: 10.1016/j.actbio.2016.11.058. [DOI] [PubMed] [Google Scholar]
- (12).Samsa LA, Yang B, Liu J. Embryonic cardiac chamber maturation: Trabeculation, conduction, and cardiomyocyte proliferation. Am J Med Genet Part C Semin Med Genet. 2013;163:157–168. doi: 10.1002/ajmg.c.31366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (13).Lindsey SE, Butcher JT, Yalcin HC. Mechanical regulation of cardiac development. Front Physiol. 2014;5:1–15. doi: 10.3389/fphys.2014.00318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (14).Hirt MN, Sörensen NA, Bartholdt LM, Boeddinghaus J, Schaaf S, Eder A, Vollert I, Stöhr A, Schulze T, Witten A, Stoll M, et al. Increased afterload induces pathological cardiac hypertrophy: a new in vitro model. Basic Res Cardiol. 2012;107:1–16. doi: 10.1007/s00395-012-0307-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (15).Bupha-Intr T, Holmes JW, Janssen PML. Induction of hypertrophy in vitro by mechanical loading in adult rabbit myocardium. Am J Physiol Heart Circ Physiol. 2007;293:H3759–H3767. doi: 10.1152/ajpheart.01267.2006. [DOI] [PubMed] [Google Scholar]
- (16).Zhang H, Cannell MB, Kim SJ, Watson JJ, Norman R, Calaghan SC, Orchard CH, James AF. Cellular hypertrophy and increased susceptibility to spontaneous calcium-release of rat left atrial myocytes due to elevated afterload. PLoS One. 2015;10:1–17. doi: 10.1371/journal.pone.0144309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (17).Kim SJ, Choisy SCM, Barman P, Zhang H, Hancox JC, Jones SA, James AF. Atrial remodeling and the substrate for atrial fibrillation in rat hearts with elevated afterload. Circ Arrhythmia Electrophysiol. 2011;4:761–769. doi: 10.1161/CIRCEP.111.964783. [DOI] [PubMed] [Google Scholar]
- (18).Toischer K, Rokita AG, Unsöld B, Zhu W, Kararigas G, Sossalla S, Reuter SP, Becker A, Teucher N, Seidler T, Grebe C, et al. Differential cardiac remodeling in preload versus afterload. Circulation. 2010;122:993–1003. doi: 10.1161/CIRCULATIONAHA.110.943431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (19).Hirt MN, Werner T, Indenbirken D, Alawi M, Demin P, Kunze A-C, Stenzig J, Starbatty J, Hansen A, Fiedler J, Thum T, et al. Deciphering the microRNA signature of pathological cardiac hypertrophy by engineered heart tissue-and sequencing-technology. J Mol Cell Cardiol. 2015;81:1–9. doi: 10.1016/j.yjmcc.2015.01.008. [DOI] [PubMed] [Google Scholar]
- (20).Hansen A, Eder A, Bönstrup M, Flato M, Mewe M, Schaaf S, Aksehirlioglu B, Schwörer A, Uebeler J, Eschenhagen T. Development of a drug screening platform based on engineered heart tissue. Circ Res. 2010;107:35–44. doi: 10.1161/CIRCRESAHA.109.211458. [DOI] [PubMed] [Google Scholar]
- (21).Eder A, Vollert I, Hansen A, Eschenhagen T. Human engineered heart tissue as a model system for drug testing. Hum Eng Hear Tissue as a Model Syst Drug Test. 2016;96:214–224. doi: 10.1016/j.addr.2015.05.010. [DOI] [PubMed] [Google Scholar]
- (22).Mirsky I. Left Ventricular Stresses in the Intact Human Heart. Biophys J. 1969;9:189–208. doi: 10.1016/S0006-3495(69)86379-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (23).Johnson P, Maxwell DJ, Tynan MJ, Allan LD. Intracardiac pressures in the human fetus. Heart. 2000;84:59–63. doi: 10.1136/heart.84.1.59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (24).Gagnon C, Bigras JL, Fouron JC, Dallaire F. Reference Values and Z Scores for Pulsed-Wave Doppler and M-Mode Measurements in Fetal Echocardiography. J Am Soc Echocardiogr. 2016;29:448–460. doi: 10.1016/j.echo.2016.01.002. [DOI] [PubMed] [Google Scholar]
- (25).St Sutton J MG, Gewitz MH, Shah B, Cohen A, Reichek N, Gabbe S, Huff DS, St MGJ, Sutton MRCP. Quantitative assessment of growth and function of the cardiac chambers in the normal human fetus: a prospective longitudinal echocardiographic study. Circulation. 1984;69:645–654. doi: 10.1161/01.cir.69.4.645. [DOI] [PubMed] [Google Scholar]
- (26).Struijk PC, Mathews VJ, Loupas T, Stewart PA, Clark EB, Steegers EAP, Wladimiroff JW. Blood pressure estimation in the human fetal descending aorta. Ultrasound Obstet Gynecol. 2008;32:673–681. doi: 10.1002/uog.6137. [DOI] [PubMed] [Google Scholar]
- (27).Wladimiroff JW, Vosters R, McGhie JS. Normal cardiac ventricular geometry and function during the last trimester of pregnancy and early neonatal period. Br J Obstet Gynaecol. 1982;89:839–844. doi: 10.1111/j.1471-0528.1982.tb05037.x. [DOI] [PubMed] [Google Scholar]
- (28).Colan SD, Parness IA, Spevak PJ, Sanders SP. Developmental modulation of myocardial mechanics: Age- and growth-related alterations in afterload and contractility. J Am Coll Cardiol. 1992;19:619–629. doi: 10.1016/S0735-1097(10)80282-7. [DOI] [PubMed] [Google Scholar]
- (29).Chung CS, Granzier HL. Contribution of titin and extracellular matrix to passive pressure and measurement of sarcomere length in the mouse left ventricle. J Mol Cell Cardiol. 2011;50:731–739. doi: 10.1016/j.yjmcc.2011.01.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (30).Vliegen HW, van der Laarse a, Cornelisse CJ, Eulderink F. Myocardial changes in pressure overload-induced left ventricular hypertrophy. A study on tissue composition, polyploidization and multinucleation. Eur Heart J. 1991;12:488–494. doi: 10.1093/oxfordjournals.eurheartj.a059928. [DOI] [PubMed] [Google Scholar]
- (31).Olivetti G, Melissari M, Balbi T, Quaini F, Cigola E, Sonnenblick EH, Anversa P. Myocyte cellular hypertrophy is responsible for ventricular remodelling in the hypertrophied heart of middle aged individuals in the absence of cardiac failure. Cardiovasc Res. 1994;28:1199–1208. doi: 10.1093/cvr/28.8.1199. [DOI] [PubMed] [Google Scholar]
- (32).Elzinga C, Westerhof N. Isolated cat trabeculae in a simulated feline heart and arterial system. Contractile basis of cardiac pump function. Circ Res. 1982;51:430–438. doi: 10.1161/01.RES.51.4.430. [DOI] [PubMed] [Google Scholar]
- (33).Leonard A, Bertero A, Powers JD, Beussman KM, Bhandari S, Regnier M, Murry CE, Sniadecki NJ. Afterload promotes maturation of human induced pluripotent stem cell derived cardiomyocytes in engineered heart tissues. J Mol Cell Cardiol. 2018;118:147–158. doi: 10.1016/j.yjmcc.2018.03.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (34).Campbell P. Permanent Magnet Materials and their Application. Cambridge University Press; 1996. [DOI] [Google Scholar]
- (35).Honshima TM, Y M, M Improvement of the corrosion resistance on Nd-Fe-B magnet with nickel plating. IEEE Trans Magn. 1989;25:3776–3778. doi: 10.1109/20.42430. [DOI] [Google Scholar]
- (36).Wei J, Sun J, Xu H, Shi L, Sun L, Zhang J. Effects of extremely low frequency electromagnetic fields on intracellular calcium transients in cardiomyocytes. Electromagn Biol Med. 2015;34:77–84. doi: 10.3109/15368378.2014.881744. [DOI] [PubMed] [Google Scholar]
- (37).Lenzi A, Gimmelli R, Fassina L, Isidori AM, Naro F, Gianfrilli D, Taglialatela M, Di Siena S, Soldovieri MV, Ambrosino P, Pellegrini M, et al. β-Adrenergic response is counteracted by extremely-low-frequency pulsed electromagnetic fields in beating cardiomyocytes. J Mol Cell Cardiol. 2016;98:146–158. doi: 10.1016/j.yjmcc.2016.07.004. [DOI] [PubMed] [Google Scholar]
- (38).Gulch RW, Lutz O. Influence of strong static magnetic fields on heart muscle contraction. Phys Med Biol. 1986;31:763–769. doi: 10.1088/0031-9155/31/7/006. [DOI] [PubMed] [Google Scholar]
- (39).Takahashi M, Saito A, Jimbo Y, Nakasono S. Evaluation of the effects of power-frequency magnetic fields on the electrical activity of cardiomyocytes differentiated from human induced pluripotent stem cells. J Toxicol Sci. 2017;42:223–231. doi: 10.2131/jts.42.223. [DOI] [PubMed] [Google Scholar]
- (40).Holden AV. The sensitivity of the heart to static magnetic fields. Prog Biophys Mol Biol. 2005;87:289–320. doi: 10.1016/j.pbiomolbio.2004.08.015. [DOI] [PubMed] [Google Scholar]
- (41).High WB, Sikora J, Ugurbil K, Garwood M. Subchronic in vivo effects of a high static magnetic field (9.4 T) in rats. J Magn Reson Imaging. 2000;12:122–139. doi: 10.1002/1522-2586(200007)12:1<122::AID-JMRI14>3.0.CO;2-C. [DOI] [PubMed] [Google Scholar]
- (42).Zablotskii V, Dejneka A, Kubinová Š, Le-Roy D, Dumas-Bouchiat F, Givord D, Dempsey NM, Syková E. Life on magnets: stem cell networking on micro-magnet arrays. PLoS One. 2013;8:e70416. doi: 10.1371/journal.pone.0070416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (43).Li F, Yuan Y, Guo Y, Liu N, Jing D, Wang H, Guo W. Pulsed magnetic field accelerate proliferation and migration of cardiac microvascular endothelial cells. Bioelectromagnetics. 2015;36:1–9. doi: 10.1002/bem.21875. [DOI] [PubMed] [Google Scholar]
- (44).Ma S, Zhang Z, Yi F, Wang Y, Zhang X, Li X, Yuan Y, Cao F. Protective Effects of Low-Frequency Magnetic Fields on Cardiomyocytes from Ischemia Reperfusion Injury via ROS and NO/ONOO. Oxid Med Cell Longev. 2013;2013 doi: 10.1155/2013/529173. 29173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (45).Bekhite MM, Figulla H-R, Sauer H, Wartenberg M. Static magnetic fields increase cardiomyocyte differentiation of Flk-1 + cells derived from mouse embryonic stem cells via Ca 2+ influx and ROS production. 2012 doi: 10.1016/j.ijcard.2012.02.020. [DOI] [PubMed] [Google Scholar]
- (46).Ma F, Li W, Li X, Tran B, Suguro R, Guan R, Hou C, Wang H, Zhang A, Zhu Y, Zhu Y. Novel protective effects of pulsed electro magnetic field ischemia/reperfusion injury rats. Biosci Rep. 2016;36:e00420. doi: 10.1042/bsr20160082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (47).Ventura C, Maioli M, Asara Y, Santoni D, Mesirca P, Remondini D, Bersani F. Turning on stem cell cardiogenesis with extremely low frequency magnetic fields. FASEB J. 2004;19:155–157. doi: 10.1096/fj.04-2695fje. [DOI] [PubMed] [Google Scholar]
- (48).Godier-Furn emont AF, Tiburcy M, Wagner E, Dewenter M, El-Armouche A, Lehnart SE, Vunjak-Novakovic G, Zimmermann W-H, Godier-Furnemont AFG, Tiburcy M, Wagner E, et al. Physiologic force-frequency response in engineered heart muscle by electromechanical stimulation. Biomaterials. 2015;60:82–91. doi: 10.1016/j.biomaterials.2015.03.055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (49).Sonnenblick EH. Force-velocity relations in mammalian heart muscle. Am J Physiol. 1962;202:931–939. doi: 10.1152/ajplegacy.1962.202.5.931. [DOI] [PubMed] [Google Scholar]
- (50).Siegel JH, Sonnenblick EH. Isometric Time-Tension Relationships as an Index of Myocardial Contractility. Circ Res. 1963;12:597–610. doi: 10.1161/01.RES.12.6.597. [DOI] [PubMed] [Google Scholar]
- (51).Sonnenblick EH, Evans S. Afterload as a primary determinant of ventricular performance. Am J Physiol. 1963;204:604–610. doi: 10.1152/ajplegacy.1963.204.4.604. [DOI] [PubMed] [Google Scholar]
- (52).Holubarsch C, Lüdemann J, Wiessner S, Ruf T, Schulte-Baukloh H, Schmidt-Schweda S, Pieske B, Posival H, Just H. Shortening versus isometric contractions in isolated human failing and non-failing left ventricular myocardium: Dependency of external work and force on muscle length, heart rate and inotropic stimulation. Cardiovasc Res. 1998;37:46–57. doi: 10.1016/S0008-6363(97)00215-0. [DOI] [PubMed] [Google Scholar]
- (53).Boudou T, Legant WR, Mu A, Borochin MA, Thavandiran N, Radisic M, Zandstra PW, Epstein JA, Margulies KB, Chen CS. A Microfabricated Platform to Measure and Manipulate the Mechanics of Engineered Cardiac Microtissues. TISSUE Eng Part A. 2012;18:910–919. doi: 10.1089/ten.tea.2011.0341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (54).Sonnenblick EH, Braunwald E, Morrow A. The Contractile Properties of Human Heart Muscle: Studies on Myocardial Mechanics of Surgically Excised Papillary Muscles. J Clin Invest. 1965;44:966–977. doi: 10.1172/JCI105214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (55).Ross J, Covell JW, Sonnenblick EH, Braunwald E. Contractile State of the Heart Characterized by Force-Velocity Relations in Variably Afterloaded and Isovolumic Beats. Circ Res. 1966;18:149–163. doi: 10.1161/01.RES.18.2.149. [DOI] [Google Scholar]
- (56).Quinones MA, Gaasch WH, Alexander AK. Influence of acute changes in preload, afterload, contractile state and heart rate on ejection and isovolumic indices of myocardial contractility in man. Circulation. 1976;53:293–302. doi: 10.1161/01.CIR.53.2.293. [DOI] [PubMed] [Google Scholar]
- (57).Dorn GW. The fuzzy logic of physiological cardiac hypertrophy. Hypertension. 2007;49:962–970. doi: 10.1161/HYPERTENSIONAHA.106.079426. [DOI] [PubMed] [Google Scholar]
- (58).von Anrep G. On the part played by the suprarenals in the normal vascular reactions of the body. J Physiol. 1912;45:307–317. doi: 10.1113/jphysiol.1912.sp001553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (59).Rosenblueth A, Alanís J, López E, Rubio R. The adaptation of ventricular muscle to different circulatory conditions. Arch Physiol Biochem. 1959;67:358–373. doi: 10.3109/13813455909072295. [DOI] [PubMed] [Google Scholar]
- (60).Parmley WW, Chuck L. Length-dependent changes in myocardial contractile state. Am J Physiol. 1973;224:1195–1199. doi: 10.1152/ajplegacy.1973.224.5.1195. [DOI] [PubMed] [Google Scholar]
- (61).Cingolani HE, Pérez NG, Cingolani OH, Ennis IL. The Anrep effect: 100 years later. Am J Physiol Hear Circ Physiol. 2013;304:H175–182. doi: 10.1152/ajpheart.00508.2012. [DOI] [PubMed] [Google Scholar]
- (62).Brunello E, Lombardi V, Irving M, Narayanan T, Reconditi M, Caremani M, Piazzesi G, Fusi L, Linari M. Force generation by skeletal muscle is controlled by mechanosensing in myosin filaments. Nature. 2015;528:276–279. doi: 10.1038/nature15727. [DOI] [PubMed] [Google Scholar]
- (63).Gsell MAF, Augustin CM, Prassl AJ, Karabelas E, Fernandes JF, Kelm M, Goubergrits L, Kuehne T, Plank G. Assessment of wall stresses and mechanical heart power in the left ventricle: Finite element modeling versus Laplace analysis. Int j Numer Method Biomed Eng. 2018;34:e3147. doi: 10.1002/cnm.3147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (64).Zhang Z, Tendulkar A, Sun K, Saloner DA, Wallace AW, Ge L, Guccione JM, Ratcliffe MB. Comparison of the young-laplace law and finite element based calculation of ventricular wall stress: Implications for postinfarct and surgical ventricular remodeling. Ann Thorac Surg. 2011;91:150–156. doi: 10.1016/j.athoracsur.2010.06.132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (65).Denys BG, Aubert AE, Denef B, Van de Werf F, De Geest H, Kesteloot H. Relationship between apexcardiogram, left ventricular pressure and wall stress. J Biomed Eng. 1982;4:9–16. doi: 10.1016/0141-5425(82)90020-6. [DOI] [PubMed] [Google Scholar]
- (66).Burns JW, Covell JW, Myers R, Ross J. Comparison of directly measured left ventricular wall stress and stress calculated from geometric reference figures. Circ Res. 1971;28:611–621. doi: 10.1161/01.RES.28.6.611. [DOI] [PubMed] [Google Scholar]
- (67).Zhong L, Ghista DN, Tan RS. Left ventricular wall stress compendium. Comput Methods Biomech Biomed Engin. 2012;15:1015–1041. doi: 10.1080/10255842.2011.569885. [DOI] [PubMed] [Google Scholar]
- (68).Yin FCP. Ventricular Wall Stress. Circ Res. 1981;49:829–842. doi: 10.1161/01.RES.49.4.829. [DOI] [PubMed] [Google Scholar]
- (69).Jackman CP, Carlson AL, Bursac N. Dynamic culture yields engineered myocardium with near-adult functional output. Biomaterials. 2016;111:66–79. doi: 10.1016/j.biomaterials.2016.09.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (70).Vollert I, Seiffert M, Bachmair J, Sander M, Eder A, Conradi L, Vogelsang A, Schulze T, Uebeler J, Holnthoner W, Redl H, et al. In vitro perfusion of engineered heart tissue through endothelialized channels. Tissue Eng Part A. 2014;20:854–863. doi: 10.1089/ten.TEA.2013.0214. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.