Effects of Collagen Heterogeneity on Myocardial Infarct Mechanics in a Multiscale Fiber Network Model

Abstract

The scar that forms after a myocardial infarction is often characterized by a highly disordered architecture but generally exhibits some degree of collagen fiber orientation, with a resulting mechanical anisotropy. When viewed in finer detail, however, the heterogeneity of the sample is clear, with different subregions exhibiting different fiber orientations. In this work, we used a multiscale finite element model to explore the consequences of the heterogeneity in terms of mechanical behavior. To do so, we used previously obtained fiber alignment maps of rat myocardial scar slices (n = 15) to generate scar-specific finite element meshes that were populated with fiber models based on the local alignment state. These models were then compared to isotropic models with the same sample shape and fiber density, and to homogeneous models with the same sample shape, fiber density, and average fiber alignment as the scar-specific models. All simulations involved equibiaxial extension of the sample with free motion in the third dimension. We found that heterogeneity led to a lower degree of mechanical anisotropy and a higher level of local stress concentration than the corresponding homogeneous model, and also that fibers failed in the heterogeneous model at much lower macroscopic strains than in the isotropic and homogeneous models. Taken together, these results suggest that scar heterogeneity may impair myocardial mechanical function both in terms of anisotropy and strength, and that individual variations in scar heterogeneity could be an important consideration for understanding scar remodeling and designing therapeutic interventions for patients after myocardial infarction.

1. Introduction

Each year, nearly 1 million Americans experience a myocardial infarction (MI), wherein a region of myocardial ischemia results in cardiomyocyte death and subsequent replacement by collagenous scar tissue [1]. Past work has shown that the mechanical properties of the resulting scar are important for determining long-term cardiac function and risk for post-MI complications such as cardiac rupture and heart failure [2,3]. As is the case for many collagenous tissues, the particular mechanical properties of MI scar are largely determined by the underlying structure of its primary matrix component—collagen fibers. Therefore, many studies have extensively measured healing infarcts for global properties such as bulk collagen density, cross-linking, orientation, and alignment [4–10]. Recently, we also assessed localized variations in collagen structures and found stark spatial heterogeneities of fiber orientations [11]. Specifically, collagen fibers from rat infarct scar samples displayed high alignment within small subregions (∼250 × 250 μm), but the orientation of those fibers varied greatly from subregion to subregion such that the global alignment for the bulk scar appeared more random.

Structural heterogeneity has been observed in a variety of tissues including heart valves, facet capsular ligaments, aortic aneurysms, and tendon-to-bone insertion points [12–15]. Aneurysms, for example, exhibit significant variation in matrix and cellular compositions around the circumferential direction, which is consistent with similar spatial variation in matrix protease activity and spatial variation in the tensile moduli and strengths of aneurysm samples taken from different regions [15,16]. From a mechanical perspective, fiber heterogeneity could likely alter how infarct scar material redistributes stress and strain under loading, potentially giving rise to stress/strain concentrations, failure points, altered apparent stiffness, and/or altered degrees of anisotropy. Thus, the objective of this study was to test the effects of collagen fiber orientation heterogeneity on both local and global mechanical responses of infarct scar tissue. Herein, we applied a previously published, computational model of multiscale fiber network mechanics to explore the mechanical responses of subject-specific scar orientation maps obtained from rat MI tissue sections.

2. Methods

2.1. Fiber Map Generation From Scar Samples.

In a previously reported study, Fomovsky and Holmes obtained scar samples from healing rats at 1, 2, 3, and 6 weeks after permanent coronary artery ligation [10]. Upon sacrifice of each animal, they arrested and excised the rat hearts, then sectioned samples (7 μm thick) in parallel to the epicardial plane, and stained collagen fibers with picrosirius red. In a follow-up study, we previously imaged a selection of those midwall sections under 20× magnification with automated stitching (Aperio ScanScope, Leica Biosystems Inc., Buffalo Grove, IL), and used a gradient-based image processing method (MatFiber, code freely available at the given website,1 and implemented in matlab) to generate collagen orientation maps for each sample (Fig. 1(a)) [11].

Fig. 1.

(a) Excised rat scar samples stained with picrosirius red to show collagen fiber orientations in the circumferential (C)–longitudinal (L) plane. (b) Collagen fiber orientation extracted from the tissue sample using gradient-based image processing. Each pixel was assigned an angle from –90 deg to 90 deg, representing the angle deviation from the circumferential direction (C = 0 deg, L = –90 deg or 90 deg). (c) A 2D finite element mesh was created to encompass the entire tissue area, and a nearest-neighbor linear interpolation was performed to complete the data set where fiber angle data was previously missing in (b). (d) The 2D mesh was extruded into the third dimension to create a tissue slab of uniform thickness. Aligned networks were created for each of the elements based on the fiber angle data, and each sample was subjected to uniform biaxial extension, indicated by the arrows.

Due to sectioning artifacts in the samples, tissue was not present in some areas, leading to gaps in the raw fiber maps (Fig. 1(b)). To fill the entirety of the tissue geometry and prepare the sample for our finite element simulations, the two-dimensional (2D) outline of each tissue piece was traced, extruded into three-dimensional, and then meshed with roughly 600 hexahedral elements to create a finite element mesh of the tissue sample (Fig. 1(c)). Each sample had an extruded thickness of 0.25 mm, to represent a myocardial tissue slab of uniform thickness. A linear interpolation was performed on the 2D fiber orientation scatter data to produce a full fiber orientation map for the entire sample within the finite element mesh (Fig. 1(c)). After the image analysis, a fiber-based multiscale finite element model was generated and solved (Fig. 1(d)) as described in Sec. 2.3.

2.2. Fiber Network Model Generation.

Three different types of networks (Fig. 2) were created to compare the effects of network orientation:

Fig. 2.

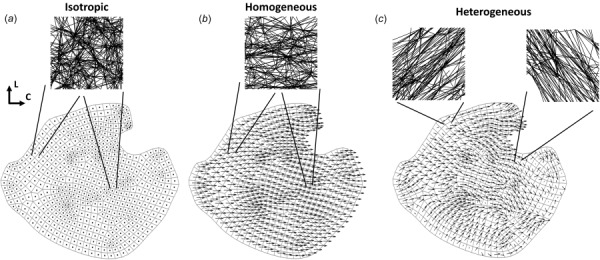
An example of the three different network cases used for each sample. The 2D finite element mesh is shown, with a quiver plot of fiber orientation overlaid on each element. Quiver plot arrows indicate the fiber direction, and the arrow length corresponds to degree of alignment (i.e., dots indicate no degree of alignment (isotropic), while longer arrows indicate higher degree of alignment (homogeneous and heterogeneous)): (a) the same isotropic network was used for every element in the isotropic case, where the network had no degree of alignment, (b) likewise, the same network was used for every element in the homogeneous case, where the network was now aligned in the average fiber direction, with the average degree of alignment in that direction. In the example shown here, the average fiber direction is close to the circumferential direction, and (c) different networks were used for each element in the heterogeneous case, where networks were constructed based on local fiber orientations and degrees of alignment for each element.

• (1)The same isotropic network used for every element (the isotropic case, Fig. 2(a)).
• (2)The same aligned network used for every element, where the network was aligned in the average fiber direction for the whole sample with the average degree of alignment (the homogeneous case, Fig. 2(b)).
• (3)Differently aligned networks for each finite element (the heterogeneous case, Fig. 2(c)).

Networks were comprised of collagen fibers defined by the constitutive relation

$$F=\frac{EA}{B}(e^{(B*{\mathrm{ϵ}}_G)}-1)$$ (1)

where F was fiber force, E was fiber modulus, A was fiber cross-sectional area, B was fiber nonlinearity, and ϵ_G was the fiber green strain. Each fiber also had a critical failure stretch, λ_f, where the fiber failed if it exceeded the critical stretch, and was removed from the network by reducing its modulus ten orders of magnitude. A neo-Hookean component was also included in parallel to collagen fibers, resembling nonfibrous material. Collagen fiber parameters were based on previous values used for aortic tissue [17] and collagen gels [18], where E = 10 MPa, A = 0.0314 mm², B = 2.5, and λ_f = 1.42. The volume fraction of collagen fibers was 10% for all of the networks, based on Ref. [10]. These parameters remained constant for all the network cases in order to isolate the specific effect of network alignment on mechanical response.

The use of an orientation tensor (Ω) was selected to define network alignment, as it naturally arises in physical systems [19], and contains the information for both the direction and strength of alignment. In a general case, the orientation tensor takes the form of

$$\Omega =\left[\begin{array}{cc}\hspace{0.17em}{\text{cos}}^2(\varphi )& \hspace{0.17em}\text{sin}(\varphi )\text{cos}(\varphi )\\ \hspace{0.17em}\text{sin}(\varphi )\text{cos}(\varphi )& \hspace{0.17em}{\text{sin}}^2(\varphi )\end{array}\right]$$ (2)

where ϕ is the angle that specifies the direction of alignment. For the isotropic case, the same Delaunay isotropic network was used for each of the 15 samples, and was created with the orientation tensor

$$\Omega =\left[\begin{array}{cc}0.495& 0.004\\ 0.004& 0.505\end{array}\right]$$ (3)

producing no preferred fiber direction or degree of alignment.

The network for each homogeneous case was an aligned Delaunay network, created according to the overall sample orientation tensor

$$\langle \Omega \rangle =\frac{1}{N}\sum _{i=1}^N\left[\begin{array}{cc}{\Omega }_{11}^{\left(i\right)}& {\Omega }_{12}^{\left(i\right)}\\ {\Omega }_{21}^{\left(i\right)}& {\Omega }_{22}^{\left(i\right)}\end{array}\right]$$ (4)

where i is the element number and N is the number of elements. The average fiber direction (θ) and degree of alignment (α) were calculated as

$$\theta ={\text{tan}}^{-1}\left(\frac{v_y}{v_x}\right)$$ (5)

$$\alpha ={\Lambda }_1-{\Lambda }_2$$ (6)

where v_y and v_x are the components of the eigenvector corresponding to the largest eigenvalue, Λ₁ is the largest eigenvalue, and Λ₂ is the smallest eigenvalue. θ is taken as the angle relative to the circumferential direction (horizontal), and ranges from –90 deg to 90 deg, while α ranges from 0 to 1, where 0 = no alignment, and 1 = fully aligned. Average angle and degree of alignment for each sample are shown in Table 1. The heterogeneous networks were created according to the orientation tensor and degree of alignment for each element, Ω⁽ⁱ⁾ and α⁽ⁱ⁾, where Ω is of the same form as the homogeneous case, created by averaging over the space of each individual finite element instead of the entire sample. Thus, the heterogeneous case contains differing local angles and degrees of alignment for each element, but on average has the same overall preferred fiber direction and degree of alignment as the homogeneous case.

Table 1.

The average angle and degree of alignment for each of the 15 samples

Angle (θ)	Degree of alignment (α)
25.8 deg	0.22
75.6 deg	0.04
–7.5 deg	0.20
45.0 deg	0.35
8.9 deg	0.43
–0.56 deg	0.33
65.9 deg	0.11
23.3 deg	0.25
–7.6 deg	0.44
34.2 deg	0.41
24.0 deg	0.25
15.7 deg	0.25
58.2 deg	0.15
16.6 deg	0.16
5.0 deg	0.16

2.3. Model Simulations.

A custom multiscale finite element model [17,18] was used to simulate each sample (n = 15) in uniform biaxial extension by displacing the boundary nodes of the mesh outward (Fig. 1(d)), with no shear stress on the boundaries. Results were considered at 20% strain to allow for comparison among all samples, as this was the maximum strain reached prior to failure in one sample. Simulations were run on 256-core parallel processors at the University of Minnesota Supercomputing Institute.

2.4. Statistics.

Paired t-tests were performed (graphpad, prism 6) on the homogeneous and heterogeneous data to compare results, as the differences between these two groups are of primary concern. A linear regression was performed on the homogeneous and heterogeneous data to determine the strength of trends for the anisotropy ratio and peak stress in the sample.

3. Results

Following biaxial extension to 20% strain, samples were analyzed for each of the three network cases. The stress (P_ii) and strain (E_ii) for each sample were calculated in the direction of the overall average fiber direction, n₁₁, and the perpendicular direction, n₂₂ (Figs. 3(a) and 4(a)). A representative sample with strong alignment (Fig. 3) demonstrates a few trends present in the highly aligned samples: (1) the macroscale stresses for the homogeneous case exhibit a higher degree of anisotropy compared to the heterogeneous and isotropic case (Fig. 3(b)), (2) homogeneous and isotropic strains, stresses, and fiber failure are homogeneous throughout the sample, while the heterogeneous case displays localized hotspots of strain, stress, and fiber failure (Fig. 3(c)), and (3) the peak strain, stress, and percentage of failed fibers is significantly higher in the heterogeneous case (Fig. 3(c)). These trends are similar, but less pronounced in samples with weaker alignment, as shown in Fig. 4 for a representative weakly aligned sample. Mechanical anisotropy for the homogeneous and heterogeneous cases is weaker (Fig. 4(b)), accompanied by lower strains, stresses, and percentage of failed fibers (Fig. 4(c)) in the heterogeneous case.

Fig. 3.

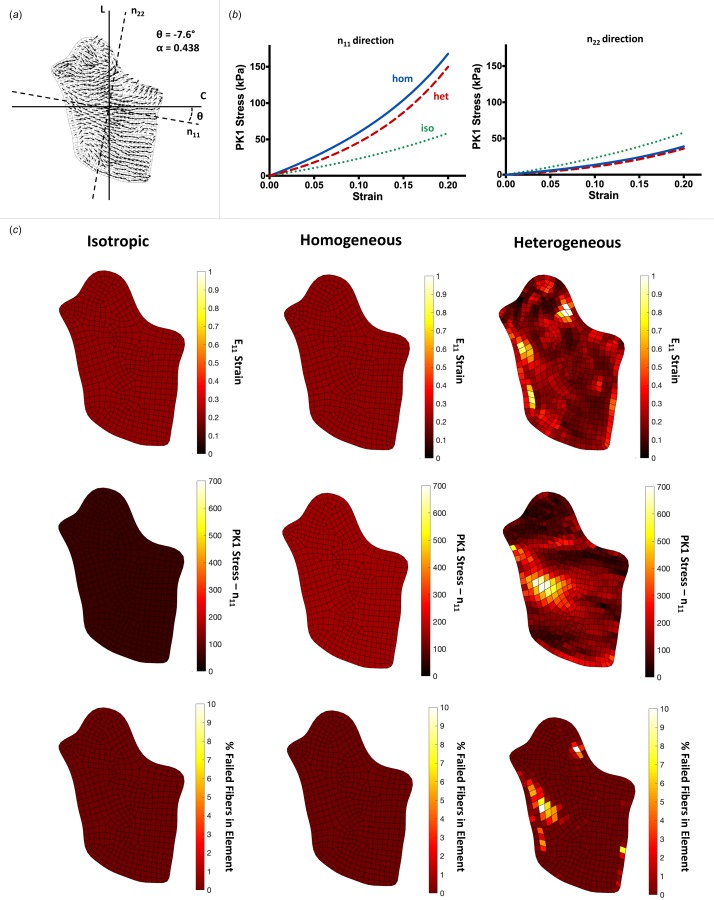
A representative, comprehensive analysis of the data, shown for an image with a high degree of alignment: (a) the 2D mesh and quiver plot is shown for the sample, where the n₁₁ direction indicates the average fiber orientation for the sample, and the n₂₂ direction is perpendicular to n₁₁. The angle relative to circumferential (θ) and the degree of alignment (α) are shown, (b) averaged macroscale stress plots shown in the n₁₁ (left) and n₂₂ (right) directions for each of the three cases, isotropic (green, dotted line), homogeneous (blue, solid line), and heterogeneous (red, dashed line). For highly aligned samples, the homogeneous case was more anisotropic on average, displaying higher stresses than the heterogeneous or isotropic stress for the n₁₁ direction, but lower stresses in the n₂₂ direction, and (c) heatmaps shown on the sample for the isotropic (left column), homogeneous (middle column), and heterogeneous (right column) cases, displaying the E₁₁ strain (top row), PK1 stress in the n₁₁ direction (P₁₁, middle row), and % of fibers failed in each element (bottom row). Isotropic and homogeneous cases displayed homogeneous strain, stress, and fiber failure throughout all of the samples, while the heterogeneous case experienced localized areas of high strain, stress, and fiber failure.

Fig. 4.

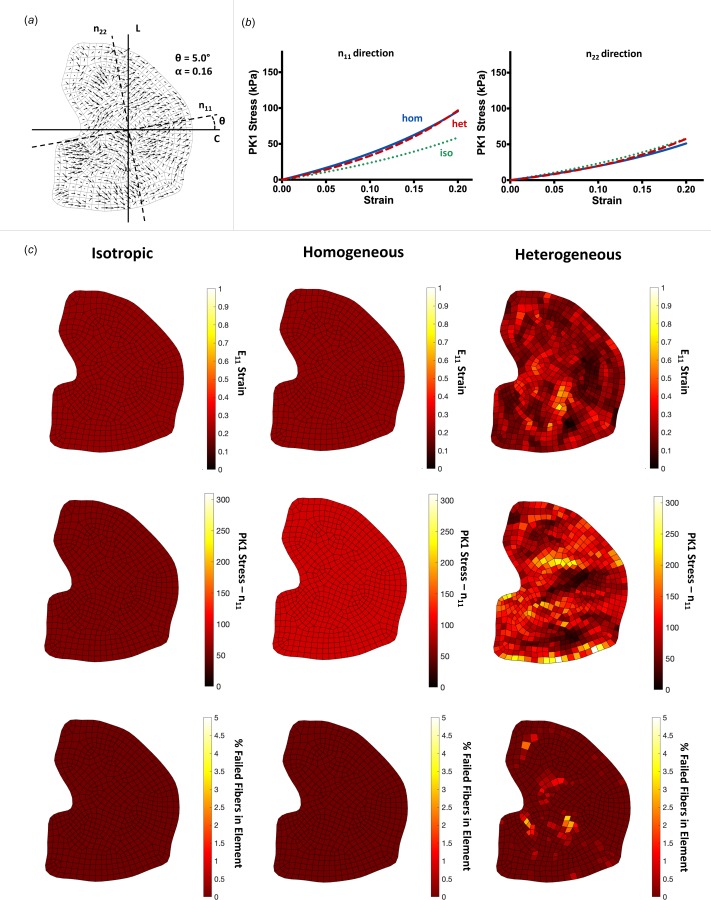
A representative analysis of the same from as Fig. 3, shown for a sample with degree of alignment: (a) the quiver plot shows a lesser degree of preferred fiber angle and degree of alignment, (b) averaged macroscale stresses are very similar between the three network cases for both the n₁₁ and n₂₂ directions. The amount of anisotropy is similar between the homogeneous and heterogeneous samples, on average, and (c) heatmaps shown again for each of the network cases. As in the highly aligned images, the isotropic and homogeneous cases display homogeneous strains, stresses, and fiber failure. The heterogeneous case shows the same trend as the highly aligned case, to a lesser degree. The maximum strain, stress, and % of failed fibers are lower in cases with low degree of alignment.

The interactions between anisotropy and heterogeneity can be seen in the plots of Fig. 5. For these plots, the location of a point indicates a sample's degree of alignment (y-axis) and heterogeneity (quantified as the standard deviation of orientation over the finite elements and measured on the x-axis), and the color of the point shows the degree of the resulting effect. Throughout all the samples, there is a trend of increasing anisotropy linked to increasing degree of alignment (Fig. 5(b)). As the degree of alignment rises, the anisotropy ratio (P₁₁/P₂₂) increases in both the homogeneous (R² = 0.97) and heterogeneous (R² = 0.86) conditions. The maximum stress in the sample also has an increasing trend with increasing degree of alignment for the homogeneous case (R² = 0.96, Fig. 5(c)). There was no trend, however, related to the peak stress experienced in the sample with increasing degree of alignment for the heterogeneous case (R² = 0.03, Fig. 5(c)). When considering fiber failure, the heterogeneous case consistently required less strain (22.2%±0.79%, mean ±95% CI) to initiate failure in the sample compared to homogeneous (31.4%±1.27%) and isotropic (32%±0%) cases (Fig. 5(d)).

Fig. 5.

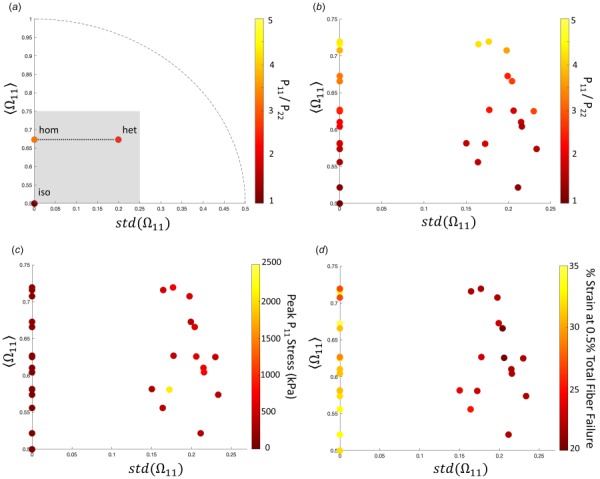
Plots analyzing the differences between each of the network cases for all the samples: (a) a representative plot for one sample is shown to illustrate how the plots work. The y-axis displays the average Ω₁₁ for the sample, while the x-axis displays the standard deviation of Ω₁₁ over all elements within the sample. Thus, the y-axis represents how strongly aligned the sample is on average (0.5 = isotropic, 1 = perfectly aligned), and the x-axis represents how strongly the sample deviates from its average alignment (0 = no deviation (homogeneous), 0.5 = strong deviation (heterogeneity)). Each sample has the three network cases plotted for the given variable. The isotropic case always corresponds to (0, 0.5), as there is no degree of alignment, or deviation from the average. The homogeneous and heterogeneous cases lie on a horizontal line, as they have the same average degree of alignment, but differing variation from the alignment in the heterogeneous case. The dotted line shows the range of possible ($\langle {\Omega }_{11}\rangle ,\hspace{0.17em}\text{std}({\Omega }_{11})$) pairs. The gray box contains all of the samples that were studied and sets the zoomed-in plot area shown for (b), (c), and (d). (b) The ratio of P₁₁ to P₂₂ is shown at 20% strain for each of the samples, as a measure of anisotropy. As degree of alignment increases, so does the degree of anisotropy. The effect is slightly more pronounced in the homogeneous case. (c) Peak P₁₁ stresses are consistently higher in the heterogeneous case compared to homogeneous and isotropic cases but do not show any obvious trend within the heterogeneous model results. (d) The % strain required to fail 0.5% of the fibers in the sample is shown for each case. For the isotropic and homogeneous cases, a much higher strain must be reached in order to initiate failure in the sample. In the heterogeneous cases, the strain to initiate failure is much lower.

When pooling all samples and comparing differences between the network cases, the heterogeneous condition exhibited a significant difference in maximum strain (Fig. 6(a)) and stress (Fig. 6(b)) compared to the isotropic and homogeneous conditions. The isotropic and homogeneous cases showed a similar maximum strain, but the homogeneous case displayed higher peak stress than the isotropic case. As seen in the representative samples (Figs. 3 and 4), the homogeneous and heterogeneous cases present higher anisotropy compared to the isotropic case, with the homogeneous case showing a trend of higher anisotropy compared to the heterogeneous case (Fig. 6(c)). Furthermore, fiber failure is overwhelmingly more present in the heterogeneous case, exhibiting higher total fibers failed (Fig. 6(d)), percentage of elements with failed fibers (Fig. 6(e)), and percentage of fibers failed within the worst element (Fig. 6(f)) compared to the homogeneous case, which has limited fiber failure at 20% strain. The isotropic case experienced no fiber failure in any elements at 20% strain.

Fig. 6.

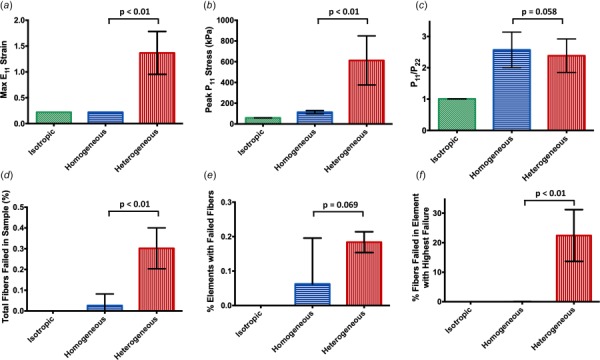
Bar plots containing the mean ±95% CI for each of the three network cases at 20% strain, with p-values shown for the comparison between the homogeneous and heterogeneous case: (a) and (b) the maximum E₁₁ strain and P₁₁ stress experienced in a single element for the samples was much higher in the heterogeneous case compared to the homogeneous and isotropic case, (c) the degree of anisotropy in the homogeneous and heterogeneous case was much higher than the isotropic case. The homogeneous case displayed a slightly higher degree of anisotropy overall compared to the heterogeneous case, and (d), (e), and (f) the amount of fiber failure and elements containing failed fibers was significantly higher for the heterogeneous case.

Overall, the results show that fiber heterogeneity vastly affects the mechanical behavior of the tissue on the macroscopic level. Despite the same average fiber direction and degree of alignment in the homogeneous and heterogeneous cases, the results show a decrease in anisotropy for the heterogeneous case, joined by an increase in local peak strains, stress, and fiber failure. These localized events of high strain, stress, and fiber failure within the heterogeneous samples emphasize the notion that overall tissue behavior (and thus, tissue failure) is highly dependent on the underlying fibrous structure.

4. Discussion

4.1. Heterogeneous Collagen Structure Produces Heterogeneous Stresses and Strains.

After an MI, ischemic myocardium is infiltrated by a swift and large inflammatory wave that serves to degrade necrotic myocytes and recruit cardiac fibroblasts into the wound site for collagen production [20,21]. The resulting fiber network structure within the collagenous scar is a key determinant of infarct mechanical properties and critically affects cardiac performance. Prior studies have observed a range of scar structures with variable collagen densities and alignments across infarcts from different cardiac locations and different experimental models, but these reported structures typically represented bulk measurements of the global, aggregate scar [7–10]. Recently, we observed and quantified regional heterogeneity of collagen fiber orientations within individual scar samples [11]. We specifically found that both collagen fibers and cells demonstrated strong alignment in small subregions of rat scars from 1 to 6 weeks post-MI, but fiber and cell orientations varied greatly from subregion to subregion resulting in clearly observable spatial heterogeneities.

From an electrical perspective, previous work has shown that spatial variations in scar geometry can lead to dangerous arrhythmias in the heart as tortuous paths can produce nonuniform and re-entrant currents [3]. But, no other study (to our knowledge) has examined the effects of heterogeneity on mechanical properties of the scar, so our current objective was to test mechanical behaviors of subject-specific infarct orientation maps. In the current fiber network simulations, heterogeneous fiber orientations resulted in corresponding heterogeneous stress and strain fields. While homogeneous scars exhibited uniformly low stresses/strains, heterogeneous scars led to high regional variations with some subregions under very low stress/strain and other subregions under very high stress/strain likely due to the redistribution of loads (e.g., stress shielding).

It is currently unknown how fiber heterogeneity emerges and evolves in healing scars. Collagen is deposited and arranged by fibroblasts that infiltrate the wound during the healing cascade, and it is of course possible that the wound environment presents heterogeneous chemical gradients or heterogeneous pre-existing structural cues that direct fibroblasts into a heterogeneous arrangement, which the collagen network then follows. However, we previously used an agent-based computational model to support an alternative hypothesis that structural heterogeneity can emerge even from an initially homogeneous environment due to cell–cell and cell–matrix interactions within the system [11]. Specifically, long-range cell sensing and long-range remodeling were predicted to produce local self-reinforcing pockets of cell and matrix alignment. Perturbing these interactions, therefore, may offer a therapeutic approach for controlling the degree of fiber heterogeneity. To guide potential therapeutic modulation of this heterogeneity, we sought to test the mechanical implications of fiber orientation heterogeneity on tissue anisotropy and failure.

4.2. Effect of Heterogeneity on Scar Tissue Anisotropy.

Isotropic samples displayed isotropic material properties (i.e., same stress–strain behavior in all directions), whereas the homogeneous samples displayed anisotropic properties with stiffer behavior parallel to the direction of global fiber alignment (i.e., higher P₁₁ versus P₂₂ at the same levels of strain). Not surprisingly, the samples with higher degrees of alignment demonstrated higher degrees of anisotropy. Scar anisotropy is clinically interesting as a potential therapeutic target—both computational and experimental reports have indicated that highly anisotropic scars oriented in the longitudinal direction may benefit left ventricular function much more than isotropic scars [9,22].

Heterogeneity within sample orientations usually dampened anisotropy. In other words, the anisotropic stress ratio P₁₁/P₂₂ was lower in the majority (11/15) of heterogeneous samples compared to their corresponding homogeneous counterparts, even though both samples across each pair demonstrated identical global fiber alignment. This finding is consistent with previous results and presumably due to the ability for stiff and compliant regions to redistribute loads/displacements [23,24]. Given that a high degree of anisotropy may provide a therapeutic benefit for improving MI properties, our current results suggest that orientation heterogeneity in the infarct may act as a deterrent to achieving this benefit.

4.3. Effect of Heterogeneity on Scar Tissue Failure.

Infarct rupture is a rare but catastrophic event occurring when the infarct is too weak to support the ventricle's cavity pressure, leading to mechanical failure of the tissue. Though it only afflicts <3% of infarct patients, left ventricle free wall rupture carries a 60%–90% mortality rate, and typically occurs very early in the healing time course within the first few days [25]. The early occurrence is thought to coincide with a narrow window when inflammation and protease-mediated degradation of the necrotic myocardium has peaked but prior to the influx of fibroblasts and newly generated matrix material [2].

While the imbalance in infarct mass turnover is likely to contribute to scar tissue vulnerability, our current results suggest that fiber orientation heterogeneity might also lead to infarct rupture. Heterogeneous samples exhibited substantially higher failure rates compared to their homogeneous counterparts, measured by total percentage of failed fibers across the sample, percentage of elements with failed fibers, and percentage of failed fibers in the weakest element. Such failure rates were not surprising given the elevated peak stresses in heterogeneous versus homogeneous samples. The fiber failure rate was very high in just a few elements that corresponded to the locations of peak stresses and strains (i.e., failure was a localized event). However, we should note that the degree of stretch subjected in our simulations (∼20%) is considerably higher than most in vivo strains measured in these healing rat infarcts, which averaged ∼5% (though some infarcts did reach up to 16% in vivo) [10]. Also, since the earliest obtained samples were acquired at 1 week post-MI, it is unknown whether fiber heterogeneity actually emerged during the rupture-prone window around 2–3 days.

4.4. Limitations of This Study.

There are a few important limitations to our model predictions. First, since the goal of this study was to explore the effects of orientation heterogeneity on scar mechanics, we chose to ignore other structural heterogeneities like spatial variations in collagen density and other coronary blood vessels. These other heterogeneous inclusions may also contribute interesting and important roles in scar mechanics. We also assumed each sample had identical collagen densities, which we know is not true, but enabled us to isolate the role of fiber orientation heterogeneity alone. Now that we have isolated the effects of orientation heterogeneity, future work can combine other sources of heterogeneous mechanics for improved predictions.

A second limitation is that our current simulations focused on single “slabs” of scar tissue with uniform collagen structure throughout the 0.25 mm thickness of the material. The free wall thickness of an unloaded, healthy left ventricle in rats is approximately 1–2 mm, and thickness of unloaded, infarct scar tissue drops as low as 0.4 mm [3]. Across the full thickness of healthy myocardium, average myocyte orientation varies from around –60 deg at the epicardium to around +60 deg at the endocardium; this transmural variation is also present in scar collagen structure but the variation is reduced to approximately –30 deg to +30 deg [26]. We have not yet analyzed how localized heterogeneities vary through the full thickness of the infarct scar (i.e., variation in the radial direction); the samples used herein were sections taken near the midwall so our current simulations describe the planar heterogeneous behavior within a scar slab representing a partial thickness (i.e., variation in the circumferential–longitudinal plane). Future work with three-dimensional orientation maps of the full thickness (capturing heterogeneity in all three directions) will enable predictions of the full scar behavior.

As a third limitation, we are simulating acute mechanical responses as a single snapshot of scar behavior versus structure. Of course, scar tissue in vivo is dynamically remodeling as cells continue to deposit, degrade, and rearrange collagen fibers in response to chemical, structural, and mechanical signals. Here, we show that heterogeneous structure gives rise to heterogeneous stress and strain fields with increased peak stresses and increased failure rates. However, long-term implications of this structure will also depend on how cells continue to remodel their local matrix across the spatially varying mechanics. In our previous agent-based simulations of scar heterogeneity, we showed that cell–matrix interactions over long ranges could give rise to heterogeneous structures, but those simulations assumed homogeneous mechanical cues for the entire tissue over the remodeling time course [11]. Future modeling work that couples cell behaviors with heterogeneous mechanics will help predict the evolving interplay of scar structure and properties over the chronic, healing time course.

5. Conclusions

In summary, this work highlights the importance of microenvironment considerations within the larger scope of macroscopic infarct tissue mechanics. Our results show a striking dependence on local fiber orientation and degree of alignment, where samples with heterogeneous networks exhibit significantly different deformation patterns and overall mechanics when compared to samples with homogeneous and isotropic networks. Most notably, while homogeneous and heterogeneous cases share the same average fiber direction and degree of alignment for the entire sample, several factors, such as anisotropy, peak strain, peak stress, and fiber failure, differ between the two cases. These results support the conclusion that infarct mechanics depend on the underlying fiber orientation and degree of alignment, which affect the tissue behavior and tissue failure on a whole.

Funding Data

• National Science Foundation Graduate Research Fellowship Program (Grant No. 00039202; Funder ID: 10.13039/501100008982).

• National Institutes of Health (Funder ID: 10.13039/100000002).

• Achievement Rewards for College Scientists (ARCS) (Funder ID: 10.13039/100008227).