On the Relative Impact of Intraluminal Thrombus Heterogeneity on Abdominal Aortic Aneurysm Mechanics

Abstract

Intraluminal thrombus (ILT) is present in the majority of abdominal aortic aneurysms (AAA) of a size warranting consideration for surgical or endovascular intervention. The rupture risk of AAAs is thought to be related to the balance of vessel wall strength and the mechanical stress caused by systemic blood pressure. Previous finite element analyses of AAAs have shown that ILT can reduce and homogenize aneurysm wall stress. These works have largely considered ILT to be homogeneous in mechanical character or have idealized a stiffness distribution through the thrombus thickness. In this work, we use magnetic resonance imaging (MRI) to delineate the heterogeneous composition of ILT in 7 AAAs and perform patient–specific finite element analysis under multiple conditions of ILT layer stiffness disparity. We find that explicit incorporation of ILT heterogeneity in the finite element analysis is unlikely to substantially alter major stress analysis predictions regarding aneurysm rupture risk in comparison to models assuming a homogenous thrombus, provided that the maximal ILT stiffness is the same between models. Our results also show that under a homogeneous ILT assumption, the choice of ILT stiffness from values common in the literature can result in significantly larger variations in stress predictions compared to the effects of thrombus heterogeneity.

Introduction

Abdominal aortic aneurysms (AAAs) are common and can rapidly result in death if it rupture [1,2]. Maximum aneurysm diameter serves as a metric to assess aneurysm rupture risk, but it is imperfect, and a subset of aneurysms will still rupture despite not meeting the common 5.5 cm threshold for surgical or endovascular intervention [3]. A growing body of work suggests that imaging-based biomechanical assessment of AAA stability may have utility in identifying patients at risk for rupture and who would benefit from early intervention [4–8]. The sophistication of imaging-based finite element modeling of patient-specific AAAs has increased through the years, and the representation of many aneurysm features and relevant physiology have become more realistic and complex. Advances in constitutive relations for the vessel wall, estimations of the zero-pressure state and incorporation of residual stresses, specification of variable vessel wall thickness, and fluid–structure interaction are increasingly common in the literature [9–13]. Other aneurysm features, such as intraluminal thrombus (ILT), have received comparatively little attention.

Intraluminal thrombus is nearly ubiquitous in larger aneurysms, and its deposition has been related to shear-mediated activation of platelets, exposure to thrombogenic factors at the vessel wall, and increased flow residence time and decreased wall shear stress within the aneurysm belly [14–16]. ILT has been examined at open AAA repair and at autopsy and is noted to take a variety of forms: (1) largely solid and with a relatively homogeneous appearance and gradual changes in stiffness through its thickness; (2) heterogeneous, with a solid luminal component and disintegrated or disorganized outer/abluminal component; (3) solid, but with a discretely layered appearance and layer-specific mechanical characteristics [16–18].

In the earliest investigations of AAA mechanics, ILT was largely excluded from the analysis. Later, the influence of ILT in AAA wall mechanics was disputed. Conflicting theories and observations were presented regarding: transmission of luminal pressure through the thrombus to the vessel wall; the role of thrombus in “cushioning” the underlying wall from stress; and the concept of an ILT-mediated reduction in underlying wall strength, thought to be secondary to induced hypoxia and inflammation [19–22].

Over the past several years, AAA finite element analysis has typically included ILT, as several studies have demonstrated its role in reducing and homogenizing wall stress despite, transmitting nearly the entire luminal pressure to the underlying wall [20,22–24]. The vast majority of imaging-based analyses rely on computed tomography (CT) for geometric boundary conditions and material distributions. Since CT cannot resolve thrombus heterogeneity [25,26], ILT is most commonly treated as a homogenous material. Relatively few studies consider idealized variation of ILT stiffness throughout its thickness. Magnetic resonance imaging (MRI) is capable of resolving ILT features, and several studies have reported signal characteristics that correlate with distinct ILT types [17,18,27,28]. Those studies have focused on ILT signal as it might pertain to thrombus organization in the excluded aneurysm sac status post endovascular repair, or as it might relate to AAA expansion rate. To the best of our knowledge, no study has used this patient-specific ILT heterogeneity information to refine the AAA mechanical analysis. In this work, we use MRI to delineate ILT heterogeneity and then apply this information in patient-specific finite element analyses. Results obtained under differing assumptions of ILT mechanical character are compared to assess the relative influence of ILT heterogeneity on AAA wall mechanics.

Materials and Methods

Magnetic Resonance Imaging and Subject Selection.

Our group follows a cohort of subjects with AAA, performing longitudinal comprehensive MRI evaluation of their aneurysms. Among the imaging data collected, MRI sequences useful to construct finite element models including 3D MRA, 1.3 mm isotropic resolution; T1W black blood (DANTE-SPACE), 1.3 mm in-plane and 1.3 mm interpolated through-plane resolution; contrast enhanced VIBE, 1.3 mm isotropic resolution. Details of the imaging parameters can be found in previous publications [26,29]. TrueFISP was also acquired for improved outer wall boundary delineation, with 1.2 mm isotropic resolution.

In order to explore a range of physiological conditions, seven subjects were selected from our larger cohort as their AAAs demonstrated delineations between two dominant ILT layers on T1-weighted black blood imaging and spanned a range of ILT volumes, heterogeneity, and spatial distribution. Inclusion of subjects was based solely on these ILT features and image data quality suitable for constructing computational models. For all cases, the luminal component of the ILT demonstrated predominantly decreased signal intensity compared to the more peripheral abluminal component, as shown in Fig. 1. All medical imaging was performed and subject data collected following approval by our institutional review board and informed subject consent. The geometric, compositional, and demographic information for the seven cases is provided in Table 1, in which “% inner ILT” refers to the fraction of total thrombus volume contributed by the inner layer.

Fig. 1.

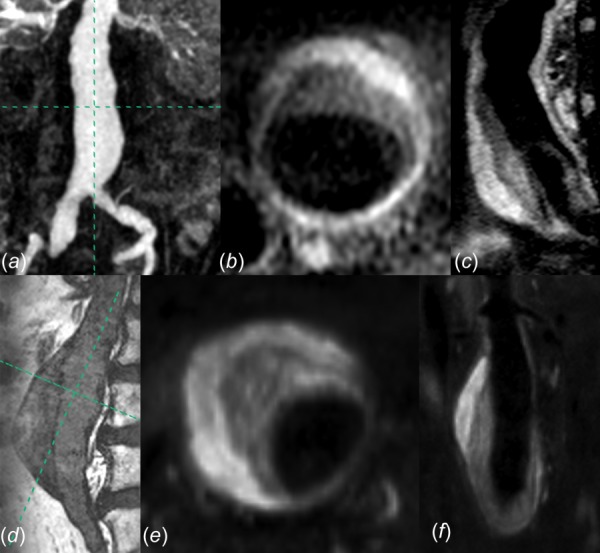
(a) Coronal maximum intensity projection image of MRA for AAA-3, with axial (b) and sagittal (c) T1 weighted imaging demonstrating ILT heterogeneity. (d) Sagittal TrueFISP image of AAA-2, with axial (e) and coronal (f) T1 weighted imaging demonstrating ILT heterogeneity.

Table 1.

Geometric, compositional, and demographic data for AAAs 1–7. % ILT denotes the fraction of total ILT volume contributed by the stiffer inner layer. M = “Male,” N = “No.”

	AAA-1	AAA-2	AAA-3	AAA-4	AAA-5	AAA-6	AAA-7
Max diameter (cm)	4.6	4.9	5.7	4.9	4.6	6.6	5.5
ILT volume (cm3)	23	85	118	31	54	208	29
Max ILT thickness (cm)	1.8	2.7	2.8	1.7	2.7	3.4	1.5
% Inner ILT	51	63	73	68	33	62	79
Gender	M	M	M	M	M	M	M
Age (years)	74	65	67	73	64	69	80
Family history of AAA	N	N	N	N	N	N	N

Finite Element Model Generation.

In the 3D Slicer environment,2 the MR datasets for each case were cropped, resampled to 0.5 mm isotropic resolution, and manually coregistered. After median filtering, the lumen was segmented automatically from the MRA using a thresholding technique. The outer wall was segmented manually from the MR acquisition that showed the highest contrast between the wall and surrounding fat and bowel, which was generally VIBE or TrueFISP. The boundary between inner and outer ILT components was traced manually, ignoring smaller internal features to achieve two confluent ILT layers. Laplacian smoothing was then applied to the segmentations, and triangulated bounding surfaces were generated. Examples of vessel wall, lumen, and ILT segmentation (presmoothing) are shown for AAAs 3 and 5 in Fig. 2.

Fig. 2.

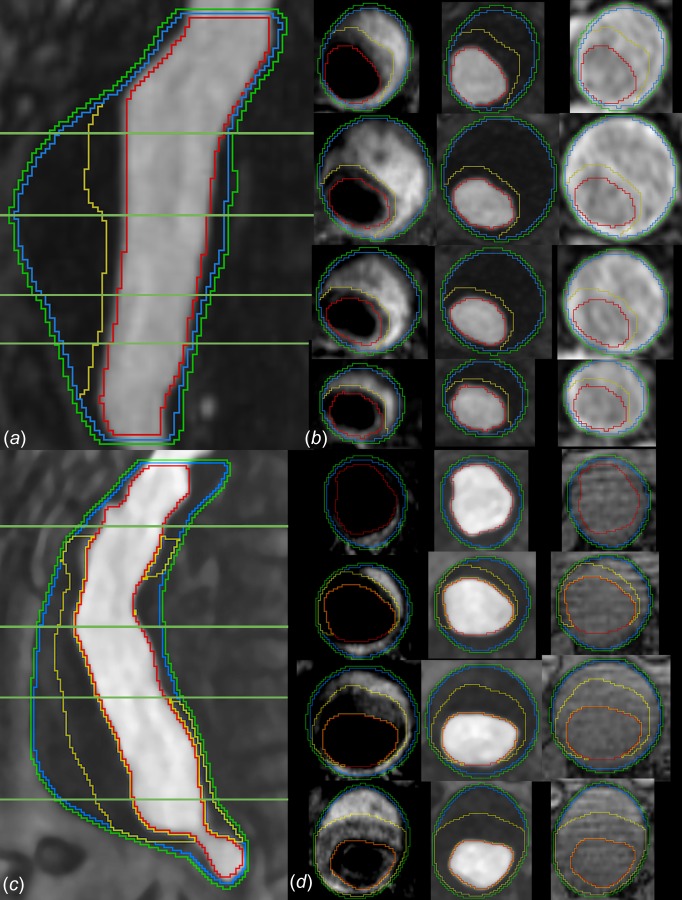
Segmentations of AAA 5 and AAA 3 in sagittal plane ((a) and (c)), respectively) and at the four specified levels in axial plane ((b) and (d), respectively). The segmentation curves are, from outermost to innermost: outer wall, representation of the inner wall, boundary between ILT layers, lumen. In the axial images ((b) and (d)) MRI acquisitions are, from left to right: black-blood T1-weighted, CE-MRA, and VIBE.

The triangulated surfaces representing the lumen, outer wall, and ILT boundaries were remeshed for uniformity, and an inner wall surface was generated as an offset from the outer wall, for a uniform wall thickness of 1.5 mm [30]. The geometry was then trimmed normal to the vessel centerline at the inlet and outlet(s) and converted to initial graphics exchange specification format for mesh generation, performed using Hypermesh (Altair Engineering, Troy, MI). The inner wall was meshed in a four-node quadrilateral-dominant fashion with edge length 0.9 mm, and the lumen and ILT boundaries were meshed with three-node triangles. The surface mesh of the inner wall was extruded outward 1.5 mm for a solid wall mesh consisting of four linear hexahedral elements (0–3% prisms) through the wall thickness. Element size and number were guided by a prior mesh sensitivity analysis where inner and outer wall stress results and displacements were within 2.6% and 1.3% error, respectively, from results obtained with a fourfold increase in mesh density as shown in Fig. 1, which is available in the Supplemental Materials on the ASME Digital Collection. The volume defined by the set of lumen and inner wall surfaces, as well as vessel endcaps (when appropriate) was designated ILT, with the previously segmented intra-ILT boundary used to delineate inner and outer layers. Conforming linear tetrahedral meshes represented inner and outer ILT layers, with nominal element edge length 1 mm. The proximal aspect of the segmented geometries was no more than 2 cm inferior to the lower of the two main renal arteries, and all geometries included relevant inlet shoulders where applicable. All geometries except AAA-5 included at least the proximal common iliac arteries, while AAA-5 was truncated at the aortoiliac bifurcation.

A hybrid element formulation, in which pressure stress is interpolated as a separate solution variable, suitable for representing incompressible biologic materials, was used for all elements. A representative mesh for AAA-3 is shown in Fig. 3. Element counts ranged from 52,000 to 143,000 for the vessel wall, and from 219,000 to 736,000 for ILT depending on aneurysm size, wall curvature, thrombus burden, and local ILT feature sizes, as shown in Table 1, which is available in the Supplemental Materials on the ASME Digital Collection.

Fig. 3.

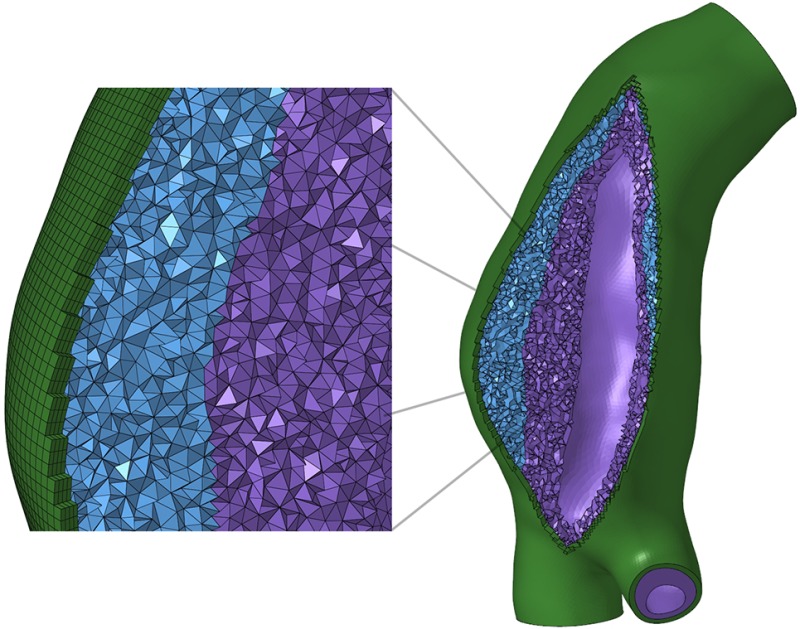
Mesh for AAA-3. In the magnified view, the mesh components are, from left to right: vessel wall, weaker outer ILT, stiffer inner ILT.

Material Models.

The AAA wall was modeled as isotropic, hyperelastic, and incompressible with the second-order Yeoh-type strain-energy density function (SEDF) proposed by Raghavan and Vorp [31]

$$W_{\mathrm{Wall}}=\hspace{0.17em}\alpha \left(I_1-3\right)+\beta {\left(I_1-3\right)}^2$$ (1)

where α = 17.4 N/cm² and β = 188.1 N/cm².

As patient-specific ILT material properties, and the relative stiffnesses of the inner and outer ILT layers, are not known, multiple modeling paradigms were considered

• (1)High disparity between layer compliance—weak and stiff
• (2)Low disparity between layer compliance—each relatively weak
• (3)Low disparity between layer compliance—each relatively stiff

For the stiff class of ILT materials, the SEDF proposed by Wang et al. [32] was used

$$W_{\mathrm{ILT}-\mathrm{Stiff}}=c_1\left(I_{\mathrm{II}}-3\right)+c_2{\left(I_{\mathrm{II}}-3\right)}^2$$ (2)

where $I_{\mathrm{II}}$ is the second invariant of the left Cauchy–Green stretch tensor. The parameters describing the stiff class of ILT materials are based on population averages of longitudinal and circumferential testing data of luminal and medial ILT specimens from the original study of Wang et al. [32], as previously applied by DiMartino and Vorp [33]. The stiff ILT models and their parameters ${\mathrm{Sf}}_1,\hspace{0.17em}{\hspace{0.17em}\mathrm{Sf}}_2,\hspace{0.17em}{\hspace{0.17em}\mathrm{Sf}}_{\mathrm{avg}}$ are listed in Fig. 4(a), with stress–stretch curves in Fig. 4(b) demonstrating relative stiffnesses. ${\mathrm{Sf}}_1$ corresponds to the luminal thrombus layer in Ref. [33], and ${\mathrm{Sf}}_2$ corresponding to their medial thrombus layer. ${\mathrm{Sf}}_{\mathrm{avg}}$, representing thrombus of average stiffness with respect to the luminal and medial layers is also considered.

Fig. 4.

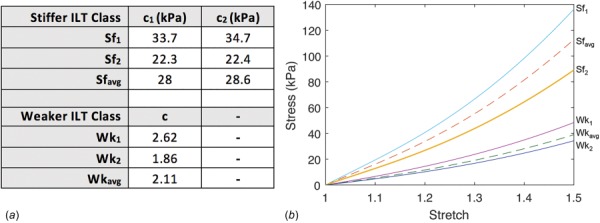
(a) Material parameters of stiffer and weaker class ILT models as defined by Eqs. (2) and (3) and (b) Cauchy stress versus stretch for all ILT material models.

For the weak class of ILT materials, the SEDF proposed by Gasser et al. [34] was used

$$W_{\mathrm{ILT}-\mathrm{Weak}}=c\sum _{i=1}^3\left({\lambda }_i^4-1\right)$$ (3)

where ${\lambda }_i$ is the $i$th principal stretch. For this class of ILT materials, material parameters were adapted from those described in Gasser et al. [34], in which three distinct thrombus layers (luminal, medial, and abluminal) were characterized. As only two thrombus layers are considered herein, ${\mathit{Wk}}_1$ corresponds to the luminal thrombus layer in Ref. [34], while ${\mathit{Wk}}_2$ corresponds to the average stiffness of their medial and abluminal layers. The ${\mathrm{Wk}}_{\mathrm{avg}}$ model corresponds to the average material parameters of the luminal, medial, and abluminal ILT layers tested in Ref. [34]. The material parameters describing the weak class of ILT considered, and their stress–stretch curves are also listed in Figs. 4(a) and 4(b), respectively.

For modeling paradigm 1, the average stiff (${\mathrm{Sf}}_{\mathrm{avg}})$ and weak (${\mathrm{Wk}}_{\mathrm{avg}})$ ILT models were assigned to the inner and outer ILT layers, respectively. For modeling paradigms 2 and 3, the pairs ${(\mathrm{Wk}}_1,\hspace{0.17em}{\mathrm{Wk}}_2)$ and ${(\mathrm{Sf}}_1,\hspace{0.17em}{\mathrm{Sf}}_2)$ were assigned to inner and outer ILT layers, respectively. In addition to explicitly modeling ILT heterogeneity in each paradigm, ILT was considered uniform for additional simulations, with ${\mathrm{Wk}}_1,\hspace{0.17em}{\mathrm{Wk}}_2,\hspace{0.17em}{\hspace{0.17em}\mathrm{Wk}}_{\mathrm{avg}}$ and ${\mathrm{Sf}}_1,\hspace{0.17em}{\hspace{0.17em}\mathrm{Sf}}_2,\hspace{0.17em}{\hspace{0.17em}\mathrm{Sf}}_{\mathrm{avg}}$ each considered separately for comparative purposes.

Boundary Conditions and Analysis.

For each model, the aortic inlet and aortic/iliac outlet cut surfaces were constrained to be distensible in only the radial direction with respect to the local vessel centroid. A nodal “tie” constraint was used to enforce a no-slip condition between the nodes of the ILT outer boundary and the inner surface of the vessel wall since nodal conformity was not enforced during mesh generation.

A fixed point iterative technique was used to estimate the unloaded configuration of each aneurysm, for each ILT modeling scenario, assuming a diastolic pressure of 80 mm Hg at imaging as previously described [12,35]. This is important, as changing ILT stiffness is expected to alter the reference configuration for finite element modeling and has been shown to influence stress results significantly [24]. Once established, the unloaded aneurysm configuration in each thrombus modeling scenario was loaded statically to 120 mmHg for wall stress analysis. The assumed systemic blood pressure of 120/80 mm Hg was used since patient-specific blood pressures were not fully available.

Nine stress analyses were run for each of the seven cases, for a total of 63 simulations. All finite element analyses were conducted using abaqus 2017 (Dassault Systemes, Simulia, Providence, RI).

Statistical Methods.

Von Mises wall and ILT stresses were analyzed for all simulations. Owing to small sample sizes in each ILT modeling paradigm and the inherent pairing of data, comparison of peak wall stresses was made between simulations using the nonparametric Wilcoxon signed-rank test, with statistical significance considered at α = 0.05.

Wall Strength and Rupture Potential Index.

Peak AAA wall stress is commonly observed where ILT is thinnest or absent and may incompletely capture the effects of modeling ILT heterogeneity. The rupture potential index (RPI) introduced by Vande Geest et al. [36] is the ratio of local wall stress to local wall strength, and was also calculated for vessel wall elements for each simulation, with wall strength defined as

$$\begin{array}{c}\mathrm{Strength}\left(\mathrm{kPa}\right)=719-379\mathrm{*}\left({\mathrm{ILT}}^{\frac{1}{2}}-0.81\right)\\ -156\mathrm{*}\left(\mathrm{NORD}-2.46\right)\\ -\hspace{0.17em}213\mathrm{*}\mathrm{HIST}+\hspace{0.17em}193\mathrm{*}\mathrm{SEX}\end{array}$$ (4)

where ILT is the local ILT thickness in centimeter, NORD is the normalized local vessel diameter, HIST = ±½ is assigned for positive or negative family history of AAA, respectively, and SEX is assigned as ±½ for male and −½ for female subjects. From Eq. (4), it is noted that regions where ILT is thickest are predicted to have lower wall strength and correspond to regions where ILT heterogeneity may have a larger impact on RPI.

Results

Wall Stress.

The wall stress distributions for all cases in the high-disparity heterogeneous ILT paradigm are shown in Fig. 5 and are each highly nonuniform, strongly influenced by large variations in local aneurysm features such as diameter, wall curvature, and ILT thickness. Peak stress is noted at the inlet shoulder for AAAs 1 and 4, at gentle concavities posteriorly for AAAs 3, 4, and 6, and laterally for AAA-2 and AAA-7. Table 2 lists peak and mean Von Mises wall stresses for simulations considering heterogeneous ILT in the three paradigms, with Table 2 which is available in the Supplemental Materials on the ASME Digital Collection listing all peak and mean Von Mises wall stresses. The ILT types incorporated in each simulation in Table 2 are listed as a set (i.e., (Sf_avg, Wk_avg)), with the stiffer type assigned to the inner ILT layer. For each AAA case and each ILT modeling paradigm, the simulation including ILT heterogeneity serves as the reference to which simulations assuming only “all-stiffer” or “all-weaker” ILT are compared.

Fig. 5.

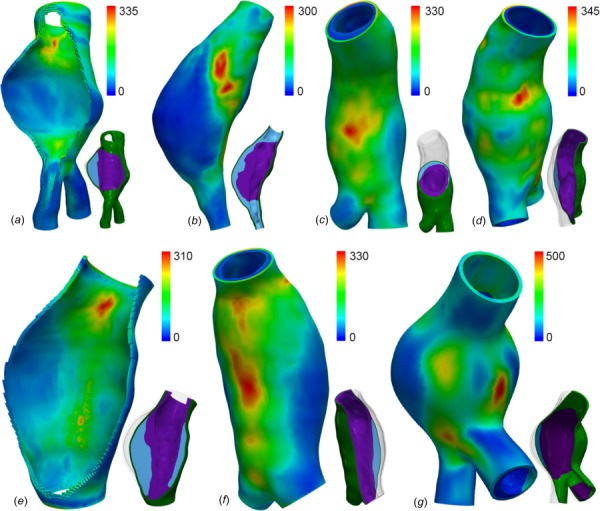
Von Mises stress (kPa) distributions for AAAs 1–4 (a)–(d) and 5–7 (e)–(g) in the high ILT stiffness disparity paradigm. To the lower right of each stress plot, a cutplane visualization of the model gives an impression of the ILT type distribution: inner = stiffer ILT (SF_avg), outer = weaker ILT (Wk_avg).

Table 2.

Peak and mean Von Mises wall stress (kPa) for simulations considering heterogeneous ILT in three modeling paradigms of differing ILT stiffness disparity. (Sf_avg, Wk_avg) = high stiffness disparity; (Wk₁, Wk₂) = low stiffness disparity, both ILT models relatively weak; (Sf₁, Sf₂) = low stiffness disparity, both ILT models relatively stiff.

	Peak Von Mises wall stress (kPa)	Mean stress (kPa)		Peak Von Mises wall stress (kPa)	Mean stress (kPa)
AAA-1			AAA-2
(Sfavg , Wkavg)	335	79.0	(Sfavg , Wkavg)	301	65.7
(Wk1, Wk2)	330	98.9	(Wk1, Wk2)	310	89.9
(Sf1, Sf2)	338	73.5	(Sf1, Sf2)	294	57.1
AAA-3			AAA-4
(Sfavg, Wkavg)	329	102	(Sfavg, Wkavg)	344	131
(Wk1, Wk2)	366	137	(Wk1, Wk2)	403	149
(Sf1, Sf2)	293	91.1	(Sf1, Sf2)	338	123
AAA-5			AAA-6
(Sfavg , Wkavg)	309	71.2	(Sfavg , Wkavg)	330	96.3
(Wk1, Wk2)	351	98.9	(Wk1, Wk2)	449	144
(Sf1, Sf2)	300	61.0	(Sf1, Sf2)	301	83.5
AAA-7
(Sfavg , Wkavg)	615	123
(Wk1, Wk2)	661	143
(Sf1, Sf2)	606	118

As shown in Fig. 6, for all three ILT modeling paradigms, no statistically significant difference in peak wall stress is realized when comparing results from simulations incorporating heterogeneous ILT or “all stiffer” ILT (p ≥ 0.22). Comparisons between models assuming heterogeneous ILT and “all weaker” ILT show varying magnitudes of sensitivity to differing thrombus arrangements, with peak wall stress differences reaching statistical significance in all three ILT modeling paradigms (p = 0.016). The greatest differences in peak wall stress between heterogeneous and all weaker ILT models are observed in the high ILT stiffness disparity paradigm, with all-weak ILT models predicting 15% higher peak wall stresses, on average (range 1–40%, SD = 13%). It is noted that in each of the lower disparity paradigms, modeling thrombus as homogeneously stiff tends to predict peak wall stresses closer to the reference heterogeneous ILT peak wall stress compared to modeling thrombus as homogenous with an average stiffness (0.83% average difference (SD = 1%) from reference, compared to 2.3% (SD = 1.3%)).

Fig. 6.

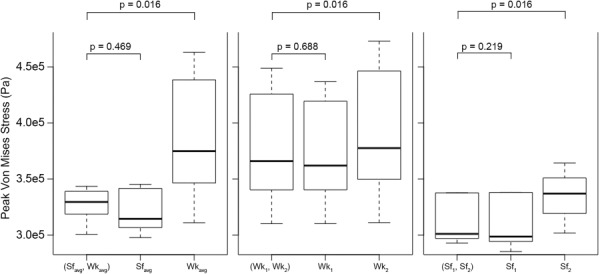
Boxplots of peak Von Mises wall stresses in different ILT stiffness paradigms for cases considering heterogeneous and homogeneous ILT arrangements. Please note: outlying stress values for AAA-7 models (average ∼ 640 kPa) are not plotted for clarity.

Mean wall stress shows a greater sensitivity to differing thrombus configurations. Again, assuming a homogeneously stiffer ILT affords stress predictions very close to those obtained with explicitly modeled ILT heterogeneity, with the average difference of −3.7% (SD = 3.2%). There is an average 17% increase in mean wall stress when a homogeneously weaker ILT is assumed compared to heterogeneous ILT when results from all ILT modeling paradigms are considered, with the high disparity paradigm showing the greatest differences in average wall stress (mean = +35%, SD = 15%) . The enhanced sensitivity of average wall stress to ILT configuration predominantly reflects changing stress at wall segments overlying the thickest ILT, where changes in thrombus stiffness have the greatest effect. Similar to prior works comparing the effects of varying stiffness of homogeneous ILT, stiffer thrombus is associated with relatively lower peak and mean wall stresses than those predicted in the setting of weaker thrombus.

Rupture Potential Index.

Rupture potential index was calculated for vessel wall elements, as shown for AAA-6 in Fig. 7, with peak RPI for all simulations listed in Table 3. Local relative changes in RPI (normalized to peak RPI per model) were calculated using the heterogeneous ILT case as the reference and are provided in Table 3, which is available in the Supplemental Materials on the ASME digital collection. For each modeling paradigm, specifying either heterogeneous ILT or all-stiffer ILT resulted in no difference in peak RPI for the majority of cases, with minimal change (<7% for AAA3 and <4% for AAA-6 and AAA-7 in the lower disparity paradigms) in 6 of 21 cases. Peak RPI predicted using an all-weaker ILT strategy can differ more substantially, an average +9% with range 0–31% when compared to peak RPI from the reference heterogenous ILT simulation. This finding is again heavily influenced by these results of the high disparity paradigm modeling, and peak RPI changes resulting from an all-weaker ILT approach in the lower disparity paradigms average +5.2%. Local changes in RPI, calculated per element as a percentage of the reference peak RPI, vary moderately with changing ILT configuration. For the low disparity paradigms, local RPI changes range from −9.6% to +17.3% of the peak reference RPI when all-weaker ILT is considered. Local RPI changes range −11.4% to +4.5% of the peak reference RPI when all-stiffer ILT is considered in the low disparity setting. As expected, in the high disparity paradigm, local RPI changes are more sensitive to ILT arrangement, ranging from −25.6 to +57.2% of the peak reference RPI when all-stiffer or all-weaker ILT is considered, respectively.

Fig. 7.

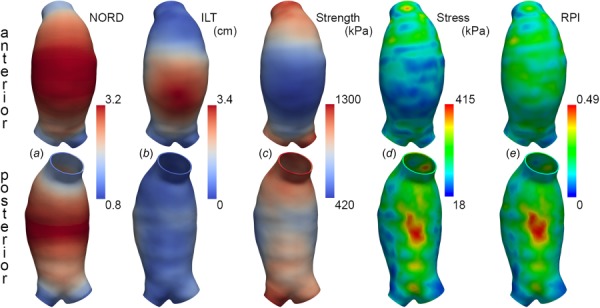
Determinants of RPI for AAA-6 in the low ILT stiffness disparity paradigm, with inner ILT layer represented by ${\mathrm{Wk}}_1$ and the outer ILT layer represented by ${\mathrm{Wk}}_2.$ From left to right: (a) local diameter normalized to expected diameter for sex and age (NORD), (b) local ILT thickness, (c) wall strength (kPa) distribution, (d) Von Mises wall stress (kPa) distribution, and (e) RPI.

Table 3.

Peak rupture potential indices predicted under each ILT modeling paradigm. The ILT configuration of each simulation is denoted by the ILT material model(s) listed.

	AAA-1	AAA-2	AAA-3	AAA-4	AAA-5	AAA-6	AAA-7
Paradigm 1 (high disparity)
(Sfavg , Wkavg)	0.22	0.26	0.32	0.29	0.23	0.39	0.48
Sfavg	0.22	0.26	0.30	0.29	0.23	0.34	0.48
Wkavg	0.26	0.28	0.36	0.36	0.28	0.51	0.53
Paradigm 2 (low disparity)
(Wk1, Wk2)	0.25	0.27	0.36	0.35	0.27	0.49	0.51
Wk1	0.25	0.27	0.35	0.35	0.27	0.47	0.52
Wk2	0.26	0.29	0.37	0.37	0.28	0.52	0.53
Paradigm 3 (low disparity)
(Sf1, Sf2)	0.24	0.25	0.29	0.28	0.22	0.32	0.48
Sf1	0.24	0.25	0.28	0.28	0.22	0.31	0.48
Sf2	0.24	0.26	0.31	0.30	0.24	0.36	0.48

Intraluminal Thrombus Stress.

Differing ILT stiffness distributions also result in changes in 99th percentile peak stress experienced in the inner ILT layer. Explicitly modeling ILT heterogeneity predicts the highest 99th percentile ILT stress in each paradigm. Similar to peak wall stress predictions, assuming a homogeneously stiff ILT approximates the results of the explicitly modeled ILT heterogeneity simulations with highest accuracy (mean difference −5.9%), while assuming a homogeneously weaker ILT reduces 99th percentile ILT stress predictions more substantially (mean difference −30.1%). No configuration of ILT for any case demonstrated peak stresses surpassing the luminal ILT ultimate strength of 157 kPa as described by Gasser, nor did any peak stress exceed the lower failure stress 94 kPa relevant in pulsatile loading [34].

Discussion

Patient-specific AAA risk stratification based on aneurysm features beyond maximum diameter necessitates a careful determination of what known factors are most influential to aneurysm evolution and rupture. A variety of geometric factors [37–39], as well as compositional [28,40] and biologic factors [41,42] have been examined recently with hopes of improving the clinical assessment and care of patients with AAA. Inclusion of biomechanical factors in this assessment, most commonly through finite element modeling, is complex and the fidelity with which an aneurysm must be modeled for biomechanical characterization to be of benefit is not yet fully known. In this work, we have explored the importance of spatially heterogeneous intraluminal thrombus within the AAA, something that has not been considered in a nonidealized patient–specific sense previously, in an effort to improve this knowledge.

Intraluminal thrombus is most commonly considered a homogeneous material in models of AAA mechanics, and this is especially true in patient–specific models based on CT, which is incapable of resolving internal ILT features. This is despite observations during open surgery and at advanced imaging that ILT can be quite heterogeneous, appearing either disorganized or demonstrating two or more distinct layers. Previous studies investigating the effects of ILT on AAA wall stress distributions have most commonly compared wall stress distributions in models either including or disregarding ILT or have assessed the dependence of wall stress predictions on the assumed ILT constitutive properties [22,24,33,43,44]. These studies demonstrate that ILT reduces and spatially homogenizes wall stress, with the stiffer thrombus causing a greater effect than more compliant thrombus. Only a small number of studies have examined the influence of ILT heterogeneity but have been restricted to idealized aneurysm geometries and idealized distributions of different ILT types [24,33,44].

In this work, we have explored the impact of ILT heterogeneity on AAA mechanics by using MRI to delineate distinct inner and outer ILT layers on a patient–specific basis. These cases presented demonstrate a range of relative ILT volumes by layer, with complex spatial distributions and ILT layer thicknesses. Three different paradigms of ILT layer stiffnesses were considered to both account for an unknown disparity between layer-specific mechanics and to extend the analysis over a range of ILT material models commonly employed in the literature.

We find that with regard to peak stress predictions, explicitly modeling ILT heterogeneity as seen at MRI is unlikely to substantially change simulation results compared to a model assuming a homogenous ILT with mechanical characteristics corresponding to the stiffer ILT layer. Peak rupture potential index is similarly insensitive to the explicit incorporation of ILT heterogeneity compared to modeling a uniformly stiff ILT. Thus, for modeling efforts where the considered ILT constitutive properties are not more disparate in stiffness than those considered here, explicitly modeling ILT heterogeneity (rather than assuming the class' stiffest material parameter) is likely to add little value since the predictions of greatest interest in the literature are peak stress and peak RPI. This provides, in some sense, back validation of prior CT-based studies of patient-specific AAAs where ILT has been considered spatially homogeneous, and suggests that idealizations of spatially varying ILT properties, which can be challenging to implement, are not likely to impact study conclusions. The additional time and effort required to model patient-specific ILT heterogeneity can therefore likely be avoided in many cases.

Our results show that when ILT is heterogeneous with a marked stiffness disparity between layers, larger changes in simulation predictions can result from inappropriately applying a uniformly weaker ILT material model. The range of magnitude of these changes is wide (1–41% for peak wall stress, 8–31% for peak RPI, and 22–57% for local nonpeak RPI), and the location of changes is not predictable in real geometries where the absolute and relative layer thickness have complex distributions. The peak RPIs for the aneurysms considered here do not in general suggest a high rupture potential, and the peak RPI changes when uniformly weaker ILT is considered do not reach the 44.9% noted by Maier et al. [45] to distinguish symptomatic/ruptured AAAs from asymptomatic AAAs. However, the change in nonpeak RPIs under an incorrect all-weaker ILT assumption could alter analysis conclusions if secondary sites of concern are considered, based on local rather than global maxima of rupture potential.

MRI characterization of intraluminal thrombus has received increasing attention in recent years [17,18,28,46], and correlations between imaging features and gross mechanical character are encouraging. However, no large studies have been conducted to assess any quantitative relationship between the mechanical stiffness and thrombus appearance at MRI. Advances in this area could help to identify heterogeneous ILTs of high stiffness disparity and markedly degenerated weaker ILTs, allowing for a more deliberate assignment of stiff or weak thrombus material properties in the mechanical analysis. This is important, as the range of thrombus stiffness represented in the literature is likely narrower than that found in vivo, owing to difficulties in mechanical testing of markedly degenerated and gel-like thrombus. In our cohort of 80 subjects, 18 ILTs (22.5%) have a near-uniform signal intensity commonly associated with weak and degenerated thrombus, similar to the 11/45 AAAs (24%) with degenerated thrombus in the study by Castrucci et al. [17]. This relatively common subset of ILTs could benefit from imaging-based ILT material property inference, as assignment of an inappropriately stiff material model may also lead to inaccurate stress predictions, as shown in our results.

Our study has a number of limitations. First, we consider only a small number of discrete AAA geometries. In our database from our larger cohort, additional cases with ILT heterogeneity were identified, but imaging data were either incomplete or of insufficient quality for finite element modeling. Despite this, our sample includes a range of AAA diameters near the commonly accepted intervention threshold of 5.5 cm, and a range of ILT volumes and configurations. As additional data on AAAs with MRI discernable ILT heterogeneity become available, further analyses should be made so that our results and conclusions from this limited cohort can be examined in the context of greater variation in aneurysm shape, size, thrombus distribution, and thrombus heterogeneity.

We considered three paradigms of ILT heterogeneity, one with widely disparate material models as in Riveros et al. [24], and the others using ILT material models of lower disparity and different average stiffness. The choice of material models was motivated by their use in the literature and does not exhaustively evaluate the range of feasible stiffness disparities. This limitation is justified by the fact that the majority of AAA studies consider ILT of a similar stiffness range and that any attempt to specify an even weaker or gel-like ILT would be hypothetical, as there is a sparsity of suitable constitutive relations and as yet no definite way to make this assignment based on imaging.

Although we have incorporated an estimate of the aneurysms' unloaded state for each considered ILT configuration, we did not account for residual stresses within the vessel. There are relatively few AAA studies in the literature that incorporate residual stress [47,48], and as yet there is no consensus on the most suitable and physiologically realistic approach in the case of heavily diseased vascular segments, for which foundational experimental data are lacking.

Because patient–specific blood pressures were not fully available at the time of imaging, and blood pressure can naturally be quite variable, an assumed 120/80 mmHg was applied for each model in determining the unloaded aneurysm configuration and wall stress distribution. There is no doubt that changes in the applied pressure loading will alter the wall stress magnitude, and to a lesser extent its distribution; however, the use of consistent boundary conditions while varying only the ILT modeling strategy is considered the most important factor in our analysis.

Spatially varying wall thickness was also not considered. Although MRI has superior soft tissue contrast compared to CT, the limited spatial resolution of our current MRI techniques hampers an accurate and reliable wall thickness assessment presently. Technical development is underway to permit this imaging capability and thereby reduce the number of assumptions included in the modeling process. Additionally, while our multisequence MRI exam can distinguish vessel wall from surrounding tissues, the distinction between vessel wall and thrombus can still be challenging in some cases. It is expected that spatially variable wall thickness could increase the local impact of specifically accounting for ILT heterogeneity in the stress analysis. According to a commonly employed statistical wall thickness model, wall thickness is linearly reduced as local ILT thickness increases. ILT heterogeneity is commonly greatest where ILT is thickest, and so accounting for its layered structure could affect the mechanical environment in the thinned underlying wall. Further work could be done to characterize this sensitivity.

In summary, we have investigated that the relative impact of ILT heterogeneity on the mechanics of AAAs, using patient specific geometries and distributions of ILT types delineated with multisequence MRI. Our results provide some assurance that treating ILT as a homogeneous material in imaging-based modeling is reasonable provided that a relatively stiffer ILT material model is used, and including more realistic stiffness distributions is unlikely to change major results. This serves as a back-validation of CT-based finite element AAA modeling where ILT is most commonly regarded as homogeneous. At the same time, our results demonstrate that more substantial changes in peak wall stresses and rupture potential index might result if a uniformly weak ILT were specified, and that MRI may serve a role in guiding that choice. Further studies quantitatively relating ILT mechanical character to imaging features are needed to demonstrate this potential.

Supplementary Material

Supplementary Material

Supplementary Tables 1-3 and Figure 1

Funding Data

• National Institutes of Health (NIH) (Grant Nos. 5T32EB001631-13, 5R01HL123759-03, and 5R01HL114118-04, Funder ID: 10.13039.100000002).