Abstract
Hydrostatic pressure (HP) regulates diverse cell behaviors including differentiation, migration, apoptosis, and proliferation. Abnormal HP is associated with pathologies including glaucoma and hypertensive fibrotic remodeling. In this review, recent advances in quantifying and predicting how cells respond to HP across several tissue systems are presented, including tissues of the brain, eye, vasculature and bladder, as well as articular cartilage. Finally, some promising directions on the study of cell behaviors regulated by HP are proposed.
Keywords: cell micro-environment, mechanobiology, mechanotransduction, cell volume
1. Introduction
Cells in their native micro-environments experience a broad range of mechanical cues, including stretch, compression, hydrostatic pressure, and shear stress[1–5]. Micro-environmental hydrostatic pressure (HP) is an important cellular cue both in vivo and in vitro, playing a vital role in regulating cell behaviors such as differentiation, migration, apoptosis, and proliferation [6–11]. HP is an especially important cue for the development and homeostasis of cells in the central nervous system, eyes, cardiovascular system, cartilage, and bladder [12–19]. The range of physiological HP differs substantially across tissues, and the source of cell type-specific regulation has been the focus of significant research efforts [20–24]. Despite this broad range, locally abnormal HP can induce disease: high HP can induce vesicoureteral reflux and deterioration of the upper urinary tract [25]. HP is an important cue for development and for reconstitution of gradations of cell phenotypes in tissue engineering [26–32]. It is thus necessary to understand how both physiological and pathological HP affect cell behaviors.
Quantitatively, HP is related to the trace of the stress tensor at a point within a tissue: , where the negative sign represents the definition that positive pressure is compressive. However, what is typically important for a biological system is what is sometimes termed gage pressure, p, namely the differential between absolute HP and atmospheric pressure.
Recent, significant experimental efforts in vitro have uncovered how HP regulates key cell behaviors in brain, eye, vascular, bladder, and articular cartilage tissues, and shown how the responses of cells in these tissues to HP can differ substantially. In bovine aortic endothelial cells (BAECs), elevated HP elongates cells without inducing cell orientation or cytoskeletal rearrangement [33]. Increasing HP promotes proliferation of human bladder smooth muscle cells (SMCs) by upregulating micro ribonucleic acid (RNA) 4323 and MiR 3180-5p [34,35]. Elevated HP increases intracellular Ca2+ and upregulates the transient receptor potential vanilloid-1 channel of retinal ganglion cells, resulting in cell apoptosis [36]. Loading with long-term HP enhances the differentiation of ATDC5 cells to chondrocyte [37]. Elevated HP increases the volume of lung cancer A549 and CL1-5 cells [38], but decreases the volume of leukemia K562 and HL60 cells [39]. There is a pressing need to understand what drives these diverse HP-regulated cell behaviors.
Although reviews of HP in articular cartilage tissue engineering exist [27], and a review of the role of ion channels in cellular mechanotransduction of HP does as well [40], there is still a need for a large-scale overview of observations of and models for HP-regulated cell behaviors, which is the thrust of this paper. The review begins with an introduction of HP as an important mechanical cue in the cell micro-environment. In the Sec. 2, the state-of-art advances in the in vitro experimental approaches and results about HP-regulated cell behaviors are reviewed, with focus on cells in brain, vascular, cartilaginous, eye, and bladder tissues. Thereafter, theories about how cells respond to HP through tuning cell volume are briefly summarized. The review concludes with some future perspectives.
2. Hydrostatic Pressure in Native Cell Micro-Environments
Hydrostatic pressure plays significant roles across in function across hierarchies, from tissue/organs to cells. We begin discussion of the roles of HP in pathology with a summary of hierarchical structures of several key tissues, and of the physiological range of HP in the cell micro-environment of these tissues. In each of these, a change to the relevant physiological HP can lead to a complicated multi-axial change to the stress field in the cell micro-environment.
2.1. Brain.
The brain contains a multitude of tissues, separated by substantial barriers including the falx and tentorium, and heavily vascularized (Fig. 1(a)). Intracranial pressure (ICP) is the HP inside the cranium (Fig. 1(b)), which is normally in the range of 7–15 mmHg (0.93–1.99 kPa) for a supine adult at rest [41]. A key factor in brain pressure is the balance between production and drainage of cerebrospinal fluid. Elevated ICP in the cranium (20–25 mmHg, 2.66–3.33 kPa) can shift brain structures such as the tencephalon, diencephalon, cerebellum, and medulla, and restrict blood supply to the brain [42]. Human brain is composed primarily of two broad classes of cells, i.e., neurons (Fig. 1(c)) and glial cells. Elevated ICP is associated with a range of severe pathologies, including hydrocephalus, hypoxemia, and herniation of the brain.
Fig. 1.
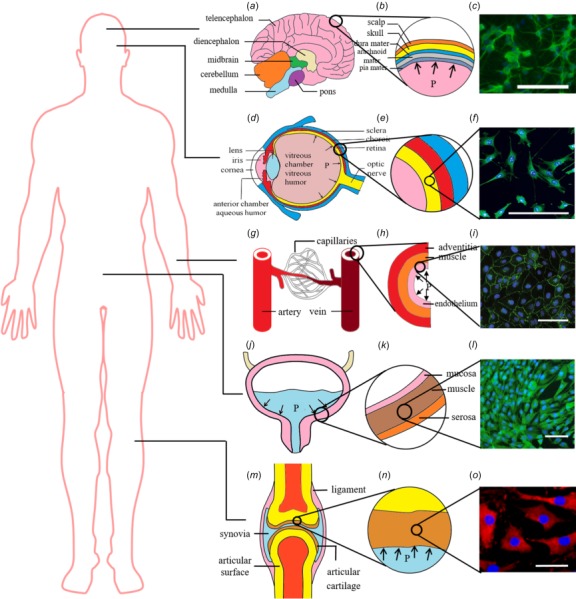
Native cell micro-environments for cells that commonly experience substantial hydrostatic pressure: (a) the brain, (b) brain parenchyma, and (c) neurons [43]; (d) the eye, (e) eye wall tissue, and (f) retinal cells [17]; (g) blood vessel, (h) blood vessel wall tissues, and (i) blood vessel endothelial cells [44]; (j) the bladder, (k) bladder wall tissues, and (l) bladder wall smooth muscle cells [35]; and (m) joints, (n) articular cartilage, and (o) chondrocyte cells [45]. Scale bar is 100 μm. Image (i) reproduced, with permission, from Ref. [44].
2.2. Eye.
The eye contains an anterior segment, made up of the iris and lens, the cornea, and a posterior segment (Fig. 1(d)). The wall of posterior segment has three layers, i.e., sclera, choroid, and retina layers, from distal (outer) to proximal (inner) (Fig. 1(e)). Intraocular pressure (IOP) is the fluid pressure inside the eye, which is mainly determined by the difference between the production and the drainage of aqueous humor [46]. The normal range of IOP is about 10–20 mmHg (1.33–2.66 kPa), while elevated IOP (>21 mmHg, 2.79 kPa) is recognized as a threat for retinal ganglion cell pathology (Fig. 1(f)) and associated optic nerve damage and vision loss [47].
2.3. The Cardiovascular System.
There are three main types of blood vessels, i.e., veins, arteries, and capillaries (Fig. 1(g)). Arteries and veins have three layers [48] (Fig. 1(h)): the tunica adventitia (largely collagen and elastin), the tunica media (largely smooth muscle cells, elastin, and collagen), and the tunica intima (largely endothelial cells) (Fig. 1(i)). The blood vessel in vivo is exposed to various mechanical stimulations, specifically, shear stress as induced by blood flow, mechanical stretch due to vascular wall compliance, and blood pressure resulting from containment of blood within the vasculature. Normal adult blood pressure is about 120 mmHg (16 kPa) at the peak of the cardiac cycle (systole), and 80 mmHg (11 kPa) at diastole [49]. HP for endothelial cells is the blood pressure, which varies over the cardiac cycle and may change due to normal variations in daily activity and due to pathologies that induce hypotension (blood pressure less than 90 mmHg (11.97 kPa) in systole or less than 60 mmHg (7.98 kPa) in diastole [50]) and hypertension (blood pressure more than 160 mmHg (21.3 kPa) in systole or more than 100 mmHg (13.3 kPa) in diastole [51]). Hypertension thickens and stiffens the blood vessel wall and increases the risk of rupture. Further, hypertension induces fibrotic remodeling, including cardiac fibrosis.
2.4. Bladder.
The bladder is a hollow distensible organ for collecting and storing urine from the kidneys (Fig. 1(j)). Urine enters the bladder via the two ureters that are connected to the kidneys and exits via the urethra. Typically, the adult human bladder can hold 300–500 mL of urine. The bladder wall has four layers, i.e., mucosa, submucosa, muscularis, and serosa, from inside to outside (Fig. 1(k)). Because the contraction of SMCs in the muscularis plays an important role in maintaining bladder function, these SMCs have attracted the most attention (Fig. 1(l)). SMCs of the bladder are subjected to periodic HP, which increases when the urine volume increases in the bladder. When HP rises up to ∼40 cm H2O (4 kPa) [52] (Table 1), SMCs will be stimulated to contract, resulting in the expulsion of urine through the urethra. Finally, HP will return to the point at which there is nearly no differential with atmospheric pressure, and another cycle starts. Spinal cord injury can cause elevated HP, which further induces vesicoureteral reflux and deterioration of the upper urinary tract [25].
Table 1.
Hydrostatic pressure micro-environment in native cell micro-environment
| Tissues | Value | Period |
|---|---|---|
| Blood vessel | Adult | 0.6–1 s [56] |
| 10.6–16.0 kPa (systolic pressure) [53–55]; | ||
| 7.98–12.0 kPa (diastolic pressure) [53–55] | ||
| Infant | Shorter than adult [57] | |
| 9.31–13.3 kPa (systolic pressure) [57]; | ||
| 3.99–5.99 kPa (diastolic pressure) [57] | ||
| Bladder | 0–4.00 kPa [52,58] | |
| Eye | 1.33–2.93 kPa (adult) [59] | 24 h [61,62] |
| 1.06–2.93 kPa (infant) [60] | ||
| Articular cartilage | 5–6 MPa (gait) [63] | 0.1–1 s [64] |
| 18 MPa (running or jumping) [63] | ||
| Brain | 0.67–2.00 kPa (healthy supine adult) [36,65] | 0.82–1 s [57,66] |
| 0.4–0.93 kPa (child) [65] | 0.56–0.73 s [57] | |
| 0.20–0.80 kPa (infant) [65] | 0.42–0.51 s [57] | |
| Lung | −0.5 to 2.5 kPa (transpulmonary pressure) [67,68] | 3.5–9.5 s [69] |
2.5. Articular Cartilage.
Articular cartilage is an avascular tissue that transfers compressive mechanical load in a joint (Fig. 1(m)). The tissue consists of chondrocyte cells in a matrix of proteoglycans and collagen fibers (Figs. 1(n) and 1(o)). The mechanical micro-environment of chondrocytes is well modeled by the biphasic model of tissue mechanics [70,71], with compressive stress borne by hydraulic resistance of the flow of interstitial fluid. The key determinant of the time-varying micro-environment of chondrocytes is thus time-dependent HP [72,73]. In vivo, the range of HP in articular cartilage is about 5–6 MPa in gait and can reach 18 MPa during running and jumping [74].
3. Engineering Cell Micro-Environment of Hydrostatic Pressure In Vitro
For the aforementioned range of tissues, HP is a critical driving force for the cell micro-environment. Technologies for modulating HP in vitro are thus crucial to mimicking the native cell mechanical micro-environment. Three techniques have been used to modulate HP in vitro: the gas pressure method, the syringe method, the media height method [40].
3.1. Gas Pressure Method (Gas Pressurization).
Hydrostatic pressure can be applied by gas pressure supplied by gas pump. A gas pressurization system can consist of a cell culture chamber, a pressure gage, a pressure-control, and a pump supplying a mixture of 95% air and 5% CO2 [75] (Fig. 2(a)). More intricate designs are available as well, including electronic controls and a pressure transducer to enable cyclic HP [25]. In this method, pH, pO2, and pCO2 are controlled based off of measurements from a blood gas analyzer to ensure that these factors do not affect the HP-regulated cell behavior. This approach can provide a relatively large range of pressure change (∼0–10 MPa).
Fig. 2.
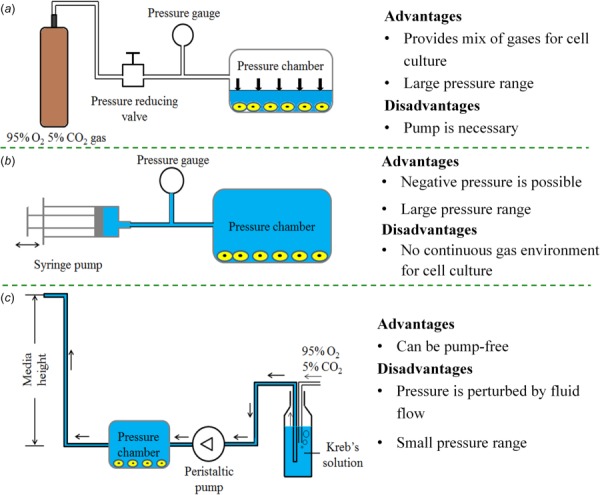
Existing approaches for altering hydrostatic pressure in the cell micro-environment: (a) the gas pressure method [25,75], (b) the syringe method [44,76], and (c) the media height method [77,78]
3.2. Syringe Method (Solid Pressurization).
The syringe method achieves HP loading by pressurizing cell culture media into a pressure chamber via a syringe, and monitoring the pressure via a gage [76] (Fig. 2(b)). This method can provide both positive (compressive) pressure and negative (tensile) pressure. The application of negative pressure has certain benefits for wound healing, and existing systems can apply negative pressures to both wounds and cultured cells at pressures of –50 mmHg (–6.65 kPa) [44]. Cyclic HP can be obtained by driving a syringe pump. A challenge associated with this method is maintaining the 5% CO2 and 95% air mixture used for long-term cell culture.
3.3. Media Height Method (Liquid Pressurization).
The media height uses a static column of cell culture media to modulate HP. One shortcoming of this method is that the nutrition, pH, pO2, pCO2, and gas concentration distribution can change with the height of media. For instance, the pO2 and pCO2 can increase by 3% and 7%, respectively, as HP increases from 0.3 to 10 cm H2O (30 Pa–1 kPa) [77]. To address this, a HP platform is designed to maintain constant gas concentration by perusing Kreb's solution (Fig. 2(c)) [78]. An additional shortcoming that has yet to be addressed is that flowing cell culture media brings the issue of potential shear stress effects on the cells under study. It is worth noting that the HP may dependently vary with the gas tension (e.g., oxygen tension) in culture medium [79]. Specially designed apparatus is needed to separate the effects of HP and gas tension.
4. Response of Cells to Hydrostatic Pressure In Vitro
The responses of cells to HP vary dramatically from tissue to tissue. A number of these responses have been studied in vitro. In this section, experimental findings about HP-regulated cell behaviors in brain tissues, eye tissues, blood vessels, bladder tissues, and articular cartilage are summarized.
4.1. Hydrostatic Pressure-Regulated Behaviors of Brain Cells.
Exploring the injury mechanism of central nervous system cells caused by HP might improve understanding of the pathophysiology in brain tissues. Here, some current studies on HP-induced behaviors of neurons and glial cells are summarized. HP of 40 kPa with 25 μM of hemoglobin significantly decreases neuron viability (Fig. 3(a)) and increases lactate dehydrogenase release (Fig. 3(b)) [43]. Furthermore, these conditions upregulate piezo-2 expression, which reaches a plateau at 8 h [43], and increases adenosine triphosphate (ATP) release of human neurons (Fig. 3(c)) [80]. In contrast, HP has little influence on the ATP release of human astrocytes [80]. Increased HP increases expression of messenger RNA (mRNA) for aquaporin (AQP1), serotonin receptor 5 A (HTR5A), and voltage-gated ion channels (KCNS1) in single pyramidal cells.
Fig. 3.
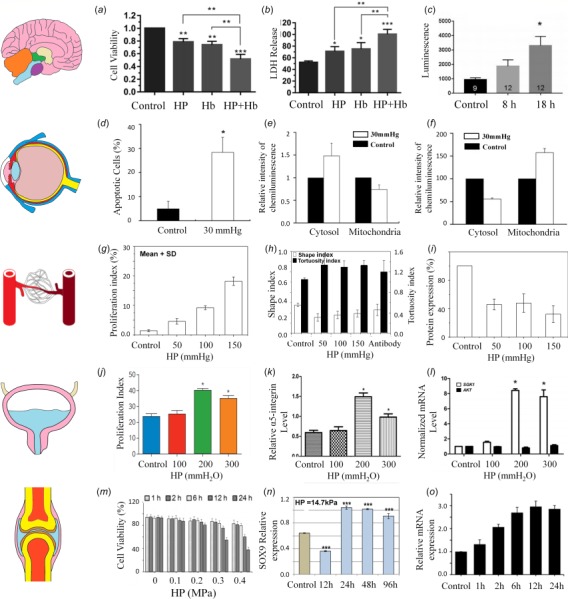
Hydrostatic pressure regulated cell behaviors in vitro: (a) neuron viability varies with HP of 40 kPa and application of 25 μM hemoglobin (Hb) [43], as does (b) lactate dehydrogenase release by neurons [43] and (c) bioluminescence indicating ATP release [80]. (d) Apoptosis of retina ganglion precursor-like cells is affected by HP [17], as is the chemiluminescence intensity of cytochrome C [17] (e) and Drp-1 [81] (f) in the cytosol and mitochondria of retina cells. (g) In blood vessel endothelial cells, proliferation increases with HP [33], while (h) they become less round (lower shape index) and more tortuous [33] and (i) VE-cadherin expression decreases [33]. (j) In the bladder, proliferation of smooth muscle cells increases with sufficient HP [16], and (k) expression of -integrin is elevated at HP of 200 mmH2O (2 kPa) [82], while (l) SGK1 but not protein kinase B (AKT) mRNA levels increase with HP above this level [58]. (m) In articular cartilage, chondrocyte viability decreases with both the magnitude and duration of HP [19], but (n) expression of the transcription factor SOX9 increases with sufficient HP exposure [37] and time-dependent variation of GRP78 protein expression in chondrocytes induced by HP [19]. Images (c, j, k, l, g, h, i, m, o, n) reproduced, with permission, from Refs. [80], [16], [58], [33], [19], and [37].
4.2. Hydrostatic Pressure-Regulated Behaviors of Eye Cells.
Glaucoma is the main cause of blindness, which is characterized by irreversible and progressive retinal ganglion cell (RGC) loss [83]. The biggest threat to RGC death is the elevated IOP in glaucoma [84]. In vitro, apoptosis of cells similar to the mouse retinal ganglion precursor-like cell line 661W (often incorrectly reported as the rat RGC-5 retinal ganglion cell line [85,86]) is enhanced under HP of 30 mmHg (3.99kPa) for three days (Fig. 3(d)) [17]. At the same time, cytochrome C content in cytosol increases by ∼150% fold, but decreases in mitochondria by 3/4-fold (Fig. 3(e)), likely contributing to cell death. In addition, Drp-1 translocation, abnormal cristae depletion, and cell ATP reduction is triggered in these cells under HP of 30 mmHg (3.99 kPa) [81]. After elevating hydrostatic pressure, Drp-1 was decreased by 55.6%±2.2% in the cytosol while increased by 57.4%±8.7% in mitochondria [81] (Fig. 3(f)). It was also shown that directly applied HP does not cause detectable changes in survival of human RGCs [87]. These conflicting data suggest the possibility of redundant pathways for HP-induced cell death, and point to a need for additional research in the area.
4.3. Hydrostatic Pressure-Regulated Behaviors of Vascular Cells.
Under both physiologic and pathologic conditions, HP has been found to affect form and function of vascular endothelial cells, including morphology, cytoskeletal structure, and proliferation (Fig. 3(g)). BAECs exhibit elongated cell shape and remodel their cytoskeletal structure and multilayering under HP of 12 mmHg (1.60 kPa) for 7 days [18]. Furthermore, BAECs exposed to HP of 50, 100, or 150 mmHg (6.65, 13.3, or 20.0 kPa) for 24 h become less circular and more tortuous [33,88] (Figs. 3(h)–3(i)). Vascular endothelial (VE) cadherin expression reduces under HP stimulation, and VE cadherin inhibition causes elongated and tortuous cell shapes, suggesting a role for VE cadherin in regulating endothelial cell morphology under HP. HP stimulates the proliferation of endothelial cells. Human umbilical vein endothelial cells increase in proliferation when exposed to 400 Pa to HP for 4 days [89]. Under these conditions, these cells upregulate expression of integrin subunit . antagonists block HP-induced proliferation, suggesting a role for integrin in mechanotransduction of HP by endothelial cells. However, some other studies have found no detectable effect of elevated hydrostatic pressure (with slow depressurization) on cell functions of BAECs by using similar methodologies [90].
4.4. Hydrostatic Pressure-Regulated Behaviors of Bladder Cells.
Bladder SMCs and endothelial cells are subjected to dynamic HP over a physiological range whose magnitude varies over time. This physiological range of HP environment is required for bladder cell function. Pathologies such as certain spinal cord injuries or bladder outlet obstruction can elevate bladder HP sufficiently to negatively influence bladder cell function or lead to degenerative disease of the upper urinary tract.
Dynamic HP of 10, 20, or 30 kPa over 24 h enhances proliferation of human bladder SMCs in vitro (Fig. 3(j)) [16,58,82]. Furthermore, expression of integrin α5 and phosphorylation of focal adhesion kinase (FAK) also increase with HP stimulation (Fig. 3(k)), while inhibition of integrin α5 decreases the level of p-FAK expression and eliminates HP-induced proliferation of human bladder SMCs [82], suggesting an integrin α5-FAK signaling pathway for HP-induced proliferation of these cells. SGK1 expression and activity are similarly increased by HP stimulation (Fig. 3(l)), and silencing SGK1 abolishes HP-induced human bladder SMC proliferation, suggesting a role for the PI3K/SGK1 signaling pathway in this mechanotransduction [58]. Recently, both microRNA 4323 and MiR 3180-5p have also been found to promote proliferation of human bladder SMCs under HP [34,35].
4.5. Hydrostatic Pressure-Regulated Behaviors of Articular Cartilage Cells.
Articular cartilage injury is a widespread problem, with defects and degeneration commonly arising from injury, overuse, and arthritis. Cartilage tissue engineering aims to treat or replace injured or degraded cartilage. Some of the most promising cartilage repair strategies include application of HP to mimic the native mechanical micro-environment of chondrocytes for tissue engineering [27].
Hydrostatic pressure influences differentiation and viability of chondrocytes. Excessive HP reduces chondrocyte viability (Fig. 3(m)) [19]. Chondrocyte differentiation, as measured by expression of the transcription factor SOX9, is enhanced by long-term HP stimulation (Fig. 3(n)) [37]. Compared to static HP, dynamic HP generally has superior effects on the function of chondrocytes. Dynamic HP of 0.8 MPa (5 min on, 30 min off, for only ten times) increases proteoglycan synthesis mRNA expression in bovine chondrocytes, while no change in collagen synthesis occurs under static HP [91]. Similarly, aggrecan and collagen II increase under 1 Hz HP of 10 MPa for 4 h, while collagen mRNA levels decrease under static HP [92]. Collagen II and aggrecan expression is significantly upregulated by combined treatment with HP and growth factor TGF-β [93]. Induced by HP, the mRNA expression of GRP78 increased significantly with a maximum of 2.96 time than the control at 12 h [19] (Fig. 3(o)).
4.6. Hydrostatic Pressure Responses Across Cell Types.
Proliferation and apoptosis are, in general, affected by HP across cell types, but the effects vary substantially depending upon cell types (Fig. 4). Positive HP enhances proliferation of most kinds of cells (e.g., osteosarcoma cells [94], bladder smooth muscle cells [82], vascular endothelial cells [89], and jurkat cells [95]), but leads to apoptosis of others at sufficient magnitude (e.g., retina cells [17], jurkat cells [95]). Negative HP enhances proliferation of a few kinds of cells (e.g., epidermal cells [96]), while apoptosis under negative HP has not yet been reported.
Fig. 4.
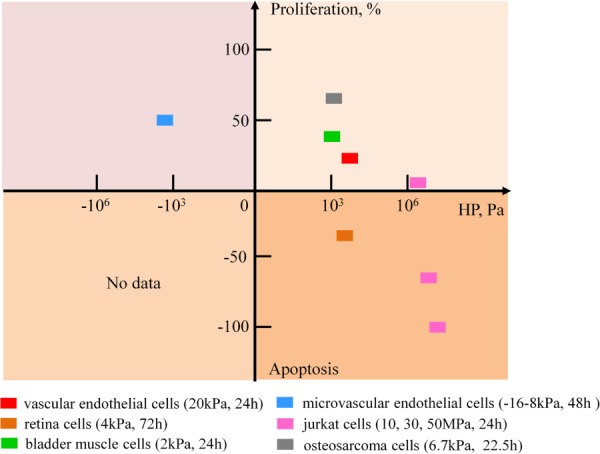
HP regulates proliferation and apoptosis differently for different types of cells [17,82,89,94–96]. Most types of cells proliferate at positive hydrostatic pressure, but some types of cells are apoptotic at positive (compressive) hydrostatic pressure. A few types of cells proliferate at negative (tensile) hydrostatic pressure; apoptosis of cells under negative hydrostatic pressure has not been reported.
5. Mathematical Models of Hydrostatic Pressure-Regulated Cell Behaviors
In Sec. 4, we summarized the main experimental observations of cell behaviors regulated by HP. Mathematical models are very important to quantitatively understand cell behaviors and predict new phenomena. In spite of the massive body of experimental studies in vitro, there are few theories for HP-regulated cell behaviors. Compared to other types of mechanical cues (e.g., stretch, compression, twist), HP predominantly induces the volumetric deformation without shear deformation. Theories of HP-regulated cell volume have been developed (Fig. 5(a)) that predict cell volume responses under HP. Control of cell volume by HP could be a target for cancer treatment [38,97].
Fig. 5.
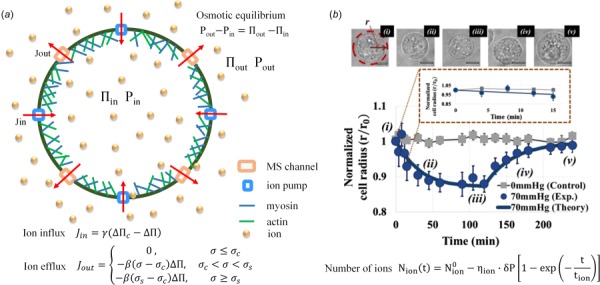
Hydrostatic pressure-regulated cell volume: (a) theoretical model of cell volume and pressure regulation for a spherical cell. A spherical cell enclosed by an actomyosin cortex and the cell membrane. Embedded in the membrane are several families of passive mechanosensitive ion channels (ions efflux) and active ion pumps (ions flux). The mechanosensitive channels and active ion pumps can change the internal osmotic pressure, , leading to changes in internal HP, . Figure modeled after Ref. [98] (b) experimental and theoretical results [39]. (upper) the volume of K562 cells changed under HP of 70 mmHg (9.3 kPa), which was then removed after 2 h; (lower) comparison of theoretical normalized cell radius with the experimental data. Image (b) reproduced, with permission, from Ref. [39].
5.1. Osmotic Pressure.
The starting point of these theories is the work of Jacobus van't Hoff, who received the first Nobel Prize in Chemistry for his theory of osmotic pressure in chemical equilibrium [99]. When two solutions of different concentration are separated by a semipermeable membrane (e.g., a cell membrane) that allows water but not solute to pass through it, the concentration difference forces the water into the solution of higher concentration, which exerts an extra pressure on the membrane. This extra pressure is defined as osmotic pressure and can be estimated by van't Hoff's theory.
A living cell in a medium with solute concentration differing from that of the extracellular medium will have the turgor pressure (, the force per unit area bearing on the cell wall or membrane) equal to the osmotic pressure difference (), namely
| (1) |
The turgor pressure () equals the hydrostatic pressure difference: , where and are the hydrostatic pressure inside and outside the cell, respectively. The osmotic pressure is , being the osmotic pressure inside the cell and being the osmotic pressure outside the cell. van't Hoff observed that nonelectrolyte solute molecules in such a situation obey the ideal gas law so that the osmotic pressure difference can be estimated as:
| (2) |
where N is the number of extra sugar molecules in the volume V, (molecules/volume) is the concentration difference of sugar, is the concentration inside the cell, is the concentration outside the cell, is the Boltzmann's constant, and is the absolute temperature.
5.2. Water Flux in Response to Osmotic Pressure.
For nonequilibrium living cells exposed to external stimuli, Jiang et al. [98] systemically discuss the cellular pressure and volume regulation by considering ion regulation, cortical tension, and water flow. For a spherical cell with radius r, the volume change is controlled by
| (3) |
where is the volumetric flux across the cell membrane, and is a constant representing membrane permeability.
Mechanosensitive channels and ion transporters on cell membranes control the influx and efflux of ions and other osmolytes, which play a role in cell volume and pressure regulation. The simplest phenomenological model considers only one species of mechanosensitive channel as
| (4) |
where is a constant, is the (biaxial) membrane and cortical stress, is a threshold stress below which is zero, and is the saturating stress above which all mechnosensitive channels open. The model considers one species of ion transporter as
| (5) |
where is the critical osmotic pressure difference and is a constant.
Assuming the cell membrane adheres to the cell cortex and neglecting the dynamics of membrane structures, the cell membrane and cortex are treated as a single layer. The cortical stress that appears in the mechanical force balance is
| (6) |
where h is the cortical thickness. In many cells, actin under the membrane interacting with myosin molecular motors forms a cortical layer. The cortex is actively controlled through internal stresses in the cortical layer generated by actomyosin motors [100–102].
5.3. Models of Cortical Actin Contractility.
There exist a series of intricate models of cellular mechanics and contractility exist, which have been reviewed elsewhere [103]. Although much more intricate models of passive [104] and active [105,106] cellular mechanics exist, we review here one model of how active contractility of the cortex plays a major role in controlling cell pressure [107,108]. In mammalian cells, cortex is just below the cell membrane, containing a large amount of actin [90,109–111]. In many cells, this actin interacts with myosin molecular motors to form an actively contracting cortical layer [101,102,111]. Active stress generated in cortex varies with calcium influx induced by change of membrane tension [112], with stress-induced changes to the number of actin cross-linkers [113,114], with cytoskeletal depolymerization due to cell stretch [103,115], membrane domain dynamics [116], and force-dependent myosin kinetics [117]. All of these point to a feedback mechanism whereby changes of cell membrane tension lead to changes of myosin contraction, Tao et al. [107,108] propose that membrane tension can trigger Rho activation and, in turn, further activate the myosin assembly. The contraction of myosin monofilaments is related to the active stress
| (7) |
where is a maximum contractile stress that cells exert and M is the fraction of activated myosin. This relates to the kinetics of Rho by
| (8) |
| (9) |
where and are the activation and deactivation rates of Rho, respectively, and M are fractions of activated Rho and myosin, respectively, and are assembly and disassembly rates of the myosin. is an activation function of depending on membrane tension. As above, is the critical membrane tension where Rho activation starts and is a saturating tension.
The process of myosin assembly and contraction influenced by the sudden change of force that cell experience is modeled as
| (10) |
where is a constant, is the passive transient stress, which is proportional to the flow rate in the cortex, and is an activation function. Active stress in the cell cortex can restore membrane tension (maintain homeostasis). From the perspective of Sun and coworkers model [107,108], it is not the cell membrane but the cortical tension generated by cell contraction that balances most of the pressure difference.
Additionally, actin networks in cells are viscoelastic fluids with both solid and fluid mechanical properties [107]. The polymerization and depolymerization of actin network are regulated by actin crosslinking proteins [118,119]. The dynamic binding and unbinding of cross-linking proteins also regulate the mechanical properties of the actin network [120,121]. The binding process will contribute to the elasticity of the network while unbinding process will contribute to hysteresis. In addition, factors such as filament stiffness, entropic fluctuations, and myosin molecular motors could also regulate actin network rheology [122–127]. An active literature exists on active actin network contractility at the cell membrane [128,129].
These factors all fall under the broad rubric of mechanotransduction, the transduction of mechanical force into intracellular biochemical signals. Actin cytoskeleton dynamics plays a key role in this [103,130]. Recently, using a microfluidic device that mechanically compresses live cells, He et al. [131] find that uniaxial compression can influence RhoA activity through a Ca2+ dependent pathway regulated by TRPV4 channels. This is modeled by considering membrane tension, myosin contraction, and TRPV4 and RhoA kinetics in response to compression. The membrane tension could be found using a force balance normal to the surface
| (11) |
where H is the cell surface mean curvature, is the external mechanical force, and A is the area over which the external force is distributed. A Hill function is used to represent how stress-dependent TRPV4 opening affects RhoA kinetics
| (12) |
where are rate constants for activation and deactivation, is an activation threshold for membrane tension, and ρ is the proportion of active RhoA.
5.4. Models of How Cortical Actin Contractility Affects Pressure-Volume Relations.
The volume of cells of leukemia cell lines K562 and HL60 in suspension decreases under HP stimulation [39] (Fig. 5(b)). To explain this phenomenon, Hui et al. [39] modify Jiang's model [98] (Eq. (3)) to include bending, surface energy, and ion transport
| (13) |
where represents membrane permeability, represents the cross-membrane difference in ionic concentrations (number of extra ions within the volume ), is the membrane tension multiplied by the membrane thickness, r is the cell radius, is the radius that the cell would adopt in the absence of mechanical stress, and K is an areal modulus. Osmotic pressure is expressed, following van't Hoff, as:
| (14) |
Before the pressure shock is introduced, Eqs. (3), (6), and (13) combine to yield
| (15) |
For each species of ion, the ionic concentrations vary with time according to an experimentally motivated phenomenological function
| (16) |
where is the applied hydrostatic pressure spike, is a time constant for a specific ion species, and is a constant. The overall membrane tension is assumed to take the form
| (17) |
where is the tension generated by actomyosin contraction in the actin cortex (treated as constant) and represents the passive stress from the deformation of the cell membrane:
| (18) |
where is the surface area of the cell, and is the area of a cell with vanishing . The unstretched cell radius can be written in terms of and .
5.5. More Detailed Representations of Ion Transport in Volume Regulation.
Ionic flows play a vital role in regulating cell size and shape, including Cl– ions [132,133], and Ca2+ ions, which affect cell shape oscillations [134]. Additionally, at least one volume-regulated anion channel, SWELL1, has been identified [135].
Florence et al. [136] systematically investigated Na+, K+, and Cl– ions and transmembrane electrical potential in cell volume regulation. By controlling the electrical potential through a whole-cell patch clamp experiment, they find that cell volume increases with depolarization. Decreasing extracellular chloride concentration decreases cell volume, and exchanging sodium and potassium in the medium increases cell volume. To model this, they consider both the concentrations of permeable ions and the membrane potential, and write the following for ionic fluxes:
| (19) |
where n is an ionic species (Na+, K+, or Cl−), is the total number of ions in species n, and is the associated ion flux across the cell membrane. Considering both the passive and active processes, the transportation is modeled as
| (20) |
| (21) |
| (22) |
where the passive ion fluxes, represented by the superscript p, are related to electrochemical potential as
| (23) |
in which and are the ion species n concentrations outside and inside the cell, is the membrane potential, F is the Faraday's constant, is the rate of ion permeation, and is the valence of the ionic species.
The flux of cotransporter (NKCC) is
| (24) |
where is s constant of transport rate. Active fluxes arise from Na+/K+ pump:
| (25) |
where is the pump transport rate constant, is the ATP concentration, and are constants that scale and , and describes the pump activity depending on the potential voltage
| (26) |
where and are constants. Models such as this that incorporate specific ion channel activity are important for the long-term goal of identifying specific ion channels that can be blocked to tailor the volumetric responses of healthy and pathological cells.
6. Conclusions and Future Perspectives
Hydrostatic pressure is an important mechanical cue in cell micro-environment, playing significant roles in regulating cell behaviors including differentiation, migration, apoptosis, and proliferation. Models of how these are regulated through volumetric response of cells are still emerging, but are important to understand a range of pathologies. We conclude with thoughts on the challenges and opportunities in understanding HP-regulated cell behaviors in the future.
The first challenge is quantifying the local mechanical micro-environment of living cells and their extracellular matrix. Advanced technologies for doing so have potential to transform the field. New tools are emerging continuously, such as elastic, round microgels, which have been used to quantify compressive forces between living cell layers and within tissues [137]. The stress fields in a three-dimensional (3D) matrix and dynamical mechanical behavior in living mammalian cytoplasm have been characterized by using a nonlinear stress inference microscopy with optical tweezers [138] and [139]. The local intracellular pressure has been directly measured by using a micropressure system [140]. Tools for measuring and specifying the time dependence of the mechanical micro-environment are coming online [141,142]. Advanced technologies to measure local HP in living cells and extracellular matrix can contribute to diagnosis and understanding of pathobiology.
Although there are several in vitro HP loading platforms, these cannot reconstitute the full complexity and heterogeneity of cells in vivo. 3D micro-environments are essential but notoriously difficult to construct [143,144]. To solve the problem, cells can be encapsulated in hydrogels, which are now the most promising method to mimic 3D cell micro-environment in vivo [29]. In addition, the cell mechanical micro-environment in vivo also varies with time; however, most existing studies cultured cells under static HP in vitro. Tools to prescribe and characterize the viscoelastic properties and development of tissues are emerging [141,145,146], and represent an important need. An omission in the many models currently in the literature is the role of extracellular matrix elasticity in regulating these HP-induced volumetric responses.
One major motivation for engineering HP in vitro is the development of in vivo applications, such as regeneration of functional tissues. For instance, craniofacial bone substitutes for implantation purposes can be fabricated by culturing chondrocytes under HP stimulation [147]. Optimized HP stimulation is required in regeneration of functional articular cartilage tissue. Negative HP method significantly promotes wound healing effect by enhancing the migration of epidermal cells [148] and epidermal cells proliferation [96]. The optimized parameters of HP for wound healing are also required. Positive HP leads to the apoptosis of some cell types (e.g., jurkat cells [95]), and the ability to quantify and alter HP-related volume regulation of cells may someday hold promise for killing cancer cells.
Finally, the detailed mechanisms by which HP affects cell behaviors continue to be a source of debate, and detailed relationships between electrophysiology and volumetric response are needed to resolve, as well as further characterization of downstream biochemistry. For instance, for in retinal ganglion cell death, debate exists between whether cytochrome C or mitochondrial fission, Drp-1 translocation, abnormal cristae depletion, and cell ATP reduction play crucial roles in HP regulation. For the HP-induced cell proliferation in the bladder, debate exists about the relative roles of integrin α5, the level of p-FAK [82], or SGK1, MicroRNA 4323, and MiR 3180-5p [34,58,82]. To address this, it is necessary to characterize in situ, real time and even long-term cells behaviors in response to HP. Additionally, decoding the detailed intracellular responses at the molecular and genetic levels that together build intracellular and extracellular signaling communication networks to HP will provide valuable insight.
Contributor Information
Shaobao Liu, State Key Laboratory of Mechanics and, Control of Mechanical Structures, , Nanjing University of Aeronautics and Astronautics, , Nanjing 210016, China;; The Key Laboratory of Biomedical Information, Engineering of Ministry of Education, , School of Life Science and Technology, , Xi'an Jiaotong University, , Xi'an 710049, China; Department of Biomedical Engineering, Bioinspired Engineering and Biomechanics Center (BEBC), , Xi'an Jiaotong University, , Xi'an 710049, China
Ru Tao, The Key Laboratory of Biomedical Information, Engineering of Ministry of Education, , School of Life Science and Technology, , Xi'an Jiaotong University, , Xi'an 710049, China;; Department of Biomedical Engineering, Bioinspired Engineering and Biomechanics Center (BEBC), , Xi'an Jiaotong University, , Xi'an 710049, China
Ming Wang, The Key Laboratory of Biomedical Information, Engineering of Ministry of Education, , School of Life Science and Technology, , Xi'an Jiaotong University, , Xi'an 710049, China;; Department of Biomedical Engineering, Bioinspired Engineering and Biomechanics Center (BEBC), , Xi'an Jiaotong University, , Xi'an 710049, China
Jin Tian, Department of Biomedical Engineering, Bioinspired Engineering and Biomechanics Center (BEBC), , Xi'an Jiaotong University, , Xi'an 710049, China;; State Key Laboratory for Strength and, Vibration of Mechanical Structures, , Xi'an Jiaotong University, , Xi'an 710049, China
Guy M. Genin, The Key Laboratory of Biomedical Information , Engineering of Ministry of Education, , School of Life Science and Technology, , Xi'an Jiaotong University, , Xi'an 710049, China; Department of Biomedical Engineering, Bioinspired Engineering and Biomechanics Center (BEBC), , Xi'an Jiaotong University, , Xi'an 710049, China; Department of Mechanical Engineering & , Materials Science, , National Science Foundation Science and , Technology Center for Engineering Mechanobiology, , Washington University, , St. Louis, MO 63130
Tian Jian Lu, State Key Laboratory of Mechanics and, Control of Mechanical Structures, , Nanjing University of Aeronautics and Astronautics, , Nanjing 210016, China;; Department of Structural Engineering & Mechanics, , Nanjing Center for Multifunctional Lightweight, Materials and Structures, , Nanjing University of Aeronautics and Astronautics, , Nanjing 21006, China; , State Key Laboratory for Strength and, Vibration of Mechanical Structures, , Xi'an Jiaotong University, , Xi'an 710049, China
Feng Xu, The Key Laboratory of Biomedical Information, Engineering of Ministry of Education, , School of Life Science and Technology, , Xi'an Jiaotong University, , Xi'an 710049, China;; Department of Biomedical Engineering, Bioinspired Engineering and Biomechanics Center (BEBC), , Xi'an Jiaotong University, , Xi'an 710049, China , e-mail: fengxu@mail.xjtu.edu.cn
Funding Data
National Natural Science Foundation of China (Grant Nos. 11522219 and 11532009; Funder ID: 10.13039/501100001809).
New Faculty Foundation of NUAA (Grant No. 1001-YAH19016; Funder: 10.13039/501100004193).
Foundation of “Jiangsu Provincial Key Laboratory of Bionic Functional Materials” (Grant No. 1001-XCA1816310; Funder ID: 10.13039/501100004193).
Foundation for the Priority Academic Program Development of Jiangsu Higher Education Institutions (Funder ID: 10.13039/501100012246).
National Science Foundation through the Science and Technology Center for Engineering Mechanobiology (Grant No. CMMI 1548571; Funder ID: 10.13039/100000001).
NIH (Grant No. U01EB016422; Funder ID: 10.13039/100000002).
References
- [1]. Chang, L. , Azzolin, L. , Di Biagio, D. , Zanconato, F. , Battilana, G. , Lucon Xiccato, R. , Aragona, M. , Giulitti, S. , Panciera, T. , Gandin, A. , Sigismondo, G. , Krijgsveld, J. , Fassan, M. , Brusatin, G. , Cordenonsi, M. , and Piccolo, S. , 2018, “ The SWI/SNF Complex is a Mechanoregulated Inhibitor of YAP and TAZ,” Nature, 563(7730), pp. 265–269. 10.1038/s41586-018-0658-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2]. Vining, K. H. , and Mooney, D. J. , 2017, “ Mechanical Forces Direct Stem Cell Behaviour in Development and Regeneration,” Nat. Rev. Mol. Cell Biol., 18, pp. 728–742. 10.1038/nrm.2017.108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3]. Huang, G. , Xu, F. , Genin, G. M. , and Lu, T. J. , 2019, “ Mechanical Microenvironments of Living Cells: A Critical Frontier in Mechanobiology,” Acta Mechanica Sinica, 35(2), pp. 265–269. 10.1007/s10409-019-00854-1 [DOI] [Google Scholar]
- [4]. Chen, J. , and Wang, N. , 2019, “ Tissue Cell Differentiation and Multicellular Evolution Via Cytoskeletal Stiffening in Mechanically Stressed Microenvironments,” Acta Mechanica Sinica, 35(2), pp. 270–274. 10.1007/s10409-018-0814-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5]. Xia, Y. , Pfeifer, C. R. , and Discher, D. E. , 2019, “ Nuclear Mechanics During and After Constricted Migration,” Acta Mechanica Sinica, 35(2), pp. 299–308. 10.1007/s10409-018-00836-9 [DOI] [Google Scholar]
- [6]. Wolfe, R. P. , and Ahsan, T. , 2013, “ Shear Stress During Early Embryonic Stem Cell Differentiation Promotes Hematopoietic and Endothelial Phenotypes,” Biotechnol. Bioeng., 110(4), pp. 1231–1242. 10.1002/bit.24782 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7]. Wolfe, R. P. , Leleux, J. , Nerem, R. M. , and Ahsan, T. , 2012, “ Effects of Shear Stress on Germ Lineage Specification of Embryonic Stem Cells,” Integr. Biol. UK, 4(10), pp. 1263–1273. 10.1039/c2ib20040f [DOI] [PubMed] [Google Scholar]
- [8]. Messina, S. L. , 2015, “ Effects of Oscillatory Shear Stress on Early Differentiation and Mechanotransduction,” ProQuest Dissertations Publishing, Ann Arbor, MI. [Google Scholar]
- [9]. Hsu, H. J. , Lee, C. F. , Locke, A. , Vanderzyl, S. Q. , and Kaunas, R. , 2010, “ Stretch-Induced Stress Fiber Remodeling and the Activations of JNK and ERK Depend on Mechanical Strain Rate, but Not FAK,” PLoS One, 5(8), p. e12470. 10.1371/journal.pone.0012470 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10]. Yang, M. , Xiao, L. W. , Liao, E. Y. , Wang, Q. J. , Wang, B. B. , and Lei, J. X. , 2014, “ The Role of Integrin-β/FAK in Cyclic Mechanical Stimulation in MG-63 Cells,” Int. J. Clin. Exp. Pathol., 7(11), pp. 7451–7459.https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4270589/pdf/ijcep0007-7451.pdf [PMC free article] [PubMed] [Google Scholar]
- [11]. Wu, Y. , van der Schaft, D. W. J. , Baaijens, F. P. , and Oomens, C. W. J. , 2016, “ Cell Death Induced by Mechanical Compression on Engineered Muscle Results From a Gradual Physiological Mechanism,” J. Biomech., 49(7), pp. 1071–1077. 10.1016/j.jbiomech.2016.02.028 [DOI] [PubMed] [Google Scholar]
- [12]. Stewart, M. P. , Helenius, J. , Toyoda, Y. , Ramanathan, S. P. , Muller, D. J. , and Hyman, A. A. , 2011, “ Hydrostatic Pressure and the Actomyosin Cortex Drive Mitotic Cell Rounding,” Nature, 469(7329), pp. 226–230. 10.1038/nature09642 [DOI] [PubMed] [Google Scholar]
- [13]. Stewart, M. P. , Mueller, D. J. , Helenius, J. , and Hyman, A. A. , 2010, “ Opposing Activities of Hydrostatic Pressure and Actomyosin Contraction Drive Mitotic Cell Rounding,” Biophys. J., 98(3), p. 367a. 10.1016/j.bpj.2009.12.1979 [DOI] [Google Scholar]
- [14]. Zonia, L. , and Munnik, T. , 2007, “ Life Under Pressure: Hydrostatic Pressure in Cell Growth and Function,” Trends Plant Sci., 12(3), pp. 90–97. 10.1016/j.tplants.2007.01.006 [DOI] [PubMed] [Google Scholar]
- [15]. Steward, A. J. , Thorpe, S. D. , Vinardell, T. , Buckley, C. T. , Wagner, D. R. , and Kelly, D. J. , 2012, “ Cell–Matrix Interactions Regulate Mesenchymal Stem Cell Response to Hydrostatic Pressure,” Acta Biomater., 8(6), pp. 2153–2159. 10.1016/j.actbio.2012.03.016 [DOI] [PubMed] [Google Scholar]
- [16]. Wu, T. , Chen, L. , Wei, T. , Wang, Y. , Xu, F. , and Wang, K. , 2012, “ Effect of Cyclic Hydrodynamic Pressure-Induced Proliferation of Human Bladder Smooth Muscle Through Ras-Related C3 Botulinum Toxin Substrate 1, Mitogen-Activated Protein Kinase Kinase 1/2 and Extracellular Regulated Protein Kinases 1/2,” Int. J. Urol., 19(9), pp. 867–874. 10.1111/j.1442-2042.2012.03043.x [DOI] [PubMed] [Google Scholar]
- [17]. Ju, W.-K. , Kim, K.-Y. , Lindsey, J. D. , Angert, M. , Patel, A. , Scott, R. T. , Liu, Q. , Crowston, J. G. , Ellisman, M. H. , and Perkins, G. A. , 2009, “ Elevated Hydrostatic Pressure Triggers Release of OPA1 and Cytochrome C, and Induces Apoptotic Cell Death in Differentiated RGC-5 Cells,” Mol. Vis., 15, pp. 120–134. [PMC free article] [PubMed] [Google Scholar]
- [18]. Acevedo, A. D. , Bowser, S. S. , Gerritsen, M. E. , and Bizios, R. , 1993, “ Morphological and Proliferative Responses of Endothelial Cells to Hydrostatic Pressure: Role of Fibroblast Growth Factor,” J. Cell. Physiol., 157(3), pp. 603–614. 10.1002/jcp.1041570321 [DOI] [PubMed] [Google Scholar]
- [19]. Xu, T. , Xu, G. , Gu, Z. , and Wu, H. , 2017, “ Role of Endoplasmic Reticulum Stress Pathway in Hydrostatic Pressure-Induced Apoptosis in Rat Mandibular Condylar Chondrocytes,” Mol. Cell. Biochem., 429(1–2), pp. 22–31. 10.1007/s11010-016-2933-5 [DOI] [PubMed] [Google Scholar]
- [20]. Markiewicz, L. , Pytel, D. , Mucha, B. , Szymanek, K. , Szaflik, J. , Szaflik, J. P. , and Majsterek, I. , 2015, “ Altered Expression Levels of MMP1, MMP9, MMP12, TIMP1, and IL-1β as a Risk Factor for the Elevated IOP and Optic Nerve Head Damage in the Primary Open-Angle Glaucoma Patients,” Biomed. Res. Int., 2015, p. 812503. 10.1155/2015/812503 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21]. Brockhaus, K. , Melkonyan, H. , Prokosch, V. , and Thanos, S. , 2017, “ Elevated Intraocular Pressure Induces Cellular Responses in the Retinal Capillaries,” Klinische Monatsblätter Für Augenheilkunde, 234(10), pp. 1266–1275. [DOI] [PubMed] [Google Scholar]
- [22]. Sampathkumar, S. , Schieber, A. T. , and Toris, C. B. , 2016, “ A Schlemm's Canal Scaffold for the Treatment of Elevated IOP,” Expert Rev. Ophthalmol., 11(4), pp. 259–266. 10.1080/17469899.2016.1210006 [DOI] [Google Scholar]
- [23]. Nusbaum, D. M. , Wu, S. M. , and Frankfort, B. J. , 2015, “ Elevated Intracranial Pressure Causes Optic Nerve and Retinal Ganglion Cell Degeneration in Mice,” Exp. Eye Res., 136, p. 38. 10.1016/j.exer.2015.04.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24]. Kershen, R. T. , Azadzoi, K. M. , and Siroky, M. B. , 2002, “ Blood Flow, Pressure and Compliance in the Male Human Bladder,” J. Urol., 168(1), pp. 121–125. 10.1016/S0022-5347(05)64843-4 [DOI] [PubMed] [Google Scholar]
- [25]. Stover, J. , and Nagatomi, J. , 2007, “ Cyclic Pressure Stimulates DNA Synthesis Through the PI3K/Akt Signaling Pathway in Rat Bladder Smooth Muscle Cells,” Ann. Biomed. Eng., 35(9), pp. 1585–1594. 10.1007/s10439-007-9331-9 [DOI] [PubMed] [Google Scholar]
- [26]. Thomopoulos, S. , Das, R. , Birman, V. , Smith, L. , Ku, K. , Elson, E. L. , Pryse, K. M. , Marquez, J. P. , and Genin, G. M. , 2011, “ Fibrocartilage Tissue Engineering: The Role of the Stress Environment on Cell Morphology and Matrix Expression,” Tissue Eng. Part A, 17(7–8), pp. 1039–1053. 10.1089/ten.tea.2009.0499 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27]. Elder, B. D. , and Athanasiou, K. A. , 2009, “ Hydrostatic Pressure in Articular Cartilage Tissue Engineering: From Chondrocytes to Tissue Regeneration,” Tissue Eng. Part B: Rev., 15(1), pp. 43–53. 10.1089/ten.teb.2008.0435 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28]. Mauck, R. L. , Nicoll, S. B. , Seyhan, S. L. , Ateshian, G. A. , and Hung, C. T. , 2003, “ Synergistic Action of Growth Factors and Dynamic Loading for Articular Cartilage Tissue Engineering,” Tissue Eng. Part A, 9(4), p. 597. 10.1089/107632703768247304 [DOI] [PubMed] [Google Scholar]
- [29]. Huang, G. , Li, F. , Zhao, X. , Ma, Y. , Li, Y. , Lin, M. , Jin, G. , Lu, T. J. , Genin, G. M. , and Xu, F. , 2017, “ Functional and Biomimetic Materials for Engineering of the Three-Dimensional Cell Microenvironment,” Chem. Rev., 117(20), pp. 12764–12850. 10.1021/acs.chemrev.7b00094 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30]. Hall, A. C. , Urban, J. P. , and Gehl, K. A. , 1991, “ The Effects of Hydrostatic Pressure on Matrix Synthesis in Articular Cartilage,” J. Orthop. Res., 9(1), pp. 1–10. 10.1002/jor.1100090102 [DOI] [PubMed] [Google Scholar]
- [31]. Smith, L. , Xia, Y. , Galatz, L. M. , Genin, G. M. , and Thomopoulos, S. , 2012, “ Tissue-Engineering Strategies for the Tendon/Ligament-to-Bone Insertion,” Connect. Tissue Res., 53(2), pp. 95–105. 10.3109/03008207.2011.650804 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32]. Thomopoulos, S. , Birman, V. , and Genin, G. M. , 2013, Structural Interfaces and Attachments in Biology, Springer, Berlin.
- [33]. Ohashi, T. , Sugaya, Y. , Sakamoto, N. , and Sato, M. , 2007, “ Hydrostatic Pressure Influences Morphology and Expression of VE-Cadherin of Vascular Endothelial Cells,” J. Biomech., 40(11), pp. 2399–2405. 10.1016/j.jbiomech.2006.11.023 [DOI] [PubMed] [Google Scholar]
- [34]. Sun, Y. , Luo, D. , Zhu, Y. , and Wang, K. , 2017, “ MicroRNA 4323 Induces Human Bladder Smooth Muscle Cell Proliferation Under Cyclic Hydrodynamic Pressure by Activation of Erk1/2 Signaling Pathway,” Exp. Biol. Med., 242(2), pp. 169–176. 10.1177/1535370216669837 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35]. Sun, Y. , Luo, D. Y. , Zhu, Y. C. , Zhou, L. , Yang, T. X. , Tang, C. , Shen, H. , and Wang, K. J. , 2016, “ MiR 3180-5p Promotes Proliferation in Human Bladder Smooth Muscle Cell by Targeting PODN Under Hydrodynamic Pressure,” Sci. Rep., 6, p. 33042. 10.1038/srep33042 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36]. Sappington, R. M. , Sidorova, T. , Long, D. J. , and Calkins, D. J. , 2009, “ TRPV1: Contribution to Retinal Ganglion Cell Apoptosis and Increased Intracellular Ca2+ With Exposure to Hydrostatic Pressure,” Invest. Ophthalmol. Vis. Sci., 50(2), pp. 717–728. 10.1167/iovs.08-2321 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37]. Karamesinis, K. , Spyropoulou, A. , Dalagiorgou, G. , Katsianou, M. A. , Nokhbehsaim, M. , Memmert, S. , Deschner, J. , Vastardis, H. , and Piperi, C. , 2017, “ Continuous Hydrostatic Pressure Induces Differentiation Phenomena in Chondrocytes Mediated by Changes in Polycystins, SOX9, and RUNX2,” J. Orofacial Orthop., 78(1), pp. 1–11. 10.1007/s00056-016-0061-1 [DOI] [PubMed] [Google Scholar]
- [38]. Kao, Y. C. , Jheng, J. R. , Pan, H. J. , Liao, W. Y. , Lee, C. H. , and Kuo, P. L. , 2017, “ Elevated Hydrostatic Pressure Enhances the Motility and Enlarges the Size of the Lung Cancer Cells Through Aquaporin Upregulation Mediated by Caveolin-1 and ERK1/2 Signaling,” Oncogene, 36(6), pp. 863–874. 10.1038/onc.2016.255 [DOI] [PubMed] [Google Scholar]
- [39]. Hui, T. H. , Zhou, Z. L. , Qian, J. , Lin, Y. , Ngan, A. H. , and Gao, H. , 2014, “ Volumetric Deformation of Live Cells Induced by Pressure-Activated Cross-Membrane Ion Transport,” Phys. Rev. Lett., 113(11), p. 118101. 10.1103/PhysRevLett.113.118101 [DOI] [PubMed] [Google Scholar]
- [40]. Champaigne, K. D. , and Nagatomi, J. , 2012, The Role of Ion Channels in Cellular Mechanotransduction of Hydrostatic Pressure, Springer, Cham, The Netherlands. [Google Scholar]
- [41]. Steiner, L. A. , and Andrews, P. J. , 2006, “ Monitoring the Injured Brain: ICP and CBF,” Brit. J. Anaesth., 97(1), pp. 26–38. 10.1093/bja/ael110 [DOI] [PubMed] [Google Scholar]
- [42]. Graham, D. I. , Adams, J. H. , and Doyle, D. , 1978, “ Ischemic Brain-Damage in Fatal Non-Missile Head-Injuries,” J. Neurol. Sci., 39(2–3), pp. 213–234. 10.1016/0022-510X(78)90124-7 [DOI] [PubMed] [Google Scholar]
- [43]. Guo, T. , Ren, P. , Li, X. , Luo, T. , Gong, Y. , Hao, S. , and Wang, B. , 2018, “ Neural Injuries Induced by Hydrostatic Pressure Associated With Mass Effect After Intracerebral Hemorrhage,” Sci. Rep., 8(1), p. 9195. 10.1038/s41598-018-27275-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44]. Yoshino, D. , Sato, K. , and Sato, M. , 2015, “ Endothelial Cell Response Under Hydrostatic Pressure Condition Mimicking Pressure Therapy,” Cell Mol. Bioeng., 8(2), pp. 296–303. 10.1007/s12195-015-0385-8 [DOI] [Google Scholar]
- [45]. Pascarelli, N. A. , Collodel, G. , Moretti, E. , Cheleschi, S. , and Fioravanti, A. , 2015, “ Changes in Ultrastructure and Cytoskeletal Aspects of Human Normal and Osteoarthritic Chondrocytes Exposed to Interleukin-1β and Cyclical Hydrostatic Pressure,” Int. J. Mol. Sci., 16(11), pp. 26019–26034. 10.3390/ijms161125936 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46]. Aptel, F. , Weinreb, R. N. , Chiquet, C. , and Mansouri, K. , 2016, “ 24-H Monitoring Devices and Nyctohemeral Rhythms of Intraocular Pressure,” Prog. Retinal Eye Res., 55, pp. 108–148. 10.1016/j.preteyeres.2016.07.002 [DOI] [PubMed] [Google Scholar]
- [47]. Mantravadi, A. V. , and Vadhar, N. , 2015, “ Glaucoma,” Primary Care, 42(3), pp. 437–449. 10.1016/j.pop.2015.05.008 [DOI] [PubMed] [Google Scholar]
- [48]. Bendayan, M. , Sandborn, E. , Rasio, E. , Inoue, S. , Michel, R. P. , Hogg, J. C. , Hammersen, F. , Osgood, C. P. , Dujovny, M. , and Barrionuevo, P. J. , 1976, Blood Vessel Structure, Springer, Berlin. [Google Scholar]
- [49]. Ogedegbe, G. , and Pickering, T. , 2010, “ Principles and Techniques of Blood Pressure Measurement,” Cardiol. Clin., 28(4), pp. 571–586. 10.1016/j.ccl.2010.07.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50]. Hiitola, P. , Enlund, H. , Kettunen, R. , Sulkava, R. , and Hartikainen, S. , 2009, “ Postural Changes in Blood Pressure and the Prevalence of Orthostatic Hypotension Among Home-Dwelling Elderly Aged 75 Years or Older,” J. Hum. Hypertens., 23, pp. 33–39. 10.1038/jhh.2008.81 [DOI] [PubMed] [Google Scholar]
- [51]. Xie, X. , Atkins, E. , Lv, J. , Bennett, A. , Neal, B. , Ninomiya, T. , Woodward, M. , MacMahon, S. , Turnbull, F. , Hillis, G. S. , Chalmers, J. , Mant, J. , Salam, A. , Rahimi, K. , Perkovic, V. , and Rodgers, A. , 2016, “ Effects of Intensive Blood Pressure Lowering on Cardiovascular and Renal Outcomes: Updated Systematic Review and Meta-Analysis,” Lancet, 387(10017), pp. 435–443. 10.1016/S0140-6736(15)00805-3 [DOI] [PubMed] [Google Scholar]
- [52]. Mcguire, E. J. , Woodside, J. R. , Borden, T. A. , and Weiss, R. M. , 1981, “ Prognostic Value of Urodynamic Testing in Myelodysplastic Patients,” J. Urol., 126(2), pp. 1049–1053. 10.1055/s-2003-814725 [DOI] [PubMed] [Google Scholar]
- [53]. Naqvi, S. , Potluri, P. , Mandal, P. , and Lewis, P. , 2018, “ Effect of Different Cuff Types on Blood Pressure Measurement: Variation in BP Values for Different Cuff Types,” J. Ind. Text., 47(7), pp. 1478–1495. 10.1177/1528083717695838 [DOI] [Google Scholar]
- [54]. Zheng, Y. L. , Yan, B. P. , Zhang, Y. T. , and Poon, C. C. Y. , 2014, “ An Armband Wearable Device for Overnight and Cuff-Less Blood Pressure Measurement,” IEEE Trans. Biomed. Eng., 61(7), pp. 2179–2186. 10.1109/TBME.2014.2318779 [DOI] [PubMed] [Google Scholar]
- [55]. Bakx, C. , Oerlemans, G. , Van, D. H. H. , Van, W. C. , and Thien, T. , 1997, “ The Influence of Cuff Size on Blood Pressure Measurement,” J. Hum. Hypertens., 11(7), pp. 439–445. 10.1038/sj.jhh.1000470 [DOI] [PubMed] [Google Scholar]
- [56]. Giannoglou, G. D. , Chatzizisis, Y. S. , Zamboulis, C. , Parcharidis, G. E. , Mikhailidis, D. P. , and Louridas, G. E. , 2008, “ Elevated Heart Rate and Atherosclerosis: An Overview of the Pathogenetic Mechanisms,” Int. J. Cardiol., 126(3), pp. 302–312. 10.1016/j.ijcard.2007.08.077 [DOI] [PubMed] [Google Scholar]
- [57]. Finley, J. P. , and Nugent, S. T. , 1995, “ Heart Rate Variability in Infants, Children and Young Adults,” J. Autonom. Nerv. Syst., 51(2), pp. 103–108. 10.1016/0165-1838(94)00117-3 [DOI] [PubMed] [Google Scholar]
- [58]. Chen, L. , Wei, T. Q. , Wang, Y. , Zhang, J. , Li, H. , and Wang, K. J. , 2012, “ Simulated Bladder Pressure Stimulates Human Bladder Smooth Muscle Cell Proliferation Via the PI3K/SGK1 Signaling Pathway,” J. Urol., 188(2), pp. 661–667. 10.1016/j.juro.2012.03.112 [DOI] [PubMed] [Google Scholar]
- [59]. Rathore, D. , Shree, S. , Mukherjee, A. , and Jameel, S. , 2014, “ Wireless Measurement of Intraocular Pressure,” Int. J. Adv. Eng. Technol., 7(4), pp. 1342–1346, http://www.e-ijaet.org/media/26I22-IJAET0722610_v7_iss4_1342-1346.pdf [Google Scholar]
- [60]. Reddy, S. C. , and Alias, R. , 2014, “ Tono-Pen Measurement of Intraocular Pressure Under Topical Anaesthesia in Full Term Normal Newborns,” Int. J. Ophthalmol., 7(1), pp. 92–94. 10.3980/j.issn.2222-3959.2014.01.16 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [61]. Li, R. , and Liu, J. H. K. , 2008, “ Telemetric Monitoring of 24 h Intraocular Pressure in Conscious and Freely Moving C57BL/6J and CBA/CaJ Mice,” Mol. Vis., 14(87–89), pp. 745–749. 10.1186/1471-2199-9-40 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [62]. Nickla, D. L. , Wildsoet, C. , and Wallman, J. , 1998, “ The Circadian Rhythm in Intraocular Pressure and Its Relation to Diurnal Ocular Growth Changes in Chicks,” Exp. Eye Res., 66(2), pp. 183–193. 10.1006/exer.1997.0425 [DOI] [PubMed] [Google Scholar]
- [63]. Correia, C. , Pereira, A. L. , Duarte, A. R. , Frias, A. M. , Pedro, A. J. , Oliveira, J. T. , Sousa, R. A. , and Reis, R. L. , 2012, “ Dynamic Culturing of Cartilage Tissue: The Significance of Hydrostatic Pressure,” Tissue Eng. Part A, 18(19–20), pp. 1979–1991. 10.1089/ten.tea.2012.0083 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [64]. Finger, A. R. , Sargent, C. Y. , Dulaney, K. O. , Bernacki, S. H. , and Loboa, E. G. , 2007, “ Differential Effects on Messenger Ribonucleic Acid Expression by Bone Marrow-Derived Human Mesenchymal Stem Cells Seeded in Agarose Constructs Due to Ramped and Steady Applications of Cyclic Hydrostatic Pressure,” Tissue Eng., 13(6), pp. 1151–1158. 10.1089/ten.2006.0290 [DOI] [PubMed] [Google Scholar]
- [65]. Raboel, P. H. , Bartek, J. , Andresen, M. , Bellander, B. M. , and Romner, B. , 2012, “ Intracranial Pressure Monitoring: Invasive Versus Non-Invasive Methods—A Review,” Crit. Care Res. Practice, 2012(12), p. 950393. 10.1155/2012/950393 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [66]. Bruce, D. A. , Langfitt, T. W. , Miller, J. D. , Schutz, H. , Vapalahti, M. P. , Stanek, A. , and Goldberg, H. I. , 1973, “ Regional Cerebral Blood Flow, Intracranial Pressure, and Brain Metabolism in Comatose Patients,” J. Neurosurg., 38(2), pp. 131–144. 10.3171/jns.1973.38.2.0131 [DOI] [PubMed] [Google Scholar]
- [67]. Wilson, T. A. , 2016, Lung Mechanics, Springer, Berlin. [Google Scholar]
- [68]. Washko, G. R. , O'Donnell, C. R. , and Loring, S. H. , 2006, “ Volume-Related and Volume-Independent Effects of Posture on Esophageal and Transpulmonary Pressures in Healthy Subjects,” J. Appl. Physiol., 100(3), pp. 753–758. 10.1152/japplphysiol.00697.2005 [DOI] [PubMed] [Google Scholar]
- [69]. Blumgart, H. L. , and Yens, O. C. , 1927, “ Studies on the Velocity of Blood Flow—I: The Method Utilized,” J. Clin. Invest., 4(1), pp. 1–13. 10.1172/JCI100106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [70]. Guilak, F. , and Mow, V. C. , 2000, “ The Mechanical Environment of the Chondrocyte: A Biphasic Finite Element Model of Cell–Matrix Interactions in Articular Cartilage,” J. Biomech., 33(12), pp. 1663–1673. 10.1016/S0021-9290(00)00105-6 [DOI] [PubMed] [Google Scholar]
- [71]. Jones, B. , Hung, C. T. , and Ateshian, G. , 2016, “ Biphasic Analysis of Cartilage Stresses in the Patellofemoral Joint,” J. Knee Surg., 29(2), pp. 92–98. 10.1055/s-0035-1568989 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [72]. Smith, R. L. , Lin, J. , Trindade, M. C. , Shida, J. , Kajiyama, G. , Vu, T. , Hoffman, A. R. , van der Meulen, M. C. , Goodman, S. B. , Schurman, D. J. , and Carter, D. R. , 2000, “ Time-Dependent Effects of Intermittent Hydrostatic Pressure on Articular Chondrocyte Type II Collagen and Aggrecan mRNA Expression,” J. Rehabil. Res. Dev., 37(2), pp. 153–161. 10.1084/jem.37.2.153 [DOI] [PubMed] [Google Scholar]
- [73]. Andriacchi, T. P. , 2002, “ Dynamic Function and Imaging in the Analysis of Osteoarthritis at the Knee,” The Many Faces of Osteoarthritis, Springer, Birkhäuser, Basel, pp. 443–452. 10.1007/978-3-0348-8133-3_43 [DOI] [Google Scholar]
- [74]. Rushfeldt, P. D. , Mann, R. W. , and Harris, W. H. , 1981, “ Improved Techniques for Measuring In Vivo the Geometry and Pressure Distribution in the Human Acetabulum—II: Instrumented Endoprosthesis Measurement of Articular Surface Pressure Distribution,” J. Biomech., 14(5), pp. 315–323. 10.1016/0021-9290(81)90041-5 [DOI] [PubMed] [Google Scholar]
- [75]. Yu, J. , Zhong, Y. , Cheng, Y. , Shen, X. , Wang, J. , and Wei, Y. , 2011, “ Effect of High Hydrostatic Pressure on the Expression of Glutamine Synthetase in Rat Retinal Muller Cells Cultured In Vivo,” Exp. Ther. Med., 2(3), pp. 513–516. 10.3892/etm.2011.239 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [76]. Liu, C. , Zhao, Y. , Cheung, W.-Y. , Gandhi, R. , Wang, L. , and You, L. , 2010, “ Effects of Cyclic Hydraulic Pressure on Osteocytes,” Bone, 46(5), pp. 1449–1456. 10.1016/j.bone.2010.02.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [77]. Haberstroh, K. M. , Kaefer, M. , Retik, A. B. , Freeman, M. R. , and Bizios, R. , 1999, “ The Effects of Sustained Hydrostatic Pressure on Select Bladder Smooth Muscle Cell Functions,” J. Urol., 162(6), pp. 2114–2118. 10.1016/S0022-5347(05)68136-0 [DOI] [PubMed] [Google Scholar]
- [78]. Mandal, A. , Shahidullah, M. , and Delamere, N. A. , 2010, “ Hydrostatic Pressure–Induced Release of Stored Calcium in Cultured Rat Optic Nerve Head Astrocytes,” Invest. Ophthalmol. Vis. Sci., 51(6), pp. 3129–3138. 10.1167/iovs.09-4614 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [79]. Lei, Y. , Rajabi, S. , Pedrigi, R. M. , Overby, D. R. , Read, A. T. , and Ethier, C. R. , 2011, “ In Vitro Models for Glaucoma Research: Effects of Hydrostatic Pressure,” Investigative ophthalmology & visual science, 52(9), pp. 6329–6339. 10.1167/iovs.11-7836 [DOI] [PubMed] [Google Scholar]
- [80]. Smith, M. E. , and Eskandari, R. , 2018, “ A Novel Technology to Model Pressure-Induced Cellular Injuries in the Brain,” J. Neurosci. Meth., 293, pp. 247–253. 10.1016/j.jneumeth.2017.10.004 [DOI] [PubMed] [Google Scholar]
- [81]. Ju, W.-K. , Liu, Q. , Kim, K.-Y. , Crowston, J. G. , Lindsey, J. D. , Agarwal, N. , Ellisman, M. H. , Perkins, G. A. , and Weinreb, R. N. , 2007, “ Elevated Hydrostatic Pressure Triggers Mitochondrial Fission and Decreases Cellular ATP in Differentiated RGC-5 Cells,” Invest. Ophthalmol. Vis. Sci., 48(5), pp. 2145–2151. 10.1167/iovs.06-0573 [DOI] [PubMed] [Google Scholar]
- [82]. Wei, T. Q. , Luo, D. Y. , Chen, L. , Wu, T. , and Wang, K. J. , 2014, “ Cyclic Hydrodynamic Pressure Induced Proliferation of Bladder Smooth Muscle Cells Via Integrin Alpha5 and FAK,” Physiol. Res., 63(1), pp. 127–134.https://www.ncbi.nlm.nih.gov/pubmed/24182341 [DOI] [PubMed] [Google Scholar]
- [83]. Agar, A. , Li, S. , Agarwal, N. , Coroneo, M. T. , and Hill, M. A. , 2006, “ Retinal Ganglion Cell Line Apoptosis Induced by Hydrostatic Pressure,” Brain Res., 1086(1), pp. 191–200. 10.1016/j.brainres.2006.02.061 [DOI] [PubMed] [Google Scholar]
- [84]. Guo, L. , Moss, S. E. , Alexander, R. A. , Ali, R. R. , Fitzke, F. W. , and Cordeiro, M. F. , 2005, “ Retinal Ganglion Cell Apoptosis in Glaucoma is Related to Intraocular Pressure and IOP-Induced Effects on Extracellular Matrix,” Investigative Opthalmol. Visual Sci., 46(1), pp. 175–182. 10.1167/iovs.04-0832 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [85]. Sayyad, Z. , Sirohi, K. , Radha, V. , and Swarup, G. , 2017, “ 661W is a Retinal Ganglion Precursor-Like Cell Line in Which Glaucoma-Associated Optineurin Mutants Induce Cell Death Selectively,” Sci. Rep., 7(1), p. 16855. 10.1038/s41598-017-17241-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [86]. Krishnamoorthy, R. R. , Clark, A. F. , Daudt, D. , Vishwanatha, J. K. , and Yorio, T. , 2013, “ A Forensic Path to RGC-5 Cell Line Identification: Lessons Learned,” Investigative Ophthal. Visual Sci., 54(8), pp. 5712–5719. 10.1167/iovs.13-12085 [DOI] [PubMed] [Google Scholar]
- [87]. Osborne, A. , Aldarwesh, A. , Rhodes, J. D. , Broadway, D. C. , Everitt, C. , and Sanderson, J. , 2015, “ Hydrostatic pressure does not cause detectable changes in survival of human retinal ganglion cells,” PloS one, 10(1), p. e0115591. 10.1371/journal.pone.0115591 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [88]. Sugaya, Y. , Sakamoto, N. , Ohashi, T. , and Sato, M. , 2003, “ Elongation and Random Orientation of Bovine Endothelial Cells in Response to Hydrostatic Pressure: Comparison With Response to Shear Stress,” JSME Int. J. Ser. C Mech. Syst. Mach. Elem. Manuf., 46(4), pp. 1248–1255. 10.1299/jsmec.46.1248 [DOI] [Google Scholar]
- [89]. Schwartz, E. A. , Bizios, R. , Medow, M. S. , and Gerritsen, M. E. , 1999, “ Exposure of Human Vascular Endothelial Cells to Sustained Hydrostatic Pressure Stimulates Proliferation. Involvement of the AlphaV Integrins,” Circ. Res., 84(3), pp. 315–322. 10.1161/01.RES.84.3.315 [DOI] [PubMed] [Google Scholar]
- [90]. Tworkoski, E. , Glucksberg, M. R. , and Johnson, M. , 2018, “ The Effect of the Rate of Hydrostatic Pressure Depressurization on Cells in Culture,” PloS one, 13(1), p. e0189890. 10.1371/journal.pone.0189890 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [91]. Suh, J.-K. , Baek, G. H. , Arøen, A. , Malin, C. M. , Niyibizi, C. , Evans, C. H. , and Westerhausen-Larson, A. , 1999, “ Intermittent Sub-Ambient Interstitial Hydrostatic Pressure as a Potential Mechanical Stimulator for Chondrocyte Metabolism,” Osteoarthritis Cartilage, 7(1), p. 71. 10.1053/joca.1998.0163 [DOI] [PubMed] [Google Scholar]
- [92]. Smith, R. L. , Rusk, S. F. , Ellison, B. E. , Wessells, P. , Tsuchiya, K. , Carter, D. R. , Caler, W. E. , Sandell, L. J. , and Schurman, D. J. , 1996, “ In Vitro Stimulation of Articular Chondrocyte mRNA and Extracellular Matrix Synthesis by Hydrostatic Pressure,” J. Orthop. Res., 14(1), pp. 53–60. 10.1002/jor.1100140110 [DOI] [PubMed] [Google Scholar]
- [93]. Miyanishi, K. , Trindade, M. C. , Lindsey, D. P. , Beaupré, G. S. , Carter, D. R. , Goodman, S. B. , Schurman, D. J. , and Smith, R. L. , 2006, “ Effects of Hydrostatic Pressure and Transforming Growth Factor-Beta 3 on Adult Human Mesenchymal Stem Cell Chondrogenesis In Vitro,” Tissue Eng., 12(6), pp. 1419–1428. 10.1089/ten.2006.12.1419 [DOI] [PubMed] [Google Scholar]
- [94]. Nathan, S. S. , Di Resta , R. G., Casas-Ganem, J. E. , Hoang, B. H. , Sowers, R. , Yang, R. , Huvos, A. G. , Gorlick, R. , and Healey, J. H. , 2005, “ Elevated Physiologic Tumor Pressure Promotes Proliferation and Chemosensitivity in Human Osteosarcoma,” Clin. Cancer Res., 11(6), p. 2389. 10.1158/1078-0432.CCR-04-2048 [DOI] [PubMed] [Google Scholar]
- [95]. Frey, B. , Janko, C. , Ebel, N. , Meister, S. , Schlücker, E. , Meyer-Pittroff, R. , Fietkau, R. , Herrmann, M. , and Gaipl, U. S. , 2008, “ Cells Under Pressure—Treatment of Eukaryotic Cells With High Hydrostatic Pressure, From Physiologic Aspects to Pressure Induced Cell Death,” Curr. Med. Chem., 15(23), pp. 2329–2336. 10.2174/092986708785909166 [DOI] [PubMed] [Google Scholar]
- [96]. Baldwin, C. , Potter, M. , Clayton, E. , Irvine, L. , and Dye, J. , 2009, “ Topical Negative Pressure Stimulates Endothelial Migration and Proliferation: A Suggested Mechanism for Improved Integration of Integra,” Ann. Plast. Surg., 62(1), pp. 92–96. 10.1097/SAP.0b013e31817762fd [DOI] [PubMed] [Google Scholar]
- [97]. Stroka, K. , Jiang, H. , Chen, S. H. , Tong, Z. , Wirtz, D. , Sun, S. , and Konstantopoulos, K. , 2014, “ Water Permeation Drives Tumor Cell Migration in Confined Microenvironments,” Cell, 157(3), pp. 611–623. 10.1016/j.cell.2014.02.052 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [98]. Jiang, H. , and Sun, S. , 2013, “ Cellular Pressure and Volume Regulation and Implications for Cell Mechanics,” Biophys. J., 105(3), pp. 609–619. 10.1016/j.bpj.2013.06.021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [99]. van't Hoff, J. , 1901, “ Osmotic Pressure and Chemical Equilibrium,” Nobel Prize Lecture, Sweden, accessed July 8, 2019, https://www.nobelprize.org/uploads/2018/06/hoff-lecture.pdf
- [100]. Joanny, J. F. , and Prost, J. , 2009, “ Active Gels as a Description of the Actin-Myosin Cytoskeleton,” HFSP J., 3(2), pp. 94–104. 10.2976/1.3054712 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [101]. Holzbaur, E. L. , and Goldman, Y. E. , 2010, “ Coordination of Molecular Motors: From In Vitro Assays to Intracellular Dynamics,” Curr. Opin. Cell Biol., 22(1), pp. 4–13. 10.1016/j.ceb.2009.12.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [102]. Cruz, E. M. D. L. , and Ostap, E. M. , 2004, “ Relating Biochemistry and Function in the Myosin Superfamily,” Curr. Opin. Cell Biol., 16(1), pp. 61–67. 10.1016/j.ceb.2003.11.011 [DOI] [PubMed] [Google Scholar]
- [103]. Elson, E. L. , and Genin, G. M. , 2013, “ The Role of Mechanics in Actin Stress Fiber Kinetics,” Exp. Cell Res., 319(16), pp. 2490–2500. 10.1016/j.yexcr.2013.06.017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [104]. Marquez, J. P. , Elson, E. L. , and Genin, G. M. , 2010, “ Whole Cell Mechanics of Contractile Fibroblasts: Relations Between Effective Cellular and Extracellular Matrix Moduli,” Philos. Trans. R. Soc. A, 368(1912), pp. 635–654. 10.1098/rsta.2009.0240 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [105]. Cao, X. , Moeendarbary, E. , Isermann, P. , Davidson, P. , Wang, X. , Chen, M. , Burkart, A. , Lammerding, J. , Kamm, R. , and Shenoy, V. , 2016, “ A Chemomechanical Model for Nuclear Morphology and Stresses During Cell Transendothelial Migration,” Biophys. J., 111(7), pp. 1541–1552. 10.1016/j.bpj.2016.08.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [106]. Mcgarry, J. P. , Fu, J. , Yang, M. T. , Chen, C. S. , Mcmeeking, R. M. , Evans, A. G. , and Deshpande, V. S. , 2009, “ Simulation of the Contractile Response of Cells on an Array of Micro-Posts,” Philos. Trans. R. Soc. A, 367(1902), pp. 3477–3497. 10.1098/rsta.2009.0097 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [107]. Tao, J. , Li, Y. , Vig, D. K. , and Sun, S. X. , 2017, “ Cell Mechanics: A Dialogue,” Rep. Prog. Phys., 80(3), p. 036601. 10.1088/1361-6633/aa5282 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [108]. Jia, X. T. , and Sun, S. X. , 2015, “ Active Biochemical Regulation of Cell Volume and a Simple Model of Cell Tension Response,” Biophys. J., 109(8), pp. 1541–1550. 10.1016/j.bpj.2015.08.025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [109]. Jean-Yves, T. , Ulrike, S. , Guillaume, S. , Julia, R. , Jean-François, J. , and Ewa, P. , 2009, “ Role of Cortical Tension in Bleb Growth,” Proc. Natl. Acad. Sci. U. S. A., 106(44), pp. 18581–18586. 10.1073/pnas.0903353106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [110]. Guillaume, C. , and Ewa, P. , 2008, “ Blebs Lead the Way: How to Migrate Without Lamellipodia,” Nat. Rev. Mol. Cell Biol., 9(9), pp. 730–736. 10.1038/nrm2453 [DOI] [PubMed] [Google Scholar]
- [111]. Jülicher, F. , Kruse, K. , Prost, J. , and Joanny, J. F. , 2007, “ Active Behavior of the Cytoskeleton,” Phys. Rep., 449(1), pp. 3–28. 10.1016/j.physrep.2007.02.018 [DOI] [Google Scholar]
- [112]. Matthews, B. D. , Overby, D. R. , Mannix, R. , and Ingber, D. E. , 2006, “ Cellular Adaptation to Mechanical Stress: Role of Integrins, Rho, Cytoskeletal Tension and Mechanosensitive Ion Channels,” J. Cell Sci., 119(3), pp. 508–518. 10.1242/jcs.02760 [DOI] [PubMed] [Google Scholar]
- [113]. Tianzhi, L. , Krithika, M. , Iglesias, P. A. , and Robinson, D. N. , 2013, “ Molecular Mechanisms of Cellular Mechanosensing,” Nat. Mater., 12(11), pp. 1063–1070. 10.1038/nmat3772 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [114]. Rodrigo, F. G. , and Zallen, J. A. , 2009, “ Cell Mechanics and Feedback Regulation of Actomyosin Networks,” Sci. Signal., 2(101), pp. 5306–5313. 10.1126/scisignal.2101pe78 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [115]. Nekouzadeh, A. , Pryse, K. M. , Elson, E. L. , and Genin, G. M. , 2008, “ Stretch-Activated Force Shedding, Force Recovery, and Cytoskeletal Remodeling in Contractile Fibroblasts,” J. Biomech., 41(14), pp. 2964–2971. 10.1016/j.jbiomech.2008.07.033 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [116]. Elson, E. L. , Fried, E. , Dolbow, J. E. , and Genin, G. M. , 2010, “ Phase Separation in Biological Membranes: Integration of Theory and Experiment,” Annu. Rev. Biophys., 39(1), pp. 207–226. 10.1146/annurev.biophys.093008.131238 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [117]. Greenberg, M. J. , Arpağ, G. , Tüzel, E. , and Ostap, E. M. , 2016, “ A Perspective on the Role of Myosins as Mechanosensors,” Biophys. J., 110(12), pp. 2568–2576. 10.1016/j.bpj.2016.05.021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [118]. Wagner, B. , Tharmann, R. , Haase, I. , Fischer, M. , and Bausch, A. R. , 2006, “ Cytoskeletal Polymer Networks: The Molecular Structure of Cross-Linkers Determines Macroscopic Properties,” Proc. Natl. Acad. Sci. U. S. A., 103(38), pp. 13974–13978. 10.1073/pnas.0510190103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [119]. Yi, X. R. , Effler, J. C. , Melanie, N. , Tianzhi, L. , Firtel, R. A. , Iglesias, P. A. , Rock, R. S. , and Robinson, D. N. , 2009, “ Mechanosensing Through Cooperative Interactions Between Myosin II and the Actin Crosslinker Cortexillin I,” Curr. Biol., 19(17), pp. 1421–1428. 10.1016/j.cub.2009.07.018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [120]. Humphrey, D. , Duggan, C. , Saha, D. , Smith, D. , and Käs, J. , 2002, “ Active Fluidization of Polymer Networks Through Molecular Motors,” Nature, 416(6879), pp. 413–416. 10.1038/416413a [DOI] [PubMed] [Google Scholar]
- [121]. Falk, W. , Stefan, S. , Bryan, L. , Revathi, A. , Maren, R. , Jochen, G. , and Josef, K. S. , 2005, “ Optical Rheology of Biological Cells,” Phys. Rev. Lett., 94(9), p. 098103. 10.1103/PhysRevLett.94.098103 [DOI] [PubMed] [Google Scholar]
- [122]. Cornelis, S. , Pastore, J. J. , Mackintosh, F. C. , Lubensky, T. C. , and Janmey, P. A. , 2005, “ Nonlinear Elasticity in Biological Gels,” Nature, 435(7039), pp. 191–194. 10.1038/nature03521 [DOI] [PubMed] [Google Scholar]
- [123]. Daisuke, M. , Catherine, T. , Schmidt, C. F. , and Mackintosh, F. C. , 2007, “ Nonequilibrium Mechanics of Active Cytoskeletal Networks,” Science, 315(5810), pp. 370–373. 10.1126/science.1134404 [DOI] [PubMed] [Google Scholar]
- [124]. Chen, P. , and Shenoy, V. B. , 2011, “ Strain Stiffening Induced by Molecular Motors in Active Crosslinked Biopolymer Networks,” Soft Matter., 7(2), pp. 355–358. 10.1039/C0SM00908C [DOI] [Google Scholar]
- [125]. Carlsson, A. E. , 2010, “ Actin Dynamics: From Nanoscale to Microscale,” Annu. Rev. Biophys., 39(39), pp. 91–110. 10.1146/annurev.biophys.093008.131207 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [126]. Dasanayake, N. L. , and Carlsson, A. E. , 2012, “ General Mechanism of Actomyosin Contraction,” Biophys. J., 102(3), p. 349a. 10.1016/j.bpj.2011.11.1913 [DOI] [Google Scholar]
- [127]. Dasanayake, N. L. , Michalski, P. J. , and Carlsson, A. E. , 2011, “ General Mechanism of Actomyosin Contractility,” Phys. Rev. Lett., 107(11), p. 118101. 10.1103/PhysRevLett.107.118101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [128]. Naganathan, S. R. , Fürthauer, S. , Nishikawa, M. , Jülicher, F. , and Grill, S. W. , 2014, “ Active Torque Generation by the Actomyosin Cell Cortex Drives Left–Right Symmetry Breaking,” eLife, 3, p. e04165. 10.7554/eLife.04165 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [129]. Mirjam, M. , Martin, D. , Bois, J. S. , Frank, J. , and Grill, S. W. , 2010, “ Anisotropies in Cortical Tension Reveal the Physical Basis of Polarizing Cortical Flows,” Nature, 467, pp. 617–621. 10.1038/nature09376 [DOI] [PubMed] [Google Scholar]
- [130]. Carlsson, A. , 2018, “ How Actin Polymerization Bends the Cell Membrane to Drive Endocytosis,” Biophys. J., 114(3), p. 388a. 10.1016/j.bpj.2017.11.2145 [DOI] [Google Scholar]
- [131]. He, L. , Tao, J. , Maity, D. , Si, F. , Wu, Y. , Wu, T. , Prasath, V. , Wirtz, D. , and Sun, S. X. , 2018, “ Role of Membrane-Tension Gated Ca2+ Flux in Cell Mechanosensation,” J. Cell Sci., 131(4), p. jcs208470. 10.1242/jcs.208470 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [132]. Else Kay, H. , Niels Bjerre, H. , and Ian Henry, L. , 2014, “ Functions of Volume-Sensitive and Calcium-Activated Chloride Channels,” IUBMB Life, 66(4), pp. 257–267. 10.1002/iub.1266 [DOI] [PubMed] [Google Scholar]
- [133]. Sardini, A. , Amey, J. S. , Weylandt, K. H. , Nobles, M. , Valverde, M. A. , and Higgins, C. F. , 2003, “ Cell Volume Regulation and Swelling-Activated Chloride Channels,” BBA-Bioenergy, 1618(2), pp. 153–162. 10.1016/j.bbamem.2003.10.008 [DOI] [PubMed] [Google Scholar]
- [134]. Salbreux, G. , Joanny, J. F. , Prost, J. , and Pullarkat, P. , 2007, “ Shape Oscillations of Non-Adhering Fibroblast Cells,” Phys. Biol., 4(4), pp. 268–284. 10.1088/1478-3975/4/4/004 [DOI] [PubMed] [Google Scholar]
- [135]. Qiu, Z. , Dubin, A. , Mathur, J. , Tu, B. , Reddy, K. , Miraglia, L. , Reinhardt, J. , Orth, A. , and Patapoutian, A. , 2014, “ SWELL1, a Plasma Membrane Protein, is an Essential Component of Volume-Regulated Anion Channel,” Cell, 157(2), pp. 447–458. 10.1016/j.cell.2014.03.024 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [136]. Yellin, F. , Li, Y. , Sreenivasan, V. K. A. , Farrell, B. , Johny, M. B. , Yue, D. , and Sun, S. X. , 2018, “ Electromechanics and Volume Dynamics in Nonexcitable Tissue Cells,” Biophys. J., 114(9), pp. 2231–2242. 10.1016/j.bpj.2018.03.033 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [137]. Mohagheghian, E. , Luo, J. , Chen, J. , Chaudhary, G. , Chen, J. , Sun, J. , Ewoldt, R. H. , and Wang, N. , 2018, “ Quantifying Compressive Forces Between Living Cell Layers and Within Tissues Using Elastic Round Microgels,” Nat. Commun., 9(1), p. 1878. 10.1038/s41467-018-04245-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [138]. Han, Y. L. , Ronceray, P. , Xu, G. , Malandrino, A. , Kamm, R. D. , Lenz, M. , Broedersz, C. P. , and Guo, M. , 2018, “ Cell Contraction Induces Long-Ranged Stress Stiffening in the Extracellular Matrix,” Proc. Natl. Acad. Sci. U. S. A., 115(16), pp. 4075–4080. 10.1073/pnas.1722619115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [139]. Hu, J. , Jafari, S. , Han, Y. , Grodzinsky, A. J. , Cai, S. , and Guo, M. , 2017, “ Size- and Speed-Dependent Mechanical Behavior in Living Mammalian Cytoplasm,” Proc. Natl. Acad. Sci. U. S. A., 114(36), pp. 9529–9534. 10.1073/pnas.1702488114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [140]. Petrie, R. J. , Koo, H. , and Yamada, K. M. , 2014, “ Generation of Compartmentalized Pressure by a Nuclear Piston Governs Cell Motility in a 3D Matrix,” Science, 345(6200), pp. 1062–1065. 10.1126/science.1256965 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [141]. Rodell, C. B. , MacArthur, J. W. , Dorsey, S. M. , Wade, R. J. , Wang, L. L. , Woo, Y. J. , and Burdick, J. A. , 2015, “ Shear-Thinning Supramolecular Hydrogels With Secondary Autonomous Covalent Crosslinking to Modulate Viscoelastic Properties In Vivo,” Adv. Funct. Mater., 25(4), pp. 636–644. 10.1002/adfm.201403550 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [142]. Babaei, B. , Velasquez-Mao, A. J. , Pryse, K. M. , McConnaughey, W. B. , Elson, E. L. , and Genin, G. M. , 2018, “ Energy Dissipation in Quasi-Linear Viscoelastic Tissues, Cells, and Extracellular Matrix,” J. Mech. Behav. Biomed., 84, pp. 198–207. 10.1016/j.jmbbm.2018.05.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [143]. Mulhall, H. J. , Hughes, M. P. , Kazmi, B. , Lewis, M. P. , and Labeed, F. H. , 2013, “ Epithelial Cancer Cells Exhibit Different Electrical Properties When Cultured in 2D and 3D Environments,” BBA-Gen. Subj., 1830(11), pp. 5136–5141. 10.1016/j.bbagen.2013.07.008 [DOI] [PubMed] [Google Scholar]
- [144]. Elson, E. L. , and Genin, G. M. , 2016, “ Tissue Constructs: Platforms for Basic Research and Drug Discovery,” Interface Focus, 6(1), p. 20150095. 10.1098/rsfs.2015.0095 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [145]. Mohammadalipour, A. , Burdick, M. M. , and Tees, D. F. J. , 2017, “ Viscoelasticity Measurements Reveal Rheological Differences Between Stem-Like and Non-Stem-Like Breast Cancer Cells,” Cell. Mol. Bioeng., 10(3), pp. 235–248. 10.1007/s12195-017-0485-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [146]. Babaei, B. , Davarian, A. , Lee, S. L. , Pryse, K. M. , Mcconnaughey, W. B. , Elson, E. L. , and Genin, G. M. , 2016, “ Remodeling by Fibroblasts Alters the Rate-Dependent Mechanical Properties of Collagen,” Acta Biomater., 37, pp. 28–37. 10.1016/j.actbio.2016.03.034 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [147]. Bruens, M. L. , Pieterman, H. , de Wijn, J. R. , and Vaandrager, J. M. , 2003, “ Porous Polymethylmethacrylate as Bone Substitute in the Craniofacial Area,” J. Craniofac. Surg., 14(4), pp. 596–598. 10.1097/00001665-200301000-00011 [DOI] [PubMed] [Google Scholar]
- [148]. Hsu, C. C. , Tsai, W. C. , Chen, C. P. , Lu, Y. M. , and Wang, J. S. , 2010, “ Effects of Negative Pressures on Epithelial Tight Junctions and Migration in Wound Healing,” Am. J. Physiol. Cell Physiol., 299(2), pp. C528–C534. 10.1152/ajpcell.00504.2009 [DOI] [PubMed] [Google Scholar]


