Abstract
Medical image resolution has been a serious limitation in plaque progression research. A modeling approach combining intravascular ultrasound (IVUS) and optical coherence tomography (OCT) was introduced and patient follow-up IVUS and OCT data were acquired to construct three-dimensional (3D) coronary models for plaque progression investigations. Baseline and follow-up in vivo IVUS and OCT coronary plaque data were acquired from one patient with 105 matched slices selected for model construction. 3D fluid–structure interaction (FSI) models based on IVUS and OCT data (denoted as IVUS + OCT model) were constructed to obtain stress/strain and wall shear stress (WSS) for plaque progression prediction. IVUS-based IVUS50 and IVUS200 models were constructed for comparison with cap thickness set as 50 and 200 μm, respectively. Lumen area increase (LAI), plaque area increase (PAI), and plaque burden increase (PBI) were chosen to measure plaque progression. The least squares support vector machine (LS-SVM) method was employed for plaque progression prediction using 19 risk factors. For IVUS + OCT model with LAI, PAI, and PBI, the best single predictor was plaque strain, local plaque stress, and minimal cap thickness, with prediction accuracy as 0.766, 0.838, and 0.890, respectively; the prediction accuracy using best combinations of 19 factors was 0.911, 0.881, and 0.905, respectively. Compared to IVUS + OCT model, IVUS50, and IVUS200 models had errors ranging from 1% to 66.5% in quantifying cap thickness, stress, strain and prediction accuracies. WSS showed relatively lower prediction accuracy compared to other predictors in all nine prediction studies.
Keywords: vulnerable plaque, OCT, IVUS, plaque progression, patient-specific model, FSI
1. Introduction
Current bottleneck of patient-specific coronary plaque model construction is the resolution of in vivo medical imaging. The threshold of cap thickness of vulnerable coronary plaques is 65 μm, while the resolution of in vivo coronary intravascular ultrasound (IVUS) images is 150–200 μm, which is not enough to identify vulnerable plaques with thin caps and construct accurate biomechanical plaque models [1–3]. Optical coherence tomography (OCT) with a 15–20 μm resolution has the capacity to identify thin fibrous cap. A modeling approach combining IVUS and OCT was introduced in our previous publication for cap thickness quantification and more accurate cap stress/strain calculations [3]. In this paper, patient baseline (time 1, or T1) and follow-up (time 2, or T2) IVUS and OCT data were acquired and three-dimensional (3D) coronary models were constructed using above approach for plaque progression investigations. Morphological and mechanical factors were combined together to identify best predictors and plaque progression prediction accuracies.
The pioneered research of Clarkson, Zarins, and Glagov and others mainly focused on the relationship between plaque morphology and plaque progression or remodeling based on histologic sections from autopsy [4–6]. They performed several large-scale studies to investigate the relationship between plaque area (PA), lumen cross-sectional area (called lumen area (LA) for simplicity), and the plaque remodeling [5–7]. As imaging technologies advances, Mintz et al. and Nakamura et al. among others were able to use medical imaging such as IVUS and angiography in their investigation and their results also indicated that plaque area and lumen area were closely related to plaque progression [8–10]. Besides plaque morphology, there have been intensive interests in understanding the mechanism of plaque growth from the mechanical perspective. By using ideal fluid models, Ku et al. indicated that the early growth of plaque had a positive correlation with low and oscillating flow shear stress [11]. When it comes to predicting future plaque progression, histological or ex vivo experimental approaches encounter an obstacle: they could only have one-time data which could not provide data for plaque progression. Patient (or animal) follow-up studies using advanced medical images can provide multitime data to measure the growth of plaque over time. These data can be used to investigate associations between risk factors and plaque progression for possible plaque progression prediction.
In recent years, several groups acquired follow-up in vivo images (mainly IVUS in the current literature) to obtain quantitative plaque morphological data including lumen area, plaque area, and plaque burden (PB) changes (used as measurements of plaque progression) and study their correlations with fluid hemodynamics, particularly wall shear stress (WSS) [12–15]. Stone et al. showed that large plaque burden and low local endothelial shear stress could provide independent and additive prediction accuracy in identifying plaques that develop progressive enlargement and lumen narrowing, where additive prediction had 41% positive and 92% negative predictive accuracies [16]. Corban et al. used follow-up virtual histology IVUS (VH-IVUS) data and indicated that combination of plaque burden, WSS, and plaque phenotype had incremental value for prediction of coronary plaque progression and increased plaque vulnerability in patients with nonobstructive coronary artery disease [15]. Plaque progression may be influenced by interactions of various morphological and mechanical factors including structural and flow conditions, and its mechanism has not been fully understood [17,18]. Wang et al. were among the few that considered structural biomechanics in their prediction analysis. They used fluid–structure interaction (FSI) models with follow-up VH-IVUS data and showed that the combination of morphological and biomechanical factors could improve prediction accuracy, compared to predictions using only morphological features [19]. These IVUS-based predictive studies have provided fruitful achievements in our knowledge in the prediction of plaque progression.
In recent years, OCT with high resolution is gradually becoming a powerful tool in plaque research for its ability in identifying the thin fibrous cap (cap thickness < 65 μm), inflammation and calcification which are primary determinants of positive remodeling [2,20]. Using OCT, Uemura et al. found 69 nonsignificant coronary plaques (diameter stenosis < 50%) from 53 patients to study the relation between morphological characteristics and plaque progression during 7-month follow-up period [21]. The univariate regression analysis showed that thin-cap fibroatheroma and microchannel images had a high correlation with subsequent luminal progression [21]. Some groups studied plaque remodeling after placing stent using OCT follow-up data and fluid dynamics models [22–24]. Plaque progression study using OCT follow-up data and prediction methods which include morphological factors, structural stress/strain, and fluid shear stress is lacking in the current literature.
In this paper, patient follow-up IVUS and OCT data were acquired and 3D FSI models based on combined IVUS, OCT, and angiography data were constructed to obtain more accurate human coronary atherosclerotic plaque morphology and plaque stress/strain conditions and investigate the relationship between plaque progression and morphological and mechanical factors. Lumen area, plaque area, and plaque burden changes were used as measures of plaque progression. Machine learning method was used to fit the morphological and mechanical factors to predict plaque progression. Prediction accuracies of key morphological and mechanical predictors and their combinations were compared to identify best predictors.
2. Data, Models, and Methods
2.1. Intravascular Ultrasound and Optical Coherence Tomography Data Acquisition.
Baseline and 10-month follow-up in vivo IVUS/OCT/Angiography data were acquired from two arteries (left circumflex coronary artery and right coronary artery) of one participant (female, 80 age) at Cardiovascular Research Foundation using approved protocol with informed consent obtained. A total of 8620 IVUS images (2 pullbacks) and 813 OCT images (3 pullbacks) were acquired from two arteries at baseline. A total of 11,017 IVUS images (3 pullbacks) and 813 OCT images (3 pullbacks) were acquired from two arteries at follow-up. Different pullbacks from one artery could have different overlap in same artery. A total of 105 matched baseline slices (51 slices from left circumflex coronary and 54 slices from right coronary artery) were used in our model construction and progression prediction analysis. IVUS catheter was traversed distally through the artery to the region of interest and performed by an automatic pullback speed of 0.5 mm/s using a motorized transducer from OptiCross, Boston Scientific/SCIMED Corporation (Natick, MA). Aortic pressure was recorded through catheter and used as pressure boundary condition in the model. Following IVUS image acquisition, OCT catheter (St. Jude, Minnesota, MN) was also traversed to the region of interest and an automatic pullback at 20 mm/s was performed. The positions of both catheters were recorded with angiography prior to pullback. The IVUS/OCT/angiography data at baseline (time 1, T1) and follow-up (time 2, T2) were acquired uniformly according to the above descriptions. All image slices were segmented into three plaque elements: fibrotic plus fibro-fatty, necrotic core (lipid), and dense calcium (calcification). The coregistration of IVUS and OCT images were performed following the procedure described in Ref. [25]. We used a framework that uses dynamic time warping for the longitudinal coregistration and dynamic programming for the circumferential coregistration of images. The segmentation of paired IVUS and OCT was performed by experts. OCT segmentation methods have been previously reported [26]. More details in image registration and segmentation can be found in Refs. [3,25,26]. Figure 1 shows samples of paired IVUS and OCT images at T1 and T2 and corresponding segmented IVUS + OCT contours. Paired IVUS and OCT images were merged into IVUS + OCT slices and denoted as IVUS + OCTT1 and IVUS + OCTT2, with IVUS providing whole slice (lumen and out-boundary) contours, and OCT providing cap thickness and plaque component contours (see Fig. 1). Furthermore, the merged IVUS + OCT data at the two time points (IVUS + OCTT1 and IVUS + OCTT2) were coregistered for plaque progression measurements between T1 and T2. This registration of IVUS + OCT at T1 and T2 was performed by an expert using branches as the main landmarks.
Fig. 1.
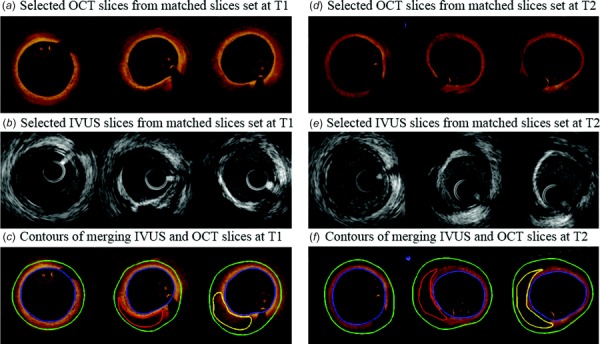
Samples of paired IVUS and OCT images at T1 and T2 with segmented contours. Contour color: blue lumen contour, green out-boundary, red lipid contour, yellow calcification.
2.2. The Three-Dimensional Fluid–Structure Interaction Model and Mooney–Rivlin Model for Material Properties.
The IVUS + OCTT1 and IVUS + OCTT2 slice contours were used to make 3D coronary geometries combing the angiography images at T1 and T2. Time-dependent vessel centerlines which had curvature change and cyclic bending information were extracted from angiography for modeling use (Fig. 2). Segmented IVUS + OCT slices were assembled to the vessel centerline with minimum curvature to construct vessel 3D geometry using the segment location identified through coregistration. These models are referred to as IVUS + OCT models. Figure 2 shows the angiography images, vessel bending curves and 3D vessel segment with stacked contours at maximum and minimum pressure. The time-dependent displacement of the centerline obtained from angiography was imposed to the vessel segment to implement cycle bending in our FSI models. Aortic pressure (max, min pressure: 136, 88 mmHg) obtained by catheter were used as inlet pressure conditions. Axial retraction (also called axial shrink-stretch process in our previous publications) was set at 5% in our models because atherosclerotic vessels were stiffer than healthy vessels. Details of our FSI models can be found in Ref. [3,26].
Fig. 2.
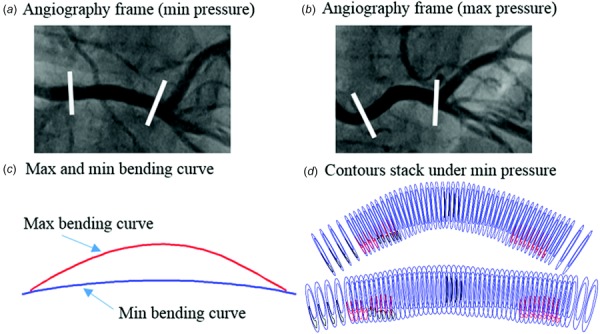
Curvature variation data from angiography of right coronary artery. (a) The angiography image with minimum pressure. (b) The angiography image with maximum pressure. (c) Vessel bending curves with maximum and minimum curvature. (d) Stacked contours plot with minimum and maximum pressure. Contour color: red lipid, black calcification, blue lumen, and out-boundary.
For comparison purposes, models were also made using IVUS data alone. Due to the limitation of IVUS resolution, when cap thickness is under 200 μm, IVUS does not see it. In this paper, two IVUS-based models were made with cap thickness set as 50 and 200 μm (denoted by IVUS50 and IVUS200), respectively, following procedures and justifications given in Ref. [3]. IVUS50 and IVUS200 models were constructed and solved, and results were compared with that from the IVUS + OCT model to observe improvements from our IVUS + OCT approach. It should be noted that results from IVUS + OCT model is taken as a benchmark to measure the errors generated by IVUS50 and IVUS200 models with artificially added cap.
The anisotropic Mooney–Rivlin model was used for the vessel tissue. Its strain energy density function is
| (1) |
| (2) |
where I1 and I2 are the first and second invariants of right Cauchy–Green deformation tensor C defined as C = [Cij] = XTX, X = [Xij] = [∂xi/∂aj]; (xi) is current position; (ai) is original position, I4 = Cij(nc)i(nc)j; nc is the unit vector in the circumferential direction of the vessel; and c1, c2, D1, D2, K1, and K2 are material parameters [27–29] whose values were determined using in vivo IVUS data [3]: c1 = −262.6 kPa, c2 = 22.9, D1 = 125.9 kPa, D2 = 2, K1 = 7.19 kPa, K2 = 23.5.
Plaque components were assumed to be isotropic and the isotropic Mooney–Rivlin material model was used to describe their material properties
| (3) |
The material constants from existing literature were used in this paper [27,30,31]: lipid: c1 = 0.5 kPa, c2 = 0, D1 = 0.5 kPa, D2 = 1.5. Calcification: c1 = 92 kPa, c2 = 0, D1 = 36 kPa, and D2 = 2.
The models were solved by a commercial finite element software adina (Adina R & D, Watertown, MA) following established procedures [27,32].
2.3. Data Extraction and Plaque Measurements.
Morphological and plaque stress, strain and flow shear stress were extracted for all 105 slices from our 3D FSI models (IVUS + OCT, IVUS50, and IVUS200) for model comparisons and progression prediction use. Each slice contained 100 evenly spaced nodal points taken on the lumen. Each lumen nodal point was connected to a corresponding point on vessel out-boundary (see Fig. 3). The length of the connecting line is defined as the wall thickness (WT). If the line passes through a lipid or calcification region, the distance between lumen nodal point and first time the line meets the lipid or calcification is defined cap thickness. The average and minimum values of cap thickness from one slice were obtained and recorded as mean cap thickness and min cap thickness, respectively. The length of the line segmented within the lipid or calcification is defined as the lipid or calcification depth. If slice contained the lipid or calcification, there are two lines tangent to lipid or calcification, which pass the position traversed by centerline. The angle between the two tangent lines is defined as the lipid or calcification angle.
Fig. 3.
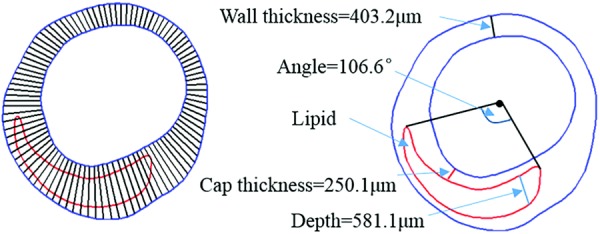
Diagrammatic sketch of the definition of WT, cap thickness, lipid depth, and angle
The area of lipid or calcification in a slice was recorded as lipid or calcification area. The area enclosed by lumen contour was denoted as LA. The area between lumen and out-boundary was defined as plaque area (denoted as PA). And, the PB was defined by the following formula:
| (4) |
Therefore, morphological factors used in this study included LA, PA, PB, WT, mean cap thickness (MeanCT), min cap thickenss (MinCT), mean calcification cap thickness (MeanCaCap), min calcification cap thickness (MinCaCap), mean lipid/calcification depth (LipidDepth/CaDepth), lipid/calcification angle (LipidAngle/CaAngle), and lipid/calcification area (LipidArea/CaArea), altogether 14 morphological risk factors (used as predictors in the prediction study).
For mechanical risk factors, WSS, plaque wall stress (PWS), and plaque wall strain (PWSn) values were extracted from 3D FSI model solution at 100 lumen nodal points of all slices. Average values of WSS, PWS, and PWSn over 100 lumen nodals on each slice were recorded for analysis. It should be noted that PWS, PWSn, and WSS were all taken at the lumen wall (solid and flow) as that is where the attention has been for both plaque remodeling, progression, and vulnerability (possibility to rupture) investigations. If slice contains cap, mean cap PWS (CapPWS) and PWSn (CapPWSn) values from all cap nodal points were calculated and also recorded. If a slice did not contain lipid or calcification, its CapPWS and CapPWSn were defined as 0. Altogether, we have five mechanical risk factors to be used as predictors.
2.4. Plaque Progression Quantifications.
For all paired slices (T1 slices paired with T2 slices), lumen area increase (LAI), plaque area increase (PAI), and plaque burden increase (PBI) from T1 to T2 were selected as measures for plaque progression
| (5) |
| (6) |
| (7) |
For the sake of simplification, for each progression measure which would be the prediction target, plaque slices were classified into two types. Using PAI as an example, for a given slice, if PAI > 0, this slice would be labeled 1. If the slice had PAI ≤ 0, it would be labeled −1. Slices were labeled “1” and “−1” for LAI and PBI following the same procedures.
2.5. Plaque Progression Prediction.
The sample size was 105 slices using slice as analysis unit in this study. The least squares support vector machine (LS-SVM), suitable for small sample size (100's), was used for our plaque progression prediction study. More details about LS-SVM can be found in Ref. [33]. In this study, LS-SVM used Gaussian radial basis function as the kernel function and steepest descent method for searching optimal parameters. A standard fivefold cross-validation procedure was employed using all 105 slices as the training and testing sets. The 105 slices were randomly divided into five groups. Each time, any four groups of slices would take turns to be the training set to determine parameter values in the prediction model with the remaining group (the testing group) was reserved to validate the prediction accuracy of the model. This procedure was repeated 100 times to stabilize the prediction results. Nineteen morphological and mechanical predictors identified in Sec. 2.3 were used to determine their prediction accuracies. Different combination of risk factors was used in LS-SVM to compare the prediction ability and find the best combination for plaque progression prediction.
For our prediction method, prediction accuracy (Acc) is defined as follows:
| (8) |
where we set plaque increase and plaque no-increase as positive and negative pattern, respectively, TP is the number of true positive outcomes, FP is the number of false positive outcomes, TN is the number of true negative outcomes, and FN is the number of false negative outcomes. Sensitivity (Sen) and specificity (Spe) were also calculated using the formulas below to avoid the reliance of the uneven distributed data in two classes
| (9) |
| (10) |
Results are reported in the next section.
3. Results
3.1. Plaque Progression Prediction Using Single Risk Factors.
Using three models (IVUS + OCT, IVUS50, and IVUS200) and three progression measures (LAI, PAI, and PBI), nine prediction studies were performed for all the predictors. For each prediction study, 5-fold prediction experiments were repeated 100 times for better stability. After averaging the prediction results from the 100 repeated experiments, prediction accuracy of LAI, PAI, and PBI by nine most popular predictors using results from the three models were given by Fig. 4. Values of prediction accuracy, sensitivity and specificity were summarized by Table 1. According to the accuracy values of 19 single factors using IVUS + OCT data, PWSn showed the best prediction accuracy (0.766) for LAI, with accompanying sensitivity and specificity at 0.787 and 0.756, respectively. For PAI prediction, CapPWS had the best prediction accuracy (0.838) with its sensitivity and specificity at 0.939 and 0.603, respectively. For PBI prediction, MinCT gave the best prediction accuracy (0.890) with its sensitivity and specificity at 0.863 and 0.900, respectively. The best prediction accuracy of PBI was 12.4% higher than the best accuracy of LAI. The best sum of sensitivity and specificity of PBI was 22% higher than the best value of LAI.
Fig. 4.
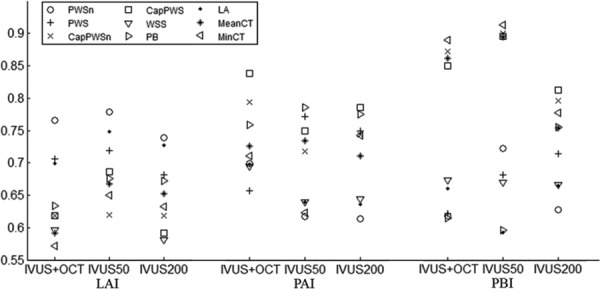
Prediction accuracies of nine single factors from IVUS + OCT, IVUS50, and IVUS200 models according to three measurements of plaque progression
Table 1.
Nine single factors with prediction accuracy, sensitivity and specificity from IVUS + OCT, IVUS50, and IVUS200 models according to three measurements of plaque progression
| LAI | PAI | PBI | ||
|---|---|---|---|---|
| Predictor | (Acc, Sen, Spe) | (Acc, Sen, Spe) | (Acc, Sen, Spe) | |
| IVUS + OCT | PWSn | (0.766, 0.787, 0.756) | (0.699, 0.829, 0.415) | (0.619, 0.170, 0.840) |
| PWS | (0.706, 0.653, 0.761) | (0.657, 0.842, 0.256) | (0.622, 0.212, 0.828) | |
| CapPWSn | (0.619, 0.420, 0.792) | (0.794, 0.936, 0.467) | (0.872, 0.857, 0.881) | |
| CapPWS | (0.619, 0.418, 0.804) | (0.838, 0.939, 0.603) | (0.850, 0.805, 0.872) | |
| WSS | (0.596, 0.617, 0.594) | (0.695, 0.961, 0.061) | (0.673, 0.250, 0.890) | |
| PB | (0.699, 0.674, 0.729) | (0.698, 0.959, 0.072) | (0.660, 0.135, 0.915) | |
| LA | (0.634, 0.542, 0.731) | (0.759, 0.840, 0.582) | (0.615, 0.101, 0.874) | |
| MeanCT | (0.591, 0.356, 0.802) | (0.726, 0.897, 0.342) | (0.862, 0.853, 0.861) | |
| MinCT | (0.572, 0.360, 0.770) | (0.711, 0.884, 0.307) | (0.890, 0.863, 0.900) | |
| IVUS50 | PWSn | (0.779, 0.759, 0.807) | (0.617, 0.322, 0.788) | (0.722, 0.871, 0.467) |
| PWS | (0.719, 0.835, 0.575) | (0.772, 0.609, 0.862) | (0.681, 0.802, 0.484) | |
| CapPWSn | (0.620, 0.798, 0.404) | (0.718, 0.405, 0.885) | (0.900, 0.897, 0.907) | |
| CapPWS | (0.686, 0.876, 0.445) | (0.750, 0.518, 0.876) | (0.896, 0.900, 0.891) | |
| WSS | (0.542, 0.595,0.513) | (0.639, 0.049, 0.951) | (0.670, 0.878, 0.316) | |
| PB | (0.748, 0.768, 0.727) | (0.640, 0.092, 0.927) | (0.593, 0.839, 0.190) | |
| LA | (0.676, 0.761, 0.581) | (0.786, 0.699, 0.837) | (0.596, 0.871, 0.141) | |
| MeanCT | (0.667, 0.888, 0.387) | (0.734, 0.398, 0.913) | (0.895, 0.900, 0.889) | |
| MinCT | (0.650, 0.838, 0.414) | (0.623, 0.223, 0.842) | (0.913, 0.921, 0.902) | |
| IVUS200 | PWSn | (0.739, 0.739, 0.752) | (0.614, 0.338, 0.773) | (0.628, 0.544, 0.540) |
| PWS | (0.682, 0.740, 0.619) | (0.750, 0.587, 0.839) | (0.714, 0.697, 0.575) | |
| CapPWSn | (0.619, 0.818, 0.372) | (0.744, 0.403, 0.927) | (0.796, 0.585, 0.885) | |
| CapPWS | (0.592, 0.803, 0.336) | (0.786, 0.517, 0.929) | (0.812, 0.657, 0.858) | |
| WSS | (0.581, 0.633, 0.536) | (0.644, 0.037, 0.963) | (0.666, 0.343, 0.720) | |
| PB | (0.727, 0.757, 0.693) | (0.636, 0.093, 0.925) | (0.665, 0.391, 0.666) | |
| LA | (0.672, 0.765, 0.566) | (0.775, 0.690, 0.826) | (0.755, 0.775, 0.636) | |
| MeanCT | (0.652, 0.873, 0.374) | (0.711, 0.353, 0.904) | (0.754, 0.518, 0.873) | |
| MinCT | (0.633, 0.820, 0.397) | (0.742, 0.436, 0.906) | (0.778, 0.586, 0.860) |
Acc-accuracy; Sen-sensitivity; Spe-specificity.
For IVUS200 model, PWSn, PWS, and CapPWSn were the best predictors for LAI, PAI, and PBI predictions, respectively. Using LAI as measure, PWSn was the best single risk factor IVUS200. This is the same for IVUS + OCT, and IVUS50. Although WSS was commonly accepted as an important factor for plaque progression, it showed relatively lower accuracies for prediction of plaque progression in our nine prediction studies compared to other predictors.
3.2. Plaque Progression Prediction Using Combinations of Morphological Risk Factors.
Lumen cross section area, plaque area, and plaque burden were all associated with plaque progression [4–6]. The combination of WT, LA, PA, and PB (denoted as Com.1) was used for plaque progression prediction. To emphasize the importance of mean cap thickness (lipid) and min cap thickness (lipid) due to their strong associations with plaque vulnerability and progression, these two factors were added to Com.1 to make Com.2 [2,3,20]. To get best possible accuracy, we combined the all 14 morphological risk factors (denoted as Com.3) mentioned in Sec. 2.3 to obtain its accuracy of plaque progression prediction. The accuracy, sensitivity and specificity values using three combinations and three measurements of plaque progression were showed in Table 2. For IVUS + OCT model, Com.3 using LAI as the measure showed the highest accuracy (0.910) and highest sum of sensitivity (0.880) and specificity (0.938). The accuracy of Com.3 was all higher than the values of Com.1 and Com.2 using each one of the each measures. For IVUS + OCT model, the accuracy of Com.1 using PBI was the worst and 20.8% less than the value of Com.3 using LAI. Using Com.3 as predictors, the accuracy difference between IVUS + OCT, IVUS50, and IVUS200 was tiny (<3%) for all three measures.
Table 2.
Prediction accuracy, sensitivity, and specificity using three combination of morphological risk factors according to three measurements of plaque progression from IVUS + OCT, IVUS50, and IVUS200 models. Com.1 is a combination of WT, LA, PA, and PB. Com.2 is a combination of mean cap thickness, min cap thickness, WT, LA, PA, and PB. Com.3 is made of a combination of 14 morphological risk factors used in this study.
| LAI | PAI | PBI | ||
|---|---|---|---|---|
| Predictor | (Acc, Sen, Spe) | (Acc, Sen, Spe) | (Acc, Sen, Spe) | |
| IVUS + OCT | Com.1 | (0.774, 0.754, 0.803) | (0.845, 0.906, 0.708) | (0.702, 0.494, 0.816) |
| Com.2 | (0.849, 0.834, 0.869) | (0.838, 0.909, 0.682) | (0.883, 0.820, 0.918) | |
| Com.3 | (0.910, 0.880, 0.938) | (0.866, 0.929, 0.719) | (0.904, 0.854, 0.931) | |
| IVUS50 | Com.1 | (0.812, 0.776, 0.843) | (0.810, 0.872, 0.694) | (0.648, 0.468, 0.764) |
| Com.2 | (0.862, 0.830, 0.891) | (0.806, 0.865, 0.701) | (0.887, 0.832, 0.921) | |
| Com.3 | (0.901, 0.869, 0.930) | (0.854, 0.919, 0.741) | (0.890, 0.839, 0.919) | |
| IVUS200 | Com.1 | (0.801, 0.758, 0.842) | (0.813, 0.703, 0.874) | (0.871, 0.376, 0.946) |
| Com.2 | (0.867, 0.893, 0.840) | (0.808, 0.877, 0.680) | (0.879, 0.748, 0.941) | |
| Com.3 | (0.898, 0.925, 0.865) | (0.878, 0.923, 0.797) | (0.917, 0.819, 0.960) |
3.3. Plaque Progression Prediction Using Combinations of Both Morphological and Mechanical Risk Factors.
Mechanical risk factors play an essential role in the process of plaque progression. The combination of five mechanical risk factors including local stress/strain, stress/strain and WSS and 14 morphological risk factors denoting as Com.4 was used to predict plaque progression. Table 3 gave the accuracy, sensitivity and specificity of Com.4 with LAI, PAI, and PBI as the measures, respectively. For IVUS + OCT model, using LAI as the measure, Com.4 showed the highest accuracy (0.911) and highest sum (1.819) of sensitivity and specificity, while PAI gave the worse accuracy (0.881) which was 3% less than the value of Com.4 using LAI. No matter which measure were employed for plaque progression, the prediction accuracy of Com.4 from IVUS + OCT model were always higher than 0.88, and accuracies from IVUS50 and IVUS200 models were slightly less, but still exceeded 0.87.
Table 3.
Prediction accuracy, sensitivity and specificity using 14 morphological risk factors and five mechanical risk factors according to three measurements of plaque progression from three models. Com.4 means the combination of all mechanical and morphological risk factors.
| LAI | PAI | PBI | ||
|---|---|---|---|---|
| Predictor | (Acc, Sen, Spe) | (Acc, Sen, Spe) | (Acc, Sen, Spe) | |
| IVUS + OCT | Com.4 | (0.911, 0.879, 0.940) | (0.881, 0.933, 0.760) | (0.905, 0.860, 0.930) |
| IVUS50 | Com.4 | (0.917, 0.899, 0.936) | (0.874, 0.915, 0.806) | (0.884, 0.851, 0.906) |
| IVUS200 | Com.4 | (0.909, 0.888, 0.929) | (0.874, 0.910, 0.815) | (0.907, 0.805, 0.955) |
3.4. Comparison of IVUS + OCT, IVUS50, and IVUS200 Models.
Cap thickness has a significant effect on the accuracy of stress/strain prediction based on computational modeling studies. Table 4 shows the comparison of MinCT, MeanCT, CapPWS, and CapPWSn of four representative slice samples from IVUS + OCT, IVUS50, and IVUS200 models. The cap thickness of IVUS + OCT was from the measurement of OCT data. As could be seen from Table 4, IVUS50 underestimated MinCT by 66.5% and overestimate CapPWS by 58.6%, compared to IVUS + OCT. IVUS200 overestimated the MeanCT by 25.1% and underestimate CapPWS by 17.0%, compared to IVUS + OCT. It should be noted that IVUS50 and IVUS200 estimated the cap thickness with errors which are unknown without OCT in practice, thereby likely lead to the erroneous estimation of CapPWS and CapPWSn values. Cap thickness decrease could be seen from the cap thickness values of the same slice at T1 and T2 in Table 4. Another item to be aware of is that IVUS50 and IVUS200 cannot give accurate values of cap thickness increase from T1 to T2, when the real cap thickness is under 200 μm. The fact that, IVUS50 and IVUS200 were not capable of measuring cap thickness increase since their cap thickness were artificially made in the modeling process due to limitation of IVUS resolution.
Table 4.
Four slice samples from IVUS + OCT, IVUS50, and IVUS200 models showing comparisons of MinCT, MeanCT (unit: mm), CapPWS (unit: kPa), and CapPWSn. The subscripted represents time. Notation S12T1 means slice 12 at T1, same for other slices.
| Slice at T1 | MinCT | Mean CT | Cap PWS | Cap PWSn | Slice at T2 | MinCT | Mean CT | Cap PWS | Cap PWSn | |
|---|---|---|---|---|---|---|---|---|---|---|
| IVUS + OCT | S12T1 | 0.177 | 0.242 | 60.8 | 0.150 | S12T2 | 0.124 | 0.134 | 139.7 | 0.212 |
| S13T1 | 0.190 | 0.223 | 60.1 | 0.141 | S13T2 | 0.090 | 0.109 | 138.1 | 0.215 | |
| S58T1 | 0.190 | 0.269 | 161.6 | 0.189 | S58T2 | 0.100 | 0.169 | 166.0 | 0.176 | |
| S59T1 | 0.177 | 0.248 | 144.3 | 0.192 | S59T2 | 0.114 | 0.181 | 172.3 | 0.177 | |
| Average | 45 slices | 0.223 | 0.289 | 88.9 | 0.163 | 45 slices | 0.208 | 0.280 | 105.6 | 0.190 |
| IVUS50 | S12T1 | 0.05 | 0.102 | 124.5 | 0.173 | S12T2 | 0.05 | 0.076 | 193.7 | 0.211 |
| S13T1 | 0.05 | 0.084 | 125.4 | 0.167 | S13T2 | 0.049 | 0.075 | 184.3 | 0.206 | |
| S58T1 | 0.048 | 0.165 | 245.1 | 0.207 | S58T2 | 0.048 | 0.126 | 277.4 | 0.190 | |
| S59T1 | 0.045 | 0.154 | 211.6 | 0.203 | S59T2 | 0.049 | 0.122 | 277.5 | 0.190 | |
| Average | 45 slices | 0.171 | 0.255 | 120.4 | 0.173 | 45 slices | 0.142 | 0.221 | 157.1 | 0.177 |
| IVUS200 | S12T1 | 0.201 | 0.246 | 50.7 | 0.141 | S12T2 | 0.203 | 0.226 | 84.0 | 0.180 |
| S13T1 | 0.202 | 0.234 | 51.8 | 0.129 | S13T2 | 0.202 | 0.225 | 81.5 | 0.174 | |
| S58T1 | 0.203 | 0.280 | 158.3 | 0.189 | S58T2 | 0.200 | 0.249 | 142.0 | 0.170 | |
| S59T1 | 0.200 | 0.263 | 147.6 | 0.190 | S59T2 | 0.200 | 0.247 | 142.5 | 0.171 | |
| Average | 45 slices | 0.268 | 0.343 | 80.5 | 0.158 | 45 slices | 0.247 | 0.316 | 92.4 | 0.162 |
4. Discussion
4.1. Significance of Multimodality Image-Based Models.
Plaque vessel wall thickness changes were normally under 200 μm and “vulnerable plaque” cap thickness threshold value defined as 65 μm. Hence, imaging resolution has been a major limitation for vulnerable plaque progression research (and other areas in a broader sense). Image resolutions at 150 μm (IVUS)–300 μm (magnetic resonance imaging) are not sufficient to accurately measure the plaque progression. OCT and IVUS could combine and complement each other for more accurate plaque morphology, which, in turn, could provide better calculations of stress/strain [3]. Compared to IVUS-based modeling study, OCT + IVUS-based model possesses more accurate plaque information and has the potential to improve the prediction accuracy of plaque progression. Wang et al. used combination of eight morphological and mechanical risk factors to predict the plaque progression by using PAI as the measurement [19]. The results shown that the sum of sensitivity and specificity was 1.5928, which is 10% less than 1.693 using Com.4 from our IVUS + OCT model.
4.2. Combination of Morphological and Mechanical Factors Could Lead to Higher Prediction Accuracy.
Although most plaque progression research paid attention to plaque morphology and fluid flow factors, Tang et al. have demonstrated that structural stress/strain and critical stress/strain may play an important part in plaque vulnerability and progression [16,18]. By using follow-up IVUS and OCT data to make FSI models, we could obtain more accurate stress and strain calculation which will improve the prediction of plaque progression. Results given by Table 1 demonstrated that mechanical factors, particularly stress, and strain conditions are important for prediction of plaque progression. Regardless of which plaque progression measurement was used, combination of morphological and mechanical risk factors provided the highest accuracy and highest sum of sensitivity and specificity. The prediction accuracy of Com.4 for LAI was approximately 91%. Combing morphological factors and mechanical factors demonstrated great ability in plaque progression prediction.
4.3. The Relationship Between Risk Factors and Prediction of Lumen Area Increase, Plaque Area Increase, and Plaque Burden Increase.
Values of LAI, PAI, and PBI could reflect plaque progression from the views of plaque area and stenosis. For a single risk factor, the prediction accuracy of PBI was generally higher than the values of LAI and PAI. From the results of IVUS + OCT model, the five best factors of PBI (MinCT, LipidAngle, CapPWSn, LipidDepth, and LipidArea) were all associated with lipid. Lipid features had an important impact on the prediction of PBI. For Com.3 and Com.4, prediction accuracy of LAI was higher than the values of PAI and PBI. Using LAI as the measure, prediction accuracy improved gradually following the order of single factor, Com.1, Com.2, Com.3, and Com.4. PWSn provided the highest accuracy for LAI among in all single risk factors. Morphological and mechanical factors all affected the prediction of LAI.
4.4. Limitations.
(a) Sample size. The sample was small in our studies since it was challenging to get IVUS and OCT data for two time points. Only two arteries from one patient were used to make follow-up FSI model. That was why we used slice as our analyzing unit. (b) Modeling conditions and assumptions. Many factors can affect model stress/strain predictions, such as image data resolution, lack of flow conditions, pressure conditions, patient-specific material properties, residual stress, cardiac motion, vessel shrinkage (longitudinal shrinkage can be 30–50% for healthy vessel), and others. These features should definitely be cooperated in our modeling procedure when data become available. (c) 3D FSI model construction is very time consuming and automation is needed for potential implementation for clinical application. (d) Neither IVUS nor OCT is gated, so it is likely that coregistered images were acquired at difference points in the cardiac cycle. That is a common problem in OCT imaging and modeling. This is a pilot study and large-scale patient studies are needed for further validation.
Acknowledgment
Dr. Yuan-Cheng Fung provided guidance to Dalin Tang during Tang's entire career. Tang first met Dr. Fung in 1992 when Tang flew to La Jolla and asked Fung for guidance. Fung asked Tang a question: “You want to learn swimming, do you want to stay on the bank or you want to get in the water?” Ever since then Tang has been trying to get into the “water.” It is really not easy for a math person to get into engineering, biological, and clinical water. Tang has tried very hard to collaborate with engineers, radiologists and clinicians and conduct patient-specific research seeking answers to clinical questions. This paper is our modest progress as a report to Dr. Fung at his 100th birthday, an update of Tang's “getting into water” effort.
Tang and Guo received support from Jiangsu Province Science and Technology Agency grant BE2016785.
Contributor Information
Xiaoya Guo, Department of Mathematics, , Southeast University, , Nanjing 210096, China.
Don P. Giddens, Department of Medicine, School of Medicine, , Emory University, , Atlanta, GA 30307; The Wallace H. Coulter Department , of Biomedical Engineering, , Georgia Institute of Technology, , Atlanta, GA 30332
David Molony, Department of Medicine, , School of Medicine, , Emory University, , Atlanta, GA 30307.
Chun Yang, Mathematical Sciences Department, , Worcester Polytechnic Institute, , Worcester, MA 01609.
Habib Samady, Department of Medicine, , School of Medicine, , Emory University, , Atlanta, GA 30307.
Jie Zheng, Mallinckrodt Institute of Radiology, , Washington University, , St. Louis, MO 63110.
Mitsuaki Matsumura, The Cardiovascular Research Foundation, , Columbia University, , New York, NY 10022.
Gary S. Mintz, The Cardiovascular Research Foundation, , Columbia University, , New York, NY 10022
Akiko Maehara, The Cardiovascular Research Foundation, , Columbia University, , New York, NY 10022.
Liang Wang, Mathematical Sciences Department, , Worcester Polytechnic Institute, , Worcester, MA 01609.
Dalin Tang, Department of Mathematics, Southeast University, , Nanjing 210096, China;; Mathematical Sciences Department, Worcester Polytechnic Institute, , Worcester, MA 01609
Funding Data
NIH (Grant No. R01 EB004759; Funder ID: 10.13039/100000002).
Nomenclature
- FSI =
fluid–structure interaction
- IVUS =
intravascular ultrasound
- LA =
lumen area
- LAI =
lumen area increase
- LS-SVM =
least squares support vector machine
- OCT =
optical coherence tomography
- PA =
plaque area
- PAI =
plaque area increase
- PB =
plaque burden
- PBI =
plaque burden increase
- PWS =
plaque wall stress
- PWSn =
plaque wall strain
- VH-IVUS =
virtual histology IVUS
- WSS =
wall shear stress
References
- [1]. Virmani, R. , Ladich, E. R. , Burke, A. P. , and Kolodgie, F. D. , 2006, “ Histopathology of Carotid Atherosclerotic Disease,” Neurosurgery, 59(Suppl. 5), p. S3-219. 10.1227/01.NEU.0000239895.00373.E4 [DOI] [PubMed] [Google Scholar]
- [2]. Brown, A. J. , Obaid, D. R. , Costopoulos, C. , Parker, R. A. , Calvert, P. A. , Teng, Z. , Hoole, S. P. , West, N. E. , Goddard, M. , and Bennett, M. R. , 2015, “ Direct Comparison of Virtual-Histology Intravascular Ultrasound and Optical Coherence Tomography Imaging for Identification of Thin-Cap Fibroatheroma,” Circ.: Cardiovasc. Imaging, 8(10), p. e003487. 10.1161/CIRCIMAGING.115.003487 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3]. Guo, X. , Giddens, D. P. , Molony, D. , Yang, C. , Samady, H. , Zheng, J. , Mintz, G. S. , Maehara, A. , Wang, L. , Pei, X. , Li, Z. Y. , and Tang, D. , 2018, “ Combining IVUS and Optical Coherence Tomography for More Accurate Coronary Cap Thickness Quantification and Stress/Strain Calculations: A Patient-Specific Three-Dimensional Fluid-Structure Interaction Modeling Approach,” ASME J. Biomech. Eng., 140(4), p. 041005. 10.1115/1.4038263 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4]. Burke, A. P. , Kolodgie, F. D. , Farb, A. , Weber, D. , and Virmani, R. , 2002, “ Morphological Predictors of Arterial Remodeling in Coronary Atherosclerosis,” Circulation, 105(3), pp. 297–303. 10.1161/hc0302.102610 [DOI] [PubMed] [Google Scholar]
- [5]. Clarkson, T. B. , Prichard, R. W. , Morgan, T. M. , Petrick, G. S. , and Klein, K. P. , 1994, “ Remodeling of Coronary Arteries in Human and Nonhuman Primates,” JAMA, 271(4), pp. 289–294. 10.1001/jama.1994.03510280051032 [DOI] [PubMed] [Google Scholar]
- [6]. Glagov, S. , Weisenberg, E. , Zarins, C. K. , Stankunavicius, R. , and Kolettis, G. J. , 1987, “ Compensatory Enlargement of Human Atherosclerotic Coronary Arteries,” New Engl. J. Med., 316(22), pp. 1371–1375. 10.1056/NEJM198705283162204 [DOI] [PubMed] [Google Scholar]
- [7]. Zarins, C. K. , Weisenberg, E. , Kolettis, G. , Stankunavicius, R. , and Glagov, S. , 1988, “ Differential Enlargement of Artery Segments in Response to Enlarging Atherosclerotic Plaques,” J. Vasc. Surg., 7(3), pp. 386–394. 10.1016/0741-5214(88)90433-8 [DOI] [PubMed] [Google Scholar]
- [8]. Gerber, T. C. , Erbel, R. , Gorge, G. , Ge, J. , Rupprecht, H. J. , and Meyer, J. , 1994, “ Extent of Atherosclerosis and Remodeling of the Left Main Coronary Artery Determined by Intravascular Ultrasound,” Am. J. Cardiol., 73(9), pp. 666–671. 10.1016/0002-9149(94)90931-8 [DOI] [PubMed] [Google Scholar]
- [9]. Mintz, G. S. , Kent, K. M. , Pichard, A. D. , Satler, L. F. , Popma, J. J. , and Leon, M. B. , 1997, “ Contribution of Inadequate Arterial Remodeling to the Development of Focal Coronary Artery Stenoses: An Intravascular Ultrasound Study,” Circulation, 95(7), pp. 1791–1798. 10.1161/01.CIR.95.7.1791 [DOI] [PubMed] [Google Scholar]
- [10]. Nakamura, Y. , Takemori, H. , Shiraishi, K. , Inoki, I. , Sakagami, M. , Shimakura, A. , Usuda, K. , Kubota, K. , Takata, S. , and Kobayashi, K. I. , 1996, “ Compensatory Enlargement of Angiographically Normal Coronary Segments in Patients With Coronary Artery Disease: In Vivo Documentation Using Intravascular Ultrasound,” Angiology, 47(8), pp. 775–781. 10.1177/000331979604700804 [DOI] [PubMed] [Google Scholar]
- [11]. Ku, D. N. , Giddens, D. P. , Zarins, C. K. , and Glagov, S. , 1985, “ Pulsatile Flow and Atherosclerosis in the Human Carotid Bifurcation. Positive Correlation Between Plaque Location and Low Oscillating Shear Stress,” Aeterioscler., Thromb., Vasc. Biol., 5(3), pp. 293–302. 10.1161/01.ATV.5.3.293 [DOI] [PubMed] [Google Scholar]
- [12]. Samady, H. , Eshtehardi, P. , McDaniel, M. C. , Suo, J. , Dhawan, S. S. , Maynard, C. , Timmins, L. H. , Quyyumi, A. A. , and Giddens, D. P. , 2011, “ Coronary Artery Wall Shear Stress Is Associated With Progression and Transformation of Atherosclerotic Plaque and Arterial Remodeling in Patients With Coronary Artery Disease,” Circulation, 124(7), pp. 779–788. 10.1161/CIRCULATIONAHA.111.021824 [DOI] [PubMed] [Google Scholar]
- [13]. Spence, J. D. , Eliasziw, M. , DiCicco, M. , Hackam, D. G. , Galil, R. , and Lohmann, T. , 2002, “ Carotid Plaque Area: A Tool for Targeting and Evaluating Vascular Preventive Therapy,” Stroke, 33(12), pp. 2916–2922. 10.1161/01.STR.0000042207.16156.B9 [DOI] [PubMed] [Google Scholar]
- [14]. Stone, G. W. , Maehara, A. , Lansky, A. J. , de Bruyne, B. , Cristea, E. , Mintz, G. S. , Mehran, R. , McPherson, J. , Farhat, N. , Marso, S. P. , Parise, H. , Templin, B. , White, R. , Zhang, Z. , and Serruys, P. W. , 2011, “ A Prospective Natural-History Study of Coronary Atherosclerosis,” New Engl. J. Med., 364(3), pp. 226–235. 10.1056/NEJMoa1002358 [DOI] [PubMed] [Google Scholar]
- [15]. Corban, M. T. , Eshtehardi, P. , Suo, J. , McDaniel, M. C. , Timmins, L. H. , Rassoul-Arzrumly, E. , Maynard, C. , Mekonnen, G. , King, S. , Quyyumi, A. A. , Giddens, D. P. , and Samady, H. , 2014, “ Combination of Plaque Burden, Wall Shear Stress, and Plaque Phenotype Has Incremental Value for Prediction of Coronary Atherosclerotic Plaque Progression and Vulnerability,” Atherosclerosis, 232(2), pp. 271–276. 10.1016/j.atherosclerosis.2013.11.049 [DOI] [PubMed] [Google Scholar]
- [16]. Stone, P. H. , Saito, S. , Takahashi, S. , Makita, Y. , Nakamura, S. , Kawasaki, T. , Takahashi, A. , Katsuki, T. , Nakamura, S. , Namiki, A. , Hirohata, A. , Matsumura, T. , Yamazaki, S. , Yokoi, H. , Tanaka, S. , Otsuji, S. , Yoshimach, F. , Honye, J. , Harwood, D. , Reitman, M. , Coskun, A. U. , Papafaklis, M. I. , and Feldman, C. L. , 2012, “ Prediction of Progression of Coronary Artery Disease and Clinical Outcomes Using Vascular Profiling of Endothelial Shear Stress and Arterial Plaque Characteristics: The Prediction Study,” Circulation, 126(2), pp. 172–181. 10.1161/CIRCULATIONAHA.112.096438 [DOI] [PubMed] [Google Scholar]
- [17]. Maurice, R. L. , Ohayon, J. , Finet, G. , and Cloutier, G. , 2004, “ Adapting the Lagrangian Speckle Model Estimator for Endovascular Elastography: Theory and Validation With Simulated Radio-Frequency Data,” J. Acoust. Soc. Am., 116(2), pp. 1276–1286. 10.1121/1.1771615 [DOI] [PubMed] [Google Scholar]
- [18]. Tang, D. , Kamm, R. D. , Yang, C. , Zheng, J. , Canton, G. , Bach, R. , Huang, X. , Hatsukami, T. S. , Zhu, J. , Ma, G. , Maehara, A. , Mintz, G. S. , and Yuan, C. , 2014, “ Image-Based Modeling for Better Understanding and Assessment of Atherosclerotic Plaque Progression and Vulnerability: Data, Modeling, Validation, Uncertainty and Predictions,” J. Biomech., 47(4), pp. 834–846. 10.1016/j.jbiomech.2014.01.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19]. Wang, L. , Tang, D. , Maehara, A. , Wu, Z. , Yang, C. , Muccigrosso, D. , Zheng, J. , Bach, R. , Billiar, K. L. , and Mintz, G. S. , 2018, “ Fluid-Structure Interaction Models Based on Patient-Specific IVUS at Baseline and Follow-Up for Prediction of Coronary Plaque Progression by Morphological and Biomechanical Factors: A Preliminary Study,” J. Biomech., 68, pp. 43–50. 10.1016/j.jbiomech.2017.12.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20]. Tearney, G. J. , Regar, E. , Akasaka, T. , Adriaenssens, T. , Barlis, P. , Bezerra, H. G. , Bouma, B. , Bruining, N. , Cho, J.-M. , Chowdhary, S. , Costa, M. A. , de Silva, R. , Dijkstra, J. , Di Mario, C. , Dudeck, D. , Falk, E. , Feldman, M. D. , Fitzgerald, P. , Garcia, H. , Gonzalo, N. , Granada, J. F. , Guagliumi, G. , Holm, N. R. , Honda, Y. , Ikeno, F. , Kawasaki, M. , Kochman, J. , Koltowski, L. , Kubo, T. , Kume, T. , Kyono, H. , Lam, C. C. S. , Lamouche, G. , Lee, D. P. , Leon, M. B. , Maehara, A. , Manfrini, O. , Mintz, G. S. , Mizuno, K. , Morel, M.-A. , Nadkarni, S. , Okura, H. , Otake, H. , Pietrasik, A. , Prati, F. , Räber, L. , Radu, M. D. , Rieber, J. , Riga, M. , Rollins, A. , Rosenberg, M. , Sirbu, V. , Serruys, P. W. J. C. , Shimada, K. , Shinke, T. , Shite, J. , Siegel, E. , Sonada, S. , Suter, M. , Takarada, S. , Tanaka, A. , Terashima, M. , Troels, T. , Uemura, S. , Ughi, G. J. , van Beusekom, H. M. M. , van der Steen, A. F. W. , van Es, G.-A. , van Soest, G. , Virmani, R. , Waxman, S. , Weissman, N. J. , and Weisz, G. , 2012, “ Consensus Standards for Acquisition, Measurement, and Reporting of Intravascular Optical Coherence Tomography Studies: A Report From the International Working Group for Intravascular Optical Coherence Tomography Standardization and Validation,” J. Am. Coll. Cardiol., 59(12), pp. 1058–1072. 10.1016/j.jacc.2011.09.079 [DOI] [PubMed] [Google Scholar]
- [21]. Uemura, S. , Ishigami, K. I. , Soeda, T. , Okayama, S. , Sung, J. H. , Nakagawa, H. , Somekawa, S. , Takeda, Y. , Kawata, H. , Horii, M. , and Saito, Y. , 2012, “ Thin-Cap Fibroatheroma and Microchannel Findings in Optical Coherence Tomography Correlate With Subsequent Progression of Coronary Atheromatous Plaques,” Eur. Heart J., 33(1), pp. 78–85. 10.1093/eurheartj/ehr284 [DOI] [PubMed] [Google Scholar]
- [22]. Barlis, P. , Serruys, P. W. , Gonzalo, N. , van der Giessen, W. J. , de Jaegere, P. J. , and Regar, E. , 2008, “ Assessment of Culprit and Remote Coronary Narrowings Using Optical Coherence Tomography With Long-Term Outcomes,” Am. J. Cardiol., 102(4), pp. 391–395. 10.1016/j.amjcard.2008.03.071 [DOI] [PubMed] [Google Scholar]
- [23]. Bourantas, C. V. , Papafaklis, M. I. , Kotsia, A. , Farooq, V. , Muramatsu, T. , Gomez-Lara, J. , Zhang, Y. J. , Iqbal, J. , Kalatzis, F. G. , Naka, K. K. , and Fotiadis, D. I. , 2014, “ Effect of the Endothelial Shear Stress Patterns on Neointimal Proliferation Following Drug-Eluting Bioresorbable Vascular Scaffold Implantation: An Optical Coherence Tomography Study,” JACC: Cardiovasc. Interventions, 7(3), pp. 315–324. 10.1016/j.jcin.2013.05.034 [DOI] [PubMed] [Google Scholar]
- [24]. Matsumoto, D. , Shite, J. , Shinke, T. , Otake, H. , Tanino, Y. , Ogasawara, D. , Sawada, T. , Paredes, O. L. , Hirata, K. I. , and Yokoyama, M. , 2007, “ Neointimal Coverage of Sirolimus-Eluting Stents at 6-Month Follow-Up: Evaluated by Optical Coherence Tomography,” Eur. Heart J., 28(8), pp. 961–967. 10.1093/eurheartj/ehl413 [DOI] [PubMed] [Google Scholar]
- [25]. Molony, D. S. , Timmins, L. H. , Rassoul-Arzrumly, E. , Samady, H. , and Giddens, D. P. , 2016, “ Evaluation of a Framework for the Co-Registration of Intravascular Ultrasound and Optical Coherence Tomography Coronary Artery Pullbacks,” J. Biomech., 49(16), pp. 4048–4056. 10.1016/j.jbiomech.2016.10.040 [DOI] [PubMed] [Google Scholar]
- [26]. Guo, X. , Tang, D. , Molony, D. , Yang, C. , Samady, H. , Zheng, J. , Mintz, G. S. , Maehara, A. , Wang, L. , Pei, X. , Li, Z. Y. , Ma, G. S. , and Giddens, D. P. , 2019, “ A Machine Learning-Based Method for Intracoronary OCT Segmentation and Vulnerable Coronary Plaque Cap Thickness Quantification,” Int. J. Comput. Methods, 16(3), p. 1842008. 10.1142/S0219876218420082 [DOI] [Google Scholar]
- [27]. Yang, C. , Bach, R. G. , Zheng, J. , Naqa, I. E. , Woodard, P. K. , Teng, Z. , Billiar, K. , and Tang, D. , 2009, “ In Vivo IVUS-Based 3-D Fluid–Structure Interaction Models With Cyclic Bending and Anisotropic Vessel Properties for Human Atherosclerotic Coronary Plaque Mechanical Analysis,” IEEE Trans. Biomed. Eng., 56(10), pp. 2420–2428. 10.1109/TBME.2009.2025658 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28]. Holzapfel, G. A. , 2000, Nonlinear Solid Mechanics: A Continuum Approach for Engineering, Wiley, Chichester, UK. [Google Scholar]
- [29]. Holzapfel, G. A. , Gasser, T. C. , and Ogden, R. W. , 2000, “ A New Constitutive Framework for Arterial Wall Mechanics and a Comparative Study of Material Models,” J. Elasticity, 61(1/3), pp. 1–48. 10.1023/A:1010835316564 [DOI] [Google Scholar]
- [30]. Walsh, M. T. , Cunnane, E. M. , Mulvihill, J. J. , Akyildiz, A. C. , Gijsen, F. J. H. , and Holzapfel, G. A. , 2014, “ Uniaxial Tensile Testing Approaches for Characterisation of Atherosclerotic Plaques,” J. Biomech., 47(4), pp. 793–804. 10.1016/j.jbiomech.2014.01.017 [DOI] [PubMed] [Google Scholar]
- [31]. Teng, Z. , Zhang, Y. , Huang, Y. , Feng, J. , Yuan, J. , Lu, Q. , Sutcliffe, M. P. , Brown, A. J. , Jing, Z. , and Gillard, J. H. , 2014, “ Material Properties of Components in Human Carotid Atherosclerotic Plaques: A Uniaxial Extension Study,” Acta Biomater., 10(12), pp. 5055–5063. 10.1016/j.actbio.2014.09.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32]. Wang, Q. , Tang, D. , Canton, G. , Wu, Z. , Hatsukami, T. S. , Billiar, K. L. , and Yuan, C. , 2018, “ Stress-Based Plaque Vulnerability Index and Assessment for Carotid Atherosclerotic Plaques Using Patient-Specific Vessel Material Properties,” MCB: Mol. Cell. Biomech., 15(4), pp. 189–201. 10.32604/mcb.2018.04572 [DOI] [Google Scholar]
- [33]. Suykens, J. A. , Van Gestel, T. D. , and Brabanter, J. , 2002, Least Squares Support Vector Machines, World Scientific, Hackensack, Singapore, Chap. 3. [Google Scholar]


