Conducting an Integrative Structural Biology Study

Abstract

Integrative structure determination is a powerful approach to mapping the structures of biological systems, with implications for our understanding of cellular biology and drug discovery. Here, we provide a Primer to introduce the researcher to the theory and methods of integrative approaches, relying on examples to illustrate the practice and challenges involved. These guidelines are intended to aid the researcher in applying integrative structural methods to systems of their interest and thus take advantage of this rapidly evolving field.

Introduction

Our understanding of biological macromolecular systems comes from gathering sufficient information about them from experiments and prior models. Depictions of the spatial and temporal arrangements of these systems are especially helpful in formulating hypotheses about their function and evolution. This mindset is often summarized by two quotes: “structure without function is a corpse; function without structure is a ghost” (Vogel and Wainwright, 1969); and, “nothing in biology makes sense except in the light of evolution” (Dobzhansky, 1973).

Historically, X-ray crystallography and NMR spectroscopy allowed us to determine atomic structures of smaller systems, such as single proteins. Larger systems were depicted at a correspondingly coarser granularity, commensurate to the data used (eg, electron or light microscopy images). Now, we are trying to map systems consisting of hundreds of macromolecules (eg, nuclear pore complexes, centrosomes), which nevertheless need to be depicted at a high level of detail. Moreover, we wish to describe the dynamics of these systems as they assemble, disassemble, function, and undergo regulation via interactions with other such systems. These descriptions also have to be sufficiently informative to allow us to modulate their functions, both to further study their mechanisms and for therapeutic interventions. It is here that traditional structure determination methods can fall short, thus creating a need for different approaches.

Fortunately, one such approach already exists and has a long track record of success: integrative structural biology (Figure 1). In integrative approaches, disparate information, potentially at different scales, is synthesized into a common view of a system. The motivation behind the integrative approach is deceptively simple: namely, any system is described best (ie, most accurately, precisely, completely, and efficiently) by using all available information about it; in other words, if information about a system is available, why not use it! The integrative approach constructs a depiction of a system by simultaneously combining information from multiple sources, including varied experimental methods (Table 1) and prior models (physical theories, statistical analyses, and other models).

Figure 1: Examples of integrative structures.

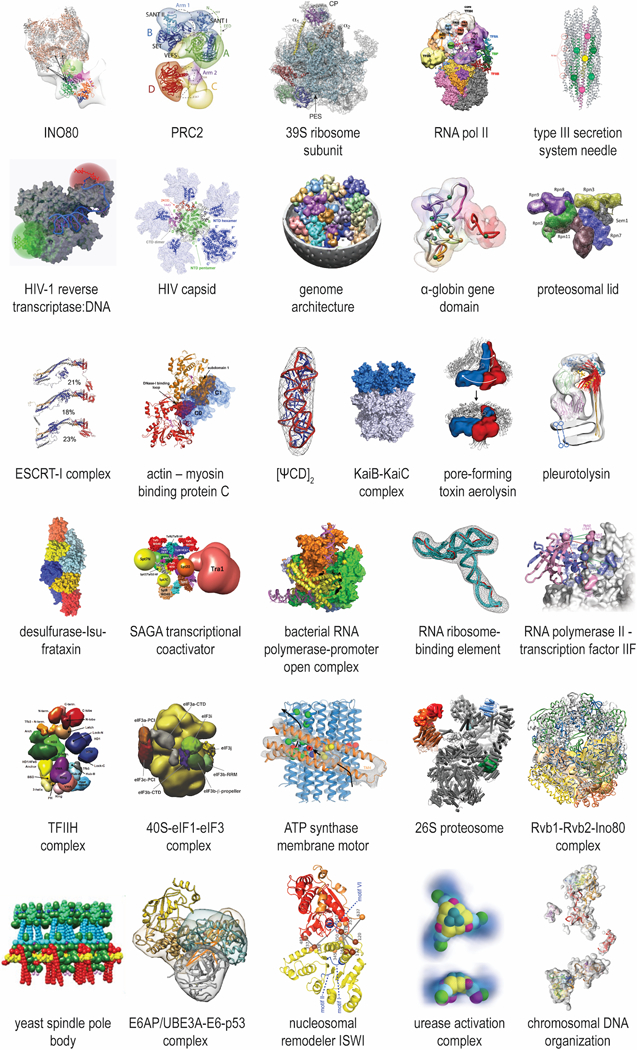
See Table 3 for details on each structure.

Table 1: Example methods that are informative about a variety of structural aspects of biomolecular systems are listed.

3DEM, 3D electron microscopy; DEER, double electron-electron resonance; EPR, electron paramagnetic resonance; FRET, Foerster resonance energy transfer; HDex, hydrogen/deuterium exchange; NMR, nuclear magnetic resonance; SAS, small-angle scattering; XL-MS, cross linking - mass spectrometry.

Structural information	Method
Stoichiometry	MS, quantitative fluorescence imaging
Atomic structures of parts of the studied system	X-ray and neutron crystallography, NMR spectroscopy, 3DEM, comparative modeling, and molecular docking
3D maps and 2D images	Electron microscopy and tomography
Atomic and protein distances	NMR, FRET, and other fluorescence techniques; DEER, EPR, and other spectroscopic techniques; XL-MS, disulfide bonds detected by gel electrophoresis
Binding site mapping	NMR spectroscopy, mutagenesis, FRET, and XL-MS
Size, shape, and distributions of pairwise atomic distances	SAS
Shape and size	Atomic force microscopy, ion mobility mass spectrometry, fluorescence correlation spectroscopy, fluorescence anisotropy, analytical ultracentrifugation
Component positions	Super-resolution optical microscopy, FRET imaging, immuno- electron microscopy
Physical proximity	Co-purification, native mass spectrometry, XL-MS, molecular genetic methods, and gene/protein sequence covariance
Solvent accessibility	Footprinting methods, including HDex assessed by MS or NMR, and even functional consequences of point mutations
Proximity between different genome segments	Chromosome Conformation Capture
Propensities for different interaction modes	Molecular mechanics force fields, potentials of mean force, statistical potentials, and sequence co-variation

Integrative approaches actually date back to the very beginning of structural biology, and in a spectacular fashion: one of the first integrative structural models was that of the double helix of DNA (Franklin and Gosling, 1953; Watson and Crick, 1953). It was possible to generate a model of DNA that elegantly explained how genetic information is stored and propagated from one generation to the next, by combining information about its chemical composition, its stoichiometry, the complementarity of its component nucleotides, and X-ray fiber diffraction data about its helical geometry. None of these individual considerations were sufficient on their own; only together did they result in an informative model. The concept of integrating different types of data then moved through a series of methodological milestones towards the current formalization, as reviewed previously (Alber et al., 2007a; Alber et al., 2008; Joseph et al., 2017; Sali et al., 2015).

Integrative modeling as an optimization problem

To introduce how integrative structure determination methods work, it is helpful to first describe modeling approaches in general (“while it may be hard to live with generalization, it is inconceivable to live without it” (Gay, 2002)); these modeling approaches include all structure determinations based primarily on experimental data (such as X-ray crystallography), computational predictions (such as comparative modeling), and even manual models (such as sketching of schematic diagrams). A “model” in this sense is a depiction of a system or process of interest that is useful for rationalizing the existing information and for making predictions about outcomes of future experiments. Thus, modeling is the process of converting input information about a system into a model of the system. All modeling methods share a common design principle: among all possible models, they aim to find those models whose computed properties match the input information (eg, structures whose interatomic distances and dihedral angles match those determined by NMR spectroscopy). Critically, modeling should also include the propagation of the uncertainty of the input information and modeling into the uncertainty of the model; this goal is achieved directly and robustly by producing a sample of all single models sufficiently consistent with the input information, not only the “best” single model (eg, the ensemble of structures found in a Protein Data Bank (PDB) entry for an NMR-derived structure, each one of which sufficiently satisfies the original data).

Modeling in general is best seen as an optimization in which input information can be used in five different ways, guided by maximizing the accuracy and precision of the model while remaining computationally feasible: (i) representing components of a model with some variables, (ii) scoring a model for its consistency with input information, (iii) searching for good-scoring models, (iv) filtering models based on input information, and (v) validating the resulting models. We now discuss each one of these ways in turn.

First, information can be used to define the representation of a model (Box 1 ). The representation specifies the variables whose values will be determined by modeling, based on input information. For an artist, this is the medium of art - whether to paint, sculpt, or photograph. For a structural biologist, the representation of a model first specifies the components of the system (eg, atoms, coarse-grained particles, and subunits in a complex), including their copy numbers. Next, it specifies the component coordinates that are fit to the input information (eg, their positions, orientations, and conformations). It also specifies if multiple structural states (eg, for heterogeneous samples) or trajectories (eg, for dynamic systems) need to be modeled. Finally, the representation of a model can also include auxiliary variables that are fit to the input information (eg, weights of different types of data and other parameters of the scoring function). The representation is generally selected based on the amount and type of information available (eg, a ~30 Å resolution EM density alone does not justify using an atomic representation), the purpose of the model (eg, questions about enzymatic mechanism generally require atomic structures), and computational feasibility (eg, a rigid representation of subunits in molecular docking enables a systematic search for the binding mode). For difficult modeling problems, a decision about the representation is often critical and can present a fall at the first hurdle, such as trying to squeeze out atomic positions from a low-resolution electron microscopy map and a dash of optimism.

Box 1. Molecular representation.

A structural model of a macromolecular assembly is defined by the relative positions and orientations of its components (eg, atoms, united atoms, residues, secondary structure elements, domains, subunits, and subcomplexes). Thus, the representation of a system is defined by all the structural variables that need to be determined based on input information, including the assignment of the system components to geometric objects such as points and spheres (Schneidman-Duhovny et al., 2014). An atomic representation can be coarsegrained by assigning unique subsets of atoms to higher level primitives (eg, beads and 3D Gaussians). Coarse-grained representations have proven useful, for example, in molecular dynamics simulations of lipid bilayers as well as structured and disordered proteins (Saunders and Voth, 2013). In our experience, selecting an appropriate representation is one of the most important decisions when performing integrative modeling, given the varied sparseness, noise, ambiguity, and resolution of the input datasets (Schneidman-Duhovny et al., 2014). An optimal representation facilitates accurate formulation of spatial restraints as well as efficient and complete sampling of good-scoring models, while still retaining sufficient detail without overfitting, so that the resulting models are maximally useful for subsequent biological analyses (Saunders and Voth, 2013; Schneidman-Duhovny et al., 2014; Viswanath and Sali, 2019).

While traditional structural biology methods usually produce a single atomic coordinate set, integrative models tend to be more complex in at least four respects (Sali et al., 2015). First, a model can be multi-scale, coarse-graining different levels of structural detail by a collection of geometrical primitives (eg, points, spheres, tubes, Gaussians, and probability densities) (Grime and Voth, 2014). Thus, the same part of the system can be described with multiple representations or different parts of the system can be represented differently. Second, a model can be multi-state, specifying multiple discrete states of the system that are needed simultaneously to explain the input information (each state may differ in structure and/or composition) (Molnar et al., 2014; Pelikan et al., 2009). Third, a model can also specify the order of states in time. This feature allows a representation of a multi-step biological process, a functional cycle (Diez et al., 2004), a kinetic network (Pirchi et al., 2011), or time evolution of a modeled system (eg, a molecular dynamics trajectory) (Bock et al., 2013). Finally, an ensemble of models is often provided to specify the uncertainty in the input information by including each model that on its own satisfies the input information within an acceptable threshold (eg, an ensemble of structures computed from a single NMR dataset). This aspect of the representation allows us to describe model uncertainty resulting from the incompleteness of input information; such ensembles are distinct from multiple states that represent actual variations in the structure, as implied by experimental information that cannot be accounted for by a single representative structure (Schneidman-Duhovny et al., 2014; Schroder, 2015). Thus, a generalized representation, already implemented in PDB-Dev (Burley et al., 2017; Vallat et al., 2018), allows us to encode an ensemble of multi-scale, multi-state, and time-ordered models.

Second, information can be used to construct and compute a value of a scoring function. The scoring function quantifies the degree of a match between a tested model and the input information, for example whether a distance in a model satisfies input information that we actually have about the distance, such as a Nuclear Overhauser Effect or chemical cross-link observation. The most common scoring function is a weighted sum of spatial restraints; each restraint is a function of the deviation of the computed property of a model from its measurement. Consequently, the greater this deviation, the less consistent is the model with the input information - and the worse the score. Optimization of the score then produces models that satisfy the encoded information as well as possible; a good-scoring model is a model that sufficiently satisfies input information by some definition (see “good-scoring models” in Box 3). Examples of spatial restraints include a potential energy function from a molecular mechanics force field, upper distance bounds in NMR spectroscopy, target functions in X-ray crystallography, and a correlation coefficient between a model and an electron microscopy map. The most objective scoring function is a Bayesian posterior model density, in which data likelihoods act as spatial restraints and noise models are effectively their weights (Box 2).

Box 3: Glossary.

Modeling: the process of converting input information into a model and its uncertainty.

Input information: experimental data and prior models used for computing a model.

Prior models: physical theories, statistical preferences, and other models (eg, X-ray structures and comparative models of subunits in a complex) used for computing a model.

Spatial restraint: a function that quantifies the degree of consistency between a model and a single piece of information; often expressed as the squared difference between the model and target value of some spatial feature, such as a distance in a traditional least-squares approach, or as a data likelihood or prior in a Bayesian approach.

Scoring function: a function that quantifies the degree of consistency between a model and input information; often expressed as a weighted sum of spatial restraints in a traditional least-squares approach or as a posterior model density in a Bayesian approach.

Model representation: the set of variables whose values are determined by modeling based on the input information.

Representation precision: a descriptor of the detail in the representation of the structural model (eg, atomic models consist of atoms).

Sampling precision: granularity of sampling used to find models consistent with input information. Model accuracy or error: the deviation of the model from the “truth”.

Good-scoring model: a model that is sufficiently consistent with given information; for example, a model whose score is better than some threshold on the scoring function used for sampling, or a model that is within all error bars on the input data. In a truly Bayesian approach, there is in principle no need to consider only good-scoring models as each sampled model can be weighted by its posterior probability.

Ensemble of models: a sample of sufficiently good-scoring models.

Precision or uncertainty of a model or ensemble of models: a measure of variability of the ensemble of models.

Single-state model: a model that specifies a single structural state and value for any other parameter.

Multi-state model: a model that specifies two or more structural states in the samples used for determining input information and values for any other parameter.

Box 2: Bayesian inference for scoring alternative models.

This solution came from a man with no direct connection to the problems of molecular cell biology. Thomas Bayes was an eighteenth century Presbyterian minister, who in his later life spent a significant amount of his spare time considering the “Doctrine of Chances”, or probability theory. In essence, he understood that the probability of a model can be updated by iteratively considering additional information. For example, if “Happy Gallop” has won ten of his last twenty horse races, we tend to be ambivalent as to his chances of trotting to a comfortable win in his next race. However, what if one found out that when a particular jockey had ridden him, the horse won every one of those races - and that this jockey will be riding him in the next race? Then this information modifies upwards our estimate of him being first past the post. The corresponding formalization is Bayesian inference, a method of statistical inference in which Bayes’ theorem is used to update the probability for a hypothesis as more information becomes available. As a structural biology exemplar, if we observe a cross-link between two residues, one can take this observation explicitly into account in formulating the likelihood of the structure having a distance between these two residues that is less than the maximal length of the cross-linker (Molnar et al., 2014). When sufficient information is available, the structure can be determined with high precision. An elegant and insightful application of Bayesian inference was described for determining protein structures based on NMR data (Rieping et al., 2005).

Formally, the posterior probability of model M given data D and prior information I isp(M|D,I) α p(D|M,I) • p(M|I). The model, M, consists of a structure X and unknown parameters Y, such as noise in the data. The prior p(M|I) is the probability density of model M given I. The prior reflects information such as excluded volume, statistical potentials, and a molecular mechanics force field. The likelihood function p(D|M,I) is the probability density of observing data D given M and I, and can be defined as a product over the individual measurements, p(D|M,I) = Π_i=1 N(d_i|f_i(X),σ_i), where f_i(X) is a forward model that predicts the data point d_i in D that would have been observed for structure X in an experiment without noise; N(d_i| f_i (X),σ_i) is a noise model that quantifies the deviation between the predicted and observed data points. A Gaussian noise model is often used, N(d_i|f_i(X),σ_i) α exp (−[d_i − f_i(X)]²/2σ_i²), where σ_i is the noise parameter in Y that can optionally be determined as part of the model. Finally, a Bayesian scoring function is defined as the negative logarithm of the posterior probability density: S(M) = –log p(M|D,I). In the Bayesian view, the output model is in fact best equated to the posterior model density that specifies a distribution of alternative single models Mwith varying probabilities, not a single model (although single representative or average models can always be proposed based on the posterior model density).

A key advantage of defining the posterior model density in a Bayesian fashion, compared to traditional least-squares-scoring functions, is that it allows for objective mixing of different types of information (ie, balancing varying uncertainties of varying input information), which is an essential requirement for integrative modeling. As a result, the output models tend to be more accurate, with more accurate estimates of their uncertainty. A Bayesian approach allows us to quantify model uncertainty in a strict sense. Repeated nonlinear least-squares minimization may produce a diverse set of solutions, but its spread will mainly reflect the power of the optimizer. Another advantage is that we know how to deal with the nuisance parameters Y, whereas least-squares minimization needs to invoke additional recipes, such as cross-validation. The Bayesian approach is also relatively robust in terms of the specific parameterization of the representation of M. Finally, multiple choices about model representation and scoring function can in principle be quantified and compared using model selection criteria (Viswanath and Sali, 2019), such as the model evidence (Knuth et al., 2015).

Third, information can be used to constrain the model search space. Given information that your keys were most likely lost in your house, you can focus your search to the house, without completely excluding other areas, just in case. Although rarely computationally feasible, the best search is a systematic enumeration of a defined search space, going through every possible model one by one with sufficient granularity. In practice, other methods, such as stochastic sampling via a Monte Carlo scheme (Allen and Tildesley, 1989; Metropolis, 1953), are often used. As an example, when modeling the quaternary structure of a complex, information that a certain domain spans the membrane can be used to constrain that domain’s position only to the membrane during sampling (Alber et al., 2007a; Alber et al., 2007b).

Fourth, some information can be used for filtering good-scoring models after they are produced by searching. Such use is often the case for information that is computationally expensive to incorporate into a scoring function, which is commonly evaluated thousands or millions of times during sampling. An example is using a negative-stain electron microscopy class of a binary complex to filter out all but those molecular docking solutions whose 2D projections match the negative-stain electron microscopy class (Fernandez-Martinez et al., 2016; Fernandez-Martinez et al., 2012; Shi et al., 2014; Velazquez-Muriel et al., 2012).

Fifth, some information can be used only to validate the good-scoring models, without changing or filtering them. Just like scoring and filtering, validation also depends on assessing a degree of consistency between a model and some information not used to compute the model. An example is testing whether or not a site-directed mutagenesis phenotype is consistent with a model (eg, whether or not a mutation in a predicted catalytic site actually kills the function in an experiment).

An occasional criticism of integrative structural modeling is that it produces “only a model, and I don’t even know what it means”. But this judgement is rash, because every structure is a model, each one of which is computed based on some information as outlined above. In other words, if it is not understood how a structure is determined, there is a tendency to call it a model rather than a structure; it also tends to be called a model when the expected uncertainty is relatively high or even unknown (eg, when the uncertainty of data is not known). Hence, this Primer: it makes no fundamental difference if the molecular model is computed “only” from X-ray crystallography data, “only” from electron microscopy particle images, or from some combination of varied data, so long as the uncertainty of the model is properly quantified and taken into account when interpreting the model (Schneidman-Duhovny et al., 2014). If anything, because integrative modeling can take all the available information into account, integrative structures are in principle more accurate, precise, and complete than structures based on only a subset of information (Lasker et al., 2010; Lasker et al., 2009). Every piece of data, regardless of its precision, is useful if it is not over-interpreted.

An Illustrative Example: Integrative structure determination of the nuclear pore complex

The existing toolbox (Table 2) has already successfully produced integrative structures for a large number of complex systems, all of which were refractory to traditional methods of structural biology (Figure 1). For convenience, however, we focus mainly on one illustrative example: the yeast nuclear pore complex (NPC), structures for which have been solved using integrative structural techniques. Biologically, the NPC encapsulates many of the challenges presented individually by other assemblies. The NPC is a large (50 – 100 MDa) octagonally symmetric cylindrical macromolecular assembly, consisting in yeast of ~500 copies of 30 different structured and intrinsically disordered proteins collectively termed nucleoporins (Alber et al., 2007a; Alber et al., 2007b; Beck and Hurt, 2017; Knockenhauer and Schwartz, 2016). Embedded in the nuclear envelope, it is the only known conduit for trafficking between the nucleoplasm and cytoplasm, mediating the active exchange of a large range of select proteins and RNAs. As such, the NPC interfaces with the nucleoplasm, cytoplasm, and both the membrane and perinuclear cisterna of the nuclear envelope. Thus, it directly interacts with enormously diverse macromolecules, including transmembrane and lumenal nuclear envelope proteins, cytoplasmic proteins, chromatin and nuclear proteins, and ribonucleoproteins. These associations can exist in a large dynamic range, from ultrafast (such as with transported macromolecules) to ultrastable (such as between scaffold components in the NPC) (Baade and Kehlenbach, 2018; Beck and Hurt, 2017; De Magistris and Antonin, 2018; Knockenhauer and Schwartz, 2016; Raices and D’Angelo, 2012). It is this diversity that also presents a string of formidable challenges to traditional structure determination approaches, as the NPC is by nature huge, flexible, heterogeneous in shape and composition, and highly dynamic (Beck and Hurt, 2017; Knockenhauer and Schwartz, 2016). Thus, we chose by necessity to solve structures for its subcomplexes and the entire NPC assembly using integrative approaches.

Table 2:

Software resources for integrative modeling.

Program	Functionality	Web Site	Reference
ISD	Bayesian modeling based on NMR data		(Rieping et al., 2005)
IMP	Integrative modeling	integrativemodeling.org	(Russel et al., 2012)
Rosetta	Integrative modeling	rosettacommons.org	(Das and Baker, 2008)
ISDB	Integrative modeling	plumed.org	(Bonomi and Camilloni, 2017)
power	Integrative modeling	lbm.epfl.ch/resources/	(Degiacomi and Dal Peraro, 2013)
cMNXL, Jwalk/MNXL	Integrative modeling	topf-group.ismb.lon.ac.uk/Software	(Bullock et al., 2018a; Bullock et al., 2018b)
PyRy3D	Integrative modeling	genesilico.pl/pyry3d/	J. M. Kasprzak, M. Dobrychtop, J. Bujnicki
PGS	Modeling genome structure	github.com/alberlab/PGS	(Hua et al., 2018)
TADBit	Modeling genome structure	sgt.cnag.cat/3dg/tadbit/	(Serra et al., 2017)
MDFF/NAMD	Fitting of molecular models into EM maps using MD simulations	ks.uiuc.edu/Research/mdff	(Trabuco et al., 2008)
ATSAS	Integrative modeling using SAXS	embl-hamburg.de/biosaxs	(Franke et al., 2017)
iFoldRNA	Integrative modeling of RNA	iFoldRNA.dokhlab.org	(Sharma et al., 2008)
HADDOCK	Integrative modeling using docking and data derived restraints	haddock.science.uu.nl	(Dominguez et al., 2003)
ATTRACT-EM	Integrative modeling using docking and EM	attract.ph.tum.de	(de Vries and Zacharias, 2012)
DireX	Flexible fitting of EM maps with data derived distance restraints.	schroderlab.org/software/direx/	(Wang and Schroder, 2012)
MDFit	MD based integrative	smog-	(Ratje et al., 2010)
	modeling using EM maps	server.org/SBMextension.html#mdfit
FPS	Integrative modeling using FRET data	www.mpc.hhu.de/en/software/fps.html	(Kalinin et al., 2012)
XPLOR-NIH	Structure determination using NMR data	nmr.cit.nih.gov/xplor-nih/	(Schwieters et al., 2018)
PatchDock	Molecular docking by shape complementarity	bioinfo3d.cs.tau.ac.il/PatchDock/	(Schneidman-Duhovny et al., 2005)
iSPOT	Structure determination using SAS, footprinting and docking	www.theyanglab.org/ispot/	(Hsieh et al., 2017)
BCL	Various servers for integrative modeling	meilerlab.org/index.php/servers	(Woetzel et al., 2011)
ChimeraX	Model visualization	rbvi.ucsf.edu/chimerax	(Goddard et al., 2018)
VMD	Model visualization	ks.uiuc.edu/research/vmd	(Humphrey et al., 1996)
Protein Model Portal	Portal to atomic models of proteins	proteinmodelportal.org	(Haas et al., 2013)
PDB-Development	Archiving of integrative structures	pdb-dev.wwpdb.org	(Burley et al., 2017)

The five ways of converting input information into a model, outlined above, are conveniently described as an iterative four stage process (Figure 2): (i) gathering input information; (ii) converting input information into system representation and spatial restraints; (iii) searching for models that satisfy the restraints; and (iv) validating the model. Next, we describe these four stages, as applied primarily to the NPC.

Figure 2: Description of the iterative integrative modeling workflow.

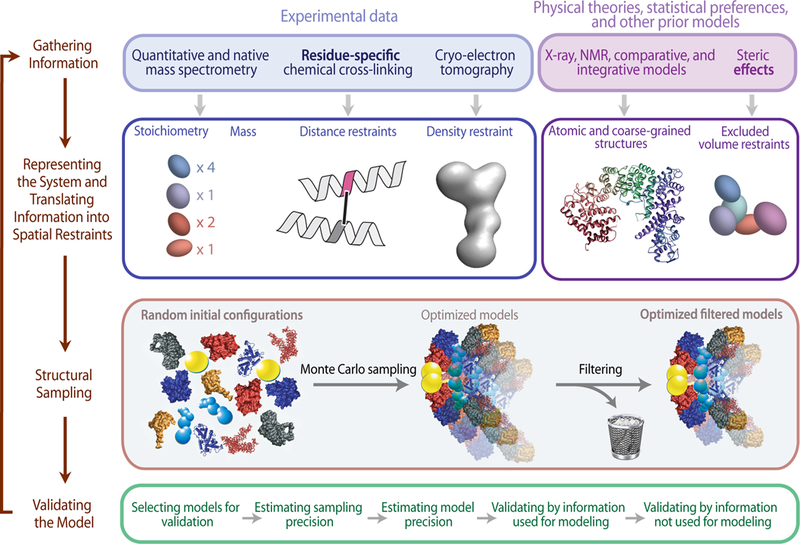
As illustrated, the four stages include: (1) gathering all available experimental data and prior information; (2) translating information into representations of assembly components and a scoring function for ranking alternative assembly structures; (3) sampling structural models; and (4) validating the model. In this example, representations of the components of a complex are based on models of its components. Some component representations are coarse-grained by using spherical beads corresponding to multiple amino acid residues, to reflect the lack of information and/or to increase efficiency of structural sampling. The scoring function consists of spatial restraints that are obtained from CX-MS experiments and a cryo-electron tomography density map. The sampling explores both the conformations of the components and/or their configuration, searching for those assembly structures that satisfy the spatial restraints as well as possible. The result is an ensemble of many good-scoring models that satisfy the input data within acceptable thresholds. The sampling is then assessed for convergence, models are clustered, and evaluated by the degree to which they satisfy the input information used to construct them as well as omitted information. The protocol can iterate through the four stages until the models are judged to be satisfactory, most often based on their precision and the degree to which they satisfy the data. Finally, the models and data are deposited into PDB-Dev (https://pdb-dev.wwpdb.org) (Burley et al., 2017; Vallat et al., 2018).

Stage 1: Information gathering

Ideally, we aim to collect all the kinds of information, at a sufficient depth and granularity, necessary to solve our structure at the highest precision (ie, smallest uncertainty). Practically speaking though, and particularly for difficult biological problems, methodological limitations mean that we often do not have the luxury of using the data we would like to have, but only the data that we can actually obtain. Nevertheless, there is still some flexibility available, in terms of deciding between which methods will give the most “bang for buck”, that is, the most useful information for modeling per unit effort.

For NPCs, the ideal information might be an X-ray crystallographic dataset for an entire native purified or reconstituted assembly. However, as indicated above, the nature of the assembly precludes gathering such information, at least for the moment. So, what information can we collect that would be most useful? This decision should be a continuing dialog between the experimentalists and modelers. In our first effort to solve an NPC structure, almost two decades ago, the available technologies were significantly more limiting than today in terms of both the amount and precision of the information; cryo-electron tomography maps had resolutions of ~100 Å (Akey and Radermacher, 1993; Beck et al., 2004; Hinshaw et al., 1992; Yang et al., 1998), and few atomic structures of nucleoporins were available (Brohawn et al., 2009). These limitations in turn set a bound on the precision of the first structure published in 2007 (Figure 3) (Alber et al., 2007b).

Figure 3: Integrative structures of the yeast NPC.

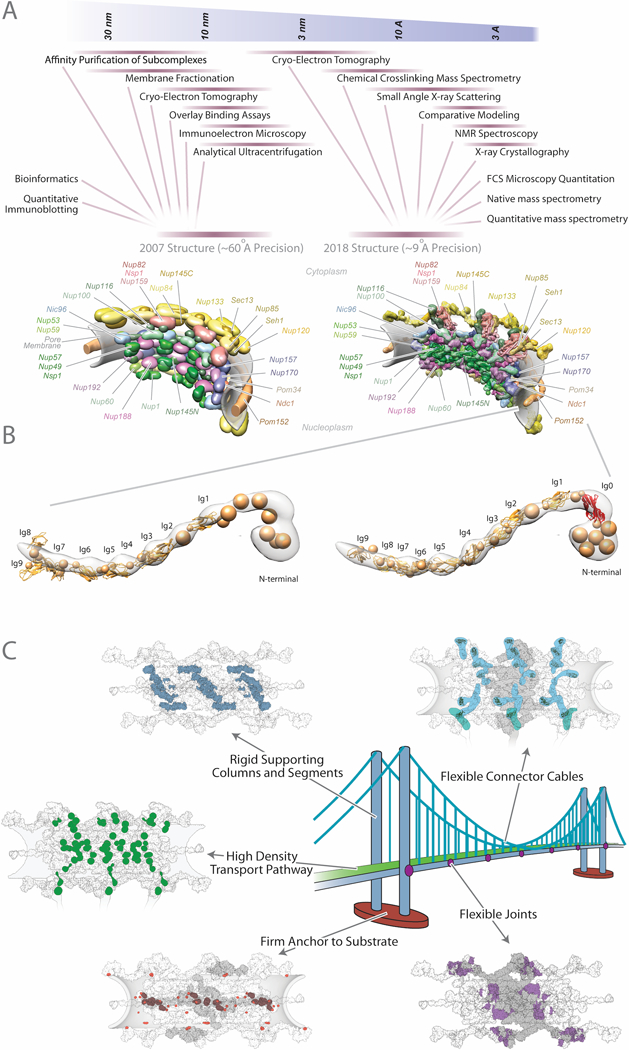
(A) A comparison of the integrative NPC structures determined in 2007 (Alber et al., 2007b) and 2018 (Kim et al., 2018) illustrates how the integration of a larger amount of more precise data led in turn to a structure with a higher precision. (B) A comparison of two representative Pom152 models, without and with an atomic model of the first Ig domain (Hao et al., 2018; Upla et al., 2017), shows how consideration of additional information (ie, knowledge of an atomic structure of the first Ig domain (Ig0)) into the representation of a protein improves its model. (C) Insights into the architectural principles and functions of the NPC. Five examples of analogous structural principles shared by an NPC and a suspension bridge are each illustrated by a specific color showing the features sharing these principles, in the NPC by panels showing three of the eight spokes of an NPC viewed from its axial center: (i) a firm anchor to a substrate (brown / orange), (ii) rigid supporting columns and segments (dark blue) that (iii) appear somewhat flexibly jointed to each other (purple), (iv) flexible connector cables that tie together all the structural elements (light blue), (v) collectively forming a transport pathway supporting a high density of trafficking routes (green).

An important benefit of integrative structure determination is that it facilitates the use of information from experiments that have generally not been used for structure determination. As a case in point, for our first coarse NPC structure, one such class of data were affinity capture experiments. In these assays, nucleoporins are genomically tagged with an affinity handle, allowing them to be copurified with subsets of other nucleoporins whose identity is then usually determined using mass spectrometry. Such experiments had been used with great success to identify other nucleoporins and even infer nearest neighbors (Grandi et al., 1993; Grandi et al., 1995a; Grandi et al., 1995b; Siniossoglou et al., 1996), but they had not been interpreted as formal spatial restraints that could be used to compute a structure. Nevertheless, these data could in fact be used as restraints; each affinity capture result, which we termed a “composite”, defined the composition of a sample of one or more complexes that share the tagged protein. Thus, a model can be scored for consistency with this data by ascertaining whether or not it contains at least one of the possible complexes implied by the composite (Alber et al., 2007a; Alber et al., 2008). However, because each composite carries relatively little spatial information, the experimentalists were challenged to produce a large number of different composites, densely covering all the nucleoporins. In other examples of input information, combined experimental and bioinformatic information defined transmembrane regions in three nucleoporins, allowing us to restrain those regions to the NPC’s pore membrane; sequence-based definition of domains and analytical ultracentrifugation of the nucleoporins informed the degree to which they were spherical versus elongated, giving us an approximate shape and size for every nucleoporin; and immunoelectron microscopy provided axial and radial distributions of the nucleoporins, albeit with a high uncertainty corresponding to approximately a third of the size of the NPC. Finally, once enough information had been gathered, integrative modeling allowed us to convert it into the molecular architecture of the complete assembly (Alber et al., 2007b). These examples illustrate how integrative modeling facilitates generating and using more information, and thus solving harder structure determination problems (Alber et al., 2007a; Alber et al., 2008; Sali et al., 2015).

With the coarse molecular architecture of the NPC in hand, we embarked on improving it by gathering additional and higher resolution data for higher resolution representations of nucleoporins and for more accurate and precise modeling of their configuration in the whole assembly (Figure 3A). An impressive repertoire of nucleoporin atomic structures was produced by X-ray crystallography and NMR spectroscopy, via the Protein Structure Initiative and sterling efforts from many groups (reviewed in refs. (Brohawn et al., 2009; Knockenhauer and Schwartz, 2016)). In addition, we determined the integrative structures of Pom152, Nup133, the heptameric Nup84 outer ring complex, and the cytoplasmic Nup82 export platform (Fernandez-Martinez et al., 2016; Kim et al., 2014; Shi et al., 2014; Upla et al., 2017). These integrative structures were informed by two additional types of data. First, we required that a good model had a projection whose shape matched 2D negative-stain electron microscopy class averages (Fernandez-Martinez et al., 2012; Velazquez-Muriel et al., 2012). Second, we also required that a good model reproduced the distances implied by chemical cross-links, detected through cross linking - mass spectrometry (XL-MS) (below).

With a more detailed representation of the NPC components in hand, two experimental technological advances enabled us to solve the 3D jigsaw puzzle of how these components fit together into a much more precise NPC depiction. The first is the dramatic improvements in cryo-electron microscopy, which needs no further explanation here, having revolutionized structural biology in the last few years (Callaway, 2015; Danev and Baumeister, 2017; Murata and Wolf, 2018; Wells and Marsh, 2018). These improvements allowed us to produce a ~28 Å density map of the entire NPC. The second is XL-MS, where substantial improvements in MS sensitivity have allowed investigators to identify large numbers of residues in peptides from a protein or complex that can be chemically cross-linked together, so setting an upper limit on the native distance between those residues based on the length of the cross-linker (Fischer et al., 2013; Gingras et al., 2007; Lauber et al., 2012; Leitner et al., 2012a; Leitner et al., 2012b; Leitner et al., 2010; Rappsilber, 2012; Sinz, 2006; Walzthoeni et al., 2013). These improvements allowed us to generate ~3100 unique cross-links in the entire NPC. We also adopted several complementary experimental methods to unambiguously establish the NPC’s composition and stoichiometry. Finally, together with the vastly improved models of NPC components and other information almost entirely distinct from that used for the first coarse structure, integrative modeling was able to produce a significantly more detailed structure of the NPC (Figure 3A) (Kim et al., 2018).

Any output structure will only be as good as its input information (“garbage in, garbage out”). We still needed a physical sample suitable for application of the new technologies discussed above, as previous methods to isolate NPCs were time-consuming and cumbersome, limiting throughput. We thus adapted our affinity capture approaches to rapidly and gently isolate preparations of entire native NPCs that were suitable for higher throughput electron microscopy and XL-MS analyses. The quality of samples for analysis is clearly crucial and integrative (or indeed any other) structural approaches cannot materialize a precise structure from low quality starting material. Even so, there are clear limitations to most samples that must be removed from their native environments for analysis. For the NPC, we remain aware that depletion of chromatin, pore membrane, and a cloud of accessory factors during the purification may have changed the structure compared to its completely native state(s).

More information can generally improve a representation of the system, its model, and the uncertainty estimate. Thus, most structures are a work in progress, especially if initially determined at lower resolution. It is often easy to overlook some valuable information that could have improved the precision of the structure. For example, we did not use our own new NMR structure (Upla et al., 2017) of an Ig domain in the pore membrane nucleoporin Pom152 for assigning the folds of the other Pom152 domains, as publicly available threading web servers could not consider our new structure at the time. This resulted in a lower precision structural model of Pom152 that lacked high resolution representation of a tenth Ig domain (Hao et al., 2018); simply updating our modeling with an atomic representation of this domain can result in an improved model of the entire Pom152 (Figure 3B). Thus, a structure and its validation should be continuously refined to reflect the data and modeling methods that are available at any given moment in time. Importantly, the structure should not be overinterpreted beyond its uncertainty, so that the key functional and evolutionary conclusions survive any adjustments in its depiction as new data and modeling methods become available (cf, improving the precision of the Pom152 model has nevertheless not altered our overall interpretation of the NPC structure (Kim et al., 2018)).

Stage 2: Converting input information into system representation and spatial restraints

As mentioned already, information from the first stage can be parsed in two ways at this second stage - into either a system representation or restraints. Deciding how to use input information for modeling is a point of much communication and synergy between the experimentalists and modelers, to make sure that input information is optimally interpreted.

Defining the representation of the modeled system is a non-automated task that depends on the available information, the experience of the researcher, and trial-and-error (Box 1); in particular, the granularity of representation should be commensurate with the amount and precision of information. The representation must also facilitate (i) answering biological questions of interest, (ii) constructing an accurate and efficiently computed scoring function to quantify the consistency of a model with the input information, and (iii) sampling of alternative models (Viswanath and Sali, 2019).

The goal of the first integrative structure determination of the NPC was to map the single static coarse configuration of the component nucleoporins, commensurate with the information available at the time (Alber et al., 2007a; Alber et al., 2007b). Thus, we used a coarse-grained representation of the nucleoporins: each nucleoporin was represented either by a single bead whose radius depended on the number of residues in its sequence or a flexible string of a small number of beads corresponding to individual sequence domains. In the absence of atomic structures or comparative models for most of the constituent nucleoporins, these representations were informed primarily by sequence comparisons to delimit individual domains and ultracentrifugation to inform the globularity of the shape. Subsequently, as X-ray, NMR, and integrative structures of the nucleoporins and their subcomplexes were determined (Knockenhauer and Schwartz, 2016), we were able to use these structures either as rigid or somewhat flexible pre-determined shapes during their computational assembly into the structure of the entire NPC (Kim et al., 2018). In addition, we incorporated information about the nuclear envelope by representing it as a rigid layer of defined shape, size, and thickness that helps to organize the nucleoporins.

Spatial restraints are defined based on a subset of input information, considering the uncertainty in this information as much as possible, and then summed into the scoring function. For the most recent NPC structure, the restraints relied on chemical cross-links, the cryo-electron microscopy density map, immuno-electron microscopy localizations, excluded volume considerations, sequence connectivity, the shape of the pore membrane, and sequence-based membrane localizations (eg, the nuclear envelope can only be spanned by transmembrane regions in a fraction of nucleoporins). Definition of the resulting restraints from different types of data was facilitated by the use of a multi-scale representation of the NPC components; for example, chemical cross-links restrained distances between pairs of residues, while membrane localizations constrained entire domains to the membrane (Kim et al., 2018).

An advantage of integrative approaches is that they can include any information about flexible or even completely unstructured regions, such as intrinsically disordered regions (IDRs) in proteins, although they cannot be seen in X-ray and electron microscopy density maps. This advantage is an important consideration, because significant IDRs are found in as much as a third of eukaryotic proteins and play fundamental and diverse roles in protein interactions and regulation (Oldfield and Dunker, 2014; Sharma et al., 2015; Uversky, 2017). IDRs make up one-fifth of the yeast NPC’s mass and are critical to its structural integrity and transport functionality (Fischer et al., 2015; Kim et al., 2018; Knockenhauer and Schwartz, 2016). Thus, being able to depict these regions as flexible strings of beads was another benefit to choosing the integrative structure determination route.

The scoring function allows us to account for uncertainties and mistakes in input information, but the same cannot be said of representation. That is, information that is used for representation must be highly certain, while scoring function can readily incorporate uncertain information. For example, an incorrect stoichiometry or assuming an incorrect rigid protein shape will result in an incorrect representation that is in turn likely to result in incorrect models. In contrast, a cross-linking dataset with some incorrect cross-links can still be used successfully via appropriate cross-linking restraints and soft thresholds in the scoring function. Fortunately for the experimentalist, the majority of the input information is usually used to formulate the scoring function, and near perfection is only required for a subset of information going towards the representation.

Potential problems with converting input information into representation and scoring can be illustrated by the considerations needed when modeling a generic, pan-species version of the system based on data about the system from different species. Using data from different species to model a single structure is clearly appropriate only if the differences in composition, stoichiometry, and structure between the species are smaller than the uncertainties in the data. For example, NPCs from different organisms can have very different stoichiometries, morphologies, and even compositions. The average human NPC is approximately twice the mass of that from yeast, and also substantially differs in the composition and arrangement of its more peripheral complexes as well conformations of its components (Alber et al., 2007b; Kim et al., 2018; Kosinski et al., 2016; Mosalaganti et al., 2018; Ori et al., 2013). Exemplifying these pitfalls, a recent generic model meant to represent “the” NPC scaffold, generated by amalgamation of human and fungal data (Lin et al., 2016), is thus not an accurate representation of either a fungal or human NPC.

Stage 3: Searching for models that satisfy the restraints

The purpose of the third stage is to find a sample of all models that are sufficiently consistent with input information, as quantified by the scoring function. If a Bayesian scoring function is used (Box 2), the goal of sampling methods is to accurately sample the posterior model density. The search for good-scoring models is often achieved by a stochastic sampling of alternative structures, avoiding the biases and limitations intrinsic to searches for good-scoring models by humans. The sampling must be done at a precision that is higher than needed for interpreting the models. Potentially, the sampling can be made more efficient by limiting or guiding it based on a subset of input information (cf, the “search for keys”, above). For example, the search for good-scoring NPC structures relied on a stochastic Monte Carlo scheme that benefited from being constrained to solutions with the 8-fold rotational symmetry of the NPC, an essentially universal feature of the assembly. Optionally, the sampling can be followed by filtering the good-scoring models from sampling based on some information not used for representation, scoring, or sampling. Such filtering may be useful when using the corresponding information for scoring is computationally costly. Using information only for filtering, however, requires that the sampling generates solutions consistent with the filter even in the absence of the corresponding information from the scoring function considered during sampling. Notably, not all existing modeling methods aim to find a representative sample of all good-scoring solutions, thus vastly overestimating the precision of their solutions. A good example of this pitfall is when modeling is done in one’s head, which assumes one can think of all possible models, even though in reality many unimagined models will simply go unexplored. Computer-assisted sampling and estimates of sampling precision can avoid such biases (Viswanath et al., 2017b).

A large variety of sampling methods have been developed. Enumeration of all possible solutions at a sufficiently high precision is an ideal sampling method, as it ensures no solution is missed (Lasker et al., 2012; Lasker et al., 2009), but it is generally not feasible for large systems with many degrees of freedom that need to be sampled finely. Efficient and well-known methods for local refinement of structures include conjugate gradients and steepest descent (Press et al., 2007). Often, however, the structural sampling does not benefit from knowing a starting structure that is close to the correct model, and thus stochastic sampling methods need to be employed. A large variety of such methods have been developed over the years, including many versions of Monte Carlo simulated annealing, replica exchange, Gibbs sampling, and Hamiltonian Monte Carlo (Betancourt, 2017). For stochastic sampling methods, it is imperative that tests of thoroughness of structural sampling are performed (below) (Viswanath et al., 2017b).

Stage 4: Validating a structural model

To avoid overinterpretation of a model, it is essential that a model is validated. Formal model validation can follow five steps: (i) selecting the models for validation; (ii) estimating sampling precision; (iii) estimating model precision; (iv) quantifying the degree to which a model satisfies the information used to compute it; and (v) quantifying the degree to which a model satisfies relevant information not used to compute it. It is anticipated that the nascent worldwide PDB effort on integrative methods will refine and implement a set of specific procedures for these steps and apply them to every integrative structure during its deposition into the PDB (Vallat et al., 2018), as is already the case for traditional atomic structures (Henderson et al., 2012; Montelione et al., 2013; Read et al., 2011; Trewhella et al., 2013; Young et al., 2017).

In the first step, we select sufficiently good-scoring models produced by sampling for validation (the ensemble). For example, a good-scoring model may be defined as a sampled model that satisfies all restraints or sets of restraints within their own uncertainties (eg, we may require that the correlation coefficient between a model and the electron microscopy density map is at least 0.8 and that a model violates at most 4% of chemical cross-links). If no such models were produced, we need to reconsider various aspects of modeling: perhaps the input information was not as precise as presumed, representation of the system was not sufficiently flexible (eg, too coarse-grained or too few states in a multi-state model), or sampling was insufficient.

In the second step, the sampling precision can be estimated for stochastic sampling methods by splitting the ensemble of models into two independent sets, followed by quantifying the difference between the two sets. The sampling precision can then be defined as this difference, in a similar fashion to that used for estimating the resolution of electron microscopy density maps (van Heel and Schatz, 2005). It is important that we properly estimate the sampling precision (uncertainty), because clearly only the features of the model larger than the sampling precision are well estimated (Viswanath et al., 2017b), just as traditional microscopy can only map features larger than the resolution of the microscope. When using stochastic sampling methods, sampling precision may often be increased simply by increasing the number of independently computed models. High sampling precision is necessary but not sufficient for exhaustive sampling (Gelman and Rubin, 1992; Viswanath et al., 2017b).

In the third step, model uncertainty (precision) is estimated. The most explicit description of model uncertainty is provided by the set of all models that are sufficiently consistent with the input information (ie, the ensemble). Model precision can be quantified by the variability among the models in the ensemble; in the end, the ensemble can be described by one or more representative models and their uncertainties. For example, good-scoring NPC models cluster in a single cluster with a root-mean-square fluctuation of ~9 Å, quantifying the average degree of uncertainty; importantly, the uncertainty is not distributed evenly across the ensemble, such that some regions were determined at a higher precision than 9 Å and others at a significantly lower precision; thus, even features larger than this estimate should be interpreted with some caution.

It is often convenient if the ensemble structures are clustered based on their structural similarity. As a result, only a structure representative of each major cluster can potentially be used for interpretation. Many clustering methods exist, varying in terms of the criterion used to quantify a similarity between two structures (eg, distance root-mean-square deviation between structure coordinates that avoids the need for structure superposition (Koehl, 2001)) as well as a method for converting such pairwise similarities into clusters (Hastie, 2001); the clustering generally also depends on an arbitrary threshold parameter that determines how many clusters are produced. Minor clusters with few structures might be ignored, especially if the scoring function approximates a Bayesian posterior model density (Viswanath et al., 2017a). In our own work (eg, (Kim et al., 2018; Viswanath et al., 2017b)), we often rely on a threshold-based clustering, where the threshold specifies the maximum distance between a cluster centroid and a model in the cluster (Daura et al., 1999); the clustering threshold is selected such that the number of major clusters is minimized for parsimony, while also requiring that their precision is worse than the sampling precision yet sufficient for interpreting the models.

The model uncertainty reflects both the actual heterogeneity of the physical sample and the uncertainties in the input information, representation, scoring for sampling, sampling itself, and scoring for filtering. It is difficult to deconvolve from each other the impact of these different uncertainties on the model uncertainty; in general, only the total model uncertainty is reported. The uncertainty of how to represent the model in particular is often not considered, but can be large and have a major impact on the model uncertainty. For example, it is often possible to explain the small-angle X-ray scattering (SAXS) profile of a protein in solution within its uncertainty by a single or a small number of structures, even when the actual sample is disordered, because the large number of degrees of freedom in the model relatively easily result in a good fit to the data, given the relatively small amount of the data and its relatively large uncertainty (Carter et al., 2015). A mistake in representation is often not recoverable (eg, when a protein subunit structure is incorrectly assumed to be rigid during modeling a structure of a complex).

As an aside, the accuracy (error) of a model is defined as the deviation of the model from the truth; the accuracy is therefore not knowable when modeling systems without known structures (in benchmarking, reference answers are of course known by design). In contrast, model precision can be estimated. A conservative assumption is that accuracy is no better than model precision. If model error is larger than its estimated uncertainty, the model is incorrect; correspondingly, a model can be deemed correct if its error is within its uncertainty.

In the fourth step, the model is assessed by quantifying the degree to which it satisfies the information used to compute it. For example, the correlation coefficient between our recent NPC structure and the electron microscopy density map that helped compute the structure is higher than 0.92; less than 10% of chemical cross-links are violated; and less than 5% of bead overlaps are larger than the standard deviation of the harmonic excluded volume restraint (Kim et al., 2018).

The fifth step represents perhaps the most convincing test of model validity. In this step, a model is tested against relevant information that was not used to compute it. For example, one can perform a jackknifing test consisting of repetitively omitting a random subset of chemical crosslinks, recomputing the model, and comparing these models against the omitted cross-links, to validate both the model and the cross-links (Brunger et al., 1993). This test is even more powerful when some information is used only for validation. For example, we took advantage of omitting the vast majority of the 2007 NPC data from the most recent structure determination of the NPC, allowing us to use this data as well as the 2007 NPC topology map to validate the 2018 structure (Kim et al., 2018) (Figure 3A).

The integrative approach is unique in providing an especially strong test of model validity: when the structure is consistent with multiple types of data that were collected independently for physically different samples using different methods, the odds of artefacts are reduced compared to structures relying on a single type of information. An example of such an artefact are the false depictions of the NPC’s organization that have arisen from reliance on biologically irrelevant intermolecular contacts in protein crystals (Debler et al., 2008; Hsia et al., 2007).

Lastly, even the input data themselves can be validated with respect to each other, via a structural model based on these data. A piece of data can be inconsistent with a model, and thus with other data, when a mistake in model representation, scoring, or sampling is made. More precisely, data can be violated when the model is represented with too few degrees of freedom, data is compared against the model too stringently, or the sampling fails to find an existing good-scoring model. As an example of a representational error, a violation of a chemical cross-link may occur when a rigid subunit in a complex is not allowed to relax, or a single-state instead of multi-state representation is used (as is required when one or more physical samples from which the data are derived contain a mixture of structures). As an example of a scoring error, a violation may also be declared when the data are presumed to be less uncertain (noisy) than they actually are. There are no general protocols for deconvolving possible reasons for a given mismatch between data and a model, although the Bayesian approach shows most promise in this regard (Box 2). Remedies include modeling with alternative representations, scoring functions, and sampling schemes, which in turn often results in a more varied ensemble of good-scoring models and thus an increased estimate of model uncertainty. Most usefully, additional experiments may shed light on the homogeneity of the physical sample(s) and noise in the data. It may be appropriate to discard some data under the explicit assumption that the omitted data applies to non-interesting states or that it is too noisy, although tacitly omitting a subset of data only because a model does not fit it is perhaps one of the worst errors a scientist can make.

Validation is thus key to the iterative nature of the integrative structure determination process (Figure 2), such that the experimentalist and modeler synergize on data and model until consistency among all datasets and the final structure is obtained.

Biological insights from validated structures

The synergistic dialog between experimentalist and modeler continues as validation becomes interpretation, with a subjective but informed consideration of whether or not the structure makes sense in light of current knowledge. If not, the iterative process of information gathering and modeling must continue. After validation is satisfactory, we then move to biological interpretation of our structure.

Ultimately, the true worth of any structure is how informative it is about architectural principles of the modeled system, its assembly and disassembly, its function (ie, interactions with other systems), regulation and modulation of its function, and evolutionary relationships. Even though integrative structures are often determined at resolutions lower than atomic, they can still be informative, or at least more informative than the data on which they are based. Once again, each structure must be interpreted biologically only within its precision. For example, being preoccupied by nanometer-scale features of the 100 nm-diameter 2007 map would completely mistake its purpose primarily as a topological representation of the nucleoporin arrangements in the NPC.

An important tool in the interpretation of any structural model is its visualization and manipulation on a computer screen. However, most existing molecular viewers for atomic structures, such as those deposited in the PDB, are of limited utility, because integrative structures are often represented as ensembles of multi-scale models (with atomistic and coarse-grained representations), multi-state models (allowing for simultaneous multiple states), and ordered states (states related by time or other order) (Sali et al., 2015). Fortunately, the ChimeraX visualization program (Goddard et al., 2018) was developed specifically to support integrative structural models stored in the common mmCIF file format upgraded for integrative models (Vallat et al., 2018). In addition to the models themselves, ChimeraX can also visualize a number of different datasets, such as density maps and chemical crosslinks, thus facilitating an assessment of how well the model fits the data.

Structures of the NPC and its subcomplexes from various organisms (Eibauer et al., 2015; Kim et al., 2018; Kosinski et al., 2016; Mosalaganti et al., 2018; von Appen et al., 2015) have led to a plethora of insights. For example, the overall architecture of the NPC as seen in our recent structure is evocative of the form and function of suspension bridges (Kim et al., 2018) (Figure 3C). In both bridge and NPC, this architecture results in a strong and resilient structure capable of resisting external forces and forces from the enormous transport flux through the pore. Moreover, both structures serve a similar purpose, namely to provide a selective conduit across a barrier. In the NPC, the “roadway” is constructed from anchors that arrange a high density of docking sites lined from cytoplasm to nucleoplasm for cargo-carrying transport factors to follow across the NPC’s central channel (Figure 3C). Future directions will add information about the dynamic behavior of these docking sites and the transport factors, to animate the process of nuclear transport and elucidate its detailed mechanisms. Another insight we obtained is that the entire scaffold of the NPC is made of nucleoporins that share their architecture with those of the major scaffold components of vesicle coating complexes, indicating a common evolutionary origin in a primordial “protocoatomer” (Alber et al., 2007b; Devos et al., 2004; Spang et al., 2017). Such coating complexes currently fall into two structurally distinct families (Dacks and Robinson, 2017; Faini et al., 2013). The fact that the NPC is comprised of representatives of both families suggests that these families evolved first, together with an already differentiated internal membrane system. Intriguingly, this pattern in turn implies that the NPC - and the nucleus as a whole as we know it – may have been among the last organelles to evolve on the path of eukaryotic cellular evolution, rather than being among the first as had been previously assumed (Kim et al., 2018).

The NPC is but one of a large number of structures solved by integrative methods that have been biologically highly informative (Figure 1). Highlights include: the complete structure of the mammalian mitochondrial ribosome large subunit, revealing how the 5S ribosomal RNA has become substituted by a tRNA, and showing how insights into unusual aspects of architectural reorganization can be garnered (Greber et al., 2014a); the complete structure of the 26S proteasome, showing how the lid structure is critical for recruiting and partially unfolding the substrate protein for subsequent proteolysis by the 20S core particle, thus showcasing how functional and catalytic insights can be achieved (Lasker et al., 2012); and visualizing how chromosomes are dynamically positioned in the nucleus and revealing the plasticity of genome structures, showing how integrative methods can be applied at different cellular spatial and temporal scales (Kalhor et al., 2011).

The integrative approach is not restricted to a particular granularity or size of the model. Indeed, the integrative structural solution of two smaller subcomplexes from the NPC, Nup82 (Fernandez-Martinez et al., 2016) and Nup84 (Shi et al., 2014), both around 650 kDa in size, preceded our most recent solution of the entire NPC structure. Similarly, numerous moderately-sized protein structures have also been solved by integration of orthogonal structural data (cf, Figure 1). For example, supplementing data from NMR spectroscopy by additional data from SAXS experiments can produce larger and more accurate protein structure models than NMR spectroscopy on its own (Sunnerhagen et al., 1996). Thus, a flexible-domain structure refinement with both NMR and SAXS data allowed the solution of a structure for the 82 kDa Malate Synthase G enzyme (Grishaev et al., 2008). More recently, a combination of data from NMR spectroscopy, SAXS, and small-angle neutron scattering (SANS) was used to determine the structure for a 34 kDa ternary SXL, UNR, and msl-2 mRNA complex (Hennig et al., 2013). Another elegant method uses augmented NMR NOESY-based restraints, which are often insufficient to calculate an accurate model, with evolutionary residue-residue couplings computed from multiple alignments of related protein sequences (Tang et al., 2015). The largest protein solved in this manner was the 41 kDa E. coli maltose-binding protein, and the method is applicable to even larger systems (Huang et al., 2019).

Outlook

There is much still to be done to improve all aspects of computing, validating, visualizing, archiving, and disseminating integrative structures (Table 2). This task includes automating as much of the modeling process as possible. It would be particularly helpful to develop better methods for objectively finding optimal representations (Viswanath and Sali, 2019; Wagner et al., 2016), given the available input information, including methods for finding the number of different states in multi-state models and optimal coarse-graining. It is also necessary to formulate all conceivable types of structural information in terms of Bayesian data likelihoods, which will facilitate proper relative consideration of varied information during modeling. Modeling will further benefit from improving the efficiency of sampling methods and computing hardware, resulting in a more thorough search for good-scoring models, especially for large systems with many degrees of freedom. Most importantly, a rigorous and extensive validation pipeline for estimating the uncertainty in integrative structures is essential for their proper interpretation. Finally, the field will benefit from a community-wide set of standards for various aspects of integrative modeling, underpinned by an archive for integrative structures as well as the data on which they are based and the modeling protocols, as spearheaded by the nascent PDB-Development community resource (Burley et al., 2017; Vallat et al., 2018). PDB-Development will further strengthen integrative structural biology, by bringing together specialists in disparate experimental methodologies (Table 1), unified by their intent to iteratively and formally combine their data into as informative models of biomolecular systems as possible.

Improving various aspects of integrative modeling, as outlined above, will further expand its applications. It will become possible to obtain useful models of the larger systems, heterogeneous systems, and dynamic processes that actually typify the organization of cells. A particular strength of integrative modeling is its potential to use all information to compute models represented in any fashion, be it single static structures, mixtures of states, molecular networks, dynamic processes, systems of ordinary differential equations, and others. Indeed, the explicit inclusion of dynamic and state-dependent information into integrative approaches holds the promise of breathing life and movement into currently mostly static representations, and so visualize the processes that actually drive living cellular systems. As a result, it is conceivable that integrative modeling will play a key role in mapping entire cellular neighborhoods and even whole cells, thus bridging the gap between biophysical methods focused on molecules and optical microscopies focused on the meso-scale organization of the cell.

As the toolbox of integrative structural biology continues to improve, it will be increasingly applied not only to discover the basic principles of biological systems, but also to drug discovery. As a result, it will allow us to rationally target larger systems, in addition to single proteins. While still largely untapped, the potential for using integrative approaches to translate from bench to bedside is surely among the most exciting new future directions open to the biomedical community (Singla et al., 2018).

Table 3:

Examples of integrative structures (shown in Figure 1).

System name	Input data	Accession	Citation
INO80	17-Å resolution cryo-electron microscopy (EM) map, 212 intra-protein and 116 inter-protein cross-links		(Tosi et al., 2013)
Polycomb Repressive Complex 2 (PRC2)	21-Å resolution negative-stain EM map and ~60 intra-protein and inter-protein cross-links		(Ciferri et al., 2012)1
Large subunit of the mammalian mitochondrial ribosome (39S)	4.9-Å resolution cryo-EM map and ~70 inter-protein cross-links	4CE4	(Greber et al., 2014b)2
RNA polymerase II transcription pre-initiation complex	16-Å resolution cryo-EM map plus 157 intra-protein and 109 inter-protein cross-links		(Murakami et al., 2013)3
Type III secretion system needle	19.5-Å resolution cryo-EM map and solid-state nuclear magnetic resonance (NMR) data	2LPZ	(Loquet et al., 2012)4
Productive HIV-1 reverse transcriptase:DNA primer-template complex in the open educt state	Foerster resonance energy transfer (FRET) positioning and screening using a known HIV-1 reverse transcriptase structure		(Kalinin et al., 2012)2
HIV-1 capsid protein	Residual dipolar couplings and small-angle X-ray scattering (SAXS) data	2M8L, 2M8N, 2M8P	(Deshmukh et al., 2013)5
Human genome	Tethered chromosome conformation capture and population-based modeling		(Kalhor et al., 2011)6
Drosophila genome	Chromosome conformation capture and lamina DamID		(Li et al., 2017)
α-globin gene domain	Chromosome Conformation Capture Carbon Copy (5C)		(Bau et al., 2011)7
Proteosomal lid	Native mass spectrometry and 28 cross-links		(Politis et al., 2014)8
ESCRT-I complex	SAXS, double electron-electron transfer, and FRET		(Boura et al., 2011)
Actin together with the cardiac myosin binding protein C	Crystallographic and NMR structures of subunits and domains, with positions and orientations optimized against SAXS and small-angle neutron scattering data to reveal information about the quaternary interactions		(Whitten et al., 2008)9
[ΨCD]2	Averaged cryo-electron tomography map, NMR	2L1F	(Miyazaki et al., 2010)
Cyanobacterial circadian timing KaiB-KaiC complex	Hydrogen/deuterium exchange and collision cross-section data from mass spectrometry		(Snijder et al., 2014)
Pre-pore and pore conformations of the pore-forming toxin aerolysin	Cryo-EM data and molecular dynamics simulations		(Degiacomi et al., 2013)10
A segment of a pleurotolysin pore map (~11 Å resolution); an ensemble of conformations shows the trajectory of β-sheet opening during pore formation	Cryo-EM, X-ray crystal subunit structures, fluorescence spectroscopy, cross-linking	4V2T	(Lukoyanova et al., 2015)11
Ternary complex of the iron-sulfur cluster assembly proteins desulfurase (orange) and scaffold protein Isu (blue) with a bacterial ortholog of frataxin (yellow)	NMR chemical shifts, SAXS, mutagenesis		(Prischi et al., 2010)12
SAGA transcription coactivator complex	199 inter- and 240 intra-subunit cross-links, several comparative models based on X-ray crystal structures, and a transcription factor IID core EM map at 31 Å resolution		(Han et al., 2014)13
Bacterial (Thermus aquaticus) RNA polymerase-promoter open complex; subsequently validated by a crystal structure (Feng et al., 2016)	FRET		Mekler, 2002 #400}
RNA ribosome-binding element from the turnip crinkle virus genome	NMR, SAXS, EM	DOI: 10.6084/m9.figshare.1295199	(Gong et al., 2015)14
Complex between RNA polymerase II and transcription factor IIF	Deposited crystal structure of RNA polymerase II, comparative models of some domains in transcription factor IIF and 95 intra-protein and 129 inter-protein cross-links		(Chen et al., 2010)15
Human and yeast TFIIH	XL-MS data, biochemical analyses, and previously published electron microscopy maps		(Luo et al., 2015)
40S-eIF1-eIF3 translation initiation complex	X-ray crystallography, EM, XL-MS		(Erzberger et al., 2014)
ATP synthase membrane motor	cryo-EM (~7.8 Å resolution), XL-MS, and evolutionary couplings		(Leone and Faraldo-Gomez, 2016)16
26S proteasome	67 inter-protein and 26 intra-protein chemical cross-links in combination with EM maps	5LN3	(Wang et al., 2017)
Ino80 insert domain bound to the Rbv1/Rvb2 dodecamer	12-Å resolution cryo-EM map, 226 chemical cross-links		(Zhou et al., 2017)
Core of the yeast spindle pole body (SPB)	in vivo FRET, SAXS, X-ray crystallography, EM, two-hybrid analysis		(Viswanath et al., 2017a)2
E6AP/UBE3A-E6-p53 enzyme-substrate complex	XL-MS data of the complex with and without E6	PDBDEV_00000022, PDBDEV_00000023	(Sailer et al., 2018)17
Nucleosome remodeler ISWI	XL-MS, SAXS, protein-protein docking		(Harrer et al., 2018)
Urease activation complex	Mobility-mass spectrometry data		(Eschweiler et al., 2018)
Chromosomal DNA organization	Super-resolution microscopy methods OligoSTORM and OligoDNA-PAINT, Hi-C data		(Nir et al., 2018)18

¹Figure panel reprinted from figure 11 of (Ciferri et al., 2012), used under the terms of the Creative Commons Attribution 3.0 license (https://creativecommons.org/licenses/by/3.0/).

²Figure panel obtained via personal communication and used with permission of the author.

³Panel from Figure 5 of (Murakami et al., 2013). Reprinted with permission from AAAS.

⁴Figure 3 reprinted by permission from Springer Nature Terms and Conditions for RightsLink Permissions Springer Nature Customer Service Centre GmbH: Nature “Atomic model of the type III secretion system needle.” Loquet A, Sgourakis NG, Gupta R, Giller K, Riedel D, Goosmann C, Griesinger C, Kolbe M, Baker D, Becker S, Lange A. Copyright Springer Nature Publishing AG (2012).

⁵Figure 9 reprinted (adapted) with permission from (Deshmukh et al., 2013). Copyright (2013) American Chemical Society.

⁶Figure 6 reprinted by permission from Springer Nature Terms and Conditions for RightsLink Permissions Springer Nature Customer Service Centre GmbH: Nature Biotechnology “Genome architectures revealed by tethered chromosome conformation capture and population-based modeling.” Kalhor R, Tjong H, Jayathilaka N, Alber F, Chen L. Copyright Springer Nature Publishing AG (2012).

⁷Figure 4 reprinted by permission from Springer Nature Terms and Conditions for RightsLink Permissions Springer Nature Customer Service Centre GmbH: Nature Structural & Molecular Biology “The three-dimensional folding of the α-globin gene domain reveals formation of chromatin globules.” Baù D, Sanyal A, Lajoie BR, Capriotti E, Byron M, Lawrence JB, Dekker J, Marti-Renom MA. Copyright Springer Nature Publishing AG (2011).

⁸Figure 2 reprinted by permission from Springer Nature Terms and Conditions for RightsLink Permissions Springer Nature Customer Service Centre GmbH: Nature Methods “A mass spectrometry–based hybrid method for structural modeling of protein complexes.” Politis A, Stengel F, Hall Z, Hernández H, Leitner A, Walzthoeni T, Robinson CV, Aebersold R. Copyright Springer Nature Publishing AG (2014).

⁹Copyright (2008) National Academy of Sciences.

¹⁰Figure 6 reprinted by permission from Springer Nature Terms and Conditions for RightsLink Permissions Springer Nature Customer Service Centre GmbH: Nature Chemical Biology “Molecular assembly of the aerolysin pore reveals a swirling membrane-insertion mechanism.” Degiacomi MT, Iacovache I, Pernot L, Chami M, Kudryashev M, Stahlberg H, van der Goot FG, Dal Peraro M. Copyright Springer Nature Publishing AG (2013).

¹¹Figure 3 from (Lukoyanova et al., 2015) used under the terms of the Creative Commons Attribution 4.0 license (https://creativecommons.org/licenses/by/4.0/).

¹²Figure 6 from (Prischi et al., 2010) used under the terms of the Creative Commons Attribution-NonCommercial-Share Alike 3.0 Unported License (https://creativecommons.org/licenses/by-nc-sa/3.0/).

¹³Figure 7 from (Han et al., 2014) is Copyright (2014) Han Y, Luo J, Ranish J, Hahn S. EMBOpress.

¹⁴Figure 3 from (Gong et al., 2015) used under the terms of the Creative Commons Attribution 4.0 license (https://creativecommons.org/licenses/by/4.0/).

¹⁵Figure 4 from (Chen et al., 2010) used under the terms of the Creative Commons Attribution‐NonCommercial‐NoDerivs License (https://creativecommons.org/licenses/by-nc-nd/3.0/).

¹⁶Figure 6 from (Leone and Faraldo-Gomez, 2016) used under the terms of the Creative Commons Attribution–Noncommercial–Share Alike 3.0 Unported license (https://creativecommons.org/licenses/by-nc-sa/3.0/).

¹⁷Figure 4 from (Sailer et al., 2018) used under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0/).

¹⁸Figure 3 from (Nir et al., 2018) used under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0/).