Data-Trace Types for Distributed Stream Processing Systems

Abstract

Distributed architectures for efficient processing of streaming data are increasingly critical to modern information processing systems. The goal of this paper is to develop type-based programming abstractions that facilitate correct and efficient deployment of a logical specification of the desired computation on such architectures. In the proposed model, each communication link has an associated type specifying tagged data items along with a dependency relation over tags that captures the logical partial ordering constraints over data items. The semantics of a (distributed) stream processing system is then a function from input data traces to output data traces, where a data trace is an equivalence class of sequences of data items induced by the dependency relation. This data-trace transduction model generalizes both acyclic synchronous data-flow and relational query processors, and can specify computations over data streams with a rich variety of partial ordering and synchronization characteristics. We then describe a set of programming templates for data-trace transductions: abstractions corresponding to common stream processing tasks. Our system automatically maps these high-level programs to a given topology on the distributed implementation platform Apache Storm while preserving the semantics. Our experimental evaluation shows that (1) while automatic parallelization deployed by existing systems may not preserve semantics, particularly when the computation is sensitive to the ordering of data items, our programming abstractions allow a natural specification of the query that contains a mix of ordering constraints while guaranteeing correct deployment, and (2) the throughput of the automatically compiled distributed code is comparable to that of hand-crafted distributed implementations.

1. Introduction

Modern information processing systems increasingly demand the ability to continuously process incoming data streams in a timely manner. Distributed stream processing architectures such as Apache Storm [28], Twitter’s Heron [38, 56], Apache Spark Streaming [27, 58], Google’s MillWheel [5], Apache Flink [19, 25] and Apache Samza [26,47] provide platforms suitable for efficient deployment of such systems. The focus of the existing systems has been mainly on providing high throughput, load balancing, load shedding, fault tolerance and recovery. Less developed, however, is a semantics for streaming computations that enables one to reason formally about the correctness of implementations and distributed deployments with respect to a specification, even in the presence of disorder in the input. This is especially important because–as we will discuss in section 2–parallelization and distribution can cause spurious orderings of the data items, and it is therefore necessary to have a formal way of reasoning about these effects. The goal of this paper is to develop high-level abstractions for distributed stream processing by relying on a type discipline that is suitable for specifying computations and that can be the basis for correct and efficient deployment.

Physically, streams are linearly ordered, of course, and computations consume one item at a time. However, this is only one of many possible logical views of streaming data. Indeed, assuming a strict linear order over input items is not the ideal abstraction for computation specification, for two reasons. First, in an actual implementation, there may be no meaningful logical way to impose a linear ordering among items arriving at different processing nodes. Second, for many computations it suffices to view the input logically as a relation, that is, a bag of unordered data items. Such lack of ordering often has computational benefits for optimization and/or parallelization of the implementation. Between linear ordering at one extreme and lack of ordering at the other we have the large space of partial orders and capturing these orders is the main focus of our type discipline.

We use partially ordered multisets (pomsets), a structure studied extensively in concurrency theory [48]. Pomsets generalize both sequences and bags, as well as sequences of bags, bags of sequences, etc., and we have found them sufficient and appropriate for our formal development. To specify the types that capture these partial orders as well as a logical type-consistent semantics for stream computations, we model–inspired by the definition of Mazurkiewicz traces [44] in concurrency theory–input and output streams as data traces. We assume that each data item consists of a tag and a value of a basic data type associated with this tag. The ordering of items is specified by a (symmetric) dependency relation over the set of tags. Two sequences of data items are considered equivalent if one can be obtained from the other by repeatedly commuting two adjacent items with independent tags, and a data trace is an equivalence class of such sequences. A data-trace type is given by a tag alphabet, a type of values for each tag, and a dependency relation.

For instance, when all the tags are mutually dependent, a sequence of items represents only itself, and when all the tags are mutually independent, a sequence of items represents the bag of items it contains. A suitable choice of tags along with the associated dependency relation, allows us to model streams with a rich variety of logical ordering and synchronization characteristics. As another example, consider a system that implements key-based partitioning by mapping a linearly ordered input sequence to a set of linearly ordered sub-streams, one per key. To model such a system the output items corresponding to distinct keys should be unordered. For this purpose, we allow the output items to have their own tags along with a dependency relation over these tags, and a sequence of outputs produced by the system is interpreted as the corresponding data trace. This representation can be easily presented programmatically and is also easily related to physical realizations.

While a system processes the input in a specific order by consuming items one by one in a streaming manner, it is required to interpret the input sequence as a data trace, that is, outputs produced while processing two equivalent input sequences should be equivalent. Formally, this means that a stream processor defines a function from input data traces to output data traces. Such a data-trace transduction is the proposed semantic model for distributed stream processing systems, and is a generalization of existing models in literature such as acyclic Kahn process networks [36, 39] and streaming extensions of database query languages [15, 40]. Our formal model is described in section 3.

In section 4 we propose a programming model where the overall computation is given as an acyclic dataflow graph, where every communication link is annotated with a data-trace type that specifies the ordering characteristics of the stream flowing through the link. In order to make the type annotation easier for the application developer, we restrict our framework to data-trace types that have two features: (1) the traces contain linearly ordered periodic synchronization markers for triggering the output of blocking operations and forcing progress (similar to the punctuations of [40] or the heartbeats of [50]), and (2) the data items of traces are viewed as key-value pairs in order to expose opportunities for key-based data parallelism. To ensure that each individual computational element of the dataflow graph respects the data-trace types of its input and output channels, we provide a set of operator templates for constraining the computation appropriately. For example, when the input data-trace type specifies that the items are unordered, their processing is described by a commutative monoid (a structure with an identity element and an associative, commutative binary operation), which guarantees that the output is independent of the order in which the items are processed.

When a programmer uses these typed abstractions to describe an application, she secures the global guarantee that the overall computation has a well-defined semantics as a data-trace transduction, and therefore its behavior is predictable and independent of any arbitrary data item interleaving that is imposed by the network or the distribution system (Theorem 4.2). Moreover, the operator templates allow for data parallelism that always preserves the semantics of the original specification (Theorem 4.3, Corollary 4.4).

We have implemented data-trace types, operator templates and typed dataflow DAGs in Java as an embedded domain-specific language. Our system compiles the specification of the computation into a “topology” [29] that can be executed using Storm (see section 5). In section 6 we present an experimental evaluation where we address the following questions: (1) Is the code that our framework generates as efficient as a handcrafted implementation? (2) Does our framework facilitate the development of complex streaming applications? To answer the first question, we used a slight variant of the Yahoo Streaming Benchmark [35] and compared a generated implementation (that we built using our typed abstractions) against a handcrafted one. The experimental results show very similar performance. This provides evidence that our approach does not impose a computational overhead, while offering guarantees of type correctness, predictable behavior, and preservation of semantics when data parallelism is introduced. To address the second question, we consider a significant case study on prediction of power usage. This case study is inspired by the DEBS’14 Grand Challenge [22], which we adapted to incorporate a more realistic prediction technique based on machine learning. This application requires a mix of ordering constraints over data items. Our system automatically deals with low-level ordering and synchronization, so our programming effort was focused on the power prediction itself.

2. Motivation

Many popular distributed stream processing systems–such as Storm [28, 54], Heron [38, 56] and Samza [26, 47]–allow the programmer to express a streaming computation as a dataflow graph, where the processing performed by each node is described in a general-purpose language such as Java or Scala. During compilation and deployment, this dataflow graph is mapped to physical nodes and processes.

As a simple example, suppose that we want to process a stream of sensor measurements and calculate every 10 seconds the average of all measurements seen so far We assume that the sensor generates the data items in increasing timestamp order, but the time series may have missing data points. The processing pipeline consists of three stages: (1) Map deserializes the incoming messages and retains only the scalar value and timestamp (i.e., discards any additional metadata), (2) LI performs linear interpolation to fill in the missing data points, and (3) Avg computes the average historical value and emits an update every 10 seconds.

The above pipeline can be programmed conveniently in Storm by providing the implementations of each node Map, LI, Avg and describing the connections between them.

The implementation described previously exposes pipeline parallelism, and thus suggests a multi-process or distributed execution where each stage of the pipeline computes as an independent process. In the case where the sensor produces messages at a very high rate, the computationally expensive deserialization stage Map becomes a bottleneck. In order to deal with such bottlenecks, Storm provides a facility for data parallelism by allowing the programmer to explicitly specify the creation of several parallel instances of the Map node. It handles automatically the splitting and balancing of the input stream across these instances, as well as the merging of the output streams of these instances.

The problem, however, with this data parallelization transformation is that it does not preserve the semantics of the original pipeline. The issue is that the linear interpolation stage LI relies on receiving the data elements in increasing order of timestamps. Unfortunately, when Storm merges the output streams of the two Map instances it introduces some arbitrary interleaving that may violate this precondition. This introduces nondeterminism to the system that causes the outputs to be unpredictable and therefore not reproducible without modifications to the computation.

Typically, a practical way to deal with these problems is to generate sequence numbers and attach them to stream elements in order to recover their order later (if they get out of order). However, this increases the size of data items. Moreover, it imposes a linear order, even in cases where a partial order is sufficient. For example, synchronization markers can be used to impose a partial order more efficiently than attaching sequence numbers. In general, many such practical fixes make the programs harder to debug, maintain, and modify correctly and thus less reliable.

In contrast, in order to facilitate semantically sound parallelization transformations and eliminate behaviors that rely on spurious ordering of the data items, our approach relies on data-trace types that classify the streams according to their partial ordering characteristics. For example, we can declare that the connection from Map to LI is “linearly ordered”, and this would indicate that the parallelization transformation of the previous paragraph is not sound because it causes the reordering of data items flowing through that channel. Alternatively, the implementation LI could be replaced by a new implementation, denoted Sort-LI, that can handle a disordered input by sorting it first according to timestamps. Then, the connection channel between Map and Sort-LI can be declared to be “unordered”, which enables sound data parallelization for the Map stage. Assuming that all connections are typed, the problem now arises of whether the computation nodes are consistent with these input/output partial ordering types. We propose later in section 4 a way of structuring the code for each node according to a set of templates, so that it respects the types of its input/output channels.

3. Types for Data Streams

We will introduce a semantic framework for distributed stream processing systems, where the input and output streams are viewed as partial orders [13]. Under this view, finite prefixes of streams are represented as data traces, and they are classified according to their ordering characteristics using types. The input/output behavior of a stream processing system is modeled as a data-trace transduction, which is a monotone function from input traces to output traces.

3.1. Data Traces

We use data traces to model streams in which the data items are partially ordered. Data traces generalize sequences (data items are linearly ordered), relations (data items are unordered), and independent stream channels (data items are organized as a collection of linearly ordered subsets). The concatenation operation and the prefix order on sequences can be generalized naturally to the setting of data traces.

A data type A = (Σ, (T_σ)_σ∈Σ) consists of a potentially infinite tag alphabet Σ and a value type T_σ for every tag σ ∈ Σ. The set of elements of type A, or data items, is equal to {(σ, d) ∣ σ ∈ Σ and d ∈ T_σ}, which we will also denote by A. The set of sequences over A is denoted as A*. A dependence relation on a tag alphabet Σ is a symmetric binary relation on Σ. We say that the tags σ, τ are independent (w.r.t. a dependence relation D) if (σ, τ) ∉ D. For a data type A = (Σ, (T_σ)_σ∈Σ) and a dependence relation D on Σ, we define the dependence relation that is induced on A by D as {((σ, d), (σ′, d′)) ∈ A × A ∣ (σ, σ′) ∈ D}, which we will also denote by D. Define ≡_D to be the smallest congruence (w.r.t. sequence concatenation) on A* containing {(ab, ba) ∈ A* × A* ∣ (a, b) ∉ D}. Informally, two sequences are equivalent w.r.t. ≡_D if one can be obtained from the other by repeatedly commuting adjacent items with independent tags.

Example 3.1. Suppose we want to process a stream that consists of sensor measurements and special symbols that indicate the end of a one-second interval. The data type for this input stream involves the tags Σ = {M, #}, where M indicates a sensor measurement and # is an end-of-second marker. The value sets for these tags are T_M = Nat (natural numbers), and T_# = Ut is the unit type (singleton). So, the data type A = (Σ, T_M, T_#) contains measurements (M, d), where d is a natural number, and the end-of-second symbol #.

The dependence relation D = {(M, #), (#, M), (#, #)} says that the tag M is independent of itself, and therefore consecutive M-tagged items are considered unordered. For example, (M, 5) (M, 5) (M, 8) # (M, 9) and (M, 8) (M, 5) (M, 5) # (M, 9) are equivalent w.r.t. ≡_D.

A data-trace type is a pair X = (A, D), where A is a data type and D is a dependence relation on the tag alphabet of A. A data trace of type X is a congruence class of the relation ≡_D. We also write X to denote the set of data traces of type X. Since the equivalence ≡_D is a congruence w.r.t. sequence concatenation, the operation of concatenation is also well-defined on data traces: [u] · [v] = [uv] for sequences u and v, where [u] is the congruence class of u. We define the relation ≤ on the data traces of X as a generalization of the prefix partial order on sequences: for data traces u and v of type X, u ≤ v iff there are u ∈ u and v ∈ v s.t. u ≤ v (i.e., u is a prefix of v). The relation ≤ on data traces of a fixed type is a partial order. Since it generalizes the prefix order on sequences (when the congruence classes of ≡_D are singleton sets), we will call ≤ the prefix order on data traces.

Example 3.2 (Data Traces). Consider the data-trace type X = (A, D), where A and D are given in Example 3.1. A data trace of X can be represented as a sequence of multisets (bags) of natural numbers and visualized as a partial order on that multiset. The trace corresponding to the sequence of data items (M, 5) (M, 7) # (M, 9) (M, 8) (M, 9) # (M, 6) is visualized as:

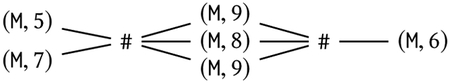
where a line from left to right indicates that the item on the right must occur after the item on the left. The end-of-second markers # separate multisets of natural numbers. So, the set of data traces of X has an isomorphic representation as the set Bag(Nat)⁺ of nonempty sequences of multisets of natural numbers. In particular, the empty sequence ε is represented as ∅ and the single-element sequence # is represented as ∅ ∅.

A singleton tag alphabet can be used to model sequences or multisets over a basic type of values. For the data type given by Σ = {σ} and T_σ = T there are two possible dependence relations for Σ, namely ∅ and {(σ, σ)}. The data traces of (Σ, T, ∅) are multisets over T, which we denote as Bag(T), and the data traces of (Σ, T, {(σ, σ)}) are sequences over T.

Example 3.3 (Multiple Input/Output Channels). Suppose we want to model a streaming system with multiple independent input and output channels, where the items within each channel are linearly ordered but the channels are completely independent. This is the setting of (acyclic) Kahn Process Networks [36] and the more restricted synchronous dataflow models [18, 39]. We introduce tags Σ_I = {I₁,…, I_m} for m input channels, and tags Σ₀ = {0₁,…, 0_n} for n output channels. The dependence relation for the input consists of all pairs (I_i, I_i) with i = 1,…, m. This means that for all indexes i ≠ j the tags I_i and I_j are independent. Similarly, the dependence relation for the output consists of all pairs (0_i, 0_i) with i = 1,…, n. Assume that the value types associated with the input tags are T₁, …, T_m, and the value types associated with the output tags are U₁, …, U_n. The sets of input and output data traces are (up to a bijection) $T_1^{\ast }\times \cdots \times T_m^{\ast }$ and $U_1^{\ast }\times \cdots \times U_m^{\ast }$ respectively.

3.2. Data-String Transductions

In a sequential implementation of a stream processor the input is consumed in a sequential fashion, i.e. one item at a time, and the output items are produced in a specific linear order. Such sequential semantics is formally described by data-string transductions, which we use as a precursor to defining data-trace transductions.

Let A and B be data types. A data-string transduction with input type A and output type B is a function f : A* → B*. A data-string transduction f : A* → B* describes a streaming computation where the input items arrive in a linear order. For an input sequence u ∈ A* the value f(u) gives the output items that are emitted right after consuming the sequence u. In other words, f(u) is the output that is triggered by the arrival of the last data item of u. We say that f is a one-step description of the computation because it gives the output increment that is emitted at every step.

The lifting of a data-string transduction f : A* → B* is the function $\overline{f}:A^{\ast }\to B^{\ast }$ that maps a sequence a₁a₂ … a_n ∈ A* to $\overline{f}(a_1{a}_2\dots a_n)=f(\epsilon )\cdot f(a_1)\cdot f(a_1{a}_2)\cdots f(a_1{a}_2\dots a_n)$. In particular, the definition implies that $\overline{f}(\epsilon )=f(\epsilon )$. That is, $\overline{f}$ accumulates the outputs of f for all prefixes of the input. Notice that $\overline{f}$ is monotone w.r.t. the prefix order: u ≤ v implies that $\overline{f}(u)\le \overline{f}(v)$ for all u, v ∈ A*. The lifting $\overline{f}$ of a data-string transduction f describes a sequential streaming computation in a different but equivalent way. For an input sequence u ∈ A* the value $\overline{f}(u)$ is the cumulative output of the computation as the stream is extended item by item.

Example 3.4. Suppose the input is a sequence of natural numbers, and we want to define the transformation that outputs the current data item if it is strictly larger than all data items seen so far. We model this as a data-string transduction f : Nat* → Nat*, given by f(ε) = ε and

$$f(a_1\dots a_{n-1}{a}_n)=\{\begin{array}{cc}{a}_n,\hfill & \mathrm{if}{a}_n>a_i\text{for all}i=1,\dots ,n-1;\hfill \\ \epsilon ,\hfill & \text{otherwise}.\hfill \end{array}\phantom{\}}$$

The table below gives the values of f and $\overline{f}$ on input prefixes:

current item	input history	f output	$\overline{f}$ output
	ε	ε	ε
3	3	3	3
1	3 1	ε	3
5	3 1 5	5	3 5
2	3 1 5 2	ε	3 5

Notice that $\overline{f}(3152)=f(\epsilon )\cdot f(3)\cdot f(31)\cdot f(315)\cdot f(3152)$.

3.3. Data-Trace Transductions

Data-trace transductions are useful for giving the meaning (semantics) of a stream processing system. Consider the analogy with a functional model of computation: the meaning of a program consists of the input type, the output type, and a mapping that describes the input/output behavior of the program. Correspondingly, the semantics for a stream processing systems consists of: (1) the type X of input data traces, (2) the type Y of output data traces, and (3) a monotone mapping β : X → Y that specifies the cumulative output after having consumed a prefix of the input stream. The monotonicity requirement captures the idea that output items cannot be retracted after they have been omitted. Since β takes an entire input history (data trace) as input, it can model stateful systems, where the output that is emitted at every step depends potentially on the entire input history.

We have already discussed how (monotone) functions from A* to B* model sequential stream processors. We will now introduce the formal notion of consistency, which captures the intuition that a sequential implementation does not depend on the relative order of any two elements unless the stream type considers them to be relatively ordered.

Definition 3.5 (Consistency). Let X = (A, D) and Y = (B, E) be data-trace types. We say that a data-string transduction f : A* → B* is (X, Y)-consistent if u ≡_D v implies that $\overline{f}(u){\equiv }_E\overline{f}(v)$ for all u, v ∈ A*.

Let f ∈ A* → B* be a (X, Y)-consistent data-string transduction. The function β : X → Y, defined by $\beta ([u])=[\overline{f}(u)]$ for all u ∈ A*, is called the (X, Y)-denotation of f.

Definition 3.6 (Data-Trace Transductions). Let X = (A, D) and Y = (B, E) be data-trace types. A data-trace transduction with input type X and output type Y is a function β : X → Y that is monotone w.r.t. the prefix order on data traces: u ≤ v implies that β(u) ≤ β(v) for all traces u, v ∈ X.

Definition 3.5 essentially says that a data-string transduction f is consistent when it gives equivalent cumulative outputs for equivalent input sequences. It is shown in [13] that the set of data-trace transductions from X to Y is equal to the set of (X, Y)-denotations of all (X, Y)-consistent data-string transductions.

Example 3.7 (Deterministic Merge). Consider the streaming computation where two linearly ordered input channels are merged into one. More specifically, this transformation reads items cyclically from the two input channels and passes them unchanged to the output channel. Recall from Example 3.3 that the set of input data traces is essentially T* × T*, and the set of output data traces is essentially T*. The data-trace transduction merge : T* × T* → T* is given by:

$$\text{merge}(x_1\dots x_m,y_1\dots y_n)=\{\begin{array}{cc}{x}_1{y}_1\dots x_m{y}_m,\hfill & \mathrm{if}m\le n;\hfill \\ x_1{y}_1\dots x_n{y}_n,\hfill & \text{if}m>n.\hfill \end{array}\phantom{\}}$$

Example 3.8 (Key-Based Partitioning). Consider the computation that maps a linearly ordered input sequence of data items of type T (each of which contains a key), to a set of linearly ordered sub-streams, one per key. The function key : T → K extracts the key from each input value. An input trace is represented as an element of T*. The output type is specified by the tag alphabet K, value types T_k = T for every key k ∈ K, and the dependence relation {(k, k) ∣ k ∈ K}. So, an output trace is represented as a K-indexed tuple, that is, a function K → T*. The data-trace transduction partition_key : T* → (K → T*) describes the partitioning of the input stream into sub-streams according to the key extraction map key: partition_key(u)(k) = u∣_k for all u ∈ T* and k ∈ K, where u∣_k denotes the subsequence of u that consists of all items whose key is equal to k. The implementation of partition_key can be modeled as a data-string transduction f : T* → (K × T)*, given by f(ε) = ε and f(wx) = (key(x), x) for all w ∈ T* and x ∈ T.

Although the computation of aggregates (e.g., sum, max, and min) is meaningful for unordered input data (i.e., a bag), if the bag is given as a stream then it is meaningless to produce partial aggregates as the data arrives: any partial aggregate depends on a particular linear order for the input items, which is inconsistent with the notion of unordered input. Therefore, for a computation of relational aggregates in the streaming setting we require that the input contains linearly ordered markers that trigger the emission of output (see [40] for a generalization of this idea). The input can then be viewed as an ordered sequence of bags (each bag is delineated by markers), and it is meaningful to compute at every marker occurrence the aggregate over all items seen so far. Our definition of data-trace transductions captures these subtle aspects of streaming computation with relational data.

Example 3.9. Suppose that the input stream consists of unordered natural numbers and linearly ordered markers #. Consider the computation that emits at every occurence of # the maximum of all numbers seen so far. More specifically, the input type is given by Σ = {σ, τ}, T_σ = Nat, T_τ = Ut (unit type), and D = {(σ, τ), (τ, σ), (τ, τ)}. So, an input data trace is essentially an element of Bag(Nat)⁺, as in Example 3.2. The streaming maximum computation is described by the data-trace transduction smax : Bag(Nat)⁺ → Nat*, where for a sequence of bags B₁… B_n, smax(B₁… B_n) := max(B₁) max(B₁ ⋃ B₂) … max(B₁ ⋃ B₂ ⋃ ⋯ ⋃ B_n–1). In particular, the output does not include the bag of items B_n since the last occurrence of #. The implementation of smax is modeled as a data-string transduction f : (Nat ⋃ {#})* → Nat*, which outputs at every # occurrence the maximum number so far. That is, f(ε) = ε and

$$f(a_1\dots a_n)=\{\begin{array}{c}\epsilon \mathrm{if}{a}_n\in \mathrm{Nat};\hfill \\ \text{max of}\{a_1,\dots ,a_n\}\{\#\},\text{if}{a}_n=\#.\hfill \end{array}\phantom{\}}$$

for all sequences a₁a₂ … a_n ∈ (Nat ⋃ {#})*.

4. Type-Consistent Programming

Complex streaming computations can be naturally described as directed acyclic graphs (DAGs), where the vertices represent simple operations and the edges represent streams of data. Such a representation explicitly exposes task and pipeline parallelism, and suggests a distributed implementation where every vertex is an independent process and inter-process communication is achieved via FIFO channels.

The semantic framework of section 3, which includes the notions of data-trace types and data-trace transductions, will serve a dual purpose. First, it will allow us to give a formal denotational semantics for streaming computation DAGs that respect the input/output stream types. Second, it will enable reasoning about equivalence and semantics-preserving transformations, such as data parallelization. We will focus here on a subset of data-trace types that emphasizes two crucial elements that are required by practical streaming computations: (1) a notion of synchronization markers, and (2) viewing the data items as key-value pairs in order to expose opportunities for data parallelization.

The synchronization markers can be thought of as events that are periodically generated by the input sources. The period is configurable and can be chosen by the application programmer depending on the time-granularity requirements of the computation (e.g. 1 msec, 1 sec, etc). The purpose of the markers is similar to the punctuations of [40] or the heartbeats of [50]. They are used for triggering the output of nonmonotonic operations (e.g., the streaming aggregation of Example 3.9) and making overall progress, as well as for merging streams in a predictable way by aligning them on corresponding markers. These synchronization markers are always assumed to be linearly ordered, and they occur in order of increasing timestamp.

We define two kinds of data-trace types for streams of key-value pairs: unordered types of the form U(K, V), and ordered types of the form O(K, V). For a set of keys K and a set of values V, let U(K, V) denote the type with alphabet K ⋃ {#}, values V for every key, values Nat for the # tag (i.e., marker timestamps), and dependence relation {(#, #)} ⋃ {(k, #), (#, k) ∣ k ∈ K}. In other words, U(K, V) consists of data traces where the marker tags # are linearly ordered and the elements between two such tags are of the form (k, v), where k ∈ K and v ∈ V, and are completely unordered. We define O(K, V) similarly, with the difference that the dependence relation also contains {(k, k) ∣ k ∈ K}. That is, in a data trace of O(K, V), elements with the same key are linearly ordered between # markers, but there is no order across elements of different keys.

A transduction DAG is a tuple (S, N, T, E, →, λ) which represents a labelled directed acyclic graph, where: S is the set of source vertices, T is the set of sink vertices, N is the set of processing vertices, E is the set of edges (i.e., connections/channels), → is the edge relation, and λ is a labelling function. The function λ assigns: (1) a data-trace type to each edge, (2) a data-trace transduction to each processing vertex that respects the input/output types, and (3) names to the source/sink vertices. We require additionally that each source vertex has exactly one outgoing edge, and each sink vertex has exactly one incoming edge.

Next we define the denotational semantics of a transduction DAG G with source vertices S₁,…, S_m and sink vertices T₁, …, T_n. Suppose that e_i is the unique edge emanating from the source vertex S_i (for i = 1, …, m), and ${\overline{e}}_i$ is the unique edge leading to the sink vertex T_i (for i = 1, …, n). The graph G denotes a data-trace transduction, where the set of input traces is (up to a bijection) ${\prod }_{i=1}^m\lambda (e_i)$ and the set of output traces is (up to a bijection) ${\prod }_{i=1}^n\lambda ({\overline{e}}_i)$. Given an input trace, we will describe how to obtain the output data trace (representing the entire output history of G on this input trace). We will gradually label every edge e of the DAG with a data trace u(e). First, label every edge emanating from a source vertex with the corresponding input trace. Then, consider in any order the processing vertices whose incoming edges have already been labeled. For such a vertex n, apply the data-trace transduction λ(n) to the input traces and label the outgoing edges with the corresponding output traces. After this process ends, the output is read off from the data traces which label the edges that point to sinks.

Example 4.1 (Time-Series Interpolation). Consider a home IoT system where temperature sensors are installed at a residence. We wish to analyze the sensor time series to create real-time notifications for excessive energy loss through the windows. The sensor time series sometimes have missing data points, and therefore the application requires a preprocessing step to fill in any missing measurements using linear interpolation. We assume that the sensors first send their measurements to a hub, and then the hub propagates them to the stream processing system. The stream that arrives from the hub does not guarantee that the measurements are sent in linear order (e.g., with respect to a timestamp field). Instead, it produces synchronization markers every 10 seconds with the guarantee that all elements with timestamps < 10·i have been emitted by the time the i-th marker is emitted. That is, the i-th marker can be thought of as a watermark with timestamp 10·i. The input stream is a data trace of U(Ut, M), where M is the type of measurements (id, value, ts) consisting of a sensor identifier id, a scalar value value, and a timestamp ts. This is a transduction DAG that describes the pre-processing computation:

The vertex HUB represents the source of sensor measurements, and the vertex SINK represents the destination of the output stream. ID is the type of sensor identifiers, and V is the type of timestamped values (value, ts). The processing vertices are described below:

• The stage Join-Filter-Map (JFM) joins the input stream with a table that indicates the location of each sensor, filters out all sensors except for those that are close to windows, and reorganizes the fields of the input tuple.

• Recall the guarantee for the synchronization markers, and notice that it implies the following property for the input traces: for any two input measurements that are separated by at least one marker, the one on the left has a strictly smaller timestamp than the one on the right. The sorting stage SORT sorts for each sensor the measurements that are contained between markers.

• The linear interpolation stage LI considers each sensor independently and fills in any missing data points.

We have described informally the data-trace transductions JFM, SORT and LI. The transduction DAG shown earlier denotes a data-trace transduction U(Ut, M) → O(ID, V).

The computation performed by a processing node is given in a structured fashion, by completing function definitions of a specified operator template. Table 1 shows the three templates that are supported, which encompass both ordered and unordered input streams. Each operator is defined by a sequential implementation, which we describe informally below. This means that each operator can be modeled as a data-string transduction. It can then be proved formally that these data-string transductions are consistent w.r.t. their input/output data-trace types (Definition 3.5). It follows that each operator that is programmed according to the template conventions has a denotation (semantics) as a data-trace transduction of the appropriate type.

Table 1.

Operator templates for data-trace transductions.

U(K, V): unordered key-value pairs between markers O(K, V): for every key, ordered values between markers

Type parameters: K, V, L, W OpStateless: transduction U(K, V) → U(L, W) Ut onItem(K key, V value) { } Ut onMarker(Marker m) { }

Type parameters: K, V, W, S OpKeyedOrdered: transduction O(K, V ) → O(K, W) S initialState() { } S onItem(S state, K key, V value) { } S onMarker(S state, K key, Marker m) { } // Restriction: Output items preserve the input key.

Type parameters: K, V, L, W, S, A OpKeyedUnordered: transduction U(K, V) → U(L, W) A in(K key, V value) { } A id() { } // identity for combine A combine(A ×, A y) { } // associative, commutative S initialState() { } S updateState(S oldState, A agg) { } Ut onItem(S lastState, K key, V value) { } Ut onMarker(S newState, K key, Marker m) { } // Restriction: in, id, combine, initialState, and // updateState are all pure functions.

OpStateless:

The simplest template concerns stateless computations, where only the current input event—not the input history—determines the output. The programmer fills in two function definitions: (1) onItem for processing key-value pairs, and (2) onMarker for processing synchronization markers. The functions have no output (the output type is Ut, i.e. the unit type) and their only side-effect is emitting output key-value pairs to the output channel by invoking emit(outputKey, outputValue).

OpKeyedOrdered:

Assuming that the input is ordered per key, this template describes a stateful computation for each key independently that is order-dependent. The programmer fills in three function definitions: (1) initialState for obtaining the initial state, (2) onItem for processing a key-value pair and updating the state, and (3) onMarker for processing a synchronization marker and updating the state. The functions have output S, which is the type of the data structure for representing the state. As for stateless computations, the functions allow the side-effect of emitting output key-value pairs to the output channel. This template requires a crucial restriction for maintaining the order for the output: every occurrence of emit must preserve the input key. If this restriction is violated, e.g. by projecting out the key, then the output cannot be viewed as being ordered.

OpKeyedUnordered:

Assuming that the input is unordered, this template describes a stateful computation for each key independently. Recall that the synchronization markers are ordered, but the key-value pairs between markers are unordered. To guarantee that the computation does not depend on some arbitrary linear ordering of the key-value pairs, their processing does not update the state. Instead, the key-value pairs between two consecutive markers are aggregated using the operation of a commutative monoid A: the programmer specifies an identity element id(), and a binary operation combine() that must be associative and commutative. Whenever the next synchronization marker is seen, updateState is used to incorporate the aggregate (of type A) into the state (of type S) and then onMarker is invoked to (potentially) emit output. The behavior onItem may depend on the last snapshot of the state, i.e. the one that was formed at the last marker. The functions onItem and onMarker are allowed to emit output data items (but not markers), but the rest of the functions must be pure (i.e., no side-effects).

Table 2 shows how some streaming computations (which are based on the setting of Example 4.1) can be programmed using the operator templates of Table 1. The first example is the stateless computation joinFilterMap, which retains the measurements of temperature sensors that are placed near windows. The second example is the per-sensor ordered stateful computation linearInterpolation, which fills in the missing data points of a sensor time series by performing linear interpolation. The last example is the persensor unordered (between markers) stateful computation that takes the average of the measurements between markers and reports the maximum over all the averages so far.

Table 2.

Examples of data-trace transductions.

M = { id: ID, scalar: Float, ts: Int } V = { scalar: Float, ts: Int }

joinFilterMap: OpStateless U(Ut, M) → U(ID, V) Ut onItem(Ut key, M value) { if (location(value.id) = "window") emit(value.id, (value.scalar, value.ts)) } Ut onMarker(Marker m) { }

linearInterpolation: OpKeyedOrdered O(ID, V) → O(ID, V) Precondition: items arrive in order of increasing timestamp V initialState() { return nil } V onItem(V state, ID key, V value) { if (state == nil) then // first element emit(key, value) else // not the first element Float x = state.scalar Int dt = value.ts - state.ts for i = 1 … dt do Float y = x + i * (value.scalar - x) / dt emit(key, (y, state.ts + i)) return value } V onMarker(V state, ID key, Marker m) { return state }

maxOfAvgPerID: OpKeyedUnordered U(ID, V) → U(ID, V) AvgPair = { sum: Float, count: Nat } AvgPair in(ID key, V value) { return (value.scalar, 1) } AvgPair id() { return (0.0, 0) } AvgPair combine(AvgPair x, AvgPair y) { return (x.sum + y.sum, x.count + y.count) } Float initialState() { return -infinity } Float updateState(Float oldState, AvgPair agg) { return max(oldState, agg.sum / agg.count) } Ut onItem(Float lastState, ID key, V value) { } Ut onMarker(Float newState, ID key, Marker m) { emit(key, (newState, m.timestamp - 1)) }

Theorem 4.2. Every streaming computation defined using the operator templates of Table 1 is consistent w.r.t. its input/output type (see Definition 3.5).

Proof. We will prove the case of the OpKeyedUnordered template, since it is the most interesting one, and we will omit the rest. A template OpKeyedUnordered<K, V, L, W, S, A> describes a data-string transduction f : A* → B*, where:

$$A=(K\times V)\cup (\{\#\}\times \mathrm{Nat})B=(L\times W)\cup (\{\#\}\times \mathrm{Nat})$$

This data-string transduction was informally described earlier and is defined operationally by the pseudocode shown in Table 3. The streaming algorithm of Table 3 maintains a per-key store and also tracks the state that should be given to keys that have not been encountered yet.

Table 3.

Implementation of OpKeyedUnordered.

R = { agg: A, state: S } // record type Map<K, R> stateMap = ∅ // state map S startS = initialState() // state when key is first seen next(K key, V value) { // process data item R r = stateMap.get(key) if (r == nil) then // first time key is seen r = { agg = id(), state = startS } onItem(r.state, key, value) r.agg = combine(r.agg, in(key, value)) stateMap.update(key, r) } next(Marker m) { // process marker for each (key, r) in stateMap do: r.state = updateState(r.state, r.agg) r.agg = id() stateMap.update(key, r) onMarker(r.state, key, m) startS = updateState(startS, id()) emit(m) }

We write M for the memory of the streaming algorithm of Table 3. The function next: M × A → M describes how the algorithm updates its memory every time it consumes an element. We also write next: M × A* → M to denote the function that describes how the algorithm updates the memory after consuming a sequence of elements. If a₁, a₂ ∈ A are key-value pairs, then we have a₁a₂ ≡ a₂a₁. It is easy to see that next(m, a₁a₂) = next(m, a₂a₁) for every m ∈ M. If the items a₁ and a₂ have the same key, then the property holds because of the associativity and commutativity of combine. If the items a₁ and a₂ have different keys, then the property holds because different keys cause the modification of disjoint parts of the memory. It follows by an inductive argument (on the construction of ≡) that next(m, u) = next(m, v) for all m ∈ M and u, v ∈ A* with u ≡ v.

Suppose now that out : M × A → B* gives the output generated by the algorithm when it consumes a single element. We lift this function to out: M × A* → B* as follows: out(m, ε) = ε and out(m, ua) = out(m, u) · out(next(m, u), a) for all m ∈ M, u ∈ A* and a ∈ A. The crucial observation is that for every key-value item (k, v) ∈ (K × V), the value out(m, (k, v)) depends only on the part of memory that holds the state for k, which we denote by m[k].state. Moreover, this part of the memory does not get modified when key-value pairs are processed. For memories m₁, m₁ ∈ M and key k, we write m₁ ≡_k m₂ when m₁[k].state = m₂[k].state. Our previous observations can be written as m₁ ≡_k m₂ ⇒ out(m₁, (k, v)) = out(m₂, (k, v)) and m ≡_k′ next(m, (k, v)) for all m, m₁, m₂ ∈ M, all k, k′ ∈ K, and every v ∈ V. For key-value pairs a₁, a₂ ∈ (K × V) we have that

$$\begin{gathered} out(m,a_1{a}_2)=out(m,a_1)\cdot out(next(m,a_1),a_2)\in (L\times W{)}^{\ast } \\ out(m,a_2{a}_1)=out(m,a_2)\cdot out(next(m,a_2),a_1)\in (L\times W{)}^{\ast } \end{gathered}$$

and by virtue of the properties discussed previously we obtain that out(m, a₁a₂) ≡ out(m, a₂a₁). By an inductive argument on the construction of ≡, we can generalize this property to: out(m, u) ≡ out(m, v) for every memory m ∈ M and all sequences u, v ∈ A* with u ∈ v.

In order to establish the consistency property we have to show that: u ≡ v implies $\overline{f}(u)\equiv \overline{f}(v)$ for all u, v ∈ A*. We have that $\overline{f}(u)=out(m_0,u)$, where m₀ is the initial memory for the algorithm. From u ≡ v and earlier results we conclude that $\overline{f}(u)=out(m_0,u)\equiv out(m_0,v)=\overline{f}(v)$. □

The templates of Table 1 define data-trace transductions with only one input channel and output channel. The operation merge, which we denote by MRG or M, combines several input streams into one by aligning them on synchronization markers and taking the union of the key-value pairs that are in corresponding blocks. We consider two variants of merge, which we will not distinguish notationally. The first one has unordered input channels with the same input keys and values, i.e. MRG : U(K, V)×⋯× U(K, V) → U(K, V). The second variant of merge has ordered input channels with pairwise disjoint sets of input keys K₁, K₂,…, K_n, so we write MRG : O(K₁, V )×⋯× O(K_n, V) → O(K₁ ⋃⋯⋃ K_n, V).

To enable parallelization, we also need to consider operations that split one input stream into several output streams. The round-robin splitter, denoted RR : U(K, V) → U(K, V)×⋯× U(K, V), sends every input key-value pair to one output channel by cycling through them and sends a synchronization marker to all output channels. The hash-n splitter, denoted HASH or H : U(K, V) → U(K_0/n, V)×⋯× U(K_n–1/n, V) sends a key-value pair (k, v) with k ∈ K_i/n with the i-th output channel where K_i/n = {k ∈ K ∣ hash(k) = i (mod n)}. We write K_i instead of K_i/n when no confusion arises. As for the round-robin splitter, H sends a synchronization marker to all output channels. The ordered version H : O(K, V) → O(K₀, V)× ⋯ × O(K_n–1, V) behaves similarly.

In order to convert an unordered trace of type U(K, V) to an ordered trace of O(K, V), we also consider the sorting data-trace transduction SORT^< : U(K, V) → O(K, V). The transformation SORT^< uses the linear order < to impose a total order for every key separately on the key-value pairs between synchronization markers. Even when the stream source is ordered, the parallelization of intermediate processing stages can reorder the key-value pairs between markers in an arbitrary way. So, if a later stage of the processing requires the original ordered view of the data, SORT^< must be applied immediately prior to that stage.

The templates of Table 1 not only enforce the data-trace type discipline on the input and output channels, but they also expose explicitly opportunities for parallelization and distribution. Computations that are described by the templates OpKeyedOrdered and OpKeyedUnordered can be parallelized on the basis of keys, and stateless computations can be parallelized arbitrarily.

Theorem 4.3 (Semantics-Preserving Parallelization). Let β : U(K, V) → U(L, W), γ : O(K, V) → O(K, W), and δ : U(K, V) → U(L, W) be data-trace transductions that are implemented using the OpStateless, OpKeyedOrdered, and OpKeyedUnordered templates, respectively. Then, we have:

$$\begin{gathered} \mathrm{MRG}\gg \beta =(\beta \Vert \cdots \Vert \beta )\gg \mathrm{MRG} \\ \gamma =\mathrm{HASH}\gg (\gamma \Vert \cdots \Vert \gamma )\gg \mathrm{MRG} \\ \delta =\mathrm{HASH}\gg (\delta \Vert \cdots \Vert \delta )\gg \mathrm{MRG} \\ \mathrm{SORT}=\mathrm{HASH}\gg (\mathrm{SORT}\Vert \cdots \Vert \mathrm{SORT})\gg \mathrm{MRG} \end{gathered}$$

where ≫ denotes streaming composition and ∥ denotes parallel composition [13]:

$$\frac{f:X\to Yg:Y\to Z}{f\gg g:X\to Z}\frac{f:X\to Yg:Z\to W}{f\Vert g:X\times Z\to Y\times W}$$

Proof. First, we observe that all the considered data-trace transductions are well-typed by Theorem 4.2. We will only give the proof for the equation involving β, since the other cases are handled similarly. For simplicity, we ignore the timestamps of the # markers. We can view the traces of U(K, V) as nonempty sequences of bags of elements of K × V (recall Example 3.2), i.e. U(K, V) = Bag(K×V)⁺. Since β is implemented by the template OpStateless, there is a function out: (K × V) → Bag(L×W) that gives the output of β when it processes a single key-value element. Then, we have $\beta (B)={\bigcup }_{(k,v)\in B}out(k,v)$ and β(B₁B₂…B_n) = β(B₁)β(B₂)… β(B_n) for all B, B₁,…, B_n ∈ Bag(K × V). Assuming we have m input channels, we obtain:

$$\begin{gathered} ((\beta \Vert \cdots \Vert \beta )\gg \mathrm{MRG})(B_{11}\dots B_{1n},\dots ,B_{m1}\dots B_{mn}) \\ =\mathrm{MRG}(\beta (B_{11}\dots B_{1n}),\dots ,\beta (B_{m1}\dots B_{mn})) \\ =\mathrm{MRG}(\beta (B_{11})\dots \beta (B_{1n}),\dots ,\beta (B_{m1})\dots \beta (B_{mn})) \\ =(\beta (B_{11})\cup \dots \cup \beta (B_{m1}))\dots (\beta (B_{1n})\cup \dots \cup \beta (B_{mn})) \\ =\beta (B_{11}\cup \dots \cup B_{m1})\dots \beta (B_{1n}\cup \dots \cup B_{mn}) \\ =\beta ((B_{11}\cup \dots \cup B_{m1})\dots (B_{1n}\cup \dots \cup B_{mn})) \\ =(\mathrm{MRG}\gg \beta )(B_{11}\dots B_{1n},\dots ,B_{m1}\dots B_{mn}) \end{gathered}$$

using elementary properties of β and of MRG. So, we conclude that MRG ≫ β = (β ∥ ⋯ ∥ β) ≫ MRG. □

We say that a data-trace transduction f : U(K, V) → U(K, V)×⋯×U(K, V) is a splitter if f ≫ MRG : U(K, V) → U(K, V) is the identity function on data traces (identity transduction). Informally, a splitter splits (partitions) the input stream into several output streams. The data-trace transductions RR and H (defined earlier) are splitters. If SPLIT is a splitter, then Theorem 4.3 implies that for stateless β, β = SPLIT ≫ (β ∥ ⋯ ∥ β) ≫ MRG.

The processing pipeline for the sensor input stream of Example 4.1 can be parallelized. Figure 1 shows two equivalent processing graphs, where every stage of the pipeline is instantiated two times. The input for the JFM stage is partitioned in a round-robin fashion, and the input for the SORT and LI stages is partitioned based on the key (sensor identifier). All the vertices of the graph have a formal denotational semantics as data-trace transductions (Theorem 4.2), which enables a rigorous proof of equivalence for the DAGs of Example 4.1 and Figure 1. The top graph of Figure 1 is obtained from the graph of Example 4.1 by applying the parallelizing transformation rules of Theorem 4.3. The bottom graph of Figure 1 is obtained from the top one using the transformation rules of the following table:

Figure 1.

A transduction DAG that is equivalent to the one of Example 4.1 and allows data parallelism.

Each box above shows two equivalent transduction DAGs. These rules are specialized to two input channels and three output channels for the sake of easy visualization. They extend in the obvious way to an arbitrary number of input and output channels. The bottom right graph of the table is equivalent to the identity transduction when the number of output channels is equal to the number of input channels, because HASH_n : O(K_i/n, V) → O(K_0/n, V)×⋯× O(K_n–1/n, V) sends the entire input stream to the i-th output channel.

Corollary 4.4 (Correctness of Deployment). Let G be a transduction DAG that is built using the operator templates of Table 1. Any deployment of G, regardless of the degree of parallelization, is equivalent to G.

Proof. The idea of the proof is that every deployment can be obtained from the original description G of the computation by applying a sequence of semantics-preserving transformation rules on specific subgraphs. This requires examining several cases. We will limit this proof to one case that illustrates the proof technique, and we will omit the rest since they can be handled with very similar arguments. First of all, we observe that the original graph G (and every graph obtained via transformations) has a denotational semantics in terms of data-trace transductions (Theorem 4.2). Let us examine the case of a subgraph of the form β ≫ γ, where β is programmed using OpStateless and γ is programmed using OpKeyedUnordered. Let SPLIT be an arbitrary splitter, which means that SPLIT ≫ MRG is the identity transduction. Using the equations of Theorem 4.3 we can obtain the equivalent SPLIT ≫ (β ∥ β) ≫ MRG ≫ HASH ≫ (γ ∥ γ ∥ γ) ≫ MRG. Using the transformation rules for “reordering MRG and HASH” mentioned earlier, we obtain:

Finally, each subgraph β ≫ HASH is fused into a single node β; HASH, and similarly each subgraph MRG ≫ γ is fused into MRG; γ. These fusion transformations can be easily checked to be semantics-preserving. □

5. Implementation in Apache Storm

In the previous section we proposed an abstraction for describing a distributed streaming computation as a transduction DAG, where each processing element is programmed using one of three predefined templates. This principled manner of defining computations enforces a data-trace type discipline that disallows operations which depend on a spurious ordering of the data items. Additionally, it enables a number of equivalence-preserving parallelization transformations.

We have implemented a compilation procedure that converts a transduction DAG into a deployment plan for the distributed streaming framework Storm [28, 54]. In Storm, a computation is structured as a DAG (called topology) of source vertices called spouts and processing/sink vertices called bolts. Each vertex (bolt or spout) may be instantiated multiple times, across different physical nodes or CPU threads. In such settings, the connections between vertices specify a data partitioning strategy, which is employed when the vertices are instantiated multiple times. These connections are called groupings in Storm’s terminology, and the most useful ones are: (1) shuffle grouping, which randomly partitions the stream in balanced substreams, (2) fields grouping, which partitions the stream on the basis of a key, and (3) global grouping, which sends the entire stream to exactly one instance of the target bolt. We refer the reader to [29] for more information on the programming model of Storm.

Figure 2 shows a concrete example of programming a transduction DAG (and thus obtaining a Storm topology) using our framework. In this example, the user first describes the data source using an Iterator object and converts it to a Source vertex. Then, the operator vertices are described using the templates OpStateless and OpKeyedUnordered. A transduction DAG is represented as a DAG object, which exposes methods for adding new vertices and edges. For example, the method call dag.addOp(op, par, v1, v2, …) adds the vertex op to dag with the parallelism hint par, and it also adds edges from the vertices v1, v2,… to op. Finally, dag.getStormTopology() performs all necessary checks for type consistency and returns a StormTopology object that can be passed to Storm for deployment on the cluster.

Figure 2.

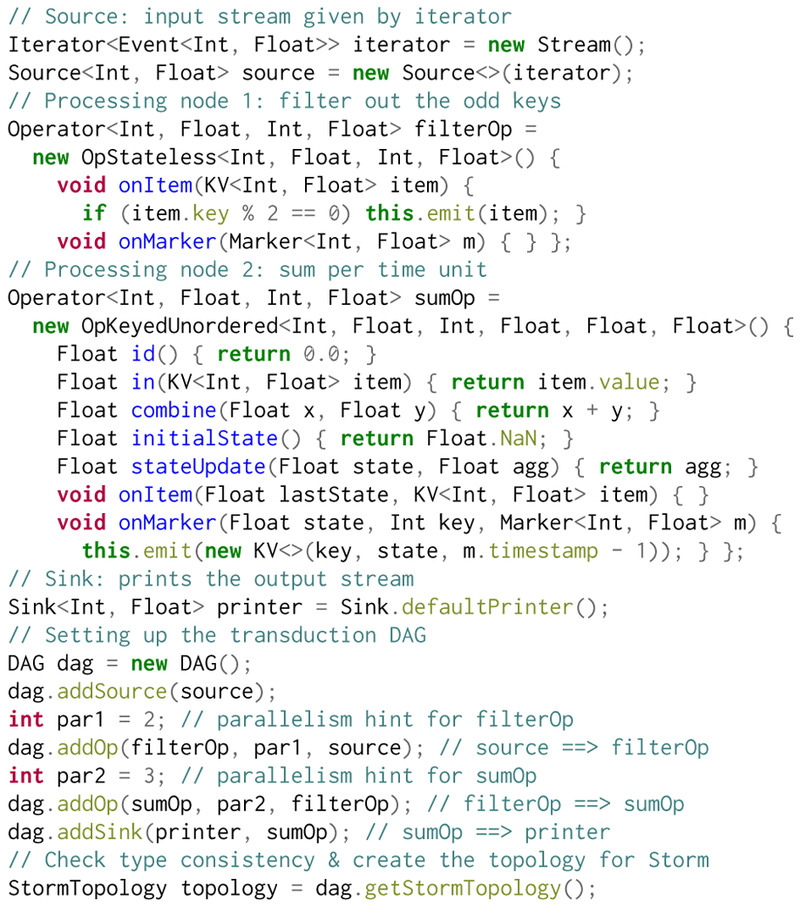
An extended programming example.

Our framework ensures that the data-trace types of input, output and intermediate streams are respected. The compilation procedure automatically constructs the glue code for propagating synchronization markers throughout the computation, merging input channels, partitioning output channels, and sorting input channels to enforce a per-key total order on the elements between markers. We use Storm’s built-in facilities for the parallelization of individual processing vertices, but we have replaced Storm’s “groupings” because they inhibit the propagation of the synchronization markers. For efficiency reasons, we fuse the merging operator (MRG) and the sorting operator (SORT) with the operator that follows them in order to eliminate unnecessary communication delays.

We chose Storm as the deployment platform because (1) it is a widely adopted “pure streaming” system that is used for many industry workloads, (2) it naturally exposes parallelism and distribution, and (3) it is extensible. Due to its similarity to alternative systems, it would not be difficult to compile transduction DAGs into topologies for these other platforms.

6. Experimental Evaluation

In this section we experimentally evaluate our data-trace type-based framework. We address two questions:

• Can our system generate code that is as efficient as a handcrafted implementation, while automatically adapting to whatever levels of parallelism are available?

• Does our framework facilitate the development of complex streaming applications?

To answer the first question, we used an extension of the Yahoo Streaming Benchmark [21]. We compared an implementation generated using our framework against a hand-tuned one. To address the second question, we consider a significant case study: the Smart Homes Benchmark [22] used in the Grand Challenge of the DEBS 2014 conference, which we have modified to include a more realistic power prediction technique based on a machine learning model.

Our focus in the experiments is to determine how well stream applications scale. To do this, we used the following experimental setup: We ran our implementation on top of Storm on a cluster of several virtual machines. Each virtual machine has 2 CPUs, 8 GB of memory, and 8 GB of disk each and runs CentOS 7. Across multiple trials and configurations, we measured maximum throughput for each configuration.

Yahoo Streaming Benchmark.

The streaming benchmark of Yahoo [21] defines a stream of events that concern the interaction of users with advertisements, and suggests an analytics pipeline to process the stream. There is a fixed set of campaigns and a set of advertisements, where each ad belongs to exactly one campaign. The map from ads to campaigns is stored in a database. Each element of the stream is of the form (userId, pageId, adId, eventType, eventTime), and it records the interaction of a user with an advertisement, where eventType is one of {view, click, purchase}. The component eventTime is the timestamp of the event.

The basic benchmark query (as described in [21]) computes, at the end of each second, a map from each campaign to the number of views associated with that campaign within the last 10 seconds. For each event tuple, this involves an expensive database lookup to determine the campaign associated with the advertisement viewed. The reference implementation published with the Yahoo benchmark involves a multi-stage pipeline: (i) stage 1: filter view events, project the ad id from each view tuple, and lookup the campaign id of each ad, (ii) stage 2: compute for every window the number of events (views) associated with each campaign. The query involes key-based partitioning on only one property, namely the derived campaign id of the event.

To compare the effectiveness of our framework, we next re-implemented this analytics pipeline as a transduction DAG, where every processing vertex is programmed using a template of Table 1. This is shown in the top graph of Figure 3, where YItem is the type of input tuples and CID is the type of campaign identifiers. The system is configured so that the stream sources emit synchronization markers at 1 second intervals, i.e. exactly when the timestamps of the tuples cross 1 second boundaries. To evaluate our framework more comprehensively, we have implemented six queries:

Figure 3.

Query IV: Transduction DAG for a variant of the Yahoo Streaming Benchmark [21], and its deployment on Storm with parallelization 2 and 3 for the processing vertices Filter-Map and Count(10 sec) respectively.

• Query I: A single-stage stateless computation that enriches the input data items with information from a database (we use Apache Derby [24]).

• Query II: A single-stage per-key aggregation, where the intermediate results are persisted in a database.

• Query III: A two-stage pipeline that enriches the input stream with location information and then performs a per-location summarization of the entire stream history.

• Query IV: A re-implementation of the analytics pipeline of the original Yahoo streaming benchmark (see Figure 3).

• Query V: A modification of Query IV, where the percampaign aggregation is performed over non-overlapping windows (also called tumbling windows), instead of the overlapping (or sliding) windows of Query IV.

• Query VI: A three-stage pipeline that performs a machine learning task. First, it enriches the stream with location information from a database. Then, it performs a per-user feature extraction (i.e., per-key aggregation). Finally, for every location independently it clusters the users periodically using a k-means clustering algorithm.

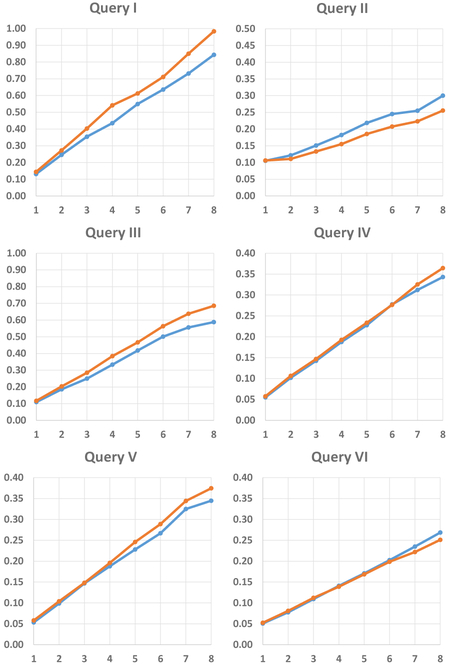
For every query, we have created a handwritten implementation using the user-level API of Apache Storm, as well as an implementation using our framework of data-trace transductions. Figure 4 shows the experimental comparison of the handcrafted implementations (blue line) and the data-trace-transduction-based implementations (orange line). We have varied the degree of parallelization from 1 up to 8 (shown in the horizontal axis), which correponds to the number of virtual machines assigned to the computation. The vertical axis shows the maximum throughput for each configuration. Observe that the hand-written implementation and the generated implementation have similar performance.

Figure 4.

Queries inspired by the Yahoo Streaming Benchmark. The orange (resp., blue) line shows the throughput of the transduction-based (resp., handcrafted) implementation. The horizontal (resp., vertical) axis shows the number of machines (resp., throughput in million tuples/sec).

The experiments reported in Figure 4 involve compute-heavy operators, but our observations also apply to computationally cheaper operators: our framework incurs a small performance penalty in the range of 0%-20%. In the results for Query I, the generated code is slightly more efficient than the handwritten code (by 10%-15%). This is because we use a routing mechanism that balances the load in a way that minimizes the communication cost, whereas Storm balances the load more evenly across the replicated nodes but incurs a slightly higher communication cost. Overall, we conclude that our framework achieves good performance—despite the higher-level specification and additional typing requirements in the transduction-based code.

Case Study: Smart Homes Benchmark.

To examine the suitability of our framework for more expressive stream processing applications, we consider a variant of the benchmark used for the “Smart Homes” Internet of Things (IoT) competition of the DEBS 2014 conference [22]. In this benchmark, the input stream consists of measurements produced by smart power plugs. A smart plug is connected to a wall power outlet, and then an electrical device is connected to the plug. This allows the plug sensors to measure quantities that are relevant to power consumption. The deployment of these smart plugs is done across several buildings, each of which contains several units. A smart plug is uniquely identified by three numbers: a building identifier, a unit identifier (which specifies a unit within a building), and a plug identifier (which specifies a plug within a unit). For simplicity, we assume here that the plugs only generate load measurements, i.e. power in Watts. More specifically, every stream event is a tuple with the following components: (i) timestamp: timestamp of the measurement, (ii) value: the value of the load measurement (in Watts), (iii) plugId: identifier that specifies the plug, (iv) unitId: identifier that specifies the unit, (v) buildingId: identifier that specifies the building. A plug generates roughly one load measurement for every 2 seconds, but the measurements are not uniformly spaced. There can be gaps in the measurements, as well as many measurements for the same timestamp.

We implement a load prediction pipeline in the framework of data-trace transductions. The load prediction is separate for each device type (A/C unit, lights, etc.). The diagram of Figure 5 is a transduction DAG implementing the computation: (i) JFM (join-filter-map): Join the input stream with information regarding the type of electrical device connected to a plug and retain only a subset of device types. Reorganize the fields of the tuple, separating them into a plug key (plugId) of type Plug and a timestamped value of type VT. (ii) SORT: For every plug key, sort the input items (between consecutive markers) by timestamp. (iii) LI: For every plug key, fill in missing data points using linear interpolation. (iv) Map: Project every input key (a Plug identifier) to the kind of device it is connected to. (v) SORT: For every device type, sort the input items (between consecutive markers) according to their timestamp. (vi) AVG: Compute the average load for each device type by averaging all data items with the same key (device type) and timestamp. (vii) Predict: For every device type and every input value (there is exactly one value per second), predict the total power consumption over the next 10 minutes using the features: current time, current load, and power consumption over the past 1 minute. A decision/regression tree is used for the prediction (REPTree of [32]), which has been trained on a subset of the data.

Figure 5.

Transduction DAG for a variant of the Smart Home Benchmark [22] of DEBS 2014, and its deployment on Storm.

Figure 6 shows that by varying the degree of parallelism (number of virtual machines) the computation scales up linearly. As before, we conducted the experiment on a cluster of virtual machines (each with 2 CPUs, 8 GB memory, and 8 GB disk). We conclude from these results that our framework indeed can scale out to high levels of concurrency, even for complex operations such as machine learning inference over streams. Overall, our experiments have demonstrated that our framework can express the complex computations required in both enterprise and IoT streaming applications, and that it can generate an efficient implementation comparable to hand-coded solutions.

Figure 6.

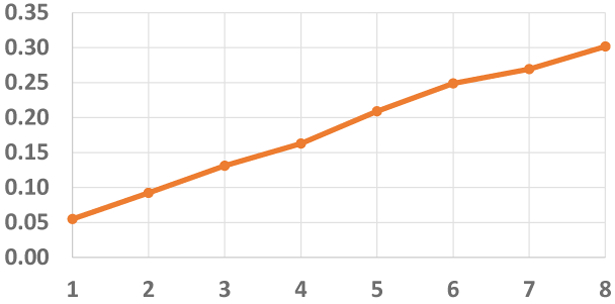
Smart Homes - Energy Prediction: The horizontal (resp., vertical) axis shows the level of parallelization (resp., throughput in million tuples/sec).

7. Related Work

Our programming model is closely related to dataflow computation models. It is a generalization of acyclic Kahn process networks (KPNs) [36]. A KPN specifies a finite number of independent linearly ordered input and output channels, and consists of a collection of processes, where each process is a sequential program that can read from its input channels and write to its output channels. Synchronous Dataflow [18, 30, 39, 53] is a special case of KPNs, which has been used for specifying and parallelizing streaming programs primarily in the embedded software domain. In a synchronous dataflow graph, each process reads a fixed finite number of items from the input channels and also emits a fixed finite number of items as output. We accommodate a finite number of independent input or output streams, but also allow more complicated dependence relations on the input and output. In particular, viewing the input or output stream as a bag of events is not possible in KPNs or their restrictions.

There is a large body of work on streaming database query languages and systems: Aurora [2] and its successor Borealis [1], STREAM [15], CACQ [42], TelegraphCQ [20], CEDR/StreamInsight [7, 17], and System S [33]. The query language supported by these systems (for example, CQL [15]) is typically an extension of SQL with constructs for sliding windows over data streams. This allows for rich relational queries, including set-aggregations (e.g. sum, max, min, average, count) and joins over multiple data streams, but requires the programmer to resort to user-defined functions in another language for richer computations such as machine learning classification. A precise semantics for how to deal with out-of-order streams has been defined using punctuations (a type of synchronization markers) [37, 40, 41, 55]. The partial ordering view supported by data-trace transductions gives the ability to view a stream in many different ways: as a linearly ordered sequence, as a relation, or even as a sequence of relations. This provides a rich framework for classifying disorder, which is useful for describing streaming computations that combine relational with sequence-aware operations. Our implementation supports at the moment only a specific kind of time-based punctuations (i.e., periodic synchronization markers), but our semantic framework can encode more general punctuations. Extending relational query languages to partially ordered multisets has been studied in [31], though not in the context of streaming.

A number of distributed stream processing engines, such as Samza [26, 47], Storm [28, 54], Heron [38, 56], Mill-Wheel [5], Spark Streaming [27, 58], and Flink [19, 25], have achieved widespread use. Spark Streaming and Flink support SQL-style queries or, equivalently, lower-level operations roughly corresponding to the relational algebra underlying SQL. Apache Beam [6, 23] is a programming model that provides relational and window-based abstractions. The other stream engines provide much lower-level abstractions in which the programmer writes event handlers that take tuples, combine the data with windows, and emit results. As with the manually coded Storm implementation used in our experiments, this provides great power but does not aid the programmer in reasoning about correctness. Naiad [45] is a general-purpose distributed dataflow system for performing iterative batch and stream processing. It supports a scheme of logical timestamps for tracking the progress of computations. These timestamps can support the punctuations of [40] and deal with certain kinds of disorder, but they cannot encode more general partial orders. Systems such as Flink [19, 25] and Naiad [45] support feedback cycles, which we do not consider here due to the semantic complexities of cycles: they require a complex denotational model involving continuous functions, as in KPNs [36].

Prior work has considered the issue of semantically sound parallelization of streaming applications [34, 49]. The authors of [49] observe that Storm [28, 54] and S4 [46] perform unsound parallelizing transformations and propose techniques for exploiting data parallelism without altering the original semantics of the computation. Our framework addresses similar issues, and our markers have a similar role to the “pulses” of [49]. Our approach, however, is based on a type-based discipline for classifying streams and a denotational method for proving the preservation of semantics.

8. Conclusion

We have proposed a type discipline for classifying streams according to their partial ordering characteristics using data-trace types. These types are used to annotate the communication links in the dataflow graph that describes a streaming computation. Each vertex of this typed dataflow graph is programmed using a pre-defined set of templates, so as to ensure that the code respects the types of the input and output channels. We have implemented this framework in Java and we have provided an automatic procedure for deployment on Apache Storm. We have shown experimentally that our framework can express complex computations required in IoT streaming applications, and that it can produce efficient implementations comparable to hand-coded solutions.

A direction for further work is to enrich the set of type-consistent templates with common patterns. For example, our templates can already express sliding-window aggregation, but a specialized template for that purpose would relieve the programmer from the burden of re-discovering and re-implementing efficient sliding-window algorithms (e.g., [16, 51, 52, 57]). Other avenues for future research are to extend the compilation procedure to target streaming frameworks other than Storm, and to automatically perform optimizations that exploit the underlying hardware.

The StreamQRE language [43] (see also [10]) consists of a set of programming constructs that allow the combination of streaming computations over linearly-ordered data with static relational operations (i.e., over unordered data). A promising direction for future work is to generalize the language to the setting of partially ordered data streams. StreamQRE is based on a notion of regular stream transformations [8, 9] that admit efficient space-bounded implementations [11, 12, 14], which is a crucial property for applications in resource-constrained environments [3, 4]. It would be interesting to investigate whether a similar notion of regularity can be formulated for the data-trace transductions that we consider here.

CCS Concepts • Information systems → Data streams; Stream management; • Theory of computation → Streaming models; • Software and its engineering → General programming languages.