Amikacin Initial Dose in Critically Ill Patients: a Nonparametric Approach To Optimize A Priori Pharmacokinetic/Pharmacodynamic Target Attainments in Individual Patients

Amikacin is commonly used for probabilistic antimicrobial therapy in critically ill patients with sepsis. Its narrow therapeutic margin makes it challenging to determine the right individual dose that ensures the highest efficacy target attainment rate (TAR) in this setting. This study aims to develop a new initial dosing approach for amikacin by optimizing the a priori TAR in this population.

ABSTRACT

Amikacin is commonly used for probabilistic antimicrobial therapy in critically ill patients with sepsis. Its narrow therapeutic margin makes it challenging to determine the right individual dose that ensures the highest efficacy target attainment rate (TAR) in this setting. This study aims to develop a new initial dosing approach for amikacin by optimizing the a priori TAR in this population. A population pharmacokinetic model was built with a learning data set from critically ill patients who received amikacin. It was then used to design an initial dosing approach maximizing a priori TAR for a target ratio of ≥8 for the peak concentration to the MIC (C_max/MIC) or of ≥75 for the ratio of the area under the concentration-time curve from 0 to 24 h to the MIC (AUC_0–24/MIC). In the 166 patients included, 53% had amikacin C_max of ≥64 mg/liter with a median dose of 23.4 mg/kg. A two-compartment model with creatinine clearance and body surface area as covariates best described the data and showed good predictive performance. Our dosing approach was successful in optimizing TAR for C_max/MIC, with a rate of 92.9% versus 67.9% using a 30-mg/kg regimen, based on an external subset of data and assuming a MIC of 8 mg/liter. Mean optimal doses were higher (3.5 ± 0.5 g) than with the 30-mg/kg regimen (2.1 ± 0.3 g). Suggested doses varied with the MIC, the target index, and desired TAR threshold. A dosing algorithm based on the method is proposed for a large range of patient covariates. Clinical studies are necessary to confirm efficacy and safety of this optimized dosing approach.

INTRODUCTION

Aminoglycosides are still used as first-line agents for empirical antimicrobial therapy in critically ill patients with sepsis, most often in combination with other agents such as beta-lactams (1, 2). Optimal dosing of aminoglycosides is primarily based on pharmacokinetic/pharmacodynamic (PK/PD) principles. These agents display concentration-dependent activity, and both the ratio of maximal aminoglycoside concentration in plasma to the bacterial MIC (C_max/MIC) and the ratio of the area under the concentration-time curve from 0 to 24 h (daily area) to the MIC (AUC_0–24/MIC) have been suggested as targets. The conventional targets are C_max/MIC of ≥8 to 10 (3) and AUC_0–24/MIC of ≥75 (4, 5). For amikacin, considering a MIC breakpoint of 8 mg/liter for most susceptible Gram-negative bacteria (8 mg/liter is the EUCAST epidemiological cutoff for several Enterobacteriaceae), a C_max of ≥64 mg/liter and AUC_0–24 of ≥600 mg/liter·h can be considered reasonable targets for empirical dosing in sepsis. Lower C_max and AUC_0–24 target values can be considered if the putative MIC is lower. The risk of nephrotoxicity should also be considered in dosing as it has been associated with high exposure. For amikacin, achieving a trough concentration of ≤2.5 mg/liter has been recommended to minimize toxicity (6, 7) although data supporting this specific value are limited.

Septic critically ill patients display impaired aminoglycoside PK. Patho-physiological changes associated with sepsis, including capillary leak syndrome and/or augmented renal clearance (ARC), may result in increased volume of distribution (V_d) and clearance (CL). Therapeutic interventions as use of intravenous (i.v.) fluids or organ support (e.g., renal replacement therapies [RRTs] or extracorporeal membrane oxygenation) are also known to alter PK in critically ill patients (8, 9). Moreover, the occurrence of acute kidney injury can lead to decreased amikacin CL. The PK variability of aminoglycosides is very large in critically ill patients, and this makes the selection of optimal doses difficult, especially at the time of initiation of treatment.

Despite extensive use of aminoglycosides, the initial dosing of these agents remains challenging, especially in critically ill patients. Weight-based dosing up to 20 to 25 mg/kg of amikacin has been associated with an insufficient C_max target attainment rate (TAR) in critically ill patients (10–13). Use of larger doses may be necessary in this special population but raises concerns about the risk of nephrotoxicity associated with high trough concentrations.

Therapeutic drug monitoring (TDM), in combination with Bayesian forecasting, is a useful method to adjust aminoglycoside dose and more consistently achieve concentration targets. However, such approaches cannot be applied for initial dosing. There is a need for precision dosing approaches in this context.

The aim of this study was to design a model-based approach to optimize the attainment of PK/PD targets for initial dosing of amikacin in individual critically ill patients.

RESULTS

Population model building and validation.

A total of 395 concentrations from 166 patients were analyzed from the two centers. Demographic, TDM, clinical, and biological characteristics of these patients are shown in Table 1. The median initial dose of amikacin was 23.4 mg/kg (range, 11 to 40 mg/kg) of total body weight (TBW). This dosage was associated with only 53% and 30% of patients achieving target C_max values of ≥64 mg/liter and ≥80 mg/liter (C_max/MIC values of ≥8 and ≥10 considering a MIC of 8 mg/liter), respectively. This is consistent with previous reports in critically ill patients (10–13).

TABLE 1.

Characteristics of patients included in the analysis (n = 166)

Variablea	Value for the variableb	IQRc	Ranged
Patients from the Lyon site (% of total)	71.7
Age (yr)	65	53–74	19–85
Male patients (% of total)	65
TBW (kg)	76.5	65.2–88.5	41.5–137.5
Height (cm)	170	164–175	137–190
BSA (m2)	1.92	1.77–2.10	1.33–2.63
BMI (kg/m2)	25.6	22.8–29.7	16–46
SAPSII score	48	34–63	13–100
SOFA score	5	3–8	0–16
Patients with a SOFA score of ≥2 (% of total)	87.3
Dose (mg)	1,985	1,500–2,000	860–3,000
Dose/TBW (mg/kg)	23.4	20.0–27.0	11.0–39.7
Cmax (mg/liter)	67.2	50.1–84.5	20.9–139.7
Cmax distribution (% of patients)
≥64 mg/liter	53
≥80 mg/liter	30
Cmin (mg/liter)	2.7	0.4–9.5	≤0.3–53.5
Serum creatinine (μmol/liter)	83	59–117	23–480
CLCG (ml/min)	79.8	53.2–124.5	11.2–300.1
GFR estimated with CKD-EPI (ml/min/1.73m2)	83.6	49.0–103.8	9.6–167.0
GFR estimated with MDRD (ml/min/1.73 m2)	77.6	49.0–110.6	9.2–300.8
Alanine amino transferase (UI/liter)	43	29–76	8–7,272
Aspartate amino transferase (UI/liter)	31	16–64	3–3,263

^aTBW, total body weight; BSA, body surface area; BMI, body mass index; C_max, amikacin concentration measured 1 h after start of infusion; C_min, amikacin concentration measured before the second planned administration; SOFA, sepsis-related organ failure assessment; SAPSII, simplified acute physiology score II; CL_CG, creatinine clearance estimated by the original Cockcroft-Gault equation; GFR, glomerular filtration rate; MDRD, Modification of Diet in Renal Disease; CKD-EPI, Chronic Kidney Disease Epidemiology Collaboration.

^bMedian values are given unless otherwise indicated.

^cIQR, interquartile range.

^dMinimum and maximum values are given.

A two-compartment model best fit the data in the learning set (n = 110 patients). As these parameters could not be well estimated, we fixed the intercompartmental clearance (Q) to 0.5 h⁻¹ and set the central (V1) and peripheral volumes of distribution (V2) as equal (V1 = V2). Significant decreases in the objective function (OF) during forward selection of 87 and 15 (likelihood ratio test [LRT], P < 0.01) were observed when creatinine clearance (CL_CR) estimated by the Cockcroft-Gault equation (CL_CG) and body surface area (BSA) were included in the model, respectively. Backward selection retained these covariates with OF increases of 102 and 15 (LRT, P < 0.01) when CL_CG and BSA, respectively, were removed from the final model. A power model best described the relationship between amikacin clearance and median-normalized CL_CG, while V1 was linearly correlated with median-adjusted BSA as follows:

$$\text{CL}={\text{CL}}_0\times {\left(\frac{{\text{CL}}_{\text{CG}}}{73.6}\right)}^{0.85}$$

$$\text{V}1=\text{V}{1}_0\times \frac{\text{BSA}}{1.93}$$

where 73.6 ml/min and 1.93 m² are the median values of CL_CG and BSA in the population, respectively, and CL₀ and V1₀ are the typical values of CL and V1 (i.e., when covariate values are equal to the medians).

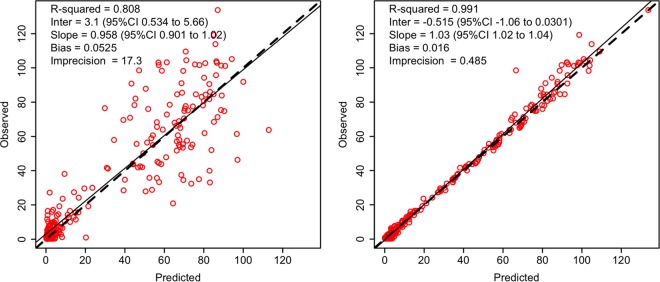
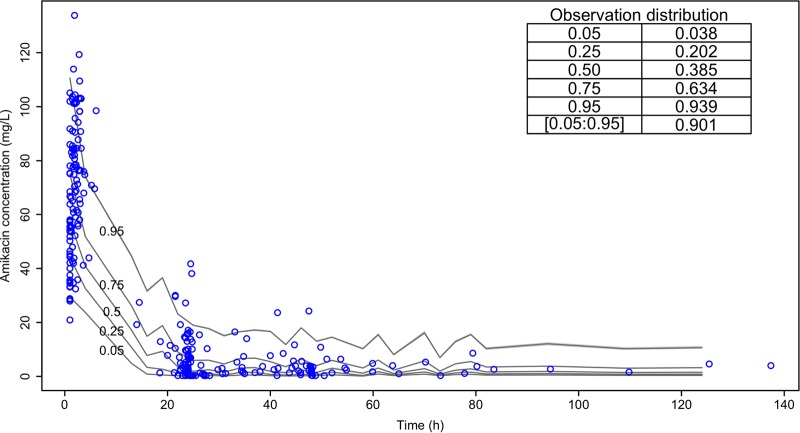
Table 2 describes the estimated PK parameter values. Fig. 1 shows the nonparametric distribution of the typical values of CL and V1. The final model adequately described the data, as shown by the plot of observations versus predictions in Fig. 2. Predictive performances were acceptable, with low bias and acceptable imprecision in the learning data set. Results were consistent in the validation data set (n = 56 patients), as shown in Table 3. Internal validation was confirmed using a visual predictive check (VPC) plot as shown Fig. 3. The proportion of observations between the 5th and the 95th simulated percentiles was 90.1%, as expected.

TABLE 2.

Population pharmacokinetic parameters of the final model

Pharmacokinetic parameter	Mean	Coefficient of variation (%)	Median	Rangeb
Typical clearance (CL0 [liters/h])	2.6	53.4	2.6	0.7–9.9
Typical central volume of distribution (V10 [liters])a	23.0	44.8	20.7	10.3–69.7
Intercompartment clearance (Q [liters/h])	0.5

^aOf note, we set the peripheral volume V2 equal to V1.

^bMinimum and maximum values are given.

FIG 1.

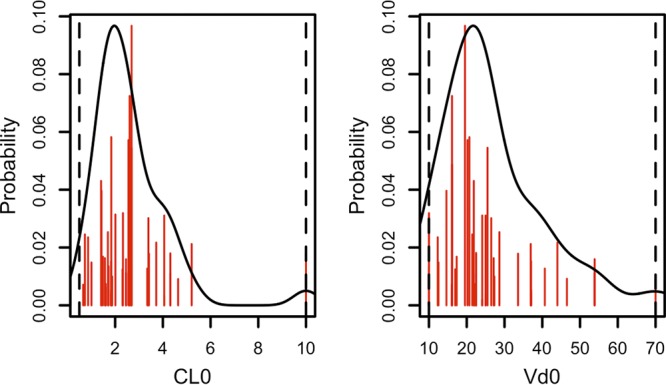
A priori amikacin clearance (left) and volume of distribution (right). CL0, typical clearance in liters/h; Vd0, typical volume of distribution in liters. Red lines represent the discrete nonparametric distribution of PK parameters, the black lines represent their smooth density function, and dotted vertical lines represent the parameter ranges.

FIG 2.

Predictive performance represented by population (left) and individual (right) predictions compared with observations. The dotted line represents the identity line; the solid black line represents the linear regression. CI, confidence interval.

TABLE 3.

Predictive performances of the population pharmacokinetic model

Parameter	Value for the parameter by data set and prediction type
	Learning data set (n = 110)		Validation data set (n = 56)
	Population	Individual	Population	Individual
Mean error (mg/liter)	−1.83	−0.52	−0.03	−0.38
Median absolute % error	34.62	8.09	49.83	16.44
Root mean squared error (mg/liter)	15.67	3.49	15.95	4.88

FIG 3.

Visual predictive check (VPC). The inset table displays the observation proportions (left column) below or within the quantile proportions (right column).

Simulations and OIAD recommendations.

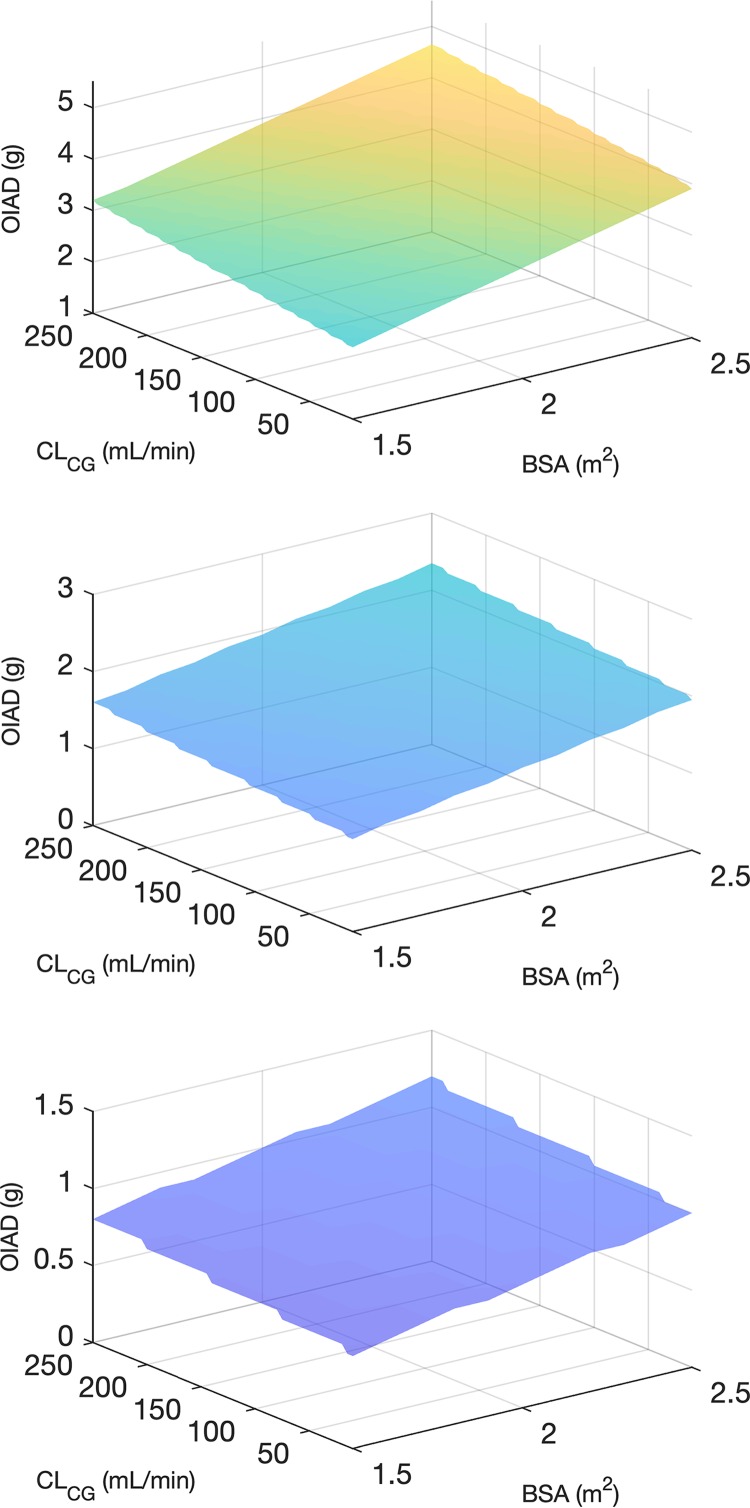
An optimal initial amikacin dose (OIAD) based on the final PK model was calculated for various values of the two covariates (see the Materials and Methods section). OIAD was defined as the lowest dose associated with the a priori probability of achieving the efficacy target of ≥90% (see Materials and Methods). OIAD recommendations are displayed in Tables S1, S2, and S3 in the supplemental material for putative MICs of 8, 4, and 2 mg/liter, respectively. Those tables also show the a priori probabilities to achieve the various efficacy and safety targets for a wide range of covariate values. Graphical representations of optimal doses targeting a C_max/MIC of ≥8 as a function of BSA and CL_CG are displayed in Fig. 4 for MIC values of to 8, 4, and 2 mg/liter. The same plot for the AUC target (AUC_0–24/MIC of ≥75) is provided in Fig. S1. For a given MIC, as expected, the optimal dose increases with increasing renal function and BSA. For a putative MIC of 8 mg/liter, doses much larger than standard appear necessary to reach the efficacy targets with a probability of ≥90%. The dose necessary to achieve the AUC_0–24/MIC target appears to be highly dependent on renal function. In patients with augmented renal clearance (CL_CG of ≥130 ml/min), doses greater than 5 g would be required. It is also interesting that achieving both the efficacy (C_max/MIC) and safety (minimum concentration [C_min] of ≤2.5 mg/liter at 24 h) concentration targets with high probabilities is impossible with once-daily dosing, except in patients with ARC (see the supplemental tables). For a putative MIC of 4 mg/liter, achievement of efficacy targets appears possible with more conventional doses. A dose of less than 2.5 g is sufficient to achieve the C_max/MIC target even for the highest CL_CG and BSA values. In contrast, a dose greater than 2.5 g would be necessary to achieve the AUC_0–24/MIC target in patients with CL_CG of ≥130 ml/min, with optimal doses up to 4.3 g for the highest CL_CR and BSA values. Obviously, achievement of the C_min target is improved when lower doses are considered.

FIG 4.

Optimal initial amikacin dose (OIAD) targeting a maximal concentration in plasma (C_max)/MIC ratio of ≥8 as a function of body surface area (BSA) and creatinine clearance estimated by the Cockcroft-Gault formula (CL_CG) for MIC values of 8 mg/liter (top), 4 mg/liter (center), and 2 mg/liter (bottom). Note that the maximal dose was capped at 5 g.

As a validation of the dosing approach, Table 4 shows the observed rates of target attainment for OIAD and a fixed-dose regimen of 30 mg per kg of corrected body weight (CBW; using a TBW correction for morbidly obese patients [see Materials and Methods]) based on individual PK parameters estimated in the validation set of 56 patients. Assuming a MIC of 8 mg/liter, the proportion of individuals achieving the C_max/MIC target with OIAD was in agreement with the a priori probability and greater than that with the 30 mg/kg of CBW. The observed target attainment rate was lower for the AUC_0–24 target. Despite a higher C_max with OIAD, trough concentrations at 24 h were not greater than those associated with the fixed dose. Importantly, the desired probability of target attainment strongly influenced the calculated OIAD. For example, the median (range, minimum to maximum) values of OIAD for a C_max of ≥64 mg/liter in the validation set were 3.5 g (2.4 to 4.6 g), 2.7 g (1.9 to 3.7 g), and 2.5 (1.8 to 3.3 g) for acceptable probabilities set at 90%, 85%, and 80%, respectively.

TABLE 4.

Comparison of observed target attainment for the OIAD approach and a standard dose of 30 mg/CBW using the real pharmacokinetic parameters from 56 patients

Parametera	Initial dose (g)		Observed target attainment rate (%)
	Mean ± SD	Median (range)	Cmax	AUC	Cmin at 24 h	Cmin at 48 h
Optimal initial amikacin dose for Cmax	3.5 ± 0.5	3.5 (2.4 to 4.5)	92.9	64.3	42.9	71.4
Optimal initial amikacin dose for AUC0–24	3.8 ± 0.5b	4.1 (1.5 to >5)	87.5	69.6b	41.2	69.6
Standard regimen (30 mg/CBW)	2.1 ± 0.3	2.2 (1.5 to 2.9)	67.9	32.1	50.0	75.0

^aAUC_0–24, daily area under the curve (target fixed to ≥600 mg/liter·h); C_max, amikacin concentration measured 1 h after start of infusion (target fixed to ≥64 mg/liter); C_min, amikacin concentration measured at 24 h or 48 h after start of infusion (target fixed to ≤2.5 mg/liter).

^bResults obtained with a maximal dose capped at 5 g.

DISCUSSION

Achieving the PK/PD targets of efficacy with the first dose of aminoglycoside in critically ill patients is challenging. The traditional dosing approach in this context is weight-based dosing or dosing based on alternative metrics of body size like CBW. Although simple, this approach is not precise enough as body size explains only a limited part of aminoglycoside PK variability. Dosing based on population PK models and Monte Carlo simulations deal better with PK variability, but their precision is questionable in individual patients. Indeed, these methods are useful to define dosing regimens for populations, but they do not maximize the probability to achieve the target in each individual patient. Here, another model-based approach has been designed to optimize a priori amikacin PK/PD target attainment in critically ill patients. This approach is based on nonparametric population PK modeling and a priori control principles.

Nonparametric population analysis identified estimated creatinine clearance and BSA as covariates influencing amikacin CL and V_d, respectively. The influence of renal function on amikacin clearance was expected, and here CL_CG was a more influential covariate than the glomerular filtration rate (GFR) estimated by equations from the Modification of Diet in Renal Disease (MDRD) Study or from the Chronic Kidney Disease Epidemiology Collaboration (CKD-EPI). This result is consistent with previous studies (8). However, estimating renal function in critically ill patients is challenging, and estimation equations may not be accurate in all patients (14). It would be interesting to investigate the value of the Jelliffe equation (15) for both the estimation of renal function and drug dosing in such a context as this equation uses a pair of serum creatinine values and might better predict unstable renal function. This was not possible in the present study as we collected only a single serum creatinine value at the time of amikacin onset, and measurement of creatinine clearance based on urine collection was not performed in most patients.

The relationship between V_d and BSA provided the best fit (lowest OF) of all of the size metrics, including total body weight, ideal body weight (IBW), corrected body weight, and adjusted body weight (AdjBW), which are widely used for empirical aminoglycoside dosing. BSA has been rarely reported as a covariate influencing aminoglycoside PK although it is widely used for drug dosing in other therapeutic areas (e.g., oncology). In obese patients, use of adjusted body weight has been recommended for aminoglycoside dosing (16, 17). It is noteworthy that our study population did not include a majority of obese patients, as the interquartile range (IQR) of the body mass index (BMI) was 22.8 to 29.7 kg/m², with 30.1% and 24.7% of overweight and obese patients (BMI values of ≥25 and 30 kg/m²), respectively. This may explain why AdjBW was not the most influential size metric in our analysis. BSA depends on both weight and height and is less variable than weight in adult patients. As a result, its use for dosing may result in a lower risk of overexposure in overweight or obese patients (18). Also, this may be of interest the in case of large intraindividual body weight fluctuations observed in intensive care settings (19). Use of composite covariates including TBW and height to calculate the aminoglycoside dosing regimen or estimate the V_d in critically ill patients has also been suggested elsewhere (13, 20, 21).

An a priori control approach based on a nonparametric population PK model was then used to design optimal dosage regimens of amikacin. With this approach, one can compute the a priori probability to reach any PK target and determine a dosage that maximizes this probability for an individual patient (22, 23). When tested with individual PK parameters from the validation cohort, the approach was successful in maximizing the probability of reaching the C_max/MIC and AUC_0–24/MIC targets. However, for the AUC_0–24 target of ≥600 mg/liter·h, the observed target attainment rate was still less than 70% when a MIC of 8 mg/liter (AUC_0–24/MIC_{8 mg/liter} of ≥75) was assumed. As shown in Table 4 and in the supplemental material, this is because a dose greater than the maximum set at 5 g would have been necessary in some patients. Indeed, we observed that patients with high CL_CG values would need very large amikacin doses to achieve such a high AUC_0–24 with a high probability.

Our dosing approach performed better in the validation group than a dosage of 30 mg/kg of CBW, which led to TARs of 67.9 and 32.1% for C_max/MIC and AUC_0–24/MIC targets, respectively, for a putative MIC of 8 mg/liter. Also, our approach suggested optimal doses much larger than standard doses, especially in patients with ARC, which may raise safety concerns. Regarding safety concentration targets, OIAD values were associated with more than 40% of patients in the validation set with a C_min of ≤2.5 mg/liter at 24 h. This proportion is a little lower than that observed with 30 mg/CBW (50%). This illustrates that our dosing approach better individualizes dosing by taking into account both body size and renal function. This also shows that achieving high C_max and low C_min at 24 h is not possible in a large proportion of patients as these objectives are conflicting, as previously stated by Drusano et al. (4). Therefore, increasing the dosage interval up to 36 or 48 h should be considered in critically ill patients with normal renal function or moderate renal impairment, but this has not been evaluated clinically to our knowledge.

The target C_min considered for safety (2.5 mg/liter) in our study is disputable. Indeed, the evidence is limited regarding the relationship between trough concentration and nephrotoxicity for once-daily amikacin, and the recommendations about the target value are not consistent. A target C_min of ≤2.5 mg/liter has been recommended by French guidelines, without any supportive reference (6). Perhaps the most convincing evidence of a relationship between C_min and nephrotoxicity has been presented in a study on isepamicin (7), which can be considered an equivalent of amikacin in terms of dosage and drug exposure. Data from 196 intensive care unit (ICU) patients with nosocomial pneumonia who received once-daily isepamicin with various dosages and durations of therapy were analyzed. Trough concentration after the first 24 h was found to be the strongest predictor of serum creatinine elevation. AUC was also a secondary predictor but not significant in the multivariate analysis. Based on their results, the authors suggest a target C_min of <5 mg/liter to minimize the risk of toxicity. For once-daily amikacin therapy, other TDM studies suggested this target C_min of <5 mg/liter (24). However, recent Australian guidelines from the state of Queensland suggest an amikacin C_min target of less than 2 mg/liter (25), and The Sanford Guide (2019 edition) (26) suggests a C_min target of less than 1 mg/liter (similar to that for gentamicin/tobramycin) for once-daily amikacin. Overall, 2.5 mg/liter appears to be a reasonable C_min target although this is not supported by strong direct evidence.

We did not consider AUC as a predictor of nephrotoxicity. While several studies reported a relationship between aminoglycoside AUC and renal toxicity (5, 7, 27, 28), no clear AUC target has been defined for once-daily amikacin. Further research is necessary about this question.

Although safety is an important issue, we believe that early achievement of a therapeutic concentration is the primary goal of amikacin initial dosing in critically ill patients. The risk of accumulation and renal toxicity can be managed by subsequent therapeutic drug monitoring and dose adjustment, including an individualized dose interval. Our approach suggests the need for very high amikacin doses under some circumstances (high MIC, BSA, and CL_CG values), and those may daunt clinicians. There is little data on the use of such a large dose of amikacin. The study of Brasseur et al. investigated high amikacin doses combined with renal replacement therapy (RRT) in order to accelerate amikacin elimination for the treatment of infections caused by multidrug-resistant (MDR) bacteria in ICUs (29). In 11 patients under amikacin therapy, the initial dose ranged from 25 to 37 mg/kg, and the maximal daily dose over therapy ranged from 26 to 67 mg/kg. For 5 out of 11 patients, increasing the dose up to more than 50 mg/kg was necessary to achieve the target C_max/MIC ratio of 8 to 12. In the 5 patients discharged who were not already under RRT before aminoglycoside therapy, one experienced acute kidney injury during therapy but did not require renal support. Those results are consistent with our dosing suggestions.

Another important finding of our study is the discrepancy between the doses required to achieve C_max/MIC and AUC_0–24/MIC targets. As shown Tables S1 to S3 in the supplemental material, achievement of the AUC_0–24 target is strongly influenced by renal function. In patients with severe renal impairment (CL_CG of <30 ml/min), the doses required to reach the AUC_0–24 target are lower than those required to achieve the C_max target. The doses are broadly similar in patients with CL_CG values of 40 to 60 ml/min. In patients with normal renal clearance and ARC, the doses required to achieve the AUC_0–24 target are larger. So, C_max and AUC_0–24 targets of amikacin are not consistent in terms of dosage requirements. Our results show that achieving the AUC_0–24/MIC target for a MIC up to 8 mg/liter is almost impossible in patients with ARC unless very large amikacin doses are used, which have never been evaluated clinically. This issue is relevant in ICU patients, considering the large prevalence of ARC. Our study has included 22.3% patients with CL_CG values of ≥130 ml/min, which is consistent with previous studies in ICUs reporting ARC prevalences of 17.9% and 25% (30, 31).

The use of the AUC_0–24/MIC as a marker of efficacy of aminoglycosides has been suggested as an alternative to use of the C_max/MIC ratio (4, 5) and is supported by a strong rationale from animal models (32) and a few clinical studies (33, 34). In a seminal clinical study from Moore et al., only the C_max/MIC was reported as a predictor of clinical response, but the AUC was not determined (35). The study from Kashuba et al. reported both the C_max/MIC and AUC/MIC as predictors of aminoglycoside effect in patients with nosocomial pneumonia (3). To our knowledge, no human studies have shown that the AUC_0–24/MIC ratio is a better predictor of clinical response than the C_max/MIC. Considering the collinearity between C_max and AUC for a given dosage regimen, only a clinical dose fractionation study could identify a difference between the two indices, and this has yet to be performed. In any case, our dosing approach can accommodate both target indices, and dose suggestions are provided accordingly.

This work has several limitations, including its retrospective design and the lack of rich PK data. Our dosing suggestions are based on calculations only and have not been validated clinically. Also, they are based on various MIC breakpoints, which may be viewed as worst-case microbiological situations. The use of local microbiology data may be better suited for dosing decisions although assuming a high putative AUC remains a reasonable approach, considering the limited accuracy of MIC determinations (36). As noted above, the C_min target used is based on limited evidence. This work can be considered a preliminary contribution toward optimal aminoglycoside initial dosing in critically ill patients. Clinical trials are necessary to assess the proposed dosing approach.

To conclude, we have designed a new dosing approach for initial dosing of amikacin in critically ill patients. Our approach maximizes the a priori probability to reach a C_max/MIC or AUC_0–24/MIC target for any individual patient and showed promising performance when simulated in patients. The optimal dose depends on patient covariates but also on the target and putative MIC considered. Further research is necessary to confirm the clinical value of this approach.

MATERIALS AND METHODS

Patients and data.

(i) Study design. Two data sets from two centers were collected. The first one was from intensive care units of Lyon-Sud hospital (Hospices Civils de Lyon, Pierre-Bénite, France) and used a retrospective methodology. Adult patients who received at least one amikacin administration from June 2014 to September 2015 and underwent amikacin TDM after that first dose (with at least one peak concentration measurement), as recommended by national French guidelines (6), were included in the study. Exclusion criteria were administration of more than one previous dose of amikacin before TDM and use of renal replacement therapy. In addition, a subset from a previous prospective study conducted by Roger et al. in Nîmes University Hospital which satisfied the same inclusion/exclusion criteria was available (10). The two data sets were pooled and then randomly divided into a learning (66.7%, n = 110) and a validation (33.3%, n = 56) data set for the PK analysis.

The study was approved by the Ethics Committee of Lyon University Hospitals that waived patient consent as it was a noninterventional study based on data collected during routine patient care.

(ii) Sampling procedure and analytical method. The amikacin initial dose was administered intravenously as a 30-min infusion with an electric syringe. C_max was sampled 1 h after the infusion start in accordance with French guidelines (6). C_min was measured before the next planned amikacin administration, i.e., after a dosing interval of 24 h in most patients. In patients with a C_min at 24 h above the target (≥2.5 mg/liter), the second amikacin dose was delayed, and another concentration measurement was obtained. The exact administration and sampling times were recorded in all patients. In the Lyon cohort, amikacin concentrations were determined using an immunoturbidimetry assay (Multigent amikacin; Abbott Diagnostics, IL, USA) on an Architect c8000 system. The limit of quantification of the method was 0.52 mg/liter. Maximum interday variability was 1.50% at mean concentrations of 4.62, 15.5, and 30.71 mg/liter.

(iii) Covariate collection. Descriptive and biological data were also recorded on the day of initial dosing, plus or minus 1 day. These covariates included age, sex, height, and total body weight (TBW). Clinical and biological data included a sepsis-related organ failure assessment (SOFA) score (37), simplified acute physiology score II (SAPSII) (38) and serum creatinine and alanine and aspartate amino transferase (ALAT and ASAT, respectively) levels.

Several metrics of renal function and body size were also calculated and considered candidate covariates in model building: creatinine clearance estimated by the original Cockcroft-Gault equation (CL_CG; in milliliters/minute) (39), glomerular filtration rate (GFR) estimated by the equation from the Modification of Diet in Renal Disease (GFR_MDRD) Study (in milliliters/minute/1.73 m²) (40), GFR estimated by the equation from the Chronic Kidney Disease Epidemiology Collaboration (GFR_CKD-EPI; in milliliters/minute/1.73 m²) (41), body surface area (BSA; in square meters) (42), body mass index (BMI; in kilograms/square meter) (43), ideal body weight (IBW) (44), and lean body weight (LBW) (45). Corrected body weight (CBW) proposed by Traynor et al. (46) was adapted according to French recommendations (6) with a weight correction factor for overweight patients (i.e., IBW/TBW ratio of ≥1.25) and calculated as CBW = 0.43(TBW − IBW) + IBW. Adjusted body weight (AdjBW) was calculated as proposed by Bauer et al.: AdjBW = 0.4(TBW − IBW) + IBW for morbidly obese patients (IBW/TBW ratio of ≥1.9) (16).

Pharmacokinetic analysis.

(i) Model building. Population pharmacokinetic analysis was performed using the nonparametric adaptive grid algorithm (NPAG) available in the R package Pmetrics (Laboratory of Applied Pharmacokinetics, University of Southern California, Los Angeles, CA) (47, 48). One- and two-compartment models were tested in the learning data set. Both gamma (multiplicative) and lambda (additive) residual error models available in Pmetrics were evaluated. The best structural and error model was identified by the change in objective function (OF), calculated as OF = −2 log likelihood, by using the likelihood ratio test (LRT).

Once the structural and error models were defined, the influence of each collected covariate on central volume of distribution (V1) and clearance (CL) was examined using a forward addition- backward deletion stepwise approach. In the end, a covariate was retained in the model if it was associated with a significant increase in the OF (LRT, significance set at P < 0.01) after deletion. Both linear and power (including allometric scaling) functions were tested for covariate modeling.

(ii) Model diagnostics. Model predictive performance was evaluated by plots of observation (obs) versus population and individual predictions (pred), as well as by computation of mean error (ME), median absolute percent error (MdAPE), and root mean squared error (RMSE) of prediction.

Simulation-based diagnostics were also performed by computation of visual predictive checks (VPCs) based on 10,000 simulated profiles per subject. The number of observations within the simulated 5th and 95th percentile profiles was computed.

Finally, external validation in the remaining data after splitting was done, based on goodness-of-fit and predictive performance (ME, MdAPE, and RMSE).

Optimal initial amikacin dose (OIAD) algorithm.

A dosing approach based on the final nonparametric model was developed to optimize the achievement of the amikacin PK/PD target with the first dose. This approach has been described in detail elsewhere (22, 23). Briefly, for any patient, the a priori distribution of PK parameters can be computed as a finite number of n parameter values, each set of parameters having a given a priori probability. These are the support points of the nonparametric distribution. The influence of individual covariates is taken into account in the a priori value. For a given candidate dosing regimen, each set of PK parameters results in a PK profile with the associated probability. As a consequence, it is straightforward to calculate the a priori probability to reach a target interval (with one or two bounds) for any PK quantity of interest (C_max, C_min, or AUC).

For a given dose (dose_j) of amikacin, the a priori probability that C_max is greater than a given target value X can be calculated as follows:

$$\text{TAR}({\text{dose}}_j)={\displaystyle \sum _{i=0}^n{\text{prob}}_i}(C_{\max ,\hspace{0.17em}i}\ge X)$$

where prob_i are the probabilities related to each of the n support points of the nonparametric model, and C_{max, i} is the concentration calculated for one possible set of PK parameter values associated with probability prob_i.

Our goal was to achieve the target C_max with a high a priori probability. We set this probability to 90%. Mathematically, this translates as follows:

$${\text{Optimal dose}}_j=\arg \left\{{\text{TAR}}_{{\text{dose}}_j}\ge 0.9\right\}$$

Of note, the method can accommodate any desired probability. The same principles were used to identify the optimal dose for achieving an AUC target. Obviously, any huge dose of amikacin may be associated with a high probability to achieve the targets. This is why we used increasing doses and selected the lowest optimal dose.

Studied dosing regimens ranged from 500 to 5,000 mg with an increment of 50 mg and were tested for different covariate values ranging from 10 to 250 ml/min for CL_CG and from 1.5 to 2.5 m² for BSA, according to the population characteristics, with increments of 10 ml/min and 0.1 m², respectively.

Studied efficacy targets were C_max/MIC of ≥8 and AUC_0–24/MIC of ≥75 (3, 4). We considered three putative MIC values for probabilistic therapy: 8 mg/liter (the epidemiological cutoff for susceptible Enterobacteriaceae from EUCAST), 4 mg/liter (the Enterobacteriaceae MIC breakpoint from USCAST), and a lower value of 2 mg/liter (5, 49). C_max was calculated as the concentration obtained 1 h after the start of the 30-min infusion (3).

In addition, attainment of a C_min of ≤ 2.5 mg/liter, considered at either 24 h (usual dosing interval) or 48 h (extended dosing interval) (C_min,24 or C_min,48, respectively), was computed. Achievement of C_min below this threshold has been suggested by French guidelines to prevent nephrotoxicity (6). Other guidelines and studies have suggested a target C_min ranging from 1 to 5 mg/liter for once-daily amikacin (7, 24–26). So, 2.5 mg/liter appears as a reasonable C_min target although the evidence supporting this specific value is limited.

The dosing approach was assessed by using PK data from the validation group of patients (n = 56). The individual Bayesian posterior estimates of PK parameter based on the final model were computed and considered the “true” PK parameters of the patients. Then, for each subject and the respective values of CL_CG and BSA, the OIAD was computed. The OIAD was then simulated in each patient using the respective true PK parameter values. Finally, we evaluated the target attainment for each subject.

In addition, using the same individual PK parameters from the validation population, we also assessed the TAR for a fixed dose of 30 mg per kg of CBW. CBW was chosen as it has been recommended for dosing in overweight patients; otherwise, for nonoverweight patients, CBW is equal to TBW (6).

Calculation of the OIAD and simulations were performed using Matlab software (version 9.3; The MathWorks, Inc., Natick, MA, USA).