Investigations into the Influence of Solvents on the Nucleation Kinetics for Isonicotinamide, Lovastatin, and Phenacetin

Abstract

A new method of data interpretation based on classical nucleation theory is proposed in this work to elucidate the influence of solvents on the pre-exponential nucleation factor and interfacial energy using the induction time data for three crystallization systems, including isonicotinamide, lovastatin, and phenacetin. In this method, the pre-exponential nucleation factor is replaced by the intrinsic nucleation factor multiplied by temperature and divided by solution viscosity. The proposed method is applied to study the nucleation kinetics of isonicotinamide, lovastatin, and phenacetin among various solvents using the induction time data measured in this work. The results indicate that the intrinsic nucleation factor increases linearly with increasing square root of interfacial energy in various solvents for each system.

Introduction

Nucleation is the initial process for the formation of crystals in solutions. In classical nucleation theory (CNT),¹⁻³ the nucleation rate is expressed in the thermally activated Arrhenius form governed by the pre-exponential nucleation factor and interfacial energy. The interfacial energy is the energy required to create a new solid liquid interface for the formation of crystals in solutions. Traditionally, the interfacial energy is determined from the induction time measurements by assuming J ∝ t_i^–1.^1,4−7 Generally, the higher the value of interfacial energy, the more difficult it is for the solute to crystallize.

As the nucleation behavior of the same solute is greatly influenced by the choice of solvent, the study of nucleation in various solvents has long been an important research subject.⁸⁻¹⁴ Recent studies have indicated an increasing trend of the interfacial energy with the increasing corresponding solute–solvent interaction for the same solute in various solvents.¹⁵⁻¹⁸ Apart from the interfacial energy, nucleation should also be influenced by the pre-exponential factor based on CNT. However, few studies have been published regarding to the influence of the solvent type on the pre-exponential factor for nucleation.

Although the pre-exponential factor is related to the solute mobility in solutions, it is also implicitly dependent on the interfacial energy of a crystalline solid according to the derivation of CNT,^2,3,19 which nevertheless has not been experimentally validated in the literature. Nucleation in various solvents for a system can provide important information for nucleation rate parameters. In this work, the influence of the solvent type on nucleation will be investigated based on CNT to examine the implicit relationship between the pre-exponential factor and interfacial energy in various solvents using the induction time data for three common model compounds widely studied in crystal engineering, including isonicotinamide, lovastatin, and phenacetin. The chemical structures of these compounds are given in Figure 1. Various common crystal structures of these compounds have been reported in the literature.²⁰⁻²³

Figure 1.

Chemical structures of (a) isonicotinamide, (b) lovastatin, and (c) phenacetin.

Theory

The nucleation rate based on CNT is expressed as¹⁻³

1

where A_J is the nucleation pre-exponential factor, γ is the interfacial energy, k_B is the Boltzmann constant, 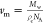is the molecular volume, and S = C₀/C_eq is the supersaturation ratio. As the solute attachment for small critical nucleus in a stirred solution should be interface-transfer control, it yields based on CNT^2,3,19

2

where D_AB is the solute diffusivity in the solution.

For simplicity, the solute diffusivity is usually estimated based on the Stokes–Einstein equation as¹

3

where r₀ is the molecular radius of solute and η is the solution viscosity. As D_AB is generally assumed to be proportional to T/η(T,S) for the same solute among various solvents,^10,13,19eq 2 becomes

4

To differentiate between the effects of γ^1/2 and T/η(T,S) on A_J, the intrinsic nucleation factor A₀ is introduced in this work as²⁴

5

Substituting eq 5 into eq 4 yields

6

Consequently, although A_J in eq 2 is dependent on D_AB among various solvents, A₀ is not related to the dependence of D_AB on T/η(T,S) among various solvents. Substituting eq 5 into eq 1 yields

7

Thus, J is expressed in terms of A₀ and γ, as opposed to J commonly adopted in terms of A_J and γ in eq 1.

In the induction time study, the nucleation event is usually assumed to correspond to a point at which the total number density of accumulated crystals in a vessel has reached a fixed (but unknown) value, f_N.²⁵⁻²⁸ Thus, one obtains at the nucleation time t_i

8

where f_N depends on the measurement device and on the substance. Note that eq 8 is consistent with J ∝ t_i^–1 reported in the literature.¹ Based on the study of 28 systems, Mersmann and Bartosch²⁹ estimated f_V = 10^–4 to 10^–3 with a detectable size of 10 μm. If the intermediate value, f_V = 4 × 10^–4, for spherical nuclei with k_V = π/6 is assumed, it leads to f_N = 7.64 × 10¹¹ m^–3 proposed by Shiau.²⁴

Substituting eq 1 into eq 8 yields

9

Experimental induction time data can be evaluated by plotting ln(1/t_i) versus 1/T³ ln²S for determination of γ from the slope and A_J from the intercept, respectively.

Substituting eq 7 into eq 8 yields

10

Experimental induction time data can be evaluated by plotting ln[η(T,S)/t_iT] versus 1/T³ ln²S for determination of γ from the slope and A₀ from the intercept, respectively.

Results and Discussion

Tables 1–3 list the experimental average induction time data of each solute in various solvents measured for various S at the specified temperature for three crystallization systems, including isonicotinamide, lovastatin, and phenacetin. The induction time measurements under each condition are repeated three times, and the deviation of the induction time is generally less than 15%. In the following, eqs 9 and 10 are applied to determine the nucleation kinetics in various solvents using the induction time data for each system.

Table 1. Experimental Induction Time Data of Isonicotinamide in Each Solvent for Various S at 303 K.

solute	solvent	S (-)	ti (s)
isonicotinamide	methanol	1.43	664
		1.45	564
		1.50	400
		1.55	370
	acetone	1.20	1077
		1.25	330
		1.30	186
		1.40	122
	acetonitrile	1.10	2879
		1.13	1338
		1.14	787
		1.20	206
	ethyl acetate	1.05	1156
		1.07	605
		1.10	589
		1.15	341

Table 3. Experimental Induction Time Data of Phenacetin in Each Solvent for Various S at 298 K.

solute	solvent	S (-)	ti (s)
phenacetin	ethanol	1.10	3507
		1.15	1223
		1.18	638
		1.20	530
	acetonitrile	1.04	3602
		1.07	842
		1.10	377
		1.113	279
	ethyl acetate	1.05	1799
		1.07	1114
		1.09	737
		1.12	504

Table 2. Experimental Induction Time Data of Lovastatin in Each Solvent for Various S at 303 K.

solute	solvent	S (-)	ti (s)
lovastatin	ethyl acetate	1.45	1139
		1.50	970
		1.60	573
		1.70	275
	ethanol	1.40	1998
		1.50	1240
		1.70	633
		1.90	357
	butyl acetate	1.40	1156
		1.45	788
		1.50	531
		1.70	363
	methanol	1.30	1389
		1.40	889
		1.50	378
		1.70	278
	acetone	1.25	846
		1.30	545
		1.40	447
		1.50	321

In the application of eq 10, the solution viscosities η(T,S) in various solvents for each system are experimentally measured in this work using a rotational viscometer (Brookfield DV2T). The measurements under each condition are repeated three times, and the deviation of the viscosity value is generally less than 6%.

Figure 2a shows the measured supersaturation dependence of solution viscosity for isonicotinamide in various solvents at 303 K, where C_eq for isonicotinamide in each solvent at 303 K is taken from a report by Hansen et al.²² (C_eq = 210 mg solute/g solvent for methanol, C_eq = 11 mg solute/g solvent for ethyl acetate, C_eq = 23 mg solute/g solvent for acetonitrile, and C_eq = 37 mg solute/g solvent for acetone). Figure 2b shows the measured induction time data fitted to eq 10 for isonicotinamide in various solvents at 303 K, where the induction time data are experimentally obtained in this work for various initial concentrations cooled to 303 K. Figure 2c shows that A₀ increases linearly with increasing γ^1/2 for isonicotinamide in various solvents at 303 K, where A₀ and γ in each solvent are determined using the corresponding induction time data fitted to eq 10. On the other hand, Figure 2d shows that no clear relationship is observed between A_J and γ^1/2 for isonicotinamide in various solvents at 303 K, where A_J and γ in each solvent are determined using the corresponding induction time data fitted to eq 9.

Figure 2.

Isonicotinamide in various solvents: (a) dependence of η on supersaturation at 303 K; (b) induction time data fitted to eq 10 at 303 K; (c) linear relationship between A₀ and γ^1/2 at 303 K; and (d) A_J vs γ^1/2 at 303 K.

As shown in Figure 2a, η increases in the order: acetone < acetonitrile < ethyl acetate < methanol. Although Figure 2c shows that A₀ increases in the order: ethyl acetate < acetonitrile < acetone < methanol, A_J in Figure 2d increases in the order: ethyl acetate < methanol < acetonitrile < acetone, which is different from the increasing order of A₀. It should be noted that η in methanol is significantly greater than that in other solvents. Consequently, although A₀ in methanol is the greatest among various solvents, A_J in methanol becomes smaller than that in acetone or acetonitrile because of eq 5.

Figure 3a shows the measured supersaturation dependence of solution viscosity for lovastatin in various solvents at 303 K, where C_eq for lovastatin in each solvent at 303 K is taken from a report by Sun et al.³⁰ (C_eq = 38 mg solute/g solvent for ethanol, C_eq = 22 mg solute/g solvent for butyl acetate, C_eq = 52 mg solute/g solvent for methanol, C_eq = 31 mg solute/g solvent for ethyl acetate, and C_eq = 105 mg solute/g solvent for acetone). Figure 3b shows the measured induction time data fitted to eq 10 for lovastatin in various solvents at 303 K, where the induction time data are experimentally obtained in this work for various initial concentrations cooled to 303 K. Figure 3c shows that A₀ increases linearly with increasing γ^1/2 for lovastatin in various solvents at 303 K, where A₀ and γ in each solvent are determined using the corresponding induction time data fitted to eq 10. On the other hand, Figure 3d shows that no clear relationship is observed between A_J and γ^1/2 for lovastatin in various solvents at 303 K, where A_J and γ in each solvent are determined using the corresponding induction time data fitted to eq 9.

Figure 3.

Lovastatin in various solvents: (a) dependence of η on supersaturation at 303 K; (b) induction time data fitted to eq 10 at 303 K; (c) linear relationship between A₀ and γ^1/2 at 303 K; and (d) A_J vs γ^1/2 at 303 K.

Figure 4a shows the measured supersaturation dependence of solution viscosity for phenacetin in various solvents at 298 K, where C_eq for phenacetin in each solvent at 298 K is taken from a report by Croker et al.²¹ (C_eq = 72 mg solute/g solvent for ethanol, C_eq = 24 mg solute/g solvent for ethyl acetate, and C_eq = 48 mg solute/g solvent for acetonitrile). Figure 4b shows the measured induction time data fitted to eq 10 for phenacetin in various solvents at 298 K, where the induction time data are experimentally obtained in this work for various initial concentrations cooled to 298 K. Figure 4c shows that A₀ increases linearly with increasing γ^1/2 for phenacetin in various solvents at 298 K, where A₀ and γ in each solvent are determined using the corresponding induction time data fitted to eq 10. On the other hand, Figure 4d shows that no clear relationship is observed between A_J and γ^1/2 for phenacetin in various solvents at 298 K, where A_J and γ in each solvent are determined using the corresponding induction time data fitted to eq 9.

Figure 4.

Phenacetin in various solvents: (a) dependence of η on supersaturation at 298 K; (b) induction time data fitted to eq 10 at 298 K; (c) linear relationship between A₀ and γ^1/2 at 298 K; and (d) A_J vs γ^1/2 at 298 K.

As shown in Figures 2a,3a, and 4a, the supersaturation dependence of solution viscosity in these systems is nearly negligible because of the narrow concentration range associated with the varied supersaturations. Table 4 lists the value of γ and the correlation coefficient R² for each line in Figures 2b, 3b, and 4b. The value of γ in each solvent for these systems agrees with the reported literature value.^27,28 Note that the correlation coefficient in each solvent for these systems exceeds the critical value of 0.900 for the 90% confidence interval and 4 points (i.e., degree of freedom = 2).

Table 4. Value of γ and the Correlation Coefficient for Each Line in Figures 2b, 3b, and 4b.

solute	solvent	γ (mJ/m2)	R2 (-)
isonicotinamide	methanol	3.32	0.973
	acetone	2.53	0.992
	acetonitrile	1.72	0.951
	ethyl acetate	0.77	0.900
lovastatin	ethyl acetate	1.94	0.915
	ethanol	1.72	0.959
	butyl acetate	1.62	0.974
	methanol	1.44	0.926
	acetone	1.08	0.965
phenacetin	ethanol	1.17	0.964
	acetonitrile	0.674	0.960
	ethyl acetate	0.632	0.943

Table 5 lists comparison between the correlation coefficient for each line in Figures 2c, 3c, and 4c and the corresponding critical value based on the 95% confidence interval. As the correlation coefficient for these systems exceeds the corresponding critical value based on the 95% confidence interval, it is concluded that A₀ increases linearly with increasing γ^1/2 in various solvents for each system. As an increasing trend of the interfacial energy with the increasing corresponding solute–solvent interaction for the same solute in various solvents has been reported in the literature,¹⁵⁻¹⁸ it is speculated that the effect of this interaction on γ is also strongly correlated with that on A₀ for the same system. Consequently, if the choice of solvent results in a greater γ because of a stronger solute–solvent interaction, it simultaneously results in a greater A₀. On the other hand, if the choice of solvent results in a smaller γ because of a weaker solute–solvent interaction, it simultaneously results in a smaller A₀.

Table 5. Comparison between the Correlation Coefficient for Each Line in Figures 2c, 3c, and 4c and the Corresponding Critical Value Based on 95% Confidence Interval.

solute	number of solvents (-)	degree of freedom (-)a	critical value (-)	R2 (-)
isonicotinamide	4	2	0.950	0.957
lovastatin	5	3	0.878	0.986
phenacetin	3	1	0.997	0.997

^aDegree of freedom = number of solvents – 2.

Conclusions

According to CNT, 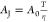is proposed in this work. Equation 10 is derived to investigate the nucleation kinetics in various solvents using the induction time data for isonicotinamide, lovastatin, and phenacetin. Although no clear relationship is observed between A_J and γ^1/2 among various solvents for each system, A₀ increases linearly with increasing γ^1/2 among various solvents for each system, which is consistent with eq 6 derived based on CNT. Based on the analyzed results of nucleation kinetics in these systems, it is proposed that A_J consists of two parts: the first part T/η is proportional to D_AB, and the other part A₀ is proportional to γ^1/2. Although A_J is dependent on D_AB among various solvents, A₀ is not related to the dependence of D_AB on T/η(T,S) among various solvents. It is speculated that both γ and A₀ are proportional to the solute–solvent interaction for the corresponding solvent.

Experimental Section

The experimental apparatus consists of a 250 mL crystallizer immersed in a programmable thermostatic water bath shown in Figure 5. The crystallizer is equipped with a magnetic stirrer at a constant stirring rate 350 rpm. The turbidity probe (Crystal Eyes manufactured by HEL limited) is used to detect the nucleation event during the induction time study.

Figure 5.

Schematic diagram of the experimental apparatus: (1) 250 mL crystallizer, (2) magnetic stirrer, (3) constant temperature water bath, (4) turbidity probe, (5) temperature probe, and (6) computer.

The induction times for three crystallization systems, including isonicotinamide (Alfa Aesar, purity 99%), lovastatin (Acros, purity 98%), and phenacetin (Acros, purity 78%) are measured in this work. Analytical grade solvents (purity 99.9%) are used to prepare the supersaturated solution. In each experiment, a 200 mL solution with the desired supersaturation is loaded into the crystallizer. The solution is held at 3 °C above the saturated temperature for 5–10 min to ensure a complete dissolution at the beginning of the experiment, which is also confirmed by the turbidity measurement. Then, the supersaturated solution is rapidly cooled to the desired temperature for the induction time measurements.

Glossary

Notation

A_J

pre-exponential nucleation factor (m^–3 s^–1)

A₀

intrinsic nucleation factor (Pa m^–3 K^–1)

C₀

initial concentration of solute molecules (m^–3)

C_eq

equilibrium concentration of solute molecules (m^–3)

D_AB

solute diffusivity (m²/s)

f_N

minimum detectable number density of accumulated crystals (m^–3)

f_V

minimum detectable volume fraction of accumulated crystals (-)

J

nucleation rate (m^–3 s^–1)

k_B

Boltzmann constant (=1.38 × 10^–23 J/K)

k_V

volume shape factor (-)

M_W

molar mass (kg/mol)

N_A

Avogadro number (=6.02 × 10²³ mol^–1)

r₀

molecular radius of solute (m)

S

supersaturation ratio (-)

T

temperature (K)

t

time (s)

t_i

induction time (s)

v_m

volume of the solute molecule (m³)

Glossary

Greek letters

γ

interfacial energy (J/m²)

ρ_C

crystal density (kg/m³)

η

solution viscosity (Pa s)

The author declares no competing financial interest.