Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2019 Oct 1;52(20):7584–7592. doi: 10.1021/acs.macromol.9b01122

Modeling Microgels with a Controlled Structure across the Volume Phase Transition

Andrea Ninarello †,‡, Jérôme J Crassous §,∥,*, Divya Paloli ∥, Fabrizio Camerin †,⊥, Nicoletta Gnan †,‡, Lorenzo Rovigatti ‡,†, Peter Schurtenberger ∥, Emanuela Zaccarelli †,‡,*
PMCID: PMC6812067  PMID: 31656322

Abstract

graphic file with name ma9b01122_0008.jpg

Thermoresponsive microgels are soft colloids that find widespread use as model systems for soft matter physics. Their complex internal architecture, made of a disordered and heterogeneous polymer network, has been so far a major challenge for computer simulations. In this work, we put forward a coarse-grained model of microgels whose structural properties are in quantitative agreement with results obtained with small-angle X-ray scattering experiments across a wide range of temperatures, encompassing the volume phase transition. These results bridge the gap between experiments and simulations of individual microgel particles, paving the way to theoretically address open questions about their bulk properties with unprecedented nano- and microscale resolution.

Introduction

As many fields of physics, colloidal science has profoundly benefited from the interplay between experiments and computer simulations. In the last decades, the epitome of colloids in suspension was represented by poly(methyl methacrylate) particles in experiments1 and by their numerical analog, the hard sphere model.2 However, in more recent years, colloids with internal degrees of freedom and tunable softness have been progressively replacing hard spheres in experimental studies.3 Among these, microgels, that is, spherical particles made of a crosslinked polymer network, with a radius ranging from 20 to 500 nm and typically synthesized with radical emulsion or precipitation polymerization, have become particularly popular4−50 for two main reasons: (i) a relatively easy preparation protocol yielding quite monodisperse particles and (ii) the possibility of finely tuning the particle properties by changing the chemical composition of the constituent polymers. In addition, in the case of thermoresponsive polymers such as poly(N-isopropylacrylamide) (PNIPAM), microgels undergo a so-called volume phase transition (VPT) at a temperature TVPT ≈ 32 °C across which they change from a swollen state at low temperature to a compact state at high temperatures. Because of their high versatility, microgels have been used to address numerous open problems in condensed matter science, including the fabrication of responsive colloidosomes,5 the nucleation of squeezable particles,6−8 the premelting within crystalline states,9 and the glass and jamming transition of soft colloids.10−13

The downside of using PNIPAM microgels is often an incomplete control on the internal particle topology,14 usually comprising a dense core and an outer corona, which is rather heterogeneous and mainly composed of long chains and few crosslinkers.4 One of the most successful descriptions of the internal topology of microgels is the so-called fuzzy sphere model, in which a strictly homogeneous core is surrounded by a loose corona.15 The use of super-resolution microscopy16−18 recently allowed the real space visualization of the internal density profiles of the microgels, revealing that the core is not really homogeneous, being denser in its inner part and progressively rarifying toward the corona.19,20

Although extensive characterization of the microgel internal structure has been provided experimentally, modeling and simulations have so far lagged behind. Indeed, the description of the inherently multiscale nature of these particles, from the polymeric constituents up to the colloidal scale, is a demanding task, even augmented by the disordered and heterogeneous structure of the network. Several numerical works modeled microgels using a polymeric crystalline lattice,21−24 whereas only recently the investigation of disordered crosslinked networks in silico has been reported.25−51 However, all methods proposed so far were unable to finely control the internal density distribution of the network and, consequently, to reproduce the properties of the experimentally available microgels in a truly quantitative fashion.

In this article, we put forward a novel numerical methodology where microgels with desired internal density profiles are generated. Building on the assembly protocol proposed in ref (26), we introduce a designing force on the crosslinkers that is able to tune the core–corona architecture independently of the system size. By carefully adjusting the force field and intensity, we obtain individual microgel particles that quantitatively reproduce the experimentally measured form factors and swelling behavior across the VPT. We also quantify the effect of coarse-graining on the structure of the in silico microgels by performing our investigation as a function of the simulated system size. Our results move numerical and experimental investigation of microgels at the single particle level closer to each other, providing a realistic description of these soft colloids at all relevant scales and paving the way to a deeper understanding of their collective behavior.

Models and Methods

Numerical Methods

We generate microgels exploiting the method put forward in ref (26) through which it is possible to obtain fully-bonded, disordered polymer networks. To this aim, we simulate the self-assembly of a binary mixture of patchy particles covered by two and four attractive patches which represent monomers and crosslinkers, respectively. During the assembly stage, the simulations are performed in a spherical cavity of radius, Z. The total number of particles is N, and the crosslinker concentration is fixed to c = 5%. Patchy particles interact via the sum of a Weeks–Chandler–Andersen (WCA) repulsion28 and a previously employed attractive patchy potential.29 In order to accelerate the network formation, we employ a bond-swapping algorithm.30 We perform NVT molecular dynamics simulations of N = 5000, 42 000, 336 000 monomers of unit mass m confined in spherical cavities, respectively, of diameter Z = 25, 50, 100 in units of bead size σ in order to maintain the final number density of the microgel roughly constant. In order to control the monomer internal density distribution, and in particular the width of the corona, we here extend the previous method of ref (26) by introducing a designing force f(r), which pulls crosslinkers toward the center of the cavity. Detailed information about the choice of the force is provided in the Results section. An illustration of the assembled microgel and of the designing force is reported in Figure 1.

Figure 1.

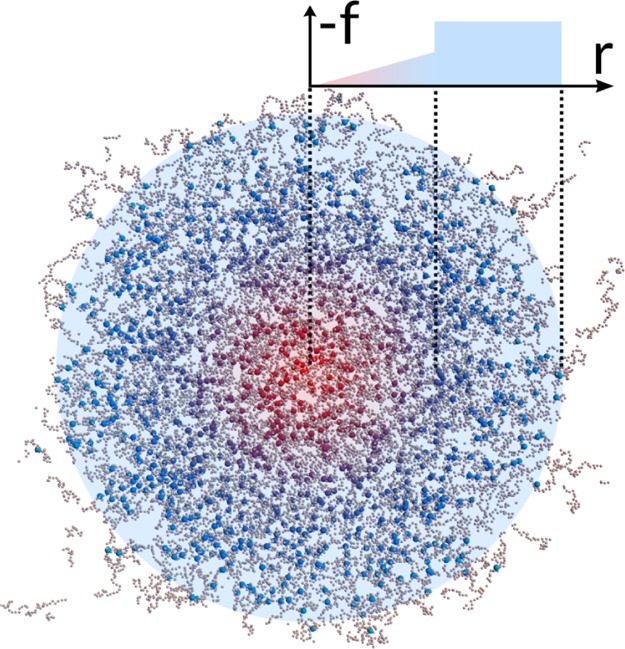
Figure 1

Open in a new tab

: Snapshot of a N ≈ 336 000 microgel slice of width 20σ. Monomers are represented in grey, whereas crosslinkers (magnified in size with respect to monomers to improve visualization) are colored from red in the center to blue in the corona, following the shape of the designing force of magnitude f, which is illustrated in the top right corner. The use of the force correctly imposes an inhomogeneous profile to the microgel, with a larger concentration of crosslinkers in the core region. At the microgel boundary, few chains are disconnected because in this representation parts of the corona are outside the field of view. The attractive force on the crosslinkers used during the assembly is made of two contributions: (i) an elastic force of spring constant k acting from the center of the cavity up to a distance Z/2 and (ii) a gravity-like force of strength g being at work between Z/2 and Z. Extensive details about this choice are provided in the Results section.

Once the network is built, we make the bonds between the monomers permanent by replacing the patchy attraction with a finite extensible nonlinear elastic potential for bonded monomers, leaving unaltered the WCA repulsion. This is the well-known Kremer–Grest potential widely employed to investigate numerically polymeric systems.31 To take into account the effect of temperature, we consider an additional solvophobic potential,26,32,33 which mimics the reduced affinity of the monomer to the solvent with increasing T, of the following form

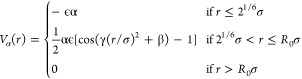graphic file with name ma9b01122_m001.jpg 1

Here, γ = π(2.25 – 21/3)−1, β = 2π – 2.25γ, R0 = 1.5, and ϵ is the unit of energy. The Vα potential is modulated by the solvophobic parameter α which controls the strength of the monomer–monomer attractive interactions. Thus, α = 0 corresponds to the case where there is no attraction and the microgel is maximally swollen.

We perform Nose–Hoover molecular dynamics runs with the LAMMPS package34 with a time step δt = 0.002 at fixed temperature kBT = 1, where kB is the Boltzmann constant. Single microgels are at first equilibrated for 1 × 106 time steps until their radius of gyration, Rg reaches a constant value. After equilibration, a production run is performed for up to 1 × 107 time steps, saving configurations every 5 × 105 steps. To improve statistics, for all system sizes, we average results over ten independent microgel topologies. We calculate the form factor of the microgels defined as

graphic file with name ma9b01122_m002.jpg 2

where the angular brackets indicate an average over independent configurations, q⃗ is the wavevector, and rij is the distance between the monomers, i and j.

From simulations, we also readily calculate the radial density profile ρ(r) as a function of the distance r from the center of mass of the microgel. The two observables, ρ(r) and P(q) allow us to compare the structure of the in silico microgels with experiments both in real and in reciprocal space.

One of the most successful models to describe microgel density distribution is the widely employed fuzzy sphere model,15 where a microgel is considered as a sphere of radius R′ with a homogeneous core surrounded by a fuzzy corona. Recent results from super-resolution microscopy have shown a slightly inhomogeneous core19 and put forward a generalization of the fuzzy sphere model with the addition of a linear dependence of the density inside the core.

In real space, this so-called extended fuzzy sphere model is represented by an error function multiplied by a linear term

graphic file with name ma9b01122_m003.jpg 3

where R′ corresponds to the radius at which the profile has decreased to half the core density, σsurf quantifies the width of the corona, and s is the slope of the linear decay. We notice that for s = 0, the standard fuzzy sphere model is recovered.

Equation 3 can be written in Fourier space as

graphic file with name ma9b01122_m004.jpg 4

We will adopt the extended fuzzy sphere model in the following to describe experimental form factors and to extract the associated density profiles that will be then compared to those directly calculated from simulations.

Experimental Details

PNIPAM microgels were synthesized by surfactant free radical polymerization as described in former studies.11,35 NIPAM (2 g) as the monomers, N,N′-methylenebisacrylamide (BIS, 0.136 g) as the cross-linker, and methacryloxyethyl thiocarbamoyl rhodamine B (2 mg dissolved in 87.8 mL of water) as the dye were polymerized by precipitation polymerization. The reaction was initiated by dropwise addition of the sodium dodecylpersulfate initiator (0.01 g in 10 mL of water) at 80 °C and run for 4 h under constant stirring at 300 rpm and nitrogen purging. The reaction mixture was passed through glass wool in order to remove particulate matter. The dispersions were purified by repeated centrifugation/redispersion cycles against an aqueous 10–3 M potassium chloride (KCl) solution. The different suspensions were further obtained by dilution of the stock suspension with the aqueous KCl solution.

Experiments were performed at the Swiss Light Source (SLS, Paul Scherrer Institute) at the cSAXS instrument. An X-ray beam with an energy of 11.2 keV was used, corresponding to a wavelength λ = 0.111 nm. The q-scale was calibrated by a measurement of silver behenate. No absolute calibration was done for the X-ray data. The sample consists of a 1 wt % microgel dispersion containing 10–3 M KCl enclosed in a 1 mm diameter sealed quartz capillary (Hilgenberg GmbH, Malsfeld, Germany) placed in a homemade thermostated aluminum sample holder ensuring temperature control with an accuracy of 0.2 °C. At least 30 2D images were taken, azimuthally integrated, transmission and background corrected, and averaged according to established procedures provided by PSI.

Experiments were carried out using a light scattering goniometer instrument from LS Instruments equipped with a HeNe laser light source with a wavelength λ = 632.8 nm and a maximum power of 35 mW. The sample was filled into a cylindrical NMR tube of diameter 5 mm and placed in the temperature-controlled index matching bath (±0.1 °C). The scattered light was detected by two APD detectors and processed by a Flex correlator in a cross-correlation configuration. A modulation unit was employed as recently described by Block and Scheffold.36 All measurements were performed on an aqueous 0.01 wt % suspension containing 10–3 M KCl. The scattering angle, θ was varied from 30° to 50° every 5°. The initial decay rate Γ0 was derived from a first cumulant analysis of the normalized field autocorrelation function. The diffusion coefficient D0 was estimated from the q2-dependence Γ0 = D0q2 and the hydrodynamic radius RH obtained via the Stokes–Einstein relation D0 = kBT/(6πηsRH), where kB, ηs, and T are the Boltzmann constant, solvent viscosity, and absolute temperature, respectively.

Results

The Choice of the Designing Force

One of the main aims of this study is to set up a protocol which is able to finely control the radial density distribution of the microgel. In this section, we discuss how to implement this feature using a designing force during the self-assembly of the patchy particles mimicking monomers (bivalent) and crosslinkers (tetravalent) in a spherical cavity.

In this work, we specifically target the reproduction of the topology of PNIPAM microgels synthesized using free radical precipitation polymerization. For these particles, the core slowly rarefies from the center toward the corona, resulting in linearly decreasing density profiles, as observed through super-resolution microscopy.19 Also, the corona should be reproduced with the correct width and shape. The fact that microgels have a denser core is the result of a faster consumption of the crosslinker with respect to NIPAM15 during the polymerization process, resulting in a larger crosslinker concentration within the core. To obtain such an inhomogenous crosslinker distribution within the microgel, we apply a force acting on the crosslinkers only. Indeed, if the force is applied on all monomers, the resulting density profiles are much more homogeneous than in experiments.

However, the exact shape that the force should assume is not obvious a priori. In order to obtain the desired density profile, we have tested different functional forms of the force and compared the results with the unperturbed case, that is, the assembly in the absence of a force that was adopted in ref (26). In all cases, the assembly is carried out by fixing the total number of particles to N = 42 000 with a fraction of crosslinkers which is equal to 5%. We confine the system in a spherical cavity of radius Z, which determines the number density and the size of the final microgel. Using too small or too large values of Z gives rise to microgels that are either too compact or too fuzzy, which is very far from the realistic core–corona structure. We thus select the intermediate value of Z = 50σ, which corresponds to a number density ρ ≈ 0.08 that provides the best conditions to reproduce experiments with the additional force on the crosslinkers. All configurations are realized using the protocol described in the Models and Methods section.

In Figure 2 we report an illustration of different choices of the designing force as a function of the distance from the center (top panels) and the associated density profiles (bottom panels) for all monomers (symbols) and for crosslinkers only (dashed lines). In the absence of a designing force, shown in Figure 2a, we find that the microgel is made of a homogeneous core and of a rapidly decaying corona. This is reflected by the flat density profile of the crosslinkers. The situation gets worse when we increase the microgel size: since the decay of the corona happens only at the microgel surface, the increase of the volume/surface ratio gives rise to an unrealistically thin corona. Ideally, instead, we would like to maintain the same ratio of the size of the corona with respect to the width of the core (corona–core ratio) when we vary the microgel size, in order to have a valid protocol that is applicable to any N. Thus, we need to control the width of the corona and to this aim, we apply an inward force with spherical symmetry inside the cavity.

Figure 2.

Figure 2

Open in a new tab

Different types of forces acting on crosslinkers (top panel) and corresponding density profiles for all particles (symbols) and for crosslinkers only (dashed lines). In the five panels, different inward forces, acting only on crosslinkers are considered: (a) no force, (b) force as in eq 5 with g = 8 × 10–3 and k = 0; (c) force as in eq 6 with m = 7 × 10–3 and t = 0.3; (d) force as in eq 5 with g = 8 × 10–3 and k = 2g1/Z = 3.2 × 10–4; and (e) force as in eq 5 with g = 8 × 10–3 and k = 4.5 × 10–5. In all cases, the integral of ρ(r) is normalized to a constant value ∫ρ(r) dr = n with n = 10, 5 for all particles and crosslinkers, respectively, to improve visualization. Data are averaged over four independent realizations obtained with the numerical protocol described in the Models and Methods section. Case (e) is the one finally adopted to compare with experiments in the following sections.

We have considered two types of forces. The first type is described by the following expression

graphic file with name ma9b01122_m005.jpg 5

where r̂ is a versor/unit vector pointing outward. Here, an elastic force with a coefficient k acts from the center up to the half radius of the cavity and a force of constant g is present for larger distances. We choose C = Z/2 as the point where the force changes type in order to reproduce a core-corona structure for the microgel. We verified that the shape of the resulting microgel is nearly the same for values of this point up to 3Z/5. The second type of force smooths out the discontinuity at Z/2, increasing continuously from the center to the cavity boundary

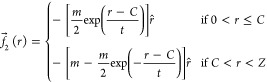graphic file with name ma9b01122_m006.jpg 6

Here, m, t determine the strength and the smoothness of the force, respectively. We use again C = Z/2.

Initially, we consider a force f of type f1 with constant g = 8 × 10–3 and k = 0, shown in Figure 2b. One can observe that, although the corona becomes larger, the core is sparser for a small r and denser close to the corona. This entails the emergence of a peak at r ≲ Z/2 showing that crosslinkers tend to accumulate around this particular distance and their number decreases toward the center of the core, which is not compatible with experimental findings for the class of microgels used in this study. As the presence of a peak could be due to the discontinuity of f at Z/2, we have also employed a smooth force of type f2 via eq 6. However, in this case, independently of the choice of the force parameters, the peak is not removed. The choice m = 7 × 10–3 and t = 0.3 provides a density profile very similar to the previous one (see Figure 2c) for both monomers and crosslinkers. One can then conclude that the additional peak is not given by the discontinuity itself but it is a consequence of the weakness or absence of the force in the region 0 < r < Z/2. Therefore, our next attempt is to maintain the corona shape of the previous examples and get rid of the peak. To this aim, we again employ a force of type f1 with g = 8 × 10–3 and k = 2g1/Z = 3.2 × 10–4. The use of k ≠ 0 corresponds to the application of an elastic force in the inner half region, eq 5 which is continuous at Z/2. Furthermore, we employ the same value of g as before in order to keep unchanged the shape of the corona. The resulting density profile is reported in Figure 2d. In this case, we notice that the density distribution inside the microgel is strongly altered, with a continuously decreasing density from the center to the cavity boundary. The absence of a core is totally different from experimental observations.

We infer that this effect is a consequence of the intensity of the force for r < Z/2, and therefore we decide to decrease the spring constant of the force as sketched in Figure 2e, resulting in a discontinuity at Z/2. Using the value k = 4.5 × 10–5, we find a density distribution in the core in agreement with the experiments, while preserving the right shape of the corona. Interestingly, in this case, the crosslinker profile is continuously decreasing from the center of the microgel and does not reflect the total profile of all monomers. This is the choice that we adopt in the following to reproduce the experimental results for all studied system sizes.

Size Effects

It is important to investigate the robustness of our results with respect to system size. Of course, the use of a large number of monomers provides a remarkable improvement in the quantitative comparison with experiments at the cost of a huge increase of the required computational resources. Hence, we need to identify the optimal system size to use in computer simulations in order to be able to tackle a specific problem. To this aim, this section is dedicated to the comparison of the structure of the three studied system sizes assembled in the presence of the force and of a large microgel in which the force has been set to zero during the assembly (unperturbed).

The effect of the microgel size is evident in the behavior of the form factors P(q), reported in Figure 3a, for the swollen state (α = 0). The numerical data for different N are compared to the experimental form factor for the lowest measured temperature (T = 15.6 °C) that we set to be the maximally swollen case in our model. In order to perform the comparison, we match the position of the first peak, qsim*, of the numerical P(q) onto that of the experiments, qexp. This procedure defines the scaling factor γ = qexp*/qsim that allows to convert numerical units into real ones.

Figure 3.

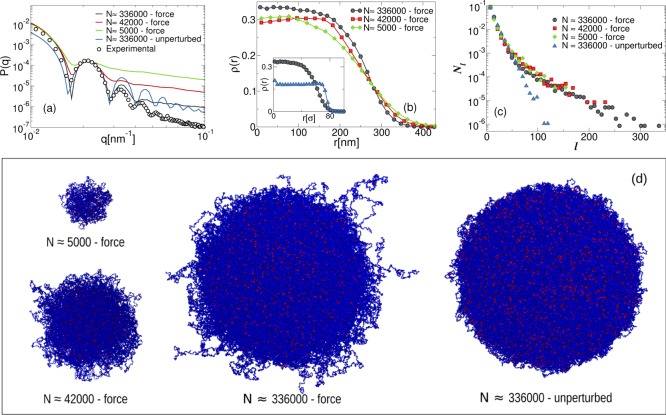
Figure 3

Open in a new tab

Size effects on the structural properties of the microgels for three system sizes obtained with the same designing force and in the unperturbed case: (a) numerical form factors P(q) in the swollen state (α = 0). The data are compared with experimental measurements for T = 15.6° C (black circles) through the rescaling factors γ336000 = 0.233, γ42000 = 0.124, γ5000 = 0.0580, and γ336000unpertubed = 0.274; (b) density profiles of the three simulated microgels, scaled on the x-axis by 1/γ for the corresponding size. Inset: density profiles for N ≈ 336 000 systems in units of σ; (c) chain length distribution Nl; and (d) snapshots with monomers represented in blue and crosslinkers in red.

We observe that the first peak of P(q) for the smallest system (N ≈ 5000) is just barely visible, whereas it becomes better defined by increasing the microgel radius by a factor of ∼2 (N ≈ 42 000), with the simultaneous appearance of a second peak. Finally, the largest system tested (N ≈ 336 000), corresponding to a further increase by a factor of ∼2 in radius, reproduces quite well three out of the four peaks observed in the experimental curve. For all sizes, the relative distance between the peaks is maintained, but upon increasing N, the high-q decay of P(q) shifts further and further down, approaching the experimental curve. It is important to point out that the observed dependence on size for P(q) is also present in real microgels of different sizes, with the peaks becoming shallower for small microgels. From the estimated values of γ for each simulated size, we get an effective size of the monomer bead, amounting to ∼4 nm for the largest microgel. We stress that in order to reach a realistic value of the PNIPAM monomer size σ ≈ 1 nm, we should increase the number of monomers up to N ≈ 2 × 107, which is unfeasible with present day computational techniques. Such a discrepancy in size between simulated and experimental microgels thus explains the high-q deviations of the numerical form factors observed in Figure 3a. In addition, the numerical form factors at large wave-vectors can be well-described by an inverse power law, P(q) ≈ q–n, with n ≈ 1 for all investigated cases. The fact that n does not vary with system size suggests that microgels with different N possess the same topological structure, at least on a mesoscopic scale. Finally, we notice that P(q) of the unperturbed microgel also shown in Figure 3a presents numerous peaks in agreement with a homogenous dense spherical system, significantly deviating from the experimental findings for both the relative position of the peaks and for the shape of the curve at small q.

To better visualize and quantify the differences between the various system sizes, we report in Figure 3b the density profiles of the three different systems as well as the corresponding snapshots in Figure 3d. As expected, the surface contributions are found to dominate for small-sized microgels of a few thousands monomers, whereas they become less and less relevant when increasing N. In all cases, the core behavior is rather similar, whereas the corona becomes more and more structured only for larger microgels. This result is the real space counterpart of the stronger pronunciation of the peaks of P(q) with increasing microgel size. In the unperturbed case, we find that the system is homogeneous and the size of the corona is rather insignificant, as it can be observed in the inset of Figure 3b and in the corresponding snapshot in Figure 3d.

Further information on the microgel internal topology is obtained by focusing on the chain length distribution as a function of N, which is reported in Figure 3c. Defining the chain length l as the sequence of monomers included between two subsequent crosslinkers, we compare its distribution Nl for all investigated cases. As shown in a previous work,37 the assembly without a designing force leads to a network structure in good agreement with the Flory theory. Instead, the introduction of the force gives rise to a larger number of chains with lengths l > 50. This effect holds for all studied N, although the probability of having longer chains clearly increases with size. Although in the absence of the force, Nl is well described by a single exponential, when the force is introduced, we have found that the same exponential only holds for relatively short chains, whereas a second exponential decay is found to describe the distribution for large chain lengths. These results confirm that, in the presence of the force upon changing N, the internal topology of the network is preserved.

Overall, on changing the system size, we observe small differences in the density profiles (also because of statistics) and more pronounced ones in the form factors. These are the consequences of the fact that the surface-to-volume contributions play a different role on the final assembled structures. Notwithstanding this, our protocol is now able to generate microgels with a similar topology and core–corona ratio independently of size and we will further show below that, thanks to this, the comparison with experiments does not depend qualitatively, but only quantitatively, on N. Consequently, the system size becomes a parameter that can be optimized in order to reproduce the properties of interest while, at the same time, reducing the computational effort.

Comparing Experiments and Simulations

Having discussed the general effect of the force on the structure of the microgels, we now perform a detailed comparison of the experimental form factors with those calculated for the largest simulated microgels for all studied temperatures. This also allows us to establish a mapping between temperature in °C and the solvophobic parameter, α.

Form Factors and Temperature Mapping

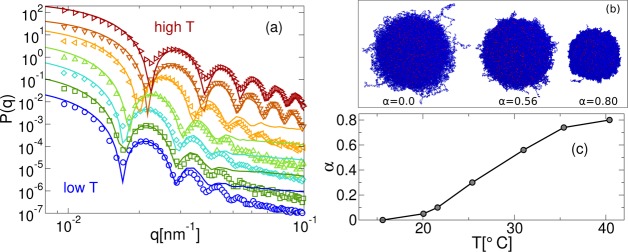
We compare the numerical and experimental P(q) for the largest studied microgels (N ≈ 336 000) in Figure 4a for several values of the temperature and corresponding α. Up to the second peak, the agreement between experiments and simulations is remarkably good at all values of T. The fact that the numerical data present peaks that are sharper and deeper could be explained by the presence of a weak polydispersity in the experimental data, that is not considered in the simulations. Most importantly, the positions of all visible peaks in the simulations are found to coincide with those in experiments. At high T, where the microgel collapses and becomes more homogeneous, the agreement improves even further, with the numerical data being able to capture the positions and heights of all measured peaks. We notice that the deviations occurring at large q are entirely attributable to the smaller size of the numerical microgels as compared to the laboratory ones, as discussed in the previous section, leading to a different structure at very short-length scales. Representative snapshots of the microgel across the VPT are shown in Figure 4b. It is evident that the inhomogeneous corona still retains a large degree of roughness even for temperatures above the VPT, differently from what was observed in the case of microgels with a more homogeneous structure.26

Figure 4.

Figure 4

Open in a new tab

(a) Comparison between experimental (empty symbols) and numerical (eq 2, full lines) form factors for N ≈ 336 000. The x-axis is rescaled by γ = qexp*/qsim = 0.2326, where q* is the position of the first peak of P(q). Different colors correspond to different temperatures, T and solvophobic parameters, α, increasing from bottom to top: T = 15.6, 20.1, 21.6, 25.4, 31.0, 35.4, 40.4 °C in experiments and α = 0.00, 0.05, 0.10, 0.30, 0.56, 0.74, 0.80 in simulations. Data at different T, α are rescaled on the y-axis with respect to the lowest temperature in order to help visualization; (b) snapshots of the N ≈ 336 000 microgels for α = 0.0, 0.56, 0.80 with monomers represented in blue and crosslinkers in red; (c) mapping between T and α.

We stress that the comparison in Figure 4a is obtained with the same value of the scaling factor, γ obtained for α = 0, that is maintained for all temperatures. However, we adjust the value of the solvophobic interaction strength α in order to capture the T-variation of P(q). The resulting relationship between α and T is illustrated in Figure 4c. We find that an approximately linear dependence holds at intermediate temperatures, showing some deviations at low and high T. Although the former may be due to the arbitrary choice of the α = 0 value with the lowest available T, the latter is more likely related to the implicit nature of the solvent employed in the simulations. These results also confirm the appropriateness of the Vα potential, tested here for the first time against experiments across the VPT.

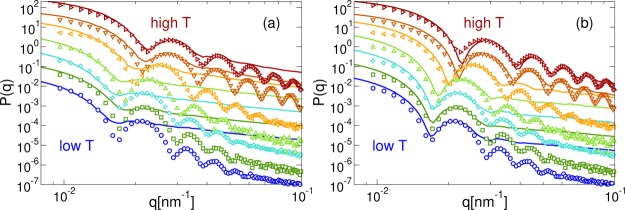
To validate the size independence of our model and the robustness of the (T,α) mapping to describe the deswelling transition of the microgels, we further compare the experimental form factors with those calculated from simulations of different system sizes using the same α values for all N. Again, we keep constant the scaling factors, γ, that we determined for α = 0. The comparisons are shown in Figure 5a,b for the small and intermediate size systems, respectively. Strikingly, we find that the swelling behavior is well captured for each system size. The peaks are indeed found in the position corresponding to those of the experimental curves, even though they are barely visible, especially for the smallest studied system. The high q deviations between experiments and simulations become more evident as N decreases, but the agreement improves at high T. From these results, we can conclude that the relationship between T and α, shown in Figure 4c is unaffected by size effects. Thus, even though smaller systems give rise to a worse q-space resolution, a size-independent swelling behavior is found for all studied N, confirming the reliability of our procedure in reproducing experimental results.

Figure 5.

Figure 5

Open in a new tab

Comparison between experimental (empty symbols) and numerical (eq 2, full lines) form factors for (a) N ≈ 5000 and (b) N ≈ 42 000. The x-axis is rescaled by γ5000 = 0.0580 and γ42000 = 0.124. Different colors correspond to different temperatures, T and solvophobic parameters, α, increasing from bottom to top: T = 15.6, 20.1, 21.6, 25.4, 31.0, 35.4, 40.4 °C in experiments and α = 0.00, 0.05, 0.10, 0.30, 0.56, 0.74, 0.80 in simulations. These are the same values used for the case N ≈ 336 000. Data at different (T, α) are rescaled on the y-axis to help visualization.

Density Profiles and Swelling Curves

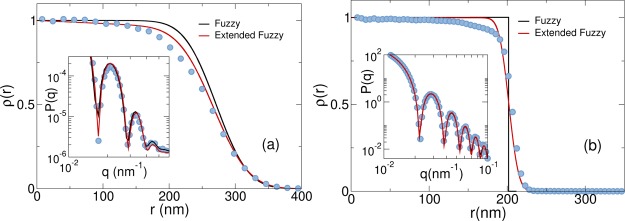
In order to directly visualize the internal structure of the microgel, we move to real space. To obtain the experimental radial density distributions from the scattering data, we need to fit the measured form factors. Building on the evidence from recent super-resolution microscopy experiments,19 we employ an extended fuzzy sphere model (eqs 3 and 4). We also calculate ρ(r) directly from simulations and then convert them to real units by rescaling the x-axis by 1/γ. We show the comparison between numerical data and the corresponding ones extracted from the fits in Figure 6 for two representative temperatures, respectively, in the swollen (a) and collapsed (b) regimes. We stress that the use of the standard fuzzy sphere model with a homogeneous core to fit the experimental P(q) not only is at odds with the super-resolution data19 but also yields density profiles that are in worse agreement with the numerical data, as shown in Figure 6. Indeed, the generalized fuzzy sphere model agrees very well with the numerical data both in the inner part of the core and in the corona. For intermediate values of r, there are some small deviations, mainly due to the nonlinear decrease of the density profile. On the other hand, the standard fuzzy sphere model shows a weaker agreement with the calculated profile, especially due to the presence of the completely homogeneous core. The disagreement becomes more evident at high T where the standard fuzzy sphere results show a step-like behavior. Instead, a continuously decreasing profile is still observed in simulations and for the generalized fuzzy sphere model, again in close agreement with each other. The quality of the extended fuzzy sphere fits to P(q) is rather good, as shown in the insets of Figure 6a,b. From the fits, we estimate the linear correction s to be always quite small, s < 5 × 10–4 nm–1. Most importantly, we find small but finite values of σsurf also above the VPT, which is consistent with the fact that, even in the collapsed state, the microgels still contain a large amount of water.38 This is confirmed by the snapshots of the collapsed state shown in Figure 4b, where many dangling ends are clearly visible in the swollen state, giving rise to a rough profile of the microgel also in the collapsed state.

Figure 6.

Figure 6

Open in a new tab

Comparing density profiles for the standard (black) and generalized (red) fuzzy sphere models with the numerical results (blue symbols) for (a) T = 15.4 °C and (b) T = 40.4 °C. All data are rescaled to 1 at x = 0 for clarity.

A summarizing comparison between numerical and experimental density profiles is reported in Figure 7a for all studied temperatures. The agreement is again found to be very good throughout the whole T range for both the core and the corona regions.

Figure 7.

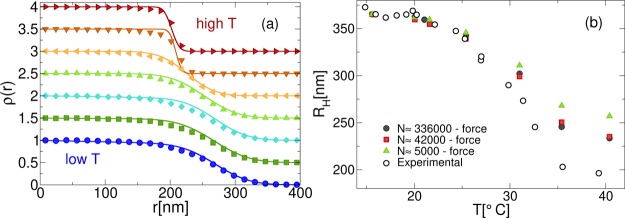
Figure 7

Open in a new tab

(a) Comparison between numerical (full symbols) and experimental (full lines) density profiles ρ(r), where the latter are obtained by fitting the form factors to the generalized fuzzy sphere model (eq 3). The numerical x-axis is rescaled by γ–1, whereas data are normalized to 1 at the center of the microgel and shifted vertically by 0.5 at different T to improve readability; (b) hydrodynamic radius, RH from experiments (black circles) and simulations (see text for its definition) for N ≈ 336 000 (blue squares), N ≈ 42 000 (red diamonds), and N ≈ 5000 (green triangles), respectively. Numerical data are rescaled to match experiments at low T.

Finally, we discuss the comparison of numerical and experimental results through the swelling curve, rather than through the form factors and/or the density profiles. This amounts to comparing the measured hydrodynamic radius, RH, measured in dynamic light scattering experiments on dilute samples, with its numerical analogue. However, the latter is not unambiguously determined in our simulations, and expensive treatments including hydrodynamic interactions would be needed for a correct assessment of its value. To circumvent this problem, we adopt an operative definition for RH, which is assumed, as in previous works,26 to be the distance at which ρ(RH) = 10–3. This choice, when converted with the determined γ factor, provides a numerical estimate of RH in good agreement with experiments for the swollen state. Experimental and numerical RH are reported in Figure 7b for the various investigated system sizes. A sharp change of RH is observed with increasing temperature both in experiments and in simulations, but for the latter, we find that the collapse is less pronounced than in experiments and it further reduces with decreasing system size. This may be due to steric effects of the bead size in the collapsed state, which are more important for small microgels. However, the dependence of RH on N seems to saturate at the largest investigated sizes, so that the discrepancy between simulations and experiments seems to remain present even by extrapolating N to realistic values (∼O(107)). A possible explanation of this result could be attributed to charge effects, which have been shown to become relevant above the VPT temperature39,40 and therefore should be taken into account for a more faithful representation of the behavior of the numerical RH at high T. A second possibility would be a fine tuning of the interaction potential between the beads beyond Vα in order to obtain a polymer chain elasticity in closer agreement with the experimental one. Such a study is currently in progress.

Conclusions

In this work, we have shown how computer simulations can realistically model thermoresponsive microgels by adopting a designing force during the network assembly, which can be tuned to quantitatively reproduce experimental form factors for a wide range of temperatures across the VPT. Even if the protocol itself is not meant to reproduce the experimental conditions of the synthesis, it is nevertheless able to generate networks with topologies that can closely match experimental data. We have shown that our method is robust in system size for swelling properties, and it reproduces very well the experimental form factors, with the agreement improving with the size of the microgels. It is worthwhile to note that the comparison is good even for microgels composed of only a few thousands monomers, which can be routinely studied in simulations. This allows us to establish a relationship between the solvophobic strength, α, used in simulations and the experimental temperature, T, finding that they are linearly related across the VPT, as expected. Such a relation is found to hold for all studied system sizes. Our results open up the possibility to address numerous questions about microgels, both at the fundamental and application levels. For example, it has already been successfully applied to the case of microgels at liquid–liquid interfaces, favorably comparing with experimental results as a function of different crosslinker concentrations.41 In addition, the protocol developed here is very general, making it possible to use it to tackle the investigation of microgels with different density profiles, such as homogeneous,42 hollow,43,44 and ultrasoft ones,45−47 synthesized in experiments nowadays. Furthermore, we plan to use the knowledge gained at the single-particle level to tailor the material properties of bulk systems in the near future.

Acknowledgments

We thank M. Paciolla for early contributions to this work. A.N., F.C., N.G., L.R., and E.Z. acknowledge financial support from the European Research Council (ERC Consolidator grant 681597, MIMIC). P.S. acknowledges financial support from the European Research Council (ERC-339678-COMPASS) and the Swedish Research Council (VR 2015-05426). J.J.C. thanks the German Research Foundation (Collaborative Research Center SFB985). SAXS experiments were performed at the cSAXS beam line of the Swiss Light Source SLS at Paul Scherrer Institute, and we gratefully acknowledge the help of the local contact, A. Menzel.

The authors declare no competing financial interest.

References

  1. Bartlett P.; van Megen W. In Granular Matter: An Interdisciplinary Approach; Mehta A., Ed.; Springer New York: New York, NY, 1994; pp 195–257. [Google Scholar]
  2. Frenkel D.; Smit B.. Understanding Molecular Simulation: From Algorithms to Applications; Computational Science Series; Academic Press, 2001; Vol. 1. [Google Scholar]
  3. Vlassopoulos D.; Cloitre M. Tunable rheology of dense soft deformable colloids. Curr. Opin. Colloid Interface Sci. 2014, 19, 561–574. 10.1016/j.cocis.2014.09.007. [DOI] [Google Scholar]
  4. Fernandez-Nieves A.; Wyss H. M.; Mattsson J.; Weitz D. A.. Microgel Suspensions: Fundamentals and Applications; Wiley-VCH, 2011. [Google Scholar]
  5. Brijitta J.; Schurtenberger P. Responsive hydrogel colloids: Structure, interactions, phase behavior, and equilibrium and nonequilibrium transitions of microgel dispersions. Curr. Opin. Colloid Interface Sci. 2019, 40, 87–103. 10.1016/j.cocis.2019.02.005. [DOI] [Google Scholar]
  6. Karg M.; Pich A.; Hellweg T.; Hoare T.; Lyon L. A.; Crassous J. J.; Suzuki D.; Gumerov R. A.; Schneider S.; Potemkin I. I.; Richtering W. Nanogels and Microgels: From Model Colloids to Applications, Recent Developments, and Future Trends. Langmuir 2019, 35, 6231–6255. 10.1021/acs.langmuir.8b04304. [DOI] [PubMed] [Google Scholar]
  7. Rovigatti L.; Gnan N.; Tavagnacco L.; Moreno A. J.; Zaccarelli E. Numerical modelling of non-ionic microgels: An overview. Soft Matter 2019, 15, 1108–1119. 10.1039/C8SM02089B. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Kim J.-W.; Fernández-Nieves A.; Dan N.; Utada A. S.; Marquez M.; Weitz D. A. Colloidal Assembly Route for Responsive Colloidosomes with Tunable Permeability. Nano Lett. 2007, 7, 2876–2880. 10.1021/nl0715948. [DOI] [PubMed] [Google Scholar]
  9. Iyer A. S. J.; Lyon L. A. Self-Healing Colloidal Crystals. Angew. Chem., Int. Ed. 2009, 48, 4562–4566. 10.1002/anie.200901670. [DOI] [PubMed] [Google Scholar]
  10. Frenkel D. Soft particles feel the squeeze. Nature 2009, 460, 465–466. 10.1038/460465a. [DOI] [Google Scholar]
  11. Scotti A.; Gasser U.; Herman E. S.; Pelaez-Fernandez M.; Han J.; Menzel A.; Lyon L. A.; Fernández-Nieves A. The role of ions in the self-healing behavior of soft particle suspensions. Proc. Natl. Acad. Sci. U.S.A. 2016, 113, 5576–5581. 10.1073/pnas.1516011113. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Alsayed A. M. Premelting at Defects Within Bulk Colloidal Crystals. Science 2005, 309, 1207–1210. 10.1126/science.1112399. [DOI] [PubMed] [Google Scholar]
  13. Mattsson J.; Wyss H. M.; Fernandez-Nieves A.; Miyazaki K.; Hu Z.; Reichman D. R.; Weitz D. A. Soft colloids make strong glasses. Nature 2009, 462, 83–86. 10.1038/nature08457. [DOI] [PubMed] [Google Scholar]
  14. Paloli D.; Mohanty P. S.; Crassous J. J.; Zaccarelli E.; Schurtenberger P. Fluid-solid transitions in soft-repulsive colloids. Soft Matter 2013, 9, 3000. 10.1039/c2sm27654b. [DOI] [PubMed] [Google Scholar]
  15. Philippe A.-M.; Truzzolillo D.; Galvan-Myoshi J.; Dieudonné-George P.; Trappe V.; Berthier L.; Cipelletti L. Glass transition of soft colloids. Phys. Rev. E 2018, 97, 040601. 10.1103/physreve.97.040601. [DOI] [PubMed] [Google Scholar]
  16. Zhang Z.; Xu N.; Chen D. T. N.; Yunker P.; Alsayed A. M.; Aptowicz K. B.; Habdas P.; Liu A. J.; Nagel S. R.; Yodh A. G. Thermal vestige of the zero-temperature jamming transition. Nature 2009, 459, 230–233. 10.1038/nature07998. [DOI] [PubMed] [Google Scholar]
  17. Lyon L. A.; Fernandez-Nieves A. The Polymer/Colloid Duality of Microgel Suspensions. Annu. Rev. Phys. Chem. 2012, 63, 25–43. 10.1146/annurev-physchem-032511-143735. [DOI] [PubMed] [Google Scholar]
  18. Stieger M.; Richtering W.; Pedersen J. S.; Lindner P. Small-angle neutron scattering study of structural changes in temperature sensitive microgel colloids. J. Chem. Phys. 2004, 120, 6197–6206. 10.1063/1.1665752. [DOI] [PubMed] [Google Scholar]
  19. Conley G. M.; Nöjd S.; Braibanti M.; Schurtenberger P.; Scheffold F. Superresolution microscopy of the volume phase transition of pNIPAM microgels. Colloids Surf., A 2016, 499, 18–23. 10.1016/j.colsurfa.2016.03.010. [DOI] [Google Scholar]
  20. Gelissen A. P. H.; Oppermann A.; Caumanns T.; Hebbeker P.; Turnhoff S. K.; Tiwari R.; Eisold S.; Simon U.; Lu Y.; Mayer J.; Richtering W.; Walther A.; Wöll D. 3D Structures of Responsive Nanocompartmentalized Microgels. Nano Lett. 2016, 16, 7295–7301. 10.1021/acs.nanolett.6b03940. [DOI] [PubMed] [Google Scholar]
  21. Conley G. M.; Aebischer P.; Nöjd S.; Schurtenberger P.; Scheffold F. Jamming and overpacking fuzzy microgels: Deformation, interpenetration, and compression. Sci. Adv. 2017, 3, e1700969 10.1126/sciadv.1700969. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Bergmann S.; Wrede O.; Huser T.; Hellweg T. Super-resolution optical microscopy resolves network morphology of smart colloidal microgels. Phys. Chem. Chem. Phys. 2018, 20, 5074–5083. 10.1039/c7cp07648g. [DOI] [PubMed] [Google Scholar]
  23. Siemes E.; Nevskyi O.; Sysoiev D.; Turnhoff S. K.; Oppermann A.; Huhn T.; Richtering W.; Wöll D. Nanoscopic Visualization of Cross-Linking Density in Polymer Networks with Diarylethene Photoswitches. Angew. Chem., Int. Ed. 2018, 57, 12280–12284. 10.1002/anie.201807741. [DOI] [PubMed] [Google Scholar]
  24. Escobedo F. A.; de Pablo J. J. Molecular simulation of polymeric networks and gels: phase behavior and swelling. Phys. Rep. 1999, 318, 85–112. 10.1016/s0370-1573(99)00012-5. [DOI] [Google Scholar]
  25. Jha P. K.; Zwanikken J. W.; Detcheverry F. A.; de Pablo J. J.; Olvera de la Cruz M. Study of volume phase transitions in polymeric nanogels by theoretically informed coarse-grained simulations. Soft Matter 2011, 7, 5965. 10.1039/c1sm05264k. [DOI] [Google Scholar]
  26. Kobayashi H.; Winkler R. Structure of Microgels with Debye-Hückel Interactions. Polymers 2014, 6, 1602–1617. 10.3390/polym6051602. [DOI] [Google Scholar]
  27. Ahualli S.; Martín-Molina A.; Maroto-Centeno J. A.; Quesada-Pérez M. Interaction between Ideal Neutral Nanogels: A Monte Carlo Simulation Study. Macromolecules 2017, 50, 2229–2238. 10.1021/acs.macromol.6b02333. [DOI] [Google Scholar]
  28. Nikolov S.; Fernandez-Nieves A.; Alexeev A. Mesoscale modeling of microgel mechanics and kinetics through the swelling transition. Appl. Math. Mech. 2017, 39, 47–62. 10.1007/s10483-018-2259-6. [DOI] [Google Scholar]
  29. Gnan N.; Rovigatti L.; Bergman M.; Zaccarelli E. In Silico Synthesis of Microgel Particles. Macromolecules 2017, 50, 8777–8786. 10.1021/acs.macromol.7b01600. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Moreno A. J.; Lo Verso F. Computational investigation of microgels: synthesis and effect of the microstructure on the deswelling behavior. Soft Matter 2018, 14, 7083–7096. 10.1039/c8sm01407h. [DOI] [PubMed] [Google Scholar]
  31. Rovigatti L.; Gnan N.; Ninarello A.; Zaccarelli E. Connecting Elasticity and Effective Interactions of Neutral Microgels: The Validity of the Hertzian Model. Macromolecules 2019, 52, 4895–4906. 10.1021/acs.macromol.9b00099. [DOI] [Google Scholar]
  32. Weeks J. D.; Chandler D.; Andersen H. C. Role of Repulsive Forces in Determining the Equilibrium Structure of Simple Liquids. J. Chem. Phys. 1971, 54, 5237–5247. 10.1063/1.1674820. [DOI] [Google Scholar]
  33. Rovigatti L.; Nava G.; Bellini T.; Sciortino F. Self-Dynamics and Collective Swap-Driven Dynamics in a Particle Model for Vitrimers. Macromolecules 2018, 51, 1232–1241. 10.1021/acs.macromol.7b02186. [DOI] [Google Scholar]
  34. Sciortino F.Three-body potential for simulating bond swaps in molecular dynamics. Eur. Phys. J. E: Soft Matter Biol. Phys. 2017, 40, DOI: 10.1140/epje/i2017-11496-5. [DOI] [PubMed] [Google Scholar]
  35. Kremer K.; Grest G. S. Dynamics of entangled linear polymer melts: A molecular-dynamics simulation. J. Chem. Phys. 1990, 92, 5057–5086. 10.1063/1.458541. [DOI] [Google Scholar]
  36. Soddemann T.; Dünweg B.; Kremer K. A generic computer model for amphiphilic systems. Eur. Phys. J. E: Soft Matter Biol. Phys. 2001, 6, 409–419. 10.1007/s10189-001-8054-4. [DOI] [Google Scholar]
  37. Verso F. L.; Pomposo J. A.; Colmenero J.; Moreno A. J. Simulation guided design of globular single-chain nanoparticles by tuning the solvent quality. Soft Matter 2015, 11, 1369–1375. 10.1039/c4sm02475c. [DOI] [PubMed] [Google Scholar]
  38. Plimpton S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. 10.1006/jcph.1995.1039. [DOI] [Google Scholar]
  39. Mohanty P. S.; Paloli D.; Crassous J. J.; Zaccarelli E.; Schurtenberger P. Effective interactions between soft-repulsive colloids: Experiments, theory, and simulations. J. Chem. Phys. 2014, 140, 094901. 10.1063/1.4866644. [DOI] [PubMed] [Google Scholar]
  40. Block I. D.; Scheffold F. Modulated 3D cross-correlation light scattering: Improving turbid sample characterization. Rev. Sci. Instrum. 2010, 81, 123107. 10.1063/1.3518961. [DOI] [PubMed] [Google Scholar]
  41. Rovigatti L.; Gnan N.; Zaccarelli E. Internal structure and swelling behaviour of in silico microgel particles. J. Phys.: Condens. Matter 2017, 30, 044001. 10.1088/1361-648x/aaa0f4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Bischofberger I.; Trappe V. New aspects in the phase behaviour of poly-N-isopropyl acrylamide: systematic temperature dependent shrinking of PNiPAM assemblies well beyond the LCST. Sci. Rep. 2015, 5, 15520. 10.1038/srep15520. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Truzzolillo D.; Sennato S.; Sarti S.; Casciardi S.; Bazzoni C.; Bordi F. Overcharging and reentrant condensation of thermoresponsive ionic microgels. Soft Matter 2018, 14, 4110–4125. 10.1039/c7sm02357j. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Del Monte G.; Ninarello A.; Camerin F.; Rovigatti L.; Gnan N.; Zaccarelli E.. Numerical Insights on Ionic Microgels: Structure and Swelling Behaviour. 2019, arXiv preprint arXiv:1905.07025 10.1039/c9sm01253b. [DOI] [PubMed] [Google Scholar]
  45. Camerin F.; Fernández-Rodríguez M. Á.; Rovigatti L.; Antonopoulou M.-N.; Gnan N.; Ninarello A.; Isa L.; Zaccarelli E. Microgels Adsorbed at Liquid-Liquid Interfaces: A Joint Numerical and Experimental Study. ACS Nano 2019, 13, 4548–4559. 10.1021/acsnano.9b00390. [DOI] [PubMed] [Google Scholar]
  46. Mueller E.; Alsop R. J.; Scotti A.; Bleuel M.; Rheinstädter M. C.; Richtering W.; Hoare T. Dynamically Cross-Linked Self-Assembled Thermoresponsive Microgels with Homogeneous Internal Structures. Langmuir 2018, 34, 1601–1612. 10.1021/acs.langmuir.7b03664. [DOI] [PubMed] [Google Scholar]
  47. Nayak S.; Gan D.; Serpe M. J.; Lyon L. A. Hollow Thermoresponsive Microgels. Small 2005, 1, 416–421. 10.1002/smll.200400089. [DOI] [PubMed] [Google Scholar]
  48. Scotti A.; Brugnoni M.; Rudov A. A.; Houston J. E.; Potemkin I. I.; Richtering W. Hollow microgels squeezed in overcrowded environments. J. Chem. Phys. 2018, 148, 174903. 10.1063/1.5026100. [DOI] [PubMed] [Google Scholar]
  49. Gao J.; Frisken B. J. Cross-Linker-FreeN-Isopropylacrylamide Gel Nanospheres. Langmuir 2003, 19, 5212–5216. 10.1021/la0269762. [DOI] [Google Scholar]
  50. Bachman H.; Brown A. C.; Clarke K. C.; Dhada K. S.; Douglas A.; Hansen C. E.; Herman E.; Hyatt J. S.; Kodlekere P.; Meng Z.; Saxena S.; Spears M. W. Jr.; Welsch N.; Lyon L. A. Ultrasoft, highly deformable microgels. Soft Matter 2015, 11, 2018–2028. 10.1039/c5sm00047e. [DOI] [PubMed] [Google Scholar]
  51. Virtanen O. L. J.; Mourran A.; Pinard P. T.; Richtering W. Persulfate initiated ultra-low cross-linked poly(N-isopropylacrylamide) microgels possess an unusual inverted cross-linking structure. Soft Matter 2016, 12, 3919–3928. 10.1039/c6sm00140h. [DOI] [PubMed] [Google Scholar]

Articles from Macromolecules are provided here courtesy of American Chemical Society

RESOURCES