Abstract
The most important index of obstructive sleep apnea/hypopnea syndrome (OSAHS) is the apnea/hyponea index (AHI). The AHI is the number of apnea/hypopnea events per hour of sleep. Algorithms for the screening of OSAHS from pulse oximetry estimate an approximation to AHI counting the desaturation events without consider the sleep stage of the patient. This paper presents an automatic system to determine if a patient is awake or asleep using heart rate (HR) signals provided by pulse oximetry. In this study, 70 features are estimated using entropy and complexity measures, frequency domain and time-scale domain methods, and classical statistics. The dimension of feature space is reduced from 70 to 40 using three different schemes based on forward feature selection with support vector machine and feature importance with random forest. The algorithms were designed, trained and tested with 5000 patients from the Sleep Heart Health Study database. In the test stage, 10-fold cross validation method was applied obtaining performances up to 85.2% accuracy, 88.3% specificity, 79.0% sensitivity, 67.0% positive predictive value, and 91.3% negative predictive value. The results are encouraging, showing the possibility of using HR signals obtained from the same oximeter to determine the sleep stage of the patient, and thus potentially improving the estimation of AHI based on only pulse oximetry.
Keywords: Computer science, Biomedical engineering, Sleep apnea, Pulse oximetry, Heart rate, Automatic sleep staging
1. Introduction
Sleep plays a very important role in well-being and physiological recovery. The gold standard test for the study of sleep pathologies is polysomnography (PSG), which consists of the simultaneous recording of several physiological signals such as electroencephalography (EEG), electrocardiography (ECG), electromiography (EMG), respiratory effort, oronasal airflow, peripheral oxygen saturation (), and electrooculography (EOG), among others. The PSG is supervised by a technician in a sleep medical center specially conditioned, and its analysis requires a tedious scoring, often by hand with the help of a software [1]. The scoring has a lot of variability among different professionals [2]. Due to these characteristics and the limited number of beds, the PSG is cost intensive and its availability is scarce, generating long waiting lists. Furthermore, many patients are reluctant to spend the night in the sleep laboratory or have difficulty to falling sleep [3].
Due to complexity, limited capacity, and high costs associated to the PSG, there is an increasing interest in reducing the need for complete PSG studies. Many approaches have been proposed to perform screening of sleep pathologies. Pulse oximeter is an ideal choice for the screening due to its low cost, accessibility and simplicity [3]. For this, it stands out among other techniques, such as cardiac and respiratory sounds [4], ECG [5], nasal airway pressure [6] and combinations of various signals [7].
Total sleep time is an important outcome of PSG for diagnosing several sleep disorders. One of these pathologies, in which the authors are currently interested, is the obstructive sleep apnea/hypopnea syndrome (OSAHS). OSAHS is one of the most prevalent sleep disorders [8] and it is characterized by repetitive interruptions of the respiratory flow, caused by pharyngeal collapses during sleep. These upper airway obstructions produce partial or total reduction in the airflow. This syndrome causes increased frequency of awakenings, reduced blood oxygen saturation, sleep fragmentation and, consequently, excessive daytime sleepiness [9]. Furthermore, it is associated with a high risk of acute pulmonary and systemic hypertension, nocturnal arrhythmias, ventricular failure and stroke, cognitive decline, and sudden death [10]. The potential social consequences of this disease, such as accidents, increased morbidity and unproductiveness, among others, make it one of the main public health problems in the world. The number of patients diagnosed and treated for OSAHS has increased drastically in the last few years [11], [12]. Sleep apnea can be easily treated applying a continuous positive airway pressure through the nose using a tight mask [9].
The most important index of OSAHS severity is the apnea/hypopnea index (AHI), which represents the number of apnea/hypopnea events per hour of sleep. The OSAHS is classified as normal, mild, moderate or severe if it belongs to the intervals [0, 5), [5, 15), [15, 30) or greater than 30 apnea or hypopnea events per hour of sleep, respectively [13]. This implies the need to know if the patient was sleeping (in any stage of sleep) or awake when an respiratory event was detected.
The upper airway obstructions associated with apnea/hypopnea events results in a drop of oxygen saturation levels [14]. Several works have been carried out with the aim of detecting these events using pulse oximeter signals [15], [16]. In these studies, the oxygen desaturation index (ODI) is estimated as an approximation to the AHI. However, it is important to point out that these works do not take into account whether the patient is or not asleep. In some of these works, the ODI was reported as a relation between the number of detected desaturations and the total sleep time (TST) estimated using the EEG, which was previously assumed as not accessible. In some other publications, the total time of the study (TT) was used, which introduces a significant bias (the value of AHI will be underestimated by this approach) [17]. TST estimation from the same signals used to estimate the number of apneas/hypopnea events could improve the reported AHI without increasing the complexity of the study. Being able to estimate the total sleep time from signals obtained with a pulse oximeter will be a great complement to improve these screening devices.
Although we are focused on the diagnosis of apnea, the results of this work may be useful for many other applications. For example, drowsy drivers is an important factor in most traffic accidents. Automatic systems with the goal of detect and prevent sleep are an active research field. Most of them use cameras to assess the level of sleepiness by detection of physiological events related to fatigue and drowsiness [18]. Due to its characteristics, our algorithm can be part of one of these systems and provide complementary information. Daily life applications related with sleep measures from personal health monitoring devices are currently under spotlight [19]. In summary, any critical work in which the sleepiness can cause accidents and material or human losses can benefit from applications such as the one developed in this paper.
In the literature, there are many researchers addressing the automatic sleep staging problem. The state of the art results are obtained using EEG signals, sometimes extracting information from other complementary signals such EOG, EMG, and others. In pursuit of obtain home-based diagnosis devices, there are many studies on automatic sleep staging with signals whose recording and processing is simpler than EEG.
Many authors have studied the dynamic of HR variability, obtaining by processing the ECG, during sleep [20], [21]. These works have made possible that Adnane et al. [22], Xiao et al. [23] and Yücelbaş [24] used ECG to classify the sleep stage. Adnane only considered two classes, awake and asleep, while Yücelbaş and Xiao considered three, awake, REM and non-REM stages. When their results are analyzed, it can be seen that the works that considered longer periods obtained better results than those that used 30 s segments, based on the rules published by the AASM [1]. However, considering longer periods is an unrealistic situation since as the length increases. There is a greater probability that the segments contain a mixture of awake and asleep stages. This problem will be addressed in more detail in the discussion section.
There are other works that try to exploit the relationship between HR and sleep stages in the same way as those that use ECG, but using photoplethysmography (PPG). Beattie et al. [25] used PPG signals and accelerometer, considering 5 classes. The database was composed by self-reported normal sleepers. The Uçar et al. research [26] used PPG and heart rate variability (HRV) from PPG. They classified in awake and asleep. An important limitation of all these works is that the size of the databases used is small, so it is difficult to clearly determine their generalization capability.
Motivated by the drawbacks of screening devices for sleep disorders, as well as by the current challenges to estimate sleep measures through mobile and wearable devices, and being inspired by these previous researchers, the aim of this work is to classify the sleep stage in awake (W) or asleep (S), regardless of the corresponding sleep stage. We only have an estimate of the heart rate (HR) from PPG, instead of ECG, which is affected by the lower temporal and frequency resolutions. Further, we use a large database with the intention that the results have the minimum risk of overfitting. The classification will be done applying machine learning techniques. In the feature extraction stage, we use information theory tools, such as dispersion [27], approximate [28], sample [29], fuzzy [30] and Renyi [31] entropies, and methods for frequency and time-frequency analysis [32]. Further, classical statistics were calculated. We suppose these features can be able to discriminate the different dynamics presented in HR series corresponding to awake and sleep stages [20], [21]. Then, we applied a feature selection scheme together with the classification. Finally, the selected system is tested with patients data never used in training.
2. Materials
2.1. Oximetry signals
PPG is an optic measurement technique widely used in both clinic and research. It detects changes in blood volume through a device consisting of a light source and a photodetector. The PPG signal results from the light interaction with biological tissues, namely, the balance between scattering, absorption, reflection, transmission and fluorescence of the signal. Several physiological variables can be estimated directly and indirectly from the PPG signal [33].
The arterial oxygen saturation () is the fraction of saturated hemoglobin relative to total hemoglobin in blood. The pulse oximeters, devices based on PPG, allow a noninvasive estimation of , commonly referred as peripheral oxygen saturation (), using two light sources (red and infrared) that presents absorption differences due to the hemoglobin presence [34]. The is very useful for the screening of OSAHS, since the number of apnea/hypopnea events can be approximate counting the number of desaturations.
In addition, pulse oximeters provide a HR estimation from the pulsatile component of PPG. The most common algorithms consist of digital filters and zeros crossing detector [33], although there are many research works with the objective of developing algorithms to reduce the movement artifacts that greatly affect the signal [35].
2.2. HR and sleep stages
The sleep has an orderly internal structure in which different stages are determined. The sleep stages are classified in wakefulness, two stages of light sleep, two of deep sleep and rapid eye movement sleep (REM), which are differentiated in the basis of typical patterns and waveforms in signals of EEG, EOC and EMG. These sleep stages are labeled in consecutive 30 s long segments. This results in a sleep profile or hypnogram.
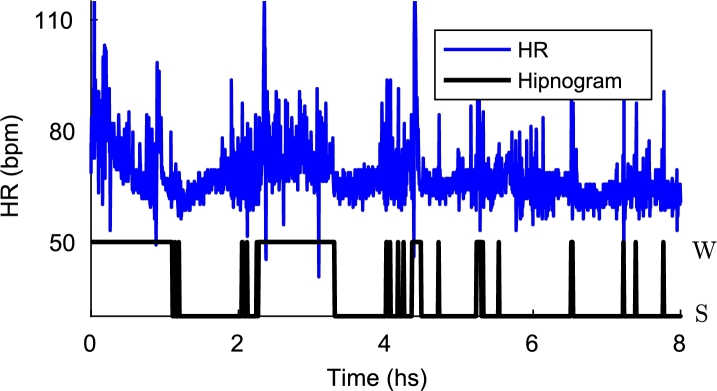
The regulation of the autonomic nervous system changes with the sleep stages. In this way, HR, blood pressure, and respiratory rate decrease to adapt a reduced metabolism during sleep. The average HR falls steadily from the waking states to deep sleep. During REM, HR increases lightly and presents greater variability than during wakefulness [20]. The relationship between sleep stages and HR is shown in the Fig. 1. This work is based on these physiological phenomena in order to discriminate the states of awake and asleep.
Figure 1.
Hypnogram and HR. The states of awake (W) and asleep (S) are shown in the hypnogram (black). The dynamical changes between these states can be noticed in the HR signal (blue).
2.3. Database
The set of biomedical signals used in this article was obtained from the Sleep Heart Health Study dataset. This dataset was designed to investigate the relationship between sleep-disordered breathing and cardiovascular consequences. SHHS database is divided into two subsets of PSG records, the SHHS Visit 1 and SHHS Visit 2, obtained several years later with the aim of studying the evolution of patients. The PSG records were acquired automatically at home of patients with supervision of specialized technicians [36]. Full details can be found in [37].
The SHHS contains several signals corresponding to a PSG study collected on twelve channels: , HR, chest wall and abdomen movement, nasal/oral airflow, body position, EEG (two central, one for redundancy in case of failure/loss), bilateral EOG, chin EMG and ECG. The oximeter provides two signals, HR and , and it also gives a quality status signal that provides information about the sensor connection status. In this work only the HR and the quality status signal are used. In future works we will incorporate the signal to detect apnea/hypopnea events.
In SHHS database, signals have a sampling rate of 1 Hz, resolution of 1% and accuracy of in the range of 70% to 100%. Their performance significantly decreases for values below this range. The HR signal based on pulse oximeter has a sampling rate of 1 Hz and a precision of 3 beats per minute.
In this work, the SHHS visit 1 was used. According to the SHHS 1 Protocol, all the records were processed with a software system to provide preliminary estimates of the AHI. Then, the recordings were manually scored on screen, with annotations of sleep stages, arousals, oxygen desaturation, and respiratory events. Table 1 shows a summary of the characteristics of the database used. 5000 patients were randomly selected to be used in the experiments detailed below. For detail on the sleep stage annotation protocol, refer to [36], [37].
Table 1.
Characteristics of the study population in SHHS Visit 1.
| SHHS 1 (min, max) | |
|---|---|
| n | 5804 |
| Age (years) | 63.1 ± 11.2 (39.0, 90.0) |
| Female (%) | 52.3% |
| Epworth sleepiness scale | 7.8 ± 4.4 (0.0, 24.0) |
| Arousal index (/hr) | 19.2 ± 10.7 (0.0, 110.4) |
| AHI (/hr) | 9.6 ± 12.7 (0.0, 115.8) |
| TST (min) | 587.7 ± 107.6 (35.0, 858.0) |
| BMI (kg/m2) | 28.2 ± 5.1 (18.0, 50.0) |
| TST/TT (%) | 74.2% |
3. Methods
3.1. System overview
The scheme of the algorithm is shown in 2. First, the HR signals from pulse oximeter were preprocessed and segmented into windows of length L for the 5000 patients, as indicated below. SHHS dataset was splitted into two subsets: 500 subjects were randomly selected in order to optimize the design and to select the features (top of Fig. 2), and the remaining 4500 subjects were used to train and test the classifier (bottom of Fig. 2).
Figure 2.
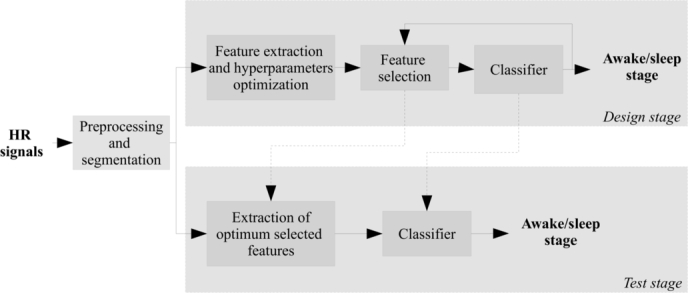
Scheme of the algorithm. In the design stage, the feature extraction and selection is performed. In the test stage, the design system is tested with new data.
In the design stage, a set of features was extracted from each window, optimizing its hyperparameters in order to maximize the area under ROC curve (AUC) [38]. Then, the features were standardized to have zero mean and unit variance. The feature selection was performed along with the classification, using two different schemes: forward feature selection (FFS) and support vector machine (SVM), and variable selection based on random forest (RF). The k-fold cross validation technique was used to validate the classifier performance.
Finally, the best system obtained in the design stage was trained and validated with the remaining 4500 subjects using a k-fold approach. There is not a formal rule to choose k as long as the size of the database allows to obtain k partitions with a sufficient number of observations to calculate the reliable statistics. We set for this problem based on recommendations from [39], [40].
3.2. Preprocessing
The pulse oximeter signals available in SHHS dataset provide a complementary signal with information about the state of the oximeter. The status signal was used to mask the HR signal, removing the invalid data. Then, we linearly interpolate between the previous and posterior valid data.
Then, the HR records were standardized in order to reduce inter-subject variability. Then, the signals were segmented into non-overlap windows of length L, considering only the segments corresponding completely to a single state: awake or asleep. The values of L were varied from to in steps of 30. No other processing for artifact or noise reduction was used, as our objective is to keep the method as simple as possible, to operate in the raw signal, aiming at low power wearable devices.
3.3. Features
The information contained in the HR signal was summarized into a set of features based on information theory, frequency and time-frequency domain, and classic statistics. In total, 70 features were extracted. A brief description of the most relevant ones is given in this section.
3.3.1. Approximate entropy
Approximate entropy (ApEn), introduced by Pincus [28], is a measure of data regularity. A greater irregularity in a signal produces a higher ApEn value, and vice versa. For an N-dimensional time series, ApEn depends on three parameters: the embedding dimension m, the embedding delay τ and the threshold r. ApEn has been widely used as a non-linear feature to classify different dynamics.
Let a time series of length N. Then, state vectors can be reconstructed doing , where [41]. Then, the ApEn is defined as [28]:
| (1) |
with
| (2) |
where is a distance measure between state vectors and is a kernel function. Usually the distance measure is the Euclidean norm or the Maximum norm. The most used kernel functions are the Heaviside step function [28] and the Gaussian kernel [42].
In this work, the Euclidean norm and Gaussian kernel were used. Three features related to ApEn were extracted. The first one is the value of ApEn estimated with the parameters r, τ and m maximizing the AUC. The other two features are the maximum of ApEn and the value of r where this maximum is located [43]. In these cases, both m and τ were selected in order to maximize the AUC, as before.
3.3.2. Sample entropy
ApEn is a highly biased estimator due to the inclusion of self-matches, and this bias is more noticeable in short data lengths. To overcome this limitation, Richman and Moorman proposed the Sample Entropy (SampEn). SampEn is largely independent of record length and shows a higher consistency than ApEn [29]. Following a notation similar to that used in ApEn, the equation for determining SampEn is given as
| (3) |
with
| (4) |
where is a distance measure between state vectors and is a kernel function. In this work, we chose an Euclidean norm and a Heaviside step function.
For high r thresholds, , and for small values of r, SampEn has a high variance. As the authors propose, we considered only the first vectors of length m when computing , ensuring that, for , and were defined.
3.3.3. Fuzzy entropy
Fuzzy entropy (FuzEn) is analogous to SampEn, but the similarity degree (kernel function ) is calculated through a fuzzy function defined by . According to [30], FuzEn is more consistent and less dependent on the data length than SampEn.
3.3.4. Dispersion entropy
SampEn is a powerful tool to assess the dynamical characteristics of time series, but it is computationally expensive. On the other hand, permutation entropy (PermEn) quantify the irregularity of the time series based on analysis of permutation patterns, which depends on comparisons of neighboring values [44]. PermEn does not consider differences between amplitudes.
Dispersion Entropy (DE) was proposed to overcome these limitations of PermEn and SampEn [27]. For a given time series of length N, the DE algorithm includes the following steps. First, is assigned to c classes. For this, is mapped to from a normal cumulative distribution function. Then, each is assigned to an integer from 1 to c as with . Finally, given an embedding dimension m and delay τ, the state vectors are reconstructed by .
Each time series is mapped to a dispersion pattern , where , , …, . Then, for each of potential dispersion pattern, relative frequency is obtained by . Finally, based on the definition of the Shannon entropy, DE is calculated by
| (5) |
3.3.5. Extension of entropy measures to the joint time-frequency () or time-scale () domains
A measure of the uniformity of signal energy distribution in the frequency domain can be defined by interpreting a power spectral density (PSD) as a quasi-probability distribution function [45], and using entropy concepts. A larger f-domain entropy value implies more uniformity and vice versa. These concepts can be extended to () or () domains in order to discriminate signals with similar bandwidth, but with different variations over time [46]. Let be a real time series of length N and its Fourier Transform (FT) of length M. The spectral entropy () is defined as
| (6) |
where .
The () or () Shannon entropy is an extension of the (). It is obtained by replacing the FT with a time-frequency or time-scale distribution . The () Shannon entropy is
| (7) |
where .
These ideas can also be used to extend the Renyi Entropy as
| (8) |
In this work, we set [46].
Inspired by these concepts and multiresolution entropy [47], we propose a measure of entropy through the scales for this application. For each scale k of the () representation , we calculate an entropy value by
| (9) |
This entropy measure allows to estimate the uniformity of signal energy distribution for a simple scale. This is maximum when the energy is constant over the time.
We normalize in order to fulfill the probability density function properties. Thus, the entropy measure does not vary with the magnitude of energy, but is only based on its distribution over time. As in the previous case, we set . From now on, these features will be called time-scale multiresolution Renyi entropy (TSMRE).
The time-scale distribution was obtained using continuous wavelet transform (CWT) using 32 scales and Haar's wavelet. Although this wavelet is very simple, and it has the disadvantage of being discontinuous and therefore not derivable, for this work it was the wavelet that showed the best performance. This is due to the fact that the HR signal provided by the pulse oximeter has a large quantization step and thus can be well approximated by piecewise constant functions.
3.3.6. Lempel-Ziv complexity
Lempel-Ziv complexity (LZ) [48] is a metric that has been widely used in biological signals for recognition of structural regularities. The LZ is nonparametric and simple to compute. First, the discrete-time signal is converted into a symbol sequence by comparison with thresholds. Then, complexity measure can be calculated as referenced in [49]. In the context of biomedical signal analysis, typically the signal is converted into a binary sequence using the median. In this work, we obtain better performance setting two thresholds using 0.33 and 0.66 quantiles. That is, we use a sequence of three different symbols.
The features described previously allow to quantify the regularity of the data. As we mentioned in the subsection 2.2, the HR shows greater variability and mean value during wakefulness. From this, these measures were proposed in order to exploit this difference in the regularity or complexity of the data. These measures have proven useful in several works on biomedical signals [50]. Further, our previous work [51] showed the potential of these features for classification.
3.3.7. Frequency domain based features
Spectral analysis of the heart rate variability signals allows to quantify the influence of the autonomic nervous system [52]. These characteristics are selected here on the assumption that they will provide information about the sleep stage, as discussed in [53]. Very low frequency (VLF) (] Hz, low frequency (LF) (] Hz and high frequency (HF) (] Hz components were obtained. Further, the ratio LF/HF, normalized HF and VF and total power (TP) are used [52]. Spectral estimation is performed using periodogram.
3.3.8. () or () signal-based features
We extracted the 15 features discussed in [54] that allow to characterize the non-stationary nature of the HR. This capability is potentially useful for discriminating sleep stages. The features are briefly explained below.
Several features are based on singular value decomposition (SVD) of the () or () representation . The SVD divides the matrix ρ into two subspaces, signal subspace and an orthogonal alternate subspace of the form , where U and V are and unitary matrices, respectively. S is an diagonal matrix with non-negative real numbers. The diagonal entries of S are known as the singular values of ρ.
The first and second features are the maximum () and variance () of the singular values of ρ. The third feature is a complexity measure given by
| (10) |
where .
The fourth feature is the energy concentration measure, and it is defined as
| (11) |
Then, 8 features related to the sub-band energy are obtained integrating over time. That is
| (12) |
where and .
Finally, in addition to these features, we calculated ()-domain mean and standard deviation by extension from classical statistics and () Renyi entropy by equation (8).
3.3.9. Autocorrelation-based features
We extracted some features related to the autocorrelation series. In general, the autocorrelation of awake segments has periodicities and is smoother than asleep segments. In order to differentiate them, we compute the first minimum and the first zero-crossing of the series. Then, we determine the coefficients of an autoregressive (AR) model of order 4 that fits the signal. These coefficients were used as features. Finally, we calculate the LZ complexity of the autocorrelation series in order to measure the regularity differences.
3.3.10. Statistical features
Further to the above-mentioned features, some classical statistics such as mean and standard deviation of the temporal signal were calculated. These features are useful for discriminate sleep stages (especially the mean value), since they vary markedly between sleep and wakefulness.
3.3.11. Summary of features
The obtained features can be summarized in:
-
•
7 variants of entropy and complexity measures: ApEn, and , SampEn, FuzEn, DispEn, and LZ.
-
•
32 entropy measures in the () domain: TSMRE.
-
•
7 frequency domain features: VLF, LF, HF, LF/HF, normalize HF and VF, and TP.
-
•
15 features in the () domain: , , , ECM, 8 , , , and .
-
•
7 autocorrelation-based features: first min, first ZC, 4 AR coefficients, and LZ of autocorrelation.
-
•
2 statistical features: mean and standard deviation.
3.4. Feature selection and classification
As mentioned above, a total of 70 features were obtained. However, system performance may vary with different combinations of features. In addition to potentially worsening performance, the presence of redundant or non-informative features increases the computational cost and makes the classifier harder to train by the “curse of dimensionality”. A feature selection routine is a popular way to resolve these problems. In this work, we propose two different schemes for the feature selection. The first scheme is a wrapper method [55] of feature selection and SVM and the second scheme is an embedding method that uses RF as classifier.
3.4.1. Forward feature selection and SVM
We use a measure of classifier performance to select the optimal subset of features. According to Kohavi and John [56], it is necessary to define how to search the space of all possible variable subsets; what performance measure to use to guide the search; and which classifier to use. An exhaustive search find the global optimum, but the problem is NP-hard. To avoid this problem, we implemented a greedy solution called forward feature selection.
Let and be the optimal feature set selected and the remaining features, respectively, in the n-th iteration. Let the number of total features and ε an error measure. Let and the set of all features. The procedure can be summarized as follows:
In this algorithm, features are progressively incorporated into larger subsets. This method yields nested subsets of features. Finally, an error measurement is obtained for each subset and from this, the “optimum” set can be selected. While the computational load is less than in an exhaustive search, reaching the solution by this method may be slow.
In this scheme we use SVM as classifier [57]. SVM involves the optimization of a convex objective function with constraints and it is unaffected by local minima. SVM produces an optimum separation hyperplane through mapping the features in a hyperdimensional space. In this work, we use a Gaussian kernel given by . Detailed explanation of SVM can be found in [57], [58].
The measure error ε was selected with the aim of maximize the AUC. Let Se and Sp be the sensitivity and specificity, respectively. Each iteration selects the feature that minimizes , that is, the minimum distance to point in the ROC curve. In addition, we evaluated the use of a criterion related with the application. We selected the feature that minimize the error in estimating the total sleep time per patient. However, the results obtained with this last measure will not be reported due to poor performance.
3.4.2. Feature importance and RF
For comparison purposes, we consider RF [59] as classifier. In RF, we can incorporate the feature selection as part of the training process and that is much more efficient because there is no need to retrain several times. To do this, after each tree is trained with all features, the values of each feature are randomly permuted. The data with the permuted variable is run down in the tree and a measure of error is calculated. By doing this for all features and calculating the percentage increase in misclassification rate compared to the resulting error with all variables intact, we can estimate a measure of variable importance.
3.5. Final classifiers
We already described the feature extraction and feature selection. The final stage is train and test the classifiers that use the subsets of selected features. However, first we need to solve one more problem: the class imbalance.
Most of the total recording time corresponds to the asleep stage. There are different approaches to prevent the classifier from biasing towards the majority class, such as resample database, synthetic samples generation by convex combination, among others. In this work, we used two different methods to overcome the drawback of class imbalance. The first method is naive: we simply randomly remove samples from the majority class until the classes are balanced. This method was applied in FFS-SVM and RF with feature importance. In the second method, we use the SVM classifier but we impose an additional cost on the model for the minority class errors during training [58]. In this way, we can bias the classifier to pay more attention to the minority class. We penalized the classification in a ratio that takes into consideration the class imbalance.
These balanced strategies were only applied in the training to avoid the classifier to have a bias towards the majority class. In the test data, no processing is done to balance the classes. In this way the classifier will be tested under conditions similar to the real application.
In conclusion, taking into account the feature selection and classification routines along with the approaches to solve class imbalance, we have three algorithms that will be trained and tested: FFS-SVM with penalty errors in minority class (FS 1), FFS-SVM with artificial balance (FS 2), and feature importance and RF with artificial balance (FS 3).
4. Results
In this section, we present the results obtained with the three proposed methods, explaining the outcomes of each of the stages that compose it.
4.1. Parameters selection
In some features described in previous section was necessary to experimentally tune a set of hyperparameters. To find the best combination of hyperparameters a set of experiments was performed over a design database (500 patients, which was described in 3.1). All hyperparameters combinations were explored using a grid search. First, we did a coarse search to get an idea of how the features behaves according to the hyperparameters and, then, we did a more detailed search to find the optimum hyperparameters. We use the AUC as an objective measure of the discriminating capacity of each single feature [38].
As mentioned above, these experiments were conducted for HR segments with a duration L of between 30 and 300 s, in steps of 30. The grid search was performed for the features ApEn, SampEn, FuzEn and DispEn. In the first three features, m was varied from 2 to 8 in steps of 1, r was varied from to varying the exponent in steps of 0.55 and τ was varied from 1 to 4 in steps of 1. For FuzEn, the exponent q of the kernel function was varied from 2 to 4 in steps of 1. In DispEn, c was varied from 2 to 4 in steps of 1, m was varied from 2 to in steps of 1, where and τ from 1 to 4 in steps of 1. The Gaussian kernel parameter used for SVM was selected varying γ with the equation , with k from 1 to 16 in steps of 2. The optimum value was , and consequently .
The hyperparameters that maximize the AUC are very similar for different values of L, but the AUC always increases with L. The consequences of this will be discussed below.
4.2. Feature selection
In order to discard irrelevant features and generate a set of optimum features for a given classifier, the feature selection routines mentioned in Section 3 were applied. The methods FS 1, FS 2 and FS 3 were applied to the different databases obtained by varying L. The two methods of FFS-SVM were applied as explained above, obtaining 70 nested subsets of features. In the RF-based method, we obtain a feature ranking. In this case, we did not consider increase the features of one by one, but we generated subsets considering groups whose ranking is similar.
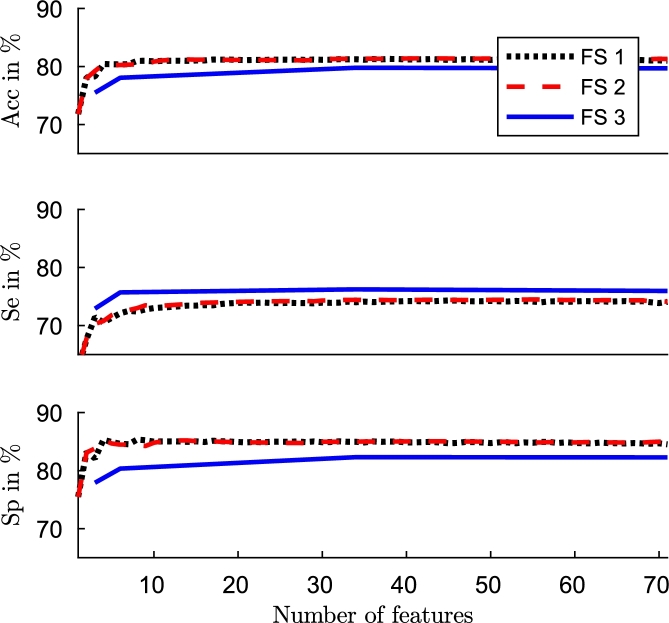
The original feature set had high redundancy. Many features are from the same family. The experiment results showed that with only a few features (approximately 10) performance is close to the best result obtained. The Fig. 3 shows accuracy, sensitivity and specificity for database with obtained with three methods. Results are very similar for the others L values.
Figure 3.
Performance (Acc, Se and Sp) versus number of features with FFS-SVM with penalty errors in minority class (black), FFS-SVM with artificial balance (red), and feature importance and RF with artificial balance (blue).
Based on these results, we selected the first 40 features obtained in each method for each database to make the classifier faster and simpler. In the Table 2, Table 3, Table 4 we show an exhaustive list of the selected features by each method. The selected features are generally very similar by each method, although the order in which they are selected are slightly different by each one. One of the most selected features is the mean value of the signal. The mean value of the HR decreases as the sleep stage is deeper, as it was established by Penzel [20]. The ApEn related features were also selected early. Being a measure of regularity, it can be able to differentiate the states of awake and asleep. During vigil there is associated a greater irregularity of the signal [20], as shown in the Fig. 1. There are other features in which it is more difficult to determine a physiological meaning directly. However, it is evident that the signal changes, and the features that we are using are able to reflect those changes. Although the interpretability of the results is always a benefit, it is not necessary that the selected features have a logical interpretation with the application, proof of this are works that use weak classifiers or the deep learning approaches [60].
Table 2.
Feature ranking. Top 40 features for different L using the algorithm FS 1.
| L | FS 1 |
|---|---|
| 30 | mean, ApEn, TSMRE5, LF, LF/HF, , rmax, AR coefficient 4, TSMRE26, TSMRE8, mean(t,s), HF, LZ of AC, FuzEn, std, TP, TSMRE7, SBE2, var S, VLF, DispEn, RE(t,s), SBE6, TSMRE27, TSMRE32, SBE1, TSMRE29, TSMRE31, TSMRE1, TSMRE25, first AC min, ESVD, LZ, TSMRE30, AR coefficient 1, TSMRE6, TSMRE23, TSMRE13, TSMRE15, TSMRE14. |
| 60 | mean, ApEn, ApEnmax, first ZC, normalize HF, std, TSMRE5, TSMRE17, rmax, SBE1, SBE8, TSMRE32, TSMRE24, ESVD, SBE6, TSMRE16, std(t,s), TSMRE25, var S, FuzEn, LF/HF, mean(t,s), TSMRE18, SBE3, VLF, TP, LZ, TSMRE19, SampEn, HF, TSMRE14, TSMRE23, TSMRE21, LZ of AC, SBE7, TSMRE12, TSMRE22, TSMRE15, TSMRE13, TSMRE27. |
| 90 | mean, ApEn, ApEnmax, first ZC, std, TSMRE3, TSMRE1, SBE8, ESVD, SBE4, TSMRE27, SampEn, TSMRE4, rmax, normalize LF, LF/HF, SBE5, LF, SBE6, TSMRE2, TSMRE27, AR coefficient 3, VLF, TP, LZ of AC, TSMRE13, FuzEn, normalize HF, TSMRE14, HF, mean(t,s), TSMRE9, TSMRE12, SBE3, SBE2, TSMRE5, SBE1, SBE7, TSMRE19, TSMRE6. |
| 120 | ApEn, mean, first ZC, ApEnmax, std, TSMRE1, SBE5, TSMRE2, SampEn, ESVD, ECM, SBE4, TSMRE16, SBE1, LZ of AC, TSMRE15, first AC min, LF, TSMRE20, TSMRE21, HF, std(t,s), TSMRE22, TP, VLF, TSMRE24, TSMRE17, FuzEn, TSMRE18, TSMRE19, TSMRE27, mean(t,s), TSMRE26, TSMRE23, TSMRE32, SBE6, AR coefficient 4, TSMRE14, SBE3, . |
| 150 | TSMRE3, mean, TSMRE5, ApEnmax, ApEn, ESVD, var S, first ZC, SBE6, TSMRE1, TSMRE2, ECM, SBE2, HF, SBE8, rmax, TSMRE9, SBE4, LZ, TSMRE7, LZ of AC, TSMRE12, FuzEn, TSMRE22, TSMRE8, SampEn, TSMRE6, SBE3, normalize LF, std, TSMRE14, TSMRE17, TSMRE15, TSMRE18, VLF, TSMRE5, TSMRE10, normalize HF, , TSMRE31. |
| 180 | TSMRE3, mean, first ZC, SBE1, LF, SBE4, ApEnmax, TSMRE1, ESVD, ECM, ApEn, TSMRE13, SBE8, TSMRE15, std, SBE2, FuzEn, SBE7, SBE5, VLF, TSMRE2, LZ of AC, TP, std(t,s), TSMRE18, SBE6, SBE3, TSMRE29, HF, normalize HF, mean(t,s), , var S, AR coefficient 2, TSMRE31, TSMRE27, normalize LF, LZ, TSMRE14, TSMRE24. |
| 210 | TSMRE3, mean, LZ of AC, ApEnmax, SBE5, TSMRE1, std, AR coefficient 4, TSMRE11, ESVD, ECM, FuzEn, LF/HF, SBE4, TSMRE13, LZ, first ZC, TSMRE2, SBE3, TSMRE12, SBE7, SBE2, TSMRE15, var S, TSMRE8, SampEn, first AC min, SBE6, , SBE8, TSMRE14, TSMRE5, TSMRE10, rmax, TSMRE19, TSMRE6, TSMRE16, RE(t,s), LF, std(t,s). |
| 240 | TSMRE3, mean, first ZC, SBE8, ApEnmax, TSMRE1, ESVD, TSMRE17, LF/HF, std, TSMRE31, TSMRE2, AR coefficient 4, TSMRE28, SBE3, LZ of AC, TSMRE13, RE(t,s), SBE6, TSMRE15, SBE2, std(t,s), SampEn, SBE7, VLF, TSMRE30, ECM, normalize LF, ApEn, mean(t,s), TP, TSMRE4, SBE4, SBE5, HF, FuzEn, SBE1, TSMRE18, TSMRE16, normalize HF. |
| 270 | TSMRE3, mean, LZ of AC, std, SBE5, ApEnmax, first ZC, TSMRE1, TSMRE10, LZ, AR coefficient 2, ESVD, ECM, AR coefficient 1, SBE4, AR coefficient 4, TSMRE4, TSMRE2, SBE2, SBE8, TSMRE32, TSMRE30, SBE7, var S, LF/HF, SBE6, SBE3, TSMRE22, VLF, DispEn, TSMRE27, TSMRE25, TSMRE31, SBE1, first AC min, TP, TSMRE19, AR coefficient 3, TSMRE29, TSMRE20. |
| 300 | TSMRE3, mean, LZ of AC, ApEnmax, TSMRE1, SBE5, AR coefficient 4, std, TSMRE2, LF/HF, ESVD, ECM, TSMRE10, DispEn, normalize LF, SampEn, TSMRE16, TSMRE12, TSMRE30, HF, AR coefficient 2, TSMRE32, SBE6, TSMRE25, TSMRE15, AR coefficient 3, mean(t,s), TP, TSMRE4, TSMRE8, std(t,s), TSMRE9, AR coefficient 1, SBE3, VLF, TSMRE18, TSMRE11, var S, LF, SBE2. |
Table 3.
Feature ranking. Top 40 features for different L using the algorithm FS 2.
| L | FS 2 |
|---|---|
| 30 | mean, ApEn, first ZC, LF, TSMRE10, AR coefficient 4, TSMRE30, rmax, normalize LF, SBE7, SBE1, TSMRE4, std(t,s), AR coefficient 1, std, SBE2, RE(t,s), TSMRE29, TSMRE8, VLF, TSMRE3, LZ, , TP, TSMRE27, AR coefficient 3, SBE6, DispEn, TSMRE23, TSMRE2, TSMRE21, TSMRE12, SampEn, FuzEn, TSMRE16, TSMRE17, var S, first AC min, ApEnmax, ESVD. |
| 60 | mean, ApEn, ApEnmax, TSMRE3, SBE5, std, rmax, first ZC, normalize HF, TSMRE8, TSMRE15, TSMRE18, SBE4, TSMRE23, DispEn, TSMRE20, AR coefficient 1, mean(t,s), TSMRE28, , TSMRE7, VLF, SBE2, first AC min, TSMRE11, SampEn, TSMRE12, TSMRE14, RE(t,s), TSMRE31, LF/HF, SBE6,TSMRE9, TSMRE32, LZ of AC, TSMRE16, ESVD, TSMRE1, FuzEn, LF. |
| 90 | mean, ApEn, ApEnmax, first ZC, TSMRE6, std, SBE4, ESVD, TSMRE11, TSMRE3, SBE6, SBE2, DispEn, TSMRE20, LZ of AC, TSMRE2, var S, AR coefficients 1, TSMRE5, SBE3, , mean(t,s), TSMRE24, TSMRE15, TSMRE17, RE(t,s), TSMRE16, LZ, TSMRE23, TSMRE13, TSMRE30, TSMRE19, normalize HF, first AC min, AR coefficients 4, rmax, AR coefficients 2, ECM, TSMRE8, TSMRE14. |
| 120 | TSMRE3, mean, first ZC, SBE1, normalize LF, SBE7, TSMRE18, ApEnmax, ESVD, TSMRE28, std, TSMRE1, FuzEn, SBE5, TSMRE2, first AC min, rmax, TSMRE27, SBE6, mean(t,s), SBE4, TSMRE26, TSMRE21, SBE8, TSMRE31, TSMRE29, TSMRE22, LF, LZ, std(t,s), var S, TSMRE25, TSMRE15, TSMRE8, LZ of AC, TSMRE20, ECM, AR coefficients 2, AR coefficients 1, TSMRE24. |
| 150 | TSMRE3, mean, first ZC, ApEnmax, SampEn, SBE5, ESVD, TSMRE1, TSMRE29, SBE6, SBE1, normalize HF, HF, LZ, LZ of AC, std, TSMRE2, ApEn, TSMRE16, first AC min, LF, var S, TSMRE13, TSMRE20, TSMRE31, TSMRE17, LF/HF, TSMRE24, SBE4, ECM, SBE2, normalize LF, FuzEn, TSMRE6, SBE3, RE(t,s), TSMRE15, rmax, SBE8, TSMRE17. |
| 180 | TSMRE3, mean, first ZC, SBE1, VLF, SBE5, ApEnmax, FuzEn, SBE4, ESVD, ECM, SBE2, TSMRE1, std, TSMRE29, TSMRE11, normalize HF, DispEn, SBE3, LZ of AC, TSMRE30, TSMRE19, SBE8, TSMRE17, SampEn, TSMRE2, SBE6, first AC min, LF, SBE7, std(t,s), var S, LZ, AR coefficients 1, TSMRE13, TSMRE24, , TSMRE10, TSMRE23, HF. |
| 210 | TSMRE3, mean, LZ of AC, ApEnmax, LF/HF, TSMRE1, SBE6, mean(t,s), ECM, AR coefficients 4, FuzEn, TSMRE12,TSMRE23, SBE7, ESVD, TSMRE2, TSMRE28, std, TSMRE17, TSMRE17, SampEn, TSMRE18, rmax, SBE8, LF, VLF, TSMRE27, SBE5, TSMRE4, TSMRE30, first ZC, TSMRE8, TSMRE15, TP, SBE4, std(t,s), LZ, SBE3, TSMRE16, TSMRE5, ApEn. |
| 240 | TSMRE3, mean, LZ of AC, SBE5, std, ApEnmax, LF/HF, TSMRE1, ESVD, TSMRE26, TSMRE2, LF, TSMRE30, first ZC, TSMRE13, TSMRE19, ApEn, SBE6, TSMRE31, SBE2, TSMRE24, TSMRE10, LZ, SBE8, TSMRE11, ECM, SampEn, AR coefficients 1, TSMRE15, TSMRE28, TSMRE29, var S, FuzEn, AR coefficients 2, , SBE7, TP, TSMRE14, TSMRE20, VLF. |
| 270 | TSMRE3, mean, LZ of AC, SBE5, std, ApEnmax, ESVD, TSMRE11, RE(t,s), first ZC, ECM, SBE4, TSMRE2, ApEn, TSMRE14, TSMRE9, LZ, AR coefficients 2, LF/HR, AR coefficients 1, SBE2, TSMRE20, TP, std, SampEn, TSMRE24, TSMRE25, TSMRE17, TSMRE31, SBE3, SBE6, , TSMRE7, TSMRE16, SBE7, TSMRE12, TSMRE11, TSMRE13, AR coefficients 3, first AC min. |
| 300 | TSMRE3, mean, LZ of AC, TSMRE1, ApEnmax, SBE5, ESVD, TSMRE2, LF/HF, ECM, FuzEn, AR coefficients 4, TSMRE14, LF, first ZC, TSMRE16, SBE4, TSMRE26, SBE7, TSMRE29, TSMRE19, normalize LF, TSMRE27, SBE2, AR coefficients 2, TSMRE8, DispEn, SBE6, std(t,s), AR coefficients 1, AR coefficients 3, TSMRE13, LZ, var S, TSMRE32, VLF, SBE8, TSMRE6, SBE1, ApEn. |
Table 4.
Feature ranking. Top 40 features for different L using the algorithm FS 3.
| L | FS 3 |
|---|---|
| 30 | mean, HF, LF, ApEnmax, TP, std, mean(t,s), VLF, TSMRE6, TSMRE5, TSMRE7, TSMRE8, TSMRE4, TSMRE9, TSMRE10, TSMRE3, TSMRE2, ApEn, ECM, normalize LF, ESVD, var S, SBE1, TSMRE1, LF/HF, max S, SBE4, FuzEn, TSMRE12, normalize HF, SBE5, SBE8, TSMRE27, TSMRE11, SampEn, AR coefficients 1, TSMRE26, TSMRE28, SBE7, TSMRE25. |
| 60 | mean, ApEnmax, TSMRE1, HF, ESVD, ECM, AR coefficients 1, TSMRE2, TSMRE19, TSMRE16, mean(t,s), TSMRE18, SBE1, TSMRE17, LF, RE(t,s), var S, , TP, TSMRE20, normalize LF, TSMRE15, VLF, SBE5, std, TSMRE14, TSMRE21, normalize HF, std(t,s), LF/HF, TSMRE22, TSMRE25, TSMRE4, TSMRE24, SBE2, TSMRE23, SampEn, rmax, SBE8, TSMRE13. |
| 90 | mean, ApEnmax, TSMRE2, TSMRE3, AR coefficients 1, ECM, first ZC, ESVD, HF, SBE1, normalize LF, LF/HF, SBE5, normalize HF, mean(t,s), TSMRE26, TSMRE30, TSMRE25, TSMRE27, TSMRE28, TSMRE29, TSMRE31, VLF, TSMRE23, LF, TSMRE24, TSMRE32, TSMRE21, std(t,s), TSMRE22, TSMRE20, TP, , TSMRE4, first AC min, std, AR coefficients 2, AR coefficients 4, TSMRE3, RE(t,s), DispEn. |
| 120 | mean, ApEnmax, TSMRE1, TSMRE2, first ZC, AR coefficients 1, ECM, SBE1, ESVD, SBE5, HF, first AC min, normalize LF, AR coefficients 4, mean(t,s), TSMRE32, normalize HF, LF/HF, AR coefficients 2, TSMRE30, TSMRE3, SBE8, TSMRE31, VLF, TSMRE4, DispEn, LF, TSMRE22, TSMRE5, SBE2, TSMRE28, TSMRE29, TP, TSMRE26, std, rmax, TSMRE20, ApEn, TSMRE24, TSMRE18. |
| 150 | mean, ApEnmax, TSMRE1, first ZC, TSMRE2, AR coefficients 1, AR coefficients 4, first AC min, normalize LF, LF/HF, ESVD, SBE1, SBE5, AR coefficients 2, normalize HF, ECM, TSMRE3, HF, LF, mean(t,s), TSMRE5, TSMRE4, SBE8, TSMRE32, SBE2, TSMRE31, rmax, VLF, TSMRE28, TSMRE29, TSMRE30, TSMRE26, SampEn, DispEn, TSMRE22, LZ of AC, TSMRE24, TSMRE20, TP, TSMRE19. |
| 180 | mean, ApEnmax, TSMRE1, first ZC, TSMRE2, AR coefficients 1, AR coefficients 4, first AC min, SBE5, AR coefficients 2, normalize LF, ESVD, SBE1, ECM, normalize HF, LF/HF, TSMRE3, HF, SBE8, mean(t,s), TSMRE4, VLF, LF, DispEn, TSMRE30, TSMRE32, SBE2, TSMRE5, TSMRE31, rmax, SBE4, ApEn, TSMRE28, TSMRE27, TSMRE29, LZ of AC, TSMRE7, TSMRE6, TSMRE25, SampEn, TSMRE26. |
| 210 | mean, ApEnmax, TSMRE1, first ZC, TSMRE2, AR coefficients 1, AR coefficients 4, first AC min, AR coefficients 2, SBE5, normalize LF, SBE1, LF/HF, normalize HF, ESVD, LZ of AC, ECM, TSMRE3, SBE8, HF, TSMRE32, TSMRE4, TSMRE5, LF, SBE4, SampEn, DispEn, mean(t,s), VLF, LZ, TSMRE6, TSMRE7, SBE6, TSMRE30, TSMRE31, SBE2, rmax, ApEn, SBE7, TSMRE29. |
| 240 | mean, ApEnmax, TSMRE1, first ZC, AR coefficients 4, first AC min, TSMRE2, AR coefficients 1, AR coefficients 2, SBE5, normalize LF, ESVD, SBE1, LF/HF, HF, normalize HF, ECM, TSMRE3, LZ of AC, DispEn, SBE8, TSMRE32, mean(t,s), TSMRE4, VLF, SBE2, TSMRE31, LF, ApEn, TSMRE5, SBE4, rmax, LZ, TSMRE29, SBE6, TSMRE30, TSMRE7, SampEn, TSMRE6, TSMRE19. |
| 270 | mean, ApEnmax, TSMRE1, first ZC, AR coefficients 4, AR coefficients 1, TSMRE2, first AC min, AR coefficients 2, SBE5, LZ of AC, normalize LF, LF/HF, normalize HF, SBE8, SBE1, ESVD, TSMRE3, HF, DispEn, ECM, TSMRE4, SBE4, TSMRE32, TSMRE5, LZ, SBE6, mean(t,s), SBE2, TSMRE31, LF, TSMRE7, ApEn, VLF, SampEn, TSMRE30, rmax, TSMRE6, SBE7, TSMRE8. |
| 300 | mean, TSMRE1, ApEnmax, first ZC, AR coefficients 4, AR coefficients 1, first AC min, AR coefficients 2, TSMRE2, SBE5, LZ of AC, normalize LF, LF/HF, SBE1, ECM, SBE8, normalize HF, ESVD, TSMRE3, DispEn, SBE4, HF, mean(t,s), TSMRE5, rmax, TSMRE7, TSMRE32, SBE2, TSMRE4, SBE6, SampEn, VLF, SBE7, ApEn, LF, TSMRE30, TSMRE31, LZ, TSMRE9, SBE3. |
4.3. Performance in unseen database
In order to evaluate the performance of the developed systems, we applied the three algorithms (FS1, FS2, and FS3) to the remaining unseen 4500 patients and we performed k-fold cross validation, with . We calculated all performances individually (per patient) and the reported results were obtained by averaging. In this way, the result obtained will be closer to the real application where the objective is to estimate the total sleep time per patient.
Table 5 shows the percentage confusion matrix obtained by applying the algorithms to the unseen database. The number of false positives (FP), true positives (TP), false negatives (FN) and true negatives (TN) was calculated for each patient and the averaged values are reported. In all algorithms a better performance was obtained in the classification of the majority class (when the patient is asleep). The performance also increases with the length of the segment L.
Table 5.
Confusion matrix of the final results in database of 4500 remaining patients for different values of L. The performance obtained can be seen in shades of gray. FS 1: FFS-SVM with penalty error in minority class. FS 2: FFS-SVM with artificial balance. FS 3: variable selection with RF. Waking and sleeping states are labeled as W and S.
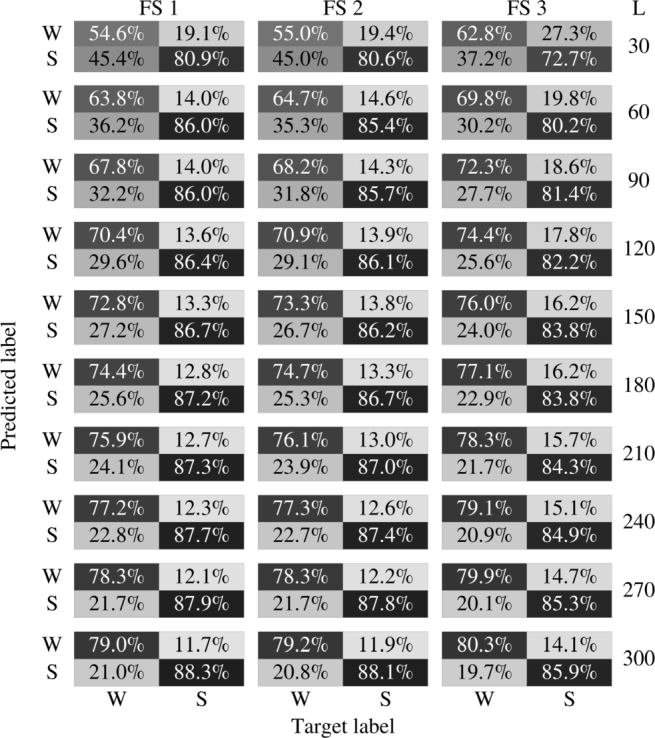
In Table 6, we summarized some common performance measures: accuracy, sensitivity, specificity, positive predictive value (PPV), and negative predictive value (NPV). These measures were reported for all three algorithms applied to databases obtained varying L. SVM-based algorithms are more sensitive and RF is more specific. It is worth noting that in this work we take the awake state as a positive class. The better accuracy of the classifiers that use SVM is explained by the fact that they classify the majority class better, which is the one that ultimately has the greater importance in this measure.
Table 6.
Performance of the algorithms in database of 4500 remaining patients for different values of L. FS 1: forward feature selection and SVM with penalty error in minority class. FS 2: forward feature selection and SVM with artificial balance. FS 3: variable selection with random forest. The best results are highlighted in bold type.
| Acc | Sp | Se | PPV | NPV | L | |
|---|---|---|---|---|---|---|
| FS 1 | 73.7 | 80.9 | 54.6 | 48.6 | 83.1 | |
| FS 2 | 73.6 | 80.6 | 55.0 | 48.4 | 83.6 | 30 |
| FS 3 | 69.7 | 72.7 | 62.8 | 43.1 | 84.65 | |
| FS 1 | 79.4 | 86.0 | 63.8 | 58.3 | 86.5 | |
| FS 2 | 79.2 | 85.4 | 64.7 | 57.6 | 86.7 | 60 |
| FS 3 | 76.6 | 80.2 | 69.8 | 52.5 | 87.6 | |
| FS 1 | 80.6 | 86.0 | 67.8 | 59.3 | 87.7 | |
| FS 2 | 80.4 | 85.7 | 68.2 | 59.0 | 87.8 | 90 |
| FS 3 | 78.2 | 81.4 | 72.3 | 54.4 | 88.6 | |
| FS 1 | 81.4 | 86.4 | 70.4 | 60.5 | 88.5 | |
| FS 2 | 81.4 | 86.1 | 70.9 | 60.3 | 88.7 | 120 |
| FS 3 | 79.4 | 82.2 | 74.4 | 56.0 | 89.4 | |
| FS 1 | 82.3 | 86.7 | 72.8 | 61.8 | 89.3 | |
| FS 2 | 82.0 | 86.2 | 73.3 | 61.1 | 89.4 | 150 |
| FS 3 | 80.3 | 83.0 | 76.0 | 57.3 | 90.0 | |
| FS 1 | 83.1 | 87.2 | 74.4 | 63.2 | 89.8 | |
| FS 2 | 82.8 | 86.7 | 74.7 | 62.4 | 89.9 | 180 |
| FS 3 | 81.2 | 83.8 | 77.1 | 58.6 | 90.4 | |
| FS 1 | 83.6 | 87.3 | 75.9 | 64.0 | 90.3 | |
| FS 2 | 83.4 | 87.0 | 76.1 | 63.4 | 90.3 | 210 |
| FS 3 | 81.9 | 84.3 | 78.3 | 59.8 | 90.8 | |
| FS 1 | 84.2 | 87.7 | 77.2 | 65.2 | 90.7 | |
| FS 2 | 84.0 | 87.4 | 77.3 | 64.6 | 90.7 | 240 |
| FS 3 | 82.6 | 84.9 | 79.1 | 61.0 | 91.1 | |
| FS 1 | 84.7 | 87.9 | 78.3 | 66.0 | 91.1 | |
| FS 2 | 84.6 | 87.8 | 78.3 | 65.7 | 91.1 | 270 |
| FS 3 | 83.1 | 85.3 | 79.9 | 62.0 | 91.4 | |
| FS 1 | 85.2 | 88.3 | 79.0 | 67.0 | 91.3 | |
| FS 2 | 85.0 | 88.1 | 79.2 | 66.7 | 91.4 | 300 |
| FS 3 | 83.6 | 85.9 | 80.3 | 63.1 | 91.5 | |
5. Discussion
The use of pulse oximetry as the only signal to diagnose OSAHS is still controversial. Different devices present a great variability for different situations and patients. The dispersion of obtained values is high. The interpretation of the measured desaturations is ambiguous without prior knowledge of the device used [61]. In addition, pulse oximetry is highly sensitive to motion artifacts [33]. However, significant results have been obtained through the use of advancing signal processing tools. As mentioned earlier, this makes the use of PPG very attractive because of its simplicity and low cost, but the algorithms designed have great difficulty in meeting its objectives due to the low quality of the signal.
Sleep classification is performed primarily using the EEG signal, although information is also extracted from other signals such as EOG, EMG to detect movement, among others. Thus, detecting whether a signal segment corresponds to awake or asleep from the HR is a very complicated task. Although there are changes in the temporal dynamics of the HR signal [20], the information we have is much more difficult to interpret. If we add to this the low accuracy of the HR reported by the pulse oximeter, we can get an idea of the difficulty in reaching an acceptable performance. Finally, in addition to all these drawbacks, we also have a low sampling frequency of HR, which makes it difficult to obtain an adequate feature extraction.
In this work we have developed an algorithm to classify the sleep stages in awake and asleep using only HR signals obtained by pulse oximetry. To summarize, the main methodological steps that must be applied to reuse the proposed scheme with other databases is as follows:
-
1.
Preprocessing HR signals to have zero mean and unit variance and segmentation into non-overlap windows of length L.
-
2.
Feature extraction and hyperparameters optimization using a subset of the database to design the system.
-
3.
Feature selection to obtain the optimum features for the chosen classifier.
-
4.
Extraction of the optimum selected features for the chosen classifier using a subset of the database to test the system and train the classifier.
In order to reuse the method described in this article with new patients, it is necessary to apply the preprocessing step so as to standardize and segment the signal Then, the selected features with the founded optimal hyperparameters should be extracted and used with the trained classifier. Although the design described in this work is computationally complex, its use is fast once the system has been designed.
We have been anticipating in previous sections the discussion about the length L of the segment to be classified. Remember that the length of the segments used in a hypnogram is 30 s. It is easy to note that the smaller L makes it easier to translate this scheme to the hypnogram.
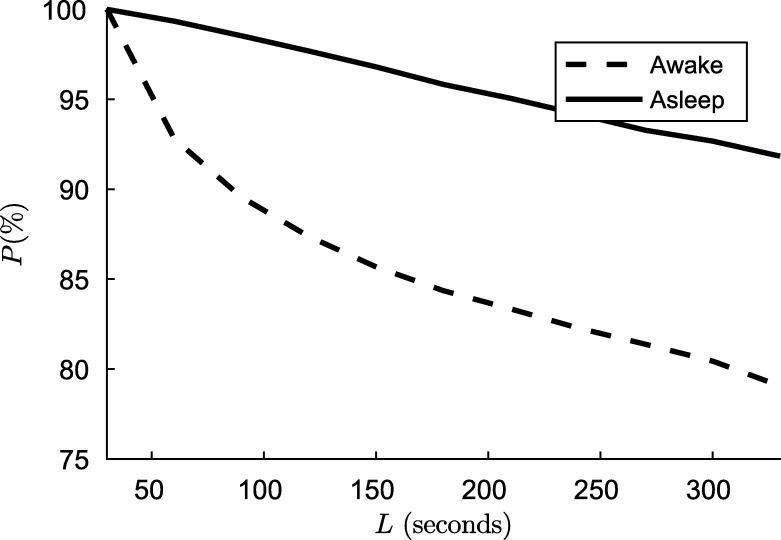
To explain this, let the hypnogram H be a sequence as , where and are the lengths of i-th awake and asleep segments. In case of awake, the Fig. 4 shows the percentage P of the total sleep time only considering segments of length greater than L, that is
Figure 4.
The percentage P(%) of the total asleep/awake time only considering segments of length greater than L.
| (13) |
where is the set of . For the case of asleep is analogous.
In the real application, the HR signal is segmented into non-overlap windows of length L, and then the segments are classified obtaining the hypnogram. If there are asleep/awake segments of length less than L, some windows will not belong to a single state. That is, when L increases, the segments with mix awake and asleep stages also increase. The classifier was not designed for these mixtures. Fig. 4 shows the magnitude of this mixture increment with L. On the other hand, as we reported in the results, as we increased L, the performance of the algorithm improves, because there is more information to detect dynamic changes and the features can be calculated more exactly. There is a trade-off between the performance and the ability to apply the algorithm in a real situation mediated by L. When choosing a larger L to obtain better classification results, we sacrifice accuracy in the boundary of the asleep/awake transition and probably will miss some short transitions.
The development of this algorithm is at an early stage. Before to be applied in clinical practice, it is necessary to perform a large scale assessment of the method to validate its use.
As mentioned previously, in this work we used the heart rate signal with a sampling frequency of 1 Hz. The AASM stipulates the use of 25 Hz in oximetry as desirable, and 10 Hz as minimum recommended, but there are no specific recommendations about the sampling frequency of the HR [1]. Considering the range of possibles HR frequencies, there is no need for a high sampling frequency.
The use of a different sampling frequency to that we use in this work could change the performance obtained, since many features vary with the sampling frequency. In the case of applying the designed system to signals with a sampling frequency greater than 1 Hz, it will be necessary to subsample the signal. Conversely, the use of signals with a sampling frequency smaller than 1 Hz is not possible without re-performing all experiments to find new optimal parameters.
There are several previous works that perform automatic sleep stage classification. EEG is generally used, but several alternatives have been proposed for ECG. However, as far as we know, there are not studies using only HR from PPG. The comparisons between studies are not simple. Different signals, databases and number of classes are used. In order to compare with our work, in cases where it was necessary, the different sleep stages were considered as unique. However, to be fair, we will report which works discriminated sleep stages in more detail.
Beattie et al. [25] used PPG signals and accelerometer. In that work the authors considered 5 classes. The database used by Beattie was composed of 60 participants were self-reported normal sleepers. We can not make a direct comparison because they have additional information. They use the PPG signal (not only the HR calculated from it), in addition to the accelerometer signals. The best accuracy, sensitivity and specificity obtained in this work were 90.6%, 69.3% and 94.6% respectively.
Uçar et al. [26] used PPG and HRV from PPG, and the combination of these two to classify in awake and asleep. The signals used in this work contain more information than those of our work. The confusion matrix was not reported in this paper, it was deduced from the data reported by the authors. The best accuracy, sensitivity and specificity were 76%, 74% and 80% respectively. The database used contains registers of 10 patients.
Adnane et al. [22] used ECG signal from 18 patients (4 normal sleepers, 6 mixed normal and insomniac sleepers, and 8 insomniac sleepers). They only considered two classes. The best accuracy, sensitivity and specificity were 80%, 69.1% and 84.5% respectively.
Xiao et al. [23] extracted 41 features from ECG and used RF to differentiate among wake, REM and non-REM stages. The results reported were 83.94%, 51.15% and 90.15% of accuracy, sensitivity and specificity, respectively. The authors only analyzed data labeled with “stationary”, that is, they classified 5-minute windows corresponding to a single class.
Yücelbaş et al. [24] used ECG signals and classify the sleep stage in wake, REM and non-REM. They used two different databases. In total, 28 patients were considered. The reported results were discriminated by healthy subjects and patients. For the first database, the accuracies was 87.11% for the healthy and 78.08% for the patient. For the second database, 77.02% and 76.79%. The reported data do not allow to compare all performance measures.
The results here obtained are encouraging, because it addresses a limitation of all apnea diagnosis methods based only on desaturation. The risk of overfitting in our algorithm is minimal, because we use a large number of records registered in real conditions. Although we have applied strategies to prevent the unbalance of classes, it can be seen that in all the developed methods there is still a bias towards the majority class that should be addressed in future work.
The Table 7 summarizes similar works. Other related results, even obtained with EEG, can be found in [24].
Table 7.
Comparison with the literature.
| Method | Signal | N. of classes | N. of patients | Epoch time | Acc | Se | Sp | Prec | NPV |
|---|---|---|---|---|---|---|---|---|---|
| Beattie et al. [25] | PPG + accelerometer | 5 | 60 | 30 s | 90.6 | 69.3 | 94.6 | 70.5 | 94.3 |
| PPG | 2 | 10 | 30 s | 76.8 | 76 | 77 | 41.2 | 93.8 | |
| Uçar et al. [26] | HRV | 2 | 10 | 30 s | 72.4 | 74 | 72 | 35.9 | 92.9 |
| PPG + HRV | 2 | 10 | 30 s | 76.7 | 80 | 76 | 41.4 | 94.7 | |
| Adnane et al. [22] | ECG | 2 | 18 | 30 s | 80 | 69.1 | 84.5 | 64.5 | 87 |
| Xiao et al. [23] | ECG | 3 | 45 | 5 min | 83.9 | 51.1 | 90.2 | 49.58 | 90.7 |
In future work, the algorithm developed for patients will be adapted and applied to obtain simplified hypnograms and total sleep time estimation. Finally, the apnea detection and sleep estimation systems for OSAHS diagnosis will be evaluated together.
6. Conclusions
In this work, we developed an automatic system to classify the sleep stage in awake or asleep using machine learning techniques from photoplethysmographic HR signals. It was shown that information theory-related features and complexity measures, and their extensions to time-frequency domain, are useful to differentiate between awake and asleep stages. It was shown that very simple and inexpensive signals such as those obtained by pulse oximetry can achieve performances comparable to those obtained with signals that contain more information. The use of a large database allows a good generalization capacity of the developed method. We developed three alternatives to eliminate the possible redundancy of the extracted features, FFS schemes based on SVM and variable selection with RF with artificial balance of training data, and FFS-SVM with penalty errors in minority class without balanced class. The FFS-SVM with penalty error in minority class has slightly better performance than the other methods. However, all performances are very similar. As future work, we will adapt the algorithm to obtain simplified hypnograms and total sleep time estimation. The ultimate aim is to use this algorithm and an apnea event detector for OSAHS diagnosis.
Declarations
Author contribution statement
Ramiro Casal: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Leandro E. Di Persia, Gastón Schlotthauer: Conceived and designed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data.
Funding statement
This work was supported by the National Agency for Scientific and Technological Promotion (ANPCyT) under projects PICT 2014-2627 and 2015-0977, Universidad Nacional del Litoral under projects CAI+D 50020150100059LI, 50020150100055LI and 50020150100082LI, Universidad Nacional de Entre Ríos under projects PID-UNER 6171, PIO-UNER-CONICET 146-201401-00014-CO and the National Council on Scientific and Technical Research (CONICET) under project PIO-UNER-CONICET 146-201401-00014-CO.
Competing interest statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
References
- 1.R.B. Berry, R. Brooks, C.E. Gamaldo, S.M. Harding, C. Marcus, B. Vaughn, The AASM manual for the scoring of sleep and associated events, in: Rules, Terminology and Technical Specifications, American Academy of Sleep Medicine, Darien, Illinois.
- 2.Norman R.G., Pal I., Stewart C., Walsleben J.A., Rapoport D.M. Interobserver agreement among sleep scorers from different centers in a large dataset. Sleep. 2000;23(7):901–908. [PubMed] [Google Scholar]
- 3.Pang K.P., Terris D.J. Screening for obstructive sleep apnea: an evidence-based analysis. Am. J. Otolaryngol. 2006;27(2):112–118. doi: 10.1016/j.amjoto.2005.09.002. [DOI] [PubMed] [Google Scholar]
- 4.Yadollahi A., Moussavi Z. Engineering in Medicine and Biology Society, 2006. EMBS'06. 28th Annual International Conference of the IEEE. IEEE; 2006. Apnea detection by acoustical means; pp. 4623–4626. [DOI] [PubMed] [Google Scholar]
- 5.Roche F., Sforza E., Duverney D., Borderies J.-R., Pichot V., Bigaignon O., Ascher G., Barthélémy J.-C. Heart rate increment: an electrocardiological approach for the early detection of obstructive sleep apnoea/hypopnoea syndrome. Clin. Sci. 2004;107(1):105–110. doi: 10.1042/CS20040036. [DOI] [PubMed] [Google Scholar]
- 6.Salisbury J.I., Sun Y. Rapid screening test for sleep apnea using a nonlinear and nonstationary signal processing technique. Med. Eng. Phys. 2007;29(3):336–343. doi: 10.1016/j.medengphy.2006.05.013. [DOI] [PubMed] [Google Scholar]
- 7.Raymond B., Cayton R., Chappell M. Combined index of heart rate variability and oximetry in screening for the sleep apnoea/hypopnoea syndrome. J. Sleep Res. 2003;12(1):53–61. doi: 10.1046/j.1365-2869.2003.00330.x. [DOI] [PubMed] [Google Scholar]
- 8.Sateia M.J. International classification of sleep disorders: highlights and modifications. Chest J. 2014;146(5):1387–1394. doi: 10.1378/chest.14-0970. [DOI] [PubMed] [Google Scholar]
- 9.Strollo P.J., Jr., Rogers R.M. Obstructive sleep apnea. N. Engl. J. Med. 1996;334(2):99–104. doi: 10.1056/NEJM199601113340207. [DOI] [PubMed] [Google Scholar]
- 10.Shahar E., Whitney C.W., Redline S., Lee E.T., Newman A.B., Javier Nieto F., O'connor G.T., Boland L.L., Schwartz J.E., Samet J.M. Sleep-disordered breathing and cardiovascular disease: cross-sectional results of the sleep heart health study. Am. J. Respir. Crit. Care Med. 2001;163(1):19–25. doi: 10.1164/ajrccm.163.1.2001008. [DOI] [PubMed] [Google Scholar]
- 11.Leger D., Bayon V., Laaban J.P., Philip P. Impact of sleep apnea on economics. Sleep Med. Rev. 2012;16(5):455–462. doi: 10.1016/j.smrv.2011.10.001. [DOI] [PubMed] [Google Scholar]
- 12.AlGhanim N., Comondore V.R., Fleetham J., Marra C.A., Ayas N.T. The economic impact of obstructive sleep apnea. Lung. 2008;186(1):7–12. doi: 10.1007/s00408-007-9055-5. [DOI] [PubMed] [Google Scholar]
- 13.Epstein L.J., Kristo D., Strollo P.J., Friedman N., Malhotra A., Patil S.P., Ramar K., Rogers R., Schwab R.J., Weaver E.M. Clinical guideline for the evaluation, management and long-term care of obstructive sleep apnea in adults. J. Clin. Sleep Med. 2009;5(03):263–276. [PMC free article] [PubMed] [Google Scholar]
- 14.Netzer N., Eliasson A.H., Netzer C., Kristo D.A. Overnight pulse oximetry for sleep-disordered breathing in adults: a review. Chest. 2001;120(2):625–633. doi: 10.1378/chest.120.2.625. [DOI] [PubMed] [Google Scholar]
- 15.Schlotthauer G., Di Persia L.E., Larrateguy L.D., Milone D.H. Screening of obstructive sleep apnea with empirical mode decomposition of pulse oximetry. Med. Eng. Phys. 2014;36(8):1074–1080. doi: 10.1016/j.medengphy.2014.05.008. [DOI] [PubMed] [Google Scholar]
- 16.Hang L.-W., Wang H.-L., Chen J.-H., Hsu J.-C., Lin H.-H., Chung W.-S., Chen Y.-F. Validation of overnight oximetry to diagnose patients with moderate to severe obstructive sleep apnea. BMC Pulm. Med. 2015;15(1):24. doi: 10.1186/s12890-015-0017-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Sabil A., Vanbuis J., Baffet G., Feuilloy M., Le Vaillant M., Meslier N., Gagnadoux F. Automatic identification of sleep and wakefulness using single-channel eeg and respiratory polygraphy signals for the diagnosis of obstructive sleep apnea. J. Sleep Res. 2018 doi: 10.1111/jsr.12795. [DOI] [PubMed] [Google Scholar]
- 18.Dong Y., Hu Z., Uchimura K., Murayama N. Driver inattention monitoring system for intelligent vehicles: a review. IEEE Trans. Intell. Transp. Syst. 2011;12(2):596–614. [Google Scholar]
- 19.Mantua J., Gravel N., Spencer R. Reliability of sleep measures from four personal health monitoring devices compared to research-based actigraphy and polysomnography. Sensors. 2016;16(5):646. doi: 10.3390/s16050646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Penzel T., Kantelhardt J.W., Chung-Chang L., Voigt K., Vogelmeier C. Dynamics of heart rate and sleep stages in normals and patients with sleep apnea. Neuropsychopharmacology. 2003;28(S1):S48. doi: 10.1038/sj.npp.1300146. [DOI] [PubMed] [Google Scholar]
- 21.Aeschbacher S., Bossard M., Schoen T., Schmidlin D., Muff C., Maseli A., Leuppi J.D., Miedinger D., Probst-Hensch N.M., Schmidt-Trucksäss A. Heart rate variability and sleep-related breathing disorders in the general population. Am. J. Cardiol. 2016;118(6):912–917. doi: 10.1016/j.amjcard.2016.06.032. [DOI] [PubMed] [Google Scholar]
- 22.Adnane M., Jiang Z., Yan Z. Sleep–wake stages classification and sleep efficiency estimation using single-lead electrocardiogram. Expert Syst. Appl. 2012;39(1):1401–1413. [Google Scholar]
- 23.Xiao M., Yan H., Song J., Yang Y., Yang X. Sleep stages classification based on heart rate variability and random forest. Biomed. Signal Process. Control. 2013;8(6):624–633. [Google Scholar]
- 24.Yücelbaş Ş., Yücelbaş C., Tezel G., Özşen S., Yosunkaya Ş. Automatic sleep staging based on SVD, VMD, HHT and morphological features of single-lead ECG signal. Expert Syst. Appl. 2018;102:193–206. [Google Scholar]
- 25.Beattie Z., Oyang Y., Statan A., Ghoreyshi A., Pantelopoulos A., Russell A., Heneghan C. Estimation of sleep stages in a healthy adult population from optical plethysmography and accelerometer signals. Physiol. Meas. 2017;38(11):1968. doi: 10.1088/1361-6579/aa9047. [DOI] [PubMed] [Google Scholar]
- 26.Uçar M.K., Bozkurt M.R., Bilgin C., Polat K. Automatic sleep staging in obstructive sleep apnea patients using photoplethysmography, heart rate variability signal and machine learning techniques. Neural Comput. Appl. 2016:1–16. [Google Scholar]
- 27.Rostaghi M., Azami H. Dispersion entropy: a measure for time-series analysis. IEEE Signal Process. Lett. 2016;23(5):610–614. [Google Scholar]
- 28.Pincus S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. 1991;88(6):2297–2301. doi: 10.1073/pnas.88.6.2297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Richman J.S., Moorman J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol., Heart Circ. Physiol. 2000;278(6):H2039–H2049. doi: 10.1152/ajpheart.2000.278.6.H2039. [DOI] [PubMed] [Google Scholar]
- 30.Chen W., Wang Z., Xie H., Yu W. Characterization of surface EMG signal based on fuzzy entropy. IEEE Trans. Neural Syst. Rehabil. Eng. 2007;15(2):266–272. doi: 10.1109/TNSRE.2007.897025. [DOI] [PubMed] [Google Scholar]
- 31.Rényi A. Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, vol. 1. 1961. On measures of entropy and information; pp. 547–561. [Google Scholar]
- 32.Mallat S. Academic Press; 1999. A Wavelet Tour of Signal Processing. [Google Scholar]
- 33.Allen J. Photoplethysmography and its application in clinical physiological measurement. Physiol. Meas. 2007;28(3):R1. doi: 10.1088/0967-3334/28/3/R01. [DOI] [PubMed] [Google Scholar]
- 34.Kyriacou P.A. Pulse oximetry in the oesophagus. Physiol. Meas. 2005;27(1):R1. doi: 10.1088/0967-3334/27/1/R01. [DOI] [PubMed] [Google Scholar]
- 35.Zhang Z., Pi Z., Liu B. TROIKA: a general framework for heart rate monitoring using wrist-type photoplethysmographic (PPG) signals during intensive physical exercise. IEEE Trans. Biomed. Eng. 2014;62(2):522–531. doi: 10.1109/TBME.2014.2359372. [DOI] [PubMed] [Google Scholar]
- 36.Redline S., Sanders M.H., Lind B.K., Quan S.F., Iber C., Gottlieb D.J., Bonekat W.H., Rapoport D.M., Smith P.L., Kiley J.P. Methods for obtaining and analyzing unattended polysomnography data for a multicenter study. Sleep. 1998;21(7):759–768. [PubMed] [Google Scholar]
- 37.Nieto E.J., O'Connor G.T., Rapoport D.M., Redline S. The sleep heart health study: design, rationale, and methods. Sleep. 1997;20(12):1077–1085. [PubMed] [Google Scholar]
- 38.Fawcett T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006;27(8):861–874. [Google Scholar]
- 39.Duda R.O., Hart P.E., Stork D.G. John Wiley & Sons; 2012. Pattern Classification. [Google Scholar]
- 40.Kuhn M., Johnson K. Springer; 2013. Applied Predictive Modeling, vol. 26. [Google Scholar]
- 41.Takens F. Detecting strange attractors in turbulence. Dynamical Systems and Turbulence; Warwick 1980; Springer; 1981. pp. 366–381. [Google Scholar]
- 42.Xu L.-S., Wang K.-Q., Wang L. Proceedings of 2005 International Conference on Machine Learning and Cybernetics, vol. 9. IEEE; 2005. Gaussian kernel approximate entropy algorithm for analyzing irregularity of time-series; pp. 5605–5608. [Google Scholar]
- 43.Restrepo J.F., Schlotthauer G., Torres M.E. Maximum approximate entropy and r threshold: a new approach for regularity changes detection. Physica A. 2014;409:97–109. [Google Scholar]
- 44.Bandt C., Pompe B. Permutation entropy: a natural complexity measure for time series. Phys. Rev. Lett. 2002;88(17) doi: 10.1103/PhysRevLett.88.174102. [DOI] [PubMed] [Google Scholar]
- 45.Boashash B., Khan N.A., Ben-Jabeur T. Time–frequency features for pattern recognition using high-resolution TFDs: a tutorial review. Digit. Signal Process. 2015;40:1–30. [Google Scholar]
- 46.Boashash B. Academic Press; 2015. Time-Frequency Signal Analysis and Processing: a Comprehensive Reference. [Google Scholar]
- 47.Torres M.E., Anino M.M., Schlotthauer G. Automatic detection of slight parameter changes associated to complex biomedical signals using multiresolution q-entropy. Med. Eng. Phys. 2003;25(10):859–867. doi: 10.1016/s1350-4533(03)00080-8. [DOI] [PubMed] [Google Scholar]
- 48.Lempel A., Ziv J. On the complexity of finite sequences. IEEE Trans. Inf. Theory. 1976;22(1):75–81. [Google Scholar]
- 49.Aboy M., Hornero R., Abásolo D., Álvarez D. Interpretation of the Lempel-Ziv complexity measure in the context of biomedical signal analysis. IEEE Trans. Biomed. Eng. 2006;53(11):2282–2288. doi: 10.1109/TBME.2006.883696. [DOI] [PubMed] [Google Scholar]
- 50.Schlotthauer G., Humeau-Heurtier A., Escudero J., Rufiner H.L. Measuring complexity of biomedical signals. Complexity. 2018 [Google Scholar]
- 51.Casal R., Schlotthauer G. 2017 XVII Workshop on Information Processing and Control (RPIC) IEEE; 2017. Sleep detection in heart rate signals from photoplethysmography; pp. 1–6. [Google Scholar]
- 52.Heart rate variability: standards of measurement, physiological interpretation, and clinical use. Task force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology. Circulation. 1996;93:1043–1065. [PubMed] [Google Scholar]
- 53.Bonnet M., Arand D. Heart rate variability: sleep stage, time of night, and arousal influences. Electroencephalogr. Clin. Neurophysiol. 1997;102(5):390–396. doi: 10.1016/s0921-884x(96)96070-1. [DOI] [PubMed] [Google Scholar]
- 54.Boashash B., Boubchir L., Azemi G. 2011 IEEE International Symposium on Signal Processing and Information Technology (ISSPIT) IEEE; 2011. Time-frequency signal and image processing of non-stationary signals with application to the classification of newborn EEG abnormalities; pp. 120–129. [Google Scholar]
- 55.Guyon I., Elisseeff A. An introduction to variable and feature selection. J. Mach. Learn. Res. March 2003;3:1157–1182. [Google Scholar]
- 56.Kohavi R., John G.H. Wrappers for feature subset selection. Artif. Intell. 1997;97(1–2):273–324. [Google Scholar]
- 57.Vapnik V. Springer Science & Business Media; 2013. The Nature of Statistical Learning theory. [Google Scholar]
- 58.Abe S. Springer; 2005. Support Vector Machines for Pattern Classification, vol. 2. [Google Scholar]
- 59.Breiman L. Random forests. Mach. Learn. 2001;45(1):5–32. [Google Scholar]
- 60.LeCun Y., Bengio Y., Hinton G. Deep learning. Nature. 2015;521(7553):436. doi: 10.1038/nature14539. [DOI] [PubMed] [Google Scholar]
- 61.Böhning N., Schultheiss B., Eilers S., Penzel T., Böhning W., Schmittendorf E. Comparability of pulse oximeters used in sleep medicine for the screening of OSA. Physiol. Meas. 2010;31(7):875. doi: 10.1088/0967-3334/31/7/001. [DOI] [PubMed] [Google Scholar]