Estimating and Testing Vaccine Sieve Effects Using Machine Learning

Abstract

When available, vaccines are an effective means of disease prevention. Unfortunately, efficacious vaccines have not yet been developed for several major infectious diseases, including HIV and malaria. Vaccine sieve analysis studies whether and how the efficacy of a vaccine varies with the genetics of the pathogen of interest, which can guide subsequent vaccine development and deployment. In sieve analyses, the effect of the vaccine on the cumulative incidence corresponding to each of several possible genotypes is often assessed within a competing risks framework. In the context of clinical trials, the estimators employed in these analyses generally do not account for covariates, even though the latter may be predictive of the study endpoint or censoring. Motivated by two recent preventive vaccine efficacy trials for HIV and malaria, we develop new methodology for vaccine sieve analysis. Our approach offers improved validity and efficiency relative to existing approaches by allowing covariate adjustment through ensemble machine learning. We derive results that indicate how to perform statistical inference using our estimators. Our analysis of the HIV and malaria trials shows markedly increased precision -- up to doubled efficiency in both trials -- under more plausible assumptions compared with standard methodology. Our findings provide greater evidence for vaccine sieve effects in both trials.

1. Introduction

The development of safe and effective vaccines is one of the greatest public health achievements of the last century. Nevertheless, several infectious pathogens responsible for substantial disease burden still lack an effective preventive vaccine. Vaccine development is often more challenging for genetically heterogeneous pathogens. Indeed, vaccines are typically constructed using only one or several pathogen sequences, and while they may stimulate immune responses that are protective to these few sequences, they may not stimulate immune responses that are more broadly protective. Consequently, vaccines may only be efficacious at preventing infection and disease due to pathogens with sequences similar to the vaccine construct. In an efficacy trial of a preventive vaccine, it is therefore important to study whether and how vaccine efficacy varies by pathogen sequence.

This field of study has been called sieve analysis, nomenclature that derives from imagining a vaccine-induced immune response as a kitchen sieve (Gilbert et al., 1998, 2001). The response presents a barrier to infection or disease, but may have “holes” that allow certain pathogen strains to break through the protective barrier. A sieve effect at a pathogen genetic locus may be defined as differential vaccine efficacy against pathogens with amino acids matched versus mismatched to the vaccine at these residues. Identification of sieve effects can guide selection of antigen sequences in future, potentially multivalent vaccines, which may offer broader protection against genetically diverse pathogens. Sieve analysis can also guide vaccine deployment. If pathogen surveillance data are available, researchers may be able to identify geographic regions where a vaccine will provide a large impact. From a policy perspective, this information is especially important for diseases for which competing partially-effective prevention strategies exist.

Two major diseases caused by highly genetically diverse pathogens for which highly efficacious preventive vaccines have yet to be developed – and therefore diseases for which vaccine sieve analysis is particularly important – are HIV and malaria. For each of these diseases, only a single vaccine has shown efficacy in a Phase III clinical trial. In the case of HIV, this is the ALVAC/AIDSVAX vaccine, whose antigen consists of three HIV-1 envelope protein sequences. The vaccine’s efficacy was evaluated in the RV144 trial, a randomized, placebo-controlled trial in Thailand (Rerks-Ngarm et al., 2009). The vaccine reduced the average instantaneous risk of HIV infection by an estimated 31% over three and a half years follow-up. Efficacy waned over time and was deemed insufficient to gain licensure. For malaria, the most advanced vaccine candidate from a regulatory perspective is the RTS,S/AS01 vaccine. The vaccine’s antigen consists of a portion of the circumsporozoite protein (CS protein) found on the surface of the plasmodium falciparum parasite during the sporozoite phase of its life cycle. The RTS,S/AS01 vaccine reduced the average instantaneous risk of clinical malaria over a follow-up of 12 months by an estimated 63% in 5–17 month old children (RTS,S Clinical Trials Partnership, 2011; Agnandji et al., 2012). As with the RV144 trial, efficacy waned and the vaccine has not been licensed by the United States Food and Drug Administration. However, due to the high morbidity and mortality associated with malaria, the vaccine may still be useful for prevention in areas of high malaria transmission (WHO, 2016).

Statistically, the setting of sieve analysis is an example of a longitudinal data structure with competing risks. After entering the study, trial participants are at risk of experiencing several “competing” endpoints, defined by the genotype of the pathogen causing the study endpoint, with each genotype representing a distinct type of endpoint. To assess the effect of a treatment on the risk of a specific type of endpoint, instantaneous or cumulative parameters may be studied. The choice of parameter depends on the scientific context (Pintilie, 2007), and both types have been used in sieve analysis (Gilbert, 2000). Instantaneous parameters are often based on the cause-specific hazard function (Prentice et al., 1978; Benichou and Gail, 1990; Gaynor et al., 1993; Lunn and McNeil, 1995), defined as the instantaneous rate at which an endpoint of a given type occurs amongst those who have not yet experienced an endpoint. The most common cumulative parameter is cumulative incidence, defined as the probability that an event occurs by a given time and is of a particular type. Cumulative incidence has also been referred to as the subdistribution function (Fine and Gray, 1999), cause-specific failure probability (Gaynor et al., 1993), and absolute cause-specific risk (Benichou and Gail, 1990). While both instantaneous and cumulative parameters are relevant for assessing vaccine sieve effects, given the waning vaccine efficacy observed in the RV144 and RTS,S/AS01 trials, cumulative parameters may have greater public health relevance.

Cumulative vaccine sieve effects are most often estimated with the Aalen-Johansen (AJ) estimator (Aalen, 1978; Aalen and Johansen, 1978; Gilbert, 2000), a generalization of the Kaplan-Meier estimator to settings with competing risks. This estimator requires few assumptions to achieve desirable statistical properties. It is consistent provided participant dropout is non-informative, and is nonparametric efficient if the data do not include any prognostic baseline covariate. However, in many preventive vaccine trials, informative censoring is present and prognostic covariates are available – opportunities for improving on the AJ estimator are therefore common. In the present work, we propose covariate-adjusted estimators that retain a desirable interpretation while offering potential improvements in both bias – by accounting for certain forms of dependent censoring – and in variance – by fully accounting for measured covariates.

In practice, covariate adjustment is often performed using methods based on parametric and semiparametric models. However, when assessing treatment efficacy in randomized trials, statisticians are often reluctant to use these methods due to the risk of model misspecffication. The overwhelming concern is that the potential benefits afforded by covariate adjustment may be offset by bias induced by the use of a misspecified model (cf. Gail et al., 1984). An alternative approach for covariate adjustment is to use flexible regression techniques, such as stacked regression (Wolpert, 1992; Breiman, 1996). Stacking evaluates many regression estimators using cross-validation and selects the best weighted combination of the various candidate estimators. Such estimators have also been referred to as super learners, because they perform essentially as well as the (unknown) best-performing combination of candidate estimators (van der Laan et al., 2004, 2007). The candidate estimators considered may include both parametric regressions, as well as more flexible, machine learning estimators, the latter potentially mitigating concerns of model misspecffication.

While flexible regression techniques are valuable for accurately adjusting for covariates, statistical inference based on the resulting estimate is theoretically challenging. In this paper, we construct flexible targeted minimum loss-based estimators of cumulative incidence for which inference can be facilitated. Relative to the existing approach for estimation of vaccine sieve effects, our method requires weaker assumptions on the censoring mechanism and exhibits markedly improved precision in both trials. Our analysis of the RTS,S/AS01 trial data additionally addresses the challenge of assessing vaccine sieve effects when multiple parasite genotypes may be observed in trial participants. Due to existing privacy policies, we are not able to provide the data used for our analyses; however, the survtmle R package available via CRAN can be used to implement our methods, and we provide an online code repository (https://github.com/benkeser/sieveml) that includes analysis of simulated data sets with identical structure to the real RV144 and RTS,S data.

2. Notation and assumptions

The RV144 and RTS,S/AS01 trials had similar designs: trial participants were enrolled, baseline covariates W were measured, and participants were randomly assigned either to vaccine (Z = 1) or placebo (Z = 0) – see Table 1 for details. After randomization, RV144 participants were asked to attend biannual clinic visits to be tested for HIV, and the endpoint of interest was time to HIV diagnosis. In the RTS,S/AS01 trial, the primary endpoint was the first episode of clinical malaria. We use T to denote the time from randomization until the study endpoint is observed. For RV144, a natural unit for time is number of clinic visits. For RTS,S the most granular unit of time available is days, although for computational simplicity we use months as the unit for the RTS,S analysis.

Table 1:

Summary of two vaccine efficacy trials. The sample size is shown indicates the number of trial participants with complete covariate and genetic sequencing information. AA = amino acid; CS = circumsporozoite.

Trial	Covariates	Endpoint	Pathogen locus
RV144 (n=15,955)	year of trial enrollment, age, gender, behavioral risk score	first diagnosis of infection with HIV-1	V2 envelope, A A 169
RTS,S/AS01 (n=6,890)	study site, age, distance from the nearest outpatient/inpatient facility, height-for-age z-score, weight-for-age z-score, weight-for-height z-score, head circumference, hemoglobin, rainy/dry season at enrollment	first episode of clinical malaria with parasite density>5000/mm3	CS protein

Regardless, our methodology applies with an arbitrarily fine time-scale. We use τ to refer to the final time-point of the analysis, which was three years post-vaccination for RV144 and one year post-vaccination for RTS,S. We use Y to denote the time until right-censoring. If a participant completed follow-up without experiencing any event, we set Y = τ; if a participant dropped out during follow-up, then Y ∈ {1, 2, …, τ − 1}. For participants who experienced the study endpoint, the genotype of the infecting pathogen was obtained. Genotypes were categorized as matched to the vaccine at the given pathogen protein locus (J = 1) or mismatched in that region (J = 2).

In the absence of right-censoring, the full data unit $X≔(W,Z,T,J)\sim {\mathbb{P}}_0$ is available for each trial participant. The cumulative incidence of type j ∈ {1, 2} endpoints at time t₀ ∈ {1, 2, …, τ} under vaccine assignment z ∈ {0, 1} is defined as ${\text{pr}}_{{\mathbb{P}}_0}(T\le t_0,J=j\mid Z=z)$ and denoted F_j,z(t₀). The cumulative vaccine efficacy against genotype j is defined as the multiplicative reduction in cumulative incidence comparing vaccine to control,

$$V{E}_j(t_0)≔1-\frac{F_{j,1}(t_0)}{F_{j,0}(t_0)}.$$

In vaccine sieve analysis, we are interested in testing the null hypothesis that V E₁(t₀) = V E₂(t₀) against various alternatives. We define the vaccine sieve effect as the ratio (match vs. mismatched) of ratios (control vs. vaccine) of cumulative incidence,

$$VSE(t_0)≔\frac{F_{1,0}(t_0)∕F_{1,1}(t_0)}{F_{2,0}(t_0)∕F_{2,1}(t_0)}.$$

To estimate the sieve effect, we estimate the cumulative incidence of each endpoint type in each treatment arm. For simplicity, we consider the statistical problem of estimating cumulative incidence of matched endpoints (i.e., of type j = 1) under assignment to the vaccine (i.e., z = 1). Because the labeling of events and treatments is arbitrary, our developments immediately apply to estimating the cumulative incidence of every other combination of endpoint and treatment arm. Our choice of t₀ is also arbitrary and our results directly apply to pointwise estimation of cumulative incidence, vaccine efficacy, and vaccine sieve effects over time.

Cumulative incidence cannot be estimated directly from the observed data because of right-censoring. In practice, we observe $O≔(W,Z,\Delta ,\tilde{T},\Delta J)\sim P_0$ , where $\tilde{T}≔\text{min}(T,Y)$ , $\Delta ≔I(\tilde{T}=T)$ , and P₀ denotes the true distribution of O. Our goal is to develop an estimator of F_1,1 (t₀) based on n independent realizations O₁, … , O_n from P₀. It will be useful to express the observed data unit in terms of discrete counting processes, i.e., O = (W, Z, {N(t), M(t), C(t) : t = 1. 2, …, τ}). where $N(t)≔I(\tilde{T}\le t,\Delta J=1)$ , $M(t)≔I(\tilde{T}\le t,\Delta J=2)$ and $C(t)≔I(\tilde{T}\le t,\Delta =0)$ .

3. Identification and estimation of cumulative incidence

Under conditions described below, cumulative incidence can be identified by the longitudinal G-computation formula (Robins, 1999; Bang and Robins, 2005), a functional of the observed data distribution P₀. Using this approach, we may identify cumulative incidence using iteratively-defined conditional means of the discrete counting process, hereafter referred to as iterated means. We define H(t) := (N(t), M(t), W) to denote a participant’s observed history through time t. We define the iterated means as

$$\begin{gathered} {\mu }_{t_0}(h(t_0-1))≔{\text{pr}}_{P_0}\{N(t_0)=1\mid Z=1,C(t_0-1)=0,H(t_0-1)=h(t_0-1)\}; \\ {\mu }_{t_0-1}(h(t_0-2))≔{\mathrm{E}}_{P_0}\{{\mu }_{t_0}(H(t_0-1))\mid Z=1,C(t_0-2)=0,H(t_0-2)=h(t_0-2)\}; \\ {\mu }_{t_0-2}(h(t_0-3))≔{\mathrm{E}}_{P_0}\{{\mu }_{t_0-1}(H(t_0-2))\mid Z=1,C(t_0-3)=0,H(t_0-3)=h(t_0-3)\}; \end{gathered}$$

and so on. In words, μ_t0 (h(t − 1)) is the true conditional probability of a matched endpoint at t₀ given vaccine, no censoring up to t₀ − 1, and history h(t − 1). Thereafter, the iterated mean at t is defined recursively as the conditional mean of μ_t+1 (H(t)) given vaccine, no censoring up to t − 1, and history h(t − 1). For example, μ_t0−2(h(t₀ − 3)) with n(t₀ − 3) = 0, m(t₀ − 3) = 0 and w = w₀ is the probability a vaccinated participant with baseline covariate vector value w₀ experienced a J = 1 endpoint at times t₀ − 2, t₀ − 1 or t₀ given no endpoint prior to t₀ − 2. While each iterated mean is implicitly dependent on the final time-point t₀, we suppress this to simplify notation. We note that μ₁ is only a function of the value of W, since no participant has yet experienced an endpoint.

We can relate the iterated means above to cumulative incidence under two key conditions. The first condition is that the observed data unit O is a random coarsening of the full data unit X (see, e.g., van der Laan and Robins, 2003). This is satisfied, for example, if (T, J) is independent of C given W and Z; in words, there are no unmeasured confounders of the relationship between the censoring mechanism and outcome process. The second condition essentially states that the conditional probability of remaining uncensored throughout the study given W = w is strictly positive for each value of w that arises in the population. This is often referred to as the positivity condition (see, e.g., Petersen et al., 2010). In Appendix A, we show that under these two conditions, for each t = 1, … , t₀, μ_t(h(t − 1)) with h(t − 1) = (0, 0, w) equals the conditional probability of a J = 1 endpoint between t and t₀ for a vaccinated participant with covariates W = w and no endpoint observed prior to t. Thus, because no participant has experienced an event at time zero, μ₁ is equal to the conditional probability of a J = 1 endpoint between 1 and t₀ for a vaccinated participant with W = w, that is, the covariate conditional cumulative incidence of matched endpoints in vaccinated participants. The marginal cumulative incidence of matched endpoints in the vaccine arm can be obtained by integrating μ₁ over the distribution of covariates. Defining G(w) := pr_P (W ≤ w) the cumulative distribution function of covariates at w and $\stackrel{‒}{\mu }≔\int {\mu }_1(w)dG(w)$ , we have that $F_{1,1}(t_0)=\stackrel{‒}{\mu }$ under coarsening at random and positivity assumptions.

A heuristic justification of the identification result is that μ_t describes what happens in the stratum of vaccinated participants under observation at t with covariate value W = w. The positivity assumption ensures that this stratum indeed exists for each choice of w, while coarsening at random ensures that at-risk participants with W = w are on average similar to previously censored participants with W = w. Thus, at any given time, participants at risk can be used to infer, on average, what would have happened to other participants in the same stratum had they remained under study.

The identification result implies that an estimator of F_1,1 (t₀) may be obtained by estimating μ := {μ_t : t = 1, …, t₀} and subsequently marginalizing the estimator of μ₁ using an estimator of the distribution of baseline covariates. When parametric regression models are used to estimate μ, this estimator is commonly referred to as a G-computation estimator, and it is an example of a plug-in estimator. For concreteness, we outline the practical construction of the G-computation estimator based on the use of the empirical distribution of covariates to estimate G and a modified version of logistic regression to estimate μ. We modify standard logistic regression in two ways. First, we account for the fact that for any observation with H(t − 1) = (1, 0, w), indicating a matched endpoint prior to t, N(t) = 1 necessarily, and thus our regression estimator μ_n,t of μ_t should equal 1 for all such observations. Similarly, if H(t − 1) = (0, 1, w), indicating a mismatched endpoint prior to t, then N(t) = 0 and so μ_n,t should equal zero for all such observations. Our second modification of logistic regression is that the outcome of our regressions may take values between zero and one. Below, we refer to such regressions as quasi-logistic. For simplicity of exposition, we assume momentarily that W is univariate. The algorithm includes the following steps:

1. Set μ_n,t0 (H_i(t₀ − 1)) = 1 for all observations with N_i(t₀ − 1) = 1 and set μ_n,t0 (H_i(t₀ − 1)) = 0 for all observations with M_i(t₀ − 1) = 1. Define a logistic regression model, logit {μ_t0(h(t₀ − 1))} = α_t0 + β,_t0w, for the remaining observations. Fit the logistic regression model by regressing outcome N_i(t₀ − 1) on W_i using all O_i with Z_i = 1, C_i(t − 1) = 0, N_i(t − 1) = 0, and M_i(t − 1) = 0. Let α_n,t0 and β_n,t0 denote the estimated parameters of the model. Set μ_n,t0 (H_i(t₀ − 1)) = expit(α_n,t0 + β_n,t0 W_i) for all observations with M_i(t₀ − 1) = 0 and N_i(t₀ − 1) = 0.

2. For t = t₀ − 1, …, 1, recursively construct an estimate μ_n,t of μ_t as follows. First, set μ_n,t(H_i(t − 1)) = 1 for all observations with N_i(t − 1) = 1 and set μ_n,t0 (H_i(t − 1)) = 0 for all observations with M_i(t − 1) = 1. Define a quasi-logistic regression model, logit{μ_t(h(t − 1))} = α_t + β_tw, for the remaining observations. Fit the quasi-logistic regression model by regressing outcome μ_n,t+1(H_i(t)) on W_i using all O_i with Z_i = 1, C_i(t − 1) = 0, N_i(t − 1) = 0, and M_i(t − 1) = 0. Let α_n,t and β_n,t denote the estimated parameters of the model. Set μ_n,t(H_i(t − 1)) = expit(α_n,t + β_n,t W_i) for all observations with M_i(t − 1) = 0 and N_i(t − 1) = 0.

3. Construct estimate ${\stackrel{‒}{\mu }}_n=\frac{1}{n}{\sum }_{i=1}^n{\mu }_{n,1}(W_i)$ by averaging μ_n,1 over observed values of W.

If the fitted logistic regression approximates μ_t well for each t, then relative to the AJ estimator, we expect this plug-in estimator to have improved bias when censoring is dependent, and reduced variability when covariates are predictive of the outcome process. Intuitively, there are two sources of variation in the time-to-endpoint of trial participants: variation due to measured versus unmeasured characteristics, the latter often referred to as noise. Covariate-averaged estimators of the type exhibited above often mitigate the former source of variation and can therefore have improved precision. Among others, Zhang et al. (2008) and Moore and van der Laan (2009) discuss efficiency improvements in randomized trials.

These arguments point to the potential for possibly important gains from using a covariate-averaged estimator of marginal cumulative incidence. However, to realize these gains, the fitted regression estimators must adequately approximate the true iterated mean at each time-point. Moore and van der Laan (2009) showed that, in studies with no right-censoring, adjusting for covariates, even via misspecified regression models, can yield unbiased treatment effect estimates that are more precise than unadjusted estimates. However, the same is not true in the presence of right-censoring. This motivates the use of flexible regression techniques to ensure that estimates of the iterated means are as close to the truth as possible. As discussed in the introduction, stacking or super learning (Wolpert, 1992; Breiman, 1996; van der Laan et al., 2007) based on a library of candidate learners may be useful towards this end. Numerous studies illustrate the advantages of this approach in practice (van der Laan et al., 2007; Rose, 2013; Pirracchio et al., 2015). In order to approximate the truth as well as possible, it appears strategic in the context of super learning to consider a large set of candidate regression estimators including both parametric and machine learning-based estimators. However, when flexible regression techniques are used, performing valid statistical inference is a more challenging task. Whereas plug-in estimators based on a parametric MLE typically have an asymptotic normal distribution, the same is not true when adaptive procedures, like the super learner, are used. This complicates greatly the construction of valid confidence intervals and hypothesis tests. The targeted minimum loss-based estimation (TMLE) framework provides a means of addressing this problem.

4. Targeted minimum loss-based estimation

To understand why plug-in estimators based on adaptive regression estimators behave poorly, we require the form of the efficient influence function (EIF), a key element in efficiency theory (Bickel et al., 1997). We define ζ(w) := pr_P0(Z = 1 ∣ W = w) as the conditional probability of receiving vaccine given covariates. For t = 1, 2,…, t₀ − 1, we define π_t(w) := pr_P0{C(t) = 0 ∣ Z = 1, N(t − 1) = 0, M(t − 1) = 0, C(t − 1) = 0, W = w} as the conditional probability of remaining uncensored at time t given vaccine, no endpoint nor censoring through t − 1, and baseline covariates, and we write π := {π_t : t}. The EIF of cumulative incidence $\stackrel{‒}{\mu }$ at P₀ relative to a nonparametric model evaluated on a typical observation O_i is

$$D^{\ast }(\mu ,G,\zeta ,\pi )(O_i)=\sum _{t=1}^{t_0}{D}_t(\mu ,\zeta ,\pi )(O_i)+D_W(\mu ,G)(O_i),$$ (1)

where, for t = 1, 2,…, t₀, we define D_t(μ, ζ, π) as the mapping

$$o\mapsto \frac{I(z=1,c(t-1)=0)}{\zeta (w){\prod }_{s=1}^{t-1}{\pi }_s(w)}\{{\mu }_{t+1}(h(t))-{\mu }_t(h(t-1))\},$$

and D_W(μ, G) as the mapping o ↦ μ₁(w) − ∫ μ₁(u)dG(u). This is also the EIF in a model with arbitrary constraints imposed on the conditional treatment or censoring distribution. If an estimator ${\stackrel{‒}{\mu }}_n$ of $\stackrel{‒}{\mu }$ is such that ${\stackrel{‒}{\mu }}_n-\stackrel{‒}{\mu }=\frac{1}{n}{\sum }_{i=1}^n{D}^{\ast }(\mu ,G,\zeta ,\pi )(O_i)+o_P(n^{-1∕2})$ , it follows that $n^{1∕2}({\stackrel{‒}{\mu }}_n-\stackrel{‒}{\mu })$ has a normal distribution in large samples, with variance at least as small as any other regular, asymptotically linear estimator of $\stackrel{‒}{\mu }$ . Valid inference based on such an estimator may be facilitated by knowledge of this asymptotic distribution.

The construction of a plug-in estimator of $\stackrel{‒}{\mu }$ only requires estimators of μ and G. However, estimators of the treatment probability ζ and censoring distribution π are also generally needed to construct efficient estimators of $\stackrel{‒}{\mu }$ . Under conditions stated in Appendix B, the estimation error of any plug-in estimator of $\stackrel{‒}{\mu }$ can be expressed as

$${\stackrel{‒}{\mu }}_n-\stackrel{‒}{\mu }=\frac{1}{n}\sum _{i=1}^n{D}^{\ast }(\mu ,G,\zeta ,\pi )(O_i)-\frac{1}{n}\sum _{i=1}^n{D}^{\ast }({\mu }_n,G_n,{\zeta }_n,{\pi }_n)(O_i)+o_P(n^{-1∕2}),$$ (2)

where ζ_n and π_n are estimators of ζ and π, respectively. Sufficient regularity conditions include that ζ_n and π_n tend in probability to ζ and π, respectively, at a sufficiently fast rate. In the case of a randomized trial, the treatment assignment probability ζ is known exactly; however, the conditional censoring distribution π is unknown and must be estimated from the data. To ensure that our estimate of the censoring distribution is as close to the truth as possible, we resort to super learning. Because in our proposed implementation μ_n and π_n are super learner-based estimators, the second summand on the right-hand side of (2), $\frac{1}{n}{\sum }_{i=1}^n{D}^{\ast }({\mu }_n,G_n,{\zeta }_n,{\pi }_n)(O_i)$ , generally does not converge to zero faster than n^−1/2. This renders ${\stackrel{‒}{\mu }}_n$ inefficient and prevents it from having a tractable distributional limit theory. Practically, this implies that ${\stackrel{‒}{\mu }}_n$ will exhibit large finite-sample bias, making it difficult, if not impossible, to perform valid inference based on ${\stackrel{‒}{\mu }}_n$ .

In the previous section, we argued that flexible estimation techniques may be useful for obtaining an accurate estimate of the iterated means. However, equation (2) makes clear that there are repercussions vis-à-vis statistical inference for adopting such an approach. The challenge is thus to construct regression estimators ${\mu }_n^{\ast }$ and π_n that (i) are flexible enough to provide a good approximation to μ and π, respectively, and (ii) have minimal finite-sample bias relative to $\stackrel{‒}{\mu }$ , in the sense that $\frac{1}{n}{\sum }_{i=1}^n{D}^{\ast }({\mu }_n^{\ast },G_n,{\zeta }_n,{\pi }_n)(O_i)=o_P(n^{-1∕2})$ . If such estimators can be constructed, then the plug-in estimator ${\stackrel{‒}{\mu }}_n^{\ast }$ based on ${\mu }_n^{\ast }$ is consistent, asymptotically normal and efficient.

The TMLE framework provides a way to update an initial estimator μ_n into a revised estimator ${\mu }_n^{\ast }$ that satisfies a set of user-specified equations. Remarkably, the idea of TMLE was first suggested in Stein (1956) as a means of constructing nonparametric efficient estimators, though, to our knowledge, examples of these estimators did not appear in the literature until Scharfstein et al. (1999). The concept was developed in generality and formally studied in van der Laan and Rubin (2006), which led to the development of the field of targeted learning (van der Laan and Rose, 2011, 2018). In the longitudinal data setting, TMLE estimators of average treatment effects based on parametric regressions were described in Robins (1999) and implemented in Bang and Robins (2005). TMLE estimators using super learning-based estimators were described and evaluated in van der Laan and Gruber (2012).

In the present problem, we use TMLE to map initial estimates (μ_n, ζ_n, π_n) into an estimate ${\mu }_n^{\ast }$ of μ that satisfies

$$\frac{1}{n}\sum _{i=1}^n{D}^{\ast }({\mu }_n^{\ast },G_n,{\zeta }_n,{\pi }_n)(O_i)=0.$$ (3)

Here, we describe how such a procedure can be implemented in practice – theoretical details follow from van der Laan and Gruber (2012) and are omitted. The targeted plug-in estimator is implemented similarly as the G-computation estimator described in Section 3, though it includes an additional univariate model-fitting step after each regression.

1. If the conditional treatment probability ζ₀ is known, set ζ_n = ζ₀; otherwise, construct estimate ζ_n of ζ₀. Construct estimate π_n of the censoring probabilities π₀.

2. Set ${\mu }_{n,t_0+1}^{\ast }(H_i(t_0))=N_i(t_0)$ for i = 1,…, n. For t = t₀, t₀ − 1,…, 1, perform recursively:

   1. construct and evaluate an initial estimate μ_n,t of μ_t. First, set μ_n,t(H_i(t − 1)) = 1 for all observations with N_i(t − 1) = 1. Similarly, set μ_n,t(H_i(t − 1)) = 0 for all observations with M_i(t − 1) = 1. For the remaining observations fit a super learner regression of the outcome ${\mu }_{n,t+1}^{\ast }(H_i(t))$ on covariates W_i using O_i with Z_i = 1, C_i(t − 1) = 0, N_i(t − 1) = 0, and M_i(t − 1) = 0. Note that at t = t₀ this outcome is simply N_i(t₀), while for other time points it is a vector of predictions from the quasi-logistic regression generated in step 2b) at time t + 1. Set μ_n,t(H_i(t − 1)) equal to the super learner-predicted value for all O_i with N_i(t − 1) = 0 and M_i(t − 1) = 0. The estimate μ_n,t has been evaluated on all observations and we have a vector of n observations containing predicted values of μ_t.
   2. fit a quasi-logistic regression with outcome ${\mu }_{n,t+1}^{\ast }(H_i(t))$ , offset term logit{μ_n,t(H_i(t − 1))} and covariate $\{{\zeta }_n(W_i){\prod }_{s=1}^{t-1}{\pi }_{n,s}(W_i){\}}^{-1}$ using only observations with Z_i = 1, C_i(t − 1) = 0, N_i(t − 1) = 0, and M_i(t − 1) = 0. Denote by ϵ_n,t the estimated regression coefficient in this model. For observations with N_i(t − 1) = M_i(t − 1) = 0, define

      $${\mu }_{n,t}^{\ast }(H_i(t-1))≔\text{expit}\left[\mathrm{logit}\{{\mu }_{n,t}(H_i(t-1))\}+\frac{{ϵ}_{n,t}}{{\zeta }_n(W_i){\prod }_{s=1}^{t-1}{\pi }_{n,s}(W_i)}\right];$$
      for all other observations set ${\mu }_{n,t}^{\ast }(H_i(t-1))={\mu }_{n,t}(H_i(t-1))$ . Thus, we again obtain a vector of n predicted values for μ_t, which will serve as outcome values in the regression at t − 1.

3. Construct estimate ${\stackrel{‒}{\mu }}_n^{\ast }=\frac{1}{n}{\sum }_{i=1}^n{\mu }_{n,1}^{\ast }(W_i)$ by averaging ${\mu }_{n,1}^{\ast }$ over observed values of W.

The targeted estimator ${\stackrel{‒}{\mu }}_n^{\ast }$ has desirable large-sample properties. If each of ζ_n, μ_n and π_n are consistent for ζ, μ and π, respectively, at a sufficiently fast rate,${\stackrel{‒}{\mu }}_n^{\ast }$ is a nonparametric efficient estimator of $\stackrel{‒}{\mu }$ , and $n^{1∕2}({\stackrel{‒}{\mu }}_n^{\ast }-\stackrel{‒}{\mu })$ tends to a mean-zero normal distribution with variance consistently estimated by ${\sigma }_n^2≔\frac{1}{n}{\sum }_{i=1}^n{D}^{\ast }({\mu }_n^{\ast },G_n,{\zeta }_n,{\pi }_n)(O_i{)}^2$ . Additionally, ${\stackrel{‒}{\mu }}_n^{\ast }$ is doubly-robust in the sense that it is consistent if at least one of μ_n and (π_n, ζ_n) is consistent (van der Laan and Gruber, 2012). If μ_n is inconsistent but the treatment and censoring mechanisms are known exactly, ${\stackrel{‒}{\mu }}_n^{\ast }$ is no longer efficient but$n^{1∕2}({\stackrel{‒}{\mu }}_n^{\ast }-\stackrel{‒}{\mu })$ tends to a normal distribution with variance still consistently estimated by ${\sigma }_n^2$ . However, if μ_n is inconsistent, ζ is known and π is consistently estimated using the observed data, the asymptotic variance is more complicated. Nevertheless, in the special case that π_n is an efficient estimator within a parametric model, then${\sigma }_n^2$ is a conservative estimate of the asymptotic variance (see, e.g., Theorem 2.3 of van der Laan and Robins, 2003). A similar result holds for the case in which π_n or ζ_n is inconsistent but μ_n is consistently estimated.

Use of the Wald interval (${\stackrel{‒}{\mu }}_n^{\ast }-z_{1-\alpha ∕2}{\sigma }_n{n}^{-1∕2}$ ,${\stackrel{‒}{\mu }}_n^{\ast }+z_{1-\alpha ∕2}{\sigma }_n{n}^{-1∕2}$ ), where z_β is the β-quantile of the standard normal distribution, is motivated by these large-sample results. This interval will typically have asymptotic coverage no smaller than 1 − α under a range of scenarios, and asymptotically exact coverage either if each of μ_n, ζ_n and π_n are consistent, or (π, ζ) is exactly known. Given a fixed ${\stackrel{‒}{\mu }}^{\circ }\in (0,1)$ , a test of the null hypothesis $\stackrel{‒}{\mu }={\stackrel{‒}{\mu }}^{\circ }$ versus the two-sided complement alternative with asymptotic size no larger than α can be constructed by rejecting the null whenever $\mid n^{1∕2}({\stackrel{‒}{\mu }}_n^{\ast }-{\stackrel{‒}{\mu }}^{\circ })∕{\sigma }_n\mid >z_{1-\alpha ∕2}$ . In Section 2 of the web supplement, we illustrate how the delta method can be used to obtain estimates of the asymptotic variance of V E_j(t₀) and V S E(t₀).

5. Simulation study

We evaluated the performance of the super learner-based TMLE estimators via simulation studies. The baseline covariate vector W had independent components W₁ ~ Uniform(−2, 2) and W₂ ~ Bernoulli(0.5). Vaccine was randomly assigned with equal probability, that is, Z ~ Bernoulli(0.5) independently of W. Given W = w and Z = z, the time T of interest was simulated as T ~ Geometric{λ_β(w, z)}, where λ_β(w, z) = expit(−2 + βw₁ − 2βw₁w₂ + z), and the time C to censoring was simulated as C ~ Geometric{η_γ(w, z)}, where η_γ(w, z) = expit(−3 + γw₁ − 2γw₁w₂ + z). The type of endpoint was randomly assigned with equal probability to types J = 1 and J = 2. The observed failure time was taken to be the minimum of T and C, with ties labeled as events.

We compared the performance of our proposed TMLE estimator using super learning to estimate the iterated means and censoring distribution to: (1) the AJ estimator, which does not adjust for covariates, and (2) a G-computation estimator that adjusts for covariates via main terms logistic regression. The super learner library included four algorithms: a main terms logistic regression, a logistic regression with forward stepwise variable selection including all two-way interactions, an intercept-only logistic regression, and multivariate adaptive regression splines (Friedman, 1991) – this represents a combination of traditional regression techniques and machine learning algorithms.

We evaluated the performance of estimators of $F_{1,0}^1(6)$ at two sample sizes, n ∈ {500, 5000}, in five different scenarios that varied how covariates related to endpoints and censoring (Table 3). In the first scenario, we set β = 0 and γ = 0, and covariates were related neither to endpoints nor censoring (W ↛ T, W ↛ C). In this scenario, all three estimators considered are consistent and asymptotically efficient, and indeed we found that the three estimators performed equally well at both sample sizes.

Table 3:

Left: theoretical properties of the Aalen-Johansen (AJ), main terms logistic regression-based G-computation (GCOMP), and super learner-based targeted minimum loss-based estimator (TMLE). Right: Monte Carlo evaluation of finite-sample performance of estimators of cumulative incidence in terms of bias, coefficient of variation, mean squared-error (MSE) and coverage probability of nominal 95% confidence intervals. Results are based on 1,000 samples from the data generating mechanism for two sample sizes and four relationships between covariates (W), time-to-endpoint (T) and time-to-censoring (C). The fifth scenario includes an unmeasured confounder U.

		Large-sample properties				n = 500			n = 5000
		AJ	GCOMP	TMLE		AJ	GCOMP	TMLE	AJ	GCOMP	TMLE
W ↛ T, W ↛ C	Consistent	✓	✓	✓	Relative Bias (%)	−0.12	−0.12	−0.95	0.14	0.14	0.03
					Coef. Var. (×10)	0.86	0.86	0.88	0.26	0.26	0.26
$F_{1,0}^1(6)$ = 0.42	Efficient	✓	✓	✓	MSE (×100)	0.74	0.74	0.78	0.07	0.07	0.07
					Coverage (%)	92.9	92.9	92.4	95.3	95.0	95.1
W ↛ T, W → C	Consistent	✓	✓	✓	Relative Bias (%)	0.02	0.26	−2.83	0.05	0.07	−0.73
					Coef. Var. (×10)	0.91	0.90	1.08	0.28	0.28	0.33
$F_{1,0}^1(6)$ = 0.42	Efficient	✓	✓	✓	MSE (×100)	0.83	0.82	1.24	0.08	0.08	0.11
					Coverage (%)	95.8	95.8	93.0	95.8	95.6	98.0
W → T, W ↛ C	Consistent	✓	✓	✓	Relative Bias (%)	−0.63	−0.62	−1.29	0.08	0.08	−0.00
					Coef. Var. (×10)	0.95	0.96	0.92	0.31	0.31	0.30
$F_{1,0}^1(6)$ = 0.33	Efficient	✕	✕	✓	MSE (×100)	0.91	0.92	0.86	0.10	0.10	0.09
					Coverage (%)	95.1	95.1	94.8	95.3	95.3	95.3
W → T, W → C	Consistent	✕	✕	✓	Relative Bias (%)	−7.96	−7.65	−1.69	−7.64	−7.60	0.52
					Coef. Var. (×10)	0.99	0.99	0.99	0.33	0.33	0.32
$F_{1,0}^1(6)$ = 0.33	Efficient	✕	✕	✕	MSE (×100)	1.74	1.67	1.01	0.80	0.79	0.10
					Coverage (%)	84.8	85.1	95.8	24.8	25.2	94.0
(W, U) → T, (W, U) → C	Consistent	✕	✕	✕	Relative Bias (%)	−6.50	−6.50	−6.81	−6.87	−6.87	−6.96
					Coef. Var. (×10)	0.09	0.09	0.09	0.29	0.29	0.30
$F_{1,0}^1(6)$ = 0.35	Efficient	✕	✕	✕	MSE (×100)	0.14	0.15	0.15	0.07	0.07	0.07
					Coverage (%)	88.1	88.4	87.9	31.5	31.5	31.6

In the second scenario, we set β = 0 and γ = 2, and covariates were related to censoring but not to endpoints (W ↛ T, W → C). Again, all estimators are consistent and asymptotically efficient, and we found that the three estimators performed well. The TMLE estimator had slightly more bias than the other two estimators, which may be due to practical violations of the positivity assumption, a known concern when implementing efficient estimators in small sample sizes (Petersen et al., 2010). In particular, for this data-generating mechanism, there were observations with < 0.0001 probability of remaining uncensored until the last time point. These observations receive large weight in both the TMLE estimation procedure and in the variance estimates for the TMLE, which may contribute to the slight deterioration in performance.

In the third simulation scenario, we set β = 2 and γ = 0, and covariates were related to endpoints but not to censoring (W → T, W ↛ C). In this scenario, all estimators are consistent; however, only the TMLE estimator, which correctly adjusts for the covariate-endpoint relationship, is asymptotically efficient. We found low bias for all estimators in this scenario, but slightly lower variability in the TMLE estimates. Though the improvements in variability are modest, they come near to achieving the theoretical efficiency gains possible for this data-generating process. The theoretical efficiency gains can be computed by contrasting the efficiency bound for covariate-adjusted estimators and for covariate-unadjusted estimators. This can be achieved by computing the variance of the efficient influence function of μ based on a data structure that does or does not include the available baseline covariate vector. We numerically evaluated these efficiency bounds – these are lower bounds for asymptotic variances – and found 0.54 and 0.48 for unadjusted and adjusted estimators, respectively. Thus, it is only theoretically possible to improve the efficiency of the unadjusted estimator in this simulation study by about 11%. The TMLE estimators nearly achieve this efficiency improvement at the sample sizes we considered.

In the fourth scenario, we set β = 2 and γ = 2, and covariates were related both to endpoints and censoring (W → T, W → C). In this case, the G-computation and AJ estimators are inconsistent, while the TMLE estimator remains consistent and asymptotically efficient. We found that the confidence intervals based on the G-computation and AJ estimators suffered from poor performance, while the TMLE-based intervals achieved approximately nominal coverage.

Finally, in the fifth scenario, we studied the performance of estimators when the coarsening at random assumption is violated. In this scenario, we additionally simulated an unobserved confounder U of T and C. Given W₁ = w₁, we drew U from a Normal(w₁, 1) distribution. Given W = w, U = u and Z = z, and time to endpoint was simulated as $T\sim \text{Geometric}\{{\lambda }_{\beta }^{\ast }(w,u,z)\}$ , where ${\lambda }_{\beta }^{\ast }(w,u,z)=\text{expit}\{-2+2(u+w_1)-4(u+w_1)w_2+z\}$ , time to censoring was simulated as $C\sim \text{Geometric}\{{\eta }_{\gamma }^{\ast }(w,u,z)\}$ , where ${\eta }_{\gamma }^{\ast }(w,u,z)=\text{expit}\{-3+2(u+w_1)-4(u+w_1)w_2+z\}$ . In this situation, all estimators are inconsistent and had equally poor performance.

6. RV144 HIV Vaccine Efficacy Trial Sieve Analysis

We studied the efficacy of the ALVAC/AIDSVAX vaccine to prevent HIV infection by viruses matched and mismatched to the vaccine at amino acid position 169 of the V2 loop of the envelope protein. We estimated the cumulative incidence, vaccine efficacy and sieve effects against matched and mismatched infections every six months from the time of vaccination until three years post vaccination. We adjusted for baseline patient characteristics (year of enrollment, age, gender, behavioral risk score) by using the super learner to estimate of the conditional censoring distribution and the iterated means. The super learner library included both parametric techniques and machine learning algorithms – details are provided in Appendix C.

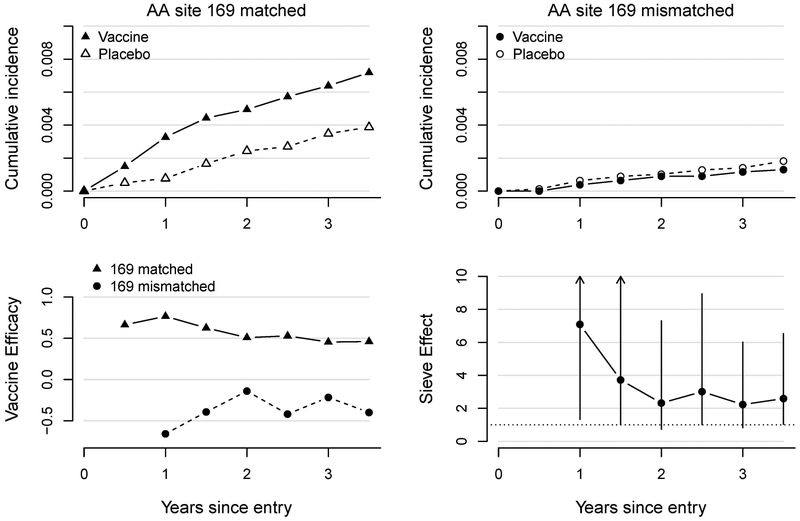
There was a clear separation between the estimated vaccine and control cumulative incidence curves for matched infections, but not for mismatched infections (top row, Figure 1), which led to positive estimates of vaccine efficacy against matched infections and negative efficacy against mismatched infections (bottom left). The efficacy against matched infections appeared to wane over time but was greater than zero at all time-points. The sieve effect comparing these efficacies is thus strongest at early time-points, when the efficacy against matched infections is highest (bottom right). At one and a half years post-vaccination, the vaccine sieve effect was estimated to be 3.0 (95% CI: 1.0, 8.9; p-value=0.05), indicating higher vaccine efficacy against matched rather than mismatched infections. Over time, the sieve effect waned along with the efficacy against matched infections. At three years post vaccination, the vaccine sieve effect was estimated to be 2.3 (95% CI: 0.9, 6.0; p-value=0.12).

Figure 1:

Results from the TMLE analysis of the RV144 trial. Top: Cumulative incidence in vaccine and control groups of HIV-1 infections matched (left) and mismatched (right) to the vaccine at AA 169. Bottom left: Vaccine efficacy against matched (triangle) and mismatched (circle) infections. Bottom right: Vaccine sieve effect with 95% confidence intervals.

We also analyzed the data using the AJ estimator for comparison. We found the point estimates to be nearly identical to those of the TMLE, which might indicate a lack of dependent censoring based on the measured covariates. The confidence intervals about the TMLE-estimated sieve effects were considerably narrower than those for the AJ estimator, as illustrated in Figure 2. By year 3 the efficiency gain is large, with a 33% narrower confidence interval, equating to a 1 − 0.67² = 45% increase in efficiency. These results are consistent with our theory and simulation results, which predict efficiency gains when adjusting for prognostic covariates. The greater precision strengthens the evidence for vaccine sieve effects at site 169 that wane over time; we interpret the scientific impact of these results in the discussion.

Figure 2:

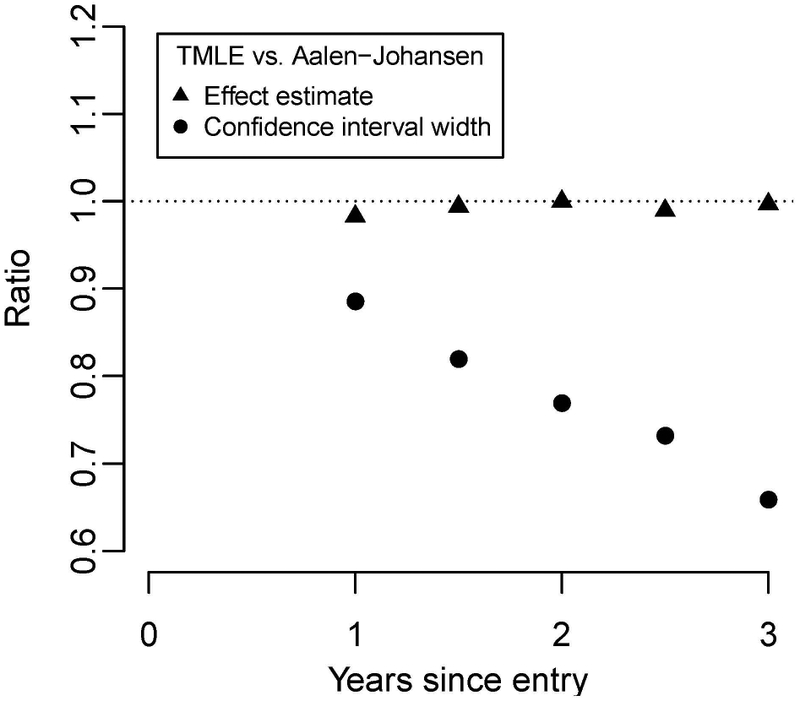
Relative sieve effect estimate (triangle) and confidence interval width (circle) from RV144 trial comparing TMLE to AJ. Values less than one indicate lower point estimate/variance for TMLE.

7. RTS,S/AS01 Malaria Vaccine Efficacy Trial Sieve Analysis

The majority of malaria endpoints in the RTS,S/AS01 trial had multiple parasite genotypes, which occurred because most children were infected by malaria parasites multiple times before presenting with clinical disease. Each strain in a multiple-genotype infection is likely caused by a separate transmission event from a different mosquito. Only clinical cases were registered as study endpoints and all of the associated parasite genomes were subsequently sequenced. The fact that many cases had both matched and mismatched genotypes along the CS protein led to an interesting question: how should vaccine efficacy and vaccine sieve effect parameters be defined?

One approach is to define each endpoint as matched to the vaccine if any of the parasites strains are matched to the vaccine. However, a vaccine sieve effect defined in this way is a mixture of the effect of (i) the vaccine on the number of parasite strains present, and (ii) genetic sieve effects, and the latter are of primary interest in our analysis. To estimate the genetic component of the sieve effect, it may be most relevant to define a parameter describing the vaccine’s effect on a randomly sampled founder parasite of a clinical malaria case. Let A_i := (A_1,i,…, A_Ki,i) denote the K_i different genotypes found in participant i, with A_i = ∅ if participant i is not a case. Let R_i denote a random index drawn from a discrete uniform distribution on {1, 2,…, K_i}, with R_i = 0 if A_i = ∅. Let J_i,Ri = 1 if A_Ri,i is matched to the vaccine and J_i,Ri = 2 otherwise. Let $F_{jr,z}(t_0)≔{\text{pr}}_{{\mathbb{P}}_0}(T\le t_0,J_R=j\mid Z=z,R=r)$ denote the cumulative incidence of clinical malaria associated with genotype r in treatment arm z. The average cumulative vaccine efficacy against parasites of type j is defined using the geometric mean over random draws of R as

$${\overline{VE}}_j(t_0)≔1-\text{exp}\left({\mathrm{E}}_R\left[\log \left\{\frac{F_{jR,1}(t_0)}{F_{jR,0}(t_0)}\right\}\right]\right).$$ (4)

The geometric mean is used so that the averaging process occurs on a scale with greater symmetry.

The multiple outputation approach of Follmann et al. (2003) can be used to estimate such parameters. In this procedure, a dataset is constructed by randomly sampling a single founder genotype from each clinical malaria endpoint, and a statistical method designed for a single genotype per endpoint is applied. For each resample r, we apply our TMLE procedure to obtain a point estimate F_n,jr,z(t₀) of F_jr,z(t₀) for j ∈ {1, 2} and z ∈ {0, 1}. The resampling process is repeated a large number B times. For this analysis, based on the guidelines of Follmann et al. (2003), the estimated number of outputations required for stable inference was B = 3, 677. The overall estimate is calculated as the average of point estimates across the resampled data sets. Specifically, the overall estimate of the true average cumulative vaccine efficacy provided in (4) is computed as

$${\overline{VE}}_{n,j}(t_0)≔1-\text{exp}\left[\frac{1}{B}\sum _{b=1}^B\log \left\{\frac{F_{n,jb,1}(t_0)}{F_{n,jb,0}(t_0)}\right\}\right],$$

for j = 1, 2, while the corresponding estimate of sieve effect is given by

$${\overline{VSE}}_n(t_0)≔\text{exp}\left[\frac{1}{B}\sum _{b=1}^B\log \left\{\frac{F_{n,1b,0}(t_0)∕F_{n,1b,1}(t_0)}{F_{n,2b,0}(t_0)∕F_{n,2b,1}(t_0)}\right\}\right].$$

The asymptotic variance of ${\overline{VE}}_{n,j}(t_0)$ and ${\overline{VSE}}_n(t_0)$ can easily be approximated via the delta method by appropriately combining the estimated influence functions for each outputation sample (details in Section 2 of the web supplement). These influence function-based variance estimators offer an improvement over the nonparametric variance estimators suggested in Follmann et al. (2003), which are not guaranteed to be positive.

Similarly as in the RV144 example, we estimated genotype-specific vaccine efficacy for each genotype and tested for differential vaccine efficacy. We used the super learner with a large library to generate initial estimates of the conditional censoring distribution and the iterated conditional means. Further details are included in Table C1.

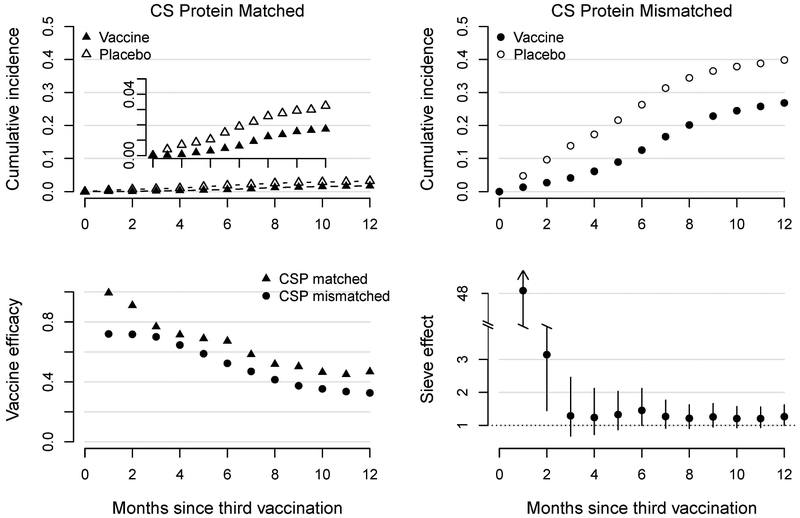
The results are displayed in Figure 3. In the top row, we illustrate the estimated cumulative incidence of disease with malaria parasites matched (left) and mismatched (right) to the RTS,S/AS01 vaccine along the CS protein (left). The cumulative incidence of matched malaria is much lower than mismatched malaria at each time-point for each treatment group. However, for both genotypes there is a clear separation between the vaccine and control curves, indicating vaccine efficacy against both types of endpoints. The vaccine efficacy wanes over time (bottom left) but remains significant through 12 months of follow-up. Vaccine efficacy is significantly higher against matched versus mismatched malaria at each time-point. For example, at 12 months the multiplicative effect of the vaccine is estimated to be 1.3 (95% CI: 1.0, 1.6; p=0.05) times stronger for preventing clinical disease caused by CS protein-matched vs. mismatched parasites.

Figure 3:

Results from the TMLE analysis of the RTS,S/AS01 trial. Top: Multiple outputation TMLE estimates in vaccine and control groups of the incidence of clinical malaria cases matched (left) and mismatched (right) to the vaccine along the CS protein. Bottom left: Vaccine efficacy against matched (triangle) and mismatched (circle) infections. Bottom right: Vaccine sieve effect with 95% confidence intervals.

Once more, our TMLE-based results yielded similar point estimates as the AJ estimator but narrower confidence intervals for the TMLE-estimated sieve effects, achieving a doubled efficiency (1 − 0.7² = 0.51) at the 10-month time-point (Figure 4).

Figure 4:

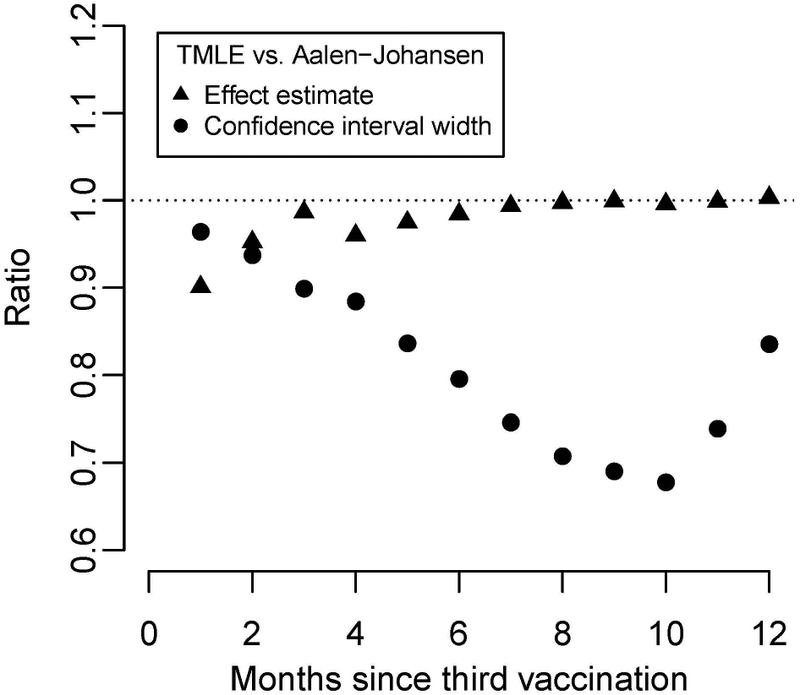
Relative sieve effect estimate (triangle) and confidence interval width (circle) from RTS,S/AS01 trial comparing TMLE to AJ. Values less than one indicate lower point estimate/variance for TMLE.

8. Discussion

For both studies we have analyzed, the identified sieve effects contribute to vaccine science in several ways. First, they motivate basic science studies of mechanisms of protection associated with antibody epitopes at site 169 for the HIV vaccine and in CSP for the malaria vaccine. Second, they support building refined versions of the vaccine that include additional antigen sequences. Third, they have generated hypotheses about sieve effects that will be tested in follow-up efficacy trials of refined vaccine regimens now being planned for both HIV and malaria.

Accurate and precise estimates of vaccine efficacy are important from a regulatory and public health perspective. In preventive vaccine trials, we can never be certain that censoring is completely random and therefore should be concerned that estimators based on this assumption may be systematically biased for efficacy in the enrolled population. Bias due to non-random participant dropout can be mitigated to some extent through the use of measured covariates that predict both dropout and events. As demonstrated in the simulation study, our proposed estimators account for such covariates and thereby reduce bias. However, the simulation also demonstrated that unmeasured confounding can have an impact on estimation, which makes developing relevant sensitivity analyses (e.g., Rotnitzky et al., 2001; Díaz and van der Laan, 2013) an important next step.

In addition to controlling bias due to informative dropout, the proposed TMLE estimators can gain precision by accounting for predictive covariates. Such gains in precision are particularly important in vaccine sieve analysis, since efficacy trials are designed to ensure adequate power to assess overall vaccine efficacy but not genotype-specific vaccine efficacy. The utilization of covariate information thus provides a means of increasing the power to detect sieve effects. For both the HIV and malaria motivating studies, use of the covariate-adjusted TMLE appears to provide sieve effect estimates that are more precise than the standard unadjusted method. On the other hand, our simulation study demonstrates that efficiency gains are not always substantial. The theoretical improvement in variance that is achievable through covariate adjustment is a function both of the covariate-conditional event process and the censoring process. Thus, when evaluating the potential for gains in a given problem, both these processes need to be taken into account.

A common alternative for identification of cumulative incidence is via cause-specific hazard functions. We also derived a TMLE estimator for this approach (details in Section 1 of the web supplement). We found that the two approaches performed similarly in simulations, and in data analyses. The iterated mean approach may be more appealing in that incorporation of time-varying covariates to the TMLE procedure is straightforward (van der Laan and Gruber, 2012), whereas this is quite challenging with the hazards-based approach (Stitelman et al., 2012).

Our simulation studies highlighted that there may be room to improve the TMLE estimators in finite samples when there are practical positivity violations. Collaborative targeted minimum loss-based estimation (C-TMLE) builds upon the TMLE framework and incorporates data-adaptive selection of estimates of the censoring distribution in order to produce iterated means estimates with reduced bias. C-TMLE appears to be a potential avenue for improving performance of the proposed estimators in the context of practical positivity violations (Sekhon et al., 2011).

Table 2:

Key notation used in theoretical development. Full data parameters refer to summaries of the population when no right-censoring is present. Observed data parameters refer to summaries of the observed population, which includes participants with right-censored outcome data. In the text, a subscript n denotes an estimate of the relevant quantity.

Quantity	Expression	Description
Full data parameters
Fj,z(t0)	${\text{pr}}_{{\mathbb{P}}_0}\{T\le t_0,J=j\mid Z=z\}$	cumulative incidence at time t0 of type j endpoints in arm z
V Ej(t0)	1 − Fj,1(t0)/Fj,0(t0)	vaccine efficacy against type j endpoints at time t0
V S E(t0)	(1 − V E1(t0))/(1 − V E2(t0))	vaccine sieve effect at time t0
Observed data parameters
μt(h(t − 1))	EP0{μt + 1(H(t)) ∣ Z = 1, C(t − 1) = 0, H(t − 1) = h(t − 1)}	iterated mean at time t given history h(t − 1)
G(w)	prP0{W ≤ w}	distribution function of baseline covariates
$\stackrel{‒}{\mu }$	∫ μ1 (w)dG(w)	mean of μ1; under assumptions, equals F1,1 (t0)
ζ(w)	prP0{Z = 1 ∣ W = w}	probability of receiving vaccine given covariate value w
πt(w)	prP0 {C(t) = 0 ∣ Z = 1, N(t − 1) = 0, M(t − 1) = 0, C(t − 1) = 0, W = w}	probability of remaining under study at time t given at risk at t − 1 and covariate value w

Appendix A. Relating iterated means to incidence

Under the assumptions stated above, the iterated mean μ_t can be expressed as an indicator plus the probability of failing due to a matched endpoint between t and t₀ given vaccine receipt and no endpoint prior to time t. We derive this result for the vaccine arm (Z = 1) and for matched endpoints (J = 1), but note that the labeling of treatment arms and endpoint type is arbitrary so that these results can also be applied to any combination of Z ∈ {0, 1} and J ∈ {1, 2}.

Defining

$$\begin{gathered} {\lambda }_{1,t}(w)≔{\text{pr}}_{P_0}\{N(t)=1\mid Z=1,C(t-1)=N(t-1)=M(t-1)=0,W=w\}\text{and} \\ {\lambda }_{2,t}(w)≔{\text{pr}}_{P_0}\{M(t)=1\mid Z=1,C(t-1)=N(t-1)=M(t-1)=0,W=w\} \end{gathered}$$

as the conditional cause-specific hazard functions for matched and mismatched endpoints, respectively, we have that μ_t(n(t − 1), m(t − 1), w) equals

$$\begin{gathered} I(n(t-1)=1,m(t-1)=0) \\ +I(n(t-1)=0,m(t-1)=0)·\left[\sum _{m=t}^{t_0}{\lambda }_{1,m}(w)\prod _{s=t}^{m-1}\{1-{\lambda }_{1,s}(w)-{\lambda }_{2,s}(w)\}\right] \end{gathered}$$

for t = 1, 2, …, t₀. Since ${\lambda }_{j,t}(w)={\text{pr}}_{{\mathbb{P}}_0}(T=t,J=j\mid Z=1,T>t-1,W=w)$ under the identification assumptions, we have that

$$\sum _{m=t}^{t_0}{\lambda }_{1,m}(w)\prod _{s=t}^{m-1}\{1-{\lambda }_{1,s}(w)-{\lambda }_{2,s}(w)\}={\text{pr}}_{{\mathbb{P}}_0}(t\le T\le t_0,J=1\mid Z=1,T>t-1,W=w).$$ (5)

The case t = 1 shows that μ₁ is indeed equivalent to the covariate-conditional cumulative incidence.

Appendix B. Conditions for asymptotic efficiency

Equation (2) will hold for estimators μ_n, G_n, ζ_n and π_n that satisfy the following conditions:

1. D*(μ_n, G_n, ζ_n, π_n) falls into a P₀-Donsker class with probability tending to one;

2. E_P0 [{D*(μ_n, G_n, ζ_n, π_n)(O) − D*(μ, G, ζ, π)(O)}²] converges to zero in probability;

3. the second-order term

   $$\begin{gathered} R_n≔\sum _{t=1}^{t_0}{\mathrm{E}}_{P_0}[\frac{I(Z=1,C(t-2)=0)}{{\prod }_{s=0}^{t-2}{\pi }_{n,s}(W)}\left\{\frac{{\pi }_{n,t-1}(W)-{\pi }_{t-1}(W)}{{\pi }_{n,t-1}(W)}\right\}\phantom{]}\times \\ \phantom{[}\left\{{\mu }_{n,t}(N(t-1),M(t-1),W)-{\mu }_t(N(t-1),M(t-1),W)\right\}] \end{gathered}$$

   is asymptotically negligible – that is, R_n = o_P(n^−1/2). In the above equation, for the sake of brevity, we let π_n,0 and π denote ζ_n and ζ, respectively, and set empty products equal to one.

Condition 3 will generally be satisfied if for t = 1,…, t₀ both

$$\begin{gathered} {\mathrm{E}}_{P_0}\left[\{{\mu }_{n,t}(N(t-1),M(t-1),W)-{\mu }_t(N(t-1),M(t-1),W){\}}^2\right]=o_P(n^{-1∕2})\text{and} \\ {\mathrm{E}}_{P_0}\left[\{{\pi }_{n,t-1}(N(t-2),M(t-2),W)-{\pi }_{t-1}(N(t-2),M(t-2),W){\}}^2\right]=o_P(n^{-1∕2}). \end{gathered}$$

Table C1:

Candidate regressions included in super learner analysis of the RV144 data. Tuning parameters for random forest and regression trees were selected from a grid of eight possible combinations using 10-fold cross-validation.

Algorithm	Tuning parameters
GLM	intercept only
GLM	main terms
Random forest	10-fold CV
Regression tree	10-fold CV

Table C2:

Candidate regressions included in super learner analysis of the RTS,S/AS01 data for estimation of censoring distribution. GLM = logistic regression; GAM = generalized additive model; GBM = gradient boosted machine. A variable selection was included in some candidate regression algorithms (third column). In some cases, variables were selected a-priori; in others, variables were selected based on their correlation with the outcome.

Algorithm	Tuning parameters	Covariates
GLM	intercept only	none
GLM	main terms	all
GLM	main terms	five highest correlations
GLM	main terms	study site, treatment, time
GLM	all two-way interactions	study site, treatment, time
GAM	main terms, df=3	five highest correlations
GAM	main terms	five highest correlations
GAM	main terms	study site, treatment, time
GAM	all two-way interactions	study site, treatment, time
Random forest	mtry=5,ntree=1000	All
GBM	int.depth=2, ntree=1000	All

Appendix C. Details of RV144 and RTS,S analyses

The super learner library for the RV144 analysis included four algorithms to estimate both the iterated means and the censoring distribution (Table C1). The RTS,S analysis used considerably more algorithms and slightly different libraries to estimate the iterated means and censoring distribution (Tables C2 and C3).

Table C3:

Candidate regressions included in super learner analysis of the RTS,S/AS01 data for estimation of iterated means. GLM = logistic regression; GAM = generalized additive model; GBM = gradient boosted machine. A variable selection was included in some candidate regression algorithms (third column). In some cases, variables were selected a-priori; in others, variables were selected based on their correlation with the outcome. Gradient boosted machine tuning parameters selected based on out-of-bag (OOB) error rate.

Algorithm	Tuning parameters	Covariates
GLM	main terms	all
GLM	intercept only	none
GLM	main terms	treatment
GLM	main terms	study site, treatment
GLM	two-way interactions	study site, treatment
Stepwise GLM	two-way interactions	five highest correlations
Forward stepwise GLM	main terms	all
GAM	main terms, df=3	five highest correlations
GAM	main terms, df=3	ten highest correlations
Random Forest	mtry=5,ntree=1000	all
GBM	OOB error rate	all