Breast Cancer Diagnosis in Digital Breast Tomosynthesis: Effects of Training Sample Size on Multi-Stage Transfer Learning using Deep Neural Nets

Abstract

In this work we developed a deep convolutional neural network (CNN) for classification of malignant and benign masses in digital breast tomosynthesis (DBT) using a multi-stage transfer learning approach that utilized data from similar auxiliary domains for intermediate-stage fine-tuning. Breast imaging data from DBT and digitized screen-film mammography (SFM), digital mammography (DM) totaling 4,039 unique ROIs (1,797 malignant and 2,242 benign) were collected. Using cross-validation, we selected the best transfer network from six transfer networks by varying the level up to which the convolutional layers were frozen. In a single-stage transfer learning approach, knowledge from CNN trained on ImageNet data was fine-tuned directly with DBT data. In a multi-stage transfer learning approach, knowledge learned from ImageNet was first fine-tuned with the mammography data and then fine-tuned with the DBT data. Two transfer networks were compared for the second-stage transfer learning by freezing most of the CNN structure versus freezing only the first convolutional layer. We studied the dependence of the classification performance on training sample size for various transfer learning and fine-tuning schemes by varying the training data from 1% to 100% of the available sets. The area under the receiver operating characteristic curve (AUC) was used as a performance measure. The view-based AUC on the test set for single-stage transfer learning was 0.85±0.05 and improved significantly (p<0.05) to 0.91±0.03 for multi-stage learning. This study demonstrated that, when the training sample size from the target domain is limited, an additional stage of transfer-learning using data from a similar auxiliary domain is advantageous.

I. INTRODUCTION

To utilize deep convolutional neural networks (CNNs) for pattern recognition tasks in medical imaging, transfer learning is commonly used due to the lack of large training data. The knowledge from a trained source domain task is transferred to improve the learning in the target domain task. Pre-trained CNNs with transferable weights are particularly suited for transfer learning. Studies have shown that fine-tuning of pre-trained CNNs can achieve higher performance than conventional feature engineering methods for a variety of medical imaging tasks. [1]

In a CNN, the convolutional layers near the input are generic and the deeper layers are specific to the target task. [2] Transfer learning from one domain (e.g., non-medical images) to another (e.g., medical images) is to utilize these generic features while transforming or fine-tuning the deeper features to a target task. However, when the available training data from the target domain are limited, the pre-trained features may not be sufficiently fine-tuned to the target task. Instead of transfer learning directly to the target domain with a small training set, additional, intermediate stages of transfer learning from related auxiliary domains may help improve learning in the target task.

CNNs are hierarchical representation of cascading feature extraction stages across the layers. The knowledge learned by training with image samples is incorporated in the weights. One common approach of transfer learning is to control the depth at which the amount of ‘knowledge’ transfer between the source and target is optimal for the target task. This type of feature transformation by freezing the weights from the input layer up to a certain layer of CNN is analogous to utilizing a set of common basis functions for decomposing image features, while training the deeper layers with the image samples from the target domain to select the specific features for the target task. Previous studies on the effects of finite sample size on classifier performance when feature selection[3] is involved shows that the bias in the classifier performance depends on the number of training samples, the number of selected features and their statistical distribution. The CNN performance thus depends on the transfer learning strategy where the level of feature transformation is controlled across multiple stages as well as on the training sample size.

In this study, we propose a multi-stage transfer leaning approach, where a pre-trained CNN on non-medical images is first fine-tuned to a related task in medical imaging domain before being fine-tuned to the target task. We also study the dependence of the effectiveness of this approach on the transfer learning strategy and the training sample size in the two stages.

As of 2013, 67% of the U.S. women population over the ages of 40 have had a mammogram in the past two years. [4] Digital breast tomosynthesis (DBT) is a promising new breast imaging modality with the potential to alleviate the limitations of conventional mammography by providing quasi 3 dimensional structural information of the breast volume. DBT has been shown to improve the detection sensitivity of invasive breast cancer while reducing the recall rate. The reduction of tissue overlap provides increased lesion conspicuity particularly in dense breasts compared to full-field digital mammography (DM). Thus the availability of DBT continues to increase in the U.S. [5] and widely used in clinical practice [6]. Research and development of computer-assisted methods in mammography had a long history [7], [8], including the use of convolution neural networks [9]–[11]. Similar studies on computer-aided detection (CADe) and diagnosis (CADx) methods for DBT have been conducted with relatively smaller data set sizes, [12]–[25] compared to the past mammography studies. The collection of medical images for development of computer-assisted methods is a complex and expensive process that requires institutional approval and annotation by experts. To collect a substantial set of DBT data for deep learning methods is difficult without a concerted effort from multiple research groups with extensive funding similar to the Lung Image Database Consortium image collection (LIDC-IDRI). [26], [27] Multi-stage transfer learning is particularly useful in this scenario, when a sufficiently large data set is not available in the target domain. Knowledge from related domains, such as digitized screen-film mammography (SFM) and DM can be transferred to train a CAD system for DBT. In our previous study on CADe of masses in DBT, we have shown that transfer learning from training on mammograms can improve the learning on DBT. [23] In the current work, we study the usefulness of the additional stage of pre-training with SFM and DM data for the target task of classifying malignant and benign masses (CADx) in DBT.

In the following sections, we describe the data characteristics of mammography and DBT images, the processes of the single-stage and multi-stage transfer learning, and the investigations of the finite sample size effects on the transfer learning strategies. We then discuss the results and observations of these investigations.

II. METHODS AND MATERIALS

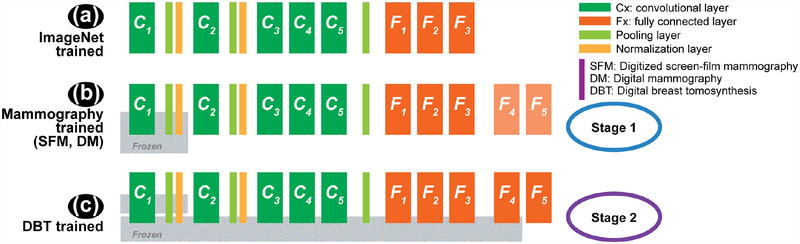
We studied multi-stage transfer learning from non-medical-image-trained CNN to medical-image-trained CNN. For the three structures shown in Fig. 1., Fig. 1(a) shows the ImageNet trained AlexNet CNN structure [28] using 1.2 million non-medical images for a 1000 class image classification problem, corresponding to an average of about 1,200 samples per class. The CNN has 150K neurons and 33M parameters trained on the 2012 ImageNet large scale visual recognition challenge (ILSVRC) data set. Fig. 1(b) shows the stage 1 fine-tuned CNN on 2,454 unique regions of interest (ROIs) with breast masses extracted from mammograms, consisting of 1,057 and 1,397 ROIs for malignant and benign classes, respectively. Fig. 1(c) shows the stage 2 fine-tuned CNN on 1,140 unique ROIs from DBT images, consisting of 590 and 550 ROIs for malignant and benign classes, respectively. A unique ROI on mammograms is defined as a mass ROI extracted from each available view. A unique ROI on DBT is defined as a mass ROI extracted from each of the five slices centered at the mass centroid on each available view. The following sections provide more details of the mammography and DBT data sets, CNN structures, transfer learning and validation methods.

Fig. 1.

Overview of the CNN structures used in the multi-stage transfer learning. (a) ImageNet trained CNN with five convolutional layers and four fully connected layers. (b) Stage 1 transfer learning using mammography data. Two fully connected layers (F₄ and F₅) are added to the ImageNet structure in (a). (c) Stage 2 transfer learning using DBT data. Note that (b) and (c) show three strategies of fine-tuning by freezing the CNN at different layers. The choice of fine-tuning layers is explained in sections II-C and II-D.

A. Data sets

In this study, breast images from SFM, DM and DBT were partitioned into training, validation and independent test sets. SFM data was collected from the University of Michigan (UM) with Institutional Review Board (IRB) approval and from the Digital Database for Screening Mammography (DDSM). [23], [29] The DM images were acquired with a GE Senographe 2000D FFDM system at the UM and collected with IRB approval. The DBT data were collected from the UM and the Massachusetts General Hospital (MGH) with IRB approval [12] from the respective institutions. The UM DBT system was a General Electric (GE) GEN2 prototype DBT system with a total tomographic angular range of 60°, 3° increments and 21 projection views. The MGH DBT system was a prototype GE DBT system with a 50°, 3° increments and 11 projection views. Both the DBT volumes were reconstructed using simultaneous algebraic reconstruction technique with a slice spacing of 1 mm and in-plane resolution of 100 μm × 100 μm. All the breast images used in the study were reduced to 200 μm × 200 μm pixel size by averaging every adjacent k × k pixels, where k depended on the original pixel size of the image. The mass on each view was marked with a bounding box by a Mammography Quality Standard Act (MQSA) qualified radiologist with over 30 years of experience in breast imaging. A 128 × 128-pixel ROI centered at the mass was extracted from the breast image and normalized using a background correction method. [11], [30] The ROI size of 128×128 pixels at a pixel size of 200 μm × 200 μm can enclose a mass up to 25.6 mm in the long diameter.

Table I and table II summarize the breast imaging data sets used in the study. The mammography training data consisted of SFM cases from UM and DDSM, and DM cases from UM and the test set consisted of SFM cases from UM. The DBT training data consisted of cases from UM and MGH and the test set consisted of cases from UM. For each lesion in a DBT volume, ROIs were extracted from five slices centered at the central slice of the lesion and within the upper and lower bounds of the box marked by the radiologist.

TABLE I.

SUMMARY OF MAMMOGRAPHY AND DBT BREAST IMAGING DATA SETS. FOR EACH LESION IN A DBT VOLUME, FIVE UNIQUE ROIS CENTERED AT THE CENTRAL SLICE WERE EXTRACTED

Data set	No. of viewa	No. of unique ROIs	No. of malignant ROIs	No. of benign ROIs	No. of ROIs after data augmentation
Mammography
Training	1,335	1,545	604	941	12, 360
UM-SFM	748	886	317	569	7,088
DDSM-SFM	277	322	191	131	2,576
UM-DM	310	337	96	241	2,696
Test	907	909	453	456	7,272
UM-SFM	907	909	453	456	7,272
Total	2,242	2,454	1,057	1,397	19,632
DBT
Training	230	1,140	590	550	9,120
UM-DBT	92	450	155	295	3,600
MGH-DBT	138	690	435	255	5,520
Test	94	445	150	295	3,560
UM-DBT	94	445	150	295	3,560
Total	324	1,585	740	845	12,680

^aA view in mammography or DBT is a compression direction of the breast during x-ray imaging. For example, a screening examination generally includes a craniocaudal (CC) view and a mediolateral oblique (MLO) view of each breast.

TABLE II.

SUMMARY OF IMAGE PROPERTIES OF THE MAMMOGRAPHY AND DBT BREAST IMAGES USED IN THIS STUDY.

Data set	Source	Device	Gray level range	Pixel size (mm)
Mammography
UM-SFM	University of Michigan	Lumiscan85 laser scanner	12 bits	0.05 × 0.05
UM-DM	University of Michigan	GE Senographe 200D FFDM	14 bits	0.1 × 0.1
DDSM-SFM	Digital Database for Screening Mammography	Lumisys 200 laser scanner	12 bits	0.05 × 0.05
DBT
UM-DBT	University of Michigan	GE GEN2 prototype DBT system	12 bits	0.1 × 0.1a
MGH-DBT	Massachusetts General Hospital	GE prototype DBT system	12 bits	0.1 × 0.1a

^aThe DBT volumes were reconstructed at 1 mm slice spacing.

B. CNN structure

As shown in Fig. 1(a), the ImageNet-trained AlexNet CNN structure has five convolutional layers and three fully connected layers connected with max-pooling and normalization layers; the last fully connected layer is a softmax layer with 1000 outputs. [28] To adapt the ImageNet CNN trained for a 1000-class task to a 2-class mammography task, two fully connected layers were appended to the end of the network with 100 and 2 nodes, respectively. A similar approach of dropping the number of nodes in the last fully connected layer by adding additional layers was proposed by Oquab et al. [31] The same CNN structure was used for both stage 1 and stage 2 transfer learning. Table III lists the number of neurons, the filter sizes and the number of nodes in each layer including the two additional fully connected layers (F₄ and F₅). The CNN was trained with mini-batch stochastic gradient descent optimization using a batch size of 128 to maximize the multinomial logistic regression objective [28] on a Tesla K40 GPU. The output score of each sample from the softmax layer of the CNN was used as a decision variable for receiver operating characteristic (ROC) analysis [32] and the area under the ROC curve (AUC) was used as a performance measure. Trapezoidal rule was used to estimate the AUC during iterations for its efficiency. From our previous study [33], we observed that a momentum of 0.9 and an initial learning rate of 0.001 would reach stable plateau within 200 epochs for our studied task. We therefore used these parameters for the current study.

TABLE III.

CNN STRUCTURE.

Layer	Num. of neurons	Filter size	Num. of nodes
C1	61,504	11 × 11	64
C2	43,200	5×5	192
C3	18,816	3×3	384
C4	12,544	3×3	256
C5	12,544	3×3	256
F1			4096
F2			4096
F3			1000
F4			100
F5			2

C. First-stage transfer learning strategy

In the first-stage transfer learning, ‘knowledge’ transfer from the CNN trained on non-medical images was transferred to the CNN to be trained for classification of malignant and benign masses in mammography. Different levels of knowledge from the pre-trained task may be transferred to the current target task by varying the number of convolutional layers allowed to be fine-tuned by the image samples of the target task. The fully connected layers were always initialized with a random seed in stage 1. To identify the best transfer learning scheme for fine-tuning the ImageNet-trained CNN to the breast mass classification task, we first conducted experiments with the mammography data as follows.

The mammography data was divided into a training set and a test set as shown in table I. A total of six transfer networks were evaluated: five from freezing C to the i^th convolutional layer C_i, where i=1,.., 5, and one from not freezing any layers (C₀). These networks are denoted as C₁, C₁-C₂, C₁-C₃, C_1-C₄, C₁-C₅, and C₀, respectively, in the following discussion. As the early convolutional layers are usually more generic and the deeper layers are more specific to the task, by varying the freezing point along the depth of the CNN layers, we attempted to find empirically the balance between transferring the generic and specific type of features for our target task. From the six transfer networks and the average performance of ten experiments, we selected the best levels for transfer learning of the mammography task.

After the network selection experiments, the training and test sets of 19,632 mammography ROIs were combined into a large training set for the rest of the experiments.

D. Multi-stage transfer learning

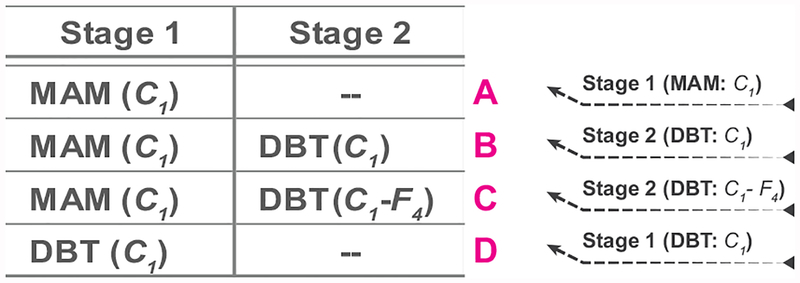
In our previous work on detection of masses in DBT, we have shown that a CNN trained on mammography images to differentiate true masses and normal breast tissue can also classify DBT masses with an AUC of 0.81 without additional fine-tuning. [23] This important observation can potentially alleviate the large data requirements for DBT when training deep learning structures. To assess the knowledge that could be gained by pre-training with mammography data for the target task of classifying malignant and benign mass in DBT, the stage-1 mammography transfer-trained CNN was tested without stage-2 fine-tuning with DBT data (Fig. 2, A).

Fig. 2.

Four transfer learning and fine-tuning strategies using the mammography and the DBT data sets to be compared in this study. ‘A’ to ‘D’ denote the plots in the graphs from the Results section. ‘A’ and ‘D’ are referred to as single-stage transfer learning by mammograms and DBT, respectively. ‘B’ and ‘C’ are referred to as multi-stage transfer learning DBT. C₁ indicates that the C₁ layer of the pre-trained CNN was frozen during transfer learning. C₁-F₄ indicates that the C₁ to F₄ layers of the pre-trained CNN were frozen during transfer learning.

We investigated two strategies for second-stage transfer learning: freezing up to C₁ (Fig. 2, B) and freezing up to F₄ (Fig. 2, C) layers. We chose these extreme situations to assess the range of variations when a relatively small set of samples for the target task was available for training. To provide a baseline for assessing the usefulness of additional pre-training with mammography data, the ImageNet-trained CNN was directly fine-tuned with DBT data (Fig. 2, D).

E. Effects of finite sample size

The generalizability of a classifier can be evaluated with respect to the mean classifier performance and variance of the classifier performance trained on a finite training sample size and validated on an independent test set, given both sets are drawn from the same population distribution. [34] In this study, the effect of finite sample size of mammography data and DBT data was investigated for various transfer learning strategies. We simulated a wide range of available training sample sizes by drawing a percentage of ROIs ranging from 1% to 100% from the mammography or DBT training set. At each percentage, ROIs by case were randomly drawn from the original training set with the constraint that the proportion of the malignant and benign classes was kept at about the same as the original set. To study the effects of training sample size without the additional variability due to different weight initialization, the fully connected layers in the CNN were initialized randomly using a single random seed for all runs under each condition. Different random seeds were used to select a desired percentage of training samples and, for each set, to batch the training samples to be input to the CNN during training.

For the study of mammography sample size effect during stage 1 pre-training of the C₁-frozen CNN, we compared three fine-tuning schemes: (A) no additional stage 2 transfer learning, (B) with stage 2 training of C₁-frozen CNN using a fixed DBT training data size (100%), and (C) with stage 2 training of C₁-to-F₄-frozen CNN using a fixed DBT training data size (100%) (Fig. 2).

For the study of DBT training sample size effect, we also compared three transfer learning schemes: (D) single-stage transfer learning by directly fine-tuning the C₁-frozen CNN using DBT data, (B) stage 1 training of C₁-frozen CNN using a fixed mammography data size (100%) data followed by stage 2 training of C₁-frozen CNN using DBT data, and (C) stage 1 training of C₁-frozen CNN using a fixed mammography data size (100%) followed by stage 2 training of C₁-to-F₄-frozen CNN using DBT data.

F. Performance evaluation

To select the optimum transfer network in stage 1 (selection of convolution layers to be frozen during transfer training) from the ImageNet-trained CNN to a mammography-trained CNN, the mammography data were partitioned into training and test sets for training and validation. After the selection, the entire mammography data set was used to study training sample size effects in stage 1 transfer learning, and the inference ability on DBT for the mammography-trained CNNs was evaluated by using the DBT training set as a validation set. To compare the single-stage and multi-stage approaches in the four transfer learning schemes (A-D), we used the mammography data and the DBT training set for transfer learning, and compared the sample size effects on the overall performance of each scheme using the same independent DBT test set that was held out during all training processes. The AUC was used as a summary performance measure. An ROI-based ROC curve was obtained when each ROI was considered an individual sample. A view-based ROC curve was obtained when the average score of all ROIs within each view was considered an individual sample. Averaging is preferred over taking maximum of the scores based on the previous studies [35], [36].

III. RESULTS

A. Selection of CNN levels for transfer learning

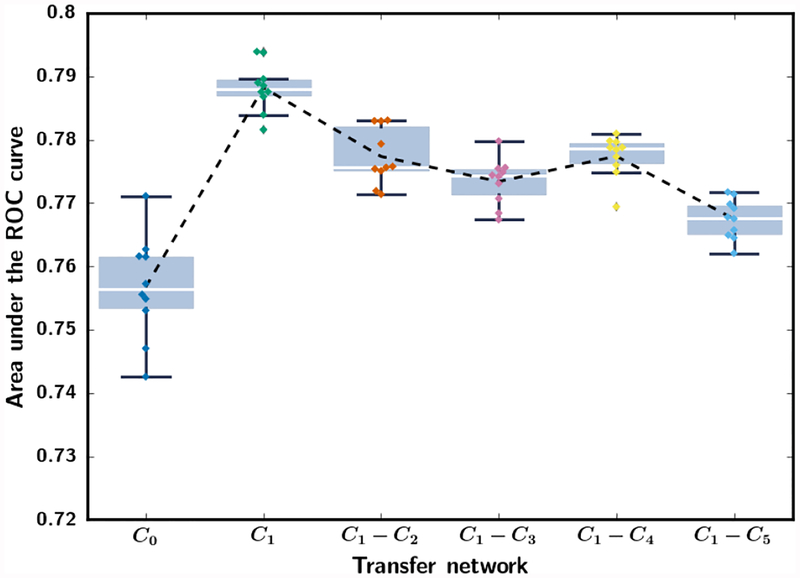
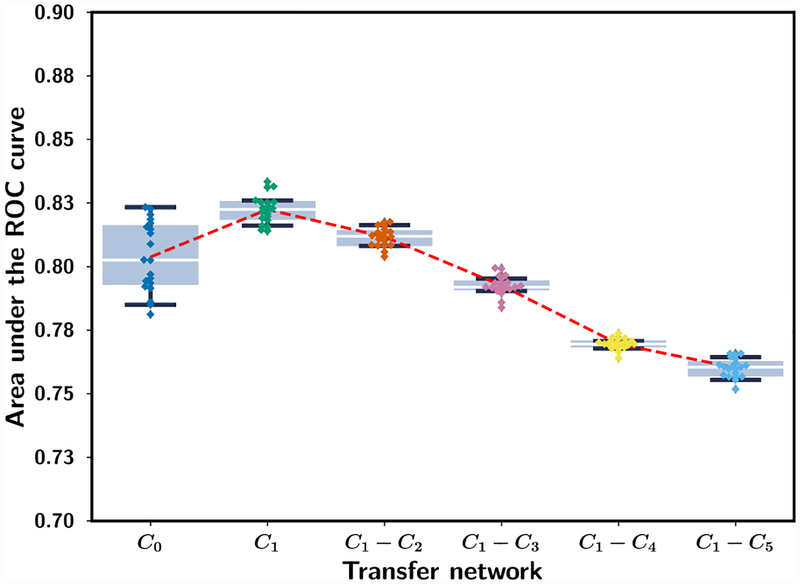
Fig. 3 shows the performance on the mammography test set for the six transfer networks, C₀, C₁, C₁-C₂, C₁-C₃, C₁-C₄ and C₁-C₅ when they were trained with the mammography training set (table I). Each transfer network was trained for ten random batchings of the training samples. When the entire network was allowed to train (C₀), the CNN had the lowest AUC and the largest variation. Freezing only C₁ resulted in the highest average AUC and the lowest variation. The transfer network C₁ was therefore chosen and used as the primary transfer learning structure in the subsequent analyses.

Fig. 3.

Box-and-whisker plots of inference results from stage 1 mammogram-trained CNN. The AUC values for classifying the mammography test ROIs (Table I) from the six transfer networks are shown for ten random batchings of the training samples. The training set and the test set consists of 12,360 and 7,272 ROIs, respectively. The 25^th percentile, median, and 75^th percentile are represented by the bottom, middle and top of the boxes, respectively. The interquartile range (IQR) is the difference between the 75^th and 25^th percentile. AUC values outside the 1.5*IQR above the 25^th percentile and below the 75^th percentile are outliers. The whiskers indicate the maximum and minimum AUC values excluding the outliers. The dotted line shows the mean AUC of the repeated experiments.

B. Inference ability of mammogram-trained CNN on DBT and finite sample size effect

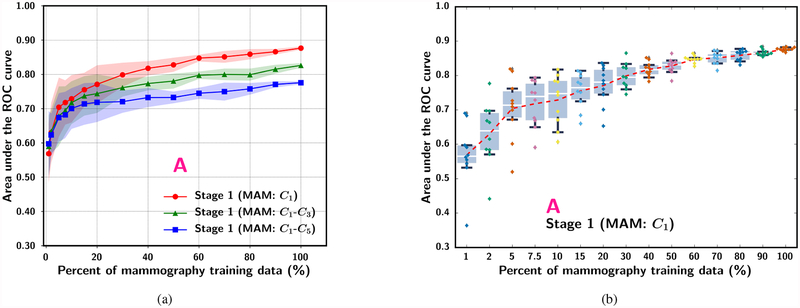
To evaluate the usefulness of knowledge learned from mammography data on the inference ability of CNN on DBT, three stage 1 transfer networks were analyzed : C₁, C₁-C₃ and C₁-C₅. The DBT training set was used as a validation set, which has not been used for training at this stage, to assess the classification performance without additional fine-tuning using the DBT data. The sample size effect was observed by varying the simulated mammography data set size from 1% to 100% for the three transfer networks as shown in Fig. 4(a). The ROI-based performances at 100% of mammography training data for the C₁, C₁-C₃ and C₁-C₅ transfer networks reached AUCs of 0.88, 0.83 and 0.78, respectively. This trend is similar to the inference performance of stage 1 mammogram-trained CNN shown in Fig. 3, where C₁ was also found to be the optimal transfer network among the six studied. These experiments show that mammography is a useful auxiliary domain for DBT. However, if the learning capacity of the CNN is constrained because too many layers (e.g., C₁-C₃ and C₁-C₅) are frozen during transfer training, the inference ability of the mammography-trained CNN on DBT can be limited due to inadequate adaptation of the features learned from non-medical images in the ImageNet-trained CNN to the breast imaging domains.

Fig. 4.

The ROI-based AUC performance for classifying the 9,120 DBT training ROIs (serve as a validation set at this stage) (Table I) for three transfer networks at stage 1. Each simulated training set size was repeated with ten random samplings from the entire training set and random batching of the training samples. (a) Dependence of mean and standard deviation of AUC on mammography training set size. (b) Box-and-whisker plots of inference results from the stage 1 mammogram-trained C₁-frozen transfer learning CNN. The entire set of 19,632 mammography ROIs was used for randomly drawing the training subsets. Note that the plot in (b) uses categorical x-axis to show details of the low percentage region.

C. Single- and multi-stage transfer trained CNN and finite sample size effect

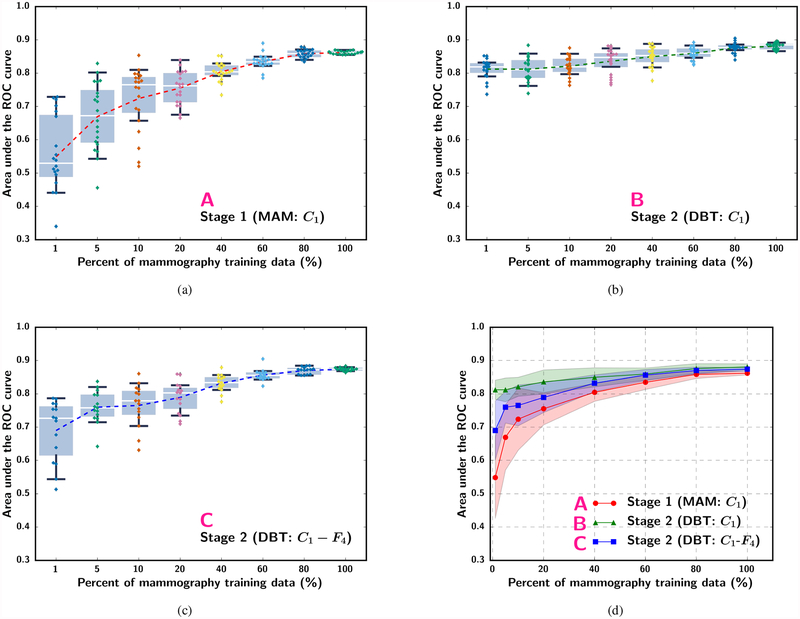
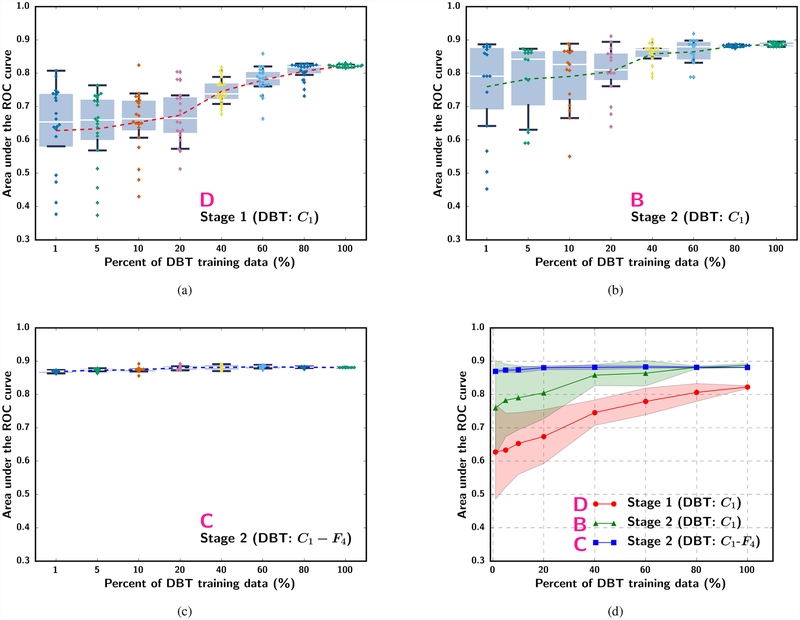
The effect of sample size was analyzed by simulating the available mammography and DBT training sample sizes from 1% to 100% of the original sets under different strategies as listed in Fig. 2. The experiment at each percentage was repeated 10 times to estimate the mean, median, range and interquartile range of AUCs. Fig. 5 and Fig. 6 show the box-and-whisker plots of the ROI-based AUCs over the training sample size range. Note that some small differences can be observed between the curves in Fig. 4(b) and Fig. 5(a) although both were obtained with scheme A because the former was evaluated with the DBT training set (used as a validation set in stage 1) while the latter was evaluated with the DBT test set. The statistical significance of the difference between pairs of the transfer learning approaches shown in fig. 5(d) and fig. 6(d) at different training sample sizes was evaluated with two-tailed paired t-test. The p-values can be found in section VI of the Supplementary Material.

Fig. 5.

Box-and-whisker plots of ROI-based AUC performance on the DBT test set while varying the simulated mammography training sample size available for stage 1 C₁-frozen transfer learning. (a) Stage 1 mammogram-trained C₁-frozen CNN without stage 2 (scheme A in Fig. 2). (b) Stage 2 C₁-frozen transfer learning at a fixed (100%) DBT training set size (scheme B). (c) Stage 2 C₁-to-F₄-frozen transfer learning at a fixed (100%) DBT training set size (scheme C). The dotted line in (a) to (c) plots the mean AUC at each simulated training set size. Note that the plots in (a) to (c) use categorical x-axis to show details of the low percentage region. (d) shows the mean and standard deviation of AUC in (a) to (c) together with the x-axis plotted in a linear scale.

Fig. 6.

Box-and-whisker plots of the ROI-based AUC performance on the DBT test set while varying the simulated DBT sample size available for training. (a) single-stage transfer learning by DBT trained C₁-frozen CNN without pre-training with mammography data (scheme D), (b) Stage 2 C₁-frozen transfer learning using DBT training set after Stage 1 transfer learning with a fixed mammography data set (100%) (scheme B), and (c) Stage 2 C₁-to-F₄-frozen transfer learning using DBT training set after Stage 1 transfer learning with a fixed mammography data set (100%) (scheme C). The dotted line in (a) and (b) plots the mean AUC at each simulated training set size. Note that the plots in (a) to (c) use categorical x-axis to show details of the low percentage region. (d) shows the mean and standard deviation of AUC in (a) and (b) together with the x-axis plotted in a linear scale.

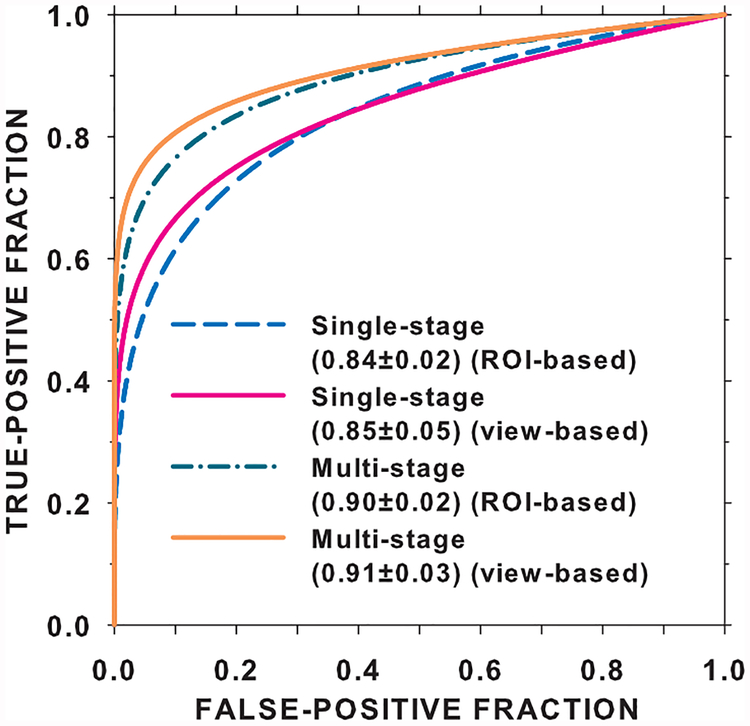
We compared the performance on the DBT test set by the single-stage transfer learning of the C₁-frozen CNN using the DBT training set (scheme D) to that by the multi-stage transfer learning (scheme B) at 100% of the training sample sizes. The ROC curves and the AUCs for both the transfer networks obtained with the ROC curve fitting software by Metz et al [32] are shown in Fig. 7. The ROI-based AUCs were 0.84±0.02 and 0.90±0.02 for the single-stage and multi-stage transfer networks, respectively, and the view-based AUCs were 0.85±0.05 and 0.91±0.03, respectively. The improvement in the view-based AUC by the multi-stage over single-stage transfer learning was statistically significant with a p-value of 0.005.

Fig. 7.

Comparison of the ROI-based and view-based ROC curves for the DBT test set using the single-stage transfer network (D in Fig. 2) versus the multi-stage transfer network (B in Fig. 2). The entire mammography set and the entire DBT training set were used for training.

IV. DISCUSSION

The increased adaptation of DBT for breast cancer screening and the possibility that the DM in the combo-mode will be replaced with a ‘synthesized’ DM necessitates innovative approaches to specifically improve the workflow of DBT interpretation. In this regard, CAD for DBT may be utilized in an intelligent visualization tool that could potentially increase the efficiency of reading DBT volumes and the diagnostic accuracy. In this paper we introduced a multi-stage transfer learning approach for classification of masses in DBT where an ImageNet-trained CNN was first fine-tuned with more readily available mammography data before a second-stage fine-tuning with an available small DBT data set. We compared the multi-stage fine-tuned CNN with a single-stage CNN directly fine-tuned with the DBT data and studied the improvement in the CNN performance when the available mammography and DBT data varied over a wide range for the different strategies of fine-tuning CNNs.

The ROC curves and AUCs for the classification of masses in the DBT test set (Fig. 7) indicate that the additional pre-training with mammography data significantly improved the performance over single-stage transfer learning with DBT data alone. Note that the AUCs in Fig. 7 are slightly different from those in Fig. 5 and Fig. 6 because they were estimated from the fitted ROC curves rather than by trapezoidal rules. In the absence of stage 1 pre-training, the single-stage transfer learning from ImageNet to DBT achieved an AUC of 0.82 at 100% sample size (Fig. 6(a)). Since the mammogram-trained CNN can classify DBT masses with an AUC of 0.86 (Fig. 5(a)), the observed low performance was mostly likely caused by the much smaller DBT training data. We expect that if a larger DBT training set is available, it is possible to achieve a higher AUC. In fact, 100% of the DBT training set contained 230 views, which corresponded to about 10% of the 2242 mammography training set (Table I). With 10% of the mammography data, the AUC on the DBT test set was only about 0.72 (Fig. 5(a)). This indicates that training with DBT data is likely more effective than training with mammography data if the sample sizes are comparable. A more detailed comparison of the performances of the CNN trained with single- and multi-stage transfer learning at a matched number of samples and a few other combined sample sizes is given in section VII of the Supplementary Material.

A number of important observations can be made from Fig. 4 to Fig. 6. First, when the sample size was small at either stage 1 or stage 2, the variations in the observed test performance were very large when the randomly drawn and randomly batched training samples were varied as indicated by the large IQRs and outliers. Occasionally the AUC could reach as high as those at 100% training sample size but the average AUC were not much better than by chance (0.5). Table IV presents a few examples of outliers observed in the different finite sample size experiments. This indicates that optimizing a CNN based on a small training set and exhaustively searching for the highest performance in a validation set could lead to overly optimistic results. The generalizability of a trained CNN therefore should be assessed with independent test cases that are not seen during parameter optimization.

TABLE IV.

EXAMPLES OF OUTLIERS WHERE THE CNN WHEN TRAINED ON SMALLER DATA SET SIZE PERFORMS EQUALLY OR BETTER THAN CNN TRAINED USING 100% OF THE TRAINING DATA.

Scheme	Percent training data	AUC at 100% training data	Minimum AUC	Mean AUC	Outlier AUC
Training on Mammography data (Fig. 5)
A	5%	0.86	0.46	0.67	0.83
A	60%	0.86	0.79	0.83	0.89
B	5%	0.88	0.74	0.81	0.88
B	10%	0.87	0.76	0.82	0.88
C	10%	0.87	0.63	0.77	0.86
C	60%	0.87	0.82	0.86	0.90
Training on DBT data (Fig. 6)
D	10%	0.82	0.43	0.65	0.82
D	60%	0.82	0.66	0.78	0.86

Second, Fig. 5 shows that, with the largest available DBT training set size (100%) in our study, the additional stage 1 pre-training with the mammography training set in scheme B (C₁-frozen) improved the AUC over training with the DBT set alone (Fig. 6, scheme D: AUC of 0.82 at 100% DBT data) even when the available mammography data set was as small as 10% (about 245 ROIs). However, if the learning capacity of the pre-trained CNN was constrained by freezing too many layers as in scheme C (C₁-to-F₄ frozen), the new knowledge in the DBT training set might not be properly utilized. This problem is particularly clear when the mammography training set was small (below about 30%); the AUCs of the C₁-to-F₄-frozen CNN (C) could not even reach the level of directly transfer learning with the DBT training set alone.

Third, Fig. 6 further confirms that the additional stage 1 pre-training by the mammography data consistently provided a substantial gain in the mean AUC over the range of simulated DBT training set size studied. The mean AUC increased by about 0.13 to 0.06 between scheme D and scheme B. It also shows that the DBT training set even at 100% was too small to train the DCNN alone (D), leaving much room for improvement. An interesting result is that the AUC achieved by the C₁-frozen CNN (B) was much lower than that by the C₁-to-F₄-frozen CNN (C) at small DBT training sample sizes. In this set of experiments, the available mammography data for stage 1 pre-training was large (100%) and the AUC on the DBT test set already achieved an AUC of 0.86 without stage 2 fine-tuning (Fig. 5, scheme A). When the DBT training set at stage 2 was small (below about 40%), allowing too many layers to be fine-tuned with DBT actually reduced the AUC to below 0.86, likely because the stage 2 fine-tuning attempted to adapt the knowledge learned from mammography to DBT but learning from such small DBT sets was insufficient to achieve robust adjustment of the large number of weights. Fine-tuning with C₁-to-F₄-frozen (C) retained the knowledge learned from the mammography data and obtain a small gain in AUC to above 0.86 by adjusting only the weights of the final fully connected layer. The results in Fig. 5 and Fig. 6 demonstrate that, to balance the knowledge retained from the source task and the knowledge learned from the target task, the optimal number of CNN layers to be frozen during transfer learning has to be chosen properly, taking into consideration the characteristics of the source and target tasks and the relative sizes of the available samples from the two domains. Visualization of the deep features extracted from the fully connected layers and examples of the activation maps from the convolutional layers trained with single- and multi-stage transfer learning are shown in sections VIII and IX of the Supplementary Material.

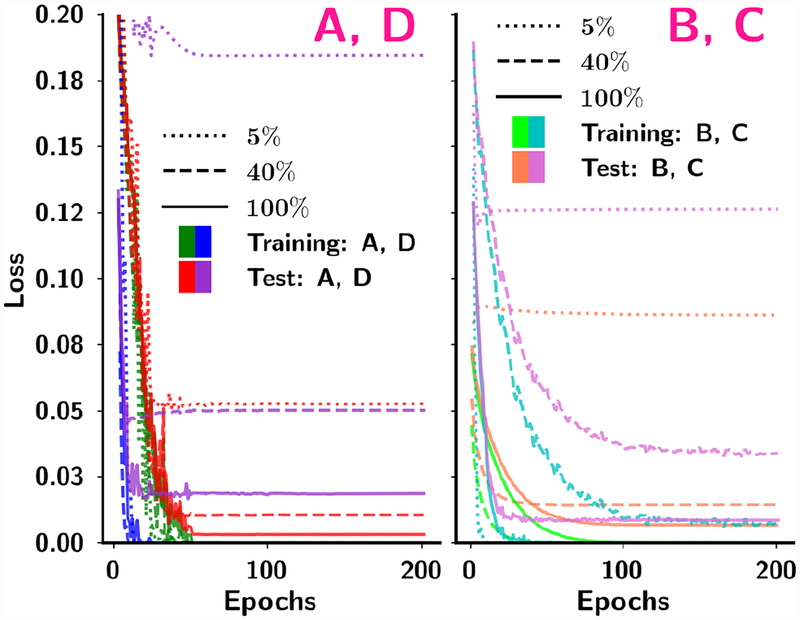
We retrospectively studied if our choice of 200 training epochs for all conditions based on experiments in stage 1 without using a validation set in stage 2 was reasonable. The mean squared error (MSE)-vs-Epochs curves for the four transfer learning strategies at 5%, 40% and 100% of the training samples sizes are shown in Fig. 8. The MSEs reached very stable values after about 100 epochs under all the conditions shown, indicating that 200 epochs could reach convergence without over-training. The CNN training was regularized using jittering, dropout in all hidden layers and random vertical flipping with probabilities of 0.2, 0.5, and 0.5, respectively, which might have reduced the risk of over-fitting.

Fig. 8.

Dependence of the mean squared error on the number of epochs for four transfer networks in four schemes (A, B, C and D) from one of the random sampling experiments. Within each scheme the training and test curves are shown for 5%, 40% and 100% of the training sample sizes. For B and C, 100% mammography data were used in the stage 1 pre-training. The DBT test set was used for testing of all four schemes and conditions.

To understand if freezing the first convolutional layer is consistently the optimal transfer network for the data used in this study, we retrospectively performed similar experiments as those shown in Fig. 3, except that the DBT training set and test set were used instead of the mammography sets. Fig. 9 shows the performance of the six transfer networks on the DBT test set. Similar to Fig. 3, the C₁-frozen transfer network was robust and consistently better than the other transfer networks.

Fig. 9.

Box-and-whisker plots of inference results from stage 1 DBT trained CNN. The mean AUC values for classifying the DBT test ROIs (Table I) from the six transfer networks are shown for 20 random batchings of the training samples. The training set and the test set consists of 9,120 and 3,560 ROIs, respectively.

There are limitations in this study. A recent study showed that, for the ImageNet classification task, if the training set was scaled from 1 million to 300 million image samples, the gain in average precision increased at best linearly as the data size increased logarithmically. [37] Because of the limited sizes of our mammography and DBT data sets at present we cannot study whether the relative performance of the various fine-tuning strategies will change when these data sets are much larger. It is possible that different training set size may change the tradeoff between the learning capacity in a transfer network and the overfitting risk. We will continue to expand the data sets and investigate these trends in future studies.

Another limitation is that we did not attempt to ”optimize” the hyperparameters such as momentum, learning rate, number of iterations, batch size, using a validation set for each condition due to the small available data sets and the computational costs. We did not exhaustively investigate the many different combinations that can be obtained by freezing different number of layers in each of the two-stage fine-tuning but selected only a few representative combinations of the two stage transfer learning. Nevertheless, our study has demonstrated the impact of training sample size in each stage and the effect of fine-tuning from related auxiliary tasks, thereby providing some useful information for transfer learning in medical imaging tasks. Although we used AlexNet in this study, the observed trends can likely be extended to other DCNN structures or tasks even if the absolute performance would differ.

A third limitation is that we did not compare the performance of deep learning methods with conventional feature engineering methods using the same data sets because our focus was to study the transfer learning strategies and sample size effects. In comparison with previous work using different data sets, Chan et al [38] developed a feature engineering approach for characterization of breast masses in a data set of 99 patients containing 56 malignant and 51 benign masses and obtained an AUC of 0.93±0.02 from the DBT reconstructed volumes and 0.84±0.04 from DBT projection view images from two-loop leave-one-case-out cross-validation. A recent work on classification of breast masses in DBT by deep machine learning methods used a combination of CNN to characterize the masses in the in-plane direction and long short term memory networks to learn the texture pattern changes in the depth direction. [24] They used 185 DBT volumes with 197 biopsy-proven malignant masses and selected the benign masses from a computer-aided detection method. The combined method achieved an improvement (AUC = 0.92±0.02) over using the pre-trained CNN (AUC = 0.87±0.03) in a five-fold cross-validation. Our current study showed that our proposed multi-stage transfer learning (AUC = 0.91±0.03) can outperform single-stage transfer learning (AUC = 0.85±0.05) in an independent test set.

V. CONCLUSION

Our work demonstrates that multi-stage transfer learning can take advantage of the knowledge gained through source tasks from unrelated and related domains. We show that the limited data availability in a target domain can be alleviated with pre-training of the CNN using data from similar auxiliary domains. We also show that the gain in CNN performance from the additional stage of fine-tuning with the auxiliary data depends on the relative sizes of the available training samples in the target and the auxiliary domains, and proper selection of the transfer learning strategy. Furthermore, when the training sample size is small, the variance in the performance of the trained CNN is large. Reporting the best performance through exhaustive search using a ”test” set can be overly optimistic. It is therefore important to validate the generalizability of the trained CNN with independent unknown cases.