A Physiologically‐Based Pharmacokinetic Model for the Prediction of Monoclonal Antibody Pharmacokinetics From In Vitro Data

Abstract

Monoclonal antibody (mAb) pharmacokinetics (PK) have largely been predicted via allometric scaling with little consideration for cross‐species differences in neonatal Fc receptor (FcRn) affinity or clearance/distribution mechanisms. To address this, we developed a mAb physiologically‐based PK model that describes the intracellular trafficking and FcRn recycling of mAbs in a human FcRn transgenic homozygous mouse and human. This model uses mAb‐specific in vitro data together with species‐specific FcRn tissue expression, tissue volume, and blood‐flow physiology to predict mAb in vivo linear PK a priori. The model accurately predicts the terminal half‐life of 90% of the mAbs investigated within a twofold error. The mechanistic nature of this model allows us to not only predict linear PK from in vitro data but also explore the PK and target binding of mAbs engineered to have pH‐dependent binding to its target or FcRn and could aid in the selection of mAbs with optimal PK and pharmacodynamic properties.

Monoclonal antibodies (mAbs) represent a major class of therapeutics with more than 50 mAbs currently in late‐stage clinical studies.1 This success is mainly because of their high specificity and affinity for the therapeutic target of interest together with their long serum half‐life (T1/2). This long T1/2 enables less frequent administration, which is appealing for some chronic indications. In preclinical stages, studies are performed to understand pharmacokinetic (PK) and pharmacodynamic (PD) properties to identify candidates with the highest chance of success in clinic, with dosing regimens that meet the target product profile.

Empirical approaches such as allometric scaling from nonhuman primates2, 3, 4, 5 and more recently a transgenic homozygous human neonatal Fc receptor (hFcRn) mouse (Tg32) model6 have been successfully used to predict mAb human PK. Many mAbs reaching the clinic have similar human PK, and it has been shown that a typical set of two‐compartmental PK parameters can predict the human PK of the majority of mAbs, reducing the need for preclinical in vivo PK studies.7 Despite this, there are several recent reports where in vivo PK can vary considerably8, 9, 10 consequently affecting target engagement, dose, and dosing regimen. Unlike in small molecule drug discovery, early optimization screening has historically focused on affinity and potency, with assays to predict PK propensity only being used at later stages. The in vitro–in vivo correlations of PK properties are therefore less well established. However, several physicochemical attributes, e.g., non‐specific charge‐based interactions, self‐association, and hFcRn binding affinity, have recently been shown to correlate with in vivo clearance (CL).11, 12 One particular in vitro assay is the affinity‐capture self‐interaction nanoparticle spectroscopy (AC‐SINS) assay.13, 14, 15 Avery et al.11 show a Spearman correlation coefficient of 0.7 between AC‐SINS and CL.

Physiologically‐based PK (PBPK) models are routinely used prospectively to inform the selection of small molecules for clinical studies.16, 17 Large molecule PBPK models have typically been descriptive, relying on in vivo tissue distribution data and generally only describe neonatal Fc receptor (FcRn) mediated kinetics.18, 19, 20 These models are built using known physiology and account for the key processes involved in mAb disposition, including (i) non‐specific uptake via fluid‐phase pinocytosis into vascular endothelial cells, (ii) pH‐dependent binding to FcRn in the acidic environment of the endosome, (iii) proteolytic degradation of unbound mAb in the lysosome, (iv) pH‐dependent release of bound mAb at the cell surface into the plasma or interstitial fluid via exocytosis, and (v) exit of interstitial mAb into the lymph via convective flow. The complex nature of mAb disposition together with the recent evolution of in vitro assays for mAb screening and the realization that mAb PK can vary in human provides an opportunity for predicting in vivo behavior using in vitro data in a PBPK framework analogous to small molecule approaches.

We have developed a PBPK model that we can use prospectively early in the drug discovery process to select mAbs with optimal PK and therefore the best chance of clinical success. The core of the PBPK model used in this work, including organs, basic topology, and physiological parameters, was based on the model described by Shah and Betts.19 We have expanded the model to include a mechanistic description of FcRn–mAb dynamics within the endothelial cell compartment and have included an additional CL mechanism to describe non‐specific interactions within each organ compartment using AC‐SINS data. The model was built for the Tg32 mouse and human using a training set of mAbs (15 in Tg32 mouse and seven in human) and then tested for prediction accuracy using a test set of mAbs (16 in Tg32 mouse and five in human).

Methods

Antibody selection

MAbs were selected based on the availability of AC‐SINS data, in vivo Tg32 mouse and/or clinical PK (plasma concentration‐time profile data). Data were available for 31 mAbs in the Tg32 mouse and 12 mAbs in human. Each data set was split into a training set and a test set. For the Tg32 mouse, the training and test set consisted of 15 (mAbs 1–15) and 16 mAbs (mAbs 16–31), respectively. For human, the training and test set consisted of 7 (mAbs 1–3, 5–8) and 5 mAbs (mAbs 11–14, 23), respectively.

In vivo PK studies (Tg32 mouse and human)

In vivo PK studies were conducted in the Tg32 homozygous mouse model as described by Avery et al.6 for mAbs 1–31. In brief, the studies were conducted at Pfizer and were designed and executed in accordance with the Animal Use Protocol and adherence to the Pfizer institutional animal care and use committee regulations. MAbs were dosed intravenously at a saturating dose (5 or 10 mg/kg). A total of 4‐6  mice were evaluated for each mAb. Serum samples were analyzed as described by Avery et al.6 PK parameters (CL, volume of distribution at steady state (Vss), and terminal T1/2) were derived from individual animal data using non‐compartmental analysis (NCA) in Phoenix^® WinNonlin^® (version 6.3; Certara L.P. (Pharsight), Saint Louis, MO). A small proportion (<10%) of plasma concentration‐time profiles showed a sharp drop in exposure (presumed as a result of anti‐drug antibodies) and were excluded. Samples below the limit of quantification of the assay were set as 0 for data analysis.

Clinical PK data were available for 12 mAbs (mAbs 1–3, 5–8, 11–14, and 23) from in‐house or literature sources.6 These studies were single‐dose intravenous PK studies and were conducted in healthy volunteers or patients. For mAb 11, only subcutaneous PK data were available; bioavailability and absorption rate constants were assumed for the purposes of modeling. Reported PK parameters (as noted previously) were derived from NCA from saturating doses where the PK was linear. All clinical studies conducted at Pfizer were approved by the institutional review board of the research center and were conducted in compliance with the principles derived from the Declaration of Helsinki including all International Conference on Harmonization Good Clinical Practice guidelines and local regulatory requirements.

In vitro data (AC‐SINS and FcRn affinity)

AC‐SINS and FcRn affinity data were generated for all mAbs in the data set (mAbs 1–31). The AC‐SINS assay has been described in the literature.11, 13 In brief, mAbs are captured by anti‐human Fc antibodies coated on the gold nanoparticles. If a mAb tends to interact with itself, there is a clustering of the nanoparticles that leads to a red shift in the absorbance wavelength. This assay was used as a surrogate for non‐specific CL. The methodology for FcRn affinity measurement was described by Avery et al.11

Overall model description

The core of the PBPK model used in this work was based on the model described by Shah and Betts.19 The model contains a plasma compartment and 15 tissue compartments. Each tissue compartment is subdivided into a vascular compartment, a vascular‐side membrane compartment, an endothelial cell compartment, an interstitial‐side membrane compartment, an interstitial fluid compartment, and a cellular space compartment. Within the endothelial cell compartment, a single‐cell mechanistic model of FcRn‐mAb dynamics has been constructed. The transit of mAb around the body and between organs is mediated via plasma flow into tissues and then returned via plasma flow except for the portion undergoing lymphatic drainage into a lymph node compartment, which then exits back into plasma. As described by Shah and Betts,19 both endogenous and exogenous immunoglobulin G (IgG) were modeled separately to account for any competition for FcRn in the endosomal space. An additional non‐specific CL mechanism was included in each organ compartment. A schematic of the model is shown in Figure  1 a–c.

Figure 1.

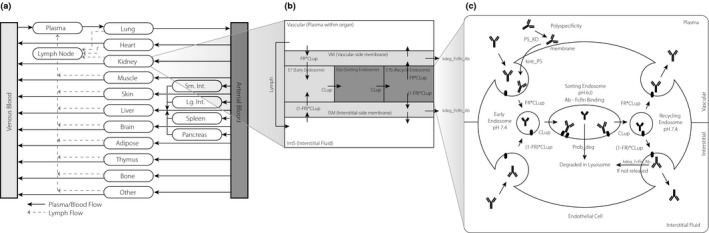
Schematic of the physiologically‐based pharmacokinetic (PBPK) model: (a) full PBPK model, (b) organ‐level model, (c) endosomal‐level model. FcRn, neonatal Fc receptor; Ab, antibody; FR, volume fraction of pinocytosis from vascular space (apical); CLup, pinocytotic uptake rate of endothelial cells; 1‐FR, volume fraction of pinocytosis from intestitial space (basolateral); kdeg_FcRn_Ab, degradation rate of FcRn bound mAb; Prob_deg, probability of mAb degradation in the absence of FcRn binding; PS_KD, equilibrium constant for mAb‐cell membrane site non‐specific interactions.

Physiological parameters including organ volumes, plasma volume, interstitial volumes, cellular volumes, plasma flow rates, and lymphatic flow rates (0.2% of plasma flow rate) were taken from Shah and Betts.19 These values and all parameters and equations are summarized in Tables S1–S3.

The FcRn mechanistic model operates within the endothelial cells located in each organ (Figure 1 c). The model is composed of membrane proximal compartments for both apical (vascular side) and basolateral (interstitial side) membranes that are in rapid equilibrium with plasma and interstitial fluid and 3 well‐mixed intracellular endosomal transit compartments: early endosome (pH 7.4), sorting endosome (pH 6.0), and recycling endosome (pH 7.4). This allows explicit modeling of mAb‐FcRn kinetics as a function of pH and time.

A series of calibration steps were performed to develop the PBPK model using the training set of mAbs. Once completed, the a priori predictability of the model was tested using the test set of mAbs. These steps are described in detail below.

Model calibration

The first calibration step involved estimating the whole‐body catabolic rate of the mAb in the absence and presence of FcRn. The catabolic rate in the absence of FcRn is a function of the total number of endothelial cells in the body (N _endo), the pinocytotic uptake rate of endothelial cells (CL_up), and the probability of mAb degradation in the absence of FcRn binding (Prob_Deg). The catabolic rate in the presence of FcRn is a function of FcRn concentration (calculated from FcRn amount, CL_up, endosomal transit time (T _endo), N _endo and volume of endosome (V _endo)), FcRn stoichiometry, and FcRn binding affinity. Several of these parameters were fixed (CL_up, Prob_deg, T _endo, V _endo, equilibrium constant for mAb‐FcRn binding (Kd) pH 6.0, dissociation rate constant for mAb‐FcRn binding (k _off) pH 6.0, degradation rate of FcRn‐mAb complex at pH 7.4 (kdeg_FcRn_Ab)), and several were calibrated to in vivo observations based on uncertainty in their values (N _endo, second association rate constant for mAb‐FcRn binding(k _{on_2nd}) and Kd pH 7.4/Kd pH 6.0 ratio). This process involved simultaneous fitting to plasma concentration‐time data from FcRn^−/− knockout mice (using mAbs 2, 6, and 16–22), humans with severely compromised FcRn function as a result of a mutation in the beta‐2‐microglobulin subunit21, 22 and mAb PK data from both Tg32 mice and human exhibiting “typical PK” with terminal T1/2 values of ~17 and ~20 days, respectively. MAbs 1, 2 (Tg32 mouse and human) and 11 (Tg32 mouse only) were used for this fitting process because non‐specific interactions were not believed to contribute to their PK properties.

The CL_up ranges from ~30 to ~667 nL/hour/1E6 cells across different cell types and studies,23, 24, 25 and in this analysis we used an intermediate value of ~150 nL/hour/1E6 cells based on endothelial cell pinocytosis measurements.23 The CL_up and recycling rate were divided between apical (vascular side) and basolateral (interstitial side) membranes by means of a fractional multiplier (FR), where the apical recycling fraction was set at 0.71519 and the basolateral fraction was set equal to the remainder (1‐FR).19, 26 Prob_deg was assumed to be 98% (>95% indicated by S. Ward, personal communication). N _endo is one of the most uncertain parameters within the model so was fit yielding values of 14.2E8 and 0.86E12 in the Tg32 mouse and human, respectively. The values of 6.25E8 in a mouse and 2.54E12 in human have been reported in the literature.27, 28, 29

The T _endo was assumed to be 10.8 minutes consistent with previous estimates19, 29 and was used to calculate total V _endo using the following equation: V _endo = CL_up × T _endo. The FcRn concentration values used in the model are based on internal mass spectrometry measurements and are ~1.1430 and ~1,022 nMoles31 of FcRn per Tg32 mouse and human, respectively. To derive an intracellular FcRn concentration, we assumed FcRn concentration = FcRn Total Amount (Moles per Body)/(V _endo × N _endo), yielding values of 29.7 μM (Tg32 mouse) and 44.1 μM (human). We made the assumption that FcRn was only expressed in endothelial cells and its concentration was the same in every endothelial cell within each organ. To determine endothelial cell allocation among the different organs, the fraction of total FcRn within each organ was used as a proxy of endothelial cell number.30, 31 We assumed FcRn concentration remains at steady state and thus did not include explicit synthesis and degradation terms.

Binding between FcRn and a mAb was allowed to occur with both 1:1 and 2:1 stoichiometry, the proportion of each being a function of binding affinities and free concentration. One would expect the two association rate constants to differ as the first binding involves a transmembrane anchored protein (FcRn) being approached by a freely diffusing mAb in solution, whereas the second binding involves the 1:1 membrane anchored complex only laterally diffusing in 2 dimensions until contacting an additional molecule of membrane anchored FcRn. Estimates of 2‐dimensional lateral diffusion rates are on the order of 10⁻⁹ − 10⁻¹¹ cm²/second for transmembrane proteins,32 significantly slower that than of IgG freely diffusing in solution at 4.9E‐7 cm²/second,33 thus we would expect the two k _on s to differ by a factor of 10–1,000 fold. The first association rate constant for mAb‐FcRn binding (k _{on_1st}) event was set to 8.06E+7 1/M/hour (forming the 1:1 complex)19 and the second association constant was fitted, yielding a value of 9.63E+5 1/M/hour. The first dissociation rate constant for mAb‐FcRn binding (k _{off_1st}) was calculated from the first association rate constant for mAb‐FcRn binding (k _{on_1st}) and Kd. The second dissociation rate constant for mAb‐FcRn binding (k _{off_2nd}) was assumed to be the same as k _{off_1st}.

The affinity between FcRn and a mAb is known to be pH specific, exhibiting tighter affinity at low pH (6.0) to allow binding within the acidified endosome and poorer affinity at neutral pH (7.4) to allow release/recycling at the cell surface. It has been shown that FcRn‐mAb affinity is correlated across pH,34 with a ratio of Kd pH 7.4 to Kd pH 6.0 typically ranging from 20‐fold to 250‐fold.34, 35 For mAbs with higher AC‐SINS scores, FcRn affinity via Biacore (GE Healthcare, Chicago, IL) was tighter than anticipated; for these mAbs, we believed the assay was not specific and was also capturing non‐specific interactions. To ensure we captured only the FcRn component, the model used a binding affinity value of 700 nM for pH 6.0 based on Biacore experimental values across a group of mAbs in the data set exhibiting no non‐specific interactions. The binding at pH 7.4 was estimated via fitting to be 220‐fold higher. The FcRn‐mAb complex that does not release at pH 7.4 because of a high affinity binding at neutral pH was subject to degradation via an additional first‐order clearance term (kdeg_FcRn_Ab), which we assumed occurs at the natural turnover rate (11.1 hours) of FcRn.31 The majority of FcRn has been shown to exist intracellularly with only a small percentage on the cell surface.36, 37 To reflect this in the model, we implemented a function (FcRn_recycle_fraction, which was set to 0.99) where any free FcRn following mAb recycling was immediately returned to the endosomal FcRn pool, whereas recycling FcRn‐mAb complex moves to the cell surface, after which it could be reinternalized upon the next pinocytosis event or degraded.

The results of the model calibration to mAb plasma concentration‐time profiles are shown in Figure 2 and exhibit good agreement, suggesting that the model has the correct whole‐body catabolic capacity required for both Tg32 mouse and human. Fixed and calibrated parameter values are shown in Table 1.

Figure 2.

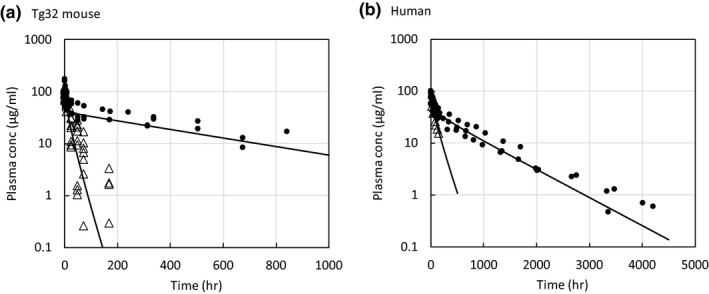
Calibration results for Tg32 mouse and human (WT and KO) pharmacokinetic profiles. conc, concentration; hr, hour;. WT, wild‐type; KO, knockout.

Table 1.

Fixed and calibrated parameters to describe whole‐body catabolic capacity for antibody

Parameter	Value	Reference
Fitted
Tg32 endothelial cell number (N endo)	14.2E8	In same range as literature reports27, 28, 29
Human endothelial cell number (N endo)	0.86E12	In same range as literature reports27, 28, 29
k on ratio (FcRn binding #1/#2)	83.7	k on_2 10–1,000 fold slower due to limited membrane diffusion
Kd 7.4/Kd 6.0 ratio	220	Literature suggests values spanning 20×–250×34, 35
Fixed
Transit time (T endo) (minutes)	11	19, 29
Uptake rate (CLup) (nL/hour/1E6 cells)	150	23
Prob_deg (%)	98	Assumed based on S. Ward personal communication (>95%)
FcRn tissue levels (nMoles)	1.1/1022	(Tg32 mouse/human)30, 31
kdeg_FcRn_Ab (FcRn turnover; min−1)	0.062	11.1 hour half life 31

CL_up, pinocytotic uptake rate of endothelial cells; FcRn, neonatal Fc receptor; Kd, equilibrium constant for mAb‐FcRn binding; kdeg_FcRn_Ab, degradation rate of FcRn‐mAb complex at pH 7.4; k _on,  association rate constant for mAb‐FcRn binding; Prob_deg, probability of mAb degradation in the absence of FcRn binding; T _endo, endosomal transit time.

The second calibration step involved incorporating the impact of non‐specific interactions on PK. These were represented in the model as a non‐specific charge‐mediated binding (association rate constant for mAb‐cell membrane site non‐specific interactions (k _onPS) and dissociation rate constant for mAb‐cell membrane site non‐specific interactions (k _offPS); k _onPS assumed equal to mAb‐FcRn association rate constant for mAb‐FcRn binding (k _on)) between the mAb and the cell membrane (cell membrane site density that can bind to mAb (C _mem)). We hypothesized that the bound mAbs on the membrane would be internalized (internalization rate of membrane‐bound mAb due to non‐specific interactions (k _{int_PS})) via pinocytosis and brought into the endosome. These mAbs will become free in the sorting endosome and available to bind with FcRn. If unbound, they will be subjected to degradation (Prob_deg). Data from the AC‐SINS assay measuring mAb self‐association were used as a basis for the affinity terms. The parameters (C _mem, k _{int_PS}) were estimated from plasma concentration‐time profiles for mAbs in the training set. The equation relating AC‐SINS score to an affinity describing these non‐specific interactions is log₁₀ Kd = exp (PS_a‐PS_b × PS_Score), where PS_a and PS_b represent empirically fitted parameters to scale an AC‐SINS score range (0–25) into a binding equilibrium constant Kd. The fitted values for PS_a, PS_b, C _mem, and k _{int_PS} are shown in Table 2. C _mem in human was set to equal C _mem in Tg32 mouse. These fitted plasma concentration‐time profiles are shown in Figure 3 a,b for Tg32 mouse and human, respectively.

Table 2.

Estimated parameters to predict in vivo non‐specific interaction‐related clearance from affinity‐capture self‐interaction nanoparticle spectroscopy scores

Parameter	Tg32 mouse	Human
PS_a	0.739	1.81
PS_b	−0.0409	−0.262
C mem (μM)	18.5
kint_PS (1/hour)	0.290	0.0380

C _mem, cell membrane site density that can bind to mAb; k_{int_PS}, internalization rate of membrane‐bound mAb due to non‐specific interactions; PS_a, empirical parameter a to scale an AC‐SINS score to a binding equilibrium constant; PS_b, empirical parameter b to scale an AC‐SINS score to a binding equilibrium constant.

Figure 3.

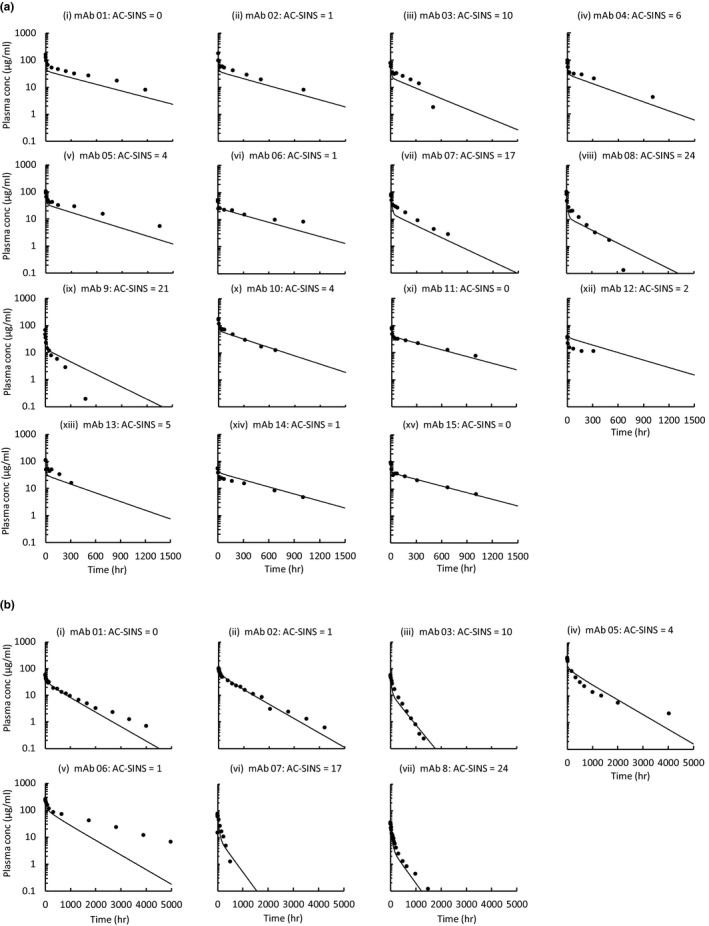
Physiologically‐based pharmacokinetic model calibration of non‐specific interaction clearance mechanism using the training set in (a) Tg32 mouse (n = 17) and (b) human (n = 9). AC‐SINS, affinity‐capture self‐interaction nanoparticle spectroscopy; conc, concentration; hr, hour; mAb, monoclonal antibody.

Model testing

Using the derived PBPK model in Tg32 mouse and human, the prospective prediction accuracy of the model was explored using the test set of mAbs where AC‐SINS data were used as input to the model. Predicted PK parameters were calculated via NCA and compared with observed values.

Model coding

The model development, simulation, and control parameterization method were implemented in J2 Dynamic Modeling and Optimization Software (RES Group, Inc, Needham, MA). The model code has also been implemented in Berkeley Madonna and can be found in the Supplemental Materials .

Results

The first calibration step involved estimating the whole‐body catabolic rate of the mAb in the absence and presence of FcRn. The results of the model calibration to mAb plasma concentration‐time profiles are shown in Figure 2 and exhibit good agreement between the observed and fitted data, suggesting that the model has the correct whole‐body catabolic capacity required for both Tg32 mouse and human. Calibrated parameter values were in reasonable agreement with estimates from the literature where available and are shown in Table 1.

The second calibration step involved incorporating the impact of non‐specific interactions on PK. The equation relating AC‐SINS score to an affinity describing these non‐specific interactions is described in the Methods section, and the fitted parameters from this equation are shown in Table 2. The fitted plasma concentration‐time profiles are shown in Figure 3 a,b for the Tg32 mouse and human, respectively. In general, the fitted plasma concentration‐time profiles were in good agreement with the observed plasma concentration‐time profiles, indicating that the model was specified correctly.

Using the final model, the Tg32 mouse and human plasma concentration‐time profiles were simulated using AC‐SINS data as input. The simulated plasma concentration‐time profiles for the test set of mAbs are shown in Figure 4 a,b for Tg32 mouse and human, respectively. In general, the predicted plasma concentration‐time profiles were in good agreement with the observed plasma concentration‐time profiles. In particular, the model was able to accurately predict the trend in PK properties across the mAbs and was able to correctly categorize those mAbs with poor in vivo properties. Predicted vs. observed PK parameters are shown in Figure 5. In general, there is a good degree of prediction accuracy with 90%, 71%, and 90% of the predicted parameters being within twofold of the observed parameters for terminal T1/2, CL, and Vss, respectively.

Figure 4.

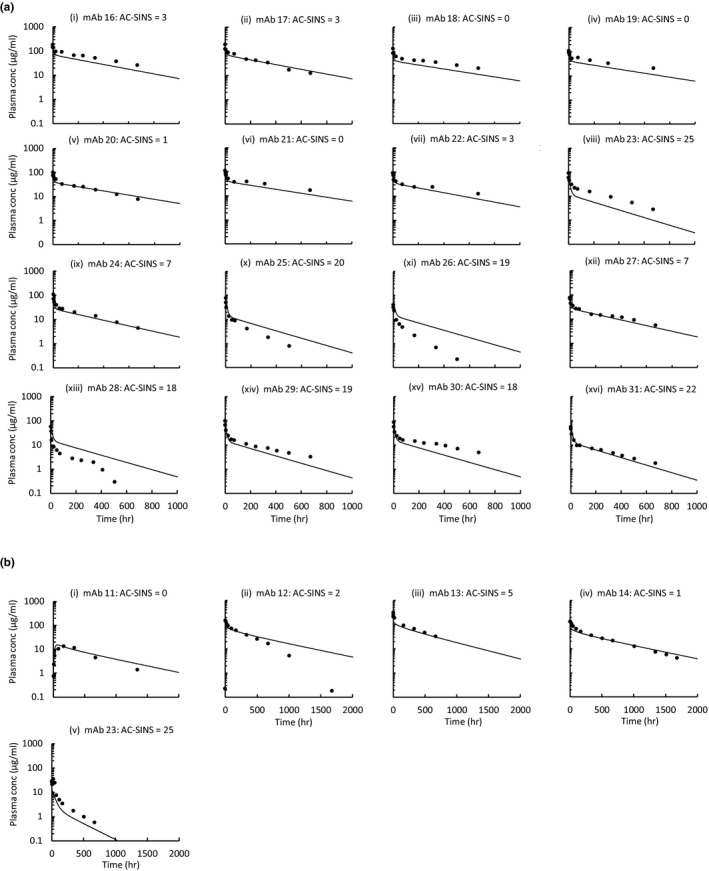
Physiologically‐based pharmacokinetic model simulations vs. observed data using the test set in (a) Tg32 mouse (n = 19) and (b) human (n = 5). AC‐SINS, affinity‐capture self‐interaction nanoparticle spectroscopy; conc, concentration; hr, hour; mAb, monoclonal antibody.

Figure 5.

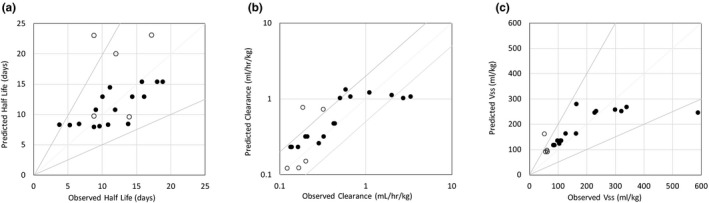
Physiologically‐based pharmacokinetic model predicted vs. observed (a) half life, (b) clearance, and (c) volume of distribution at steady state in human (open circles) and Tg32 mouse (closed circles). Vss, volume of distribution at steady state.

Discussion

The first publications on the topic of PBPK models for biotherapeutics appeared in the literature in the 1980s and 1990s.38, 39 These early models have been expanded to include the interaction of mAbs with FcRn in the endosomal compartment of tissues18, 40 and to incorporate pH‐dependent FcRn binding and tissue‐specific FcRn mRNA expression data.29 Urva and coauthors26 added a compartment to represent cells expressing the target receptor in the tissue, and recent publications by Glassman and Balthasar20, 41 illustrate the application of PBPK models for predicting target‐mediated disposition and the effect of “catch and release” mAbs.

However, despite these literature reports, the use of PBPK modeling for mAbs in the pharmaceutical industry is still limited. Most PBPK models published have relied on in vivo data for fitting as there have been few predictive in vitro assays described and few in vitro–in vivo relationships established.12, 18, 19, 20 Although these models can fit the experimental data, the models are heterogeneous, and different groups have used not only different physiological parameters but also different representations of physiology to fit the data.42, 43 Recent reports indicating a linkage between a number of physicochemical attributes and in vivo PK could enable mAb PBPK models to be used to support mAb discovery analogous to those established for supporting small molecule drug discovery. In particular, poor PK has been reported for mAbs with high positive charge10 and a correlation has been established between self‐association (as measured by the AC‐SINS assay) and in vivo CL.11

In this work we developed a PBPK model that we believe can be used prospectively in a drug discovery setting to predict human PK of mAbs with differing properties. The core of the PBPK model used in this work, including organs, basic topology, and physiological parameters was based on the model described by Shah and Betts.19 We have expanded the model to include a mechanistic description of FcRn and mAb dynamics across a pH range within the endothelial cell compartment. Unlike others, we have included an additional non‐specific CL mechanism within each organ compartment using readily available in vitro AC‐SINS data. This additional feature allows us to move beyond FcRn‐dependent mechanisms, allowing us to predict from in vitro data, the range of PK seen in vivo for mAbs as a result of non‐specific processes. Other groups have accounted for this by fitting of empirical coefficients to modulate the rate of endosomal uptake and the vascular reflection coefficient in their PBPK models.29 However, the reliance on in vivo fitting in this case limits the a priori application of such models. In addition, our model explicitly accounts for the binding of the mAb to FcRn at both acidic and neutral pH values and assumes a fixed affinity ratio between pH 6 and 7.4, which could allow for the prediction of mAbs with atypical FcRn affinity characteristics.34, 35 Given the increased use of engineering approaches to either improve the affinity of mAbs to FcRn at acidic pH or to reduce the affinity of mAb to antigen at acidic pH (“catch and release” mAbs), this could be an important feature of the model to enable in vitro–in vivo scaling early in discovery and to explore potential solutions to poor PK or target coverage.

Our PBPK model and in vitro–in vivo scaling approach were built in a systematic manner for both the Tg32 mouse and human using a training set of Pfizer mAbs and then tested for prediction accuracy using a test set of mAbs. In general, there is a good degree of prediction accuracy with 90%, 71%, and 90% of the predicted parameters being within 2‐fold of the observed parameters for terminal T1/2, CL, and Vss, respectively. In addition, for a separate set of mAbs, the model was able to accurately predict tissue concentrations (data not shown). There is a trend toward an increase in CL and Vss and a decrease in terminal T1/2 as AC‐SINS score is increased. The model is able to capture this trend and correctly rank mAbs based on PK parameters (Figure 5). Generally, those mAbs with low AC‐SINS score are predicted accurately. There is a slight trend toward over‐prediction in exposure for those mAbs with high AC‐SINS score (mAbs 26–28 in Tg32 mouse); however, these mAbs were still correctly categorized as high CL mAbs. It is possible for these high AC‐SINS score mAbs that other factors are playing a role. The prediction accuracy we have observed is comparable to that obtained by more traditional allometric scaling approaches.2, 3, 4, 5, 6 However, in contrast, our PBPK framework does not rely on the availability of preclinical in vivo PK data, which are often not available until later in the preclinical development process, which means predicted PK properties can be factored into the lead selection process.

We believe that the work described herein represents the first attempt to predict mAb in vivo PK from in vitro data using a mechanistic PBPK model framework. This approach offers the potential to screen out mAbs with poor PK properties earlier in the drug discovery process compared to current approaches that rely heavily on in vivo data. To date the in vitro–in vivo relationships between AC‐SINS and in vivo PK have been established based on a relatively small set of mAbs. Further work should focus on increasing the number of mAbs in this data set and on finding more mechanistic relationships between in vitro and in vivo CL. The mechanistic nature of this PBPK model allows for a more informed translational strategy across species and offers a framework to incorporate additional processes such as target binding, “catch and release” target binding, and enhanced FcRn binding. Such applications should be explored further.

Funding

No funding was received for this work.

Conflict of Interest

H.M.J., A.M.B., R.W., L.B.A., L.E.K., H.N., and H.A.B. are (or were at the time this work was conducted) employees of Pfizer Inc. Z.Z., P.J., and H.L. are employees of RES Group Inc and conducted part of this work under contract with Pfizer Inc. All authors declared no other competing interests for this work.

Author Contributions

H.M.J., Z.Z., and P.J. wrote the manuscript. All authors designed the research, performed the research, and analyzed the data.

Study Highlights.

• WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?

☑ There are a number of physiologically‐based pharmacokinetic (PBPK) models available in the literature to describe antibody pharmacokinetics (PK). There is no consensus with respect to model structure and model parameters, and these models rely heavily on in vivo data for application.

• WHAT QUESTION DID THE STUDY ADDRESS?

☑ This study develops a framework to predict in vivo PK for antibodies a priori using in vitro data within a PBPK model and establishes excellent prediction accuracy for this approach.

• WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?

☑ This work seeks to understand whether in vitro data can be used in a PBPK model framework to predict in vivo PK for antibodies to more efficiently support the early phases of antibody discovery.

• HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS?

☑ Our PBPK framework does not rely on the availability of in vivo PK data, which means that human PK data and possibly target engagement can be predicted from in vitro data and predicted PK properties can be factored into the lead selection process.

Supporting information

Supplementary Tables S1–S3 and PBPK Model Equations.

Model Code.