Abstract
There is a growing demand for the use of machine learning (ML) to derive fast-to-evaluate surrogate models of materials properties. In recent years, a broad array of materials property databases have emerged as part of a digital transformation of materials science. However, recent technological advances in ML are not fully exploited because of the insufficient volume and diversity of materials data. An ML framework called “transfer learning” has considerable potential to overcome the problem of limited amounts of materials data. Transfer learning relies on the concept that various property types, such as physical, chemical, electronic, thermodynamic, and mechanical properties, are physically interrelated. For a given target property to be predicted from a limited supply of training data, models of related proxy properties are pretrained using sufficient data; these models capture common features relevant to the target task. Repurposing of such machine-acquired features on the target task yields outstanding prediction performance even with exceedingly small data sets, as if highly experienced human experts can make rational inferences even for considerably less experienced tasks. In this study, to facilitate widespread use of transfer learning, we develop a pretrained model library called XenonPy.MDL. In this first release, the library comprises more than 140 000 pretrained models for various properties of small molecules, polymers, and inorganic crystalline materials. Along with these pretrained models, we describe some outstanding successes of transfer learning in different scenarios such as building models with only dozens of materials data, increasing the ability of extrapolative prediction through a strategic model transfer, and so on. Remarkably, transfer learning has autonomously identified rather nontrivial transferability across different properties transcending the different disciplines of materials science; for example, our analysis has revealed underlying bridges between small molecules and polymers and between organic and inorganic chemistry.
Short abstract
Along with the XenonPy.MDL model library, we describe the great potential of transfer learning to break the barrier of limited amounts of data in materials property prediction using machine learning.
Introduction
The ability of machine learning (ML) models, which are trained on massive amounts of data, to perform intellectually demanding tasks across various fields has reached or even surpassed that of humans.1−4 As such, ML has received considerable attention as a key driver to the next frontier of materials science, enabling us to reap substantial time and cost savings in the development of new materials.5 In particular, high-throughput screening (HTS) across extensive libraries of candidate materials, where such libraries typically contain millions or even billions of virtually created candidates, is a promising application in this context. HTS relies on a fast-to-evaluate surrogate ML model that describes physical, chemical, electronic, thermodynamic, or mechanical properties as a function of material structures. To date, ML has mostly been applied successfully in materials science via such simple workflows, e.g., in HTS-assisted discovery of new materials for organic light-emitting diodes6 and the identification of new ligands for nickel catalysis.7 Recently, a variety of materials property databases have emerged; these databases are developing continuously toward the accelerated discovery of innovative materials based on data-centric workflows. However, at present, the volume and diversity of the available data are insufficient for the exploitation of the full potential of ML. This problem of insufficient data will remain unresolved for a while, as the development of materials database is rather time-consuming and resource-intensive. Also, there is no clear incentive for broader data sharing and open-access movements among the various stakeholders in this field in industry and academia.
An ML framework called transfer learning has considerable potential to overcome the problem of limited amounts of materials data. Transfer learning is an increasingly popular ML framework, covering a broad range of methodologies in which a model trained on one task is repurposed for another related task.8,9 Among the various types of transfer learning, inductive transfer learning using artificial neural networks merits attention. Transfer learning has much less visibility in materials science than in other fields; however, a small number of studies on this topic have recently been published.10−18 In general, transfer learning is required when there is a limited supply of training data; however, many other promising applications to materials science exist, as described later. For a target property to be predicted based on a limited supply of data, a set of pretrained neural networks on its proxy properties is first obtained, where the given data are sufficiently large for training to be performed. The pretrained models autonomously acquire common features relevant to the proxy properties, which appear somewhere in the hidden layers. The features learned by solving the related tasks are partially transferable as input features for a model of the target task, if those properties are physically related. In this paper, it is demonstrated that adapting such machine-acquired features to a new task can bring a surprisingly outstanding prediction ability as highly experienced human experts can make rational inferences even on considerably less experienced tasks. There might be no materials properties as being completely independent, and every property might bear some dependencies to others directly or indirectly. This fact will create the enormous potential of transfer learning in materials science.
To facilitate the widespread use of transfer learning, we have developed a comprehensive library of pretrained models, called XenonPy.MDL,19 by feeding diverse sets of materials property data into neural networks or some other types of models such as the random forest model. In the current release (version 0.1.0), this ever-growing library contains more than 140 000 models for physical, chemical, electronic, thermodynamic, and mechanical properties of small organic molecules, polymers, and inorganic crystalline materials (15, 18, or 12 properties for each). The trained models are distributed as the MXNet20 (R) and/or PyTorch21 (Python) model objects. The distributed application programming interface (API) allows users to query the XenonPy.MDL database.
We describe the outstanding successes of transfer learning in different scenarios. In some case studies, surprisingly well-performing models were achieved even though only a few data points for polymeric properties were supplied. In addition, the enhancement of the extrapolative prediction performance through a strategic model transfer is demonstrated. Remarkably, transfer learning has autonomously identified rather nontrivial transferability across different properties transcending the different disciplines of materials science, for example, from small molecules to polymers and from inorganic to organic chemistry.
Methods
Neural Transfer Learning
In this study, we focused on specific types of transfer learning using neural networks. The task to be addressed is to learn a neural network Yt = ft(S) that predicts a target property Yt for any given material S with a considerably small data set of size nt
where {Yt,i, St,i} denotes the ith training
instance. Transfer learning provides several ways to break the barrier
of limited data in which models trained on different source property Ys with a given abundant data
set  are
reused and transferred to the model
in the target task.
are
reused and transferred to the model
in the target task.
There are two commonly applied procedures for the neural transfer learning, the frozen featurizer and fine-tuning techniques, which are briefly described below (see Yosinski et al.22 for example):
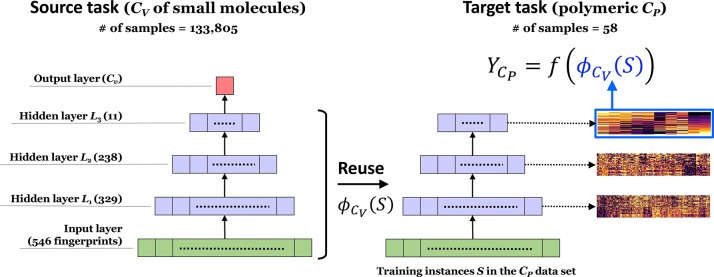
Frozen featurizer. Solving a source task on a proxy property to the target, we obtain a pretrained neural network Ys = fs(S) with L layers. In general, the function is represented as a Lth-order composite function fs(S) = (gL◦gL–1...◦g1)(S) tandemly arranged from the input g1 to the output layer gL. Earlier or shallower layers tend to acquire general features to form the basis of the material description, and only the last one or two layers are responsible for summarizing specific features for prediction of a source property. We retain the shallower layers to be frozen as a feature extractor, ϕ(S) = (gK◦gK–1...◦g1)(S) with K < L, then repurposed ϕ(S) for supervised learning of a different property, e.g., using the random forest regression as Yt = ft(ϕ(S)) (Figure 1).
Fine-tuning. In this approach, a pretrained model is used as a starting point and fine-tuned to a target task using a few given instances. In our implementation, the weights on the last few layers of the pretrained model are randomly initialized, while the learned parameters of the remaining layers are used as initial values. All those parameters are then retrained at a small learning rate, which controls the weight updating on each gradient descent iteration while preserving domain-invariant knowledge.
Figure 1.
Neural transfer learning with frozen featurizers. In this example, a fully connected pyramid neural network is first trained using training instances for the monomeric CV. A subnetwork other than the output layer is used as a feature extractor and is repurposed on a model of the polymeric CP.
The R and Python codes distributed at the XenonPy Web site enable us to perform both types of transfer learning seamlessly while utilizing the model library.
The prediction performance of a transferred model depends on the choice of source properties, source data, and architectures of the neural networks. Ideally, a resulting prediction model should be extrapolative, i.e., showing high predictability even in regions where less or no data are available. In general, the prediction of any ordinal ML models is interpolative. On the other hand, if a source model pretrained using a massive amount of training data successfully acquires generic features, which are applicable to a broad region in the landscape of structure–property relationships, a transferred target model trained with just a small data set could be extrapolative as will be demonstrated later in some applications. Besides, the more relevant the source and target tasks are, the more efficiently the source model can adapt to the target task.
Pretrained Model Library: XenonPy.MDL
To enjoy the potential benefits of transfer learning, it would be helpful to have a diverse candidate set of source models beforehand instead of building pretrained models on-demand from scratch. In conventional scenarios, we often lack a theoretical basis and empirical laws to determine source properties related to a new task. Besides, even on the same source property, pretrained models having different network architectures often show significant variations in transferability. Hence, we should take a shotgun approach, i.e., to identify a model showing the best transferability among a candidate pool of source models on a trial-and-error basis.
Currently, the pretrained model library XenonPy.MDL provides more than 140 000 pretrained neural networks, which were developed using MXNet in R and PyTorch in Python. In addition, the current release contains 16 000 pretrained random forests and 1000 gradient boosting models, which were trained using the ranger and xgboost packages in R, respectively. We classified the models into three categories according to material types: small molecules, polymers, and inorganic crystalline materials. A broad array of materials properties is covered by the library: 15, 18, and 12 properties for small molecules, organic polymers, and inorganic materials, respectively. Furthermore, we produced a set of classification models that discriminate 226 space groups (4 were neglected from the total of 230 space groups due to lack of data) or 32 point groups of crystalline materials with given input chemical compositions. The library also incorporates models successfully transferred from some of the source models.
For each source task considered in this study, we generated ∼1000 neural networks with randomly constructed network structures, using different bootstrap data sets. As will be shown, for the success of the shotgun transfer learning, it is important to have diverse candidates of pretrained models or pretrained features to be tested on the generalization capability on the trial-and-error basis. To enhance the model diversity, we used relatively small bootstrap data sets in the pretraining process. A typical model had the form of a fully connected hierarchical pyramid in which the number of layers was randomly selected from {3,4,5,6}, and the number of neurons monotonically decreased from the input layer to the output one. All neurons in the hidden layers were activated by a rectified linear unit, and a linear function was assigned to the output layers. Table 1 summarizes the trained models employed in this study and provides a list of the source data sets, descriptors, model types, and their prediction performances. Many of these models are available online and can serve as benchmarks for further developments. Prediction–observation plots of all the current best-performing models are given in Figure S1 (Supporting Information).
Table 1. Summary of Models Trained in This Studya.
| material type | database | property | model type | model parameters | no. of models | best model correlation | no. of descriptors | descriptor type |
|---|---|---|---|---|---|---|---|---|
| organic | PoLyInfo (polymer) | glass transition temperature | RF-R | RF setup 1 | 1,000 | 0.950 | max 500* | rcdk-all |
| GB-R | GB setup | 1,000 | 0.950 | max 500* | rcdk-all | |||
| EN-R | EN setup | 1,000 | 0.920 | max 500* | rcdk-all | |||
| NN-R | NN setup 1 | 1,000 | 0.950 | max 400–600# | rcdk-all | |||
| NN-Py | NN setup 2 | 500 | 0.955 | 2,048 | RDKit-5 | |||
| density | NN-R | NN setup 1 | 1,000 | 0.910 | max 400–600# | rcdk-all | ||
| NN-Py | NN setup 2 | 500 | 0.859 | 2,048 | RDKit-5 | |||
| viscosity | NN-R | NN setup 1 | 1,000 | 0.890 | max 400–600# | rcdk-all | ||
| NN-Py | NN setup 2 | 500 | 0.613 | 2,048 | RDKit-5 | |||
| melting temperature | NN-R | NN setup 1 | 1,000 | 0.880 | max 400–600# | rcdk-all | ||
| NN-Py | NN setup 2 | 500 | 0.885 | 2,048 | RDKit-5 | |||
| heat capacity (const pressure) | NN-R | TL setup 1 | 25,000 | 0.992 | max 400–600# | rcdk-all | ||
| thermal conductivity | NN-R | TL setup 1 | 25,000 | 1.000 | max 400–600# | rcdk-all | ||
| QM9 (small molecule) | heat capacity at constant volume | NN-R | NN setup 1 | ∼500 | 0.900 | max 400–600# | rcdk-all | |
| LUMO | NN-R | NN setup 1 | ∼500 | 0.950 | max 400–600# | rcdk-all | ||
| HOMO–LUMO gap | NN-R | NN setup 1 | ∼500 | 0.940 | max 400–600# | rcdk-all | ||
| zero point vibrational energy | NN-R | NN setup 1 | ∼500 | 0.940 | max 400–600# | rcdk-all | ||
| internal energy at 0 K | NN-R | NN setup 1 | ∼500 | 0.920 | max 400–600# | rcdk-all | ||
| enthalpy at 298.15 K | NN-R | NN setup 1 | ∼500 | 0.910 | max 400–600# | rcdk-all | ||
| free energy at 298.15 K | NN-R | NN setup 1 | ∼500 | 0.910 | max 400–600# | rcdk-all | ||
| HOMO | NN-R | NN setup 1 | ∼500 | 0.880 | max 400–600# | rcdk-all | ||
| internal energy at 298.15 K | NN-R | NN setup 1 | ∼500 | 0.880 | max 400–600# | rcdk-all | ||
| isotropic polarizability | NN-R | NN setup 1 | ∼500 | 0.870 | max 400–600# | rcdk-all | ||
| electronic spatial extent | NN-R | NN setup 1 | ∼500 | 0.800 | max 400–600# | rcdk-all | ||
| dipole moment | NN-R | NN setup 1 | ∼500 | 0.740 | max 400–600# | rcdk-all |
| material type | database | property | model type | model parameters | no. of models | best model correlation | no. of descriptors | descriptor type |
|---|---|---|---|---|---|---|---|---|
| Oorganic | bandgap | RF-R | RF setup 2 | 1,000 | 0.964 | max 1,500–3,000# | rcdk-all | |
| NN-R | NN setup 1 | 1,000 | 0.985 | max 400–600# | rcdk-all | |||
| NN-Py | NN setup 2 | 500 | 0.983 | 2,048 | RDKit-5 | |||
| dielectric constant | RF-R | RF setup 2 | 1,000 | 0.965 | max 1,500–3,000# | rcdk-all | ||
| NN-R | NN setup 1 | 1,000 | 0.982 | max 400–600# | rcdk-all | |||
| NN-Py | NN setup 2 | 500 | 0.958 | 2,048 | RDKit-5 | |||
| ionic dielectric constant | RF-R | RF setup 2 | 1,000 | 0.898 | max 1,500–3,000# | rcdk-all | ||
| NN-R | NN setup 1 | 1,000 | 0.934 | max 400–600# | rcdk-all | |||
| electronic dielectric constant | RF-R | RF setup 2 | 1,000 | 0.930 | max 1,500–3,000# | rcdk-all | ||
| NN-R | NN setup 1 | 1,000 | 0.947 | max 400–600# | rcdk-all | |||
| refractive index | RF-R | RF setup 2 | 1,000 | 0.953 | max 1,500–3,000# | rcdk-all | ||
| NN-R | NN setup 1 | 1,000 | 0.985 | max 400–600# | rcdk-all | |||
| NN-Py | NN setup 2 | 500 | 0.981 | 2,048 | RDKit-5 | |||
| atomization energy | RF-R | RF setup 2 | 1,000 | 0.974 | max 1,500–3,000# | rcdk-all | ||
| NN-R | NN setup 1 | 1,000 | 0.986 | max 400–600# | rcdk-all | |||
| NN-Py | NN setup 2 | 500 | 0.992 | 2,048 | RDKit-5 | |||
| polymer genome (polymer) | density | RF-R | RF setup 2 | 1,000 | 0.961 | max 1,500–3,000# | rcdk-all | |
| NN-R | NN setup 1 | 1,000 | 0.982 | max 400–600# | rcdk-all | |||
| NN-Py | NN setup 2 | 500 | 0.989 | 2,048 | RDKit-5 | |||
| ionization energy | RF-R | RF setup 2 | 1,000 | 0.922 | max 1,500–3,000# | rcdk-all | ||
| NN-R | NN setup 1 | 1,000 | 0.962 | max 400–600# | rcdk-all | |||
| NN-Py | NN setup 2 | 500 | 0.940 | 2,048 | RDKit-5 | |||
| electron affinity | RF-R | RF setup 2 | 1,000 | 0.955 | max 1,500–3,000# | rcdk-all | ||
| NN-R | NN setup 1 | 1,000 | 0.978 | max 400–600# | rcdk-all | |||
| NN-Py | NN setup 2 | 500 | 0.987 | 2,048 | RDKit-5 | |||
| cohesive energy | RF-R | RF setup 2 | 1,000 | 0.839 | max 1,500–3,000# | rcdk-all | ||
| NN-R | NN setup 1 | 1,000 | 0.943 | max 400–600# | rcdk-all | |||
| melting temperature | RF-R | RF setup 2 | 1,000 | 0.920 | max 1,500–3,000# | rcdk-all | ||
| NN-R | NN setup 1 | 1,000 | 0.94 | max 400–600# | rcdk-all | |||
| glass transition temperature | RF-R | RF setup 2 | 1,000 | 0.937 | max 1,500–3,000# | rcdk-all | ||
| NN-R | NN setup 1 | 1,000 | 0.962 | max 400–600# | rcdk-all | |||
| NN-Py | NN setup 2 | 500 | 0.931 | 2,048 | RDKit-5 | |||
| Hildebrand solubility parameter | RF-R | RF setup 2 | 1,000 | 0.951 | max 1,500–3,000# | rcdk-all | ||
| NN-R | NN setup 1 | 1,000 | 0.962 | max 400–600# | rcdk-all | |||
| NN-Py | NN setup 2 | 500 | 0.879 | 2,048 | RDKit-5 | |||
| molar heat capacity | RF-R | RF setup 2 | 1,000 | 0.989 | max 1,500–3,000# | rcdk-all | ||
| NN-R | NN setup 1 | 1,000 | 0.991 | max 400–600# | rcdk-all | |||
| molar volume | RF-R | RF setup 2 | 1,000 | 0.965 | max 1,500–3,000# | rcdk-all | ||
| NN-R | NN setup 1 | 1,000 | 0.984 | max 400–600# | rcdk-all | |||
| PHYSPROP | boiling point | NN-R | NN setup 1 | 1,000 | 0.782 | max 400–600# | rcdk-all | |
| MD database | solvation free energy | NN-R | NN setup 1 | 1,000 | 0.94 | max 400–600# | rcdk-all | |
| Jean-Claude Bradley | melting temperature | NN-R | NN setup 1 | 1,000 | 0.84 | max 400–600# | rcdk-all | |
| material type | database | property | model type | model parameters | no. of models | best model correlation | no. of descriptors | descriptor type |
|---|---|---|---|---|---|---|---|---|
| inorganic | materials project | volume | NN-Py | NN setup 3 | 3,600% | 0.997 | 290/150 | XenonPy |
| CGCNN-Py | CNN setup | 324 | 0.606 | N/A | N/A | |||
| formation energy per atom | NN-Py | NN setup 3 | 3,600% | 0.997 | 290/150 | XenonPy | ||
| CGCNN-Py | CNN setup | 324 | 0.977 | N/A | N/A | |||
| total energy per atom | NN-Py | NN setup 3 | 3,600% | 0.996 | 290/150 | XenonPy | ||
| CGCNN-Py | CNN setup | 324 | 0.963 | N/A | N/A | |||
| density | NN-Py | NN setup 3 | 3,600% | 0.994 | 290/150 | XenonPy | ||
| CGCNN-Py | CNN setup | 324 | 0.996 | N/A | N/A | |||
| Fermi energy | NN-Py | NN setup 3 | 3,600% | 0.968 | 290/150 | XenonPy | ||
| CGCNN-Py | CNN setup | 324 | 0.933 | N/A | N/A | |||
| magnetization | NN-Py | NN setup 3 | 3,600% | 0.923 | 290/150 | XenonPy | ||
| CGCNN-Py | CNN setup | 324 | 0.723 | N/A | N/A | |||
| bandgap | NN-Py | NN setup 3 | 3,600% | 0.910 | 290/150 | XenonPy | ||
| CGCNN-Py | CNN setup | 324 | 0.936 | N/A | N/A | |||
| Citrination data sets id:152062 | total dielectric constant | NN-Py | NN setup 3 | 3,600% | 0.565 | 290/150 | XenonPy | |
| electronic dielectric constant | NN-Py | NN setup 3 | 3,600% | 0.504 | 290/150 | XenonPy | ||
| refractive index | NN-Py | NN setup 3 | 3,600% | 0.762 | 290/150 | XenonPy | ||
| Shiomi data | scattering phase space | NN-Py | NN setup 3 | ∼1,200 | 0.912 | 290/150 | XenonPy | |
| lattice thermal conductivity | NN-Py | NN setup 3 | ∼1,200 | 0.998 | 290/150 | XenonPy | ||
| NN-Py | TL setup 2 | ∼200 | 0.999 | 290 | XenonPy |
RF-R, GB-R, EN-R, and NN-R denote models obtained from the ranger package (random forest), xgboost package (gradient boosting), glmnet package (elastic net), and MXNet package (neural network) in R, respectively. NN-Py and RF-Py denote neural networks trained with PyTorch and random forest trained with scikit-learn in Python, respectively. CGCNN-Py denotes the crystal graph convolution neural network in PyTorch. The hyperparameters of each model were randomly selected from fixed ranges. RF setup 1 indicates the number of trees (nTree) ∈ [100,800] and the number of randomly chosen features (mTry) ∈ [20,100]. RF setup 2 denotes nTree ∈ [50,500] and mTry ∈ [50,500]. GB setup denotes the learning rate (eta) ∈ [0.1,1], the maximum tree depth (max_depth) ∈ [3,10], and the maximum number of boosting iterations (nrounds) ∈ [50,200]. EN setup denotes the elastic net mixing parameter (alpha) ∈ [0,1] with the Gaussian-response-type family and randomly selected λ. NN setup 1 denotes the number of epochs ∈ [3,000,4,000], the number of hidden layers ∈ [3,4]. Furthermore, the maximum number of nodes in the first hidden layer equal to 400 and the number of nodes in the last layer ∈ [10,30]. NN setup 2 was the same as NN setup 1 except the maximum number of nodes in the first hidden layer was 1640. NN setup 3 denotes the number of epochs ∈ [1000, 3000], the number of hidden layers ∈ [3,6], with the maximum number of nodes in the first hidden layer given by 348 and the minimum number of nodes in the last layer given by 5. TL setup 1 denotes the use of the last hidden layer of a source neural network (N nodes) as an input for RF-R with randomly picked hyperparameters: nTree ∈ [half of the number of the training samples,the number of training samples] and mTry ∈ [N/2,N]. TL setup 2 denotes the use of a randomly chosen subset of all the hidden layers of the SPS best model as an input for RF-Py. Randomly selected hyperparameters were employed: nTree = 200, the maximum number of features = square root of the number of descriptors. For descriptor types, rcdk-all denotes combining all available fingerprints in rcdk (standard, extended, graph, hybridization, maccs, estate, pubchem, kr, circular); RDKit-5 denotes atom pairs and topological torsions fingerprints, Morgan fingerprints (with and without feature-based), and basic fingerprints in RDKit; XenonPy denotes compositional and RDF descriptors in XenonPy. The symbol * denotes cases that, after fingerprint entries showing zero in more than 90% of the training instances were removed from a total of 11 106 bits, some of the remaining entries were randomly discarded until the number of remaining entries reached at most 500. The symbol # denotes cases identical to those of *, except the remaining fingerprint entries after the filtering were randomly dropped down to, at most, X entries, where X is randomly picked from a given range. Furthermore, % indicates that the 3600 models consist of three sets of 1200 models that correspond to the compositional and RDF descriptors for stable structures and the compositional descriptor for unstable structures, respectively.
Trained model objects in R or Python were archived to RData and pickled objects, which included a set of metadata required for model reuse and retrieval, e.g., model identifier, author(s), description, property, class of materials, library to calculate descriptors, descriptors, source database, and identifiers of training samples in source database. For more details, see the XenonPy Web site.23 XenonPy is an ever-growing python library for materials informatics, including an interface for retrieval of pretrained models and application of a transfer learning module. The API allows users to work in the R or Python environments using interactive or batch queries.
The pretrained models with the source data used in the current release are summarized as follows.
Small Molecules
We used 12 properties of 133 805 small organic molecules in the QM9 data set,24,25 such as the HOMO–LUMO gap, dipole moment, and heat capacity at constant volume (CV), which were calculated using density functional theory (DFT) at the B3LYP/6-31G(2df,p) level of quantum chemistry. In addition, the second data set was taken from our previous work,26 constituting a set of the HOMO–LUMO gaps and internal energies of 16 674 chemical species in PubChem,27 which were calculated via DFT with structural optimization performed at the B3LYP/6-31+G(d) level of theory using the General Atomic and Molecular Electronic Structure System (GAMESS).28,29 We also produced an original data set of the solvation free energies of 1025 organic compounds in water solution, as calculated from molecular dynamics (MD) simulations using the Groningen Machine for Chemical Simulations (GROMACS).30 The solvation free energy was calculated from the MD trajectories using the Energy Representation Module (ERmod).31 Other than those sets, we used the melting temperatures of 28 645 chemical structures contained in the Jean-Claude Bradley open melting point data set32 and 7301 boiling points of over 40 000 structures incorporated in the Physical Properties (PHYSPROP) database.33,34 Neural networks having randomly constructed architectures were trained separately on all data sets using the MXNet package in R and PyTorch in Python. In each training, we used a randomly chosen subset of the 11 106 dimensional binary descriptor that concatenated 9 different fingerprints implemented in the rcdk library35 in R. For the RDKit package36 in Python, models were trained for each of the five fingerprints separately. See Table S1 in Supporting Information for the fingerprint descriptors.
Polymers
In this release, narrowing the focus to homopolymers, we explored mapping from the chemical structures of constitutional repeating units to polymeric properties using training data from two major polymeric properties databases, PoLyInfo37 and Polymer Genome.38 PoLyInfo provides 17 001 observations of the glass transition temperatures (Tg) for 5917 unique homopolymers and 12 374 observations of the melting temperatures (Tm) for 3234 unique homopolymers. We also extracted 13 868 observations of the density (ρ) of 1517 homopolymers, 121 observations of CP for 58 amorphous homopolymers, and 101 observations of the thermal conductivity (λ) for 19 amorphous homopolymers that correspond to room temperature (10–30◦C). Polymer Genome presents a broad range of computational and experimental properties of 853 polymers (bandgaps, diectric constants, refractive indexes (n), Hildebrand solubility parameters, atomization energies, Tg, and ρ). Pretrained models were generated in the same way as those of small molecules.
Inorganic Compounds
We generated pretrained models of 10 properties (bandgap, formation energy, n, ρ, volume, total magnetization, and so on) using 69 640 and 1056 records from the Materials Project39 and Citrination databases (id:152062),40 respectively. In addition, we used two data sets taken from our previous studies that consist of computationally calculated lattice thermal conductivity (LTC) and the related properties called the scattering phase space (SPS) for 45 and 320 inorganic crystals, respectively.59 For each task, two types of materials descriptors, referred to as the compositional and structural descriptors, were generated using XenonPy. The compositional descriptor described 290 features of the elemental compositions of the given materials. The structural descriptor was composed of topological or electronic features of a given crystal structure, such as the partial radial distribution function (pRDF)41 and orbital field matrix.42 XenonPy provided a simple-to-use interface for generation of 20 kinds of structural descriptor with the aid of a wrapper function to matminer.43 Most pretrained models in the current library describe a given materials property as a function of one or both of the compositional and structural descriptors. We also registered few descriptor-free models based on the crystal graph convolutional neural networks44 that were trained on the Materials Project database for formation energy, Fermi energy, magnetiation, bandgap, total energy per atom, volume, and density. In addition, the library contains pretrained neural networks and random forests for multiclass classification, which designates given chemical compositions into one of the 226 space groups or 32 point groups.
Results
Hereafter, successful applications of the shotgun transfer learning in four different scenarios will be described. The primary objective is to demonstrate how we learn from little data or how well pretrained off-the-shelf features work in the task of extrapolative prediction.
Illustrative Example: Prediction of Polymeric Heat Capacity
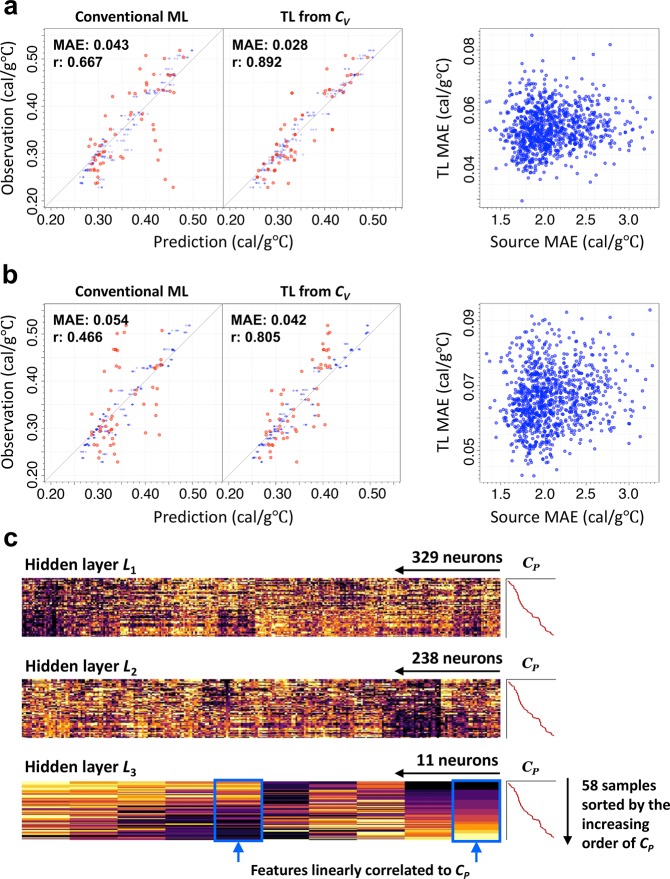
We first report a successful application that illustrates the analytic workflow of the transfer learning and some of its potential. The goal was to obtain a prediction model that describes a thermophysical property of polymers, that is, the specific heat capacity at constant pressure (CP), as a function of chemical structures in constitutional repeat units. Using a set of molecular fingerprinting algorithms in the rcdk library, the chemical structure S of a monomer was translated into a series of binary digits representing the presence or absence of specific substructures in the given molecule. To be specific, the nine fingerprint descriptors that include the Extended-Connectivity Fingerprint (ECFP) fingerprint45 and the MDL MACCS keys46 (see Table S1 in Supporting Information) were concatenated to define an augmented descriptor with the total number of elements equal to 11 106, and its randomly chosen subset was used in each of the 1000 shotgun pretrained models. These features constituted a binary vector ϕ(S) with length equal to around 400–600. The task was to identify an underlying mapping CP = f(ϕ(S)) from ϕ(S) to CP using given training instances on the structure–property relationships. PoLyInfo provides experimental values of CP at room temperature (10–30◦C) for only 58 amorphous homopolymers.37 In this study, multiple observations of the same polymer were reduced to the average value that characterizes its baseline CP. Figure 2a shows the prediction accuracy of a directly learned model that was derived by feeding the given data into the random forest algorithm. Five-fold cross validation (CV) was performed on the 58 instances to evaluate the mean absolute error (MAE), the maximum absolute error (MaxAE), the root-mean-square error (RMSE), and Pearson’s correlation coefficient (r) between the predicted and observed values. It is apparent that the generalization capability of the resulting model was significantly low (MAE = 0.043 cal/g◦C and r = 0.667). In particular, the model exhibited large prediction errors (MaxAE = 0.229 cal/g °C) for a few test polymers, such as those with a tiny monomer unit containing halogen groups (e.g., “*C(Cl)C*” and “*C(F)(F)*”); this was because of the lack of data.
Figure 2.
Illustrative example of transfer learning for prediction of polymeric CP. (a) The left two panels show prediction performance of a directly supervised random forest and the best transfer learning model using 58 instances of the polymeric CP under 5-fold CV. The predicted and experimentally measured properties are shown on the horizontal and vertical axes, respectively, color-coded in shades of red (blue: fits to the training data in the CV). The best transfer learning model is obtained from 1000 pretrained source models for the CV of small molecules, which had randomly generated different networks. The transferred polymeric CP model exhibiting the minimum MAE value was identified through the same 5-fold CV. The right panel shows a plot of the MAE values for the 1000 pretrained models on the source task (the monomeric CV) and their transferred models on the target task (the polymeric CP). (b) Same layout as (a), except the models were trained with the stratified group 6-fold CV; all the polymers were divided into nonoverlapping six subgroups according to their compositional and structural features, and the CV was looped with this grouping. (c) Heatmap display of neural descriptors acquired from CV and repurposed on CP. For each layer in the CV network, we calculated the n × p descriptor matrices with the chemical structures given in the CP data set, where p is the number of neurons and n is the number of samples on CP. In all the heatmaps, the n samples are sorted from top to bottom in increasing order of CP.
To increase the ML performance, we attempted to extract features transferable to CP by solving a different but related task. The QM9 data set contains specific heat capacities at constant volume (CV) for 133 805 small organic molecules composed of C, O, N, and F, calculated at the B3LYP/6-31G(2df,p) level of quantum chemistry. We began by using a shotgun approach to produce 1000 neural networks, which were trained on 15000–30000 randomly chosen instances representing the relationship between CV and the fingerprinted chemical structures. Each model had a fully connected pyramid network where the number of neurons monotonically decreased from the input to the output layer, and the number of hidden layers was randomly selected to be three or four. The number of neurons in each layer was also randomly chosen such that the cell size in the last hidden layers fell within the range of 10–30. For each pretrained model, its subnetwork other than the output layers, denoted by ϕCV(S), was used as a feature extractor, which was repurposed in the CP prediction model (Figure 1). By feeding the CP training set into the random forest algorithm with the randomized values of the hyperparameters, e.g., the number of trees in the forest and the number of randomly chosen features, respectively, we obtained the model CP = f(ϕCV(S)), which describes CP as a function of the reduced representation ϕCV(S) of S. We tested the transferability of each of the 1000 pretrained models on a trial-and-error basis and selected the best transferred model yielded the minimum MAE through the 5-fold CV on the foregoing CP training set. The prediction accuracy was greatly improved, as the MAE reached 0.028 cal/g °C on the validation data and the MaxAE was reduced to 0.097 cal/g °C from that of the without-transfer model (Figure 2a). It is likely that the pretraining step of transfer learning has successfully extracted generic features from the QM9 data of small molecules with F, thus improving the prediction of polymers with a tiny monomer unit containing halogens. This achievement is quite satisfactory considering the limited amount of training data and the use of highly simplified models depending only on the chemical structures in the repeating units. Notably, any other potential covariates, which could greatly affect the polymeric CP, were ignored.
The underlying transferability between the monomer-level CV and polymeric CP could be confirmed visually, as shown in Figure 2c. The test polymers in the CP data set were fed into the feature extractor learned from the monomer-level computational CV. Some neurons exhibited a clear association with the targeted CP, representing the underlying commonality between the computationally and experimentally evaluated thermophysical properties at the monomer and polymer levels.
One of the most prominent features of transfer learning lies in the potential power of extrapolative prediction. We divided the polymers into six subgroups using the K-means clustering with the fingerprinted chemical structures. After six wrongly grouped polymers were manually removed, the identified groups were annotated according to their compositional and structural features as hydrocarbon main chain polymers, phenols ethers, N containing aromatics, aliphatic esters, aromatic esters, and diphenyl substituted metals. As shown in Figure S2, between-group variability of the grouped polymers was significantly large. With this grouping, we performed a stratified group 6-fold CV: a group was treated as a validation set and the remaining five groups as a training set in the transfer learning. As expected, the prediction performance of both transferred and without-transfer models declined from the conventional CV as the task became significantly harder. However, as shown in Figure 2b, the MAE and MaxAE for the transferred models over the six validation sets (MAE = 0.042 cal/g °C and MaxAE = 0.116 cal/g °C) were still significantly lower than those of the without-transfer models (MAE = 0.054 cal/g °C and MaxAE = 0.160 cal/g °C). In general, the generalization capability of an ordinal ML model is limited to a neighboring region of a given training data set, as apparent for the case of the without-transfer models that performed rather poorly when the underlying distribution between training and test data was significantly dissimilar. This observed fact can be interpreted as follows: the pretrained model on the CV of small organic molecules successfully acquired a feature extractor generally applicable to a broader space of chemical structures than the one spanned by the rather limited training instances of polymeric CP, because the 133 805 source data included training instances that are relevant to the relationships regarding diverse chemical structures with respect to the target task.
This illustrative example demonstrates the great potential of transfer learning as a key driver to overcoming data scarcity and suggests its potential applications in various tasks relating to materials science. This example also reveals the prerequisite for full exploitation of the potential benefits of transfer learning, that is, a comprehensive set of pretrained models. In this example, the empirical knowledge that the monomeric CV is relevant to polymeric CP was already available. That is, the heat capacity of polymers is known to have a downward bias with respect to that of their monomeric states. However, conventional scenarios may lack a theoretical basis and empirical laws to determine the source properties related to a novel task. Moreover, this example highlighted the importance of using a diverse candidate set of pretrained models. As shown in Figure 2a,b, significant variation in the observed transferability from CV to CP was apparent for the 1000 pretrained models with different network architectures. In most cases, a pretrained model showing the best prediction in the source task does not always exhibit the best transferability in the target task as seen in the lack of correlations in the MAE values between the 1000 pretrained models in the source task (monomeric CV) and the transferred models in the target task (polymeric CP) (the right panels in Figure 2a,b).
Thermal Conductivity of Organic Polymers: Learning with Exceedingly Small Data Sets
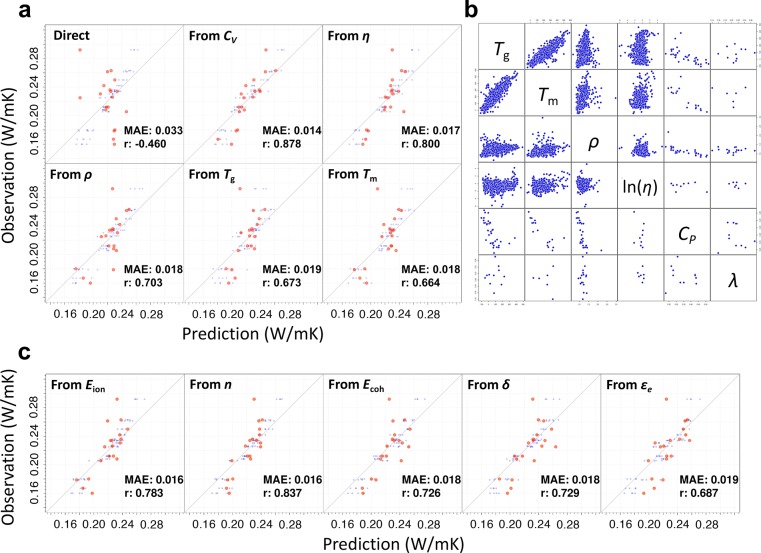
PoLyInfo records multiple observations of λ at room temperature for 19 unique amorphous homopolymers, after the removal of unreliable data based on manual inspection. The values of λ varied considerably, even for the same polymer, as shown in Wu et al.47 The observed within-polymer fluctuations would arise from unrecorded processing operations, molecular orientations, and other higher-order polymeric structures, which are known to be more influential than the chemical structures of monomers. For each polymer, the replicated observed properties were averaged to define a baseline level of λ. Both the extreme scarcity of data and the existence of unmodeled factors with considerable influence on the output property greatly increased the difficulty of obtaining accurate prediction models. As expected, none of the directly trained models yielded successful prediction of λ, as shown in Figure 3a.
Figure 3.
Transfer learning (TL) for λ of polymers using 19 observations. (a) The upper left plot shows 19 observed properties against predicted values given by directly trained random forests. The other panels present the prediction performance of transferred random forests trained using neural network features acquired from prelearning on CV (small molecules), and the viscosity, ρ, Tg, and Tm of polymers. The predicted and fitted values in the 5-fold CV are colored orange and blue, respectively. (b) Scatter plot matrix of observed properties in PoLyInfo for Tg (°C), Tm (°C), ρ (g/cm3), viscosity (η, dL/g) in log scale, CP (cal/g °C), and λ (W/mK). (c) Prediction performance of transferred random forests trained using neural network features acquired from prelearning of the ionization energy (Eion), n, cohesive energy (Ecoh), Hildebrand solubility parameter (δ), and electronic dielectric constant (ϵe) in Polymer Genome.
The procedure of transfer learning was the same as for the polymeric CP. We reused the feature extractors of all the pretrained neural networks for Tg, Tm, ρ, and the viscosity (η), which originated from PoLyInfo. In addition, we used the 1000 models of the computational CV of small organic molecules, which were trained on the QM9 data set. These pretrained models were individually repurposed for the training of random forests with only the 19 instances of λ, with the top layers being removed and swapped with the random forests. The generalization capabilities of the transferred models were measured in terms of the MAE, RMSE, MaxAE, and r, between the observed and predicted values through the 5-fold CV looped within the 19 instances. As shown in Figure 3a, the best transferable models determined through the CV, which were derived from any of the five source properties, yielded satisfactory performance on the validation sets. Rather miraculously, the transfer learning was successful with such an extremely small data set, and possibly even outperformed human capability for this task, as explained below. In previous works, ρ has been observed to have a linear relationship with λ.48 Some studies have also suggested a rule of thumb relating Tg to λ.49,50 However, none of those source properties exhibited clear dependency to λ in the observation data, as shown in Figure 3b which displays a scatter plot matrix of the observed properties of Tg, Tm, ρ, η, CP, and λ in PoLyInfo. It is apparent that the pretrained neural networks successfully acquired nontrivial commonalities transferable across these physical properties; this performance may be far beyond the human perception achievable through simple observation of the joint distribution. Furthermore, as shown in Figure 3c, which summarizes the prediction results of transferred models originating from the Polymer Genome data sets, physically uninterpretable source properties such as n, the dielectric constant, and the polymer solubility have almost comparable levels of transferability to the five properties in PoLyInfo.
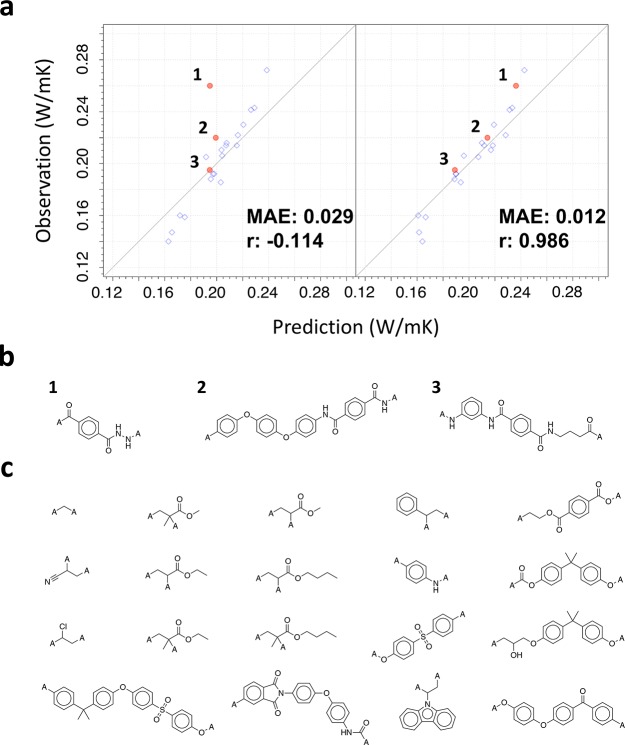
We investigated the extrapolative power of the best-performing transferred model that was originated from a source model on the computational CV of small organic molecules. In the previous work,47 we presented newly synthesized three kinds of polyamide containing mesogen groups, as depicted in Figure 4. While their chemical structures were considerably different from the 19 training instances as no mesogenic polyamides were included in the training set as displayed in Figure 4, the predicted λ of the three synthesized polymers, which were transferred from the pretrained model on the computational CV, were highly consistent with the experimental observations. As expected, the without-transfer model did not acquire such predictability.
Figure 4.
Extrapolation ability of transferred models for predicting λ. (a) Prediction of λ for three polymers that were newly synthesized in our previous study47 (left: directly learned random forest, right: the best transferred model). (b, c) Chemical structures of the three new polymers and the 19 training polymers used in the transfer learning.
Thermal Conductivity of Inorganic Crystals
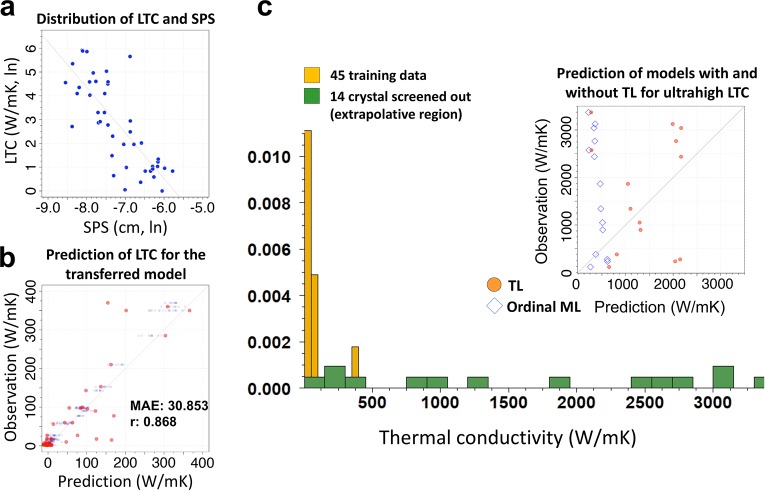
Exploration of crystalline materials with ultrahigh λ was of interest in our previous study, which aimed to facilitate efficient thermal management of electronic and optical devices. In recent decades, remarkable progress has been made with regard to first-principles calculation of the LTC using interatomic force constants (IFCs) obtained from DFT.51,52 However, performing first-principles calculations on tens of thousands of crystal compounds would be extremely time-consuming. Therefore, we selected the SPS as a proxy property for HTS, which is related to the phonon scattering rate. In theoretical speculation, the SPS should negatively correlate with the LTC. However, a rather weak negative correlation was observed, as shown in Figure 5a (r = −0.466 with a p-value of 0.00126).
Figure 5.
Transfer learning for LTC of inorganic compounds. (a) Scatter plot of data on SPS and LTC. (b) Prediction performance of model exhibiting best transferability among 1000 pretrained models. The validation and training results in the 10-fold CV are colored orange and blue, respectively. (c) Histogram showing LTC distributions for 45 training samples and 14 crystals having ultrahigh LTC identified by HTS. In the prediction-observation plot in the inset, the orange dots and blue diamonds denote the predicted values of the transferred model and of a neural network directly trained using the 45 samples, respectively, to demonstrate the extrapolation prediction performance.
For each of the 1000 neural networks trained on the 320 instances of SPS, all neurons in the top hidden layer were pipelined to a random forest regression that related the 290 compositional descriptors of XenonPy to the LTC. The restructured model was then trained on the 45 instances of LTC. For the 10-fold CV looped within the 45 training instances, the best-performing model produced predicted values that were highly consistent with the observed LTC, as shown in Figure 5b. As in the previous examples for polymers, the effectiveness of transfer learning in overcoming data scarcity was confirmed experimentally.
An alternative method of model transfer is to simply convert the predicted SPS of a pretrained model into the LTC along a straight line drawn down the middle of the SPS and LTC joint distribution, as shown in Figure 5a. However, the best prediction accuracy of such a simple calibration may be significantly lower than that of the best transferable model, because of the observed weak correlation between the source and target properties. This kind of calibration is essentially equivalent to the use of a pretrained neural network having a single neuron in the top hidden layer; the one-dimensional featurizer is mapped to the LTC through a linear function fitted on the given SPS and LTC data in Figure 5a. Transfer learning is considered to be a generalization of this approach, providing a mean of overcoming the limitation by embodying the underlying features learned from the SPS into the higher-dimensional feature space.
In our previous study, HTS was performed with a transferred model over about 60 000 candidate compounds selected from the Materials Project database. We identified 14 single crystals with LTC values that reached 115–3371 W/mK at room temperature.59 The realized LTCs resided in an extrapolative region, which is an exceedingly far tail of the training data distribution in the 1–370 W/mK range. Figure 5c shows the LTCs of the 14 crystals predicted by the transferred model and a model directly trained using the 45 data elements. Surprisingly, the transferred model successfully achieved extrapolative prediction performance. In contrast, there was a substantial difference between the observed and predicted values for the without-transfer model. In general, the generalization capability of an ordinal ML technique is limited to a neighboring region of the given training data set, as apparent for the case of the without-transfer model. This observed fact can be interpreted as follows: the pretrained SPS model can acquire a feature extractor generally applicable to a broader input space than that spanned by the given 45 training data for the LTC, because the 320 source data may contain training instances that are relevant to structure–property relationships regarding ultrahigh λ.
Transferability across Organic and Inorganic Materials
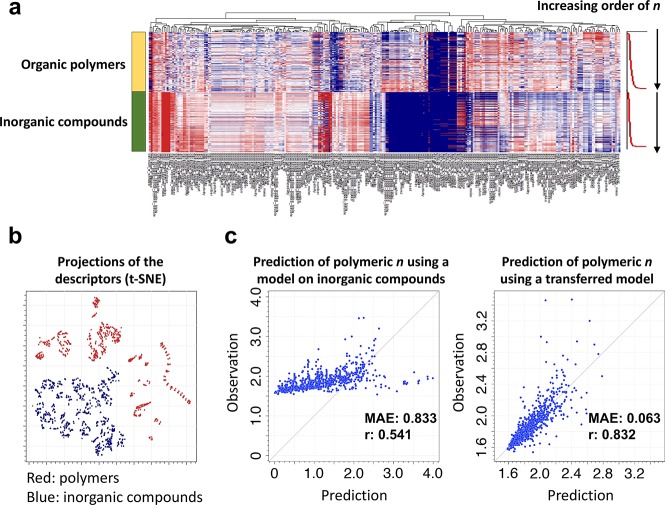
Finally, we aimed to reuse a model pretrained for inorganic materials in a new task concerning organic polymers. The target property for prediction was n (refractive index). XenonPy was used to calculate 290 features characterizing the compositional features of both inorganic compounds and polymers, with any other structural features being ignored during model building. As shown in Figure 6a, these two data sets exhibited entirely different structure–property relationships, as no common pattern was observed for each of the features (at least from a visual comparison of the polymer and inorganic data sets). Indeed, as shown in Figure 6b, which illustrates the descriptor vectors projected onto a two-dimensional subspace using t-distributed stochastic neighbor embedding (t-SNE),53 it was confirmed that the two data sets were distributed at quite distant regions in the feature space.
Figure 6.
Transfer learning across organic and inorganic materials. (a) Heatmap display of 290 compositional descriptors for 853 organic polymers (upper half) and 1056 inorganic compounds (lower half). The upper and lower half samples are separately sorted from top to bottom by increasing order n of organic polymers and inorganic compounds, respectively. (b) Projection of the 290 compositional descriptors onto two-dimensional space through t-SNE. The organic polymer and inorganic compound samples are colored red and blue, respectively. (c) Transfer learning performance from inorganic compounds to organic polymers. (Left) Prediction performance for n of organic polymers using model trained on inorganic compound data. (Right) Prediction results of best transferred model.
Before proceeding to transfer learning, we tested the direct prediction of the n values of the 853 polymers in the Polymer Genome database using the best-performing model pretrained for inorganic compounds in the current library; this model was trained on 1056 data sets. The MAE and r were 0.833 and 0.541, respectively. As shown in Figure 6c, the predicted n values of the polymers were significantly overestimated, obviously indicating a striking difference between organic and inorganic chemistry. On the other hand, the random forests trained on the polymeric property data using the transferred features yielded a reasonably precise prediction of n, with MAE and r values of 0.063 and 0.832, respectively, for 10-fold validation looped within the 853 samples.
This nontrivial transferability that breaks the barrier between organic and inorganic chemistry has been presented in this work in order to highlight a different transfer learning application scenario. By exhaustively investigating feasible transfers based on a comprehensive set of pretrained models and training instances, we can draw a directed graph that represents the physical dependence taxonomy of various properties across different materials. However, the machine-derived transferability between different material properties is not generally interpretable, and this lack of transparency makes it difficult to gain insights into explainable physicochemical mechanisms, which may be the primary interest of materials science researchers in this context. Recently, there has been increasing activity toward the creation of more transparent and interpretable ML systems, mainly inspired by legal or even ethical requirements, along with growing demand for application of ML to science.54 In the near future, emerging technology for interpretable ML will facilitate scientific understanding behind nontrivial transferability autonomously identified by ML.
Safety
No unexpected or unusually high safety hazards were encountered.
Conclusions and Outlook
We have demonstrated some outstanding successes in transfer learning, along with different application scenarios in materials science. While transfer learning is becoming increasingly popular in various fields of ML, the widespread use of this promising method in materials science has not yet been achieved. The limited availability of openly accessible big data will likely continue in the near future in this community because of the lack of incentives toward data sharing. This problem arises because of the conflicting goals of the diverse stakeholders in academia, industry, and public and governmental organizations. Therefore, transfer learning will be indispensable to the success of ML-centric workflows in materials research.
To boost the power of transfer learning, we have developed an open access library of pretrained models, XenonPy.MDL, which covers a wide variety of materials properties for small organic molecules, polymers, and inorganic compounds. This library is ever-growing. For this first release, the focus was narrowed to specific types of modeling. For example, we used only common molecular fingerprints to describe the structures of organic molecules. However, in recent years, more advanced representation techniques have been developed in related ML research fields, such as graph convolutional neural networks55−57 and the neural fingerprinting algorithm58 (a generalized version of the ECFP). For inorganic compounds, any higher-level features of these materials, such as their temperature dependency and physical, electronic, and magnetic features, have been fully ignored. In addition, only relatively shallow, pyramid-shaped neural networks have been employed in shotgun model production. Use of more diverse types of pretrained models offers more versatility and multidimensionality for material structure representation, which will be the key to a successful transfer learning.
To date, one missing component of traditional ML has been the concept of memory. The process of adapting pretrained models to a novel task seems similar to the scenario where a highly experienced expert implicitly utilizes knowledge or memory acquired in the past to perform a reasonable inference for a considerably less experienced task. Notably, it has been experimentally proven that transfer learning can often increase ML prediction performance to remarkably high levels, even for extremely small data sets. More interestingly, feasible model transitions across different properties and even cross-material adaptations have successfully revealed a dozen nontrivial connections between small molecules and polymers, organic and inorganic chemistry, and properties with unobvious dependency in terms of both observed data and physical theory. Almost all tasks in materials science are more or less connected, with no materials properties being completely independent. This trait facilitates application of transfer learning to this area. Future developments in ML are expected to further expand the applicability and usefulness of transfer learning to materials science.
Acknowledgments
This work was supported in part by the “Materials Research by Information Integration” Initiative (MI2I) project of the Support Program for Starting Up Innovation Hub from the Japan Science and Technology Agency (JST). R.Y. acknowledges financial support from a Grant-in-Aid for Scientific Research (B) 15H02672 and a Grant-in-Aid for Scientific Research (A) 19H01132 from the Japan Society for the Promotion of Science (JSPS). S.W. acknowledges financial support from JSPS KAKENHI (Grant No. JP18K18017). S.J. acknowledges financial support from JSPS KAKENHI Grant No. 19K14902. J.M. acknowledges a partial support by JSPS KAKENHI Grant No. 18H04506.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acscentsci.9b00804.
Figure S1: Prediction–observation plots for current best-performing models in XenonPy.MDL; Figure S2: Chemical structures of the 52 polymers used in the task of predicting Cp; Table S1: List of fingerprint descriptors in the rcdk and RDKit libraries that were used in building the shotgun model library (PDF)
Author Contributions
⊥ H.Y., C.L., S.W., and R.Y. contributed equally to this work.
The authors declare no competing financial interest.
Supplementary Material
References
- Silver D.; et al. Mastering the Game of Go without Human Knowledge. Nature 2017, 550, 354–359. 10.1038/nature24270. [DOI] [PubMed] [Google Scholar]
- Vaswani A.; Shazeer N.; Parmar N.; Uszkoreit J.; Jones L.; Gomez A. N.; Kaiser L.; Polosukhin I. Attention Is All You Need. Adv. Neural Inf. Process Syst. 2017, 5998–6008. [Google Scholar]
- Sutskever I.; Vinyals O.; Le Q. V. Sequence to Sequence Learning with Neural Networks. Adv. Neural Inf. Process Syst. 2014, 2, 3104–3112. [Google Scholar]
- Segler M. H. S.; Preuss M.; Waller M. P. Planning Chemical Syntheses with Deep Neural Networks and Symbolic AI. Nature 2018, 555, 604–610. 10.1038/nature25978. [DOI] [PubMed] [Google Scholar]
- Agrawal A.; Choudhary A. Perspective: Materials Informatics and Big Data: Realization of the “Fourth Paradigm” of Science in Materials Science. APL Mater. 2016, 4, 053208. 10.1063/1.4946894. [DOI] [Google Scholar]
- Gómez-Bombarelli R.; et al. Design of Efficient Molecular Organic Light-Emitting Diodes by a High-Throughput Virtual Screening and Experimental Approach. Nat. Mater. 2016, 15, 1120–1127. 10.1038/nmat4717. [DOI] [PubMed] [Google Scholar]
- Hansen E. C.; Pedro D. J.; Wotal A. C.; Gower N. J.; Nelson J. D.; Caron S.; Weix D. J. New Ligands for Nickel Catalysis from Diverse Pharmaceutical Heterocycle Libraries. Nat. Chem. 2016, 8, 1126–1130. 10.1038/nchem.2587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weiss K.; Khoshgoftaar T. M.; Wang D. A Survey of Transfer Learning. J. of Big Data 2016, 3, 1–40. 10.1186/s40537-016-0043-6. [DOI] [Google Scholar]
- Tan C.; Sun F.; Kong T.; Zhang W.; Yang C.; Liu C.. A Survey on Deep Transfer Learning. arXiv, 2018, https://arxiv.org/abs/1808.01974
- Hutchinson M. L.; Antono E.; Gibbons B.; Paradiso S.; Ling J.; Meredig B.. Overcoming Data Scarcity with Transfer Learning. arXiv, 2017, https://arxiv.org/abs/1711.05099.
- Oda H.; Kiyohara S.; Tsuda K.; Mizoguchi T. Transfer Learning to Accelerate Interface Structure Searches. J. Phys. Soc. Jpn. 2017, 86, 123601. 10.7566/JPSJ.86.123601. [DOI] [Google Scholar]
- Jalem R.; Kanamori K.; Takeuchi I.; Nakayama M.; Yamasaki H.; Saito T. Bayesian-Driven First-Principles Calculations for Accelerating Exploration of Fast Ion Conductors for Rechargeable Battery Application. Sci. Rep. 2018, 8, 5845. 10.1038/s41598-018-23852-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yonezu T.; Tamura T.; Takeuchi I.; Karasuyama M. Knowledge-Transfer Based Cost-Effective Search for Interface Structures: A Case Study on fcc-Al [110] Tilt Grain Boundary. Phys. Rev. Materials 2018, 2, 113802. 10.1103/PhysRevMaterials.2.113802. [DOI] [Google Scholar]
- Kailkhura B.; Gallagher B.; Kim S.; Hiszpanski A.; Han T. Y.-J.. Reliable and Explainable Machine Learning Methods for Accelerated Material Discovery. arXiv, 2019, https://arxiv.org/abs/1901.02717
- Segler M. H. S.; Kogej T.; Tyrchan C.; Waller M. P. Generating Focused Molecule Libraries for Drug Discovery with Recurrent Neural Networks. ACS Cent. Sci. 2018, 4, 120–131. 10.1021/acscentsci.7b00512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cubuk E. D.; Sendek A. D.; Reed E. J. Screening Billions of Candidates for Solid Lithium-ion Conductors: A Transfer Learning Approach for Small Data. J. Chem. Phys. 2019, 150, 214701. 10.1063/1.5093220. [DOI] [PubMed] [Google Scholar]
- Li X.; Zhang Y.; Zhao H.; Burkhart C.; Brinson L. C.; Chen W. A Transfer Learning Approach for Microstructure Reconstruction and Structure-property Predictions. Sci. Rep. 2018, 8, 13461. 10.1038/s41598-018-31571-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaya M.; Hajimirza S. Using a Novel Transfer Learning Method for Designing Thin Film Solar Cells with Enhanced Quantum Efficiencies. Sci. Rep. 2019, 9, 5034. 10.1038/s41598-019-41316-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- https://xenonpy.readthedocs.io/en/latest/tutorials/5-pre-trained_model_library.html (accessed Sep 3, 2019).
- Chen T.; Li M.; Li Y.; Lin M.; Wang N.; Wang M.; Xiao T.; Xu B.; Zhang C.; Zhang Z.. MXNet: A Flexible and Efficient Machine Learning Library for Heterogeneous Distributed Systems. arXiv, 2015, https://arxiv.org/abs/1512.01274.
- https://pytorch.org (accessed Sep 3, 2019).
- Yosinski J.; Clune J.; Bengio Y.; Lipson H. How Transferable are Features in Deep Neural Networks?. Adv. Neural Inf. Process Syst. 2014, 2, 3320–3328. [Google Scholar]
- https://github.com/yoshida-lab/XenonPy (accessed Sep 3, 2019).
- Blum L. C.; Reymond J.-L. 970 Million Druglike Small Molecules for Virtual Screening in the Chemical Universe Database GDB-13. J. Am. Chem. Soc. 2009, 131, 8732–8733. 10.1021/ja902302h. [DOI] [PubMed] [Google Scholar]
- Rupp M.; Tkatchenko A.; Müller K.-R.; von Lilienfeld O. A. Fast and Accurate Modeling of Molecular Atomization Energies with Machine Learning. Phys. Rev. Lett. 2012, 108, 058301. 10.1103/PhysRevLett.108.058301. [DOI] [PubMed] [Google Scholar]
- Ikebata H.; Hongo K.; Isomura T.; Maezono R.; Yoshida R. Bayesian Molecular Design with a Chemical Language Model. J. Comput.-Aided Mol. Des. 2017, 31, 379–391. 10.1007/s10822-016-0008-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim S.; Chen J.; Cheng T.; Gindulyte A.; He J.; He S.; Li Q.; Shoemaker B. A.; Thiessen P. A.; Yu B.; Zaslavsky L.; Zhang J.; Bolton E. E. PubChem 2019 Update: Improved Access to Chemical Data. Nucleic Acids Res. 2019, 47, D1102–D1109. 10.1093/nar/gky1033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmidt M.; Baldridge K.; Boatz J.; Elbert S.; Gordon M.; Jensen J.; Koseki S.; Matsunaga N.; Nguyen K.; Su S.; Windus T.; Dupuis M.; Montgomery J. General Atomic and Molecular Electronic Structure System. J. Comput. Chem. 1993, 14, 1347–1363. 10.1002/jcc.540141112. [DOI] [Google Scholar]
- Gordon M.; Schmidt M. In Theory and Applications of Computational Chemistry: The First Forty Years; Dykstra C., Frenking G., Kim K., Scuseria G., Eds.; Elsevier, Amsterdam, 2005; pp 1167–1189. [Google Scholar]
- Abraham M. J.; Murtola T.; Schulz R.; Pall S.; Smith J. C.; Hess B.; Lindahl E. GROMACS: High Performance Molecular Simulations Through Multi-Level Parallelism from Laptops to Supercomputers. SoftwareX 2015, 1–2, 19–25. 10.1016/j.softx.2015.06.001. [DOI] [Google Scholar]
- Sakuraba S.; Matubayasi N. Ermod: Fast and Versatile Computation Software for Solvation Free Energy with Approximate Theory of Solutions. J. Comput. Chem. 2014, 35, 1592–1608. 10.1002/jcc.23651. [DOI] [PubMed] [Google Scholar]
- Bradley J. C.; Williams A.; Lang A.. Jean-Claude Bradley Open Melting Point Dataset. https://figshare.com/articles/Jean_Claude_Bradley_Open_Melting_Point_Datset/1031637 (accessed Sep 3, 2019).
- Bloch D. Computer Software Review. Review of PHYSPROP Database (Version 1.0). J. Chem. Inf. Model. 1995, 35, 328–329. 10.1021/ci00024a602. [DOI] [Google Scholar]
- http://esc.syrres.com/interkow/EpiSuiteData_ISIS_SDF.htm (accessed Sep 3, 2019).
- Guha R.Chemical Informatics Functionality in R. J. Stat. Softw. 2007, 18. 10.18637/jss.v018.i05. [DOI] [Google Scholar]
- Landrum G.RDKit: Open-Source Cheminformatics; http://www.rdkit.org (accessed Sep 3, 2019).
- Otsuka S.; Kuwajima I.; Hosoya J.; Xu Y.; Yamazaki M. PoLyInfo: Polymer Database for Polymeric Materials Design. 2011. Int. Conf. on Emerg. Intell. Data Web Technol. 2011, 22–29. 10.1109/EIDWT.2011.13. [DOI] [Google Scholar]
- Mannodi-Kanakkithodi A.; Chandrasekaran A.; Kim C.; Huan T. D.; Pilania G.; Botu V.; Ramprasad R. Scoping the Polymer Genome: A Roadmap for Rational Polymer Dielectrics Design and Beyond. Mater. Today 2018, 21, 785–796. 10.1016/j.mattod.2017.11.021. [DOI] [Google Scholar]
- Jain A.; Ong S. P.; Hautier G.; Chen W.; Richards W. D.; Dacek S.; Cholia S.; Gunter D.; Skinner D.; Ceder G.; Persson K. A. Commentary: The Materials Project: A Materials Genome Approach to Accelerating Materials Innovation. APL Mater. 2013, 1, 011002. 10.1063/1.4812323. [DOI] [Google Scholar]
- https://citrination.com (accessed Sep 3, 2019).
- Ju S.; Yoshida R.; Liu C.; Hongo K.; Tadano T.; Shiomi J.. Exploring Diamond-Like Lattice Thermal Conductivity Crystals via Feature-Based Transfer Learning. ChemRxiv, 2019, https://doi.org/10.26434/chemrxiv.9850301.v1. [Google Scholar]
- Seko A.; Togo A.; Tanaka I. In Nanoinformatics; Tanaka I., Ed.; Springer: Singapore, 2018; Vol. 47; pp 3–23. [Google Scholar]
- Meroni S. M. P.; Mouhamad Y.; De Rossi F.; Pockett A.; Baker J.; Escalante R.; Searle J.; Carnie M. J.; Jewell E.; Oskam G.; Watson T. M. Homogeneous and Highly Controlled Deposition of Low Viscosity Inks and Application on Fully Printable Perovskite Solar Cells. Sci. Technol. Adv. Mater. 2018, 19, 1–9. 10.1080/14686996.2017.1406777. [DOI] [Google Scholar]
- Ward L.; et al. Matminer: An Open Source Toolkit for Materials Data Mining. Comput. Mater. Sci. 2018, 152, 60–69. 10.1016/j.commatsci.2018.05.018. [DOI] [Google Scholar]
- Xie T.; Grossman J. C. Crystal Graph Convolutional Neural Networks for an Accurate and Interpretable Prediction of Material Properties. Phys. Rev. Lett. 2018, 120, 145301. 10.1103/PhysRevLett.120.145301. [DOI] [PubMed] [Google Scholar]
- Rogers D.; Hahn M. Extended-Connectivity Fingerprints. J. Chem. Inf. Model. 2010, 50, 742–754. 10.1021/ci100050t. [DOI] [PubMed] [Google Scholar]
- https://list.indiana.edu/sympa/arc/chminf-l/2007-11/msg00058.html (accessed Sep 3, 2019).
- Wu S.; Kondo Y.; Kakimoto M.-a.; Yang B.; Yamada H.; Kuwajima I.; Lambard G.; Hongo K.; Xu Y.; Shiomi J.; Schick C.; Morikawa J.; Yoshida R. Machine-Learning-Assisted Discovery of Polymers with High Thermal Conductivity using a Molecular Design Algorithm. npj Comput. Mater. 2019, 5, 66. 10.1038/s41524-019-0203-2. [DOI] [Google Scholar]
- van Krevelen D. W. In Properties of Polymers; Nijenhuis K. T., Ed.; Elsevier Science, 2009. [Google Scholar]
- Morikawa J.; Junji T.; Hashimoto T. Study of Change in Thermal Diffusivity of Amorphous Polymers during Glass Transition. Polymer 1995, 36, 4439–4443. 10.1016/0032-3861(95)96850-8. [DOI] [Google Scholar]
- Morikawa J.; Hashimoto T. Study on Thermal Diffusivity of Poly(Ethylene Terephthalate) and Poly(Ethylene Naphthalate). Polymer 1997, 38, 5397–5400. 10.1016/S0032-3861(97)00092-X. [DOI] [Google Scholar]
- Esfarjani K.; Chen G.; Stokes H. T. Heat Transport in Silicon from First-Principles Calculations. Phys. Rev. B: Condens. Matter Mater. Phys. 2011, 84, 085204. 10.1103/PhysRevB.84.085204. [DOI] [Google Scholar]
- Esfarjani K.; Stokes H. T. Method to Extract Anharmonic Force Constants from First Principles Calculations. Phys. Rev. B: Condens. Matter Mater. Phys. 2008, 77, 144112. 10.1103/PhysRevB.77.144112. [DOI] [Google Scholar]
- van der Maaten L.; Hinton G. Visualizing Data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Ribeiro M. T.; Singh S.; Guestrin C. Why Should I Trust You?”: Explaining the Predictions of Any Classifier. Proc. of the 22nd ACM SIGKDD Inter. Conf. on Knowledge Discovery and Data Mining 2016, 1135–1144. 10.1145/2939672.2939778. [DOI] [Google Scholar]
- Li Y.; Tarlow D.; Brockschmidt M.; Zemel R.. Gated Graph Sequence Neural Networks. arXiv, 2015, https://arxiv.org/abs/1511.05493.
- Kearnes S.; McCloskey K.; Berndl M.; Pande V.; Riley P. Molecular Graph Convolutions: Moving Beyond Fingerprints. J. Comput.-Aided Mol. Des. 2016, 30, 595–608. 10.1007/s10822-016-9938-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schütt K. T.; Kindermans P.-J.; Sauceda H. E.; Chmiela S.; Tkatchenko A.; Müller K.-R. SchNet: A Continuous-Filter Convolutional Neural Network for Modeling Quantum Interactions. Adv. Neural Inf. Process Syst. 2017, 992–1002. [Google Scholar]
- Duvenaud D. K.; Maclaurin D.; Iparraguirre J. A.; anmd Timothy Hirzel R. G.-B.; Alán Aspuru-Guzik R. P. A. Convolutional Networks on Graphs for Learning Molecular Fingerprints. Adv. Neural Inf. Process Syst. 2015, 2, 2224–2232. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.