Synchrotron-based Nickel Mössbauer Spectroscopy

Abstract

We have used a novel experimental setup to conduct the first synchrotron-based ⁶¹Ni Mössbauer spectroscopy measurements in the energy domain on Ni coordination complexes and metalloproteins. A representative set of samples was chosen to demonstrate the potential of this approach. ⁶¹NiCr₂O₄ was examined as a case with strong Zeeman splittings. Simulations of the spectra yielded an internal magnetic field of 44.6 Tesla, consistent with previous work by the traditional ⁶¹Ni Mössbauer approach with a radioactive source. A linear Ni amido complex, ⁶¹Ni{N(SiMe₃)Dipp}_2, was chosen as a sample with an “extreme” geometry and large quadrupole splitting. Finally, to demonstrate the feasibility of metalloprotein studies using synchrotron-based ⁶¹Ni Mössbauer spectroscopy, we examined the spectra of ⁶¹Ni-substituted rubredoxin in reduced and oxidized forms, along with (Et₄N)₂[⁶¹Ni(SPh)₄] as a model compound. For each of the above samples, a reasonable spectrum could be obtained in about 1 day. Given that there is still room for considerable improvement in experimental sensitivity, synchrotron-based ⁶¹Ni Mössbauer spectroscopy appears to be a promising alternative to measurements with radioactive sources.

Graphical Abstract

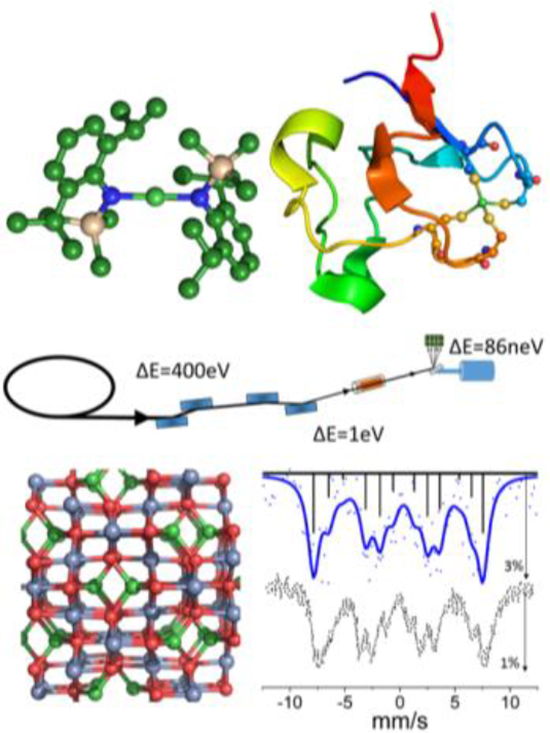
We have performed synchrotron-based ⁶¹Ni Mössbauer spectroscopy in the energy domain on a variety of samples. Our results demonstrate sensitivity to internal magnetic fields (via Zeeman splittings) and sensitivity to coordination geometry (via quadrupole splittings). Our spectra on Ni rubredoxin are the first ever ⁶¹Ni Mössbauer spectra reported for a metalloprotein.

Introduction

Despite the importance of Ni chemistry to materials¹ and battery science,² catalysis,³ inorganic chemistry,⁴ and bioinorganic chemistry,^5–7 there are relatively few reports on ⁶¹Ni Mössbauer spectroscopy. Specifically, there are tens of thousands of papers reporting the application of ⁵⁷Fe Mössbauer spectroscopy, while the ⁶¹Ni Mössbauer literature can be counted in the dozens. The reason for this discrepancy is clear – compared to ⁵⁷Fe experiments, traditional Mössbauer spectroscopy using the ⁶¹Ni 67.4 keV nuclear resonance is logistically difficult.⁸ The most appropriate parent isotopes, ⁶¹Co or ⁶¹Cu, have lifetimes of 99m or 3.3h respectively, requiring that experiments be done with frequent source changes and in close proximity to proton cyclotrons or electron accelerators where the sources are produced.^8–11

Time-domain approaches using synchrotron radiation¹² can in principle yield the same information as energy domain Mössbauer experiments. For example, nuclear forward scattering (NFS) has been used to study Ni metal at low temperatures¹³ and under high pressure,¹⁴ and synchrotron radiation perturbed angular correlation (SRPAC) measurements on Ni metal have also been successful.¹⁵ However, the interpretation of such time-domain measurements is not always straightforward, especially for mixtures. The popularity of ⁶¹Ni nuclear spectroscopy would certainly benefit from a better energy domain experiment that can be interpreted by standard Mössbauer procedures. Improvements in synchrotron x-ray generation and detection have recently made just such an experiment possible.

Energy-domain synchrotron radiation Mössbauer spectroscopy (SR-MS), first proposed in 1974,¹⁶ was first conducted in 1985¹⁷ using an ⁵⁷Fe-yttrium iron garnet nuclear Bragg diffraction monochromator.¹⁷ Monochromator development continued with work using a single line ⁵⁷FeBO₃ monochromator.^18,19 However, this diffraction approach requires near perfect isotopically-enriched single crystals with favorable magnetic properties,^17,20–22 and until now has only been achieved with ⁵⁷Fe. An alternate approach to SR-MS uses a moderately monochromatic synchrotron beam as the source, and a single line Mössbauer isotope as analyzer (Scheme 1). It was first demonstrated in 2009 by Seto and coworkers on ⁵⁷Fe and ⁷³Ge.²³ It has since been applied to ¹⁵¹Eu,^{24 174}Yb,^{25 125}Te,²⁵ and ⁴⁰K,²⁶ and it has been proposed for nearly 2 dozen lanthanide isotopes.²⁵ Recently, Seto and coworkers have applied ⁶¹Ni SR-MS to cathode materials²⁷ and nanoparticles.²⁸ This SR-MS approach is well suited to nuclei with lifetimes shorter than the typical ~10–100 ns electron bunch spacing in a synchrotron i.e. the time between radiation pulses.

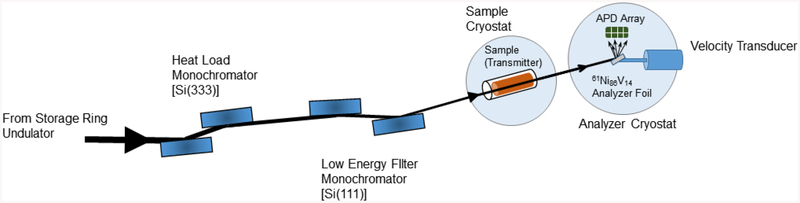
Scheme 1.

The synchrotron radiation Mössbauer spectroscopy (SR-MS) experiment.

The ⁶¹Ni nucleus, with an excited state t_1/2=5.27 ns, is an excellent candidate for SR-MS. Since ⁶¹Ni Mössbauer is relatively unfamiliar to chemists, we first compare the spectroscopic properties of this isotope with the more familiar ⁵⁷Fe. The key nuclear properties are summarized in Table 1, and we briefly discuss some of the spectroscopic consequences below.

Table 1.

Comparison of Mössbauer-relevant nuclear properties for ⁵⁷Fe and ⁶¹Ni.

	abundance (%)	E (keV)	t1/2 (ns)	2Γ (mm*s−1)	Ig	Ie	αt	μg (n.m.)	μe (n.m.)	Qg (barn)	Qe (barn)
57Fe	2.14	14.41	97.81	0.194	1/2−	3/2−	8.21	0.0906	−0.155	--	0.16
61Ni	1.19	67.40	5.27	0.77	3/2−	5/2−	0.12	−0.749	0.481	0.162	−0.2

Lifetime and energy.

The most obvious differences between ⁶¹Ni and ⁵⁷Fe are the energy and lifetimes of the first excited states. The long lifetime (98 ns) and low energy (14.4 keV) of the ⁵⁷Fe excited state lead to a natural linewidth 2Γ of 9.1 neV, while the shorter lifetime (5.3 ns) and higher energy of the ⁶¹Ni resonance (67.4 keV) lead to spectral features with a linewidth of 173 neV, nearly a factor of 20 broader.

Isomer shift (δ_IS).

For ⁶¹Ni, there is a smaller change in nuclear mean square radius (Δ<r²>/<r²>) and higher transition energy, and these lead to a significant reduction in the ⁶¹Ni isomer shift range, especially when expressed in terms of mm/s Doppler shift. Whereas common ⁵⁷Fe δ_IS values vary from −0.8 to +2.0 mm/s,⁹ the range for ⁶¹Ni δ_IS is about 30-fold smaller, from −0.06 to +0.04 mm/s.²⁹ This is more than an order of magnitude smaller than the natural linewidth 2Γ = 0.77 mm/s. Moreover, the high energy for this transition (67.4 keV) requires corrections for 2^nd order Doppler shifts (SOD) that are of comparable magnitude to the real chemical isomer shifts.²⁹ Although such corrections are possible if the lattice dynamics are well understood, as described by Gütlich,²⁹ that author has noted that so far, “the information concerning chemical bond properties was not very impressive.”²⁹ For these reasons, in this work we have not tried to exploit ⁶¹Ni isomer shifts (although others might do so in the future).

Magnetic properties.

The ⁶¹Ni nucleus has favorable magnetic properties. It has relatively large magnetic moments in its ground and excited states, μ_g = −0.75 and μ_e = 0.48 nuclear magnetons (n.m.),²⁹ compared to μ_g = +0.09 and μ_e = −0.15 n.m. for ⁵⁷Fe (Table 1). Previous work with mixed spinel type oxides, such as Cu_0.9Ni_0.1Cr₂O₄, exhibited very large splitting of ±13.6 mm/s.³⁰ Since many of the interesting problems in Ni chemistry can be framed as questions about magnetic properties, this makes observation of Zeeman splittings in ⁶¹Ni Mössbauer spectra one of the most promising applications.

Quadrupole splittings.

For ⁵⁷Fe, the transition is from I=1/2→I=3/2. Since only the excited state is split by an electric field gradient, ⁵⁷Fe Mössbauer often presents a symmetric doublet spectrum. The ⁶¹Ni resonance involves an I=3/2→I=5/2 transition. The quadrupole splitting is more complex, as the ground state (I=3/2) and excited state (I=5/2) yield two and three states respectively (Figure S1) for five non-forbidden transitions. Although the five transitions for ⁶¹Ni are not usually resolved, they can in principle provide more robust information than ⁵⁷Fe through the asymmetry of the quadrupole split spectrum (for axial systems), which is characterized by the sign of the V_zz component of the EFG and the asymmetry parameter η.

In this study we recorded SR-MS on a ferromagnetic nickel spinel – ⁶¹NiCr₂O₄, two coordination complexes with respectively linear and tetrahedral geometries – ⁶¹Ni[N(SiMe₃)C₆H₃-2,6-Pr₂]₂ and (Et₄N)₂[⁶¹Ni(SPh)₄], and a Ni protein – Ni-substituted rubredoxin. The data for these samples showcases the sensitivity of ⁶¹Ni SR-MS to the Ni internal magnetic hyperfine field, as well as to both the magnitude and the sign of the electric field gradient (EFG). The results also demonstrate that the SR-MS can be used on dilute samples such as Ni proteins – the technique should eventually be useful for catalytic studies of hydrogenase, which contain NiFe in their active site.

Experimental Methods

Synthesis of NiCr₂O₄.

⁶¹NiCr₂O₄ (1) was produced from 99% enriched ⁶¹Ni (Isoflex) and Cr₂O₃ powders. Following a previously established procedure, the two powders were mixed in an agate mortar and sintered twice in a conventional vertical furnace at atmospheric pressure and 1200° C for 24h in air.³¹ The sample composition was confirmed by powder x-ray diffraction.

Synthesis of ⁶¹NiBr₂(OEt₂).

In a Schlenk flask, ⁶¹Ni metal (0.051 g, 0.84 mmol) in ca. 10 mL Et₂O and excess Br₂ (1.36 g, 8.51 mmol) were added via a syringe.³² The reaction mixture was stirred for 16 h without light. The insoluble ⁶¹NiBr₂(OEt₂) was allowed to settle and filtered through a filter cannula. The residue was washed twice with Et₂O and dried under vacuum to afford 0.206 g (0.699 mmol) of ⁶¹NiBr₂(OEt₂).

Synthesis of ⁶¹Ni{N(SiMe₃)Dipp}₂.

⁶¹Ni{N(SiMe₃)Dipp}₂, (2) (where Dipp= C₆H₃-2,6-ⁱPr₂). 0.375 g (1.47 mmol) LiN(SiMe₃)Dipp and 0.206 g (0.699 mmol) ⁶¹NiBr₂(OEt₂) were combined as solids in a Schlenk flask and 30 mL of Et₂O was added at ca. 0 °C.³³ The reaction mixture quickly turned purple and was allowed to warm to room temperature and stirred for 18 h. All volatile material was removed under vacuum, and the residue was extracted with ca. 30 mL of pentane. The solution was filtered through a filter cannula, and the filtrate was concentrated to incipient crystallization. Storage at – 80 °C for 1 day afforded 0.172 g (0.308 mmol) of crystals.

Synthesis of [Et₄N]₂[⁶¹Ni(SPh)₄].

[Et₄N]₂[⁶¹Ni(SPh)₄] (3) was prepared as described previously,³⁴ with the following modifications: ⁶¹Ni-labeled (Et₄N)₂(NiCl₄) was used as a reagent; [Et₄N]₂[NiCl₄] and [Et₄N]SPh were combined in acetonitrile rather than propionitrile and stirred for 4 h at room temperature, isolated by filtration and then washed with cold acetonitrile.

⁶¹Ni-substituted rubredoxin purification and preparation.

Pyrococcus furiosus rubredoxin (Pf Rd) was isolated and purified according to Jenney and Adams.³⁵ The Ni form of Pf Rd (Ni Rd) was prepared essentially according to Moura et al.³⁶ except that ⁶¹Ni powder was dissolved in aqua regia, then neutralized with NaOH before addition to the denatured protein. Oxidized protein was prepared by treatment with 5 mM K₃[Fe(CN)₆], which was removed by buffer exchange. The samples were prepared by exchange into Tris buffer (100 mM, pH 8.5) and by repeated concentration/dilution using a Centricon® YM3 concentrator (Amicon). The final sample concentrations were 5–6 mM. Reduced samples contained 10 mM dithionite.

Synchrotron-based ⁶¹Ni Mössbauer Spectroscopy.

Samples were prepared in 2.0 mm inner diameter (ID) quartz tubes (for compounds 1, 2 and 3) or 1.45 mm ID (for rubredoxins). The outer diameter was 3 mm. The path lengths were 2 mm for 1, 2 cm for 2 and 3, and 10 cm for the rubredoxin samples. The longer path length for the rubredoxin samples helped compensate for the lower ⁶¹Ni concentrations. We note that the small divergence of a synchrotron beam allows the use of long narrow capillaries that would not be practical with radioactive sources (because extreme collimation would reduce the flux throughput from a radioactive source.)

The quartz sample cells were placed inside a 1 cm × 1 cm × 20.2 cm Cu block, which contained a cavity with a diameter of 3.3 mm. A temperature probe was attached to the surface of the cold-finger. The entire setup was shielded by a second Cu case with Al foil windows, which allowed for temperatures as low as 5 K.

All of the spectra were recorded using the approach illustrated in Scheme 1. The SPring-8 storage ring was running in the A bunch mode with 203 bunches spaced at 23.6 ns and a total current of 100 mA. Measurements (except for compound 3) were taken at BL19LXU, where the synchrotron radiation comes from a 27m undulator,^37,38 and the experimental setup was similar to that previously described.²³ The spectrum for 3 was collected at BL09XU with a 4.5 m long standard undulator and an otherwise identical setup.^39,40 The 9^th undulator harmonic was first monochromated by a Si(333) high heat load monochromator, followed by a Si(111) low energy filtering monochromator yielding a bandwidth of 2.3 eV with a flux of 2.2×10¹¹ photon s−¹ (4.3 eV with a flux of 1.0×10¹¹ photon s−¹ for BL09XU) at 67.4 keV. The radiation impinged on the sample in the cold finger, and the transmitted photons then passed to a second cryostat containing a ⁶¹Ni_0.86V_0.14 analyzer foil mounted onto a velocity transducer. The radiative decay of the analyzer including photons and electrons, through nuclear fluorescence and internal conversion, was captured by an 8-element Si avalanche photodiode (APD) array. The APDs were gated to restrict the collection time to between 3 ns and 18 ns after the prompt pulse to discriminate against electronic scattering unrelated to the Mössbauer effect. The resulting spectrum is a function of the analyzer Doppler velocity, and is nearly identical to a conventional Mössbauer spectrum.

The spectra were simulated using a mixed magnetic and quadrupole Hamiltonian as implemented in the MossWinn software.^41–43 Fitting parameters can be found in Tables S1, S2, S3, and S4.

Results

⁶¹NiCr₂O₄.

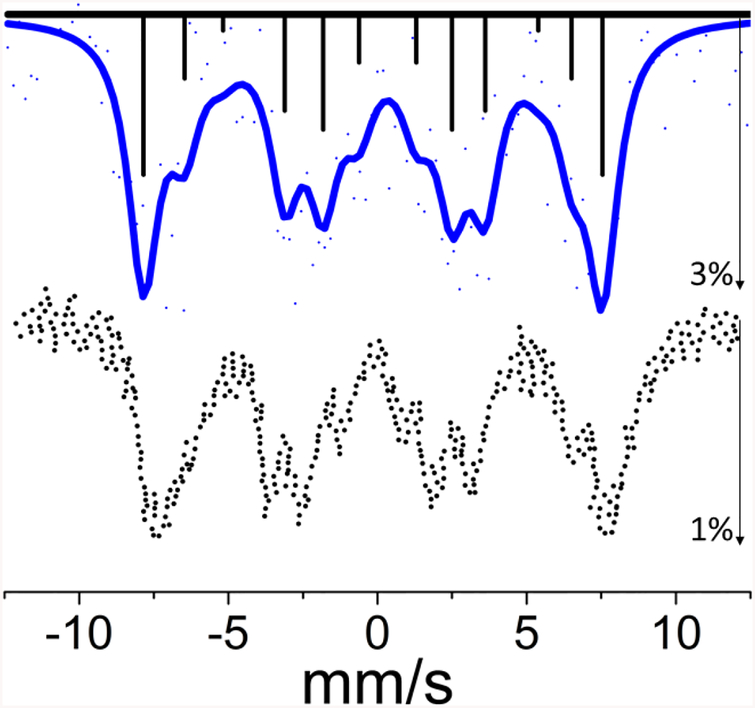
Our synchrotron Mössbauer spectrum for 1 is shown in Figure 1. It exhibits a well-resolved Zeeman splitting indicating a significant internal magnetic field in this ferromagnetic sample, which is a spinel with high-spin Ni(II) in the tetrahedral sites. There are 12 magnetically split transitions for ⁶¹Ni and the spectrum can be described as four sets of three partially resolved lines. The fit was fixed to an axial EFG as in previous studies.^44,45 The fit yielded an internal hyperfine magnetic field of 44.6 T, in agreement with the value (44.5 T) from previous Mössbauer studies using radioactive ⁶¹Co in a ⁶²Ni_0.85Cr_0.15 source that was activated by bremsstrahlung.⁴⁶ V_zz was fit to 7.23 V/m², however the fit was largely invariant of the V_zz value due to the quality of the data and the small effect of the EFG relative to the large internal magnetic field.

Figure 1.

Top: The experimental SR-MS spectrum of NiCr₂O₄ powder (points) and a simulation (solid line) using an internal hyperfine field of 44.6 T. The pattern of four sets of three partially resolved magnetic hyperfine lines results from Zeeman splitting of I=3/2 ground state and I=5/2 excited state. The sticks represent individual transition contributions, solid line represents the fit and dots indicate actual data. The maximum intensity decrease was about 3%. Bottom: a recreation of the previously reported spectrum obtained with a radioactive source.⁴⁶

⁶¹Ni{N(SiMe₃)Dipp}₂.

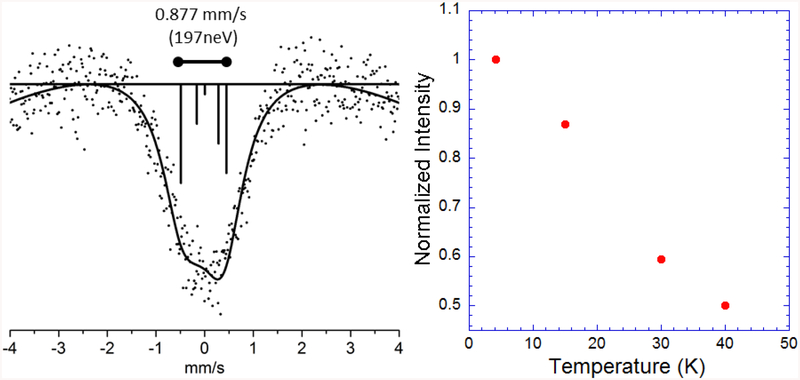
The spectrum for 2 at 4.2K is broad and asymmetric (Figure 2). The spectrum was fit with an axial EFG (Table S2), and from this simulation we found that the asymmetry can be explained by a strong quadrupole splitting with a V_zz EFG component of 11.53×10²¹ V/m² at 4.2K (The eQV_zz value for the ground state in mm/s is provided in Table S2)_. We also examined the temperature dependence of the spectral intensity, by taking additional data at 15K, 30K, and 40K (Figure 2 and Figure S4). The rapid decline in intensity with increasing temperature illustrates the importance of the Lamb-Mössbauer factor for this high-energy transition and underlines the importance of conducting experiments at near LHe temperatures. Since linear Ni(II) complexes show pronounced changes in magnetic properties between 4K and 40K,⁴⁷ the possible relevance of variable Zeeman splittings should be considered for detailed interpretation of the temperature dependent spectra. We decided that better signal-to-noise is required for such an analysis.

Figure 2.

Left: The ⁶¹Ni Mössbauer spectrum for the linear nickel complex 2. The solid line represents the fit and the vertical lines represent the energy and relative intensity of the individual transitions. The distance between the furthest transitions is shown above the spectrum in mm/s and neV. Right: A plot of the of the normalized integrated intensity for 4.2K, 15K, 30K, and 40K relative to the 4.2K integrated intensity.

⁶¹Ni-Substituted Pf Rubredoxin and 3.

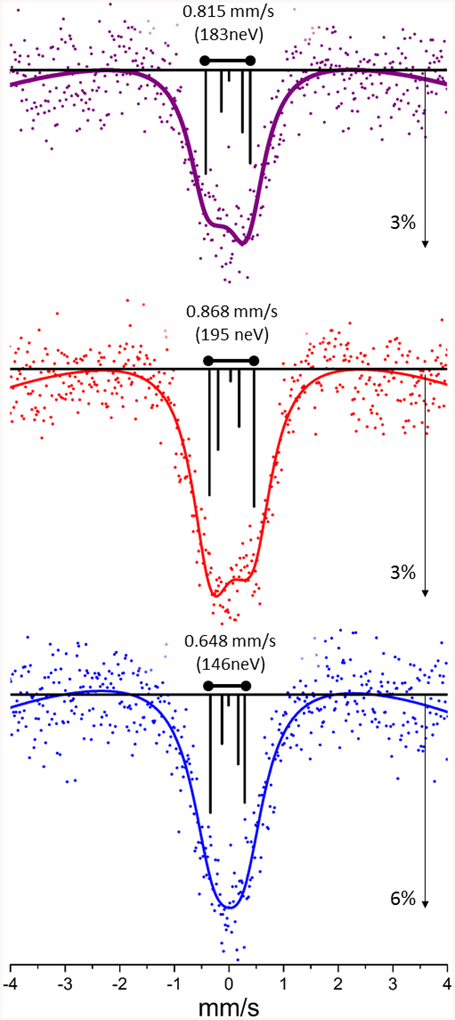
The ⁶¹Ni Mössbauer spectra for reduced and oxidized Ni Rd are compared with 3 in Figure 3 and fit parameters can be found in Table S3. The high quality of the spectra allowed them to be fit with a curved baseline to capture some of the well-known time window effect inherent in delayed coincidence Mössbauer and SR-MS.^48,49 The simulation for reduced Ni Rd resulted in a negative value for the V_zz component of the EFG, −11.2 × 10²¹V/m² (η=0.24). In contrast, the oxidized rubredoxin data were best simulated with a positive V_zz component, however a large asymmetry parameter, (7.6 × 10²¹V/m² η=0.83), consistent with higher spherical symmetry of the EFG than the reduced sample. The spectrum for 3 was best simulated by a V_zz component of 10.8 × 10²¹V/m² (η=0.000). Our results cannot exclude modest magnetic effects from a slow paramagnetic relaxation and alternative fits are supplied in Table S4.

Figure 3.

Top to bottom: ⁶¹Ni SR-MS spectra for 3, reduced, and oxidized ⁶¹Ni Pf Rd. The sticks represent individual transition contributions to the simulation using parameters from Table S3.

Discussion

In this work, we have reported the first energy domain synchrotron Mössbauer spectra for ⁶¹Ni coordination complexes and metalloproteins, with samples chosen for extremes of Zeeman splitting, quadrupole splitting, or dilution. Our first sample was nickel chromite, NiCr₂O₄, 1. This is a normal spinel with high-spin Ni²⁺ in the tetrahedral A sites and Cr³⁺ in the octahedral B sites. Apart from applications as an NOx sensor, a high emissivity coating, and as a catalyst, it has a rich variety of structural and magnetic phase transitions.³¹ For our current purposes, it served as a test for the ability of SR-MS to span a wide range of resonances caused by a large Zeeman splitting.

As was documented in Figure 1, our instrument was capable of recording Zeeman splittings out to ±10 mm/s, which arise from the internal magnetic field of ~44.6 T. The signal-to-noise could certainly have been improved with more beam time. However, an unexpected benefit of the wide range of the data was that the magnetic field derived from a least squares refinement was tightly constrained by the intensity in the wings of the spectrum and in good agreement with the previous result of 44.5 T.⁴⁶ In the future, SR-MS will be a useful probe of magnetic properties.

Our second sample was ⁶¹Ni{N(SiMe₃)Dipp}₂, 2, a high-spin linear Ni(II) complex. It belongs to a class of 2-coordinate open-shell transition metal complexes with interesting magnetic and catalytic properties (see⁵⁰ for references). For our current purposes this served as a system likely to have a strong quadrupole splitting. Although we could not resolve discrete transitions, we observed a strong asymmetry in the ⁶¹Ni Mössbauer spectrum for 2, especially at ~4.2K (Figure 2). The magnitude and sign of V_zz derived from the simulation (+11.5×10²¹ V/m²) is consistent with our predicted value. For 2, using the d-electron orbital energy order described previously,³³ the expectation value prediction of V_zz=+(4/7)e<r−³>_3d. However, it is important to note, for the interpretation of real data the sign of V_zz loses meaning as η approaches unity. Our attempts to record and interpret the temperature dependence of the spectra for 2 were less convincing. The signal dropped more than 3-fold between 4 and 40 K, illustrating the dramatic temperature dependence of the Lamb-Mössbauer factor at 67.4 keV .

Our final set of samples consisted of Ni(II) and Ni(III) Pf rubredoxin (Ni Pf Rd) and the model compound 3. In the small (6 kDa) Pf Rd protein, the natural Fe center has been replaced with Ni, yielding a high-spin Ni(II) center with four cysteine thiolate ligands in an elongated tetrahedral conformation.⁵¹ The Ni site bears some resemblance to the active site Ni in NiFe H₂ases, where the Ni also has 4 cysteine ligands, two of them bridged to Fe.⁵² Ni(II) Pf Rd can be oxidized to Ni(III) with ferricyanide,⁵³ and based on similar EPR signals, oxidized Ni Rd has been proposed as a model for the electron paramagnetic resonance (EPR) active Ni-C form of [NiFe] hydrogenases.⁵¹ It was recently shown that Ni Pf Rd shows high hydrogen turnover frequencies (20−100 s⁻¹), admittedly with a large overpotential of 540mV.⁵⁴ Our final sample, 3 has been proposed as a model for Ni(II) Rd, as it also has a high-spin Ni(II) with distorted tetrahedral thiolate ligation.⁵⁵ For 3, the distortion is an axial compression as opposed to the elongation in Ni(II) Pf Rd. For our current purposes, although interesting in their own right, these three samples are also obvious stepping stones to ⁶¹Ni Mössbauer of NiFe H₂ases and other Ni enzymes.

As mentioned in the Introduction, ⁶¹Ni has quadrupole moments of 0.16 and −0.20 barns respectively for the I=3/2 ground and I=5/2 nuclear excited states. This leads to five allowed transitions in a purely quadrupole split spectrum (Supporting Information Figures S1 and S2). Using a single electron approximation for d-electrons and a simple crystal field model, as discussed previously,²⁹ we can predict the sign of the expectation value for V_zz based on geometry. Using such a model, the prediction for a tetragonally elongated geometry becomes V_zz=-(8/7)e<r−³>)_3d. A tetragonally compressed Ni(II) complex is predicted by the same procedure to have V_zz=+(4/7)e<r−³>_3d. The net result for a tetrahedral system with an axial elongation is a stronger Mössbauer signal at high mm/s, while the converse results for a tetrahedral system with an axial elongation.

For the approximately tetrahedral Ni(II) site in Pf Rd, we observed an asymmetry in the spectral envelope (a greater dip in transmission at lower mm/s) (Figure 3). In contrast, for 3 there is also an asymmetric envelope, but this time with a greater dip in transmission at lower high mm/s. These results indicate an elongated tetrahedral distortion in Ni(II) Rd and an axial compression in 3. Such findings are consistent with the results from optical MCD spectroscopy,⁵⁵ Raman,⁵⁶ and the crystal structures⁵⁷. The structural predictions are less clear for the Ni(III) sample, where we saw a loss in the asymmetry of the Mössbauer transmission. This argues for a more spherically symmetric EFG, perhaps due to a combination of geometrical effects and a different electronic configuration.⁵¹ A high-resolution crystal structure could test this hypothesis.

Overall, we find that despite the limited resolution for ⁶¹Ni, quadrupole effects can produce a useful broadening and asymmetry of the overall spectral envelope. The asymmetry can in turn be used to determine the sign of V_zz for axial systems and thus make predictions about the type of asymmetry at the Ni site.

Summary

Overall, we have demonstrated that ⁶¹Ni SR-MS can be an effective tool in studying the magnetic properties and local geometries of ⁶¹Ni sites in solid-state materials, coordination complexes and in Ni metalloproteins. For such dilute samples, the small spot size and low divergence of a synchrotron source are an important factor. One can use cylindrical samples that are several cm long and yet only one mm in diameter, allowing for modest volumes of precious enzymes. Such a sample configuration is not possible with radioactive sources because of the large source size and divergence. As is usual with synchrotron-based experiments, there is still room for significant improvement in this technique, through brighter sources as well as faster and more efficient detectors. For energy domain experiments, ⁶¹Ni SR-MS should thus be a strong competitor to the conventional approach with radioactive sources. At synchrotron sources around the world, both energy- and time-domain nuclear techniques promise exciting opportunities for learning more about Ni chemistry through the special properties of ⁶¹Ni.