Bayesian Models for Detecting Difference Boundaries in Areal Data

Abstract

With increasing accessibility to Geographical Information Systems (GIS) software, researchers and administrators in public health routinely encounter areal data compiled as aggregates over areal regions, such as counts or rates across counties in a state. Spatial models for areal data attempt to deliver smoothed maps by accounting for high variability in certain regions. Subsequently, inferential interest is focused upon formally identifying the “diffrence edges” or “ difference boundaries” on the map, which delineate adjacent regions with vastly disparate outcomes, perhaps caused by latent risk factors. We propose nonparametric Bayesian models for areal data that can formally identify boundaries between disparate neighbors. After elucidating these models and their estimation methods, we conduct simulation experiments to assess their effectiveness and subsequently analyze Pneumonia and Influenza hospitalization maps from the SEER-Medicare program in Minnesota, where we detect and report highly disparate neighboring counties.

1. Introduction

With increasing accessibility to Geographical Information Systems (GIS), researchers and administrators in public health are increasingly encountering areal datasets that are aggregated as case counts or rates over areal units or regions (e.g. counties, census-tracts or ZIP codes). This is common practice in public health for protecting patient privacy.

Statistical models for areal data can adjust for known causes of variability in the data and also for sparsely sampled regions by smoothing across and borrowing information from its spatial neighbors (see, e.g., Anselin, 1988; Le Sage and Pace, 2009; Banerjee et al., 2004). An especially pertinent issue is to ascertain statistically significant differences among neighboring regions, hence identifying spatial barriers or difference boundaries that delineate them. Ultimately, the underlying influences responsible for these boundaries or barriers are typically of scientific and administrative interest. This ‘boundary’ detection problem is often referred to as “wombling”, after a foundational article by Womble (1951). While statistical boundary analysis has been applied extensively to point-referenced and gridded (or lattice) data (see, e.g., Banerjee and Gelfand, 2006), formal statistical inference in areal contexts present unique challenges that we outline later.

Deterministic areal wombling is often carried out using algorithms (Jacquez and Greiling, 2003a, 2003b) that are fast and straightforward to implement but fail to account for sources of uncertainty, such as extremeness in counts and rates corresponding in thinly populated regions. Li, Banerjee and McBean (2011) proposed statistical learning for boundaries using the Bayesian Information Criterion. In hierarchical model based approaches, Lu and Carlin (2004), Lu et al. (2007) and Ma, Carlin and Banerjee (2009) investigated estimating the adjacency matrix within a hierarchical framework using priors on the edges. However, inference from these models are usually highly sensitive to prior specifications on certain parameters.

Our primary contribution is a method to deliver inference for areally aggregated health outcome data, including assessment of difference boundaries, using classes of more flexible and robust nonparametric Bayesian hierarchical models. Section 2 offers a brief exposition to models for areally referenced count data. Section 3 elucidates the key issues in areal boundary analysis and our Bayesian nonparametric modeling approaches. Sections 4 and 5 discuss, respectively, a simulation study and the analysis of a Minnesota Pneumonia & Influenza (P & I) dataset to detect spatial health barriers between neighboring counties in Minnesota. Finally, Section 6 concludes the article with an eye towards future work.

2. Hierarchical Models for Areal Data

Areal data can be analyzed using Bayesian hierarchical models that incorporate geographical effects. For example, let Y_i (random) be the observed number of patients who underwent a specific preventive or clinical outcome in areal unit i, i = 1, … , n, and let E_i (fixed) be the expected number of outcomes for that unit. A commonly used likelihood is

$$Y_i\stackrel{ind}{\sim }Poisson(E_i{e}^{{\mu }_i}),i=1,\dots ,n,$$ (2.1)

where ${\mu }_i={\mathbf{x}}_i^{\prime }\beta +{\varphi }_i$ represents the log-relative risk, estimates of which are often based on the departures of observed from expected counts, x_i includes explanatory, region-level covariates or predictors for region i and β are the corresponding regression coefficients.

Each φ_i represents the spatial random effect associated with region i, which is often modeled using Markov random fields (e.g. Cressie, 1993; Banerjee et al., 2004, Ch.3) that imply the following joint distribution for φ = (φ₁, φ₂, … , φ_n)′:

$$\varphi \sim N_n\left(0,{\sigma }^2(D-\rho W{)}^{-1}\right),$$ (2.2)

where N_n denotes the n-dimensional normal distribution, D is a n×n diagonal matrix with diagonal elements m_i equal to the number of neighbors of area i, and W = {w_ij} is the adjacency matrix for the map, i.e., w_ii = 0, and w_ij = 1 if i is adjacent to j and 0 otherwise. In the joint distribution (2.2), σ² is the spatial dispersion parameter, and ρ is a spatial autocorrelation parameter. We denote this distribution concisely as CAR(ρ, σ²). A sufficient condition for D – ρW to be positive definite is that ρ ∈ (1/λ₍₁₎, 1), where λ₍₁₎ is the minimum eigenvalue of W (Banerjee et al., 2004).

The CAR model has been especially popular in Bayesian inference as its conditional specification is convenient for Gibbs sampling and MCMC schemes. The distribution in (2.2) reduces to the well-known intrinsic conditionally autoregressive (ICAR) prior if ρ = 1, or an independence model if ρ = 0. The ICAR model induces “local” smoothing by borrowing strength from the neighbors, while the independence model assumes independence of spatial rates and induces “global” smoothing. The smoothing parameter ρ in the CAR prior (2.2) controls the strength of spatial dependence among regions, though it is well-appreciated that a fairly large ρ may be required to deliver significant spatial correlation.

3. Bayesian Nonparametric Models for Areal Data

3.1. Modelling considerations for areal boundary analysis

Areal boundary analysis can be approached from different perspectives. For example, Li et al. (2011) treat the problem as one of statistical learning for the edges, where each model represents a different boundary hypothesis. Emphasizing speed of execution and ease of use, they consider a leave-one-edge-out mechanism, where each model has exactly one geographical boundary omitted from the adjacency matrix. This fails to account for the joint effects of the edges and what impact deleting one may have on the other.

More generally, one can consider models varying in their specification of the neighborhood matrix W that controls spatial smoothing. However, now we encounter an explosion in the number of models. To be precise, if W is the original geographical map, we have 2^1′W1/2 models to compare, where 1′ = (1, 1, … , 1). This will require sophisticated MCMC model composition or MC³ algorithms or other types of stochastic variable selection algorithms for selecting models (see, e.g., Hoeting et al., 1999). These methods become computationally intensive and unconducive to learning about edge effects in relatively large maps. Moreover, they work well in selection of regressors; here we are interested in choosing spatial precision matrices. Li et al. (2012) reformulate this problem as one of Bayesian hypothesis testing within a class of spatial moving average models and adjust multiple tests using false discovery rates. The method, though still computationally intensive is competitive, and will form a benchmark for our current work in the simulation studies.

A different approach seeks to estimate the adjacency matrix within a hierarchical framework using priors on the adjacency relationships. These involve incorporating “edge effects”, i.e. random effects corresponding to the edges, in addition to regional effects. These edge effects would be modelled by another CAR model, or some other MRF, leading to rather complex site-edge models (Ma et al., 2010). However, these models often involve weakly identifiable parameters that are difficult to tune causing the MCMC algorithms to be substantially slower in converging to the desired posterior distributions.

Instead of incorporating random “edge effects”, we explore an alternative stochastic mechanism that allows us detect difference boundaries by considering probabilities such as P(φ_i = φ_j ∣ i ~ j). Clearly, continuous priors for the φ_i’s will not work as they will render P(φ_i = φ_j ∣ i ~ j) = 0. A nonparametric Bayesian framework that models the spatial effects as almost surely discrete realizations of some distribution comes to mind – the Dirichlet process (Ferguson, 1973) presents itself as a natural choice, but how do we accommodate spatial (areal) dependence? We addresses this issue in the subsequent sections.

3.2. Dirichlet process mixture (DPM) models for clustered data

In the context of (2.1) and (2.2), a Dirichlet process mixture (DPM) prior specifies φ_i ~ G, where G ~ DP(α, G₀) is some unknown distribution modeled as a Dirichlet process (DP) with baseline measure G₀ (e.g., Ferguson, 1973). Blackwell and MacQueen (1973) related the Dirichlet process to a generalized Polya urn scheme that leads to effective sampling strategies if given an explicit and simple prediction rule.

The stick-breaking representation of the DP (Sethuraman, 1994) says that a draw from the Dirichlet process can be written as $G(\cdot )={\sum }_{i=1}^{\infty }{p}_i{\delta }_{{\theta }_i}(\cdot )$ a.s., where δ_θi is the Dirac measure (point mass) located at θ_i, each θ_i is a random draw from the base distribution G₀, and $p_i=V_i{\prod }_{l=1}^{i-1}(1-V_l)$ with p₁ = V₁, where each $V_i\stackrel{\mathit{iid}}{\sim }$ Beta(1, α). The p_i’s are called the “stick-breaking” weights (their infinite sum equals 1) and the θ_i’s are called atoms. In practice, the infinite sum is often replaced by the sum of the first N(N ⩽ n) terms, since the probability mass in each term decays rapidly. We can simply let V_N = 1 to truncate the sum to finite terms (Ishwaran and Zarepour, 2000). Many authors simply choose N to be a number large enough that there exists some empty components during the MCMC run or by examining the size of the last weight p_N under the prior. Following Reich and Fuentes (2007), we choose N according to the latter (see Section 4). For concerns regarding truncation bias, exact sampling can be executed using slice-sampling (Kalli, Griffin, and Walker, 2011).

The stick-breaking representation is an extremely rich framework that subsumes DP’s and other extensions (e.g. MacEachern, 2001) such as Dependent Dirichlet processes (DDP)’s. In fact, for every conceivable joint distribution on the stick-breaking weights and the atoms, there is associated a stick-breaking stochastic process. Introducing dependence is now natural. For example, the DDP introduces dependence through the stick-breaking weights and the atoms. De Iorio et al (2004) used the dependent Dirichlet process to define the desired dependence across the related random distributions in any ANOVA-type models. Gelfand Kottas and MacEachern (2005) used DDP on geostatistical data and introduced spatial dependence through an underlying base measure, where $G\sim \mathit{DP}(\alpha ,G_0^{(n)})$ and $G_0^{(n)}$ is a Gaussian process with a given covariance structure. Alternatively, Griffin and Steel (2006) proposed an order-based DDP which include dependence on predictors by permutation of elements in stick-breaking priors. Variants include kernel stick-breaking processes by Dunson and Park (2008) and the probit stick-breaking process by Chung and Dunson (2009). Spatial Dirichlet process (SDP) mixture models (Gelfand, Kottas and MacEachern, 2005) are defined on a space of surfaces that yields almost surely discrete realizations with countable support. Duan, Guindani and Gelfand (2007) extended the SDP by allowing different surface selection at different sites. Reich and Fuentes (2007) develop a spatial stick-breaking prior (SSB) to analyze hurricane surface wind fields.

The aforementioned work do not, however, apply to areal data. Our need to move into DP’s (and their extensions) is even more fundamental – accommodating non-zero probability masses for spatial random effects without sacrificing richness for areal models is problematic in any other way. The local Dirichlet process (Chung and Dunson, 2011) offers an approach to the localized spatial “sharing” of atoms and weights that could conceivably be extended to the areal setting through a suitable definition of what a neighborhood is at each areal location; also see Theorem 4 in Dunson, Pillai and Park (2007) for a related idea. The models we propose below correspond to a subclass of stick-breaking process priors that includes the DP and the SDP as special cases. In particular, we construct an areally-referenced stick-breaking process (ARSB) and an areally-referenced Dirichlet Process (ARDP) that will serve well for areal data allowing formal boundary analysis.

We make a few remarks on the more recent developments in Dependent Product Partition Models (DPPM), which refers to classes of predictor-dependent product partition models. These models encourage clustering among subjects with like covariates. Both Müller et al. (2011) and Park and Dunson (2010) require a “similarity function” g(x₁, … , x_k) which adjusts the (typically Dirichlet process) cohesion function, giving larger values for sets of covariates x₁, … , x_k that are “similar.” Park and Dunson’s (2010) model development proceeds through the consideration of similarity functions that place probability distributions on the covariates x₁, x₂, … , treating them as continuous; specifically, they consider the DPM of normals proposed by Müller, Erkanli, and West (1996). Müller, Quintana, and Rosner (2011) consider normal models for continuous covariates, and other choices for ordinal and nominal categorical predictors. For our model and application, we require a cohesion function that gives larger values for proximal counties. That is, our “predictor” is a categorical variable with spatial information, quite different from either approaches of the DPPM referenced above. We could attempt a similarity function based on, for example, average centroid distances within a group, but this is far outside the class of models we are proposing. Rather, the models we are proposing incorporate areal spatial information directly into the stick-breaking weights (ARSB) or through a copula-type formulation (ARDP).

3.3. Areally-referenced spatial stick-breaking prior

Existing dependent DP models are applicable to continuous covariates. For for areally-referenced spatial data, the underlying spatial association is built on adjacency or neighborhood structures of the regions, hence the covariates related to the spatial locations are not continuous everywhere. DDP’s allowing continuous predictor-dependent weights no longer apply. Therefore, we propose an areally-referenced stick-breaking (ARSB) prior for the spatial random effects that will apply to areal data. We adapt the point-referenced spatial stick-breaking approach of Reich and Fuentes (2007) to areal data by incorporating spatial dependence in the DP by introducing additional weights that borrow strength across the neighbors using CAR priors (Section 2)

The spatial random effects are assigned a stick-breaking prior, whose weight parameters $p_{i1}=w_{i1}{V}_1,p_{\mathit{ik}}=w_{\mathit{ik}}{V}_k{\prod }_{l=1}^{k-1}(1-w_{\mathit{il}}{V}_l)$, i = 1, …, n, k = 1, 2, …, depend not only on the V_ks, but also on “location” weight parameters w_ik. These weights lie between (0, 1) so that each p_ik is a valid stick-breaking weight (0 < p_ik < 1). Since the CAR distribution has support over the entire real line, we introduce a transformation logit(w_ik) = z_ik and allow the z_iks to be distributed as CAR. Of course, any other link mapping the unit interval to the real line could be used. For each k, we let ${\{z_{\mathit{ik}}\}}_{i=1}^n$ be distributed as a CAR distribution yielding a Markov random field (MRF) on the location weights and allowing the desired smoothing across neighbors. Usually larger values of ρ induce greater smoothing and setting ρ = 1, which is the maximum legitimate value for ρ (recall the discussion below (2.2)), yields the popular ICAR prior. This prior is improper as D – W is singular, but for a map without islands this issue can be resolved by imposing the additional constraint ${\sum }_{i=1}^n{z}_{\mathit{ik}}=0$.

The ARSB model, truncated to m terms for the stick-breaking representation, with a Poisson likelihood is

$$\begin{array}{cc}\hfill & Y_i\mid \beta ,{\varphi }_i\sim Poisson(E_i{e}^{{\mu }_i}),{\mu }_i={\mathbf{x}}_i^{\prime }\beta +{\varphi }_i;{\varphi }_i\sim G^{(i)};G^{(i)}(\cdot )=\sum _{k=1}^m{p}_{ik}{\delta }_{{\theta }_k}(\cdot ),{\theta }_k\sim N(0,{\sigma }_s^2)\hfill \\ \hfill & p_{i1}=w_{i1}{V}_1,p_{ik}=w_{ik}{V}_k\prod _{l=l}^{k-1}(1-w_{il}{V}_l),V_k\stackrel{iid}{\sim }Beta(1,\alpha ),\{z_{ik}\}\sim CAR(\rho ,{\sigma }_k^2),\hfill \end{array}$$ (3.1)

where logit{w_ik} = z_ik for k = 1, … , m. Recall that the α parameter stochastically controls the number of distinct values among the n observations. The covariance between dependent variables Y_i and Y_j is induced by the covariance of the spatial random effects φ_i and φ_j.

The ARSB model incorporates dependence between the discrete distributions on different regions but does not yield identical marginal distributions on the φ_i. Duan, Guindani and Gelfand (2007) introduced random distributions for the spatial effects associated with point-referenced data allowing different surface selection at different sites while ensuring that the marginal distribution of the effect at each sites still comes from a Dirichlet process. Here we propose an areal alternative, which we call an areally-referenced Dirichlet process (ARDP). The ARDP maintains the marginal distribution of each spatial random effect to be a regular univariate DP while incorporating the spatial dependence between these DPs.

Consider spatial random effects φ_i, i = 1, …, n each arising marginally from an identical random measure G, where G ~ DP (α, G₀). We introduce spatial dependence between these DPs by constructing dependent uniform (0, 1) random variables. Suppose γ₁, …, γ_n are jointly distributed as a CAR(ρ, σ_γ), and F⁽¹⁾(·), …, F⁽ⁿ⁾(·) denote the cumulative distribution functions of the marginal distributions of each component of the CAR random vector. Marginally, each F⁽ⁱ⁾(γ_i) is uniform (0, 1) but they will be dependent through γ₁, …, γ_n.

More explicitly, we formulate our hierarchical areally-referenced Dirichlet process (ARDP) model as follows. We use a Poisson likelihood for the first stage model, but this could be replaced by any discrete distribution in the exponential family. Thus,

$$\begin{array}{cc}\hfill & Y_i\mid \beta ,{\varphi }_i,\sim Poisson(E_i{e}^{{\mu }_i}),{\mu }_i={\mathbf{x}}_i^{\prime }\beta +{\varphi }_i;\varphi =\{{\varphi }_i{\}}_{i=1}^n\sim G_n;G_n=\sum _{u_1,\dots ,u_n}{\pi }_{u_1,\dots ,u_n}{\delta }_{{\theta }_{u_1}}\dots {\delta }_{{\theta }_{u_n}};\hfill \\ \hfill & {\pi }_{u_1,\dots ,u_n}=P\left(\sum _{k=1}^{u_1-1}{p}_k<F^{(1)}({\gamma }_1)<\sum _{k=1}^{u_1}{p}_k,\dots ,\sum _{k=1}^{u_n-1}{p}_k<F^{(n)}({\gamma }_n)<\sum _{k=1}^{u_n}{p}_k\right);{\theta }_k\stackrel{iid}{\sim }N(0,{\sigma }_s^2);\hfill \\ \hfill & p_1=V_1;p_j=V_j\prod _{k<j}(1-V_k);V_j\stackrel{i.i.d.}{\sim }\mathrm{B}\mathrm{e}\mathrm{t}\mathrm{a}(1,\alpha );\gamma =\{{\gamma }_i{\}}_{i=1}^n\sim N_n(0,\Sigma ),\hfill \end{array}$$ (3.2)

where k = 1, 2, … , K truncates the stick breaking function to K terms, $\Sigma ={\sigma }_{\gamma }^2{(D-\rho W)}^{-1}$ is the covariance matrix of a proper CAR distribution. Using the cumulative distribution function of the γ_i’s to model the weights is an adaptation of the Hybrid Dirichlet Process (Petrone et al., 2009), where copulas are used to model weights. The distinction is that we model areal dependence using Markov random fields, while the hybrid DP models dependence using continuous spatial processes for inference on uncountable sets. Both methods ensure that the marginal distribution of G⁽ⁱ⁾(φ_i), for each i, follows an identical DP

$$G^{(i)}({\varphi }_i)=\sum _{k=1}^K\sum _{u_1,\dots ,u_i=k,\dots ,u_n}{\pi }_{u_1,\dots ,u_i=k,\dots ,u_n}{\delta }_{{\theta }_{u_1}}\dots {\delta }_{{\theta }_{u_i=k}}\dots {\delta }_{{\theta }_{u_n}}=\sum _{k=1}^K{p}_k{\delta }_{{\theta }_k},$$ (3.3)

Where $p_k={\sum }_{k=1}^{K}P\left({\Sigma }_{t=1}^{k-1}{p}_t<F^{(i)}({\gamma }_i)<{\Sigma }_{t=1}^k{p}_t\right)$. How the covariance between φ_i and φ_j depends upon the probabilities p₁, …, p_K can be seen from

$$\begin{array}{cc}\hfill & \text{Cov}({\varphi }_i,{\varphi }_j)={\sigma }_s^2\sum _{l=1}^{K}P(u_i=u_j=l)\hfill \\ \hfill & ={\sigma }_s^2\sum _{l=1}^{K}P\left({\mathrm{\Sigma }}_{k=1}^{l-1}{p}_k<F^{(i)}({\gamma }_i)<{\mathrm{\Sigma }}_{k=1}^l{p}_k,{\mathrm{\Sigma }}_{k=1}^{l-1}{p}_k<F^{(j)}({\gamma }_j)<{\mathrm{\Sigma }}_{k=1}^l{p}_k\right)\hfill \\ \hfill & ={\sigma }_s^2\sum _{l=1}^K{p}_{l}P\left(F^{(i{)}^{-1}}({\mathrm{\Sigma }}_{k=1}^{l-1}{p}_k)<{\gamma }_i<F^{(i{)}^{-1}}({\mathrm{\Sigma }}_{k=1}^l{p}_k)\mid F^{(j{)}^{-1}}({\mathrm{\Sigma }}_{k=1}^{l-1}{p}_k)<{\gamma }_j<F^{(j{)}^{-1}}({\mathrm{\Sigma }}_{k=1}^l{p}_k)\right),\hfill \end{array}$$ (3.4)

where (γ_i, γ_j) follows a bivariate normal distribution with covariance specified by the CAR model. Posterior inference for the ARSB and ARDP models are based upon Markov chain Monte Carlo simulations (e.g., Gelman et al., 2004; Carlin and Louis, 2008). The details are outlined in the Supplement.

3.4. A practical FDR-based method to select difference boundaries

We offer a practical strategy to obtain a threshold for detecting difference boundaries. A decision-theoretic approach will treat the spatial boundary analysis problem as one of multiple hypothesis testing. For each pair of adjacent regions, say i and j, we seek to test φ_i = φ_j against φ_i ≠ φ_j. This produces as many hypothesis as there are edges. Recently, several authors have advocated the use of the false discovery rate (FDR) to adjust for multiplicities in hypothesis testing problems (see, e.g., Benjamini and Hochberg, 1995; Efron et al, 2001; Storey, 2002, 2003). Li et al. (2012) used the FDR on Smoothed Moving Average (SMA) models involving some awkward constraints on the random effects for model fitting. Here, we adapt this approach to the ARDP and ARSB models, which is free of such constraints.

We will want to identify a boundary (i, j) as a difference boundary if the posterior probability that P(φ_i = φ_j ∣ Y) exceeds a certain threshold t, where Y = {Y₁, Y₂, … , Y_n} is the entire collection of observed outcomes. For each pair of neighboring regions, we construct A_(i,j)(Y;t) = {Y : P(φ_i ≠ φ_j ∣ Y) > t}, a critical region that indicates evidence in favor of (i, j) being a difference boundary. The choice of t will be based upon controlling the FDR below a level δ = 0.05. If Z_(i,j) = I(φ_i = φ_j) and v_(i,j) = P(Z_(i,j) = 0 ∣ Y), then the FDR is

$$FDR=\frac{{\sum }_{i\sim j}{Z}_{(i,j)}I(v_{(i,j)}>t)}{{\sum }_{i\sim j}I(Z_{(i,j)}>t)}\text{where}i\sim j\text{if}{w}_{ij}\ne 0.$$ (3.5)

Estimation of (3.5) is straightforward. It is obtained as the posterior expectation

$$\widehat{FDR}=\mathrm{E}[FDR\mid Y]=\frac{{\sum }_{i\sim j}(1-v_{(i,j)})1(v_{(i,j)}>t)}{{\sum }_{i\sim j}1(v_{(i,j)}>t)},$$ (3.6)

where v_(i,j) is computed as a Monte Carlo mean of the posterior samples for Z_ij. Rejection rules can be then constructed to bound the FDR at target level δ: reject if v_(i,j) > t, where

$$t=\text{sup}\left\{u:\frac{{\sum }_{i\sim j}I(v_{(i,j)}>u)(1-v_{(i,j)})}{{\sum }_{i\sim j}I(v_{(i,j)}>u)}\le \delta \right\}.$$

Li et al. (2012) required estimating as many models as there are geographical boundaries making it computationally expensive. For example, for testing county boundaries in the state of Minnesota, they had to estimate 211 models. More importantly, their method does not provide posterior estimates from any single model. Obtaining model-averaged estimates is not straightforward. These drawbacks are circumvented with the ARDP and ARSB.

4. A Simulation Study

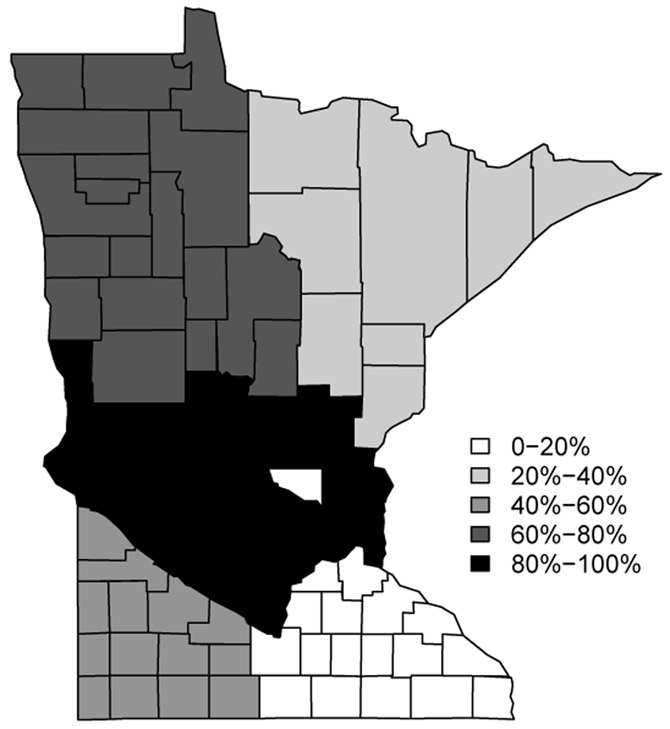
To evaluate our methods, we conduct a simulation study using the template of a Minnesota county map in Li et al. (2011). There are n = 87 counties in Minnesota, and 211 pairs of neighboring counties (i.e., geographical boundaries). We simulated 50 datasets on a map of Minnesota, where the state was divided into six regions. Each dataset was generated from (2.1), where μ_i was one of five different means corresponding the the five different shades mapped on Figure 4.1. The darker shades correspond to higher means. To add some irregularity, we also included one county (Sherburne county shaded white in Figure 4.1) that has all its boundaries as true difference boundaries. This resulted in “six” different clusters on the map and 47 “true difference boundaries” delineating the different clusters, i.e. these 47 boundaries are county borders that separate two areal units with substantially different means.

Figure 4.1:

A map of the simulated data with the grey-scales showing the six different clusters, each having its own mean. There are 47 boundary segments that separate regions with different means(shades). The percentages reflect the quantiles for the distribution of the outcomes.

For this simulation experiment, since we know the true difference boundaries we can obtain the sensitivity and specificity for each of our proposed models. Sensitivity is the probability of correctly detecting a true difference boundary, while specificity is the probability of correctly labeling a geographical boundary as not a difference boundary. To be precise, for every pair of geographical neighbors (i, j), we compute the posterior probability P(φ_i ≠ φ_j ∣ Y) and choose the top T = 35, 40, 45, 50 and 55 edges with the highest posterior probabilities. As there are 47 true difference boundaries, these choices encompass settings where we could, theoretically have obtained 100% accuracy (when T = 35, 40, 45) and also where we are assured of a few false positives (when T = 50, 55).

The prior specification and computational details of the ARDP model are in the Web Supplement. The parameter α can be fixed based upon the expected number of clusters a priori. In this case, we have six clusters which would suggest a value of α around 1.25. In fact, we experimented with α ranging from 0.25 to 1.75 and obtained very robust inference. The results presented here correspond to α = 0.5, which leads to an expected number of clusters around 3, which is half of the number of true clusters. We also fixed ρ = 0.98 in the ARDP model (ICAR is inapproriate since the covariance matrix must be proper and nonsingular). Customarily, higher values of ρ (≈ 1) yield sufficient smoothing, while values lower than 0.95 tend not to (e.g., Banerjee et al., 2004). In contrast, for ARSB, we used the ICAR model (with ρ = 1) along with the sum-to-zero constraint, which yields legitimate posterior samples. We assumed a regression structure with only an intercept (i.e. x_i ≡ 1) and placed a flat prior on the corresponding β. A weakly informative prior Γ(.01, .01) is specified for the precision parameters τ_s and τ_γ . In both models, the stick-breaking prior was computed using about 15 terms.

We compare the performance of DPM, ARSB, ARDP with three existing methods: (i) the deterministic Boundary Likelihood Value (BLV) algorithm of Jacquez and Greiling (2003a, 2003b) using the BoundarySEER software (see http://www.biomedware.com) with default thresholds set from a BLV histogram, (ii) the model-based approach of Lu and Carlin (2005), which we call the “LC method”, and (iii) a class of discrete Spatial Moving Average (SMA) models outlined in Li et al. (2011). We ran these models within the R statistical software environment running 3 parallel chains for each model and dataset. Convergence was diagnosed after 12, 000 iterations of burn-in using Gelman-Rubin diagnostics and autocorrelation plots from the coda package in R. A subsequent 5, 000 × 3 = 15, 000 samples were used for posterior inference. On a workstation using a Intel dual core 4 GHz processor, each model took less than five hours of CPU time to deliver its entire inferential output for all the 50 simulated datasets.

Table 4.1 presents the average detection rates for these different methods applied to the 50 simulated datasets. The DPM and the BLV methods do not explicitly borrow strength across neighbors, while the other four methods in Table 4.1 exploit the adjacency structure of the underlying map. There seems to be little to choose between ARDP and ARSB but both methods seem to be slightly outperforming the other methods in both sensitivity and specificity under all five scenarios. In addition, while the performance of the SMA model is perhaps comparable, it is computationally onerous and less robust to prior assumptions (Li et al., 2011) than ARDP or ARSB.

Table 4.1:

Sensitivity and specificity in the simulation study (50 datasets generated on a Minnesota map) for the ARDP, ARSB, DPM, LC and BLV methods.

T	Method	Sensitivity	Specificity		T	Method	Sensitivity	Specificity
35	ARDP	0.768	0.998		40	ARDP	0.822	0.990
	ARSB	0.771	0.991			ARSB	0.821	0.989
	DPM	0.737	0.989			DPM	0.791	0.991
	BLV	0.711	0.990			BLV	0.778	0.979
	LC	0.702	0.989			LC	0.767	0.976
	SMA	0.740	0.998			SMA	0.818	0.991
45	ARDP	0.881	0.971		50	ARDP	0.927	0.962
	ARSB	0.878	0.972			ARSB	0.930	0.968
	DPM	0.870	0.968			DPM	0.897	0.952
	BLV	0.831	0.964			BLV	0.869	0.944
	LC	0.813	0.959			LC	0.859	0.941
	SMA	0.872	0.975			SMA	0.901	0.955
55	ARDP	0.940	0.943
	ARSB	0.941	0.940
	DPM	0.895	0.915
	BLV	0.891	0.920
	LC	0.881	0.917
	SMA	0.925	0.930

The LC method is based upon a parametric CAR model that does not render itself to probabilistic boundary analysis (since P(φ_i = φ_j) will always be zero). However, one could fit parametric CAR models and use the posterior expectation of the absolute differences of the rates, i.e. E(∥η_i – η_j∥ ∣Y), where ${\eta }_i=\frac{{\mu }_i}{E_i}$ acts as a boundary difference score. Higher values will indicate spatial barriers between units i and j. The DPM, ARSB and ARDP models not only yield estimates of η_i, as in the “LC” method, but they also deliver nonzero posterior probabilities P(φ_i = φ_j ∣ Y). The LC method cannot produce these posterior probabilities. Therefore, we used the posterior expectation metric to compare its performance. The SMA model does not deliver posterior estimates of spatial effects from a single model. Hence, we exclude it from this comparison.

Table 4.2 presents the results for four of the methods. The deterministic BLV method detects 89.6% of the boundaries. The promise of our stochastic models is evident from the superior performances of the ARDP and the ARSB models. Since we know the true boundaries in Figure 4.1, we can assess the performances of these approaches in detecting the true boundaries. Using direct posterior estimates 47 difference boundaries. We find that the DPM, ARDP and the ARSB models are each able to detect about 90% of the true boundaries, which is superior to both LC and BLV. The ARDP model performs slightly better than the other two, which are approximately equally good. Using the posterior expectation metric, we again find that the proposed ARSB and ARDP models clearly outperform the LC method. The ARDP model has almost a 10% better detection rate, while the ARSB model excels by approximately 5%. Both ARDP and ARSB outperform the DPM model as well in terms of the posterior expectation metric.

Table 4.2:

Assessment of the true wombling boundaries with those produced by LC, ARDP and ARSB based on P(φ_i = φ_j ∣ Y) and E(∥η_i – η_j∥ ∣Y) in the simulation study.

	Assessment using P(φi = φj ∣ Y)	Assessment using E(∥ηi – ηj∥ ∣Y)
LC	-	78.7%
DPM	89.3%	82.2%
ARDP	91.4%	88.3%
ARSB	89.1%	83.3%

5. Analysis of Minnesota P&I Dataset

We apply our method to the Minnesota Pneumonia and Influenza (P&I) diagnosis dataset. P & I rank as the eighth leading cause of death in the United States and the sixth leading cause in people over 65 years of age with Pneumonia consistently accounting for the overwhelming majority of deaths between the two. Together, they cost the U.S. economy in 2005 an estimated $40.2 billion. Identifying difference boundaries that perform well with regard to sensitivity and specificity can help identify so-called “health barriers” more accurately and buttress an active surveillance program for an influenza-like illness.

We analyze a dataset consisting of Minnesota residents above 65 years of age who were enrolled in the Medicare fee-for-service program as of December 31, 2001. The Medicare Denominator file for 2001 was used to define the cohort, which has also been used to study the impact of vaccinations on elderly Minnesota residents. The Medicare Provider Analysis and Review (MedPAR) manages patient records based on date of discharge and supplied information regarding hospitalizations resulting from P&I. Rates of P&I hospitalization are traditional measures of the impact of influenza virus in the elderly population. We identify the ‘boundaries’ that separate the more affected areas from the less affected areas.

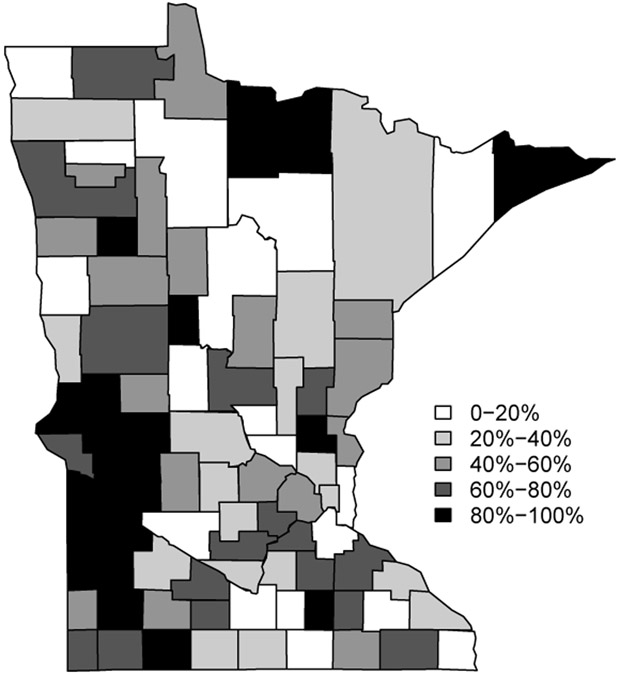
If Y_i and O_i are the observed number of hospitalizations and the population in county i respectively, then $E_i=\frac{{\sum }_{k=1}^n{Y}_i}{{\sum }_{k=1}^n{O}_i}{O}_i$ is the expected number of cases (under the assumption of no spatial variation in rates), where n is the total number of counties. The choropleth map of the raw data is shown in Figure 5.2. The high valued SMR (standard mortality ratio) counties are scattered over the map, with a clump on the southwest and some isolated regions surrounded by sparsely inhabited counties that also have lower counts.

Figure 5.2:

Choropleth map of the SMR in MN (P&I) dataset. The percentages reflect the quantiles for the distribution of the SMR.

We employed the same models in Section 4to detect boundaries on the P&I hospitalization map. The same prior specification and model settings are applied here as the simulation study, except we assign α = 1, a customary choice when one does not seek a prior distribution on this parameter (Escobar and West, 1995) or has no a priori information about the number of clusters. Three parallel MCMC chains were executed on the same computing environment as described in Section 4.Convergence was diagnosed after 10, 000 iterations of burn-in using Gelman-Rubin diagnostics and autocorrelation plots and a subsequent 5, 000 × 3 = 15, 000 samples were used for posterior inference. Each model consumed less than ten minutes of CPU time to produce its entire inferential output for the Minnesota Pneumonia and Influenza dataset with very little difference between the ARSB, ARDP and the (non-spatial) DPM model.

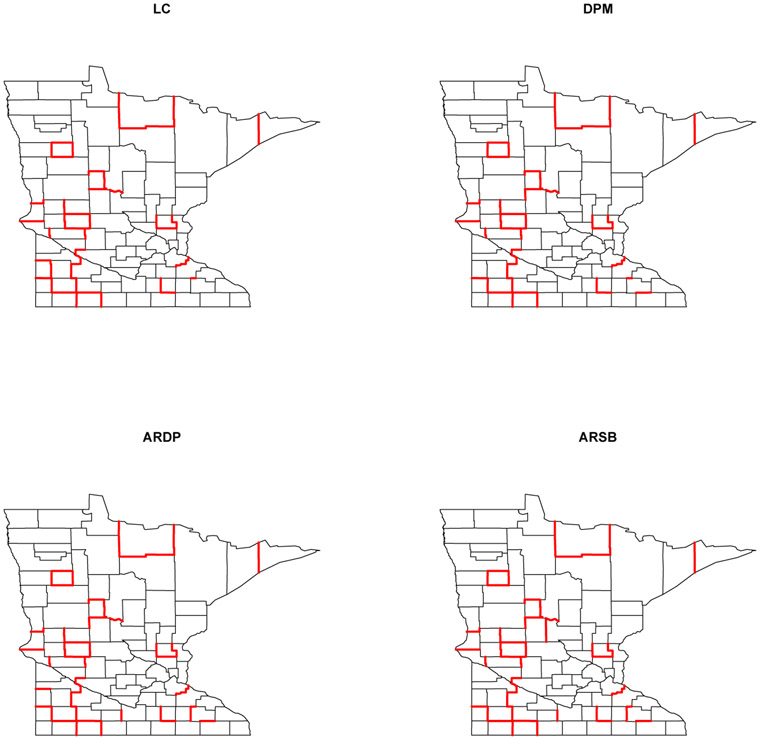
Health administrators may prefer to use a “top bracket” of most likely difference boundaries for policy formulation. The top 50 difference boundaries detected by each model are highlighted in Figure 5.3. Table 5.3 presents a comprehensive “lookup table” containing the names of adjacent counties that have been ranked in decreasing order according to 1 – P(φ_i = φ_j ∣ Data) from the ARDP model. Instead of selecting this “bracket” arbitrarily, statisticians may prefer a threshold obtained by controlling the FDR. Setting δ = 5% yields Numbers 1-33 as difference boundaries, while setting δ = 10% detects Numbers 1-42 as difference boundaries. This table offers an easy reference for health administrators and officials to identify the more substantial spatial health barriers in the state.

Figure 5.3:

Difference boundaries detected by various models in the Minnesota (P&I) dataset.

Table 5.3:

Names of adjacent counties that have significant boundary effects from the ARDP model. The numbers in the first column are the ranks according to P(φ_i = φ_j ∣ Y)

1	Beltrami , Koochiching	26	Koochiching, Lake of the Woods
2	Cass, Wadena	27	Isanti, Mille Lacs
3	Douglas , Pope	28	Chippewa, Renville
4	Freeborn , Steele	29	Murray, Pipestone
5	Goodhue , Olmsted	30	Becker ,Mahnomen
6	Itasca , Koochiching	31	Rice , Waseca
7	Kandiyohi, Pope	32	Blue Earth, Brown
8	Koochiching, St. Louis	33	Dodge, Olmsted
9	Pope, Stearns	34	Chisago , Isanti
10	Anoka , Isanti	35	Redwood , Yellow Medicine
11	Dakota, Goodhue	36	Pennington, Polk
12	Lincoln, Pipestone	37	Goodhue, Wabasha
13	Murray, Redwood	38	Pope, Swift
14	Steele, Waseca	39	Morrison, Todd
15	Renville, Yellow Medicine	40	Fillmore, Olmsted
16	Cottonwood, Murray	41	Cook , Lake
17	Jackson , Martin	42	Douglas, Grant
18	Kandiyohi, Swift	43	Mahnomen,Norman
19	Pope, Stevens	44	Grant, Wilkin
20	Todd, Wadena	45	Mahnomen, Polk
21	Lyon, Redwood	46	Jackson, Nobles
22	Murray, Nobles	47	Morrison, Todd
23	Isanti, Sherburne	48	Dodge , Olmsted
24	Otter Tail , Todd	49	Big Stone , Traverse
25	Clay, Otter Tail	50	Morrison, Stearns

About 90% of the boundaries listed in Table 5.3 are detected by all four models. As a specific example consider Cook and Koochiching county. The outcome variable in the former is substantially higher than its only neighbor, Lake, while Koochiching county is separated from all its neighbors due to its extremely high P&I SMR, even after being smoothed by the model. Among the 50 difference boundaries detected by the ARDP model, 47 are also detected by the ARSB model. The three county-pairs that went undetected by ARSB were: Goodhue and Olmsted, Freeborn and Steele, and Big Stone and Traverse. Instead, the ARSB model detected boundaries between counties Becker and Wadena, Cotton Wood and Jackson, and Cook and Lake.

The map in Figure 5.2 does not display clustering as pronounced in the simulation example. Furthermore, unlike in the simulation example, we do not know the “truth.” It does, however, reflect well on our models that the rankings in Table 5.3 are very consistent with competing methods. We already discussed the minor differences between the ARDP and the ARSB. The agreement between the ARDP and the SMA in terms of identifying the difference boundaries using FDR-based thresholds is very strong with over 95% agreement in boundary selection.

6. Conclusion and Future Work

The paper presented a class of nonparametric Bayesian hierarchical models for detecting difference boundaries on maps. An advantage of the new approach is that it permits the probabilistic estimation of an edge as a difference boundary, and improves the percentage of true detection. A disadvantage is that the model cannot be easily fit into any existing commercial software. We fit these models in R (www.r-project.org), and we wish to collect these models in an R package in the near future.

The ARDP and ARSB models in conjunction with the FDR controlled threshold selection provide a major improvement over earlier work by Li et al. (2012) by circumventing the need to estimate as many models as there are geographical boundaries and by offering comprehensive model-based posterior estimates of model parameters. The latter is precluded in Li et al. (2012) who treat this as a purely hypothesis testing problem. However, issues related to optimal selection of boundaries warrants further investigation especially regarding the sensitivity of the inference to FDR-based cutoffs and to prior specifications. Further extensions can be formulated by incorporating classes of loss functions, as discussed by Müller et al. (2008), for a more comprehensive decision-theoretic framework. Such developments may, in turn, lead to more definitive conclusions regarding the performance of these models in maps that display weaker clustering patterns.

Finally, we note that both the ARDP and ARSB models render themselves to multivariate extensions, where multiple health outcomes need to be modeled jointly. Analogous to the univariate ARSB model, we can construct a multivariate areally referenced stick breaking (MARSB) model such that the sticking breaking weights p are correlated through another type of “weight” parameter that scales the V_i’s. We place a multivariate CAR (MCAR) prior on these “weight” parameters so as to capture both spatial correlation and inter-variable correlation (Jin et al., 2005, 2007). For the ARDP, the distribution of the spatial random effects can be modeled by constructing multivariate areally referenced Dirichlet processes (MARDP). These pursuits will constitute natural extensions of our current work.