Response to Comment on “Is the nuclear refractive index lower than cytoplasm? Validation of phase measurements and implications for light scattering technologies”

Abstract

Recently, Maxim A. Yurkin commented on our paper “Is the nuclear refractive index lower than cytoplasm? Validation of phase measurements and implications for light scattering technologies” as well as on a complementary study “Cell nuclei have lower refractive index and mass density than cytoplasm” from Schürmann et al. In his comment, Yurkin concluded that quantitative phase images of cells with nuclei that are less optically dense than the cytoplasm must exhibit a characteristic concavity, the absence of which is evidence against our conclusion of a less-dense nucleus. In this response, we suggest that Yurkin’s conclusion is reached through an oversimplification of the spatial refractive index distribution within cells, which does not account for high index inclusions such as the nucleolus. We further cite recent studies in 3-dimensional refractive index imaging, in which the preponderance of studies supports our conclusion. Finally, we comment on the current state of knowledge regarding subcellular refractive index distributions in living cells.

Recently, we received notice that Maxim A. Yurkin commented on our study [1] as well as a complementary work [2], which independently found the cell nucleus to have a lower average refractive index (RI) than the cytoplasm for each cell type measured. The basic workflow of these studies was to acquire quantitative phase images of several cells and their corresponding isolated nuclei, and to image them just after plating to ensure a high degree of sphericity. From the known spherical geometry, it is possible to decouple sample thickness from the integral RI, and to infer the average RI of both the whole cell and the isolated nucleus. In our paper, we found the average nuclear RI to be less than the average whole-cell RI (and consequently, less than the cytoplasmic RI) for invasive breast ductal carcinoma (MCF-7), alveolar adenocarcinoma (A549), immortalized bronchial epithelium (BEAS-2B) and Primary Vaginal Epithelium cell types. Schürmann et al. reached a similar conclusion for human myelocytic leukemia cells (HL60/S4), leukemic T-cells (Jurkat), MCF-7 cells and human cervical cancer (HeLa) cell types. Importantly, both studies were in strong agreement regarding the overlapping cell type (MCF-7) with RI differences between the studies of approximately 0.005 for both cells and nuclei.

Yurkin’s comment can be summarized as follows. For a cell modeled as a coated sphere with homogenous compartments, the phase image in a simple transmission approximation will necessarily include a characteristic “dip” or concavity corresponding to the location of the cell nucleus. Yurkin presents a geometric derivation to support this notion, and plots example phase profiles for parameters described in both works. Yurkin is careful to note that he is not claiming that the nuclear RI is higher than that of cytoplasm, but rather, that the simple transmission and homogenous sphere approximations lead to results which appear to be self-contradictory. This results in 3 possible conclusions: (1) that the cell is inhomogenous in RI, complicating the analysis beyond his simple 2-compartment model, (2) that the simple transmission approximation is not valid in this case, and results in erroneous phase profiles or (3) that the nucleus is not less optically dense than the cytoplasm. While the first point is valid and acknowledged by both studies in question, the second two conclusions ignore a wealth of experimental evidence.

Our issue with the argument presented by Yurkin is not mathematical. Yurkin is correct in noting that a phase concavity would be observed in a phase image of a perfectly homogeneous coated sphere, in which the inner sphere (nucleus) is less optically denser than the coating (cytoplasm). The problem with this line of thinking is that biological cells, and their isolated nucleoli, exhibit substantial optical heterogeneity. In our study alone, we observed 1 to 4 high-index nucleoli per nucleus in all 4 cell types, with typical diameters between 2 and 4 microns each. Since nucleoli exist in the nucleus by definition, these high-index inclusions would appear directly within the concavity hypothesized by Yurkin in a whole-cell phase image, immediately rebutting his claim. Our observation is consistent with other works, which have quantified multiple nucleoli in HeLa cells, with RI in the range of 1.375 to 1.385, compared with the nuclear compartment RI of 1.355 to 1.365 and a cytoplasmic RI of 1.36 to 1.39 [3].

Yurkin correctly notes that his reasoning does not have implications for inhomogeneous cells. However, he states in his abstract that “the conclusions and assumptions used in retrieving the refractive index necessarily imply a characteristic dip in the center of the whole-cell phase images.” The implication of this statement is that our work assumes a homogenous RI in each cell compartment, which is required to produce the concavity central to his critique. In reality, no such assumption is made. Once a spherical geometry is confirmed (as shown by Schürmann et al. using confocal microscopy), the integral RI (ie, the RI averaged spatially along the dimension of light propagation) may be calculated for each point in the x,y-plane, and then averaged across this plane to produce mean RI values for the nucleus or whole cell.

The difference in reasoning may be summarized by noting that our study (along with Schürmann et al.) measured average RI within cells and nuclei, while Yurkin’s critique treats cells with homogeneous RI, or more specifically, RI which varies at sufficiently small length scales to be homogeneous when averaged by integration along the path of beam propagation. As described above, this is clearly not a representative description of living cells.

Yurkin also calls into question the simple transmission approximation, which approximates the cell as a phase object which modulates the illumination wave based on object height and optical density. This assumption is a fundamental consideration in the field of quantitative phase microscopy of thin samples [4, 5]. The implication of this critique is that internal reflections, refractions, and diffraction from cell borders could be sufficient to cause a substantial corruption of the resultant phase image, and lead to erroneous measurement of the mean RI. We share the commenter’s interest in Mie scattering from cell nuclei, and a substantial portion of our lab’s work has been devoted to this phenomenon in cell monolayers and tissues in a backscattering geometry [6–10]. Unfortunately, this phenomenon is not significant for a single cell in transmission geometry. To confirm the validity of the simple-transmission approximation in spherical samples, Phillips et al. acquired quantitative phase images of polystyrene microspheres immersed in fluoromount G (Δn ~ 0.2), finding very close agreement to the phase profile expected from the approximation for spheres larger than the diffraction limit [11]. Choi et al. also used projection phase images to calculate the RI of microspheres, finding excellent agreement with the expected value [3]. Schürmann et al. similarly validated their approach using hydrogel beads as a technical sample [2], as did Chowdhury et al., who found the quantitative phase projection of polystyrene microspheres to be nearly identical to that predicted by the simple-transmission approximation [12]. Because these samples are highly spherical, and often exhibit Δn values much larger than those found within cells, we would expect a failure of the simple transmission approximation caused by internal reflections to be most easily observed in these samples. However, this is not the case.

Yurkin also suggests that diffraction at the cell border may be sufficient to contaminate the phase image, even for spheres which are relatively transparent and thus exhibit negligible internal reflections. Fortunately, technical samples exist for this regime as well. Chowdhury et al. compared the phase profile of microspheres in a well-matched oil (Δn ~ 0.007 or 0.5%) to that expected from the simple-transmission approximation, finding near-perfect agreement to the expected profile, and accurately estimating the RI of the microsphere material to within 1% [12]. This regime is similar to cells measured in our study, which exhibited nuclear RI in the range of 97.8% to 99.7% of that for the cytoplasm [1].

The argument against the simple-transmission approximation made by Yurkin is based on spherical objects, which have a well-defined, rigorous scattering solution in Mie theory. However, refractive and diffractive effects occur in all samples, regardless of their specific geometry. Still, quantitative phase microscopy can produce extremely detailed maps of cellular substructure for single cells, which do not appear to be corrupted by propagation artifacts when the system is in focus. Often, intracellular phase objects correspond precisely to spatially and structurally identical objects as measured by fluorescence, such as the nucleolus and other organelles [13, 14]. The matching of structure between different imaging modes is perhaps the strongest argument for the simple-transmission approximation.

Fortunately, third-party data exist which can validate the true subcellular RI. In recent years, tomographic phase microscopy (TPM) has enabled the creation of 3-dimensional tomograms of individual cells, which use RI as an inherent contrast mechanism. As mentioned previously, Choi et al. found the nucleus of HeLa cells to be lower in index than the cytoplasm, and found similar results for HEK 293 cells, B35 neuroblastoma cells, and primary rat hippocampal neurons [3]. Lue et al. used a synthetic aperture technique to create RI tomograms of HeLa cells, also finding the RI of heterogeneous structures in the cytoplasm to be higher than those in the nucleus [15]. Kim et al. recently presented correlative RI and fluorescence tomograms, finding that the nucleus as a whole (including the nucleolus) may be lower or higher in index than the cytoplasm as a whole, with results primarily depending on cell type [13]. Interestingly, even for cells in which the mean intranuclear RI is higher than the mean cytoplasmic RI, the area immediately surrounding the nucleus is visibly more dense than the nuclear compartment aside from the nucleolus, suggesting that these nuclei will scatter light as if they were Mie scatterers with m parameter m = RI_nuc/RI_cyt < 1. This was true of all tomograms presented by Kim et al.

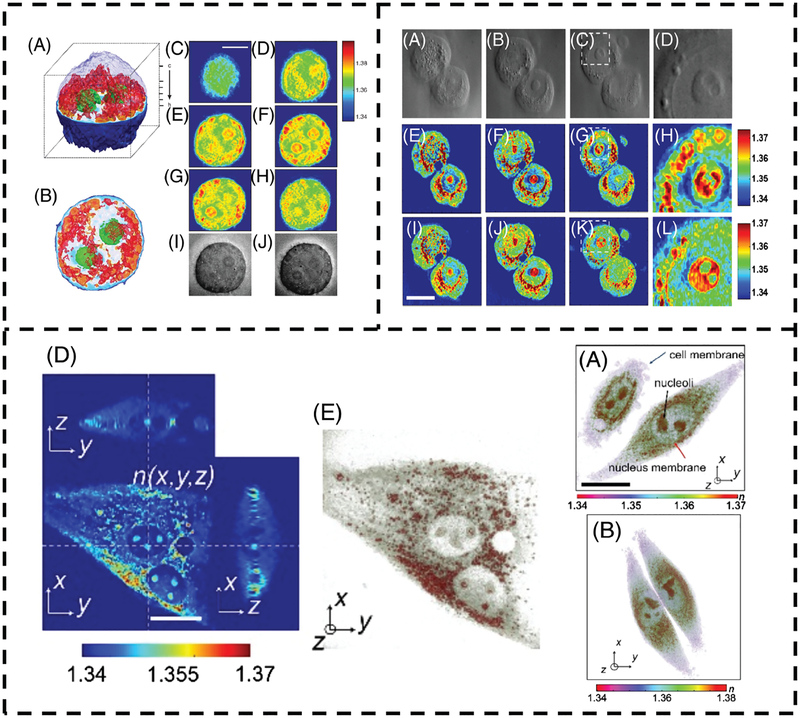
Novel methods aside from TPM have reached similar conclusions. Dardikman et al. recently developed a multimodal method to measure the integral RI distributions in cell suspensions, finding the RI of the nucleus to be lower than cytoplasm in regions other than the nucleolus [16]. An analogous method to TPM, optical diffraction tomography (ODT) uses quantitative phase images at various angles to solve an inverse scattering problem, creating diffraction-free 3-dimensional RI tomograms. Sung et al. used ODT to image living human colon adenocarcinoma (HT29) cells, with the resulting tomograms displaying a visibly less-dense nucleus [17]. A composite figure depicting some of these results is shown in Figure 1.

FIGURE 1.

(Top Left) Refractive index tomogram (A, B) and tomogram slices (C-H) from Choi et al. [3] showing a HeLa cell. The nucleus is visibly less dense than the cytoplasm. Brightfield images are shown in (I, J). (Top Right) Optical diffraction tomogram slices of HT29 cells from Sung et al. [17] with corresponding brightfield images on the top row. The middle and bottom rows represent different image reconstruction algorithms. In each case, the nucleus is visibly less dense than the perinuclear region. (Bottom) Tomographic slice (D) and 3D-rendering (E) of the refractive index distribution of an NIH-3 T3 cell from Kim et al. [13]. 3D renderings of HeLa cell RI distributions (A, B) are also displayed. In each case, the perinuclear region is more optically dense than the nucleoplasm. Subfigure lettering is referenced to the original work. Reproduced with permission refs. [3, 13, 17]. 2007, Springer Nature and 2017, 2009, The Optical Society

One weakness of our original study was the inability to correlate specific nuclei with their whole cell counterparts, a concern mitigated by the tomographic imaging studies mentioned above. To account for this, we compared populations of cells and nuclei, finding the nuclear RI to be lower on average. It is possible that some nuclei may exhibit a higher spatially averaged index than the cytoplasm in specific cells, especially if the cell has large or numerous nucleoli. In our work, a small percentage of nuclei exhibited an RI which was higher than the lowest outlier whole-cell RI of that type, though this phenomenon was only observed for a few cells in specific lines. Some cells may also invert their RI relationship to achieve a specialized function, as shown by Schürmann et al. using mouse retina cells, which have been hypothesized to act as microlenses [18]. Our conclusion was not that every individual eukaryotic cell exhibits a lower nuclear RI, but rather, that this was an accurate description of the average cell among the several populations measured in our study.

Finally, it should be mentioned that sample preparation may play a substantial role in the observed RI distributions. Each of the previously cited studies employed live cells without any potential disturbance induced by formalin fixation, permeabilization, or staining. Chowdhury et al. has examined MCF-7, HT29, and A549 cells, using structured illumination to create RI tomograms [12, 14] of these samples. Unfortunately, each sample was fixed in 4% paraformaldehyde prior to imaging, and in some cases, exposed to 0.1% Triton X-100 prior to fluorescent staining. Tomograms of several cells in this work exhibit a nucleus which appears denser than cytoplasm. However, MCF-7 cells in this work exhibit substantial blebbing and loss of cytoplasmic material, to the point of near-complete loss of the cytoplasm in some areas and visibly detached blebs. It is possible that the fixation process induces preferential loss of material in the cytoplasm, which is surrounded by only a single phospholipid bilayer compared with a double bilayer surrounding the nuclear compartment. Furthermore, the methods employed by common nuclear isolation protocols suggest that generic disturbances caused by chemical agents will disrupt and lyse the cytoplasm prior to damaging the nucleus [19, 20]. The effect of fixation on the cellular RI distribution merits further study.

To conclude, we feel that the comment by Yurkin oversimplifies the RI distribution within living cells, and ignores a substantial body of experimental literature on the subject. It is our hope that this topic receives renewed attention, both for an improved understanding of the fundamental biology involved, and as a tool for enhancing the performance of photonic diagnostic instruments based on tissue scattering.