Incorporating Prior Information with Fused Sparse Group Lasso: Application to Prediction of Clinical Measures from Neuroimages

Summary:

Predicting clinical variables from whole-brain neuroimages is a high-dimensional problem that can potentially benefit from feature selection or extraction. Penalized regression is a popular embedded feature selection method for high-dimensional data. For neuroimaging applications, spatial regularization using the l₁ or l₂ norm of the image gradient has shown good performance, yielding smooth solutions in spatially contiguous brain regions. Enormous resources have been devoted to establishing structural and functional brain connectivity networks that can be used to define spatially distributed yet related groups of voxels. We propose using the fused sparse group lasso penalty to encourage structured, sparse, and interpretable solutions by incorporating prior information about spatial and group structure among voxels. We present optimization steps for fused sparse group lasso penalized regression using the alternating direction method of multipliers (ADMM) algorithm. With simulation studies and in application to real fMRI data from the Autism Brain Imaging Data Exchange, we demonstrate conditions under which fusion and group penalty terms together outperform either of them alone.

1. Introduction

Since the earliest functional magnetic resonance imaging (fMRI) studies of the human brain were carried out in the early 1990s, there have been relatively few translations of basic neuroscience findings to clinical applications in psychiatry, such as the use of biomarkers for determining diagnosis, prognosis, or predicting treatment response (Kapur et al., 2012; Woo et al., 2017). The traditional mass univariate approach in neuroimaging, which fits a model to each voxel independently, has been successful at characterizing group-level brain structure and function. However, a predictive model approach, where neuroimage features serve as predictors and a clinical variable is modeled as the outcome, may be better suited to clinical application. Predictive models are able to exploit dependencies between brain regions and thus can potentially explain more variability in the outcome than a mass univariate approach. Moreover, predictive models can yield individual-level out-of-sample predictions with potential clinical utility.

In this paper, we show how the fused sparse group lasso, a structured, sparse estimator, can incorporate prior information into a predictive model, thereby allowing researchers to harness results from the extensive recent research on brain structural and functional connectivity. Our goals include not only predictive accuracy, but also interpretable parameter estimates, as based on the following criteria: First, model structure entails that parameter values have a straightforward meaning; e.g., linear models tend to be more interpretable than nonlinear models. Second, models are appropriately sparse, including only relevant predictors, while not excluding any relevant predictors. Third, parameter estimates are understandable in light of existing background knowledge. In a translational neuroimaging context, this would mean that the brain regions implicated by the model estimates are neuroscientifically plausible according to existing knowledge or provide new insight into the neurobiological mechanism influencing the clinical outcome, and can potentially be used to establish biomarkers.

In Section 4, we apply fused sparse group lasso to a resting state fMRI dataset from the Autism Brain Imaging Data Exchange (ABIDE), a public repository of MRI datasets (Di Martino et al., 2014). Autism spectrum disorder (ASD) is a group of developmental disorders characterized by impaired social functioning and restrictive and repetitive behavior, and affects approximately 1% of children (Di Martino et al., 2014). Neuroimaging studies report abnormal functional connectivity between brain regions in ASD, although findings are mixed regarding the specific nature of the abnormalities (Di Martino et al., 2014). In our application, we show that incorporating prior information about voxel spatial location and functional connectivity using fused sparse group lasso increases accuracy when predicting a continuous measure of autistic social impairment from resting state fMRI data.

Consider the linear regression model

$$\mathbf{y}=\mathbf{X}\beta +ϵ,$$ (1)

where $\mathbf{y}\in {\mathbb{R}}^n$ is a continuous outcome (e.g., score on a clinical depression rating scale), $\mathbf{X}\in {\mathbb{R}}^{n\times p}$ is a predictor matrix (e.g., neuroimage voxel values), $\beta \in {\mathbb{R}}^p$ is an unknown vector of coefficients, $ϵ\in {\mathbb{R}}^n$ is the error, E(ϵ) = 0, and E(ϵ^Tϵ) = σ²I_n. This represents a high-dimensional setting where the number of subjects n is much less than the number of predictors p, which can be on the order of 100,000 voxels. To obtain a unique solution for β, we can constrain the optimization problem using the penalized least squares estimator

$$\widehat{\beta }={\text{arg min}}_{\beta \in {\mathbb{R}}^p}\frac{1}{2}\Vert \mathbf{y}-\mathbf{X}\beta {\Vert }_2^2+\lambda J(\beta ),$$ (2)

where λ ⩾ 0 is a tuning parameter controlling the level of regularization. The penalty term J(β) can impose both sparsity and structure, thereby constraining the solution space according to a priori information about relationships between elements of β. Examples of unstructured and structured penalties are presented in Table 1.

Table 1.

Examples of unstructured and structured penalty terms

Unstructured penalties	J (β)
Lasso (Tibshirani, 1996)	∥β∥1
Ridge (Hoerl and Kennard, 1970)	$\Vert \beta {\Vert }_2^2$
Elastic net (Zou and Hastie, 2005)	$\alpha \Vert \beta {\Vert }_1+(1-\alpha )\Vert \beta {\Vert }_2^2;\alpha \in [0,1]$
Structured penalties	J (β)
Isotropic total variation (Rudin et al., 1992)	∥Dβ∥2,1; matrix D encodes spatial structure
Fused lasso* (Tibshirani et al., 2005)	α∥β∥1 + (1 – α)∥Dβ∥1; α ∈ [0, 1]
Graph net** (Grosenick et al., 2013)	$\alpha \Vert \beta {\Vert }_1+(1-\alpha )\Vert \mathbf{D}\beta {\Vert }_2^2;\alpha \in [0,1]$
Group lasso (Yuan and Lin, 2006)	${\sum }_{g\in \mathcal{G}}\sqrt{p_g}\Vert {\beta }_g{\Vert }_2$; groups $\mathcal{G}$ form a partition of β
Sparse group lasso (Simon et al., 2013)	$\alpha \Vert \beta {\Vert }_1+(1-\alpha ){\sum }_{g\in \mathcal{G}}\sqrt{p_g}\Vert {\beta }_g{\Vert }_2;\alpha \in [0,1]$

^*Also known as anisotropic total variation–l₁

^**Also known as sparse graph Laplacian

Simulation studies and applications to real neuroimaging datasets (mostly using fMRI) have shown that penalties enforcing spatial smoothness frequently outperform unstructured penalties (Michel et al., 2011; Fiot et al., 2014). Not only do spatially-informed penalties yield more interpretable estimates insofar as they select contiguous groups of voxels in neuroscientifically plausible brain regions, but they often show better prediction performance. In addition to spatial regularization, group-structured regularization has shown promise in predictive neuroimaging models. For example, Shimizu et al. (2015) found that group lasso and sparse group lasso were superior to lasso and random forest and comparable to SVM in terms of classification accuracy, but unlike SVM, produced sparse and more interpretable models.

For neuroimaging applications, we aim to incorporate two types of structure into the penalty term J(β) of the estimator in Equation (2): (1) local spatial information, to encourage smooth coefficient estimates across neighboring voxels; and (2) spatially distributed groups, such as those defined by functional or structural networks or anatomical regions, to allow voxels within the same group to be selected or shrunk to zero together. We achieve this by combining l₁, fusion, and group lasso penalties into a fused sparse group lasso penalty. We found one instance of this penalty in the literature, in a multi-task learning context where groups consist of repeated measures of the same task and smoothing is applied across time points within a group (Zhou et al., 2012). To our knowledge, the fused sparse group lasso penalty has never been studied via simulations or used in a predictive model with voxel-level neuroimaging data.

In the remainder of this paper, we present the fused sparse group lasso estimator in Section 2 and derive update steps to fit the fused sparse group lasso penalized least squares regression model using the alternating direction method of multipliers (ADMM) algorithm in Section 2.3. We report methods and results of a simulation study in Section 3 and apply our method to resting state fMRI data from the ABIDE repository in Section 4. We make concluding remarks in Section 5. We provide R and MATLAB functions for fitting the fused sparse group lasso estimator and additional supporting information online.

2. Fused Sparse Group Lasso

2.1. Model

Suppose we observe {(x₁, y₁), … , (x_n, y_n)} from n independent subjects, indexed by i = 1, … , n, where $y_i\in \mathbb{R}$ and ${\mathbf{x}}_i\in {\mathbb{R}}^p$. In the neuroimaging context considered here, y_i is a continuous scalar outcome for each subject such as age, depression scale score, or cognitive test score, and x_i is a vector of voxel values from a three dimensional brain image such that each element of x_i corresponds to one of p voxels. Assume that y = (y₁, … , y_n)^T and the columns of the matrix X = (x₁∣ … ∣x_n) are centered, so we do not have an intercept term. Furthermore, we standardize the columns of X to have unit standard deviation. We model the continuous outcome using standard linear regression as expressed in Equation (1).

2.2. Estimator

Since the number of voxels is typically orders of magnitude larger than the number of subjects, i.e., p ⪢ n, regularization is required to obtain a unique solution for β. We propose estimating β by minimizing the sum of the loss function and three penalty terms:

$$\widehat{\beta }={\text{arg min}}_{\beta \in {\mathbb{R}}^p}L(\beta )+{\lambda }_1\Vert \beta {\Vert }_1+{\lambda }_2\Vert \mathbf{D}\beta {\Vert }_1+{\lambda }_3{\Omega }^{\mathcal{G}}(\beta );$$ (3)

where L(β) is the loss function (e.g., least squares); $\Vert \beta {\Vert }_1={\sum }_{j=1}^p\mid {\beta }_j\mid$ the l₁ norm of β; D_m×p is the three dimensional fusion matrix for fused lasso (see Web Appendix A for example), and ∥Dβ∥₁ is the fusion penalty; ${\Omega }^{\mathcal{G}}(\beta )={\sum }_{g\in \mathcal{G}}\sqrt{p_g}\Vert {\beta }_g{\Vert }_2$ is the l_2,1 group lasso penalty, which applies the l₂ norm, $\Vert {\beta }_g{\Vert }_2=\sqrt{{\beta }_g^T{\beta }_g}$, to the coefficients β_g for each group $g\in \mathcal{G}$, each of size p_g; and λ₁, λ₂, λ₃ ⩾ 0 are regularization tuning parameters.

The three penalty terms incorporate prior information into the estimator, encouraging the solution to have both sparsity and a particular structure. The standard lasso l₁ penalty encourages overall sparsity. The fusion penalty penalizes the absolute differences between coefficients at neighboring voxels, thereby encouraging local smoothness. The group lasso penalty encourages a group-level structure; entire groups may be selected or shrunk to zero together. For example, if groups are defined by functional networks, the penalty allows voxels involved in a common network to be shrunk to zero if that network is not important for prediction. Given the overlapping structure of brain networks, overlapping groups are another possibility worth considering. With appropriate weighting and a latent variable approach (Obozinski et al., 2011), the estimator could also accommodate overlapping groups.

For ease of selecting values for the tuning parameters via cross-validation, it is convenient to reparameterize (3) as follows:

$$\begin{gathered} \widehat{\beta }={\text{arg min}}_{\beta \in {\mathbb{R}}^p}L(\beta )+\alpha \gamma \lambda \Vert \beta {\Vert }_1+(1-\gamma )\lambda \Vert \mathbf{D}\beta {\Vert }_1 \\ +(1-\alpha )\gamma \lambda {\Omega }^{\mathcal{G}}(\beta ), \end{gathered}$$ (4)

such that λ > 0 controls the overall level of regularization, α ∈ [0,1] controls the balance between the two sparsity inducing penalties (lasso and group lasso), and γ ∈ [0,1] controls the balance between the two sparsity inducing penalties and the fusion penalty. When α =1 and γ = 1, the estimator reduces to the standard lasso; when α = 0 and γ = 1, the estimator reduces to the group lasso, and so on for other subsets of the three penalty terms.

2.3. Optimization Algorithm

While a coordinate descent algorithm is often used to fit lasso penalized models, and Yuan and Lin (2006) proposed a blockwise coordinate descent algorithm for group lasso, coordinate descent does not work for the fused lasso penalty. As discussed in Friedman et al. (2007), there are two main reasons for this: (1) the fused lasso penalty is non-separable into a sum of functions of the elements of β, and (2) the fused lasso penalty is not continuously differentiable, so coordinate descent can get stuck. The accelerated gradient method algorithm employed in Zhou et al. (2012) depends on the separability of the penalty term across groups of β, which is possible because they applied the fusion penalty only within groups. We wanted to allow for fusion across groups as well. Thus, for the optimization problem expressed in Equation 3, we chose to implement an ADMM algorithm (Boyd et al., 2011).

For simplicity, we assume that the groups are non-overlapping and form a partition of β, so that each coefficient belongs to exactly one group. For applying ADMM, we follow a strategy similar to that employed in Huo and Tseng (2017) and exploit the fact that $\mid {\beta }_j\mid =\sqrt{{\beta }_j^2}$ and $\mid {\beta }_j-{\beta }_{j-1}\mid =\sqrt{({\beta }_j-{\beta }_{j-1}{)}^2}$. Then we can reformulate the lasso and fusion l₁ penalty terms as sets of l_2,1 group penalties whose groups have only one member. If there are p coefficients, D has m rows, and there are G groups that form a partition of β, then the total number of effective groups is p + m + G = N.

Using a least-squares loss function, we now write the objective function (3) as

$${\text{arg min}}_{\beta \in {\mathbb{R}}^p}\frac{1}{2}\Vert \mathbf{y}-\mathbf{X}\beta {\Vert }_2^2+\sum _{j=1}^N{\lambda }_j{w}_j\Vert {\mathbf{K}}_j\beta {\Vert }_2,$$ (5)

with

$$\{{\lambda }_j,{\mathbf{K}}_j\}=\{\begin{array}{cc}\{{\lambda }_1,{\mathbf{j}}_j\}\hfill & \text{if}j\in \{1,\dots ,p\}\hfill \\ \{{\lambda }_2,{\mathbf{d}}_j\}\hfill & \text{if}j\in \{p+1,\dots ,p+m\}\hfill \\ \{{\lambda }_3,{\mathbf{G}}_j\}\hfill & \text{if}j\in \{p+m+1,\dots ,p+m+G\},\hfill \end{array}\phantom{\}}$$

where λ_j ∈ {λ₁, λ₂, λ₃} are the regularization parameters for the lasso, fusion, and group lasso penalties, respectively; w_j are group weights (for group lasso typically $w_j=\sqrt{p_j}$ where p_j is the number of elements in group j); ${\mathbf{j}}_j\in {\mathbb{R}}^p$ corresponds to the jth row of the p × p identity matrix; ${\mathbf{d}}_j\in {\mathbb{R}}^p$ corresponds to the (j – p)th row of the fusion matrix D in the three dimensional fusion penalty; and ${\mathbf{G}}_j\in {\mathbb{R}}^{p_j\times p}$ is a sparse matrix where each row has a 1 at a column position corresponding to a member of group j.

For ADMM, we introduce the auxiliary variables θ_j = K_jβ. The optimization problem becomes minimize $\frac{1}{2}\Vert \mathbf{y}-\mathbf{X}\beta {\Vert }_2^2+{\sum }_{j=1}^N{\lambda }_j{w}_j\Vert {\theta }_j{\Vert }_2$, subject to θ_j – K_jβ = 0 for j ∈ {1,2, … , N}. Let K = (K₁∣ … ∣K_N), θ = (θ₁, … ,θ_N)^T, and μ = (μ₁, … , μ_N)^T. The augmented Lagrangian is ${\mathcal{L}}_{\mathit{\rho }}(\beta ,\theta ,\mu )=\frac{1}{2}\Vert \mathbf{y}-\mathbf{X}\beta {\Vert }_2^2+{\sum }_{j=1}^N{\lambda }_j{w}_j\Vert {\theta }_j{\Vert }_2+{\sum }_{j=1}^N[{\mu }_j^T({\theta }_j-{\mathbf{K}}_j\beta )+\frac{\rho }{2}\Vert {\theta }_j-{\mathbf{K}}_j\beta {\Vert }_2^2]$, where ρ > 0 is the step-size parameter and μ_j are the dual variables for ADMM. After initialization of β, θ, and μ, the update steps for ADMM consist of the following: ${\beta }^{t+1}={\text{arg min}}_{\beta \in {\mathbb{R}}^p}{\mathcal{L}}_{\rho }(\beta ,{\theta }^t,{\mu }^t)$; ${\theta }_j^{t+1}={\text{arg min}}_{{\theta }_j\in {\mathbb{R}}^{p_j}}{\mathcal{L}}_{\rho }({\beta }^{t+1},\theta ,{\mu }^t)$; ${\mu }_j^{t+1}={\mu }^t+\rho ({\theta }_j^{t+1}-{\mathbf{K}}_j{\beta }^{t+1})$. For β^t+1 and ${\theta }_j^{t+1}$ updates, the corresponding ${\mathcal{L}}_{\rho }$ subgradient will equal zero at the optimal solution. Thus, the update for β is β^t+1 = (X^TX + ρK^TK)⁻¹ [X^TY + K^T(μ^t + ρθ^t)], and the update for θ_j is ${\theta }_j^{t+1}=(1-{\lambda }_j{w}_j∕[\rho \Vert {\eta }_j{\Vert }_2]{)}_{+}{\eta }_j$, Where η_j = K_jβ – μ_j/ρ and (·)₊ = max(0, ·). We derive this and discuss how we implement stopping criteria and adaptive step-size in Web Appendix B.

2.4. Adaptive Fused Sparse Group Lasso

Zou (2006) showed that the lasso only exhibits consistent variable selection (i.e., identifies the right subset of non-zero coefficients asymptotically) under a certain nontrivial condition, which includes an orthogonal design matrix X and p = 2 as special cases. The adaptive lasso, on the other hand, achieves consistent variable selection by differentially scaling the tuning parameter, λ, for each coefficient by the factor $\mid {\widehat{\beta }}_j^{\ast }{\mid }^{-\gamma }$, where ${\widehat{\beta }}_j^{\ast }$ is a consistent estimator for β_j such as the ordinary least squares estimator, and γ > 0 (Zou, 2006). Adaptive versions of fused lasso (Viallon et al., 2013) and group lasso (Wang and Leng, 2008) have also been developed. In our application to a real neuroimaging dataset in Section 4, we implement an adaptive version of fused sparse group lasso using ridge regression to obtain initial coefficient estimates, ${\widehat{\beta }}^{\text{ridge}}={\text{arg min}}_{\beta \in {\mathbb{R}}^p}\frac{1}{2}\Vert \mathbf{y}-\mathbf{X}\beta {\Vert }_2^2+{\lambda }^{\text{ridge}}\Vert \beta {\Vert }_2^2$. The weights, w_j, introduced in Equation (5) are defined as

$$w_j=\{\begin{array}{cc}\Vert {\mathbf{j}}_j{\widehat{\beta }}^{\text{ridge}}{\Vert }_1^{-1}\hfill & \text{if}j\in \{1,\dots ,p\}\hfill \\ \Vert {\mathbf{d}}_j{\widehat{\beta }}^{\text{ridge}}{\Vert }_1^{-1}\hfill & \text{if}j\in \{p+1,\dots ,p+m\}\hfill \\ \Vert {\mathbf{G}}_j{\widehat{\beta }}^{\text{ridge}}{\Vert }_2^{-1}\hfill & \text{if}j\in \{p+m+1,\dots ,p+m+G\}.\hfill \end{array}\phantom{\}}$$ (6)

3. Simulation Study

3.1. Simulation Study Methods

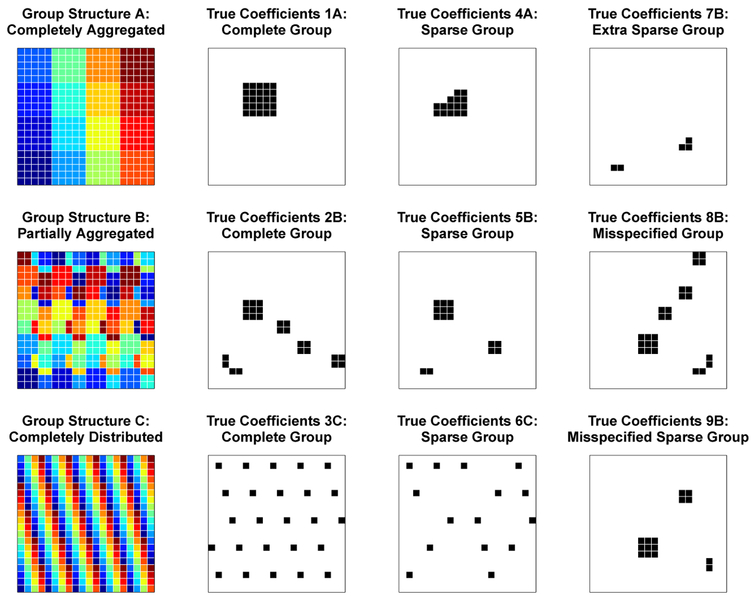
Our simulation study aimed to show that, for a given modeling scenario, the optimal weighting of the three penalty terms in the fused sparse group lasso depends on the underlying structure of the true coefficients. We also sought to characterize the optimal penalty weights for a range of different coefficient structures. Accordingly, we evenly divided the pixels of two dimensional 20 × 20 images into 16 groups of 25 and considered three spatial arrangements of the groups (Figure 1): (A) members of a group were completely aggregated into 5 × 5 squares; (B) groups were partially aggregated, consisting of one 3 × 3 square, three 2 × 2 squares, and two 1 × 2 rectangles; (C) groups were completely distributed such that no pixels from the same group were touching sides. For each of these group structures, one group was selected to have non-zero coefficients, which were all set equal to 3. We also considered sparse versions of the coefficients, where 40% of coefficients in the active group were set to zero. Additionally, we considered three more scenarios under the partially aggregated group structure: an extra sparse scenario, with 80% of active group coefficients set to zero; a misspecified group structure, where the set of true coefficients was divided among several groups; and a sparse version of the misspecified group structure. Thus, there were nine total scenarios of true coefficients (Figure 1).

Figure 1.

Simulation study group structures (top row) and true coefficients. This figure appears in color in the electronic version of the manuscript.

For each of n = 50 training subjects and n = 50 test subjects, we generated a vector of 400 independent standard normal random variables to serve as predictors, where each corresponded to a pixel in the 20 × 20 image. The responses, y, were then computed by the model y = Xβ + ϵ, where each element of ϵ was independent normal with mean zero and variance 4. To select optimal tuning parameter values, we parameterized according to Equation (4). The fusion penalty was applied between coefficients of pixels that shared an edge, and the group penalty was applied to each of the 16 groups, as previously described. For each pair of α ∈ {0, 0.2, 0.5, 0.8, 1} and γ ∈ {0, 0.2, 0.5, 0.8, 1}, we performed 5-fold cross-validation over 50 values of λ = 10^x, where values of x formed a grid on the interval [−3, 3], and selected the λ that resulted in the lowest cross-validation mean squared error. We fit the model to the entire sample of n = 50 training subjects at the given (α, γ) pair using this λ and calculated mean squared error of the estimated coefficients $(\text{MSE}(\widehat{\beta })=\Vert \widehat{\beta }-\beta {\Vert }_2^2∕400$) and mean squared prediction error for the test data $(\text{MSE}({\widehat{\mathbf{y}}}_{\text{test}})=\Vert {\widehat{\mathbf{y}}}_{\text{test}}-{\mathbf{y}}_{\text{test}}{\Vert }_2^2∕50$). We repeated the entire procedure 100 times for each of the nine scenarios. We also generated another test sample of n = 100 for the purpose of decomposing the mean squared error into squared bias and variance at each (α, γ) combination across the 100 trained models. Analyses were done using R version 3.4.0 (R Core Team, 2017).

We hypothesized that, on the basis of MSE$(\widehat{\beta })$, MSE$({\widehat{\mathbf{y}}}_{\text{test}})$, or both, (1) the fusion penalty term would perform worse and the sparsity penalty terms would perform better (i.e., optimal γ value would increase) as the groups became more spatially distributed; (2) the group penalty term would perform worse and the l₁ lasso penalty term would perform better (i.e., optimal α value would increase) as the sparsity of true coefficients increased or with misspecification of group structure. We also sought to determine whether the lowest cross-validation error would correspond to the optimal values of (α, γ).

3.2. Simulation Study Results

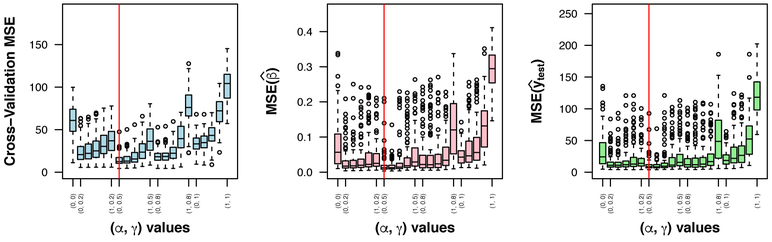
Figure 2 shows the distributions of cross-validation error, MSE$(\widehat{\beta })$, and MSE$({\widehat{\mathbf{y}}}_{\text{test}})$ across the (α, γ) combinations for true coefficient scenario 5B. Optimal (α, γ) combinations for each scenario are presented in Web Appendix C, Web Table C1; detailed simulation results are reported in Web Tables C2-C10; box plots for the other scenarios are shown in Web Figures C1-C3; and bias-variance decompositions of MSE$({\widehat{\mathbf{y}}}_{\text{test}})$ are shown in Web Figure C4.

Figure 2.

Simulation study results for true coefficients 5B. Values of γ ∈ {0, 0.2, 0.5, 0.8, 1} increase from left to right on the x-axis, corresponding to complete fusion penalty on the left (γ = 0) and complete sparsity penalties on the right (γ = 1). Intervals of increasing α ∈ {0, 0.2, 0.5, 0.8, 1} values correspond to complete group penalty on the left (α = 0) and complete l₁ lasso penalty on the right (α = 1). Vertical lines indicate (α, γ) combination yielding most frequent lowest error over 100 simulations. This figure appears in color in the electronic version of the manuscript. MSE: mean squared error.

As expected, on the basis of both MSE$(\widehat{\beta })$ and MSE$({\widehat{\mathbf{y}}}_{\text{test}})$, as groups became more spatially distributed, the optimal value of γ increased from 0.2 for the completely aggregated to 1 for the completely distributed group structure, shifting weight from the fusion penalty term to the sparsity penalty terms. This pattern was similar for the complete (1A, 2B, 3C) and sparse (4A, 5B, 6C) group scenarios. As the sparsity of true coefficients increased in the partially aggregated group scenarios (2B, 5B, 7B), the optimal value of α increased from 0 for the complete group to 0.8 for the extra sparse group scenario, shifting weight from the group penalty term to the l₁ lasso penalty term. When group structure was misspecified, the optimal α value was 1 for both scenarios (8B, 9B), putting zero weight on the group penalty term in favor of the l₁ lasso penalty term.

The results demonstrate that the combination of penalty terms in the fused sparse group lasso adapt to a wide range of spatial arrangements and sparsity levels of true coefficients. In all seven scenarios where group structure was correctly specified, the (α, γ) combination yielding the most frequent lowest cross-validation error corresponded to the most frequent lowest MSE$(\widehat{\beta })$ and MSE$({\widehat{\mathbf{y}}}_{\text{test}})$, indicating that selecting tuning parameters based on lowest cross-validation error tends to correspond to the optimal model. For the misspecified group scenarios, cross-validation error was lowest for either the first or second most frequent lowest MSE$(\widehat{\beta })$ and MSE$({\widehat{\mathbf{y}}}_{\text{test}})$ (see Web Appendix C, Web Tables C8 and C9).

4. Application to Neuroimaging Data

We applied fused sparse group lasso (FSGL) penalized regression to a resting state fMRI dataset of ASD (n = 111) and typically developing (TD, n = 108) male participants (mean (SD) age 17.4 (7.5) years, see Web Appendix D, Web Table D1 for descriptive summary) from the ABIDE repository (Di Martino et al. (2014), see Supporting Information for URL). In this set of participants, Cerliani et al. (2015) used independent components analysis to identify 19 resting state brain networks. The authors found that autistic traits as measured by Social Responsiveness Scale (SRS) scores were positively associated with functional connectivity between a subcortical network, comprising basal ganglia and thalamus, and two cortical networks: (1) dorsal and (2) ventral primary somatosensory and motor cortices. The association was only significant in the ASD group. Given that the resting state networks evaluated in Cerliani et al. (2015) represent relatively large brain regions, we used FSGL regression to more precisely define the cortical regions whose functional connectivity with a subcortical seed region best predicts SRS scores.

4.1. Application Methods

Preprocessed fMRI data was downloaded from the ABIDE I Preprocessed repository (Craddock et al., 2013). Data were preprocessed using the Connectome Computational System pipeline with no global signal regression and band pass filtering (0.01 – 0.1 Hz). The independent component resting state network data from Cerliani et al. (2015) was downloaded and resampled to 3×3×3 mm³ voxels to match the ABIDE data. (See Supporting Information for URLs.)

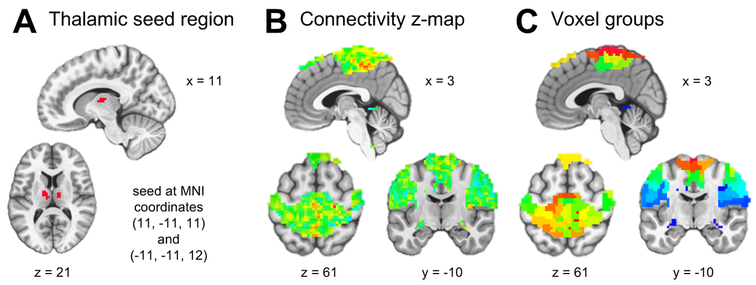
We partitioned the brain into 19 resting state networks by assigning each voxel to the maximal spatial independent component at that voxel out of the 19 components identified in Cerliani et al. (2015). We restricted our analyses to the three networks mentioned above: the basal ganglia/thalamus subcortical network and the two sensorimotor cortical networks. We defined a subcortical seed region by selecting the peak voxels in the subcortical network independent component spatial map. This yielded bilateral regions of the thalamus, with 12 voxels centered at MNI coordinates (11, −11, 11) and 11 voxels centered at (−11, −11, 12) (Figure 3A). For each participant, the first eigenvariate of the seed region time series was extracted, and its Pearson correlation was calculated with each voxel time series in the cortical regions of interest to form a seed-based connectivity map. Fisher’s r-to-z transformation was applied to each voxel. After excluding voxels where any participants had missing data, this left p = 5476 voxels to serve as predictors for FSGL regression (Figure 3B).

Figure 3.

(A) The thalamic seed region consisted of 23 3 × 3 × 3 mm³ voxels. (B) Connectivity z-maps of 5476 voxels for each participant served as predictors for fused sparse group lasso regression. (C) Voxels were partitioned into 50 groups using agglomerative hierarchical clustering on the training set resting state fMRI voxel time series. This figure appears in color in the electronic version of the manuscript.

Participant data were divided into training (n = 175) and test (n = 44) sets. Test set data was put aside until all model fitting was completed. The following steps were carried out with the training set data:

1. For the group penalty term, voxels in the cortical regions of interest were partitioned into 50 groups using agglomerative hierarchical clustering on the voxel time series. First, for each training participant, Pearson correlations between time series were calculated for all possible pairs of voxels in the cortical regions of interest. Correlation matrices were averaged across participants, and a distance matrix was formed by applying the elementwise transformation $d=\sqrt{2\ast (1-r)}$. Finally, hierarchical clustering using Ward’s method was performed based on the distance matrix, and the resulting tree was cut to form 50 groups which ranged in size from 43 to 268 voxels (Figure 3C).

2. A linear regression model adjusted raw SRS scores for age, full-scale IQ, site of acquisition, eye status at scan (open or closed), and mean framewise displacement. The residuals were used as the outcome for FSGL regression. (See Web Appendix D, Web Table D2)

3. After centering the SRS outcome and standardizing columns of the predictor matrix, 5-fold cross-validation was used to determine the λ value yielding the minimum cross-validation error at selected values of (α, γ) for the FSGL regression. We chose to compare (α, γ) equal to (1.0, 1.0) (standard lasso), (0.2, 1.0) (sparse group lasso), (0.2, 0.8) (fused sparse group lasso), and (0.0, 0.8) (fused group lasso). Cross-validation folds were stratified to ensure that they had similar distributions of the adjusted SRS outcome.

4. To estimate the coefficients, the model was fit to the entire training set at the optimal λ for selected values of (α, γ).

5. For adaptive FSGL regression, first ridge regression estimates were obtained (using R package glmnet, Friedman et al. (2010)) and adaptive weights were formed according to Equation 6, and then steps (3) and (4) were completed.

For the test set data, adjusted SRS scores were predicted for each participant by taking the dot product of the estimated FSGL regression parameters with the participant’s predictor variables, which were first standardized according to the training set column means and standard deviations. Raw test set SRS scores were adjusted using the linear regression model parameters estimated with the training set data. Prediction accuracy was assessed via mean squared error and Pearson correlation of predicted with actual adjusted SRS scores. Since prior studies have used resting state fMRI data to classify ASD and TD subjects into diagnostic groups rather than predict SRS, in order to compare our results we used receiver operating characteristic (ROC) curve analysis to find the best classification threshold for predicted SRS scores from the best-performing models and calculated the corresponding classification accuracies.

Analyses were done using a combination of AFNI version 17.1.03 (Cox, 1996), MATLAB version 9.1.0 (R2016b) (MATLAB, 2016), and R version 3.4.0 (R Core Team, 2017).

4.2. Application Results

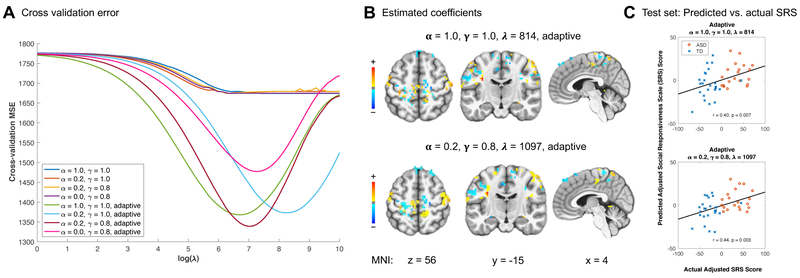
Results for non-adaptive and adaptive fused sparse group lasso as well as for ridge and elastic net penalties are summarized in Table 2. The best test set prediction was achieved by the adaptive fused sparse group lasso with (α, γ) equal to (0.2, 0.8), which gave a mean squared error of 1165.2 and Pearson correlation r = 0.437 (p = 0.003) (Figure 4C; see Web Appendix D, Web Figure D1 for other adaptive penalties). (For comparison, Cerliani et al. (2015) reported correlations of r = 0.21 and 0.25 for the respective cortical networks in ASD participants.) Cross-validation error was in general much lower for adaptive penalties than for non-adaptive penalties (Figure 4A). The superior performance of adaptive, ridge, and elastic net penalties over the non-adaptive penalties in this particular application is likely due at least in part to high multicollinearity of the predictors and the influence of many small, weak effects of predictors on the outcome rather than a few strong effects. Estimated coefficient brain maps for two sets of α and γ values are shown in Figure 4B (see Web Appendix D, Web Figure D1 for other adaptive penalties). Higher SRS scores correspond to greater autistic social impairment. Thus the coefficient maps reflect multivariate thalamic seed connectivity patterns predictive of greater social impairment. Penalties including the fusion term, i.e., with γ = 0.8, resulted in larger clusters of contiguous regions, rather than the more scattered coefficient maps resulting when γ = 1.0.

Table 2.

Comparison of estimators applied to ABIDE dataset

					Training set (n = 175)				Test set (n = 44)
Method	α	γ	Estimator	* Optimal λ	CVMSE	MSE	r	p	MSE	r	p
Glmnet	0.0		Ridge	2627	1646.7	954.3	0.879	< 0.001	1325.8	0.285	0.060
	0.01		Elastic Net	289	1661.2	935.7	0.883	< 0.001	1305.4	0.320	0.034
FSGL	1.0	1.0	Lasso	1848	1674.2	1689.1	0.159	0.036	1426.7	0.035	0.821
	0.2	1.0	Sparse Group Lasso	521	1674.4	1572.0	0.383	< 0.001	1427.8	0.069	0.654
	0.2	0.8	Fused Sparse Group Lasso	604	1673.9	1633.2	0.254	< 0.001	1434.3	0.038	0.805
	0.0	0.8	Fused Group Lasso	604	1674.3	1641.2	0.232	0.002	1435.4	0.032	0.838
Adaptive FSGL	1.0	1.0	Adaptive Lasso	814	1368.1	120.1	0.986	< 0.001	1193.1	0.406	0.006
	0.2	1.0	Adaptive Sparse Group Lasso	4041	1373.2	129.1	0.985	< 0.001	1203.1	0.397	0.008
	0.2	0.8	Adaptive Fused Sparse Group Lasso	1097	1338.9	168.6	0.977	< 0.001	1165.2	0.437	0.003
	0.0	0.8	Adaptive Fused Group Lasso	1424	1477.2	144.2	0.981	< 0.001	1211.6	0.394	0.008

^*Note: λ for glmnet R package is scaled by factor n⁻¹.

Mean total sum of squares for training set = 1697.5; Mean total sum of squares for test set = 1428.0. ABIDE: Autism Brain Imaging Data Exchange; FSGL: fused sparse group lasso; CVMSE: cross-validation mean squared error; MSE: mean squared error; r: Pearson correlation.

Figure 4.

(A) Five-fold cross-validation was carried out over a range of λ values for several sets of α and γ values. (B) Correlation of predicted and actual adjusted SRS scores for selected α and γ values. Points are distinguished by autism spectrum disorder (ASD, red circle) and typically developing (TD, blue cross) diagnosis groups. (C) Estimated coefficients at the optimal λ for selected α and γ values. Higher coefficient values contribute to higher predicted Social Responsiveness Scale (SRS) scores, which indicate greater autistic social impairment. MNI: Montreal Neurological Institute coordinates. This figure appears in color in the electronic version of the manuscript.

A couple of questions arise regarding the clinical significance of the findings. First, does the result provide insight into the neurobiology of ASD? While the sparse, structured penalty succeeded in narrowing down the predictors to a smaller subset of the most predictive voxels, it is not immediately clear why these particular scattered regions of sensorimotor cortex are most informative. We invite interested readers to further explore the coefficient brain maps available at the URL noted in the Supporting Information Section, below. Second, does the result represent a good diagnostic biomarker? We consider this question in the following context. ASD has been associated with abnormalities in connectivity between multiple brain regions (Di Martino et al., 2014). Accordingly, studies using resting state fMRI data to define ASD biomarkers have often summarized voxel-level data using regions of interest and considered connectivity between multiple regions, rather than use a focused, voxel-level approach as we did. Previous studies using such methods on the ABIDE dataset have achieved diagnostic classification (ASD versus TD) accuracies in the range of 60% to 71% (Abraham et al., 2017; Nielsen et al., 2013; Plitt et al., 2015; Kassraian-Fard et al., 2016), well below the classification accuracy that can be achieved using behavioral measures such as the SRS, which can attain accuracies of up to 95% (Plitt et al., 2015). The difficulty of identifying fMRI biomarkers for ASD may be due to the noisiness of fMRI data or the neurobiological heterogeneity of the disorder (Plitt et al., 2015). What is remarkable about our result is that, when we dichotomize our predicted outcomes for the purpose of diagnostic classification, we can achieve similar accuracies (classification accuracy of 29 to 30 out of 44 test subjects, or 66% to 68%, for the adaptive penalties), even though we only considered connectivity between a single thalamic seed region and sensorimotor cortex. This may reflect the richness imparted by voxel-level as opposed to region of interest functional connectivity data. It seems possible that adding other features to the model, e.g., using not only a thalamic seed region, but also including voxel-level connectivity data from other seed regions that have shown abnormal connectivity in ASD, such as the default mode network and regions implicated in social cognition, would likely improve prediction performance further.

5. Conclusions

The fused sparse group lasso penalty offers a flexible way to incorporate pertinent structure into a predictive model, which can lead to more interpretable coefficient estimates and better predictive performance on test data. The fusion penalty term constrains coefficients that we expect to have similar estimated values, and we can use it to enforce local spatial smoothness in an image. The group penalty term groups together coefficients that we do not necessarily expect to have similar values, but we expect to be selected simultaneously, such as voxels residing in the same functional brain networks. The l₁ penalty term allows sparse groups, and may also be useful when groups are misspecified. Cross-validation over a range of weights for the three penalty terms allows a data-driven way of incorporating information about coefficient structure into a prediction model.

In this paper we have presented an ADMM optimization algorithm to fit fused sparse group lasso. A simulation study featuring a range of coefficient structures demonstrated instances where a combination of the three penalty terms together outperforms any smaller subset, and showed that cross-validation is a reliable way to select optimal tuning parameter weights. On real fMRI data, we found that incorporating adaptive weights derived from initial ridge regression coefficient estimates greatly improved performance over non-adaptive fused sparse group lasso as well as ridge and elastic net penalties. The adaptive fused sparse group lasso produced the best test set prediction, and the addition of fusion and group penalty terms resulted in less dispersed, more clustered coefficient maps. Fused sparse group lasso, a generalization of lasso, group lasso, and fused lasso, has potential application not only to prediction problems in neuroimaging, but also to other contexts where coefficients are expected to be both smooth and group-structured.