Clinical integration of automated processing for brain quantitative susceptibility mapping: multi-site reproducibility and single-site robustness.

Abstract

Background and Purpose:

Quantitative susceptibility mapping (QSM) of the brain has become highly reproducible and has applications in an expanding array of diseases. To translate QSM from bench to bedside, it is important to automate its reconstruction immediately after data acquisition. In this work, a server system that automatically reconstructs QSM and exchange images with the scanner using the DICOM standard is demonstrated using a multi-site, multi-vendor reproducibility study and a large, single-site, multi-scanner image quality review study in in a clinical environment.

Methods:

A single healthy subject was scanned with a 3D multi-echo gradient echo sequence at 9 sites around the world using scanners from three manufacturers. A high resolution (HiRes, 0.5×0.5×1mm³ reconstructed) and standard resolution (StdRes, 0.5×0.5×3mm³) protocol was performed. ROI analysis of various white matter and gray matter regions was performed to investigate reproducibility across sites. At one institution, a retrospective multi-scanner image quality review was carried out of all clinical QSM images acquired consecutively in one month.

Results:

Reconstruction times using a GPU were 29±22s (StdRes), and 55±39s (HiRes). ROI standard deviation across sites was below 24ppb (StdRes) and 17ppb (HiRes). Correlations between ROI averages across sites were on average 0.92 (StdRes) and 0.96 (HiRes). Image quality review of 873 consecutive patients revealed diagnostic or excellent image quality in 96% of patients.

Conclusion:

Online QSM reconstruction for a variety of sites and scanner platforms with low cross-site ROI standard deviation is demonstrated. Image quality review revealed diagnostic or excellent image quality in 96% of 873 patients.

Introduction

Quantitative susceptibility mapping (QSM) enables the quantitative measurement of tissue magnetic susceptibility, which is a measure of how tissue responds to an external magnetic field.^1,2 Quantitative susceptibility mapping (QSM) has been used increasingly in clinical brain studies,^3,4 particularly for visualizing and quantifying iron in brain diseases, including multiple sclerosis (MS),^5–10 distinguishing calcifications and hemorrhage,^11–15 and preoperative planning for deep brain stimulation.¹⁶ In the brain, QSM technology has advanced to a stage of high reproducibility as demonstrated by various groups.^17–21 Accordingly, it is time to consider dissemination of brain QSM to routine clinical use, especially for measuring highly paramagnetic iron and highly-concentrated diamagnetic calcium.³

QSM data acquisition has largely converged to the 3D multi-echo gradient echo sequence (mGRE), and QSM reconstructions are generally flavors of the Bayesian optimization, which is a principled approach to the ill-posed magnetic field to susceptibility source inverse problem.²² As all Bayesian reconstruction methods are fundamentally similar, we propose for routine clinical use a basic formulation of the data fidelity and structure regularization.^1,2,23,24 The QSM reconstruction Matlab source code, along with the detailed acquisition protocols on scanners from three major manufacturers, can be downloaded freely from http://pre.weill.cornell.edu/mri/pages/qsm.html. For clinical applications, a robust automated QSM reconstruction suitable for inclusion in routine clinical MRI protocols is essential. A scanner vendor independent server system is presented that is connected to scanners for automated QSM reconstruction within a few minutes of data acquisition completion. Using this setup, a single-subject multi-site, multi-vendor reproducibility study and a large, single-site, multi-scanner image quality review study in in a clinical environment is performed.

Methods

QSM reconstruction server implementation

The nonlinear MEDI method^25,26 was used to reconstruct a susceptibility map, expressed in units of parts per million (ppm) or parts per billion (ppb). The algorithm performed the following steps. Input data was complex gradient echo signal $s\left(\mathit{r},T{E}_j\right)$, with r the voxel position and $T{E}_j$ the jth echo. For each r, a nonlinear least squares fit of the field $b\left(\mathit{r}\right)$ (rad/s)

$$b\left(\mathit{r}\right)={\text{argmin}}_{b\left(\mathit{r}\right)}{\sum }_j{\left|s\left(\mathit{r},T{E}_j\right)-|s\left(\mathit{r},T{E}_j\right)|e^{-ib\left(\mathit{r}\right)\gamma T{E}_j}\right|}^2,$$ [1]

where γ is the gyromagnetic ratio was performed using the Gauss-Newton algorithm,²⁷ as well as its standard error $n\left(\mathit{r}\right)$, followed by image quality guided unwrapping.²⁸ A magnitude image was constructed as $I\left(\mathit{r}\right)={\left({\sum }_j{\left|s\left(\mathit{r},T{E}_j\right)\right|}^2\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$. From $I\left(\mathit{r}\right)$, two masks were constructed. The Brain Extraction Tool (BET) algorithm in the FSL toolkit^29,30 was used to extract a brain mask $M\left(\mathit{r}\right)$. A binary edge mask $M_G\left(\mathit{r}\right)$ was obtained by computing the 3D gradient for each of the N voxels in $I\left(\mathit{r}\right)$, and retaining the largest $0.9N$ edges. From the multi-echo data, an $R_2^{*}$ map was computed using the ARLO method,³¹ from which the ventricular cerebral spinal fluid (CSF) regions were segmented, obtaining a binary mask $M_{CSF}$.²⁶ The Projection onto Dipole Fields³² (PDF) method was used to remove the background field: $b_L\left(\mathit{r}\right)=b\left(\mathit{r}\right)-d*{\chi }_B\left(\mathit{r}\right)$ with ${\chi }_B\left(\mathit{r}\right)={\text{argmin}}_{{\chi }_{\overline{M}}\left(\mathit{r}\right)}{\Vert M\left(b\left(\mathit{r}\right)-d*{\chi }_{\overline{M}}\left(\mathit{r}\right)\right)\Vert }_2^2$, where ${\chi }_{\overline{M}}$ was the background susceptibility on the mask $\overline{M}=1-M,\hspace{0.17em}*$ denoted convolution and $d\left(\mathit{r}\right)=\frac{1}{4\pi }{\frac{3co{s}^2\theta -1}{r^3}|}_{r\ne 0}$ was the dipole kernel with $\theta$ the angle between r and ${\mathit{B}}_{\text{0}}$. The minimization was carried out using the conjugate gradient method.²⁷ The relative difference field ${\delta }_b\left(\mathit{r}\right)=b_L\left(\mathit{r}\right)/B_0$ relative to the main magnetic field $B_0$ was computed (in rad/s). Next, the nonlinear Morphology Enable Dipole Inversion (MEDI)²⁵ with CSF zero referencing²⁶ was used to obtain the susceptibility map (in ppm). It solved

$${\chi }^{*}\left(\mathit{r}\right)={\text{argmin}}_{\chi \left(\mathit{r}\right)}\begin{array}{c}{\Vert W\left(\mathit{r}\right)\left(e^{-iS*d*\chi \left(\mathit{r}\right)}-e^{-i{\delta }_b\left(\mathit{r}\right)}\right)\Vert }_2^2\\ +{\lambda }_1{\Vert M_G\left(\mathit{r}\right)\nabla \chi \left(\mathit{r}\right)\Vert }_1+{\lambda }_2{\Vert M_{CSF}\left(\mathit{r}\right)\left(\chi \left(\mathit{r}\right)-\overline{{\chi }_{CSF}}\right)\Vert }_2^2\end{array},$$ [2]

where S is the spherical mean value operator (radius 5mm), $W\left(\mathit{r}\right)\propto M\left(r\right)/n\left(r\right)$ eflecting the reliability of ${\delta }_b\left(\mathit{r}\right)$, $\nabla$ the 3D gradient operator and $\overline{{\chi }_{CSF}}$ the average of $\chi \left(\mathit{r}\right)$ over the mask $M_{CSF}$. The spherical mean value operator is introduced to suppress remaining background field in ${\delta }_b\left(\mathit{r}\right)$ but introduces an erosion (5mm) of the mask M. Eq. 2 was solved iteratively using the Gauss-Newton method, using iterative reweighting.²⁵ ${\lambda }_1$ was set to 0.001 and ${\lambda }_2$ to 0.1. The average susceptibility $\overline{{\chi }_{CSF}^{*}}$ of the ventricular CSF in the solution ${\chi }^{*}$ was computed and subtracted from this solution to obtain the final CSF referenced susceptibility map. Pixel values on the QSM map correspond to susceptibility values measured in ppb.

The nonlinear MEDI method was implemented in C++ for both CPU and GPU. The major computational costs of the nonlinear MEDI algorithm lies in the computation of FFTs (needed to compute the dipole convolution forward problem central in QSM) and in linear algebra operations (needed for nonlinear phase to field fitting, background field removal and dipole inversion). For optimized running times, these components used the Intel Math Kernel Library (MKL)³³ on the CPU, while the cuFFT³⁴ and cuBLAS³⁵ libraries were used for the GPU. All other C++ code was identical between the CPU and GPU implementations, used multithreading where appropriate and was run on the CPU. The DCMTK toolkit library³⁶ was used for DICOM input and output. The QSM reconstruction server consisted of a DICOM server able to receive images from multiple scanners simultaneously. The DICOM protocol was chosen since this is implemented by all scanner manufacturers and requires nothing more than the setting up of DICOM destination (node) on a scanner. The technologist is then able to send the mGRE images immediately after the scan to the QSM reconstruction server, where they are stored in a temporary directory. For some scanner vendors, this was done automatically and thus required no additional action by the technologist. The QSM reconstruction server continuously polled for the presence of these temporary directories and determined whether the images were suitable mGRE images, were complete, weren’t previously received and/or processed and moved the data in a first-in-first-out queue. When images were present in the queue, the C++ program described above was invoked, one at a time. The resulting QSM images were then sent back to the originating scanner using the DICOM protocol. The QSM reconstruction server has been tested on Linux (Ubuntu 16.04, Redhat 7.0) and MacOS.

Acquisition

The QSM reconstruction server was installed at 9 sites (see Table 1) using scanners from three different vendors. Using this setup, two studies were carried out.

Table 1.

Scanners and sites with the quantitative susceptibility mapping reconstruction server installed used in this work.

1	Weill Cornell Medical College, New York, NY	General Electric (DV25)
2	Weill Cornell Medical College, New York, NY	Siemens (VE11B)
3	Aix-Marseille University, Marseille,France	Siemens (VB17)
4	Charité – Universitätsmedizin Berlin, Germany	Siemens (VE11)
5	Centre Hospitalier Universitaire, Toulouse, France	Philips Medical Systems (5.1.7.2)
6	University of Vermont Medical Center, Burlington, VT	Philips Medical Systems (5.3.1.0)
7	Icahn School of Medicine at Mount Sinai, New York, NY	General Electric (DV25)
8	Royal Melbourne Hosp, Melbourne, VIC, Australia	Siemens (VE11B)
9	Hôpital Pitié-Salpêtrière, Paris, France	Siemens (VD13)

First, between June 2017 and January 2018, a single healthy subject (male, 52 years old) visited these 9 sites, signed the local IRB-approved consent form, and was then scanned using both standard resolution (StdRes) and high resolution (HiRes) mGRE protocols at 3T. The StdRes parameters were chosen based on the clinical protocol for MS patients at Weill Cornell Medical College (WCMC). The parameters were chosen to achieve a high resolution depiction in the imaging plane (in plane resolution) as well as a sampling of the magnetic field with high signal to noise ratio (echo times up to ~45ms). The resulting long TR (~50ms) necessitated increasing the slice thickness to achieve a clinically acceptable scan time below 5 minutes. The HiRes protocol was based on a deep brain stimulation imaging protocol for preoperative planning. All imaging parameters are shown in Table 2. These parameters were considered target parameters and deviations were present depending on site and scanner vendor.

Table 2.

Imaging parameters for the standard resolution (StdRes) and high resolution (HiRes) gradient echo acquisition for quantitative susceptibility mapping.

	StdRes	HiRes
Acquired voxel size	0.95 × 0.75 × 4.0 mm3	0.8 × 0.8 × 1.0 mm3
Reconstructed voxel size	0.75 × 0.75 × 3.0 mm3	0.8 × 0.8 × 1.0 mm3
Acquisition matrix	320 × 320 × 56	320 × 320 × 172
FOV (Readout/Phase)	240/195 mm	256/208 mm
TR	49 ms	49 ms
Number of TEs	10	10
TE1/ΔTE	6.69/4.06 ms	6.73/4.06 ms
Coil	32 channel head coil	32 channel head coil
Flip angle	15°	15°
Reconstruction	Real/Imaginary or Magnitude/Phase	Real/Imaginary or Magnitude/Phase
Partial k-space $\left(k_y/k_z\right)$	100/100 %	75/75 %
Acceleration factor	2	2
Flow compensation	Readout	Readout
Readout bandwidth	260 Hz/pixel	260 Hz/pixel
Scan time	4m32s	12m19s

Abbreviations: FOV = field of view, TR = repetition time, TE = echo time, TE1 = first echo time, ΔTE = echo spacing,

Second, at WCMC, all consecutive patients for which a QSM was acquired during the month of June 2018 were selected for a retrospective review of image quality under an IRB approved protocol. Patients were scanned on 11 different scanners from two vendors (Prisma 3T, Skyra 3T, Biograph 3T PET/MR, Aera 1.5T, Siemens Healthcare, Erlangen, Germany and MR-750 3T, Architect 1.5T, and HDx 1.5T, GE Healthcare, Waukesha, WI).

Analysis

QSM reconstruction times were measured on a single server at WCMC for all data. This server used an Intel Core i9–9940X (14 Cores, 3.30 GHz) and 128G of RAM running Ubuntu 18.04. GPU reconstructions were performed using an NVIDIA GTX 1080 Ti using 3584 CUDA cores running at 1.582 GHz and 11 GB of GDDR5X memory running at 11.4 Gbps. QSM reconstruction was performed on this server for both the HiRes and StdRes healthy volunteer data from each of the 9 sites using both the CPU and GPU implementations and running times were recorded and summarized.

For each acquisition, the magnitude images $I\left(\mathit{r}\right)$ were registered to a reference magnitude image $I_{ref}\left(\mathit{r}\right)$ taken from the HiRes protocol at site #2 using FLIRT (FSL).³⁰ A HiRes protocol was chosen as reference because it provided the highest nearly isotropic resolution, thus improving image registration performance.^37,38 On the susceptibility map obtained with the HiRes protocol at site #2, an experienced neuroradiologist (SZ, 7 years of experience) segmented the following regions of interest (ROI): Caudate Nucleus (CN), Putamen (P), Globus Pallidus (GP), Thalamus (T), Substantia Nigra (SN), Red Nucleus (RN), Posterior limb of Internal Capsule (PIC), and Splenium of Corpus Callosum (SCC). These ROIs were then registered back to each of the susceptibility maps by applying the inverse transformation. An additional erosion (radius 1 voxel) of each transformed ROI in each original susceptibility map was performed to suppress potential partial volume effects. For each susceptibility map, the ROI means were recorded and their average and standard deviation across sites were recorded to assess the reproducibility of the susceptibility mapping method. Normality of the measurements was assessed using a D’Agostino & Pearson normality test. Bland-Altman, correlation analysis and two-way ANOVA analysis was performed on the ROI measurements between sites. The significance level for all tests was set at 0.05.

For the patient study at WCMC, all QSM recons were done by a reconstruction server as described above immediately after the acquisition of the mGRE data in each patient. This server used an Intel Core i7–6850K (6 Cores, 3.60GHz), 64G of RAM, and a NVIDIA GTX 1080 Ti GPU. Image quality was scored by an experienced neuroradiologist (SZ, 7 years of experience) using a 3 point scale: 3=excellent (no obvious artifacts with excellent depiction of deep gray matter regions and cortical gray-white matter contrast), 2=diagnostic (moderate artifacts but deep gray matter regions and cortical gray-white matter contrast still visualized), and 1=poor (strong artifacts and poor cortical gray-white matter contrast). QSM artifacts include those caused by motion, implants, or hemorrhage and typically manifest as streaking artifacts. Disease category, gender and age were recorded for each patient.

Results

Susceptibility maps were obtained in all cases. Reconstruction times for the StdRes procotocol (N=9) were 56±39s for the CPU recon and 29±22s for the GPU recon (p=0.003). Reconstruction times for the HiRes protocol (N=9) were 105±60s for the CPU recon and 55±39s for the GPU recon (p=0.0002).

Figure 1 shows an axial slice of the susceptibility maps through the midbrain of the subject imaged using the StdRes protocol. The corresponding HiRes images are shown in Figure 2. For both protocols, an excellent visual correspondence across the brain between the 9 sites is observed.

Figure 1.

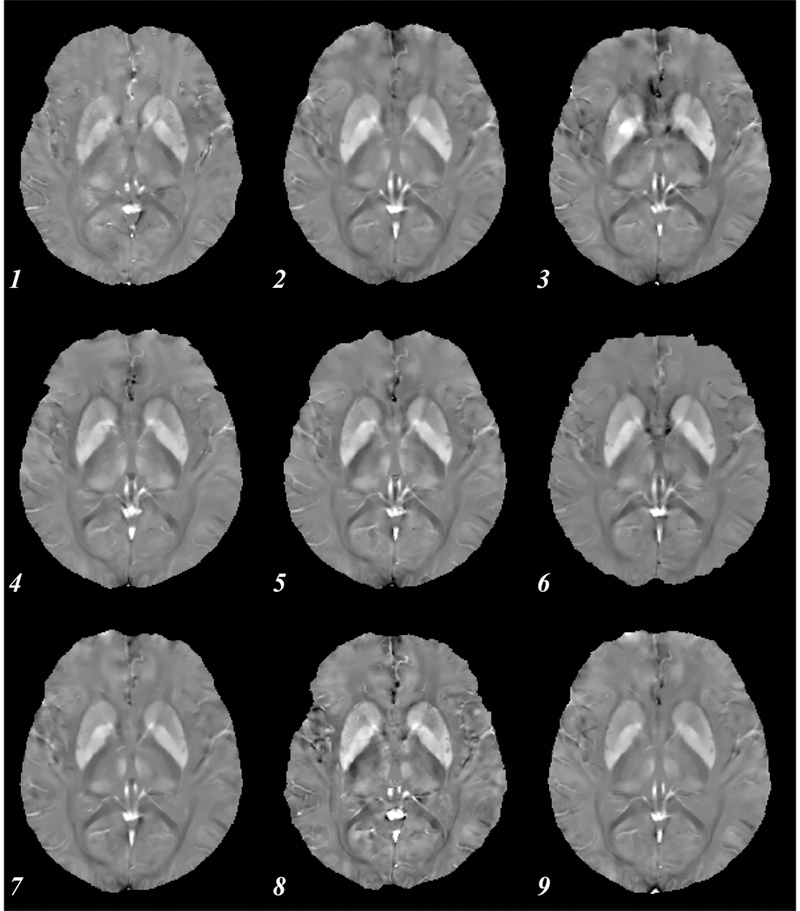
Axial susceptibility map for a single subject using the standard resolution protocol. Numbers indicate site (see Table 1). All images shown are co-registered, showing similar basal ganglia.

Figure 2.

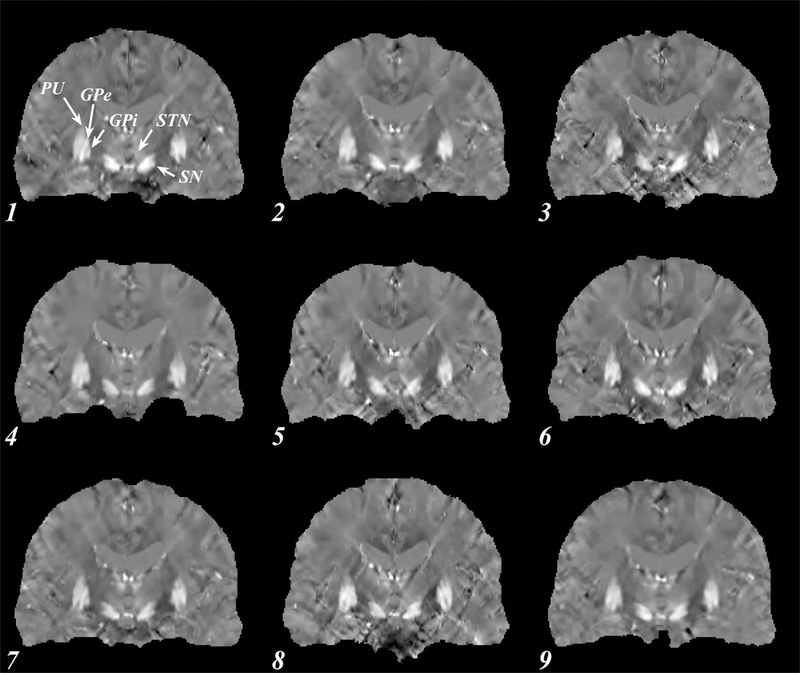
Coronal susceptibility map for a single subject using the high resolution protocol. Numbers indicate site (see Table 1). All images shown are co-registered, clearly depicting the subthalamic nuclei (STN) and the globus pallidus (GP), important targets for deep brain stimulation. Other brain regions well visualized are the putamen (PU), external and internal globus pallidus (GPe and GPi) and the substantia nigra (SN).

The measurements (in ppb) for the CN, P, GP, T, SN, RN, DN, PIC and SCC ROIs for each scan and protocol passed the normality test (p>0.11). The ROI measurement reproducibility across scanners is shown in Figure 3a for the StdRes protocol and Figure 3b for the HiRes protocol. The standard deviation of the ROI measurements across the 9 scanners ranged between 3.6 and 24.3 ppb for the StdRes protocol and between 5 and 17.6 ppb for the HiRes protocol. These numbers are consistent with the inter-scanner and same scanner reproducibility reported in the literature.¹⁸ Averaged across all possible pairs of sites, bias (in absolute value) was 4.5±2.8 ppb (StdRes protocol) and 3.4±2.4 ppb (HiRes protocol), limits of agreement were ±18.7±5.6 ppb (StdRes protocol) and ±14.3±3.8 ppb (HiRes protocol) around the bias, regression slope was 0.98±0.20 for the StdRes protocol and 0.96±0.09 for the HiRes protocol, and the corresponding average R² was 0.92±0.05 for the StdRes protocol and 0.96±0.02 for the HiRes protocol. ANOVA analysis revealed that site accounted for 1.56% of the total variance (P<0.0001) for the StdRes protocol and 0.57% (P<0.0001) for the HiRes protocol.

Figure 3.

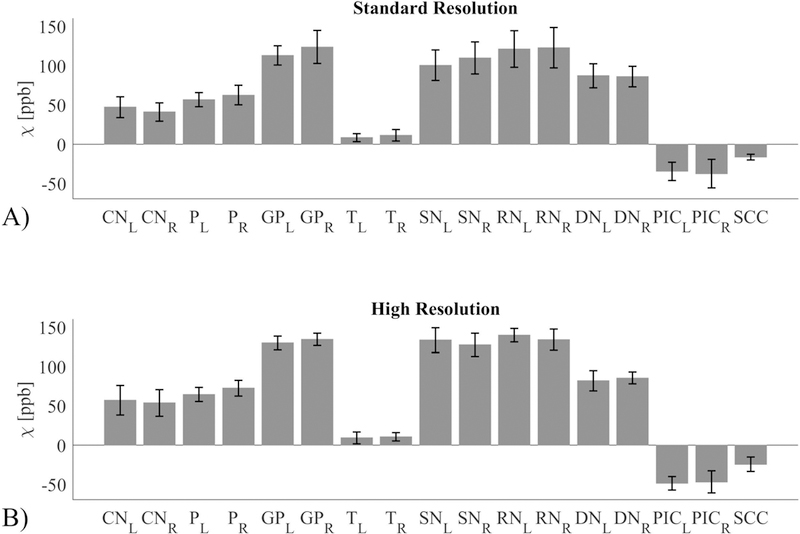
Reproducibility of susceptibility $\chi$ (expressed in units of parts per billion or ppb) for a single subject at multiple sites for A) the standard resolution protocol and B) the high resolution protocol. The analysed regions of interest are: Caudate Nucleus (CN), Putamen (P), Globus Pallidus (GP), Thalamus (T), Substantia Nigra (SN), Red Nucleus (RN), Dentate Nucleus (DN), Posterior limb of Internal Capsule (PIC), and Splenium of Corpus Callosum (SCC). Both left (L) and right (R) values are shown where appropriate.

Results for the image quality review of QSM acquired in patients are shown in Table 3. 873 patients were selected suffering from a variety of conditions. Image quality was consistently high, with 775, 67, and 31 patients having excellent image, moderate and poor image quality, respectively. Examples of QSM images for each image score are shown in Figure 4 and for a number of diseases in Figures 5 through 8. In these Figures, susceptibility values are shown within an eroded (smaller) brain mask, i.e., voxels at the cortex have been removed. Figure 5 shows a QSM of an arteriovenous malformation (arrow) in the left frontal lobe, showing the nidus of abnormal blood vessels. Figure 6 shows a QSM of an atypical meningioma located on left frontoparietal convexity. Hyperintense foci of intratumoral hemorrhage are bright on QSM. Figure 7 shows a QSM of a multiple sclerosis (MS) patient. The arrow points to a lesion that is hyperintense on QSM but non-enhancing on the contrast enhanced T1 weighted image. Recent efforts indicate that enhancement or lack thereof on QSM of lesions seen on T2 can predict T1 enhancement.^39–41 Figure 8 shows an intracranial hemorrhage. QSM is hyperintense in the hemorrhage due to its strong paramagnetism.

Table 3.

Patient demographics and image quality scores. Image quality scores used a 3-point scale: 3=excellent, 2=diagnostic, and 1=poor.

Disease category	Number	Sex (Male/Female)	Age (years, M ± SD)	Image Quality (M ± SD)
Cerebral vascular diseases (including arteriovenous malformation, e.g. Figure 5)	104	47/57	62.29±19.38	2.85±0.44
Brain tumor (including meningioma, e.g. Figure 6)	262	122/140	53.92±20.27	2.85±0.47
Demyelinating diseases (including multiple sclerosis, e.g. Figure 7)	109	31/78	43.5±14.56	2.93±0.3
Neurodegenerative diseases	45	23/22	62.09±24.22	2.93±0.33
Psychiatric diseases	12	5/7	54.25±21.9	2.33±0.89
Intracranial hemorrhage (e.g. Figure 8)	36	17/19	52.82±25.47	2.53±0.77
Intracranial infection	14	4/10	43.79±21.27	2.93±0.27
Seizure	29	19/10	33.35±24.41	2.97±0.19
Chiari malformation	11	3/8	30.91±22.68	2.91±0.3
Intracranial benign cyst	17	7/10	25.6±20.4	2.88±0.33
Nonspecific neurologic complaints (e.g., dizziness/headache)	234	91/143	48.55±22.92	2.85±0.41
Total	873	369/504	50.87±22.05	2.85±0.41

Abbreviations: M=mean, SD=standard deviation

Figure 4.

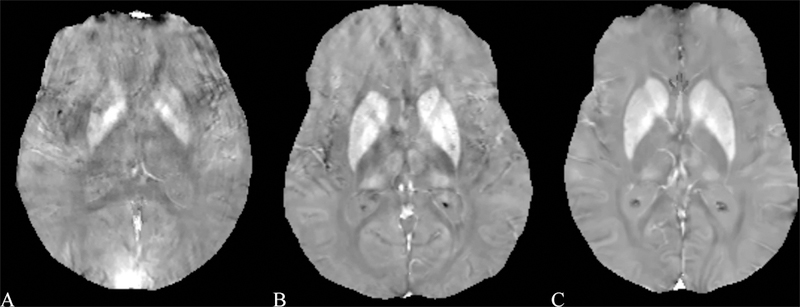
Example images for each of the scores using the image scoring analysis. A) poor image quality (score 1) in a male 64 year old patient with Multiple Sclerosis (MS), caused by large motion during the acquisition. B) diagnostic image quality (score 2) in a 55 year old female patient with MS, caused by moderate motion during the acquisition. C) excellent image quality (score 3) in a 54 year old female patient with MS.

Figure 5.

A) Brain quantitative susceptibility map of a 46 year old female with an arteriovenous malformation (arrow) in the left frontal lobe, showing the nidus of abnormal blood vessels. B) Corresponding transverse relaxation (T2) weighted image.

Figure 8.

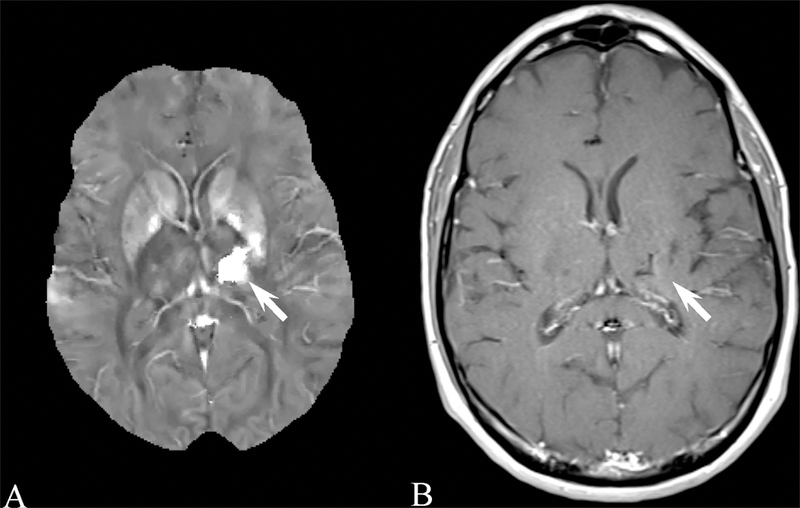
A) Brain quantitative susceptibility map of a 49 year old male with intracranial hemorrhage (arrow). The large hyperintensity indicates the strong paramagnetism of the hemorrhage. B) The corresponding contrast enhanced longitudinal relaxation (T1) weighted image.

Figure 6.

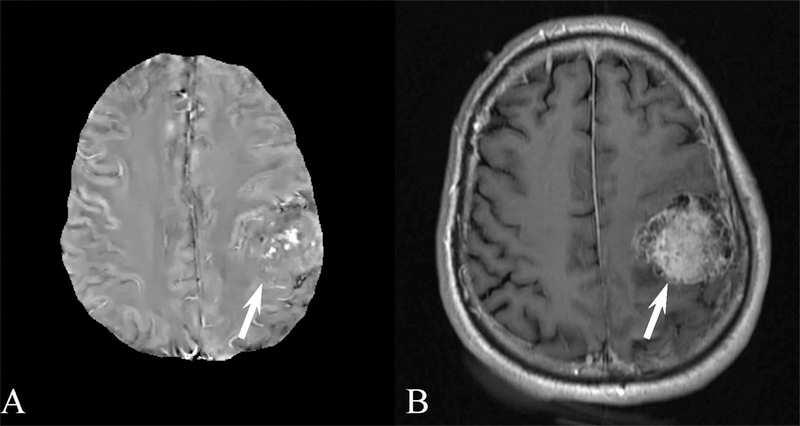
A) Brain quantitative susceptibility map (QSM) of a 61 year old male with an atypical meningioma located on left frontoparietal convexity. QSM demonstrates hyperintense foci of intratumoral hemorrhage. B) Corresponding contrast enhanced longitudinal relaxation (T1) weighted image.

Figure 7.

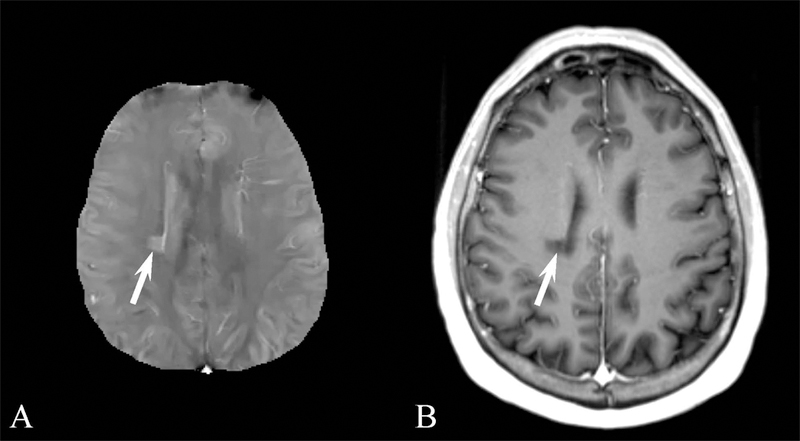
A) Brain quantitative susceptibility map (QSM) of a 46 year old male with multiple sclerosis (MS). The MS lesion indicated by the arrow in the right corona radiata is hyperintense on QSM. (B) The lesion is nonenhancing the contrast enhanced longitudinal relaxation (T1) weighted image.

Discussion

The results presented in this work show the feasibility of a clinically practical implementation of brain QSM. The same subject was scanned on scanners from 3 manufacturers at 9 different sites. ROI analysis revealed excellent reproducibility across sites, similar to intra-scanner and inter-scanner reproducibility reported previously.^17–21 Image quality in 873 consecutive patients at one site in a month revealed diagnostic or excellent quality in 96% of patients.

The data exchange with the QSM reconstruction server uses the DICOM protocol, which requires no additional software on the scanner. The QSM reconstruction itself is fully automated, including the referencing of the susceptibility values with respect the ventricular cerebral spinal fluid, chemically close to pure water. This automated zero-reference during reconstruction improves image quality, provides absolute susceptibility values and allows longitudinal and cross-center studies, which are important for monitoring disease progression and therapy of many neurological diseases including multiple sclerosis,^41–43 cerebral cavernous malformation,⁴⁴ and Parkinson’s disease,⁴⁵ and for mapping cerebral metabolic rate of oxygen consumption,⁴⁶ and biodistribution of magnetic theranostics.⁴⁷

The presented implementation is easily integrated into a clinical workflow. Indeed, at WCMC, automated QSM reconstructions are performed routinely for over 10 scanners from two vendors and two field strengths. Gradient echo acquisitions are typically near the start of the exam such that QSM is available on the scanner by the end of the exam. Then, the technologist can send all data to the Picture Archiving and Communication System (PACS) without further delay. However, connecting a server to a scanner can be problematic due to IT restrictions, maintenance of connectivity, and human error. To avoid these problems, we have now ported the codes for automated QSM reconstruction directly on some scanners (#1 in Table 1). In fact, the computing power on the latest scanners is higher than that of our server and allows QSM reconstruction of a StdRes acquisition within 3 minutes while scanning of other image contrasts continues without interruption.

Several studies have shown reproducibility of QSM in various settings and subject cohorts: in 14 healthy subjects scanned on a single 3T scanner four times over 7 days at a single site,¹⁷ in 10 MS patients on a single 3T scanner and 10 healthy subjects on a 1.5T and two 3T scanners from two vendors, all at a single site,¹⁸ in 8 healthy subjects on a 3T scanner at a single site,¹⁹ in 22 healthy subjects on both 1.5T and 3T from the same vendor at a single site,²⁰ in 9 healthy subjects both within site and between sites using 3T scanners.²¹ Reproducibility of QSM was shown in a Gadolinium phantom imaged at 7 different sites, using 12 clinical and 3 preclinical scanners, 3 field strengths (1.5T, 3T, and 7T) and 4 vendors.⁴⁸ The current study shows reproducibility in a single healthy volunteer imaged at 8 different sites using 9 3T scanners from 3 different vendors.

The Bayesian approach to QSM allows an optimal construction from noisy data and ill-posed system matrix (dipole kernel) under the prior knowledge of structural information expressed in an L1 norm.⁴⁹ It also allows constraining the ventricular CSF to have a uniform value suitable for referencing the final susceptibility values.²⁶ The field (phase) noise is commonly approximated as Gaussian, which breaks down at low signal to noise ratio; the use of a nonlinear data fidelity term ensures always the correct noise weighting for data fidelity using complex MRI data.²⁵ The proposed QSM implementation uses an image quality guided unwrapping method for phase processing.⁵⁰ The Laplacian based unwrapping method⁵¹ has been used for QSM because of its ease of implementation and speed, but can suffer from substantial errors.⁵² There are several ways to speed up QSM reconstruction. Using a GPU, we find an overall two-fold reduction in reconstruction time. Additionally, using the alternating directions of multipliers method has been shown to provide a further speed up.⁵³

There are a number of limitations in this study. The spherical mean value operation (S in Eq. 2) is used to suppress remaining background field in the estimated local field, but comes at the cost of an eroded brain mask: a border of certain width (5mm in our implementation) is removed from the original brain mask computed using BET. This brain erosion may make it difficult to study lesions near the brain border (Figure 5), particularly near the temporal bones and nasal cavity. The erosion needs to be readjusted to poor SNR in this region, or QSM without brain erosion needs to be further developed to be robust and automated.⁵⁴ Finally, it is known that the magnetic susceptibility of white matter is anisotropic, i.e., it depends on the orientation with respect to the magnetic field. In principle, anisotropic susceptibility can be resolved by acquiring data in multiple head orientations,^55,56 but this is not clinically feasible. Using a single orientation and the isotropic signal model in Eq. 2 is known to be a source of shadow artifacts that is yet to be suppressed satisfactorily in QSM.²³ In this study, a single high resolution acquisition at one scanner was used as the reference for image registration. This may have introduced a bias, and results may change should using another reference image. We have attempted to minimize this bias by choosing a high resolution acquisition, which is nearly isotropic, as reference, following the recommendations by the authors of the FSL FLIRT image registration tool used in this work.^30,37,38 In conclusion, this work demonstrates a clinically practical online QSM reconstruction method for a variety of scanner vendors with low cross-site ROI standard deviation. Excellent QSM image quality was observed in a consecutive patient cohort affected by a variety of diseases.