Dynamics of living cells in a cytomorphological state space

Significance

The cell is where life emerges from nonliving matter. How can we understand the behavior of a complicated, far-from-equilibrium system such as a living cell? By defining a state space for cells and analyzing state transitions, we find that cell behavior can be successfully predicted by an effective potential function, which suggests that although cells are complex nonequilibrium systems, this complexity can be reduced to a simple equilibrium function for predicting cell behavior.

Abstract

Cells are nonequilibrium systems that exchange matter and energy with the environment to sustain their metabolic needs. The nonequilibrium nature of this system presents considerable challenges to developing a general theory describing its behavior; however, when studied at appropriate spatiotemporal scales, the behavior of ensembles of nonequilibrium systems can resemble that of a system at equilibrium. Here we apply this principle to a population of cells within a cytomorphological state space and demonstrate that cellular transition dynamics within this space can be described using equilibrium formalisms. We use this framework to map the effective energy landscape underlying the cytomorphological state space of a population of mouse embryonic fibroblasts (MEFs) and identify topographical nonuniformity in this space, indicating nonuniform occupation of cytomorphological states within an isogenic population. The introduction of exogenous apoptotic agents fundamentally altered this energy landscape, inducing formation of additional energy minima that correlated directly with changes in sensitivity to apoptosis induction. An equilibrium framework allows us to describe the behavior of an ensemble of single cells, suggesting that although cells are complex nonequilibrium systems, the application of formalisms derived from equilibrium thermodynamics can provide insight into the basis of nongenetic heterogeneities within cell populations, as well as the relationship between cytomorphological and functional heterogeneity.

Cells are complex nonequilibrium systems that exchange matter across the cellular membrane, often against concentration gradients, allowing cells to participate in intercellular signaling, sense and respond to environmental conditions, and import and export essential biomolecules (1, 2). Mechanical nonequilibrium can be witnessed in the contraction and extension of the cytoskeletal network (3, 4), and in the complex directed movements of cell division (5). Thermal nonequilibrium is observed in the form of heat dissipation and absorption in multicellular organisms, as well as in the offset of the entropic increases produced in many biochemical reactions (e.g., metabolism, DNA synthesis) through the absorption of free energy produced in the catabolic breakdown of high-energy biomolecules (6, 7). Given the central importance of cells in biological systems, significant efforts over the years have been directed at developing nonequilibrium formalisms for describing this system; however, a unifying theory remains, at present, out of reach. In recent years, several studies have indicated that when viewed at appropriate spatiotemporal scales, the behavior of ensembles of nonequilibrium systems can, at times, be accurately approximated by equilibrium formalisms (8–11). Here, we apply this principle to explore heterogeneity in a population of isogenic mouse embryonic fibroblasts (MEFs).

We begin by identifying an appropriate state space that would allow both for testing the applicability of an equilibrium framework and for tracking the relationship between state space dynamics and functional behavior in a population of living cells. The state space of a living cell can be defined by many different feature sets. The molecular microstate represents the sum of the epigenetic, transcriptomic, proteomic, and additional molecular states of the cell. The ensemble of these states defines the functional state of a cell; as a consequence, variability in the molecular microstate can lead directly to functional heterogeneity within isogenic populations, a phenomenon known as nongenetic heterogeneity. These nongenetic heterogeneities play important roles across a diverse range of biological processes (12, 13). Examples include the selective differentiation of hematopoietic progenitor cells (14) and the appearance of subpopulations of “persister” cells with increased antibiotic resistance (15). Whole-genome methods (e.g., transcriptomics, proteomics, ChiP-Seq) offer by far the most comprehensive catalog of the microstate (16–21), but these methods are cell-destructive in nature and of limited use in live cell experiments. Fluorescent reporters linked to mRNA and protein targets can be tracked over multihour time courses in living cells (22, 23); however, reporters are limited to a few target sequences at a time and offer a limited snapshot of the molecular microstate. Here we employ cytomorphology, as defined at the cell and organelle scale, as a proxy for the molecular microstate. Cytomorphology represents the sum of many thousands of molecular processes (24, 25), providing global cell state information that offers a compromise between experimental accessibility and exhaustiveness. We note existing precedent for the development of intermediate, coarse-grained approaches in cases in which comprehensive tracking of system components is intractable, notably in the Eulerian representation of fluid mechanics (SI Appendix). Further underlining the link between the cytomorphological and functional states of the cell are numerous studies demonstrating that diseases such as cancers (26) and neurodegenerative disorders (27, 28) are characterized by concomitant functional and cytomorphological changes. By altering the scale at which we defined the cellular state, we were able to develop methods to track state space occupancy in living cells and investigate relationships between state space dynamics and functional heterogeneity.

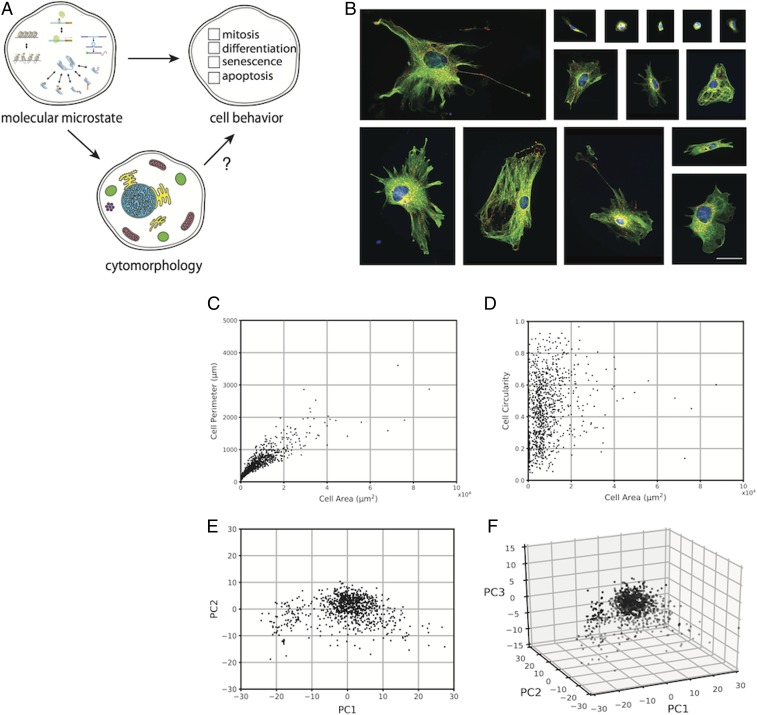
We began by developing a methodology to measure cytomorphological features and quantify state space occupancy in a population of cells. We chose MEFs as our model population, as wild-type MEFs (WT MEFs) exhibit native cytomorphological heterogeneity, rendering them ideal candidates for studying nongenetic heterogeneity in the context of cytomorphological variability. WT MEFs were harvested and grown in vitro, and then chemically fixed and fluorescently labeled for 3 cytomorphological structures: the microtubule cytoskeleton (α-tubulin), nucleus (DAPI), and mitochondria (mtHsp70; Fig. 1B). In numerous studies, morphological changes in these structures have been observed concomitant with changes in cellular function (29–31), suggesting potential links between cytomorphological and functional heterogeneity. Next, we developed image analysis algorithms to quantify 205 shape, size, and textural features (SI Appendix, Table S3) in each cell of a 904-cell dataset. The distribution of cells in cytomorphological state space were visualized using Principal Component Analysis, a technique that converts high-dimensional datasets to lower-dimensional datasets by identifying linear combinations of high-covariance features that together account for a large percentage of population-wide variance; these linear combinations are termed principal components (PCs). As discussed previously, many of our features exhibit high covariance (Fig. 1C); Principal Component Analysis allows for multiple covarying features to be linearly combined into a single PC, thereby reducing the dimensionality of the dataset. In our dataset, PC1 was dominated by cell and nuclear morphometric features, whereas PC2 was dominated by cell morphometric and textural features and PC3 was dominated by cell morphometric and mitochondrial textural features (SI Appendix, Table S4). Furthermore, plots of PC1, PC2, and PC3 (Fig. 1 E and F), together accounting for 46.9% of total variance, revealed that WT MEFs occupy a continuous set of cytomorphological states rather than a set of discrete subspaces.

Fig. 1.

Cytomorphological heterogeneity in WT MEFs. (A) Relationships between cell states at different levels of description. (B) Fluorescence images of fixed WT MEFs. The microtubule cytoskeleton (α-tubulin, green), mitochondria (mtHsp70, red), and nucleus (DAPI, blue) are labeled. (Scale bar, 50 μm.) (C and D) Scatter plots of single cell values for cell area vs. cell perimeter (C) and cell area vs. cell circularity (D) in a sample of fixed WT MEFs (n = 904). (E and F) Scatter plots of single-cell coordinates in PC1 vs. PC2 (E) and PC1 vs. PC2 vs. PC3 (F) space in a sample of fixed WT MEFs (n = 904).

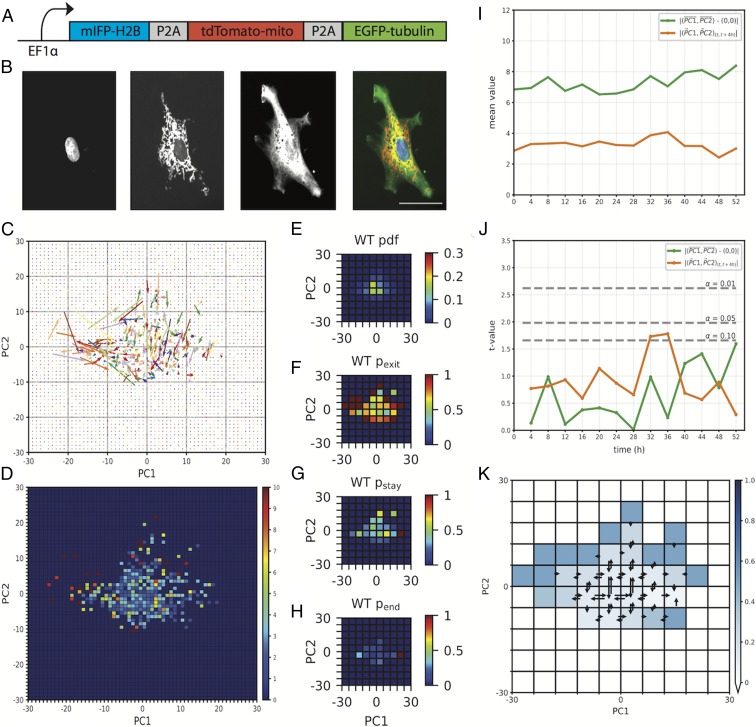
We next turned our attention to developing a dynamic map of transitions within state space by tracking cytomorphological changes in living cells. To implement live cell imaging, we employed a lentivirus-based approach to introduce fluorescent reporters targeted to our structures of interest. Our lentivirus vector consisted of an EF1α promoter driving expression of fluorescent reporters localizing to the microtubule cytoskeleton (EGFP-tubulin), nucleus (mIFP-H2B), and mitochondria (tdTomato-mito-7; Fig. 2A). Once transduced with this lentivirus, MEFs were imaged at 4-h intervals during a 60-h time course (Fig. 2B), and each cell’s location within state space calculated at each point. New PCs were calculated for living cells, and a new cytomorphological state space was constructed (SI Appendix, Fig. S2); the topography of this space bears close resemblance to that observed for fixed cells (Fig. 1 E and F). Next, cytomorphological state space transitions were plotted into a 60 × 60 bin representation of state space (Fig. 2C), where transition vectors were defined as originating at (PC1_t, PC2_t) and terminating at (PC1_{t + 4 h}, PC2_{t + 4 h}). This plot revealed nonuniform magnitudes of transition, where vectors originating more centrally in state space appeared to be of smaller magnitude than those originating peripherally. To quantify this observation, we plotted a heat map of the mean magnitude of transition of vectors originating from each bin (Fig. 2D), confirming the mean magnitude of transition varies as a function of state space. This indicates the degree of cytomorphological change within a given time interval varies as a function of the state of a cell.

Fig. 2.

State space dynamics of living cells approximate a system at equilibrium. (A) Schematic of the fluorescent reporter lentivirus cassette. (B) Fluorescence images of a WT MEF expressing the lentivirus fluorescent reporter. From left to right: mIFP-H2B (nucleus), tdTomato-mito (mitochondria), EGFP-tubulin (microtubule cytoskeleton), composite. (Scale bar, 50 μm.) (C) Experimentally observed transition vectors of WT MEFs during a 60-h time course. Vectors originate at (PC1_t, PC2_t) and terminate at (PC1_{t + 4 h}, PC2_{t + 4 h}). (D) Heat map of the mean transition vector magnitude of each bin in a 60 × 60 bin representation of state space (E–H) Heat maps of the pdf (E), p_exit (F), p_stay (G), and p_end (H) of WT MEFs. (I) The distance from the origin (0, 0) to the mean (PC1, PC2) coordinate (green) and the mean magnitude of the transition vector (PC1_t, PC2_t) to (PC1_{t + 4 h}, PC2_{t + 4 h}) (orange) at 4-h intervals in WT MEFs (n = 68). (J) Steady-state analysis. Two-sample t test comparing, at each point, the distance from the origin to the mean (PC1, PC2) coordinate (green) and the mean transition vector magnitude from (PC1_t, PC2_t) to (PC1_{t + 4 h}, PC2_{t + 4 h}) (orange) to those observed at t = 0 h. Significance values are indicated by dashed lines. (K) Detailed balance analysis. Heat map of the binomial probability, indicated by the blue color scale, of the experimentally observed ratio of forward and reverse transitions occurring given an underlying probability distribution of (p_forward = 0.5, p_reverse = 0.5). Bins for which no data were available are indicated in white. Transitions between adjacent bins are shown; a full transition map can be found in SI Appendix, Fig. S3.

To further refine our understanding of the dynamics of cytomorphology space, we plotted the probability density function (pdf) of WT MEF state space occupancy (Fig. 2E) in a 10 × 10 bin representation of state space and identified a peak in the central (0, 0) region of this space. We then plotted the probability, during a 60-h time course, that a cell occupying a bin would exit that bin by the subsequent point (p_exit; Fig. 2F) and found that WT MEFs occupying more peripheral states had a higher probability of exit compared with those occupying more central states. The probability of staying within the same bin between consecutive points (p_stay), a measure of short-term occupancy, was also higher within these central bins (Fig. 2G). However, when we plotted the probability of a cell occupying the same bin as that occupied at the end of its time course (p_end; Fig. 2H), a rough measure of long-term occupancy, the mean probability fell by more than 4-fold. These results suggest that WT MEF cytomorphology space is energetically nonuniform and supports a directional bias toward the set of states surrounding (0, 0), but that entry into this space does not impose long-term occupancy. Interestingly, in PC space, the origin (0, 0) represents the mean value of contributing features, suggesting a control mechanism acts to return cells to this morphological “mean.”

We next looked for nonequilibrium behavior in morphology space dynamics. Systems at equilibrium are at steady state, where the distribution of state variables is invariant during all timescales. Equilibrium systems are also in detailed balance, in which state transitions are accompanied by reciprocal transitions of equal magnitude (32). Violations of detailed balance have been detected in some cellular processes (33, 34). To assess the steady state characteristics of cytomorphology space, we identified 2 state variables describing the occupancy and transition dynamics of MEFs within this state space. The first state variable, representing state space occupancy, measured the distance of each cell from the origin (0, 0) in state space and calculated the mean distance at each point (Fig. 2I, green). The second state variable, representing the dynamics of state space transitions, measured the mean magnitude of transition vectors at each point (Fig. 2I, orange). At each point, the mean distance from the origin, as well as mean magnitude of transition, was compared with the mean distances and magnitudes observed at time $t_0$(0 h), using a 2-sample t test. The results indicated that both the mean distance from the origin (0, 0) and mean magnitude of transition were statistically invariant (α = 0.05) at time scales ranging from 4 to 52 h (Fig. 2J), indicating that cytomorphological state space is at steady state at the temporal resolution of our experiment. To test for detailed balance, we tabulated the frequency of state transitions between each pair of bins within our 10 × 10 bin representation of state space (Fig. 2K and SI Appendix, Fig. S3), with a binomial test revealing statistically insignificant variability in the rates of forward and reverse transitions between paired bins (α = 0.05; SI Appendix). This result was unexpected, since the cell cycle alters cell morphology (35–37). The discrepancy may be a product of dimensionality reduction (SI Appendix).

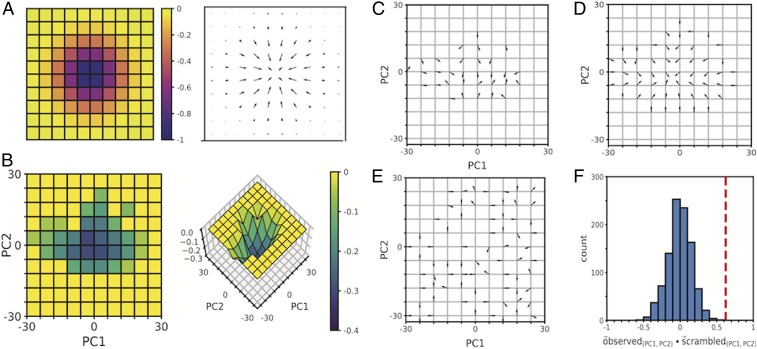
The results of the steady state and detailed balance analyses indicated that the transition dynamics of WT MEFs within cytomorphology space approximated those of a system at equilibrium. To assess the suitability of equilibrium formalisms in describing the population-level transition dynamics, we developed a framework based on an adaptation of Maxwell-Boltzmann statistics. Maxwell-Boltzmann statistics are an equilibrium statistical mechanics-based formalism for describing state occupancies of a system in terms of a single-valued state function that plays the role of a potential energy (32, 38). According to this formalism, the relative occupancies of the different energy states of a system are a function of the differences in energy levels between available states, as well as the temperature (T_b) of the system. In classical statistical mechanics, the Maxwell-Boltzmann temperature (T_b) refers to the thermodynamic temperature of the system, as measured in Kelvins (K). This concept of temperature was adapted to our system by drawing parallels between particle velocity vectors and state space transition vectors (SI Appendix), an approach that allowed us to calculate an effective temperature (T_WT) for our system. The concept of energy state occupancies was similarly adapted by drawing parallels between particle occupancy of energetic states and cell occupancy of cytomorphological states, as measured by the pdf (Fig. 2E). The effective temperature and state space occupancy data were then used to calculate the effective energy landscape underlying WT MEF cytomorphology space (Fig. 3B and SI Appendix). This energy landscape was characterized by a global minimum surrounding (0, 0), and was absent any additional local maxima or minima. In a system at equilibrium, the future behavior of the system depends on its current state, and the velocity field in state space can be predicted by the gradient of the potential energy landscape (Fig. 3A and SI Appendix). To assess the predictive power of the effective energy landscape, we plotted the vector field predicted by the gradient of the energy landscape (Fig. 3D) and compared it with the experimentally observed transition vector field (Fig. 3C). By calculating the vector dot product of corresponding bins between the observed and predicted vector fields and averaging the dot product across state space, we were able to quantify directional similarity between vector fields. Our results indicated that the experimentally observed transition vector field was more closely aligned with the transition vector field predicted by our inferred effective energy landscape than with transition vector fields predicted from any of 1,000 scrambled variations of the energy landscape, created by randomly distributing the original set of energy levels throughout state space (Fig. 3 E and F and SI Appendix, Fig. S8). Although cells are nonequilibrium systems, our results indicate equilibrium formalisms can successfully describe the behavior of an ensemble. Whether equilibrium formalisms can be applied to individual cells is a separate question not addressed here.

Fig. 3.

The gradient of the inferred effective energy landscape is predictive of experimentally observed transition dynamics. (A) Example of an energy landscape, formed by taking the inverse of a 2D Gaussian with μ_x = 0, μ_y = 0, σ_x = 1, and σ_y = 1 (Left) and the transition vector field (Right) predicted by the gradient of this landscape. (B) Heat map (Left) and surface plot (Right) of the inferred effective energy landscape of WT MEF cytomorphology space. Energy values are scaled to a range of [−0.4, 0]. (C through E) Experimentally observed transition vectors (C), vectors derived from the gradient of the inferred effective energy landscape (D), and vectors derived from a scrambled energy landscape (E). Vectors are unit normalized. (F) Histogram of the mean dot product of the observed vectors (C) and vectors derived from 100 scrambled versions of the energy landscape. The mean dot product of C and D is indicated by a dashed line (red).

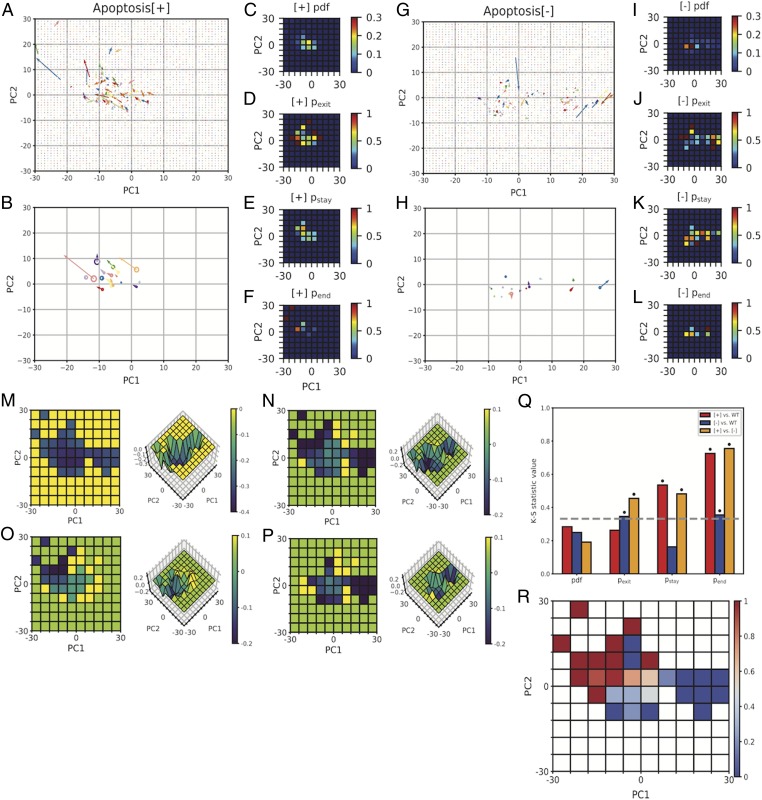
Having developed a framework for mapping cytomorphology space and a formalism for describing the energy landscape underlying this space, we were now in a position to investigate potential relationships between cytomorphological and functional variability. Given the many available examples of concomitant functional and cytomorphological changes, we hypothesized that the heterogeneity observed in cytomorphology space might correspond directly to functional heterogeneity within the population. To test this hypothesis, we screened 5 apoptosis drugs for conditions producing a heterogeneous response in a population of isogenic WT MEFs. We found that camptothecin (2 μM), a topoisomerase I inhibitor, produced such a response, with a fraction of cells undergoing apoptosis within 96 h of exposure, while others remained alive up to 21 d postexposure (SI Appendix, Fig. S9). The long duration during which some cells survived relative to the timescale of apoptosis suggests that the observed heterogeneity resulted from fundamentally different apoptotic decisions rather than a simple delay in apoptosis. To ask whether apoptotic response correlates with cytomorphology, we transduced a population of WT MEFs with our cytomorphology-targeted fluorescent reporter lentivirus and imaged cells at 4-h intervals, this time adding 2 μM camptothecin at the 2-h time. Over the course of a 64-h time course, we observed that 17 (52%) of 33 cells underwent apoptosis (Apoptosis[+]), while 16 (48%) of 33 cells did not (Apoptosis[−]). We hypothesized that the response of a cell might correlate directly with its cytomorphological state before apoptosis induction, but when the space states of Apoptosis[+] and Apoptosis[−] cells at time 0 h were plotted (SI Appendix, Fig. S10) and analyzed, they were found to be statistically indistinguishable (SI Appendix, Fig. S11). Although the initial space state was uninformative, an examination of the state transitions of each class of cell revealed characteristic differences in the dynamics of their state space transitions. The transition vectors of Apoptosis[+] cells (Fig. 4 A and B) were of larger-than-average magnitude relative to the total cell population (SI Appendix, Fig. S12), and displayed a directional bias toward the (−30, 30) region of PC space (SI Appendix, Fig. S13). In contrast, the transition vectors of Apoptosis[−] cells (Fig. 4 G and H) were of smaller-than-average magnitude (SI Appendix, Fig. S12) and displayed a directional bias toward the (30, 0) region of PC space (SI Appendix, Fig. S13). Interestingly, both groups of cells were also found to populate the central (0, 0) region of PC space. Plots of the probabilities of exit from each bin (p_exit; Fig. 4 D and J) revealed that both Apoptosis[+] and Apoptosis[−] cells exhibited higher probabilities of exit from peripheral states relative to central states. Plots of the probability of staying within the same bin between consecutive points (p_stay; Fig. 4 E and K), a measure of short-term occupancy, revealed a region of increased probability near (0, 0), in agreement with our model of an energetically favorable subspace surrounding this region. The p_stay of corresponding bins differed by no more than 1.5-fold between Apoptosis[+] and Apoptosis[−] cells, but plots of the probability of a cell occupying the same bin as that occupied at the end of its time course (p_end; Fig. 4 F and L), a measure of long-term occupancy, revealed that long-term occupancy in Apoptosis[+] and Apoptosis[−] cells was restricted to different, nonoverlapping regions in cytomorphology space. Apoptosis[+] cells exhibited increased p_end probabilities in the upper left (−30, 30) region of PC space, whereas Apoptosis[−] cells exhibited increased p_end probabilities in the central (0, 0) and far right (30, 0) regions of this space. These observations suggest variability in the occupancy of Apoptosis [+] and Apoptosis[−] cells in WT MEF cytomorphology space might contribute to functional divergence within the population. To statistically test this hypothesis, we ran 2D Kolmogorov-Smirnov significance tests (α = 0.05) between pairs of corresponding probability plots (39) (Fig. 4Q and SI Appendix, Fig. S14), revealing significant differences among the p_exit, p_stay, and p_end plots of Apoptosis[+] and Apoptosis[−] cells.

Fig. 4.

State variability in cytomorphology space corresponds to variability in apoptotic response. (A and G) Experimentally observed transition vectors of Apoptosis[+] (A) and Apoptosis[−] (G) cells during a 64-h time course. Vectors originate at (PC1_t, PC2_t) and terminate at (PC1_{t+4 h}, PC2_{t+4 h}). (B and H) Single-cell mean transition vectors and mean (PC1, PC2) coordinates of Apoptosis[+] (B) and Apoptosis[−] (H) cells during a 64-h time course. Radii of circles are scaled to the (PC1, PC2) coordinate variance. (C–F and I–L) Heat maps of the pdf (C and I), p_exit (D and J), p_stay (E and K), and p_end (F and L) of Apoptosis[+] (C–F) and Apoptosis[−] (I–L) cells. (M) Inferred effective energy landscape of camptothecin-treated WT MEFs. (N–P) Calculated differences between the effective energy landscapes of WT and camptothecin-treated (N), Apoptosis[+] (O), and Apoptosis[−] (P) cells. (Q) Bar plot of Kolmogorov-Smirnov statistic values comparing the probability plots of WT, Apoptosis[+], and Apoptosis[−] cells. The K-S statistic value at α = 0.05 is indicated by a dashed line, and statistically significant values are indicated by asterisks. (R) Heat map of the probability of apoptosis given occupancy of a particular state space bin at any point during the 64-h time course.

To identify the underlying changes to cytomorphology space driving this behavior, we calculated the effective energy landscape. The transition vectors of camptothecin-treated cells were, on average, of 36% smaller magnitude than those of untreated cells (SI Appendix, Fig. S15). In a system defined by Maxwell-Boltzmann statistics, smaller average displacements correspond to a lower effective temperature of the system. To test whether this “cooling” of morphology space could explain observed changes in the pdf, we calculated the expected pdf of WT MEFs over a range of temperatures. We then ran a series of 2D Kolmogorov-Smirnov (K-S) tests to quantify similarities between these expected pdfs and those observed experimentally under camptothecin treatment. A plot of K-S statistic values as a function of temperature (SI Appendix, Fig. S16) revealed that similarities between the observed and expected pdfs were maximized at an effective temperature of 1.04T_WT, whereas the calculated temperature of camptothecin cytomorphology space was 0.41T_WT, suggesting that a change in temperature alone was insufficient to explain observed changes in the pdf. The new camptothecin-treated energy landscape was calculated (Fig. 4M), and the difference relative to the untreated energy landscape plotted (Fig. 4N). Camptothecin treatment produced new energy minima in the upper left (−30, 30) and far right (30, 0) regions of PC space while further deepening the existing minimum at (0, 0).

Although both Apoptosis[+] and Apoptosis[−] cells effectively occupied the same camptothecin-treated energy landscape, we wanted to better understand whether specific features of this landscape could explain their divergent behaviors. To do this, we separately calculated the effective temperatures of Apoptosis[+] and Apoptosis[−] cells and plotted their effective energy landscapes (SI Appendix, Figs. S18 and S19), along with their differences relative to the untreated energy landscape (Fig. 4 O and P). The effective energy landscape of Apoptosis[+] cells resembled that of untreated cells, with the exception of a new energy well in the upper left (−30, 30) region of PC space. This well coincided with the endpoint of 92% of Apoptosis[+] cells, indicating that this energy minimum acts as a “death” well that apoptotic cells enter but do not escape. In contrast, the landscape of Apoptosis[−] cells was characterized by a dramatic deepening in the far right (30, 0) region of PC space, accompanied by a second milder deepening in the central (0, 0) region. We hypothesized that these energy minima might act as protective barriers to apoptosis by hindering cell exit and minimizing the probability of cell entry into the (−30, 30) “death” well. To test this possibility, we plotted the probability of apoptosis as a function of state space occupancy (Fig. 4R) and observed that entry at any point in the time series into states near (30, 0) corresponded to a 0% probability of apoptosis, whereas entry at any point in the time series into states in the (−30, 30) “death” well corresponded to a 100% probability of apoptosis. In between these 2 extremes were the central states surrounding (0, 0), where the probability of apoptosis was low, but nonzero. These findings support an interpretation in which the addition of camptothecin produces 3 functionally distinct energy minima in WT MEF cytomorphology space: 1 acting as an irreversible “death” well into which cells enter and do not escape, and the other 2 acting as energetically favorable subregions that serve as protective barriers to apoptosis. Comparison of observed transition vectors to those predicted by the inferred effective energy landscape (SI Appendix, Fig. S20 and SI Appendix) suggests that camptothecin alters the landscape, leading to subsequent changes in cellular transition dynamics and behavior.

Our application of equilibrium formalisms to understand nongenetic heterogeneity suggests that equilibrium statistical mechanics-based frameworks can have much to offer for studying inherently nonequilibrium systems such as living cells (40).

Materials and Methods

For imaging fixed cells, mouse embryonic fibroblasts were grown in 384-well plates, fixed with formaldehyde, and stained with antibodies, and imaged on a GE InCell 2000 imager. For imaging live cells, a custom lentivirus construct was used to express tagged proteins in MEFs. A custom image analysis pipeline was used to extract morphological features from images.