Evidence for sharp increase in the economic damages of extreme natural disasters

Significance

Observations indicate that climate change has driven an increase in the intensity of natural disasters. This, in turn, may drive an increase in economic damages. Whether these trends are real is an open and highly policy-relevant question. Based on decades of data, we provide robust evidence of mounting economic impacts, mostly driven by changes in the right tail of the damage distribution—that is, by major disasters. This points to a growing need for climate risk management.

Abstract

Climate change has increased the frequency and intensity of natural disasters. Does this translate into increased economic damages? To date, empirical assessments of damage trends have been inconclusive. Our study demonstrates a temporal increase in extreme damages, after controlling for a number of factors. We analyze event-level data using quantile regressions to capture patterns in the damage distribution (not just its mean) and find strong evidence of progressive rightward skewing and tail-fattening over time. While the effect of time on averages is hard to detect, effects on extreme damages are large, statistically significant, and growing with increasing percentiles. Our results are consistent with an upwardly curved, convex damage function, which is commonly assumed in climate-economics models. They are also robust to different specifications of control variables and time range considered and indicate that the risk of extreme damages has increased more in temperate areas than in tropical ones. We use simulations to show that underreporting bias in the data does not weaken our inferences; in fact, it may make them overly conservative.

Climate change has been convincingly linked to an increase in the frequency and intensity of natural disasters in many regions (1–4). However, whether and how this is reflected in increasing economic impacts remains unclear. Long-term upward trends in damages, when detected, have been interpreted as indicative of increasing future risks and of a need for prevention and adaptation efforts (5–7). They have also been seen as indirect evidence for climate change (8, 9). But there are still substantial disagreements on whether such trends exist. Some studies report statistically significant long-term increases in damages, but only for selected hazards (10, 11). Other studies report an increasing global trend (12, 13), though researchers have questioned the robustness of this finding with respect to methodological choices (14). These inconsistencies have led many to reject the notion that damages caused by natural disasters are growing over time (10, 15–17). Part of the debate to date has focused on how to properly normalize damage values to eliminate confounding factors (e.g., inflation, population, and wealth per capita) and ensure comparability of measurements across time and space. Recent Actual-to-Potential-Loss normalization approaches (17) did overcome problems associated with earlier techniques, which typically accounted for rates of change in confounding factors, but not for their absolute sizes. Nevertheless, these approaches did not reveal statistically significant trends in damages (17).

Inconclusive results in the literature might be due to the use of statistical techniques ill-suited to capture the evolution of the damage distribution. We hypothesize that relevant patterns may in fact correspond to changes in its right skew and tail. To investigate this, we use a different modeling and statistical strategy. First, we include control variables for socio-demographic factors as covariates in our models alongside time—this generalizes the Actual-to-Potential-Loss approach, allowing for multiple controls, and improves upon procedures that normalize damage values prior to modeling (Normalization). Second, and perhaps most importantly, we characterize the behavior of the damage distribution fitting quantile regressions over disaggregated, event-level data.

Our approach avoids 2 common pitfalls: 1) linear aggregation—i.e., summing damages associated to disasters occurring in a given year over a specified geographical area, which may lead to a substantial loss of information—and 2) the use of ordinary least squares (OLS)—i.e., mean regression, which captures only average trends in damages (changes in expected losses) (17, 18). With increasing evidence that natural disasters induce fat-tailed damage distributions (19) and that fat tails can dramatically change policy implications in a variety of climate-economics models (20), analyzing quantiles can be an effective way to inspect extreme, low-probability events. In addition, OLS regression can be a rather blunt instrument to analyze skewed data. In contrast, quantile regressions do not rely on Gaussianity or even symmetry assumptions for the error distribution and have already been used to characterize the evolution of cyclone strength (21–23).

The Devil Is in the Tails: From Climate Stressors to Damages

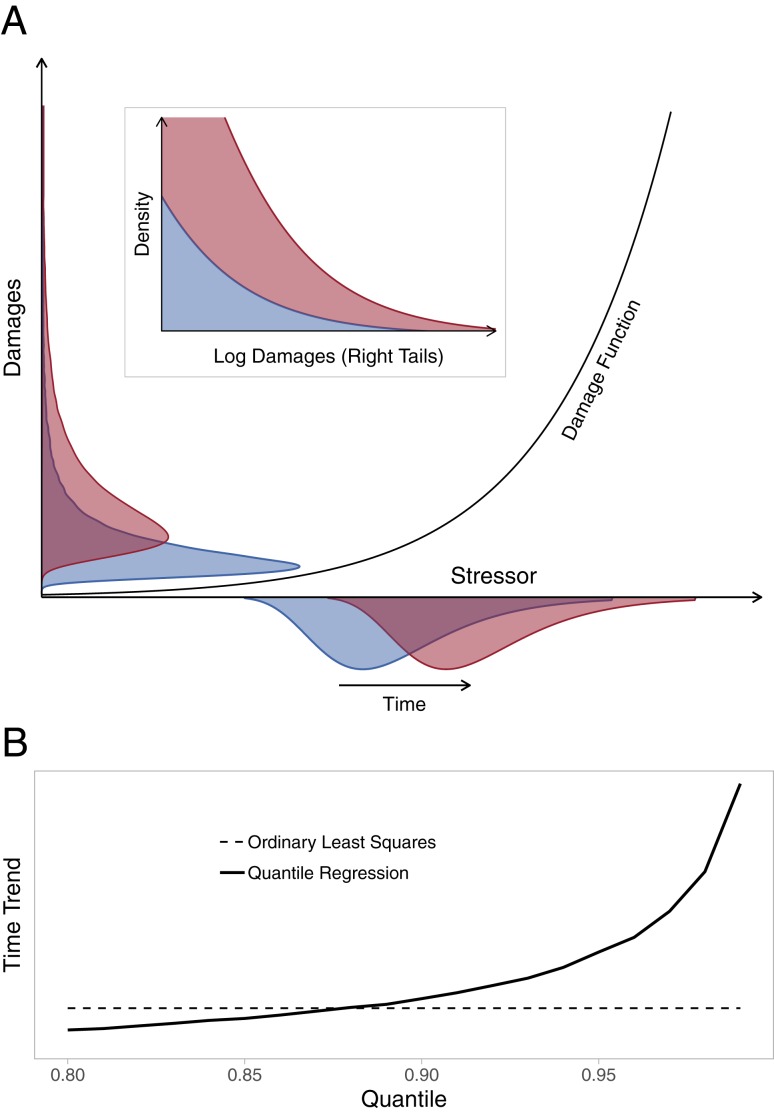
We hypothesize that what changes over time is the right skew and tail behavior (as opposed to the average) of the damage distribution. This can be explained using the concept of damage function. Damage functions are widely used in the Integrated Assessment Modeling literature to link climate-related stressors (e.g., wind speed for tropical cyclones or storm surges) to damages. Characterizing such functions poses conceptual and econometric challenges (24–27) which are specific to the economic sectors, spatio-temporal scales, and feedbacks (e.g., adaptation) under consideration. However, functions gleaned from global, regional, and local data are often convex and upwardly curved (26, 28–30), likely due to nonlinearly increasing exposure or fragility (24). Based on such a shape, a simple shift in the distribution of the underlying stressor translates into a rightward skewing and tail fattening of the damage distribution (larger damages). Fig. 1A shows a nonlinear, upwardly curved damage function mapping a hypothetical generalized extreme value (GEV)-distributed stressor into damages. GEV distributions (e.g., ref. 31) are routinely used to model block maxima for climate stressors linked to the hazards represented in the data we analyze below (e.g., riverine floods (32, 33), extreme storm surges driving coastal floods (34), or tropical cyclone maximum wind speeds (35, 36)). Shifts in the means of these distributions have been recently linked to climate change (4, 34, 37). In the illustration presented in Fig. 1A, we shift the mean of a GEV stressor and use the damage function to compute the resulting damages over time. A simple rightward shift in stressor translates into a marked rightward skewing and tail fattening of damages (Fig. 1 A, Inset). This also illustrates why mean regression techniques might be a blunt instrument to detect temporal patterns in damages. Fig. 1B shows the time trend estimates obtained through OLS (i.e., mean) and quantile regressions fitted to simulated data. The estimates obtained through quantile regressions increase exponentially along percentiles, while the OLS estimate is smaller and poorly represents the changes occurring in the damage distribution.

Fig. 1.

(A) Stylized representation of a convex, upwardly curved transfer mechanism from stressor to damages. In A, Inset, the horizontal axis shows the largest damages (upper range of the vertical axis in the main image) on the log scale. (B) Time-trend estimates from quantile (upward of 80%) and OLS (mean) regressions for a simulated dataset. The horizontal axis represents percentiles. The time-trend estimate from OLS is shown as a constant. Quantile regression estimates are obtained through the modified Barrodale–Roberts algorithm (38). The mean of a hypothetical Gumbel-distributed stressor ($GEV\left(\mu ,\sigma ,\xi \right)$ with shape parameter $\xi =0$) undergoes equal yearly shifts for 55 “years” (the time range of the data in Fig. 2). For each year, we generate i = 1,...1,000 draws and the corresponding damage values ${\text{Da}}_i$. We then consider the simple model ${\text{Da}}_i=\alpha +\beta t_i$ (where $t_i$ is the year of $i$) and fit quantile and OLS regressions. An alternative visualization is provided in SI Appendix, Fig. S1.

Rightward Skewing and Tail Fattening: Economic Impacts Are Mounting

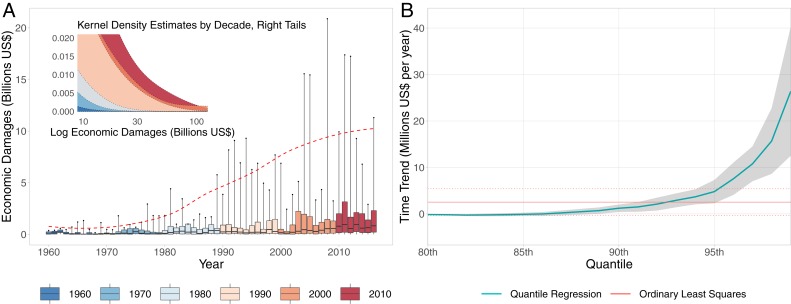
Turning from simulated to actual data, we find strong evidence of an accelerating rightward skewing and tail fattening of the damage distribution over time. We consider economic damages due to natural disasters from 1960 to 2015 as recorded in the Emergency Events Database (39), restricting attention to hazards potentially related to climate change (see Data and Code and SI Appendix, Data Treatment for details). Yearly distributions of damages from such disasters change markedly over time (Fig. 2A). In fact, their right tails appear to change in a way qualitatively similar to the one we illustrated by simulations (Figs. 1 A, Inset and 2 A, Inset). Notably, there is almost no temporal trend in the centers (medians in Fig. 2A) but upper percentiles display a striking surge.

Fig. 2.

Empirical distributions of economic damages from natural disasters (A) and estimated time trends from Model 2 (B). (A) Yearly distributions of economic damages (US$ billion) associated with n = 10,901 disasters occurred worldwide between 1960 and 2015 (see data description in Data and Code). We show partial boxplots colored by decade. Lower and upper hinges correspond to medians and 90th percentiles, respectively; middle lines to 75th percentiles; and upper whiskers to 99th percentiles; the top 1% single-event damages amounted to US$482 million in 1970 and to US$9.92 billion in 2010—an ∼20-fold increase. The red dashed line tracks the time progression of the 99th percentiles (kernel smooth), illustrating the marked increase in damages due to extreme events. A, Inset zooms into the right tails of the distributions and shows their progressive fattening over time [Gaussian kernel density estimates on log-transformed damages aggregated by decade, bandwidth fixed with Silverman’s rule (42)]. (B) Quantile and OLS (mean) regressions for the same data (but in US$ million and restricted to n = 9,495 disasters occurred between 1960 and 2014 after preprocessing; Data and Code). The model used is 2. The horizontal axis represents percentiles and the vertical one estimated time trends; e.g., at the 99th percentile, we estimate the top 1% single-event damages to increase by US$26.4 million every year. The time trend estimate from OLS (statistically nonsignificant at 5% level) is shown as a constant, with its standard 95% CI. Quantile regressions estimates are obtained through the modified Barrodale– Roberts algorithm (38) and a 95% confidence band around them is produced with r = 1,000 bootstrap samples [joint resampling of response and predictor pairs (40)]. Full results on estimates and standard errors are given in SI Appendix, Table S2.

Building on such descriptive evidence, we estimate a set of models with various control specifications. In our most general set-up (Model 1; Regression Models), economic damages depend on a pure time trend (the main object of interest), gross domestic product (GDP) in the affected area (commonly used as a proxy for wealth at risk, given the sparse quality of capital estimates (17)), additional control covariates (e.g., population size and climate zone of the affected area), and interaction terms. This formulation disentangles a pure time trend from one whose magnitude is modulated by the wealth at risk in the affected area (the interaction term). Indeed, we generalize the Actual-to-Potential-Loss normalization approach, which de facto corresponds to modeling damages as affected by GDP and its interaction with time, but not by time per se (the interaction is then interpreted as the time trend for damages over GDP; Normalization). Table 1 reports the estimates for Model 1 obtained through OLS (mean) and quantile fits with time, GDP, and their interaction, but no additional covariates.

Table 1.

Quantile and OLS (mean) regressions for damages, Model 1

	Quantile
Variable	80th	90th	95th	99th	OLS
Intercept	15.404*** (3.586)	31.023** (15.06)	38.196 (51.671)	220.579 (256.765)	29.974 (61.525)
Trend	−0.317*** (0.071)	0.936* (0.483)	4.795*** (1.677)	23.252** (10.162)	0.885 (1.59)
GDP	0.005 (0.014)	0.093** (0.042)	0.28*** (0.098)	0.747 (0.834)	0.01 (0.024)
Trend$\times$GDP	0.001*** ($<$0.001)	0.001 (0.001)	0 (0.003)	0.011 (0.022)	0.001*** (0.001)
Fit quality	$R^1=0.06$	$R^1=0.111$	$R^1=0.155$	$R^1=0.267$	$R^2=0.028$

Results on n = 9,495 disasters occurred between 1960 and 2014 (damages in US$ million). Quantile regression estimates are obtained through the modified Barrodale–Roberts algorithm (38). Standard errors (between parentheses) are produced with r = 1,000 bootstrap samples [joint resampling of response and predictor pairs (40)]. Fit quality is indicated by R¹ (41) for quantile regressions and by R² for OLS. *P < 0.10; **P < 0.05; ***P < 0.01 (2-tailed).

The pure time trend is not statistically significant for the OLS, but it is positive, statistically significant, and approximately exponentially increasing along percentiles for quantile regressions (e.g., P $<$ 1% at the 95th percentile; see Table 1 for other P values). The interaction term is not statistically significant for large percentiles (P $>$ 10%), suggesting that the increasing pattern we document for extreme damages is not due to increases in wealth at risk. Also, while fit quality is poor for the bulk of the distribution (OLS and percentiles up to 80%), it increases considerably for the upper percentiles.

Given its small effect size and limited statistical significance, we remove the interaction term and use the more parsimonious Model 2 (Regression Models) comprising only time and GDP. As can be seen in Fig. 2B, estimation results are entirely consistent with those of Model 1. In a format analogous to that of Figs. 1B and 2B shows time trend estimates obtained through OLS and quantile regressions for percentiles $\ge$80%. Remarkably, observations from 55 years of disasters around the world reveal patterns that are qualitatively similar to those from our synthetic experiment with a shifting GEV stressor and a prototypical damage function: The change in the mean is small (and statistically nonsignificant at 5% level), while upper percentiles have strong, positive, and statistically significant time trends (e.g., P $<$ 1% at the 95th percentile; see SI Appendix, Table S2 for other P values), whose magnitude increases exponentially with the percentiles. Such results indicate that the economic impacts of natural disasters are indeed growing, but not at all scales. The hallmark is a sharp increase in the risk of extreme damages, which induces a weak and hard-to-detect signal in the mean loss. This highlights the importance of considering the distribution of economic damages, not just its mean, and suggests—at a global scale—poor adaptation capacity to extreme events.

Our findings are robust to a wide range of model specifications. Modifying the control component in Model 2 (e.g., adding population or using GDP per capita instead of GDP) produces similar patterns (SI Appendix, Tables S3 and S4), as does modifying the time span (e.g., fitting our regressions on data from 1960, 1970, or 1980; SI Appendix, Tables S2 and S3).

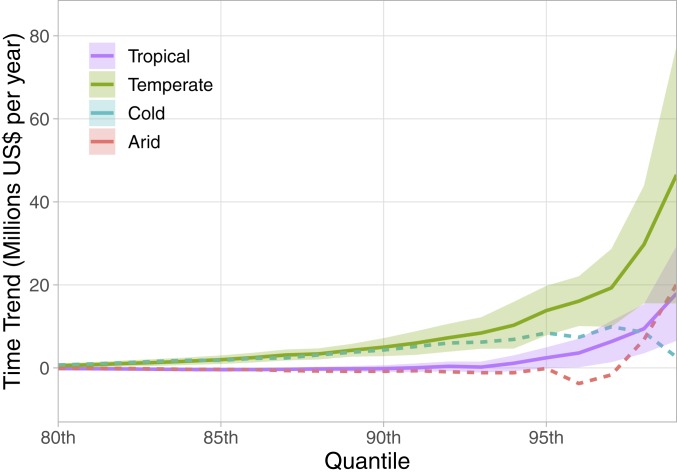
Next, we refine the analysis considering climate zones. Specifically, after geo-localizing all events in our sample, we estimate Model 3 (Regression Models), which comprises categorical control covariates for the Köppen–Geiger climate zones where disasters occurred (see Data and Code for details; SI Appendix, Table S1 documents a mild association between climate zones and income). For cold and arid zones, the time trends estimated from quantile regressions are small and statistically nonsignificant across most percentiles, possibly due to smaller sample sizes (SI Appendix, Table S1). However, in line with our results at a global scale, Fig. 3 shows upper percentiles of the damage distributions growing considerably and significantly in temperate and tropical zones (e.g., P value at the 95th percentile $<$1% for the former and $<$10% for the latter; see SI Appendix, Table S5 for other P values). Interestingly, the pattern is stronger for temperate than tropical zones, where disasters are instead more frequent* ; even the OLS detects a statistically significant time trend in temperate zones, while it still fails to do so in tropical ones (SI Appendix, Table S5). The stronger patterns may be due to the rising number of extreme weather events occurring in temperate zones (3), as well as to effective adaptation in tropical ones.^†

Fig. 3.

Quantile regressions for damages (US$ million) associated with n = 9,495 disasters occurred between 1960 and 2014 in different Köppen–Geiger climate zones (excluding the polar class). The model used is 3. The horizontal axis represents percentiles and the vertical one estimated time trends: e.g., at the 99th percentile, we estimate the top 1% single event damages to increase by US$17.9 million every year in tropical areas and by US$46.5 million in temperate ones. Quantile regressions estimates are obtained through the modified Barrodale–Roberts algorithm (38) and a 95% confidence band around them is produced with r = 1,000 bootstrap samples [joint resampling of response and predictor pairs (40)]. Time trend estimates for cold and arid zones are shown with dashed lines and without confidence bands because they were statistically nonsignificant for most percentiles. Full results on estimates and standard errors are given in SI Appendix, Table S5.

Notably, the explanatory power of the quantile regressions used in both Figs. 2B and 3 increases along percentiles (SI Appendix, Fig. S2), confirming that most of the loss dynamics occurs in the right tail of the damage distributions.

Beyond Economic Impacts: Lives Lost

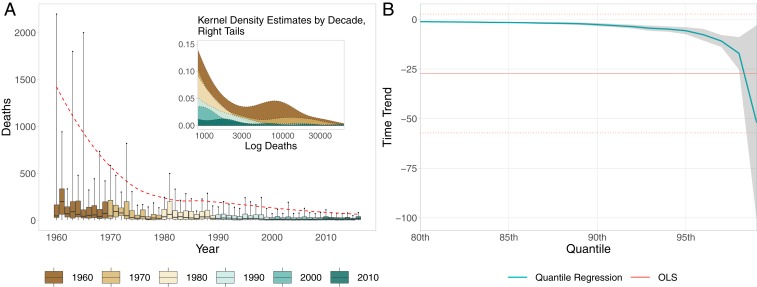
Human losses (casualties) are another important impact of natural disasters. When binned across years, they are also right skewed, but less so than economic damages, and instead of fat tails, they present extremely large isolated outliers—for example, a 1965 drought in India caused a famine that led to the death of 1.5 million people (39). Moreover, in contrast to damages, casualties display a discernible downward trend over time (Fig. 4A). We investigate this behavior using Model 4, which comprises time, population (as the key control covariate), and their interaction. As shown in Fig. 4B, the trend is negative and statistically significant for the upper percentiles (e.g., P $<$ 1% at the 95th percentile; see SI Appendix, Table S6 for other P values), with the size of the estimate increasing monotonically. Results do not qualitatively change when controlling also for GDP or varying the time span (SI Appendix, Tables S6 and S7).

Fig. 4.

Empirical distribution of deaths from natural disasters (A) and estimated time trend from Model 4 (B). (A) Yearly distributions of deaths associated with n = 10,901 disasters occurred worldwide between 1960 and 2015. We show boxplots colored by decade. Lower and upper hinges correspond to the 25th and 75th percentiles, respectively; middle lines to medians and upper whiskers to 90th percentiles; the top 10% single-event deaths amounted to 585 in 1970 and to 114 in 2010—an ∼5-fold decrease (the top 1% single-event deaths decreased by more than 80-fold from 156,744 to 18,51; not shown in the graph). The red dashed line tracks the time progression of the 90% percentile (kernel smooth), illustrating the marked decrease in deaths due to extreme events. A, Inset zooms into the right tails of the distributions and shows their progressive thinning [Gaussian kernel density estimates on log-transformed deaths aggregated by decade, bandwidth fixed with Silverman’s rule (42)]. (B) Quantile and OLS mean regressions for the same data (but restricted to n = 9,495 disasters between 1960 and 2014 after preprocessing; Data and Code). The model used is 4. The horizontal axis represents percentiles and the vertical one estimated time trends; e.g., at the 99th percentile, we estimate the top 1% single-event deaths to decrease by 52.1 every year. The time trend estimate from OLS (statistically nonsignificant) is shown as a constant, with its standard 95% CI. Quantile regression estimates are obtained through the modified Barrodale–Roberts algorithm (38), and the 95% confidence band around them is produced with r = 1,000 bootstrap samples [joint resampling of response and predictor pairs (40)]. Full results on estimates and standard errors are given in SI Appendix, Table S6.

While this global evidence for decreasing casualties over time is good news, interesting patterns emerge when breaking down the analysis by hazard type and country income class. For instance, the strongest fall in the 99th percentile of yearly casualties per inhabitant is observed for droughts (SI Appendix, Fig. S3), suggesting an increased ability to cope with this natural hazard. Despite slightly higher frequencies and strength (43), in recent decades, extreme droughts have become less fatal (39). So have extreme floods, but only in rich countries. We observed an increasing polarization between poor and rich areas of the world also for casualties caused by storms. Finally, and concerningly, extreme temperature events have become more deadly in poor and rich countries alike (SI Appendix, Fig. S3).

Biases in Data May Hide Even Larger Economic Impacts

Our assessment of the trends in economic damages may be overly conservative due to a number of issues affecting disaster data. Difficulties in data collection in the aftermath of disasters impact statistical analyses (44, 45); events dating back several decades, especially when less severe, were often entirely unreported or reported with no damage information (44). Accuracy, however, has improved (46, 47), with more institutions involved in data collection and better imputation and validation techniques. An immediate consequence of the reduction in underreporting over time, ceteris paribus, is to decrease the upper percentiles of the damage distributions. Fig. 5 illustrates this with a simple simulation exercise (details are provided in the legend). Using stationary data as a reference, the simulation shows how a reduction in underreporting (which we mimic as a decreasing left truncation of the data) induces a distinct downward bias in trend estimation, particularly for upper percentiles. Thus, in reality, the pattern of rightward skewing and tail fattening of damages may be more pronounced than the one we assessed using available data.

Fig. 5.

Quantile regressions for simulated datasets. The widening distance between estimates obtained on data from the “True Model” and on data with a decreasing “Logistic Truncation” shows how past damage underreporting can induce a downward bias for upper percentiles, making our assessments of mounting damages conservative. To create the simulated data labeled “True Model” in the plot, we pooled damages from 2000 to 2014 (a period when underreporting was negligible) and used this empirical distribution “stationarily” to draw 318 disasters (the average number of disasters per year in the 1960–2014 span covered by our study) for 55 consecutive years. To create the simulated data labeled “Logistic Truncation,” we pooled damages in the same fashion, but left-truncated them with an intensity decreasing over time (the percentage of bottom values removed starts at 50% in the first year, and coverage is increased according to a logistic, reaching 96% in the last year). This mimics a progressive reduction in underreporting. The horizontal axis represents percentiles and the vertical one estimates time trends. The model used is ${\text{Da}}_i=\alpha +\beta t_i$ (where $D{a}_i$ and $t_i$ are damage and year of disaster $i$). Quantile regressions estimates are obtained through the modified Barrodale–Roberts algorithm (38). The 95% confidence bands are produced through 500 Monte Carlo replications of the whole procedure.

Conclusions

We document an increasing trend in extreme damages from natural disasters, which is consistent with a climate-change signal. Increases in aggregated or mean damages have been modest, but evidence for a rightward skewing and tail fattening of the distributions is statistically significant and robust—with most pronounced increases in the largest percentiles (e.g., 95% and 99%), i.e., the catastrophic events. This pattern is strongest in temperate regions, suggesting that the prevalence of devastating natural disasters has broadened beyond tropical regions and that adaptation measures in the latter have had some mitigating effects on damages.

Our results motivate additional efforts to acquire better data on natural disasters and their economic impacts, increasing accuracy and spatial resolution of proxy variables for fast-evolving factors (e.g., wealth at risk or adaptation measures). Such data will allow validation and extensions of our analyses.

In contrast to the increase in economic damages, casualties linked to natural disasters have decreased. This may be due to lower vulnerabilities, improved early warning systems, and/or disaster relief. The overall downward trend in mortality is good news, but we observed a concerning increase in casualties linked to extreme temperatures.

Our study offers simple, yet relevant, implications. First, public disaster risk management and the insurance industry may face increasingly large economic losses. Second, adaptation efforts may be critical in temperate (not only tropical) areas. Third, if part of the increases in the frequency and strength of natural disasters is attributable to climate change, mitigation is a logical instrument to reduce trends in damages. From a methodological perspective, we find empirical support for the use of a convex, upwardly curved damage function in integrated climate-economics models (see also 30) and for the importance of tail risks (48).

Materials and Methods

Data and Code.

We consider monetary damages and casualties for disasters occurred between 1960 and 2015, as recorded in the Emergency Events Database (39). This data were provided by the Center for Research on the Epidemiology of Disasters (Université Catholique de Louvain) under an agreement of non-third-party disclosure. We restricted attention to 10,901 disasters belonging to the 6 categories most directly associated with climate change: floods, extreme temperatures, droughts, storms, wildfires, and landslides. We geolocalized these disasters with Google Maps API, using the location information originally present in the Emergency Events Database. Köppen–Geiger climate zones are obtained through spatial matching with ref. 49 (resolution 5° × 5°) and, in 371 point-to-cell mismatches, with ref. 50 (resolution 1° × 1°). GDP and population (at the country level) are obtained from the Penn World Table dataset (51) and income classes (also at the country level) from the taxonomy by the World Bank. We express damages in current Purchasing Power Parity (PPP) US$; since GDP is expressed in current PPP US$, too, this also controls for inflation. We remove some events during data preprocessing, resulting in a sample size of 9,495 for our regression analyses. See SI Appendix, Data Treatment for details. Code for our analyses is available at https://github.com/mcoronese/extreme-disasters.

Regression Models.

Let $i$ be an event occurring at time $t_i$ in location ${\ell }_i$. Let ${\text{Da}}_i$ and ${\text{De}}_i$ be its damages and deaths, and $c\left({\ell }_i\right)$ and $k\left({\ell }_i\right)$ the country and geolocalization cell where it occurred. Finally, let ${\mathbf{x}}_{i,t_i,{\ell }_i}$ be a generic vector of covariates measured on the event itself, and/or at its time/location. Examples of (categorical) covariates include event types, cell-level climate zones, or country-level income classes. For damages, we considered

$${\text{Da}}_i=\alpha +\beta t_i+\gamma {\text{GDP}}_{c\left({\ell }_i\right),t_i}+\delta \hspace{0.17em}{t}_i\times {\text{GDP}}_{c\left({\ell }_i\right),t_i}+\theta {\mathbf{x}}_{i,t_i,{\ell }_i}$$ [1]

and eliminating the interaction term

$${\text{Da}}_i=\alpha +\beta t_i+\gamma {\text{GDP}}_{c\left({\ell }_i\right),t_i}+\theta {\mathbf{x}}_{i,t_i,{\ell }_i}.$$ [2]

In the baseline versions of these models, we use only GDP as control, with no other covariate. When introducing a categorical covariate as a vector of dummies ${\mathbf{h}}_{i,t_i,{\ell }_i}$, the model becomes

$${\text{Da}}_i=\alpha +\beta t_i+\gamma {\text{GDP}}_{c\left({\ell }_i\right),t_i}+\sum _j\left({\alpha }_j+{\beta }_j{t}_i\right)h_{i,t_i,{\ell }_i}^{\left(j\right)}.$$ [3]

For deaths, we considered

$${\text{De}}_i=\alpha +\beta t_i+\gamma {\text{POP}}_{c\left({\ell }_i\right),t_i}+\delta \hspace{0.17em}{\text{t}}_i\times {\text{POP}}_{c\left({\ell }_i\right),t_i}+\theta {\mathbf{x}}_{t_i,{\ell }_i}.$$ [4]

In the baseline version of this model, we used only population as control, again with no other covariates. Categorical covariates were introduced in the same way as for damage models. For each model, in addition to a standard OLS (mean) regression, we fit quantile regressions for percentiles from the 70th to the 99th. Note that covariate sets and spatial resolutions different from the ones we employed can be easily accommodated in these models and fits. Robustness checks with additional covariates are included in SI Appendix.

Normalization.

Our models have easy-to-interpret parameters, do not require aggregation over events, and allow us to introduce any type of controls (e.g., the potential effect of population dynamics on total destroyable wealth, as in refs. 52 and 53). We thus overcame the need for (premodeling) normalization and generalized the Actual-to-Potential-Loss approach (17), which normalizes monetary damages by dividing every observation by the GDP of the area affected by the disaster. This produces a nondimensional measure of wealth destroyed as a fraction of the maximum potentially destroyable wealth. Based on the normalized damages ${\text{Da}}_i*$, the effect of time is then evaluated with a model of the kind

$${\text{Da}}_i*\equiv \frac{{\text{Da}}_i}{{\text{GDP}}_{c\left({\ell }_i\right),t_i}}=a+b{t}_i,$$ [5]

which is a special case of Model 1, since it can be rewritten as

$${\text{Da}}_i=\gamma {\text{GDP}}_{c\left({\ell }_i\right),t_i}+\delta \hspace{0.17em}{t}_i\times {\text{GDP}}_{c\left({\ell }_i\right),t_i}.$$ [6]

Model 6 has no intercept and no pure time effect, only wealth and its interaction with time. The more general Model 1 allows us to test whether wealth and time interact in affecting damages and provides both estimates and inference for the pure time term.