Linking scaling laws across eukaryotes

Significance

Metabolic scaling theory has had a profound influence on ecology, but the core links between species characteristics have not been formally tested across the full domain to which the theory claims to apply. We compiled datasets spanning all eukaryotes for the foremost body mass scaling laws: metabolism, abundance, growth, and mortality. We show that metabolism and abundance scaling only follow the canonical ±3/4 slopes within some taxonomic groups, but across eukaryotes reveal reciprocal near ±1 slopes, broadly supporting the “energetic equivalence rule.” In contrast to metabolism, growth follows consistent ∼3/4 scaling within many groups and across all eukaryotes. Our findings are incompatible with a metabolic basis for growth scaling and instead point to growth dynamics as foundational to biological scaling.

Abstract

Scaling laws relating body mass to species characteristics are among the most universal quantitative patterns in biology. Within major taxonomic groups, the 4 key ecological variables of metabolism, abundance, growth, and mortality are often well described by power laws with exponents near 3/4 or related to that value, a commonality often attributed to biophysical constraints on metabolism. However, metabolic scaling theories remain widely debated, and the links among the 4 variables have never been formally tested across the full domain of eukaryote life, to which prevailing theory applies. Here we present datasets of unprecedented scope to examine these 4 scaling laws across all eukaryotes and link them to test whether their combinations support theoretical expectations. We find that metabolism and abundance scale with body size in a remarkably reciprocal fashion, with exponents near ±3/4 within groups, as expected from metabolic theory, but with exponents near ±1 across all groups. This reciprocal scaling supports “energetic equivalence” across eukaryotes, which hypothesizes that the partitioning of energy in space across species does not vary significantly with body size. In contrast, growth and mortality rates scale similarly both within and across groups, with exponents of ±1/4. These findings are inconsistent with a metabolic basis for growth and mortality scaling across eukaryotes. We propose that rather than limiting growth, metabolism adjusts to the needs of growth within major groups, and that growth dynamics may offer a viable theoretical basis to biological scaling.

Scaling laws relating body mass to a variety of species characteristics are among the most general quantitative patterns in biology (1–3). These scaling laws encompass such core ecological characteristics as metabolism (1, 2, 4–9), abundance (10–13), growth (14–18), and mortality (1, 2, 19, 20). The relationship between a species characteristic (y) and its body mass (m) is often expressed as a power law, y = cm^k, where c is a constant for a given variable and k is a dimensionless scaling exponent, given by the slope of a straight line on a plot of log y vs. log m. Many of these relationships are increasingly used to better understand and make large-scale predictions of the effects of the most critical global environmental problems, since they represent simple and efficient predictors of fundamental variables that hold across broad taxonomic groups (1, 2). Moreover, these relationships raise basic and persistently enigmatic problems: how are they linked, and where do they originate?

Body mass scaling research largely began with the study of basal metabolism across mammals, which found an exponent near k = 3/4, known as Kleiber’s law (1, 2, 9, 21) and termed “allometry” (k ≠ 1). This value did not match expectations of a constant energy flux per unit tissue mass (“isometry”; k = 1) nor of surface-volume constraints on heat dissipation over the surface of geometrically similar body plans (“surface law”; k = 2/3). These mismatches provoked questions as to the origin of near 3/4 metabolic scaling but also the generality of the exponent, which is now known to depend on many factors, including metabolic activity level, taxonomic group, taxonomic level, body mass range, temperature, other environmental conditions, life stage, and regression methods (1, 6, 8–10, 22, 23). Despite these many factors, an exponent value of 3/4 has become a canonical expectation for body mass scaling, especially as additional taxonomic groups and additional species characteristics have been found to scale with similar or related values (1–3, 7, 17, 18).

Most prevailing theories of metabolic scaling (with k < 1) are based on physical constraints on the structure of a body (3, 9, 24, 25), which in turn are thought to constrain the scaling of other variables with body mass (1, 2, 7, 11, 15, 18, 20, 26). For example, limits on energy supply can proximally limit abundance (2, 10–12) and the energy allocated to growth and reproduction (1, 2, 15, 18, 26–28). Metabolism is also known to produce harmful byproducts that hasten senescence and shorten life span (2, 9, 29). However, the many dependencies of the metabolic exponent, listed above, suggest that metabolism is also flexible and can adjust to different factors, some of which have been found to be growth factors. This has prompted some authors to suggest that basal metabolic scaling adjusts to growth rather than exerting fundamental control on growth and other characteristics (9, 14, 23, 27, 30–32).

One way to better understand the origin of near 3/4 scaling is to consider the generality of circumstances over which such scaling holds. For example, similar scaling both within and across taxonomic groups is consistent with a single underlying process, whereas different scaling regimes within or across groups are consistent with multiple factors dominating under different circumstances but inconsistent with a single universal process.

In this work, we tested several of the principal assumptions and/or predictions of metabolic theories in ecology by linking scaling relationships for different characteristics, with a view toward the ultimate origin of ∼3/4 scaling. These theories assume that metabolism is the “master rate,” thus limited solely by physical factors related to body mass and so should apply to all eukaryotes. The most comprehensive test of current theory thus calls for data over the full eukaryote domain. Here we first consider the data for each characteristic separately and then examine the links between them.

Scaling Across Eukaryotes

We compiled data across eukaryotes for 4 core ecological variables, comprising 22,761 estimates drawn from nearly 2,800 published sources and meta-analyses (Fig. 1 and Table 1). These data are of varying quality, with unequal representation across the size spectrum. While data for mammals and birds are generally extensive, data are particularly limited for unicellular protists and less complete for some groups of invertebrates. Data often exhibit considerable residual variability, limiting the accuracy with which exponent values can be determined within particular taxonomic groups. At the largest scales, however, estimated exponent values are typically robust to different assumptions, measurement techniques, and regression methods, as well as more specific considerations (Methods and SI Appendix). These relationships offer a comprehensive view to distinguish the scaling across and within major groups, which helps delimit the generality of any underlying process.

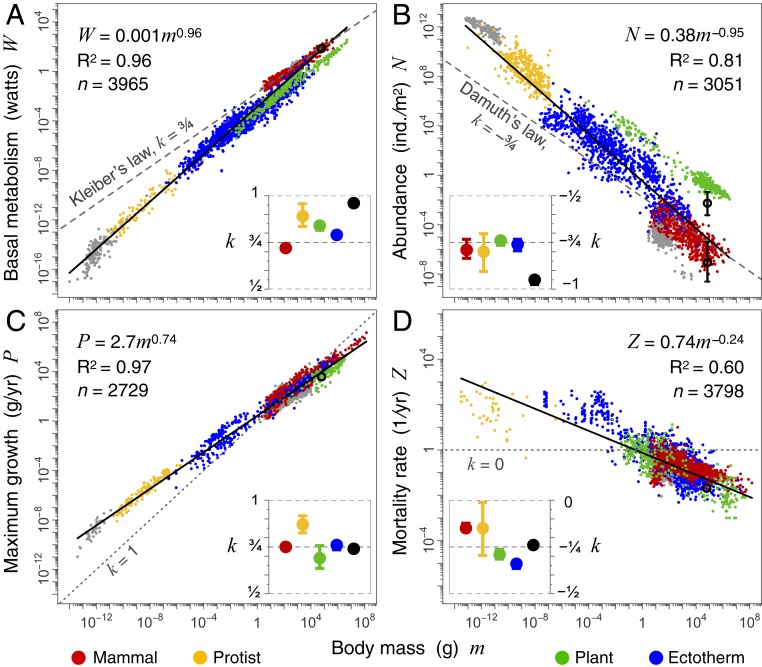
Fig. 1.

Scaling of basic variables with body mass. (A) Basal metabolism, (B) population abundance, (C) maximum growth, and (D) mortality rate. Points (n) in all plots (A–D) are separate species values, except for plants represented by multiple points for the same species. Ectotherms and protists were also not aggregated into species values in D, due to limited mortality data among smaller sized species. For illustration, we have split eukaryotes into mammals, protists, plants, and ectotherm vertebrates and invertebrates. More resolved groups down to taxonomic orders are detailed in SI Appendix, Figs. S1–S3 and Tables S1–S4. Birds (gray points) often have similar rates to mammals and thus are difficult to see in the plots (SI Appendix). We show bacteria (also gray points) for reference, where available, but limit our discussion to eukaryotes. Scaling exponents k and 95% CIs are shown in the insets for major groups (these exclude birds and bacteria). Black empty circles are humans, with ranges shown in B for cities and hunter-gatherer communities (not included in the analysis).

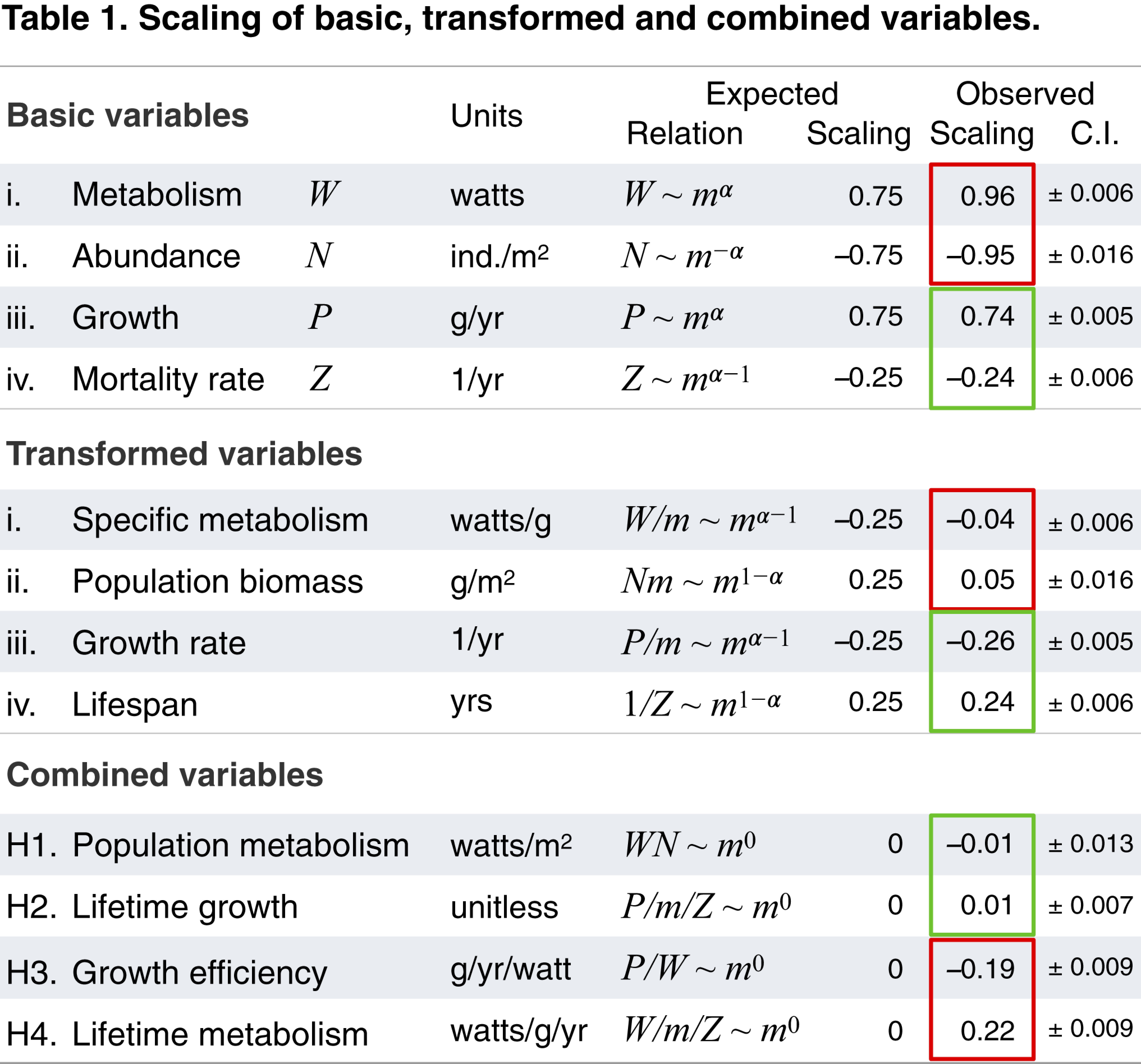Each basic variable scales with body mass m raised to a power, often expected to be α = 3/4. Observed scaling exponents are for all eukaryote data shown in Figs. 1 and 2 (with 95% CIs). Exponents that differ significantly from expectations (α ≉ 3/4) are boxed in red, while matches (∼3/4) are boxed in green. Basic variables can be transformed and combined to yield 4 hypothesized equivalence relationships with expected mass exponents near 0 (H1 to H4). H1 is supported even though W and N do not themselves match expectations, because both basic variables remain inverse to one another. H3 and H4 are rejected because α ≉ 3/4 for metabolism (W) across eukaryotes.

Metabolism (W).

Consistent with prior work (1, 2, 7, 21), we find that basal metabolism scales near 3/4 within some major groups (Kleiber’s law), but when viewed across 20 orders of magnitude, it is clear that distinct shifts in elevation occur between major and minor groups (e.g., ectotherms and mammals). These shifts are such that across all taxa, metabolism scales near isometrically, with an exponent near 1 (k = 0.96; Fig. 1A) (4, 5). These shifts between groups are partially reduced by correcting metabolism to a standard temperature (2, 5, 6), but even correcting endotherm metabolism still results in slopes k > 0.92 across the full eukaryote domain (SI Appendix, Fig. S4). This implies that mass-specific basal metabolism is strongly bounded across eukaryotes (Fig. 2A), consistent with previous studies on smaller but equally broad datasets (4, 5).

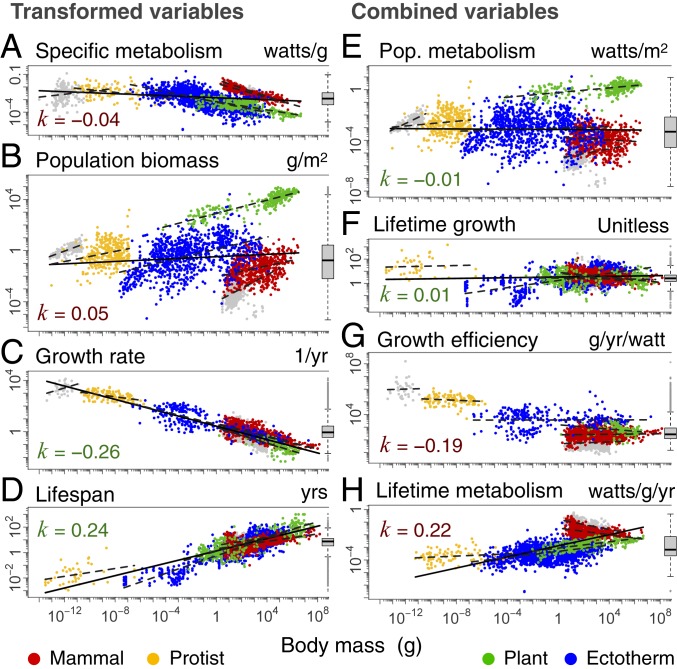
Fig. 2.

Scaling of transformed and combined variables with body mass. Data are the same as in Fig. 1 but transformed (A–D) and combined (E–H) as per Table 1, using taxonomic information down to the species level, where available. The dashed lines show within-group relationships, while the solid line shows the cross-group relationship. Colors of the exponent k correspond to colors of boxes in Table 1. The x- and y-axes have equal order of magnitude spacing. Boxplots are shown for each variable.

Abundance (Individuals/m²).

Abundance (i.e., population density of a species) data are drawn from different ecosystems globally, with each estimate representing a snapshot for a species or an average value of several such points (SI Appendix). Consistent with prior work (1, 10, 11, 13), we find that abundance scales with body mass near −3/4 within some major groups (Damuth’s law) (2, 10, 11, 13), but that across eukaryotes, the exponent is closer to −1 (k = −0.95; Fig. 1B). Surprisingly, we find that the slopes within groups and the shifts in elevation between groups are largely reciprocal to basal metabolism (Fig. 1A).

Species abundance is known to vary greatly through time or along an environmental gradient, and thus it is not surprising that the abundance-mass relationship reveals large residual variation. Contributing to this residual variation is the trophic level of a species, with, for example, carnivorous mammals approximately 10-fold less abundant than herbivorous mammals (Box 1), which themselves are at least 10-fold less abundant than plants (SI Appendix, Fig. S8). Further accounting for their very high densities, the plant data in Fig. 1B are for monoculture stands of trees rather than natural, more diverse assemblages (SI Appendix). Birds exhibit a very weak abundance-mass relationship with high residual variation, which is not fully understood (12). Much of the remaining residual variation reflects species population fluctuations rather than systematic variation between species, suggesting that residual variation across species is only marginally greater than that within species (SI Appendix, Fig. S5).

Both the scaling and residual variation in the abundance-mass relationship can also be linked to several other well-known abundance patterns. In Box 1, we transform the abundance data in Fig. 1B (N ∼ m^k) by applying simple functions to N and m, which allows predictions for other types of relationships and distributions widely studied in ecology. Overall, the abundance data reveal broad consistency with other patterns, but also highlight several critical mismatches calling for further attention (SI Appendix, section 8 and Fig. S8).

Growth (g/yr).

To ensure that data are comparable across very different groups, measures of growth were integrated over the entire life cycle and are equivalent to the maximum population growth rate (intrinsic growth rate, or r_max) multiplied by individual adult body mass (2, 15, 16, 33). Alternative measures of growth that apply only to particular groups or life stages tend to converge on similar measures, so that our confidence in the growth relationship across eukaryotes and within most major groups is relatively high (SI Appendix). Consistent with prior work (2, 15–17), maximum growth exhibits ∼3/4 scaling within major groups, similar to within-group metabolic scaling. However, in contrast to metabolism, robust ∼3/4 growth scaling is also preserved across groups (15–17) (Fig. 1C).

Mortality (1/yr).

In general, mortality rate is the inverse of life span (years), but life span is commonly defined in different ways. Maximum life span is often measured in captivity under ideal conditions and represents an intrinsic physiological potential, often quite distinct from the extrinsic ecological reality. In contrast, average field life span is measured over a population in the wild and represents a more realistic but more variable measure. Estimating mortality in the wild is more difficult for species such as trees and fish that produce large numbers of offspring, most of which die in early ontogeny. Our data include both measures of mortality and, following previous studies, are normalized to field mortality rates when possible (20). As might be expected from the challenges in measuring mortality, there is significant dispersion in the relationship. However, consistent with prior work (1, 2, 19, 20), we find that mortality scales near −1/4, both across and within many major groups. Data are limited among smaller-sized species, so that we are less confident of the scaling within some groups, such as protists and invertebrates (Fig. 1D).

Testing Equivalence Hypotheses

By variously combining any 2 of these 4 scaling relationships through multiplication or division, we can obtain combined variables that have previously been proposed to be invariant with body mass, termed “equivalence relationships” (Table 1). By “equivalence,” we do not mean to imply that everything is equal and residual variation is small, but simply that there is no significant trend with body mass. These equivalence relationships form core assumptions and/or predictions of the metabolic theory of ecology (2), but so far have only been validated within major groups. We treat these as hypotheses that can be formally tested across eukaryotes, where the null expectation is a mass exponent of 0 (k = 0). We have combined variables using taxonomic information down to the species level when available, to preserve as much of the residual variation as possible (Methods and SI Appendix). This allows us to characterize the scaling and coefficients both within and across major groups for each of 4 equivalence hypotheses, H1 to H4 (Table 1 and Fig. 2 E–H).

H1: Population Metabolism.

Population metabolism (W/m²) estimates the total amount of basal energy used by a population per unit area. This hypothesis, also known as the “energetic equivalence rule,” suggests an energetic basis of abundance, whereby energy partitioning among species in space exhibits no trend with body mass (2, 10, 12, 13). Although prior work has shown that within major groups, the product of the reciprocal ±3/4 scaling of basal metabolism and abundance gives an equivalence in population metabolism (10–13), this has not been previously tested across all eukaryotes. We find that the exponents and the shifts in elevation between groups of each variable are reciprocal. Specifically, the residual variation in each of the metabolism-mass and abundance-mass relationships (Fig. 1 A and B) is partly compensatory, so that when a species (or group) is above the line in 1 variable, it tends to be below the line in the other variable and vice versa. As a result, the product of these 2 variables shows an equivalence in energy use at the population level that appears to hold across 20 orders of magnitude in body mass (combining Fig. 2 A and B gives E).

H2: Lifetime Growth.

Lifetime growth (dimensionless) estimates the maximum number of offspring produced over the average lifetime of an individual. This hypothesis, also known as “lifetime reproductive effort” (33) or the “equal fitness paradigm” (17), suggests that populations are broadly near a steady state in abundance, such that reproductive rates multiplied over an average life span in the wild should be nearly constant across species (2, 17, 33). Combining reproduction and survival in this way has been proposed as a key component of fitness (17, 33). Data are limited for field estimates of reproductive rates, and our use of maximum reproductive growth will tend to overestimate actual lifetime growth in the wild (SI Appendix). Moreover, data remain limited among smaller-sized classes for fully evaluating this hypothesis among protists and invertebrates. Despite these limitations, and consistent with prior work (2, 17, 33), we find broad support for this equivalence relationship across eukaryotes (combining Fig. 2 C and D gives F).

H3: Growth Efficiency.

Growth efficiency (g/yr/W) estimates the maximum amount of mass produced per unit energy of basal metabolism. This hypothesis, also known as the “cost of growth,” suggests that an approximately constant fraction of metabolism is allocated to growth (27, 28, 32), which forms a basic assumption in many growth models, going back to that of Bertalanffy (18, 25, 26, 34). Our use of basal metabolism for estimating growth efficiency may underestimate the energy needed to fuel maximum growth, so that this measure represents a possible upper limit of growth efficiency (27, 28). Consistent with prior work (27, 28), we find that within major groups, growth efficiency is largely equivalent but that across groups, this hypothesis is not supported, with clear shifts between groups, such that mammals and birds are several orders of magnitude less efficient than unicells in converting energy into new biomass (combining Fig. 2 A and C gives G).

H4: Lifetime Metabolism.

Lifetime metabolism (W/g/yr) estimates the amount of basal energy used per gram of tissue over the maximum lifetime of an individual. This hypothesis, also known as the “rate of living” hypothesis (and characterized as “live fast, die young”), is based on oxygen radicals produced as byproducts of metabolism that are known to accelerate senescence and thus reduce life span (2, 9, 29). Whereas H2 applies to average ecological lifetimes, this hypothesis relates to the maximum physiological lifetime. While prior work has shown mixed support for this hypothesis (9, 29), data remain limited for fully rejecting this hypothesis within groups (SI Appendix, Fig. S7), but across groups, our data do not support this hypothesis (combining Fig. 2 A and D gives H).

In summary, our data support 2 previously proposed equivalence relationships connected to the population energetics (H1) and steady-state dynamics (H2) of abundance but are inconsistent with 2 other equivalence hypotheses often used to argue for a metabolic basis for growth and mortality scaling (H3 and H4). This raises the question of the ultimate basis for the scaling of these variables and in particular the origin of k ∼ 3/4 growth scaling across eukaryotes.

Linking Growth and Metabolism

Many of the theories for body mass scaling are based on structural dimensions of the body thought to limit the flux of raw materials or products of metabolism (3, 9, 24, 25). The flux of energy needed to support all life processes is in turn assumed to dominate the scaling of other characteristics (1, 2, 7, 11, 15, 18, 20, 26). While our results are indeed consistent with a metabolic basis for abundance both across and within groups (H1), it is only within groups that metabolism can account for the allometric scaling of other variables, such as growth and mortality (H3 and H4).

Basal metabolism exhibits 2 scaling regimes: an allometric regime within groups (k < 1, and typically k ∼ 3/4) and a near-isometric regime across groups (k ∼ 1). These 2 scaling regimes are also observed in mammals in different activity states. Basal metabolism across mammals scales near 3/4, as has long been known (1, 2, 7, 21), while maximum (35) and minimum (torpor) (36) metabolic rates scale as k ∼ 1 (Fig. 3B). Mass-specific metabolic rates across eukaryotes and across activity levels in mammals are thus limited over the same 3 orders of magnitude. This isometric regime suggests the existence of strict metabolic boundaries above which eukaryote cells may be damaged by metabolites or unable to pack mitochondria and below which tissues cease to maintain function or become unviable (4, 5, 8, 25). Within this broad 3 orders of magnitude scope, basal metabolism exhibits a tendency to scale near 3/4 within groups but is systematically staggered in elevation across groups so as to remain within near-isometric metabolic boundaries (Fig. 3C). These 2 distinct scaling regimes are suggestive of multiple underlying processes.

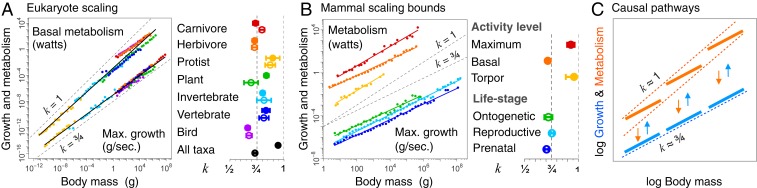
Fig. 3.

Growth and metabolism size class scaling. In A and B, original data from Fig. 1 A and C are binned into logarithmic body size classes to highlight the principal relationships and give equal representation to different size classes. Exponents and 95% CIs are shown to the right of each plot for the nonbinned data, with filled circles for metabolism (above) and empty circles for growth (below). (A) Scaling relationships for basal metabolism (W) and maximum growth (g/s) from Fig. 1 A and C (with additional taxonomic groups) reveal scaling similarities for most groups but a systematic divergence at larger body mass across groups. (B) Mammal scaling relationships for metabolism across activity levels and maximum growth across life stages shows the boundaries in which these characteristics vary. (C) The prevailing view is that metabolism determines growth scaling (orange arrows of causality) on the basis that within a given major group, both variables scale as k ∼ 3/4 (parallel thick lines). The metabolic view, however, cannot explain why growth follows the same universal k ∼ 3/4 scaling both within and across groups, given that metabolism often shows shifts in elevation between groups. A more parsimonious view is that across groups, metabolism adheres to isometric bounds (k ∼ 1), but that within major groups, metabolism adjusts to growth scaling of k ∼ 3/4 (blue arrows of causality).

Growth, on the other hand, appears to exhibit a single scaling regime (k ∼ 3/4) both within and across species, with no systematic shifts in elevation, which is consistent with a single underlying process. Similar growth scaling is also observed in mammals at different life stages. Maximum reproductive growth (mammals in red in Fig. 1C) (15, 16) scales very similarly to maximum ontogenetic (14) and prenatal (19) growth (Fig. 3B). We also observe similar ∼3/4 scaling in the growth of whole communities across large biomass gradients in grasslands, forests, lakes, and oceans (16). These community-level growth relationships represent a higher level of organization that cannot be accounted for by any strictly individual-level constraint. This single scaling regime, describing growth across and within groups and across life stages and levels of organization, eludes any single metabolic explanation and instead may point to a more general underlying process.

Several authors have suggested that basal metabolic scaling is rather underpinned by growth scaling and not the reverse (9, 14, 23, 27, 30–32). The idea that metabolism adjusts to growth factors rather than growth being limited by structural constraints on metabolism has been proposed for a variety of different reasons. In SI Appendix, section 9, we summarize some of the different lines of evidence for this proposal. In addition, we list growth phenomena at different levels of organization and stages of development, be they normal, abnormal, or experimentally induced, that are known to have downstream effects on metabolism. Extreme limits on metabolism can always limit growth, but except in some cancers (e.g., the Warburg effect) (37), normal or experimental changes in metabolism rarely cause downstream changes in growth. Growth is often seen to be regulated upstream of metabolism, which adjusts to fuel protein synthesis and cell replication and ensures coregulation in both variables (SI Appendix, Fig. S8). Despite the many indications that metabolism adjusts to growth, so far no quantitative theory for ∼3/4 growth scaling has been proposed that encompasses the numerous instances in which such scaling is observed.

Outlook.

We believe there may be a universal process underlying the ubiquitous tendency for growth to scale near 3/4. This single growth scaling regime suggests something fundamental in the dynamics of how mass changes over time across very different kinds of living systems. The idea that metabolism adjusts to fuel growth within groups and adheres to metabolic boundaries across groups appears to provide a more parsimonious explanation for the link between the growth and metabolism relationships shown in Fig. 3 and is supported by multiple lines of evidence (SI Appendix, section 9 and Fig. S8). We propose that basal metabolism in part reflects ontogenetic adjustments and evolutionary adaptations to efficiently fuel growth and turnover within groups, and that groups are staggered to remain within energetic limits. This could account for why basal metabolism and maximum growth within groups have such similar scaling (Fig. 3A), but it does not solve the problem of how this scaling arises.

We are not prepared to speculate as to what general process might underpin growth scaling, but in many of the instances in which such scaling is observed, we are essentially seeking an explanation for the relationship between mass m and its derivative, $\frac{dm}{dt}=c{m}^{\alpha }$, where α ∼3/4 and c is a constant (33). For α < 1, this relationship implies a continually diminishing growth rate and, more specifically, a characteristic scale-free form of subexponential growth. Integrating this relationship, we see how mass changes over time and approaches $m\left(t\right)\sim t^{\frac{1}{1-\alpha }}$. Thus, this solution predicts how the timing of life history events will scale with body mass as $t\sim m^{1-\alpha }$, consistent with the timing of gestation, maturity, and life span (1, 2, 20, 38) (Fig. 2D). Understanding the origin of this simple growth relationship may shed light on a number of other linked characteristics and represents a critical area for further research.

Conclusion

The data that we report here provide a comprehensive view of the most general boundaries within which life exists. Although the data are of varying quality, gathered over many decades using different methods and for different objectives, the patterns exhibit remarkable regularity and surprising connections between core species characteristics.

Population abundance is known to be highly variable, but when viewed at the largest scales reveals a reciprocal pattern with metabolism, mirroring both the slopes and shifts in elevation within and across major groups. This supports an equivalence in population-level energy use, consistent with a fundamental energetic basis to abundance that spans all eukaryotes (H1). The maintenance of steady state in abundance is necessarily mediated by the dynamics of birth and death, which also results in an equivalence in lifetime growth (H2). These relationships are intriguing given that so many presumably adaptive traits scale with body size, and yet across eukaryotes, their combined influence has a relatively neutral net effect on population energy use (H1) and individual lifetime growth potential (H2). These 2 broadly supported equivalence relationships, in connection with other known abundance patterns (Box 1), suggest the possibility for a more synthetic understanding of the different aspects of abundance in ecology.

The widely held view that a metabolic basis underpins the allometric scaling of growth and mortality is not supported across eukaryotes (H3 and H4). Most importantly, the consistent ∼3/4 scaling of growth found across groups cannot be explained by a single set of metabolic constraints, given that metabolic scaling exhibits different scaling regimes within and across groups. In contrast to metabolic scaling, the striking similarities in growth scaling within and across groups, and also across life-stages and levels of organization, are indicative of a single generating process, begging further understanding. We propose considering the dynamics of growth as presenting a general basis for biological scaling.

Methods

Additional details for all data sources, methods, and limitations, along with regression statistics for more than 200 major and minor group relationships, are provided in SI Appendix. Further analysis is possible using the raw data and source code available at https://zenodo.org/record/3145281.

Metabolism measurements were normalized to 20 °C for all taxa except mammals and birds, using both published values of Q₁₀ and the Arrhenius factor with standard activation energies, revealing only slight differences among methods that do not alter our conclusions (SI Appendix, Fig. S4). All abundance data were gathered over a relatively large area and originally reported in aerial units (e.g., m²), including aquatic species, normalized over multiple depths in the water column. The mammal growth shown in Fig. 3B was calculated for each life stage as follows: (i) maximum reproductive growth is from population time series data or, more commonly, calculated from life history measurements, integrated over the entire life cycle; (ii) maximum ontogenetic growth is obtained from near the inflection point of somatic growth curves of different mammal species (14); and (iii) prenatal growth is calculated as birth mass divided by gestation period (19) (SI Appendix).

We used ordinary least squares (OLS; type I regression) to calculate regression statistics, which is the standard approach in bivariate regression when the dependent variable is measured with greater error than the independent variable (1) (SI Appendix). Exponents from reduced major axis (type II regression) are similar to OLS for all cross-taxa regressions, although differences are apparent among more resolved groups, and can be obtained from SI Appendix, Tables S1–S4. The binning of data shown in Fig. 3 was achieved by taking the geometric mean value in each logarithmic size class, which allows equal representation for different size classes when data are not evenly distributed across the size range (7).

We combined variables to test equivalence hypotheses (Table 1) using several taxonomic levels to ensure that residual variability in combined variables is largely preserved. When direct species matches could not be made in both datasets, we combined measurements from the more-dispersed variable with order-level regression predictions from the less-dispersed variable, which preserves the majority of residual variation while ensuring that regression equations are comparatively reliable. In the relatively few cases where limited taxonomy precluded order-level regressions, we then combined estimates with regression predictions for major groups, and we linked all variables using the same 3 taxonomic levels for all hypotheses in Table 1. More specific treatments for particular groups and paired variables are described in SI Appendix.