Probing force in living cells with optical tweezers: from single-molecule mechanics to cell mechanotransduction

Abstract

The invention of optical tweezers more than three decades ago has opened new avenues in the study of the mechanical properties of biological molecules and cells. Quantitative force measurements still represent a challenging task in living cells due to the complexity of the cellular environment. Here, we review different methodologies to quantitatively measure the mechanical properties of living cells, the strength of adhesion/receptor bonds, and the active force produced during intracellular transport, cell adhesion, and migration. We discuss experimental strategies to attain proper calibration of optical tweezers and molecular resolution in living cells. Finally, we show recent studies on the transduction of mechanical stimuli into biomolecular and genetic signals that play a critical role in cell health and disease.

Mechanical energy is one of the driving forces of cell life that shapes cell morphology and adaptation to mechanical environment by providing signals that are fundamental regulators of cell development and homeostasis (Sachs 2018). The invention of optical tweezers (OT) by Arthur Ashkin (Ashkin 1970; Ashkin et al. 1986; Ashkin and Dziedzic 1971) opened up the possibility to observe single biological molecules at work and investigate their mechanical properties. Since that demonstration, single-molecule biophysics has seen unprecedented development in the last two decades. A myriad of experimental configurations has been developed to study isolated biomolecules in vitro, such as molecular motors or DNA (Capitanio and Pavone 2013).

Although the very first biological application of optical tweezers was live cell manipulation (Ashkin et al. 1990; Ashkin and Dziedzic 1989), quantitative force measurements in cells have developed slower than in in vitro reconstituted systems since the reliability of the measurements and methods are constantly challenged by the complexity of cell environment. Nevertheless, optical tweezers are a very powerful tool for quantifying molecular forces in vivo and recent developments have expanded the range of available tools. Compared to alternative techniques, such as atomic force microscopy (AFM) and magnetic tweezers, optical tweezers combine unique features including high-resolution position and force measurements that allow measurement of Angstrom-scale movements and sub-pN forces (Abbondanzieri et al. 2005; Greenleaf et al. 2005; Moffitt et al. 2008), dynamic measurements at microsecond temporal resolution (Capitanio et al. 2012; Gardini et al. 2018), and trapping of intracellular structures, which make them an ideal choice in several applications (Neuman and Nagy 2008). Optical tweezers are easily implemented in an optical microscope by focusing a laser beam through the microscope objective to create a large gradient of light intensity. Dielectric microparticles are stably trapped near the beam focus owing to the interaction between the light intensity gradient and the particle itself. A polystyrene or silica microsphere is usually trapped and used as a handle to manipulate biological molecules or cells bound to it. The bead position is used to probe the movements, while the force applied to the molecule or cell is simultaneously measured. Several papers describe the working principle of OT in details (Capitanio 2017; Neuman and Block 2004). Here, we review different strategies and experimental configurations to apply and measure force in living cells. We show how optical tweezers can be used as an efficient tool to stimulate cells or specific membrane proteins mechanically, as well as to measure the mechanical and contractile properties of cells and quantify the strength of molecular bonds between membrane proteins and binding partners, or also to investigate the activity of molecular motors in living cells. Finally, we present the latest developments which allow for the application and measurement of forces up to the nN scale and the simultaneous monitoring of mechanotransduction signals within a cell by a combination of laser tweezers and fluorescence microscopy.

Calibration of optical tweezers in living cells

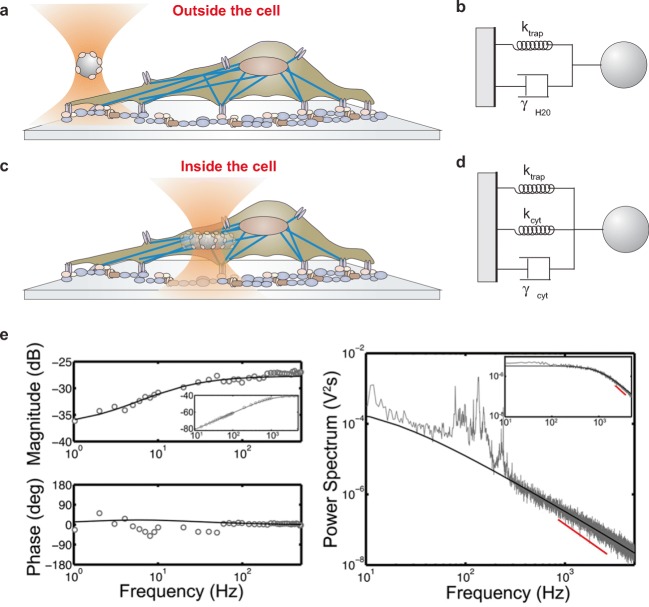
Optical tweezers are commonly used to apply and measure forces on the outer cell membrane, either to probe specific membrane proteins or to measure elastic properties of the cell. Typically, polystyrene beads of variable size (from a few hundred nanometers to several microns) are chosen depending on the area of the plasma membrane under investigation. When specific membrane proteins or receptors are interrogated, the beads are covered with target ligands. Different measurement configurations are reviewed in the following sections and the calibration of optical tweezers is straightforward in each condition. Usually, a position detector based on a quadrant detector photodiode is used to measure the bead position at high temporal and spatial resolution. In this case, beads are trapped in solution far from the cell and bead thermal fluctuations are analyzed to readily determine both the trap stiffness k_trap (pN/nm) and the position detector conversion factor β (nm/V) (Capitanio 2017; Capitanio et al. 2002). Alternatively, a fast CCD camera can be used to monitor the bead position. In such configurations, the viscous properties of the bead surrounding medium are well known and the elastic response is entirely prescribed by the stiffness of the optical trap, allowing simple modeling and interpretation of the data (Fig. 1a, b).

Fig. 1.

Calibration of optical tweezers inside and outside a cell. a Sketch of a bead trapped by optical tweezers outside a cell. b Diagram representing the forces acting on a trapped bead outside a cell surrounded by water solution (k_trap is the optical tweezers stiffness, γ_H20 is the viscous drag coefficient of the water solution). c Schematic of a trapped bead inside the cytoplasm responding to sinusoidal oscillations. d Diagram of forces acting on a bead inside a cell (k_trap is the optical tweezers stiffness, k_cyt and γ_cyt are, respectively, the stiffness and viscous drag coefficient of the cytoplasm). e Calibration of optical tweezers inside living cells is made by global fitting forced oscillation (left panels) and thermal motion (right panel) of trapped phagocytosed beads. Thermal motion fitting is limited to frequencies > 300 Hz because spontaneous fluctuations below 300 Hz indicate biological processes in the cell and vibrations of the stage due to the coupling of the stage and the bead in the cytoplasm. Bead motion in the cell is subdiffusive resulting to a slope < 2 (red line denotes a slope of 2). Inset: Spectra from a bead immersed in water (reproduced from Hendricks et al. 2012)

Although manipulating cells from the outer membrane is the most common and easily used configuration, direct manipulation and force measurement inside living cells is a unique feature of optical tweezers that has seen great progress recently. Micron-sized beads can be easily internalized by phagocytosis or, alternatively, cell organelles such as vesicles, lipid droplets, mitochondria or the cell nucleus can be directly manipulated by light and used as force probes. In such cases, one of the main issues for quantitative force measurement is the trap calibration. In fact, several viscoelastic components including the cytoskeleton, cell membrane, and various molecules that interact with the force probe potentially contribute to the elastic and viscous response. Moreover, since k_trap and β vary largely with probe size in the micrometer to submicrometer range (Capitanio 2017), it is extremely difficult to precisely calibrate traps for cell organelles of unknown size. Although the position detector calibration factor for a force probe of unknown size in a cell can be obtained by comparing its movements detected with a camera with known pixel size and the position detector signal (Barak et al. 2013), the trap stiffness cannot be easily determined. Fischer et al. proposed a general calibration method to obtain k_trap and β for particles of unknown size in a medium with unknown viscoelastic properties (Fischer and Berg-Sorensen 2007) and experimentally demonstrated it in a simple viscous medium and in a solution of entangled F-actin (Fischer et al. 2010). The method (herein named active-passive calibration) employs a combination of passive (thermal fluctuation) and active (forced oscillations) recordings to determine both trap calibration parameters and viscoelastic properties of the medium (Fig. 1c–e). More recently, this method was further extended to measure stall force of dynein and kinesin in vivo (Blehm et al. 2013; Hendricks et al. 2012). This approach is particularly interesting because it also provides measurement of the viscoelastic properties of the cell. We discuss this application further in the sections below. Alternative approaches are also possible and different methods were recently compared by Jun et al. (2014). One of these approaches attains direct measurement of force in living cells through measurement of the light momentum change. In this case, knowledge of the index of refraction of the cytoplasm is required. In a different approach, the trap is calibrated outside the cell in a medium of known index of refraction and the calibration parameters in the cell are obtained from the refractive index mismatch between the cytoplasm and the medium.

Measuring the strength of ligand-receptor bonds on the cell membrane with single-molecule sensitivity

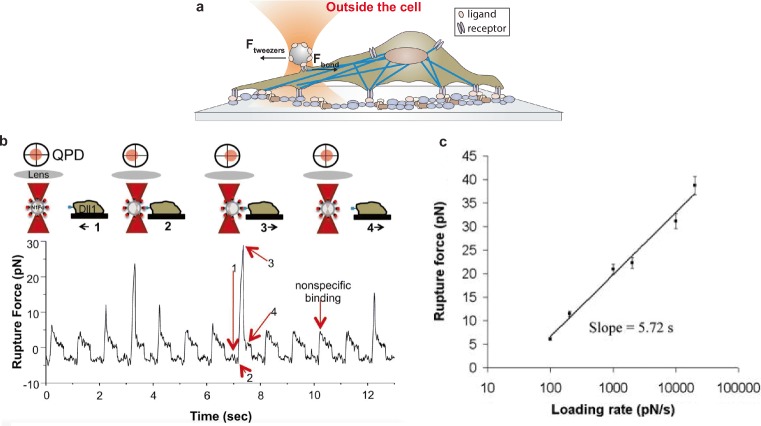
Communication between cells and between cells and their environment is mediated via specific membrane receptors and adhesion complexes, which establish connections to signaling molecules, neighboring cells, and extracellular components. Since such connections work under varying mechanical load, it is fundamental to quantify how their binding kinetics is regulated by force. Although conventional ensemble methods have extensively been used to determine unloaded binding rates and affinity constants, optical tweezers yield direct quantitative information on the lifetime and force dependence of individual biomolecular complexes. Mechanical manipulation on the cell membrane at the level of individual receptor–ligand molecular pairs is possible through the use of nanoparticles functionalized with a variety of ligands (Fig. 2a), and this approach has been applied to investigations on the bond strength of a variety of ligand–receptor pairs (Weisel et al. 2003).

Fig. 2.

Measuring molecular bond strength on the cell membrane. a Schematic of an optically trapped bead covered by ligands forming a bond with receptors on the cell membrane. The optical tweezers apply a force to probe the rupture force of the molecular bond. b Representation of the experimental setup having a trapped sphere in the vicinity of a live cell and the corresponding acquired force signal in real-time. The experiment proceeds in four steps, as indicated by the corresponding numbers and arrows: (1) cell moves towards the bead; (2) cell membrane interacts with the trapped bead; (3) cell moves away until rupture is observed; (4) bead position is restored in the trap and cell continues to move away. Force is calculated by the trap stiffness and bead displacement (reproduced from Shergill et al. 2012 with permission from Dev. Cell.). c Example of a rapture force versus loading rate plot for the A1/GB Ib-IX interaction (reproduced from Arya et al. 2005 with permission from Biophys. J.)

The interaction between a receptor and its ligand can be described, from a biochemical perspective, as a reversible chemical reaction characterized by association and dissociation rates that occur in a range that spans several order of magnitudes, from min⁻¹ up to kHz (Thoumine et al. 2000). Generally, the reaction rates depend on the potential energy profile of the molecular bond and the disruptive force applied on it. The bond strength can be measured as the dissociation rate of the ligand from the receptor at a constant force F (force-clamp measurement) or as the rupture force at constant loading rate r (dynamic force spectroscopy) (Capitanio and Pavone 2013).

Under constant force, the dissociation rate, k_off, is given by:

$$k_{\mathit{off}}\left(F\right)=k_{\mathit{off}}^{0}exp\left(\frac{F·x_{\beta }}{k_{B}T}\right)$$ 1

where k⁰_off is the unloaded dissociation rate, k_B is Boltzmann’s constant, T is the absolute temperature, and x_β is the distance parameter, i.e., the distance between the bound state and transition state along the reaction coordinate (Dudko et al. 2008). Under constant loading rate, the rupture force F_r is given by (Evans and Ritchie 1997):

$$F_r\left(r\right)=\frac{k_{B}T}{x_{\beta }}ln\left(\frac{r{x}_{\beta }}{k_{\mathit{off}}^0{k}_{B}T}\right)$$ 2

Therefore, from a measurement of k_off(F) or F_r(r), we can derive x_β and k⁰_off, which characterize the strength of the molecular bond. Pioneering studies on the strength of cadherin bonds to the cytoskeleton mediated by catenins using OT were performed by Sako et al. (Sako et al. 1998). E-cadherin is a fundamental transmembrane protein that localizes at adherens cell-cell junctions. The extracellular domain of E-cadherin links to neighbor extracellular cadherin domains on adjacent cells, whereas the cytoplasmic tail binds to the actin cytoskeleton through catenins. A single-beam gradient optical trap was used to capture and randomly drag E-cadherin complexes laterally along the plasma membrane, allowing quantification of different dragging distances as a measure of bond strength, which increased in the presence of a connection between E-cadherin and actin mediated by catenins (Sako et al. 1998).

The strength of the integrin-fibronectin bond, a fundamental component of cell-extracellular matrix adhesion, has been also characterized by optical tweezers. In a first study, direct trapping of a single fibroblast was achieved to measure cell adhesion forces on a fibronectin-coated surface (Thoumine et al. 2000). Rupture of fibronectin-integrin linkages under forces in the 13–28 pN range were identified at loading rates between 5 and 100 pN · s⁻¹. Several limitations are intrinsic of the described experimental approach, including difficulties in accurate force calibration, nonspecific interactions with the cell membrane, and cell photodamage through absorption of laser light. To overcome these limitations, Jiang et al. employed a different approach in which the movement of fibronectin-coated beads restrained by a laser trap at the leading edge of a lamellipodia was recorded over time (Jiang et al. 2003). The bead moved at about 60 nm · s⁻¹ exerting force on the linkage from the bead to the cytoskeleton. Following pulling, beads continued to move out of the trap until the breaking force was reached (2 pN), and then abruptly returned to the center of the laser trap as a result of the breakage of the cytoskeleton linkage. In another study, optically trapped fibrinogen-coupled latex beads were repeatedly reacted with either purified surface-bound αIIbβ3 or αIIbβ3 integrins on living platelets (Litvinov et al. 2002). Following serial contacts, rupture forces on the surface of living platelets were in the 60–150 pN range with a peak yield strength of 80–100 pN, at a loading rate (20,000 pN · s⁻¹) in the same order of magnitude to that imposed on platelets under physiologic shear rates.

The methodology published by Litvinov and collaborators was successively modified allowing collection of large data sets for statistical analyses to accurately determine rupture force as a measure of bond strength of single Notch-ligand bonds (Meloty-Kapella et al. 2012; Shergill et al. 2012). Notch signaling, induced by cell surface ligands, is critical to development and maintenance of many eukaryotic organisms. In this experimental configuration, cells expressing the Notch ligand Delta-like1 (Dll1) were repeatedly bound and detached to laser-trapped Notch1 (N1) beads allowing serial measurements of rupture force (Fig. 2b). Single-molecule interactions were promoted by limiting the bead–cell contact time to 20 ms. Rupture force spectra were consistent with a Poisson distribution model, indicating that the 19-pN mode represents single-bond ruptures using a loading rate of 250 pN · s⁻¹.

Optical tweezers were also used to investigate the binding of the glycoprotein (GP) Ib-IX complex to the von Willebrand factor (VWF), which mediates the formation of platelet plugs for arterioles and is associated with the bleeding disorder von Willebrand disease (Arya et al. 2002). CHO cells that stably express GP Ib-IX complexes were used to examine the binding to polystyrene bead-bound VWF multimers and determine the bond strength. A more appropriate characterization of bond strength was achieved in a following study by using dynamic force spectroscopy (Arya et al. 2005). Unbinding forces were measured under various loading rates ranging from 100 to 20,000 pN · s⁻¹ and rupture values increased logarithmically with the loading rate, as prescribed by Eq. 2 (Fig. 2c).

Measuring active forces and movement on the cell surface

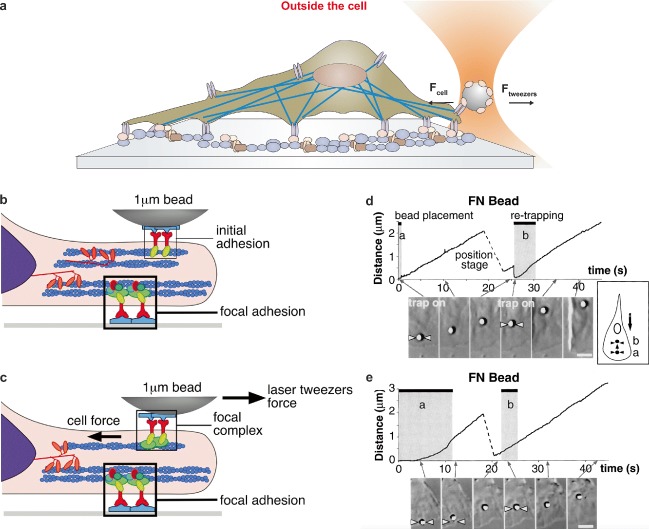
Cells actively apply forces to neighbor cells and/or to the extracellular matrix (ECM). Such forces are pivotal to drive cell motility and contractility, sense the mechanical properties of the surrounding environment, and reinforce connections to it (Grashoff et al. 2010). Optical tweezers enable the precise measurement of localized mechanical force on the cell surface (Fig. 3a). Pioneering experiments were performed by Sheetz’s lab using beads coated with fibronectin on fibroblasts to mimic extracellular attachment sites of different resistance (Fig. 3b, c). An optical gradient trap was used to place the beads on the cells and apply calibrated forces. Plots of bead displacement from the leading edge versus time with reference to the point and time at which the bead initially came into contact with the lamellipodia are shown in Fig. 3d, c. Bead movement was restrained with the optical trap to model integrin attachment to a more rigid site in the ECM. They found that cells sense the restraining force on fibronectin beads and respond by a localized, proportional strengthening of the cytoskeleton linkages, allowing stronger force to be exerted on the integrins. Thus, the strength of integrin–cytoskeleton linkages is dependent on matrix rigidity and on its biochemical composition (Choquet et al. 1997). In a later study, it was shown that the application of mechanical force induced the development of focal complexes. The mechanical stimuli strengthen initial integrin–ECM adhesions into focal complexes and regulate the amount of migration force applied to individual adhesions at localized regions of the advancing lamella (Galbraith et al. 2002).

Fig. 3.

Measuring active forces on the cell membrane. a Schematic of an optically trapped ligand-coated bead applying force while in contact with cell’s lamellipodia. b Initial adhesion between a ligand-coated bead and integrin receptors. c Focal complexes are formed when an external force is applied by the optical trap (b and c are reproduced from Galbraith et al. 2002 with permission from J. Cell Biol.). d, e Experimental data of FN7-10–coated bead displacement as a function of time and sequential images of the cell during experiments. Shaded areas indicate time intervals in which the trap was turned on. Traces are from separate experiments: d the trap was turned off 1.5 s after initial bead–cell contact (shaded area labeled [a]). Re-trapping immediately moved the bead back towards the trap center (shaded area labeled [b]); e the trap remained on (shaded area labeled [a]) until the bead escaped its radius of action (about 2.0 μm away from its center) at 12 s. Re-trapping did not move the bead back to the trap center (shaded area labeled [b]) (d and e are reproduced from Choquet et al. 1997 with permission from Cell)

In the studies mentioned above, force development of adhesion sites in a limited cell region was monitored with conventional single-trap optical tweezers. However, in more recent works, Schwingel and Bastmeyer extended the investigation to multiple locations on a single cell by establishing a custom-built multiple trap optical tweezers setup (Schwingel and Bastmeyer 2013). With such an approach, they were able to measure the temporal development and strength of cellular traction forces at an extended number of individual fibronectin-integrin adhesion sites, showing the highest traction forces in the foremost protrusions, and lower values towards the leading edge (Schwingel and Bastmeyer 2013) (Schwingel Dekan et al. 2012). A similar approach was employed to investigate dynamic cytoskeletal rearrangements involved in neuronal growth cone motility (Mejean et al. 2009). An important question is how growth cone progression on adhesive substrates is coupled to actin motility. In the “molecular clutch” mechanism, the mechanical coupling between ligand-bound adhesion receptors and the actin flow allows traction forces to be transmitted to the substrate, resulting in local diminution of the retrograde flow and forward progression. Such a mechanism was investigated in the Aplysia growth cone by placing eight beads functionalized with the neuronal cell adhesion molecule, apCAM, on different membrane regions of a single cell using holographic optical tweezers. Observed forces varied significantly from bead to bead and over time, however, some beads moved at a constant rate towards the axon shaft revealing a strong mechanical coupling between the bead and the cytoskeleton. Similar results were also observed in neurons, where the mechanical coupling between ligand-bound N-cadherin receptors and cytoskeleton was investigated by restraining microsphere motion using optical tweezers (Bard et al. 2008). At low forces, slow slippage of cadherin–cytoskeleton bonds occurred, whereas at higher forces local actin accumulation was observed. Together, these data support a direct transmission of actin-based traction forces to N-cadherin adhesions, through catenin partners, driving growth cone advancement and neurite extension.

A novel experimental approach to measure cell contractility was developed by Mizuno et al., by using double tweezers to suspend and stretch osteocyte-like MLO-Y4 cells between two beads, similar to the cell stretching configuration described in a following section (Mizuno et al. 2009). In this way, the authors measured simultaneously the cell’s viscoelastic response, the overall force produced by the cell, and the fraction of that force transmitted to the environment. They further demonstrated how the transmitted force is a direct measure of the environmental stiffness, suggesting a mechanism by which cells calibrate their own mechanosensing machinery. Using a similar strategy, 3T3 fibroblasts were suspended between two fibronectin-coated beads in order to measure cell’s elastic properties and force fluctuations (Schlosser et al. 2014). In a force-clamp experiment, cell shape changed at a clamped force of 20 pN. To check whether these deformations were actively driven by the actin/myosin cortex, the experiment was performed in the presence of blebbistatin which blocks NNM II motors. Under these conditions, cell contractions were prevented, and cell relaxation was favored. Cell stiffness decreased substantially with myosin inhibition but not with microtubule depolymerization by nocodazole, indicating that cortical forces generated by non-muscle myosin II were responsible for regulation of cell shape.

Finally, a unique and noninvasive model system for studying force and movement produced by intracellular motors from outside living cells was developed by Laib et al. (2009). A laser trap was used to position microspheres coated with the transmembrane protein FMG-1on the plasma membrane of immobilized paralyzed Chlamydomonas flagella. The anterograde and retrograde movements of the microsphere were measured with nanometer resolution as microtubule-based motors engaged the transmembrane protein FMG-1, showing that transport in each direction was driven by around 10 motors engaged simultaneously.

Measuring active forces and movement inside the cell

The unique capability of optical tweezers for manipulating particles inside living cells has opened up the possibility for the investigation of force and movement produced by molecular motors and cytoskeletal filaments inside the cell. After the pioneering work by Ashkin on mitochondria (Ashkin et al. 1990), there has been great progress into the study of organelle and protein movement in vivo. As previously discussed, precise quantitative force measurements inside cells is now possible with accurate calibration within the cell’s viscoelastic cytoplasm. Therefore, the actual performance of molecular motors in their natural environment can be directly measured, whereas it cannot be deduced from in vitro measurements. In this respect, recent experiments, reported below, surprisingly revealed that motor proteins in cells are not only responsible of directed motion and intracellular trafficking, but also for collective organization of vesicles and the cytoskeleton, as well as random position fluctuations of intracellular organelles. This and other findings underline the need to reproduce quantitative biophysical experiments inside living cells to take into account all the environmental variables and ongoing processes involved in organelle movements and intracellular transport, like local stoichiometry, cytoplasm viscosity, and molecular co-factors.

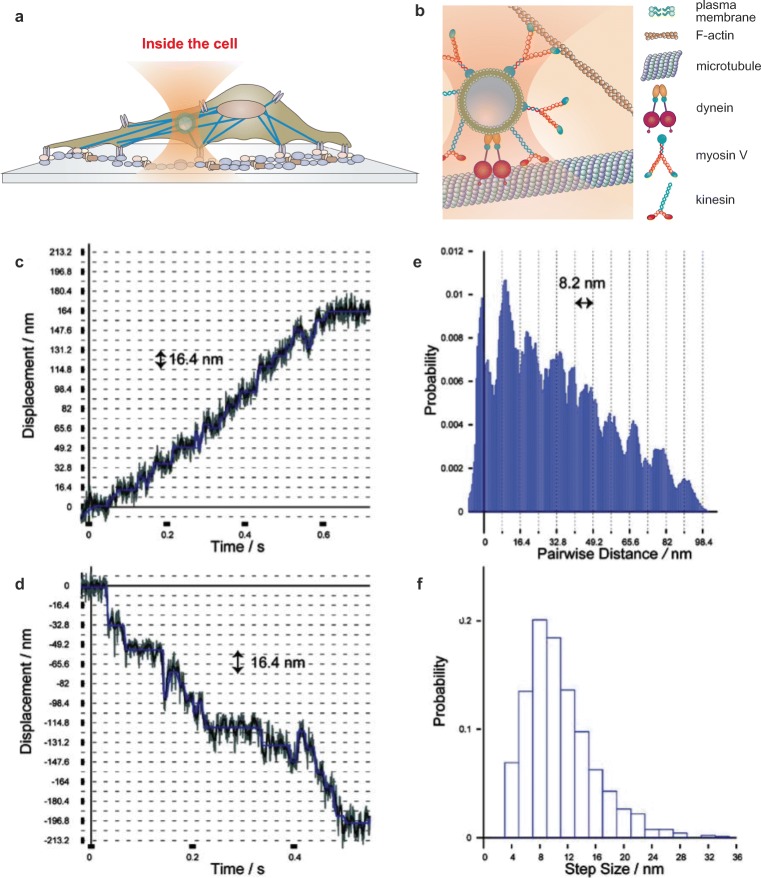
Directed motion of intracellular organelles has been long studied using optical tweezers. A range of external loads can be applied to molecular motors in vivo by using directly the motor cargo itself (Welte et al. 1998). One example of intracellular handles for micromanipulation is lipid droplets (LD), which have been extensively used in Drosophila embryos and living mammalian cells (Welte et al. 1998; Gross et al. 2002; Sims and Xie 2009; Leidel et al. 2012) (Fig. 4a, b). Such droplets have sizes ranging from 300 to 1 μm and a high refractive index with typical values in the range of 1.48–1.53, whereas the cytoplasm refractive index is in the range of 1.37–1.40 (Sims and Xie 2009). Despite their size, the relatively high refractive index makes LDs suitable for intracellular optical trapping experiments enabling the application of a range of forces relevant for molecular motor studies. By using fast camera tracking, measurements with sub-millisecond time resolution have been performed in different force regimes in order to quantify both stall forces and individual steps of motor proteins including kinesin and dynein (Sims and Xie 2009) (Fig. 4c–f). It has been widely assumed that cellular cargos can simultaneously engage multiple kinesins and increased motor numbers can affect transport speed; however, a study showed that transport properties can be unaffected by variation in motor number in vivo (Gardini et al. 2018; Shubeita et al. 2008). Molecular details of motor dynamics such as processivity and the pulling direction of a motor can be investigated through optical tweezers in order to associate each event to a particular motor type. The location of individual droplets as a function of time can be assessed with nanometer-level resolution using centroid analysis as described above (Gross et al. 2002). As previously discussed, calibration of the force probe in living cells is crucial for accurate quantification of force. The in vivo active-passive calibration on each individual cargo described above allowed Blehm et al. to compare directional stall forces in vivo and in vitro, showing that cytoplasmic dynein is active during minus- and plus-end directed motion, whereas kinesin is only active in the plus direction (Blehm et al. 2013). Hendricks et al. used a similar calibration method to examine latex beads phagocytosed into living mammalian macrophages that moved bidirectionally along microtubules, driven by teams of plus-end–directed kinesin-1, kinesin-2 motors, and minus-end–directed dynein motors (Hendricks et al. 2012). They found plus- and minus-directed forces of similar magnitude, with maximum forces of ∼ 20 pN, and 8-nm steps at forces greater than the maximum force produced by a single motor, indicating that the stepping of multiple motors is correlated. Rai et al. used phagocytosed latex beads of uniform size to circumvent the calibration uncertainty given by the variable size of LDs (Rai et al. 2013). Ex situ trap stiffness calibration was achieved by trapping the beads in a sucrose solution matching the cytosol refractive index. In this way, the number, forces, and collective force generation of endogenous dynein and kinesin motors transporting single phagosomes were measured inside macrophage cells.

Fig. 4.

Measuring active forces inside living cells. a Schematic of a trapped vesicle inside a cell by optical tweezers. b Close up representation of the trapped vesicle inside the cell showing cytoskeletal filaments and motor proteins (drawing not to scale). c, d Stepping trajectories of lipid droplets under known force load: c Outward-directed trajectory with stall force of 3.9 pN. d Inward-directed trajectory with stall force of 3.6 pN. e Pairwise distance histogram calculated from c after low pass filtering. f Step size histogram for all high-resolution trajectories. (c, d, e, and f are reproduced from Sims et al. 2009 with permission from Chemphyschem.)

Non-classical modes of intracellular transport recently emerged. In mouse oocytes, it has been shown that vesicles organize an extensive actin network that connects them with each other and with the cell surface. Movement along the network driven by myosin-5b enables them to converge and to collectively move towards the cell surface (Schuh 2013). In such a novel mechanism, long-range transport occurs in an actin-dependent and microtubule-independent manner. In a following study, the role of cytoskeleton and F-actin in spindle positioning during asymmetric divisions in mouse oocytes has been investigated, leading to the discovery of an unprecedented mechanism of nucleus positioning, named “active diffusion” (Almonacid et al. 2015). The authors observed that myosin-5b propelled vesicles actively diffused with an average squared velocity 〈ν²〉 that decreased with the distance from the oocyte center. A fluid mechanics-based model was proposed in which the nucleus experiences a propulsion force proportional to the squared velocity gradient Fp =  − α ∇ 〈ν²〉, where α is a constant. F_p is balanced by a viscous friction force F_f = − λV that depends on the viscosity of the cytoplasm, λ, resulting in a nucleus velocity $V=-\left(\frac{\alpha }{\lambda }\right)\nabla 〈{\nu }^2.〉$ In accordance with this model, active diffusion of actin-coated vesicles, driven by myosin-5b, generates a pressure gradient and a propulsion force sufficient to move the oocyte nucleus at a speed of 0.08 μm min⁻¹. This study provides evidence of an actin-dependent mechanism for nucleus positioning that involves neither actin flow nor myosin-II-dependent contractility but instead relies on active diffusion, which works as a prominent source of intracellular transport, able to move large organelles such as nuclei. In a different study, the molecular motions of kinesin-1 motor proteins in COS-7 cells were followed over times from milliseconds to hours via noninvasive tracking accomplished by imaging highly stable near-infrared luminescence of kinesin-1-targeted single-walled carbon nanotubes (Fakhri et al. 2014). At times greater than 100 milliseconds, nonequilibrium dynamics dominated. In addition to directed transport along microtubules, strong random dynamics driven by myosins was observed that result in enhanced nonspecific transport.

Active forces produced by molecular motors, thus, result in different modes of cellular and intracellular motility, as well as changes in the stiffness and mechanical properties of cells, which are discussed in the next sections.

Measuring the mechanical properties of the cell

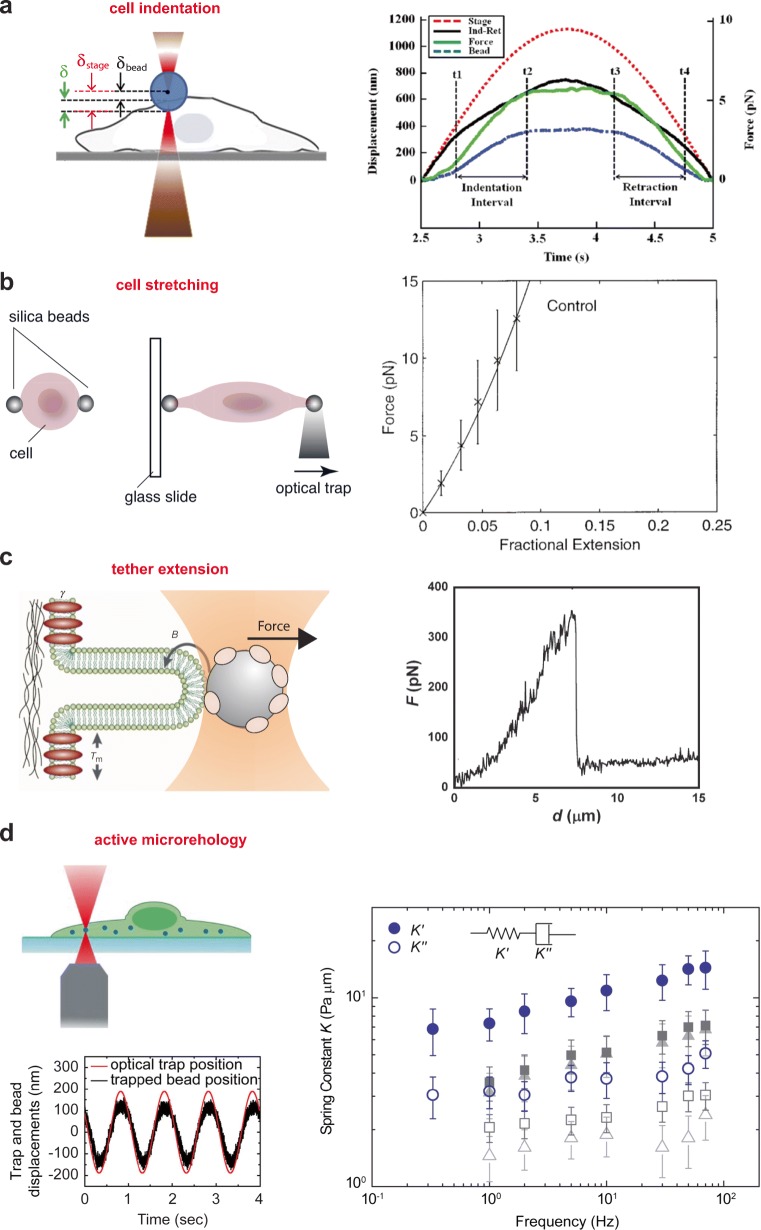
The mechanical properties of cells or cell substructures can be sampled by a force probe trapped in optical tweezers. The mechanical response of the force probe bound to a cell structure, which is usually the cell membrane, can be probed along different directions and under varying loading rates to fully characterize its viscoelastic properties. Nanoindentation, cell stretching, and tether extension are the most common modalities used to this end. Moreover, trapping of intracellular organelles, such as LDs, allows for investigation of the viscoelasticity of cell cytosol under a variety of conditions.

Nanoindentation

Nanoindentation experiments involve measuring cell deformation (indentation) induced by an external force probe, to derive the mechanical properties of the cell, which are defined through a mechanical model. Different configurations have been developed to perform nanoindentation with optical tweezers on cells. Indentation can be performed axially by moving the sample through a piezoelectric stage against a trapped dielectric microsphere (Coceano et al. 2016; Yousafzai et al. 2016), or by moving the trap towards the cell either in a linear (Dy and Sugiura 2013) or in an oscillatory way (Falleroni et al. 2018). Another possibility is to use a lateral indentation approach, where the sample or the trap is moved along the image plane against a perpendicular cell membrane (Zhou et al. 2014).

In the axial indentation configuration, the stage is moved axially against a trapped bead until contact with the cell is reached (Fig. 5a). At this stage, the trapped bead tries to resist any further movement of the cell, thus producing indentation. The depth of indentation δ can be quantified using the relation:

$$\delta ={\delta }_{\mathit{\text{stage}}}-{\delta }_{\mathit{\text{bead}}}$$ 3

where δ_stage and δ_bead are the stage and bead displacement respectively. δ_stage is known, while δ_bead can be measured, most commonly by back focal plane (BFP) interferometry, through which it is possible to reach nanometer accuracy along any direction (Gittes and Schmidt 1998; Pralle et al. 1999). The force applied by the tweezers can be readily obtained as F =  − k_i · δ_bead once the trap stiffness k_i along the direction i is calibrated outside the cell, as described above.

Fig. 5.

Measuring the mechanical properties of cells. a (left) Schematic of the experimental procedure where the stage is displaced upwards by δ_stage so the cell and bead can interact. The bead is displaced by a distance δ_bead while it is indenting the cell by δ = δ_stage − δ_bead; (right) Indentation and retraction experiment, where the stage is moved sinusoidally against the cell membrane. Stage displacement (red), measured bead displacement (blue), the calculated force (green), calculated indentation (black) (reproduced from Yousafzai et al. 2016 with permission from Opt. Lasers Eng.). b (left) Schematic of a rounded red blood cell being stretched by optical tweezers. The two beads are bound non-specifically to the erythrocyte. One bead is deforming the cell by moving the trap while the other is fixed on a stationary glass surface (reproduced from Van Vliet et al. 2003 with permission from Acta Mater.). (right) Force-extension curve obtained from experiments on sets of red blood cells (reproduced from Sleep et al. 1999 with permission from Biophys. J.). c (left) Diagram illustrating tether formation. The membrane–cytoskeleton adhesion energy, γ, and the tension in the bilayer plane, T_m, must be overcome by the optical tweezers in order to bend the membrane and form a tether. B is the membrane bending stiffness (modified from Sheetz et al. 2001 with permission from Nat. Rev. Mol. Cell Biol.). (right) Force-extension curve of tether extraction experiment on fibroblast NIH 3 T3 cells (reproduced from Pontes et al. 2011 with permission from Biophys. J.). d (left) Schematic of the experimental setup used to measure the cytoplasm viscoelastic properties and typical displacements of the trapped bead while the optical trap is oscillating at 1 Hz. (right) Spring constant K of the cytoplasm measured by active microrheology using optical tweezers. Solid symbols represent the intracellular elastic stiffness which dominates over the dissipative resistance (open symbols). Blue circles, gray squares, and light gray triangles represent untreated, 10 mM blebbistatin-treated, and ATP-depleted A7 cells, respectively (reproduced from Guo et al. 2014 with permission from Cell)

Different models are used to derive the cell’s mechanical properties from measurements of force and indentation depth; however, the Hertz model is the most commonly used in AFM and OT indentation studies (Chen 2014; Nawaz et al. 2012; Yousafzai et al. 2016). Here, the cell is modeled as a homogeneous elastic solid object and the indentation depth is small. Under these assumptions, one can omit the velocity-dependent viscous components and describe the cell by means of only two parameters, the Young elastic modulus, E, and the Poisson ratio, ν. The Young modulus, defined as the stress to strain ratio along the longitudinal direction in which the force is applied, is a measure of cell’s stiffness. The Poisson ratio, defined as the negative transverse to longitudinal strain ratio, is a measure of cell’s compressibility. In this case, nanoindentation measurements are performed slowly to exclude velocity-dependent effects. Under the assumption of rigid spherical indenters of radius R, the Young modulus is given by Eq. 4 (Yousafzai et al. 2016):

$$E=\frac{3\left(1-{\nu }^2\right)}{4\sqrt{\mathit{\delta R}}}\frac{F}{\delta }$$ 4

From the displacement/time graphs, as shown in Fig. 5a, it is possible to find the indentation and retraction intervals in the linear regime (time intervals t1–t2 and t3–t4, respectively, in Fig. 5a) and, by knowing the trap stiffness, obtain the force/indentation curves. The typical range of the Poisson ratio of soft materials is within 0.3–0.5 and a constant value in this range is chosen to quantify the Young modulus. The maximum uncertainty in the calculation of E, due to the unknown Poisson ratio, is expected to be less than 10% (Guz et al. 2014). Thus, by defining the slope of these curves as $S=\frac{\mathit{dF}}{\mathit{d\delta }}$, we can approximate the previous equation for Young modulus and obtain a relation where indentation is the only variable:

$$E=\frac{3\left(1-{\nu }^2\right)}{4\sqrt{\mathit{\delta R}}}S$$ 5

Measuring cell’s elasticity is important since it is an indicator of cellular alterations that can occur in different diseases. This technique has been used in different kind of cells, including HBL-100 cells, myelogenous leukemia cells and normal leukocytes (Zhou et al. 2014), Balb 3T3 cells (Dy and Sugiura 2013), luminal breast cancer, and basal breast cancer cells (Coceano et al. 2016). Different measurements have shown that elasticity is affected by environmental conditions such as the substrate or the number of neighboring cells, as well as the subregion where indentation is performed as shown in previous studies on human breast cancer cell lines (Yousafzai et al. 2016). Historically, indentation was first performed with other manipulation techniques, in particular Atomic Force Microscopy (AFM), which allows application of forces in the nN range. In another study, AFM and optical tweezers were combined to compare the mechanics of three different human breast cell lines. At high forces, cell response was viscoelastic and dissipation of energy occurred, whereas at low forces the cellular response was entirely elastic (Coceano et al. 2016).

Cell and subcellular structures stretching

Optical tweezers can be used to globally stretch cells or subcellular structures and study their elastic and viscoelastic properties. In the single-trap configuration (Schreiner et al. 2015; Van Vliet et al. 2003), as shown in Fig. 5b, two beads are positioned at opposite sides of the cell along the joint line: one is fixed to a stationary glass slide and used as the reference position, whereas the other bead is trapped through OT and moved to apply force and induce cell stretching. Another possible configuration is the dual trap optical tweezers (Sleep et al. 1999; Tan et al. 2012), in which one bead is held in place by a trap, while a second trap is used to move the other one in order to induce tension in the cell. A two-trap configuration has been also employed in the absence of beads by directly focusing the laser beam on a cell (Agrawal et al. 2016). A different approach, which uses laser light to stretch cells is the optical stretcher, in which two opposed non-focused laser beams apply surface forces resulting in cell stretching (Guck et al. 2000, 2001). We do not discuss this powerful technique here as it diverges from traditional optical tweezers and is extensively described elsewhere (Guck et al. 2010; Yang et al. 2016).

In these techniques, geometric changes induced in the cell are quantified through image or video processing. A mechanical model describing the cell shape and mechanically induced deformations is necessary to extract the elastic or viscoelastic properties of cells. Optical stretching was largely used to investigate red blood cells (RBCs). The RBC membrane is connected to an intracellular skeleton structure composed of spectrin, actin, and other anchoring proteins. Svoboda et al. investigated the structure and elasticity of membrane skeletons derived from these cells by extraction of RBC ghosts with detergents (Svoboda et al. 1992). Results showed that skeletons have a lower bending stiffness with respect to the whole membrane consisting of both the lipid bilayer and the skeleton (for the definition of bending stiffness see the next section). In a complementary study, Sleep et al. concentrated on the elasticity of permeabilized spherical ghosts after interruption of the skeletal network by dissociation of spectrin tetramers or extraction of the actin junctions (Sleep et al. 1999). To extract elastic constants from the measured force-extension curves, they used a mechanical model developed previously (Parker and Winlove 1999). Several studies by Suresh and coworkers investigated the mechanical properties of RBCs using optical tweezers and developed mechanical models to describe the observed force-induced deformations (Dao et al. 2003; Lim et al. 2004). Later, the same group investigated the relation between cell mechanics and disease states related to pancreatic cancer in epithelial cells and malaria infection in RBCs (Mills et al. 2007; Suresh et al. 2005). The role of RBCs deformability in diabetic retinopathy was also studied: RBCs from patients with type 2 diabetes without retinopathy showed significant differences in initial and final cell sizes, and deformability was compared to patients with diabetic retinopathy (Agrawal et al. 2016). Finally, differences in the mechanical stiffness between non-differentiated human embryonic stem cells (hESC) and differentiated cardiomyocytes hESC (hESC-CM) were quantified (Tan et al. 2012). Results showed that the elastic modulus and viscosity coefficient of hESC-CM are larger than those of hESC, indicating that the structure of these cells becomes better organized after differentiation, probably because of the loss of pluripotency. An interesting assay was developed to investigate the mechanical properties of nuclei extracted from Schizosaccharomyces pombe cells (Schreiner et al. 2015). The authors applied a range of oscillatory stress at various frequencies, finding a prevalently elastic response of wild type nuclei and a small viscous component. They then used nuclei-lacking lamins, thus untethering chromatin from the inner nuclear membrane, which resulted in highly deformable and more compliant nuclei.

Tether extension

Membrane tethers (or nanotubes) are spontaneously generated by cells or can be artificially extracted from the cell membrane by application of local force (Hochmuth et al. 1973; Waugh and Hochmuth 1987). The spontaneous generation of membrane tethers is at the base of important biological processes, among which included filopodia extension, endocytosis, and nanotube connections between cells (Baker 2017). On the other hand, the artificial generation of membrane tethers is an important means to study the biophysical properties of spontaneously generated tethers and obtain information about the membrane mechanical properties. Tether extension is achieved by attaching a trapped microbead to the membrane and applying a force by moving either the stage or the trap. Force-elongation curves can be measured and the membrane mechanical properties can be determined through membrane mechanical models (Hochmuth et al. 1996) (Fig. 5c). Some recent reviews provide a comprehensive survey of this approach (Derényi et al. 2007; Nussenzveig 2018).

An important experimental parameter that can be easily measured using optical tweezers is the force needed to hold a plasma membrane tether at constant length (F₀), which is related to two key membrane mechanical properties. The first one is the membrane surface tension (T), defined as the force per unit length acting on a cross-section of the membrane. The second one is the membrane bending stiffness (B), defined as the constant of proportionality between the torque applied to the membrane and its curvature (the inverse of the curvature radius) (see Fig. 5c). Membrane models developed by Hochmuth et al. provide a relationship between the tether force F₀, T, B, and R_t, the tether radius (Hochmuth et al. 1996):

$$F_0=2\pi R_t\left(T+\frac{B}{2R_t^2}\right)$$ 6

Solving with respect to T and B:

$$T=\frac{F_0}{4\pi R_t};B=\frac{F_0{R}_t}{2\pi }$$ 7

These equations allow for the obtainment of the membrane mechanical parameters, once the tether force and radius are measured. The tether force can be easily measured with optical tweezers. However, measurement of the tether radius is complicated by its minute size, which is below the light diffraction limit. Dai and Sheetz measured R_t using differential interference contrast (DIC) microscopy (Dai and Sheetz 1995). Later work by Pontes et al. used electron microscopy images of the tether to get a more accurate estimate of R_t (Pontes et al. 2011). Nevertheless, if the membrane bending stiffness B has been measured and can be reasonably considered constant between measurements, R_t can be eliminated between the two Eqs. (6) and (7) to give:

$$T=\frac{F_0^2}{8{\pi }^{2}B}$$ 8

Using Eq. (8), differences in membrane tension can be found in different cell areas, cells under different conditions and between different cell types by measuring F₀.

On the other hand, the membrane surface tension derives from the sum of T = T_m + γ the membrane tension in the bilayer plane, T_m, and the membrane–cytoskeleton adhesion energy per unit area, γ (Sheetz 2001): T = T_m + γ (Fig. 5c). Separation of the in-plane tension T_m and the cytoskeleton adhesion term γ is difficult and requires an additional measurement on membrane blebs lacking cytoskeleton support, where the adhesion term is zero (Sheetz 2001).

Cell’s mechanical properties measured in this way vary among different types of cells, including neurons (Hochmuth et al. 1996), fibroblasts (Pontes et al. 2011; Raucher and Sheetz 1999), human embryonic kidney cells (Khatibzadeh et al. 2013), axons (Datar et al. 2015), red cells (Hochmuth et al. 1973), and many others. Membrane tension can also diverge among different regions of the same cell (Sheetz 2001) and especially in moving cells, as observed in fish epithelial keratocytes where a ~30 % ~30% difference is observed between the leading and the trailing edge (Lieber et al. 2015). Differences can also occur as a consequence of variations in the composition of the plasma membrane or in the composition of cellular substrates (Khatibzadeh et al. 2013; Mandal et al. 2019). A combination of tether extraction and fluorescence microscopy allowed for the identification of the presence of actin in the tethers, in contrast with previous knowledge, even after disruption of the cytoskeleton with cytochalasin B or D (Pontes et al. 2011). In recent work, tether extension was employed to calibrate a novel fluorescent membrane tension probe, which is now available to measure changes in membrane tension from changes in its fluorescence lifetime (Colom et al. 2018).

As previously shown, there is a similarity between the mechanisms of tethers and an endocytic vesicle formation: in both cases, mechanical forces applied to the membrane bend the membrane and either form the tether protrusion, when the force points outward, or the endocytic vesicle, when the force points inward (Sheetz 2001). In both cases, the force must overcome the binding energy of membrane–cytoskeleton adhesion. In vitro experiments revealed that force produced by molecular motors can lead to formation of membrane tubes, indicating this as a possible cell mechanism at the base of endocytic vesicle and tether formation (Derényi et al. 2007). First, Roux et al. demonstrated that membrane tubes can be generated from giant unilamellar vesicles (GUVs), pulled by kinesin motors attached by means of small polystyrene beads and moving on immobilized microtubules in the presence of ATP (Roux et al. 2002). Later, Koster et al. directly linked purified kinesins to the lipids of GUVs. When the vesicles were brought into contact with microtubules, membrane tubes were again formed and optical tweezers were used to directly quantify the forces involved in tube formation (Koster et al. 2003). They proposed a model in which clusters of motors spontaneously form through dynamic association of single molecular proteins. In both experiments, a higher concentration of molecular motors resulted in a greater extent of tubes network. More recently, it was shown that protein scaffolds have a role in membrane scission after tube formation (Simunovic et al. 2017). The binding between the protein scaffold and the tube gives rise to a frictional barrier that limits lipid diffusion and yields to membrane scission through lysis. They provided a model, called friction-driven scission (FDS), by which molecular motors can not only extend membrane tubes, but can also cut them to form endocytic vesicles.

Passive and active microrheology

Microrheology deals with the investigation of the flow of matter at the micrometer level and, in particular, its mechanical properties, such as viscosity and elasticity. Microrheological experiments can be performed in situ, for instance inside living cells, and they are classified into “active” or “passive” experiments. Active microrheology (AMR) is realized by inducing bead displacement by an external force applied through OT, whereas in passive microrheology (PMR) the displacement is naturally generated by thermal fluctuations of the environment surrounding the probe particle. A generalization of the Young’s modulus for viscoelastic materials, in which there is a time (phase) lag between stress and strain, is the shear complex modulus:

$$G^{\ast }\left(\omega \right)=G^{\prime }\left(\omega \right)+i{G}^{\prime \prime }\left(\omega \right)$$ 9

which depends on the frequency f = ω/2π. The real part G^′(ω) is known as the storage modulus and provides information on elasticity, while the complex part G^′′(ω) describes the viscous nature of the material due to dissipation and is called the loss modulus. When performing passive microrheology (PMR), information about the viscoelastic properties of the medium can be derived through the analysis of the trajectory of an injected particle or an embedded vesicle, and in particular its mean squared displacement (MSD). Calculation of the complex shear modulus is derived through the equation:

$$G^{\ast }\left(\omega \right)=\frac{1}{6\mathit{\pi R}}\left[\frac{6k_{B}T}{\mathit{i\omega }\widehat{〈∆r^2\left(\omega \right)〉}}+m{\omega }^2\right]$$ 10

where R is the bead radius and $\widehat{〈∆r^2\left(\omega \right)〉}$ is the Fourier transform of the MSD (Tassieri 2019). Concerning active microrheology (AMR), a sinusoidal trap oscillation with a force F at a frequency ω is applied to a trapped bead (Fig. 5d). From the measurement of the displacement x(ω) of the bead and the applied force F(ω), the effective spring constant K(ω) = F(ω)/x(ω) is derived and, if the material presents dissipation, x(ω) and F(ω) are not in phase, which results in a complex spring constant related to the shear modulus through a generalization of Stokes’ relation (Guo et al. 2013):

$$K=6\pi G^{\ast }R,$$ 11

The complex spring constant also consists of an elastic K^′(ω) and a viscous K^′′(ω) component (Fig. 5d). Some recent reviews provide a full derivation of these formulas (Eqs. 10 and 11), range of applicability, and advantages and limitations of the technique (Brau et al. 2007; Guo et al. 2014; Tassieri 2019).

Microrheology has been widely used to characterize the mechanical properties of the cytosol, both in vitro (Gittes et al. 1997; Mizuno et al. 2007; Ricketts et al. 2018) and in vivo (Guo et al. 2013). The in vitro measurements were made by creating model systems consisting of myosin II, actin filaments and cross-linkers (Mizuno et al. 2007), F-actin biopolymer solution and polyacrylamide (PAAm) gels (Gittes et al. 1997), or well-mixed networks of co-entangled actin-microtubule composites (Ricketts et al. 2018). Mitzuno et al. showed that a cross-linked actomyosin network strongly violates a fundamental statistical theorem, the fluctuation-dissipation theorem, which relates the thermal fluctuations of systems to their response to forces, because of the actomyosin contractility. Moreover, the authors showed that the in vitro model system employed exhibited a dynamic behavior, adjusting its own mechanical stiffness via internal forces generated by the contractile activity of motors. Later, an in vivo study investigated the role of the third major cytoskeletal component, vimentin intermediate filaments (VIFs), using mouse embryonic filaments (mEFs) (Guo et al. 2013). Results obtained from AMR showed that the presence of vimentin doubles the value of the cytoplasmic shear modulus, while PMR studies showed that VIFs also have a role in stabilizing organelles in the cell. In a subsequent study, Guo et al. investigated random forces and motor activity in A7 melanoma cells using a combination of independent measurements of the fluctuating movement of injected particles together with measurements of the mechanics of the cytoplasm through OT-based AMR (Guo et al. 2014). They showed that random motion is not induced by thermal fluctuation, but by the aggregate motor activity in cells, which results in random forces.

Microrheology has been largely used to show that there is significant difference in the mechanical properties of different cells, especially between tumorigenic cells and healthy controls. In particular, comparison between benign (MCF-10A) and malignant (MCF-7) breast cancer cells indicates that tracer-particle motion is significantly higher and that cytoplasmic stiffness is ~30% smaller in malignant cells with respect to benign ones (Guo et al. 2014). Results from Mandal et al., which compared nontumorigenic breast cells (MCF-10A) and highly metastatic cells (MDA-MB-231), are in good agreement with the previous results as they observed a global reduction in the shear modulus of malignant cells (Mandal et al. 2016). In the same work, the authors developed a technique which combines OT-based AMR with soft lithography micropatterning to probe the cytoplasm in different regions. Experiments evidenced that the shear modulus decreases from the center to the periphery of the cell and, along the polarity axis of the micropattern, from the cell rear to its front. With a similar aim, holographic optical tweezers were used to simultaneously control different beads in different regions (Hörner et al. 2017). One bead was taken as a reference and differences between phases in the oscillation of the other beads measured variances in the mechanics of the microenvironment. A study of viscoelastic properties in different locations of the same cell was also performed on cultured alveolar epithelial cells, in which optical trapping and bead oscillation was applied both on a submicron endogenous intracellular organelle and a silica bead bound to the cytoskeleton by mean of transmembrane integrin receptors (Wei et al. 2008). Results showed higher mean values of shear and storage moduli on the external part of the cell. Finally, great insights in understanding the mechanical nature of the cytoplasm were achieved by using OT to drag microspheres in the cytoplasm of living normal rat kidney epithelial cells (NRK), varying the bead diameter and its speed (Hu et al. 2017). The authors were able to demonstrate that the cytoplasm can be considered as a size-independent viscoelastic medium as long as the effective strain rate V/a is maintained under a certain value, whereas when this threshold value is overcome the cytoplasm exhibits size-dependent poroelasticity.

In general, the presence of both thermal fluctuations and active processes occurring within living cells poses a fundamental concern about microrheology measurements related to the difference between the experimental time-scale and the timing of biological reactions occurring inside the cells (Tassieri 2015). Athermal fluctuations caused by active processes that dissipate energy within a cell drive the system out of thermodynamic equilibrium. Their existence may substantially alter the viscoelastic response of the system occurring at rates that may vary not only from different kinds of cells, but also within the same cell line (Bunea and Glückstad 2019).

Measuring mechanotransduction signals in living cells

In recent years, several hybrid instruments combining optical tweezers with fluorescence detection have been developed. These instruments potentially allow simultaneous detection of sub-nanometer displacements, sub-piconewton forces, and single-molecule fluorescence signals (Fig. 6a). Mechanical forces both between cells, and between cells and the ECM, are mediated by a large number of different receptors, and recent studies have demonstrated the use of laser tweezers to study intracellular mechanotrasduction pathways. Certain mechanical stimulations through specific receptor complexes induce biochemical responses in cells that have critical implications in normal physiology and disease. The molecular mechanisms behind the triggering of the biochemical response upon force are still not well characterized; however, it is well established that adhesion receptors, such as integrin and cadherin, as well as mechanosensitive channels are essential players in force transduction and so are potential targets for such investigations.

Fig. 6.

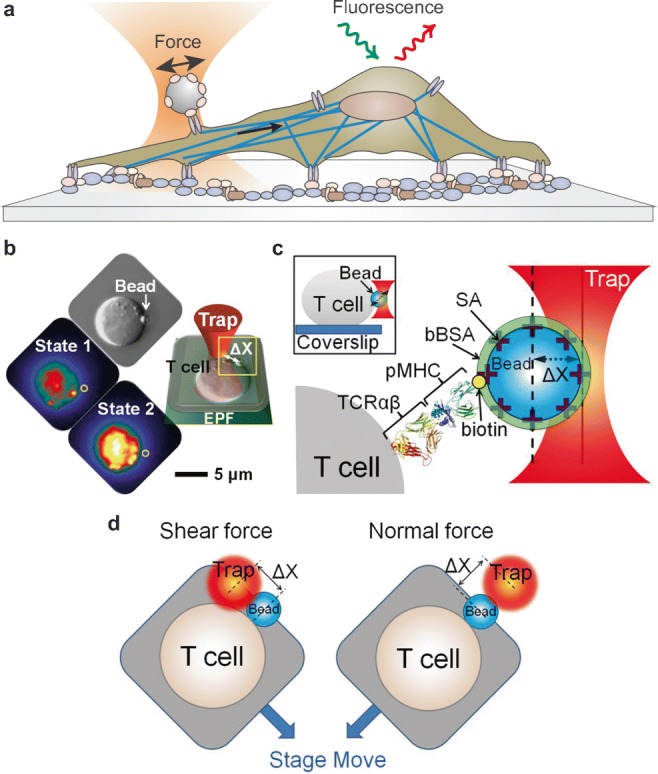
Probing mechanotransduction signals in living cells. a Combination of optical tweezers and fluorescence imaging to detect intracellular signals induced by an external force applied on the cell membrane. b Mechanical force F = − k·Δx is applied on individual T lymphocytes using an optical trap. The ligand-coated bead abutting the T cell surface is shown in the DIC image indicated by a white arrow and the fluorescence image as a gray sphere and yellow circle. The optimal force along the T cell surface triggers a rise in free Ca²⁺ shown as an increase in yellow intensity (state 2) compared with the initial state of the same T cell (state 1). EPF, epifluorescence. c Cartoon detailing the bead–cell contact interface as expanded from the yellow box in b. Optical traps are used for application of force to a streptavidin (SA)-coated polystyrene bead arrayed with specific biotinylated TCRαβ ligand (pMHC) and then saturated with bBSA to prevent potential nonspecific streptavidin binding to cells. (Inset) Side view of a bead-attached T cell. d Cartoon showing optimal shear and normal force directions of the bead relative to the cell (b–d are reproduced from Feng et al. 2017)

Different approaches for such studies can be undertaken. The development of genetically encoded FRET-based reporters allows the investigation of different mechanically induced signals with high sensitivity within living cells but it is a challenging process due to the need of calibration and control experiments. A first step in this direction was taken by Wang et al. who developed a FRET-based reporter for the activation of the Src protein, a regulator of the integrin–cytoskeleton interaction (Botvinick and Wang 2007; Wang et al. 2005). Application of a pulling force via laser tweezers on human umbilical vein endothelial cells (HUVECs) expressing the membrane-targeted Src reporter led to a directional FRET response, with the majority of activations transmitted towards distal areas of the cell opposite to the force direction (Botvinick and Wang 2007; Wang et al. 2005).

In a different study, a FRET-based calcium biosensor combined with optical tweezers was employed to investigate the force-induced calcium signals in human mesenchymal stem cells (hMSCs) at different subcellular locations (Kim et al. 2015). A mechanical force of 300 pN applied to hMSCs via fibronectin-coated beads induced Ca²⁺ release from the endoplasmic reticulum through two separate mechanisms: one occurring through the cell cytoskeleton and necessitating actomyosin contractility, and a second one triggered at the plasma membrane by the mechanosensitive channel TRPM7 and requiring support by the cell cytoskeleton, but not by actomyosin contractility.

Experiments directly testing the role of mechanical force in activating αβ T cell receptor (TCR) were provided by Kim et al., in which they used an optically trapped bead to present an antigenic peptide bound to a major histocompatibility complex molecule (pMHC) to a T cell, mimicking T lymphocyte activation during initial stages of immune surveillance (Kim et al. 2009). They applied oscillating forces with a 50-pN amplitude to trigger T cell Ca²⁺ flux, which was monitored using a Fluo4 Ca²⁺ indicator. They found that TCR is an anisotropic mechanosensor, which responds to tangential but not normal forces. In later work, an optical trap was employed to present pMHC-bound beads to T cells and apply vectoral pN forces in order to investigate chemical thresholds depending on applied load and force direction, controlling the pMHC surface concentration, force magnitude, and direction (Feng et al. 2017) (Fig. 6b–d). In the absence of force, chemical thresholds required much higher pMHC density than observed physiologically. In contrast, force applied in the shear direction could activate T lymphocytes with ∼ 10 pN per TCR molecule, mimicking native shear motions involving only two pMHC molecules at the interaction surface. The observed active transport of beads showing 8-nm steps through an actomyosin-based mechanisms is in contrast with the original concept of serial engagement-based triggering in which pMHC molecules are recycled over time. Initial TCR activation was rather dependent on external mechanical force, thus supporting a mechanosensitive-based regulation of cell activation (Feng et al. 2017).

It has been recently demonstrated that cellular calcium transients can be precisely induced in mouse neuroblastoma NG108-15 cells with a periodic mechanical stimulation method employing an oscillatory optical trap to apply gentle forces perpendicularly to the cell membrane (Falleroni et al. 2018). The induced calcium transients depended on the stimulus strength: the mechanical forces exerted in experiments had maximum values in the range 10–18 pN and induced detectable changes of intracellular Ca²⁺; a decrease in the trap stiffness by a factor of 2, led to maximum forces in the range 4–10 pN, and no calcium activation was observed (Falleroni et al. 2018).

Besides force-triggered signals, optical tweezers can be used to trigger specific signals with high spatio-temporal resolution by positioning ligand-coated beads on the cell membrane. This technique was used to monitor early signaling events upon E-cadherin engagement using beads coated with functional E-cadherin extracellular domain (Perez et al. 2008). Individual beads were placed onto lamellipodia of single-MDCK epithelial cells through a laser trap to precisely control the timing and location of initiation events, and then protein dynamics were rapidly imaged using fluorescent tagged proteins. Actin reorganization around sites of E-cadherin engagement was erratic and not coordinated with E-cadherin recruitment, indicating a dynamic model of how cell adhesion is initiated by transient accumulation of Rac1 to cause further E-cadherin accumulation on active membranes and subsequently a loss of Rac1 to maintain weak E-cadherin adhesion on quiescent membranes (Perez et al. 2008).

Conclusions and future perspectives

The study of the mechanical properties of cells, their subcellular compartments, and, ultimately, cell’s molecular components has greatly advanced during the last few decades thanks to the development of experimental methodologies that exploit the potentialities of optical tweezers. Our understanding of cell mechanics has grown enormously in recent years and has revealed its pivotal role in regulating crucial processes in cell development, health, and disease. In particular, the tight interconnection between mechanical, electrical, biochemical, and genetic signals is emerging as a fundamental element of all living organisms, which is far from being fully understood. In this respect, the development of experimental tools for the investigation of mechanotransduction signals in living cells and organisms will be crucial for further advancements. Optical tweezers still represent an ideal instrument to quantify mechanical forces in living cells while its combination with techniques for imaging different cell signals, will potentially lead to the development of important novel methods for the study of mechanotransduction signals in the forthcoming years.