Abstract
The visual image quality metric the visual Strehl ratio (VSX) combines a comprehensive description of the optics of an eye (wavefront error) with an estimate of the photopic neural processing of the visual system, and has been shown to be predictive of subjective best focus and well correlated with change in visual performance. Best-corrected visual image quality was determined for 146 eyes, and the quantitative relation of VSX, age, and pupil size is presented, including 95% confidence interval norms for age groups between 20 and 80 years and pupil diameters from 3 to 7 mm. These norms were validated using an independently collected population of wavefront error measurements. The best visual image quality was found in young eyes at smaller pupil sizes. Increasing pupil size caused a more rapid decrease in VSX than increasing age. These objectively determined benchmarks represent the best theoretical levels of visual image quality achievable with a sphere, cylinder, and axis correction in normal eyes and can be used to evaluate both traditional and wavefront-guided optical corrections provided by refractive surgery, contact lenses, and spectacles.
Keywords: (330.5370) Physiological optics; (330.7323) Visual optics, aging changes; (170.4460) Ophthalmic optics and devices; (110.3000) Image quality assessment; (140.3490) Lasers, distributed-feedback
1. INTRODUCTION
The optical quality of the eye has been studied in increasing detail and complexity from geometric schematic eyes [1,2] and dioptric refractive error [3,4], to optical metrics such as line spread functions [5–7], point spread functions (PSFs) [8,9], modulation transfer functions (MTFs) [10–14], root mean square (RMS) wavefront error (WFE) [14–16], and metrics of retinal image quality [17–20].
Normative references are essential to the use of these various metrics as benchmarks in scientific and clinical inquiry. A widely used set of normative values, for instance, is that of RMS WFE and higher-order aberrations (HOAs) as a function of pupil size and age [16], which has, for example, been used in studies of traditional [21] and wavefront-guided [22,23] contact lens corrections, reading speed [24], intra-ocular lenses (IOLs) [25], and the optical properties of the cornea [26].
Although satisfactory in many cases, a drawback of this normative dataset is that RMS WFE does not consider the visual interaction of aberrations [18,27]. Figure 1 illustrates an example where the addition (interaction) of aberrations causes an increase (worsening) in RMS WFE, but actually results in an improvement in image quality. For the same reason, the calculation of equivalent dioptric defocus from RMS [27] can be misleading. Moreover, any description of the quality of an eye in diopters is generally troublesome because the visual effect of diopters varies with pupil size, that is, the same dioptric refractive error causes much larger retinal blur and has a more detrimental effect on vision at large pupil sizes than at small pupils [28,29].
Fig. 1.

The shortcoming of root mean square (RMS) wavefront error (WFE) is that it does not capture the visual interaction of aberrations. (a) Spherical aberration alone, RMS = 0.200 μm. (b) Defocus alone, RMS = 0.451 μm. (c) Spherical aberration + defocus, RMS = 0.493 μm. Note that with the addition of these aberrations, RMS WFE increases (worsens), while image quality actually improves.
Some studies have published normative results for the MTF of the eye: Artal et al. [11] used two age groups of five subjects and one pupil size, while Guirao et al. [13] used larger samples from three age groups and three pupil sizes, and others [30,31] have modeled MTFs across pupil sizes and age. Although the MTF metric combines the effect of all aberrations on contrast transfer, it considers neither the sensitivity and limits of the neural processing of the visual system, nor phase errors, which have been shown to influence visual quality [32,33].
The evolution of optical metrics, such as the MTF, to include consideration of the neural processing of the visual system gave rise to visual image quality metrics [17–19,34,35], which combine a comprehensive description of the optics of an eye—provided by wavefront sensing—with a measure of the neural transfer function of the human visual system.
Therefore, the purpose of this paper is to provide normative best-corrected values for a visual image quality metric, which incorporates both the optical and neural components of the visual system, as a function of pupil size and age. Given the reported variability of subjective methods of refraction [36–38], these benchmarks are determined objectively—therefore unaffected by subjective performance and adaptation—and represent the best theoretical level of visual image quality [as measured by the visual Strehl ratio (VSX)] that is achievable with a sphere, cylinder, and axis (SCA) correction in a normal eye.
The particular metric that will be presented is VSX, which has been shown to be predictive of subjective best focus [18,39], well correlated with change in visual acuity (VA) [40–42], and able to identify a SCA prescription that performs equivalently to subjective refraction [43], independent of pupil size and underlying WFE [42]. We have calculated VSX according to its original definition (equation A23 from Thibos et al. [18], also included below). As shown in Eq. (1), VSX is the ratio of the volume under the weighted PSF of an eye at a given pupil size to the volume under the weighted diffraction-limited PSF for the same pupil size. The weighting function in both cases is the inverse Fourier transform of the photopic neural contrast sensitivity function (nCSF) deter-mined using interference fringes [10]. In this form, VSX ranges from 0 to 1, with 1 being best.
It has been suggested [44,45] that visual image quality metrics should be normalized using the neurally weighted PSF for a diffraction-limited 3 mm pupil diameter irrespective of the pupil size of the eye (this metric could be referred to as VSX*). The virtues of VSX and VSX* are considered in the Discussion; however, their values were found to be very similar and, therefore, data from the original definition of VSX are presented throughout the Results,
| (1) |
2. METHODS
The study followed the tenets of the Declaration of Helsinki and University of Houston Institutional Review Board approval.
Wavefront error data collected during the Texas Investigation of Normal and Cataract Optics (TINCO) study were analyzed. Collection of the TINCO data and description of subjects are described in detail elsewhere [16,46]; briefly, the TINCO study investigated the aberration structure of normal healthy eyes as crystalline lens opalescence increases naturally with aging.
Subjects with cortical and/or posterior subcapsular cataracts graded (independently by five masked clinicians) as >2 according to The Lens Opacities Classification System III (LOCS-III) [47] were excluded, as were subjects with any ocular pathology or abnormality (such as strabismus or amblyopia), previous ocular surgery, or neurological or systemic condition that affected the visual system. The preferred eyes of 146 normal subjects between the ages of 20 and 80 years of age were dilated with one drop of tropicamide 1% and one drop of neo-synephrine 5%. Wavefront error measurements were recorded using a custom-built Shack–Hartmann wavefront sensor over the maximum dilated pupil, described by a 10th radial order normalized Zernike polynomial fit, and algebraically scaled down (concentrically using the center of the dilated pupil) to 7, 6, 5, 4, and 3 mm pupil diameters [48]. It has been shown that scaling down from a larger pupil size is preferable to refitting the wavefront error over a smaller pupil using fewer points [49]. Two eyes did not dilate to a 6 mm pupil diameter, and an additional 32 eyes did not dilate to 7 mm. The number of subjects per pupil size and age group is shown in Table 1.
Table 1.
Number of Subjects per Pupil Diameter (mm) and Age Group (years)
| Age Group |
Mean Age ± SD |
Maximum Age |
Minimum Age |
Subjects per Pupil Size |
||
|---|---|---|---|---|---|---|
| 3, 4, 5 | 6 | 7 | ||||
| 20–29 | 25.2 ± 2.3 | 29.8 | 21.6 | 20 | 20 | 18 |
| 30–39 | 35.0 ± 2.4 | 38.7 | 30.1 | 18 | 18 | 15 |
| 40–49 | 45.2 ± 2.8 | 49.9 | 40.5 | 32 | 32 | 29 |
| 50–59 | 54.4 ± 2.9 | 58.7 | 50.5 | 32 | 31 | 18 |
| 60–69 | 62.9 ± 1.9 | 67.4 | 60.3 | 21 | 20 | 16 |
| 70–79 | 72.9 ± 2.4 | 78.4 | 70.0 | 23 | 23 | 16 |
| Total Count | 146 | 144 | 112 | |||
For each eye at each pupil size, the second-order defocus term was mathematically compensated for the shift due to chromatic aberration from the measured 840 nm to the desired 555 nm by extrapolating the flattening portion of the hyperbolic equation defined in Ref. [50] to 840 nm. Validation of this extrapolation has been confirmed experimentally [51,52]. Changes in HOAs due to change in wavelength have been found to be non-uniform [53], rendering a single adjustment factor inappropriate. However, these changes in HOAs have also been shown to be insignificant [51,54], and therefore no other terms were adjusted.
The SCA combination (sphere and cylinder to the nearest 0.25 D and axis in 2° increments) that maximized visual image quality (VSX) was then objectively identified using a simulated through focus experiment as previously described [43], by calculating VSX for a set of 95454 SCA prescriptions. Although this meant that eyes with low astigmatism were sampled at small dioptric increments, our intention was to frame the analyses using units (sphere, cylinder, and axis) that were clinically available and familiar rather than using units of one of the mathematically uniform dioptric spaces. Consequently, instead of searching the axis in increments that varied with cylinder magnitude, the highest accuracy, that is 2°, specified by the American National Standards Institute (ANSI Z80.1–2015) [55] was used as the axis increment for all eyes.
Subjects’ refractive errors varied from +4.75 to −6.75 D sphere and 0 to −3.50 D cylinder. Younger eyes tended to be slightly more myopic than older eyes, but both spherical and astigmatic refractive errors were generally well distributed across age groups.
Means and 95% confidence intervals for SCA best-corrected VSX were determined for each pupil size and age group. The mean best-corrected VSX, as well as the base 10 logarithm of VSX (logVSX), for each unique age group and pupil size combination were used to determine the multiple (two-element) regression of VSX (and logVSX) as a function of age and pupil size.
Toward normative validation of these data, best-corrected VSX was calculated for an independently collected WFE dataset (the Rochester Ocular Wave Aberration Study; Porter et al. [56]) of 218 normal eyes that spanned a similar age range (21 to 65 years old). These WFEs underwent a similar defocus correction for chromatic aberration (from 780 to 555 nm) [50] and the resultant SCA best-corrected image quality values were compared with the confidence intervals of the TINCO dataset.
3. RESULTS
The quantitative relationship between visual image quality, pupil size, and age, shown in Fig. 2, agrees with the prevailing qualitative clinical understanding of how these variables interact. Best VSX was found in young eyes (20 to 30 years old) at small pupil diameters (3 mm), and VSX decreased as age increased and as pupil size increased, with pupil size causing a more rapid decrease. Both pupil size and age had statistically significant influence on visual image quality (p < 0.0001), and the multiple regressions for the mean and 95% confidence intervals of the three variables were
| (2) |
| (3) |
| (4) |
Fig. 2.
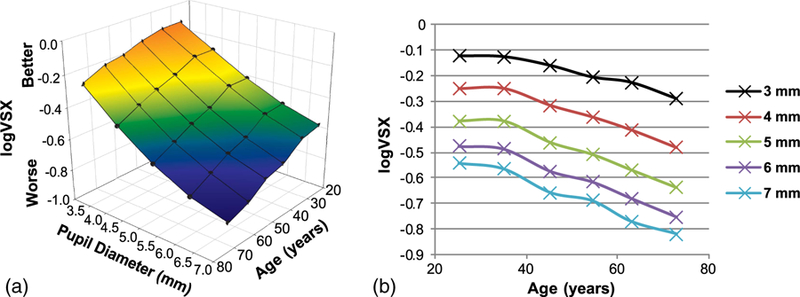
(a) Quantitative relationship between best-corrected visual image quality (logVSX), pupil diameter, and age. Black circles are the mean logVSX for the corresponding pupil sizes and means of each age group. (b) Two-dimensional depiction of the same data as in (a). Best visual image quality (logVSX) was found in young eyes (20 to 30 years old) and at small pupil diameters, and decreased as age increased and as pupil size increased, with pupil size causing a more rapid decrease.
In the above regressions, as well as in Fig. 2, logVSX is used rather than VSX, because logVSX has been shown to have a linear relationship with logMAR VA. [42] The regressions for the upper and lower confidence intervals facilitate the calculation of normative best SCA corrected visual image quality ranges for any pupil size and age. Corresponding multiple regressions for VSX can be found in Appendix A.
The full set of best-corrected VSX and logVSX results as a function of pupil size and age, including means, standard deviations, maximum and minimum values, and 95% confidence intervals are presented in reference format in Tables 2 and 3 of Appendix A.
Table 2.
Best-Corrected VSX Values as a Function of Pupil Diameter (mm) and Age (years)
| Age | Pupil Diameter | Mean VSX ± SD | Upper 95% CI | Lower 95% CI | Max VSX | Min VSX |
|---|---|---|---|---|---|---|
| 20–29 | 3 | 0.762 ± 0.111 | 0.979 | 0.545 | 0.919 | 0.531 |
| 20–29 | 4 | 0.574 ± 0.116 | 0.801 | 0.346 | 0.745 | 0.331 |
| 20–29 | 5 | 0.432 ± 0.099 | 0.625 | 0.238 | 0.584 | 0.229 |
| 20–29 | 6 | 0.344 ± 0.084 | 0.509 | 0.179 | 0.491 | 0.173 |
| 20–29 | 7 | 0.294 ± 0.068 | 0.428 | 0.161 | 0.412 | 0.159 |
| 30–39 | 3 | 0.757 ± 0.114 | 0.980 | 0.535 | 0.922 | 0.484 |
| 30–39 | 4 | 0.578 ± 0.138 | 0.849 | 0.306 | 0.859 | 0.341 |
| 30–39 | 5 | 0.434 ± 0.122 | 0.674 | 0.194 | 0.724 | 0.264 |
| 30–39 | 6 | 0.338 ± 0.102 | 0.538 | 0.137 | 0.575 | 0.207 |
| 30–39 | 7 | 0.283 ± 0.087 | 0.454 | 0.112 | 0.470 | 0.170 |
| 40–49 | 3 | 0.701 ± 0.116 | 0.929 | 0.473 | 0.877 | 0.497 |
| 40–49 | 4 | 0.496 ± 0.114 | 0.720 | 0.272 | 0.680 | 0.307 |
| 40–49 | 5 | 0.356 ± 0.086 | 0.525 | 0.188 | 0.496 | 0.206 |
| 40–49 | 6 | 0.275 ± 0.067 | 0.407 | 0.143 | 0.385 | 0.156 |
| 40–49 | 7 | 0.228 ± 0.057 | 0.340 | 0.115 | 0.325 | 0.129 |
| 50–59 | 3 | 0.640 ± 0.148 | 0.929 | 0.351 | 0.876 | 0.370 |
| 50–59 | 4 | 0.457 ± 0.147 | 0.745 | 0.169 | 0.798 | 0.230 |
| 50–59 | 5 | 0.331 ± 0.124 | 0.573 | 0.088 | 0.646 | 0.155 |
| 50–59 | 6 | 0.257 ± 0.094 | 0.441 | 0.072 | 0.506 | 0.118 |
| 50–59 | 7 | 0.213 ± 0.066 | 0.341 | 0.084 | 0.387 | 0.140 |
| 60–69 | 3 | 0.601 ± 0.097 | 0.790 | 0.412 | 0.773 | 0.468 |
| 60–69 | 4 | 0.395 ± 0.083 | 0.559 | 0.231 | 0.585 | 0.261 |
| 60–69 | 5 | 0.277 ± 0.068 | 0.410 | 0.145 | 0.444 | 0.165 |
| 60–69 | 6 | 0.215 ± 0.054 | 0.320 | 0.110 | 0.354 | 0.126 |
| 60–69 | 7 | 0.175 ± 0.046 | 0.265 | 0.086 | 0.296 | 0.104 |
| 70–79 | 3 | 0.525 ± 0.116 | 0.753 | 0.297 | 0.785 | 0.352 |
| 70–79 | 4 | 0.342 ± 0.095 | 0.527 | 0.156 | 0.551 | 0.190 |
| 70–79 | 5 | 0.240 ± 0.076 | 0.389 | 0.092 | 0.421 | 0.128 |
| 70–79 | 6 | 0.185 ± 0.059 | 0.301 | 0.069 | 0.325 | 0.097 |
| 70–79 | 7 | 0.158 ± 0.049 | 0.254 | 0.063 | 0.267 | 0.098 |
| All Ages | 3 | 0.661 ± 0.143 | 0.941 | 0.380 | 0.922 | 0.352 |
| All Ages | 4 | 0.469 ± 0.142 | 0.748 | 0.190 | 0.859 | 0.190 |
| All Ages | 5 | 0.341 ± 0.118 | 0.572 | 0.110 | 0.724 | 0.128 |
| All Ages | 6 | 0.266 ± 0.094 | 0.451 | 0.081 | 0.575 | 0.097 |
| All Ages | 7 | 0.226 ± 0.078 | 0.378 | 0.074 | 0.470 | 0.098 |
Table 3.
Best-Corrected logVSX Values as a Function of Pupil Diameter (mm) and Age (years)
| Age | Pupil Diameter | Mean logVSX ± SD | Upper 95% CI | Lower 95% CI | Max logVSX | Min logVSX |
|---|---|---|---|---|---|---|
| 20–29 | 3 | −0.123 ± 0.067 | 0.000 | −0.255 | −0.037 | −0.275 |
| 20–29 | 4 | −0.251 ± 0.096 | −0.062 | −0.439 | −0.128 | −0.480 |
| 20–29 | 5 | −0.377 ± 0.111 | −0.160 | −0.594 | −0.233 | −0.641 |
| 20–29 | 6 | −0.477 ± 0.118 | −0.246 | −0.709 | −0.309 | −0.761 |
| 20–29 | 7 | −0.543 ± 0.107 | −0.333 | −0.753 | −0.386 | −0.799 |
| 30–39 | 3 | −0.126 ± 0.070 | 0.000 | −0.264 | −0.035 | −0.316 |
| 30–39 | 4 | −0.250 ± 0.104 | −0.047 | −0.454 | −0.066 | −0.467 |
| 30–39 | 5 | −0.377 ± 0.115 | −0.152 | −0.602 | −0.140 | −0.579 |
| 30–39 | 6 | −0.488 ± 0.120 | −0.253 | −0.723 | −0.241 | −0.685 |
| 30–39 | 7 | −0.565 ± 0.125 | −0.320 | −0.811 | −0.328 | −0.770 |
| 40–49 | 3 | −0.160 ± 0.074 | −0.016 | −0.305 | −0.057 | −0.304 |
| 40–49 | 4 | −0.317 ± 0.104 | −0.113 | −0.520 | −0.168 | −0.512 |
| 40–49 | 5 | −0.461 ± 0.111 | −0.243 | −0.680 | −0.305 | −0.685 |
| 40–49 | 6 | −0.575 ± 0.113 | −0.353 | −0.797 | −0.414 | −0.808 |
| 40–49 | 7 | −0.657 ± 0.117 | −0.429 | −0.886 | −0.488 | −0.890 |
| 50–59 | 3 | −0.206 ± 0.105 | 0.001 | −0.412 | −0.057 | −0.432 |
| 50–59 | 4 | −0.362 ± 0.139 | −0.089 | −0.635 | −0.098 | −0.639 |
| 50–59 | 5 | −0.508 ± 0.157 | −0.201 | −0.815 | −0.190 | −0.811 |
| 50–59 | 6 | −0.616 ± 0.151 | −0.320 | −0.913 | −0.296 | −0.930 |
| 50–59 | 7 | −0.689 ± 0.123 | −0.448 | −0.930 | −0.412 | −0.853 |
| 60–69 | 3 | −0.227 ± 0.069 | −0.091 | −0.362 | −0.112 | −0.330 |
| 60–69 | 4 | −0.412 ± 0.090 | −0.236 | −0.589 | −0.233 | −0.583 |
| 60–69 | 5 | −0.569 ± 0.104 | −0.364 | −0.774 | −0.352 | −0.782 |
| 60–69 | 6 | −0.680 ± 0.108 | −0.468 | −0.892 | −0.451 | −0.900 |
| 60–69 | 7 | −0.770 ± 0.111 | −0.553 | −0.987 | −0.528 | −0.983 |
| 70–79 | 3 | −0.290 ± 0.097 | −0.101 | −0.479 | −0.105 | −0.453 |
| 70–79 | 4 | −0.482 ± 0.120 | −0.247 | −0.717 | −0.259 | −0.720 |
| 70–79 | 5 | −0.638 ± 0.132 | −0.380 | −0.897 | −0.376 | −0.894 |
| 70–79 | 6 | −0.753 ± 0.134 | −0.491 | −1.016 | −0.487 | −1.011 |
| 70–79 | 7 | −0.819 ± 0.129 | −0.565 | −1.073 | −0.574 | −1.010 |
| All Ages | 3 | −0.191 ± 0.100 | 0.000 | −0.386 | −0.035 | −0.453 |
| All Ages | 4 | −0.349 ± 0.136 | −0.083 | −0.615 | −0.066 | −0.720 |
| All Ages | 5 | −0.493 ± 0.152 | −0.195 | −0.791 | −0.140 | −0.894 |
| All Ages | 6 | −0.603 ± 0.155 | −0.299 | −0.906 | −0.241 | −1.011 |
| All Ages | 7 | −0.671 ± 0.149 | −0.379 | −0.963 | −0.328 | −1.010 |
Best-corrected logVSX values determined for an independently collected set of WFE data [56] from 218 eyes at a 5.7 mm pupil diameter are shown (as black circles) in Fig. 3 along with the 95% confidence interval determined for the TINCO dataset at 5.7 mm using the regressions provided in Eqs. (1)–(4). No statistically significant difference was found between datasets: the best-corrected logVSX values of 95.4% of the independently measured eyes (208 eyes) were within the 95% confidence interval defined by the TINCO dataset; as expected for normative data, the remaining eyes were split almost equally above and below the confidence interval [2.8% (6 eyes) above and 1.8% (4 eyes) below].
Fig. 3.
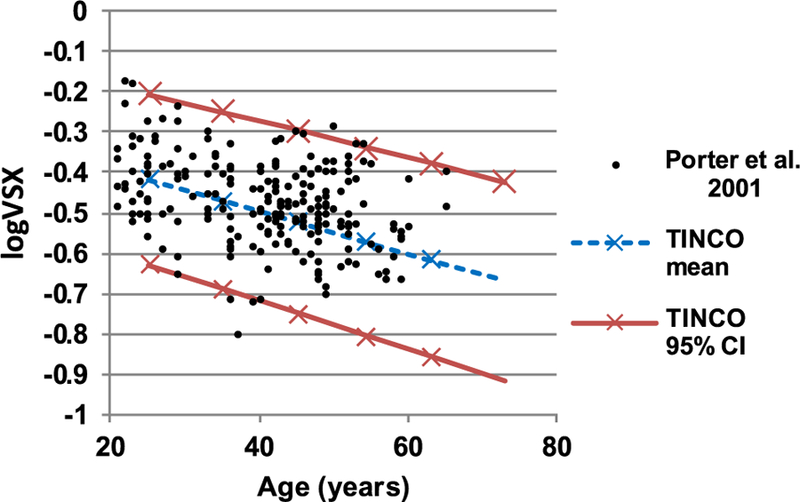
Best-corrected logVSX for an independently collected set of WFE data (the Rochester Ocular Wave Aberration Study [56]) from 218 eyes at 5.7 mm pupil diameter (black circles) and mean and 95% confidence interval determined from the TINCO dataset. Best-corrected logVSX of 95.4% of these independently measured eyes were within the TINCO 95% confidence interval.
4. DISCUSSION
We have presented mean and confidence interval values for the objectively determined best-corrected visual image quality (VSX) provided to normal eyes by sphere and cylinder prescriptions as a function of pupil size and age, and have validated these normative values using a large independently collected dataset [56]. The means and confidence intervals provided here constitute a normative reference with which the visual image quality of an individual eye at a given age and pupil size can be compared and has the potential to be useful in sample size calculations as well as the design and manufacture of ophthalmic products across different correction modalities.
A. Comparison with Other Studies
A cross-sectional reference of normative values of VSX is given by Thibos [57], where visual image quality was calculated for 1000 simulated eyes generated from a statistical model [58] and for 100 real eyes (from the Indiana Aberration Study) [27]. Unfortunately, the age distribution of the 100 real eyes was very homogeneous—most were in the 20 to 29 and 30 to 39 age groups—and the statistical model [58] was based on the same sample. Metric values were presented for a 6 mm pupil diameter.
The mean ± SD log VSX values were −0.51 ± 0.19 for the 100 real eyes and −0.55 ± 0.21 for the 1000 simulated eyes, which are similar to the corresponding values of this study, −0.48, −0.49, and −0.58, for the 20 to 30, 30 to 40, and 40 to 50 age groups, respectively (see Table 3).
The findings of this study were also in general agreement with the literature: the best visual image quality was found in young eyes and at small pupil sizes, which confirms findings of optical metrics such as higher-order (HO) RMS [16] and MTF [11,13], as well as measures of total visual performance (combining the optical and neural components) such as contrast sensitivity (CSF) (see Owsley [59] for a review) and VA [60].
The literature is divided on the cause of the abovementioned decrease in overall visual performance with age. Some studies [14,61,62] suggest that neural changes have a significant contribution, while others [11,63,64] suggest that optical changes are primarily responsible and that neural changes are insignificant.
Certain optical changes, such as scatter due to crystalline lens opalescence, increase with age [46] and are not captured by VSX. Although large amounts of scatter could be expected to reduce retinal image quality [65,66], visual acuity has been shown to be largely unaffected by scatter [66]. We believe the effect of scatter on the interpretation of the present data to be minimal because subjects with cortical and/or posterior subcapsular cataracts graded as >2 according to LOCS-III were excluded, and the data agreed with an independently collected WFE set with a similar age distribution. A full description of the nature and degree of lens opacification present in the TINCO subjects can be found in Table 4 of Applegate et al. [16].
The photopic neural transfer function used in the calculation of VSX is derived from the nCSF of Campbell and Green, [10] which was measured on a 27-year-old subject. Given the uncertainty in the stability of the neural processing with age, all visual image quality metrics should be framed as describing the optical quality of an eye in terms of the sensitivity of a healthy normal visual system. Work is underway in our laboratory to evaluate the personalization of these metrics for eyes that are not considered healthy or normal.
B. Are These Normative Levels of Visual Image Quality Clinically Achievable?
The eyes analyzed here (both the TINCO eyes and the eyes from Porter et al. [56]) underwent an objective simulated through focus refraction that identified the SCA combination that optimized VSX. This method has been shown to provide equivalent VA to subjective refraction [43]. The question arose as to whether the normative confidence intervals presented here establish benchmarks of visual image quality that would be achievable with other SCA combinations not optimized for VSX but still considered clinically acceptable, given the variability of clinical subjective refraction [36–38].
Toward this end, for each of the 218 eyes from Porter et al. [56], all SCA combinations (sphere and cylinder in 0.25 D steps and axis in 2° steps) that provided VSX better than the lower 95% confidence interval of the TINCO norms were identified. The mean ± SD number of prescriptions was 264 ± 183; the median was 240. (The four eyes that did not surpass the TINCO lower 95% confidence interval had zero SCA combinations for this analysis.) In other words, although adaptation and other factors can influence subjective refraction, for the majority of these eyes there are many SCA combinations (in addition to the one that optimized VSX) that would provide a VSX level within the 95% TINCO confidence intervals. However, the number of prescriptions in this group is dependent on the dioptric increments that are used (for instance, fewer SCA combinations would correct an eye to within the 95% confidence interval if the axis was sampled in 5° steps). Consequently, the dioptric distance from the best SCA correction to the TINCO lower 95% confidence interval was estimated (using power vectors [67]) by calculating the dioptric difference between the best SCA combination (that optimized VSX) and the “worst” SCA prescription that still corrected an eye to within the confidence interval. The mean ± SD dioptric distance was 0.41 ± 0.23 D; the median was 0.36 D. Despite that dioptric spaces are not visually uniform, and a given dioptric difference could have different visual interactions with the underlying aberrations of different eyes, this Euclidean dioptric distance provides an indication of how dioptrically different a refraction can be from the optimal objective refraction and still provide an eye with visual image quality within the TINCO 95% confidence interval norms. It is also likely that eyes with high astigmatism will have fewer SCA combinations that correct them to within the normative levels of visual image quality presented here.
The SCA prescriptions that maximized VSX for the TINCO eyes generally did not change by a clinically significant amount across the range of pupil sizes examined. The mean variability (SD) of the spherical and astigmatic components (in power vectors) [67] across all 148 eyes were less than 0.08 D. This is consistent with the finding that subjective refraction of normal eyes does not vary significantly across pupil sizes [68].
The VSX metric presented here describes monochromatic visual image quality, which would be degraded by chromatic aberration in natural viewing conditions. Chromatic aberration of the eye has been shown to be essentially constant across studies and populations [50]. Although the use of polychromatic metrics has been advocated [69], they have been found to not provide a significant benefit over monochromatic metrics [19].
While the VSX metric tracks subjective image quality for pupil sizes greater than 3 mm, it may not accurately describe subjective visual image quality over smaller pupil diameters. At such small pupil sizes, the diffraction-limited PSF (the denominator) used in normalizing the metric is significantly deteriorated by diffraction, while the aberrations of normal eyes (the numerator) are also greatly reduced. As a result, metric values may approach 1 (excellent) while visual image quality is actually quite poor due to diffraction. In these situations, normalizing the metric (VSX*) to a constant pupil size, such as 3 mm, as has been done for other visual image quality metrics [44,45], could provide a more realistic assessment of visual image quality.
However, for pupil sizes greater than 3 mm (such as the normative data presented here) renormalizing to a 3 mm pupil diameter (VSX*) was only minimally different to the VSX values. Renormalization increased the metric value as the numerator pupil size increased, but the maximum increase was less than 5% of the VSX value. This increase was small chiefly due to the effect of the neural weighting of the PSFs in the calculation of VSX and VSX*. Thus, the choice between fixed and variable pupil size for normalization is of no practical importance for computing VSX for pupil sizes greater than 3 mm. However, other metrics that do not incorporate a visual or neural weighting, such as the traditional Strehl ratio, are more affected by the choice of reference pupil size. In those metrics, normalization by a fixed standard may be preferred in applications where absolute image quality is more important than image quality relative to a standard that varies with pupil size.
5. CONCLUSIONS
The quantitative relation of SCA best-corrected visual image quality (logVSX), pupil size, and age is presented and 95% confidence interval norms are provided for pupil size from 3 to 7 mm and for age groups between 20 and 80 years, as well as regression equations for the calculation of logVSX at any individual age and pupil size. These objectively determined benchmarks represent the best theoretical levels of visual image quality that normal eyes can achieve with conventional sphere, cylinder, and axis corrections and can be useful in evaluating both traditional and wave-front-guided optical corrections across different modalities.
Acknowledgment.
The authors thank Dr. Jason Porter for kindly providing the supplementary wavefront error data analyzed here and Kimberly Thompson for assistance with figures. Portions of these findings were presented at the Association for Research in Vision and Ophthalmology (ARVO) meeting in Baltimore, Maryland, May 2017.
Funding. National Eye Institute (NEI) (R01EY008520, R01EY019105, P30 EY 07551); U.S. Navy (N00259-10-P-1354); University of Houston (UH) (Borish Endowment).
APPENDIX A
Regressions
These multiple regressions allow the calculation of normative VSX [mean and 95% confidence interval (CI)] values for any particular pupil size and age. The corresponding regressions for logVSX are presented in the Results section.
VSX
| (A1) |
| (A2) |
| (A3) |
REFERENCES
- 1.Almeida M and Carvalho L, “Different schematic eyes and their accuracy to the in vivo eye: a quantitative comparison study,” Braz. J. Phys 37, 378–387 (2007). [Google Scholar]
- 2.Schwartz S, Geometrical and Visual Optics: A Clinical Introduction, 2nd ed. (McGraw/Medical, 2013). [Google Scholar]
- 3.Smith G, “Angular diameter of defocus blur discs,” Am. J. Optom. Physiol. Opt 59, 885–889 (1982). [DOI] [PubMed] [Google Scholar]
- 4.Raasch T, “Spherocylindrical refractive errors and visual acuity,” Optom. Vis. Sci 72, 272–275 (1995). [DOI] [PubMed] [Google Scholar]
- 5.Westheimer G and Campbell F, “Light distribution in the image formed by the living human eye,” J. Opt. Soc. Am 52, 1040–1045 (1962). [DOI] [PubMed] [Google Scholar]
- 6.Krauskopf J, “Light distribution in human retinal images,” J. Opt. Soc. Am 52, 1046–1050 (1962). [Google Scholar]
- 7.Campbell F and Gubisch R, “Optical quality of the human eye,” J. Physiol 186, 558–578 (1966). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Santamaría J, Artal P, and Bescós J, “Determination of the point-spread function of human eyes using a hybrid optical-digital method,” J. Opt. Soc. Am. A 4, 1109–1114 (1987). [DOI] [PubMed] [Google Scholar]
- 9.Artal P, “Calculations of two-dimensional foveal retinal images in real eyes,” J. Opt. Soc. Am. A 7, 1374–1381 (1990). [DOI] [PubMed] [Google Scholar]
- 10.Campbell F and Green D, “Optical and retinal factors affecting visual resolution,” J. Physiol 181, 576–593 (1965). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Artal P, Ferro M, Navarro R, and Miranda I, “Effects of aging in retinal image quality,” J. Opt. Soc. Am. A 10, 1656–1662 (1993). [DOI] [PubMed] [Google Scholar]
- 12.Navarro R, Artal P, and Williams D, “Modulation transfer of the human eye as a function of retinal eccentricity,” J. Opt. Soc. Am. A 10, 201–212 (1993). [DOI] [PubMed] [Google Scholar]
- 13.Guirao A, Gonzalez C, Redondo M, Geraghty E, Norrby S, and Artal P, “Average optical performance of the human eye as a function of age in a normal population,” Invest. Ophthalmol. Visual Sci 40, 203–213 (1999). [PubMed] [Google Scholar]
- 14.Calver R, Cox M, and Elliott D, “Effect of aging on the monochromatic aberrations of the human eye,” J. Opt. Soc. Am. A 16, 2069–2078 (1999). [DOI] [PubMed] [Google Scholar]
- 15.Salmon T and van de Pol C, “Normal-eye Zernike coefficients and root-mean-square wavefront errors,” J. Cataract Refract. Surg 32, 2064–2074 (2006). [DOI] [PubMed] [Google Scholar]
- 16.Applegate R, Donnelly III W, Marsack J, Koenig D, and Pesudovs K, “Three-dimensional relationship between high-order root-mean-square wavefront error, pupil diameter, and aging,” J. Opt. Soc. Am. A 24, 578–587 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Guirao A and Williams D, “A method to predict refractive errors from wave aberration data,” Optom. Vis. Sci 80, 36–42 (2003). [DOI] [PubMed] [Google Scholar]
- 18.Thibos L, Hong X, Bradley A, and Applegate R, “Accuracy and precision of objective refraction from wavefront aberrations,” J. Vis 4, 329–351 (2004). [DOI] [PubMed] [Google Scholar]
- 19.Kilintari M, Pallikaris A, Tsiklis N, and Ginis H, “Evaluation of image quality metrics for the prediction of subjective best focus,” Optom. Vis. Sci 87, 183–189 (2010). [DOI] [PubMed] [Google Scholar]
- 20.Iskander D, “A subjective refraction-based assessment of image quality metric,” Photon. Lett. Pol 3, 150–152 (2011). [Google Scholar]
- 21.Plainis S, Atchison D, and Charman W, “Power profiles of multifocal contact lenses and their interpretation,” Optom. Vis. Sci 90, 1066–1077 (2013). [DOI] [PubMed] [Google Scholar]
- 22.Marsack J, Parker K, and Applegate R, “Performance of wavefront-guided soft lenses in three keratoconus subjects,” Optom. Vis. Sci 85, E1172 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Marsack J, Ravikumar A, Nguyen C, Ticak A, Koenig D, Elswick J, and Applegate R, “Wavefront-guided scleral lens correction in keratoconus,” Optom. Vis. Sci 91, 1221–1230 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Chung S, Jarvis S, and Cheung S, “The effect of dioptric blur on reading performance,” Vis. Res 47, 1584–1594 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Fujikado T and Saika M, “Evaluation of actual retinal images produced by misaligned aspheric intraocular lenses in a model eye,” Clin. Ophthalmol 8, 2415–2423 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Navarro R, Rozema J, and Tassignon M, “Optical changes of the human cornea as a function of age,” Optom. Vis. Sci 90, 587–598 (2013). [DOI] [PubMed] [Google Scholar]
- 27.Thibos L, Hong X, Bradley A, and Cheng X, “Statistical variation of aberration structure and image quality in a normal population of healthy eyes,” J. Opt. Soc. Am. A 19, 2329–2348 (2002). [DOI] [PubMed] [Google Scholar]
- 28.Atchison D, Smith G, and Efron N, “The effect of pupil size on visual acuity in uncorrected and corrected myopia,” Am. J. Optom. Physiol. Opt 56, 315–323 (1979). [DOI] [PubMed] [Google Scholar]
- 29.Smith G, “Relation between spherical refractive error and visual acuity,” Optom. Vis. Sci 68, 591–598 (1991). [DOI] [PubMed] [Google Scholar]
- 30.IJspeert J, van den Berg T, and Spekreijse H, “An improved mathematical description of the foveal visual point spread function with parameters for age, pupil size and pigmentation,” Vis. Res 33, 15–20 (1993). [DOI] [PubMed] [Google Scholar]
- 31.Watson A, “A formula for the mean human optical modulation transfer function as a function of pupil size,” J. Vis 13(6):18, 1–11 (2013). [DOI] [PubMed] [Google Scholar]
- 32.Piotrowski L and Campbell F, “A demonstration of the visual importance and flexibility of spatial-frequency amplitude and phase,” Perception 11, 337–346 (1982). [DOI] [PubMed] [Google Scholar]
- 33.Sarver E and Applegate R, “The importance of the phase transfer function to visual function and visual quality metrics,” J. Refract. Surg 20, S504–S507 (2004). [PubMed] [Google Scholar]
- 34.Watson A and Ahumada A, “A standard model for foveal detection of spatial contrast,” J. Vis 5(9), 717–740 (2005). [DOI] [PubMed] [Google Scholar]
- 35.Iskander D, “Computational aspects of the visual Strehl ratio,” Optom. Vis. Sci 83, 57–59 (2006). [DOI] [PubMed] [Google Scholar]
- 36.Goss D and Grosvenor T, “Reliability of refractiona literature review,” J. Am. Optom. Assoc 67, 619–630 (1996). [PubMed] [Google Scholar]
- 37.Bullimore M, Fusaro R, and Adams C, “The repeatability of automated and clinician refraction,” Optom. Vis. Sci 75, 617–622 (1998). [DOI] [PubMed] [Google Scholar]
- 38.Pesudovs K, Parker K, Cheng H, and Applegate R, “The precision of wavefront refraction compared to subjective refraction and auto-refraction,” Optom. Vis. Sci 84, 387–392 (2007). [DOI] [PubMed] [Google Scholar]
- 39.Cheng X, Bradley A, and Thibos L, “Predicting subjective judgment of best focus with objective image quality metrics,” J. Vis 4, 310–321 (2004). [DOI] [PubMed] [Google Scholar]
- 40.Marsack J, Thibos L, and Applegate R, “Metrics of optical quality derived from wave aberrations predict visual performance,” J. Vis 4(4), 322–328 (2004). [DOI] [PubMed] [Google Scholar]
- 41.Schoneveld P, Pesudovs K, and Coster D, “Predicting visual performance from optical quality metrics in keratoconus,” Clin. Exp. Optom 92, 289–296 (2009). [DOI] [PubMed] [Google Scholar]
- 42.Ravikumar A, Sarver E, and Applegate R, “Change in visual acuity is highly correlated with change in six image quality metrics independent of wavefront error and/or pupil diameter,” J. Vis 12(10):11, 1–13 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Hastings G, Marsack J, Nguyen L, Cheng H, and Applegate R, “Is an objective refraction optimised using the visual Strehl ratio better than a subjective refraction?” Ophthalmic Physiol. Opt 37, 317–325 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.López-Gil N, Martin J, Liu T, Bradley A, Díaz-Muñoz D, and Thibos L, “Retinal image quality during accommodation,” Ophthalmic Physiol. Opt 33, 497–507 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Sreenivasan V, Aslakson E, Kornaus A, and Thibos LN, “Retinal image quality during accommodation in adult myopic eyes,” Optom. Vis. Sci 90, 1292–1303 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Pesudovs K, Marsack J, Donnelly W, Thibos L, and Applegate R, “Measuring visual acuity—mesopic or photopic conditions, and high or low contrast letters?” J. Refract. Surg 20, S508–S514 (2004). [PubMed] [Google Scholar]
- 47.Chylack L, Wolfe J, Singer D, Leske M, Bullimore M, Bailey I, Friend J, McCarthy D, and Wu S, “The lens opacities classification system III,” Arch. Ophthalmol 111, 831–836 (1993). [DOI] [PubMed] [Google Scholar]
- 48.Campbell C, “Matrix method to find a new set of Zernike coefficients from an original set when the aperture radius is changed,” J. Opt. Soc. Am. A 20, 209–217 (2003). [DOI] [PubMed] [Google Scholar]
- 49.Bará S, Pailos E, Arines J, López-Gil N, and Thibos L, “Estimating the eye aberration coefficients in resized pupils: is it better to refit or to rescale?” J. Opt. Soc. Am. A 31, 114–123 (2014). [DOI] [PubMed] [Google Scholar]
- 50.Thibos L, Ye M, Zhang X, and Bradley A, “The chromatic eye: a new reduced-eye model of ocular chromatic aberration in humans,” Appl. Opt 31, 3594–3600 (1992). [DOI] [PubMed] [Google Scholar]
- 51.Llorente L, Diaz-Santana L, Lara-Saucedo D, and Marcos S, “Aberrations of the human eye in visible and near infrared illumination,” Optom. Vis. Sci 80, 26–35 (2003). [DOI] [PubMed] [Google Scholar]
- 52.Fernández E, Unterhuber A, Prieto P, Hermann B, Drexler W, and Artal P, “Ocular aberrations as a function of wavelength in the near infrared measured with a femtosecond laser,” Opt. Express 13, 400–409 (2005). [DOI] [PubMed] [Google Scholar]
- 53.Nam J, Rubinstein J, and Thibos L, “Wavelength adjustment using an eye model from aberrometry data,” J. Opt. Soc. Am. A 27, 1561–1574 (2010). [DOI] [PubMed] [Google Scholar]
- 54.Fernández E and Artal P, “Ocular aberrations up to the infrared range: from 632.8 to 1070 nm,” Opt. Express 16, 21199–21208 (2008). [DOI] [PubMed] [Google Scholar]
- 55.American National Standards Institute, “Ophthalmics-prescription ophthalmic lenses-recommendation,” Standard: ANSI Z80.1 (2015).
- 56.Porter J, Guirao A, Cox I, and Williams D, “Monochromatic aberrations of the human eye in a large population,” J. Opt. Soc. Am. A 18, 1793–1803 (2001). [DOI] [PubMed] [Google Scholar]
- 57.Thibos L, “Retinal image quality for virtual eyes generated by a statistical model of ocular wavefront aberrations,” Ophthalmic Physiol. Opt 29, 288–291 (2009). [DOI] [PubMed] [Google Scholar]
- 58.Thibos L, Bradley A, and Hong X, “A statistical model of the aberration structure of normal, well-corrected eyes,” Ophthalmic Physiol. Opt 22, 427–433 (2002). [DOI] [PubMed] [Google Scholar]
- 59.Owsley C, “Aging and vision,” Vis. Res 51, 1610–1622 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Elliott D, Yang K, and Whitaker D, “Visual acuity changes throughout adulthood in normal, healthy eyes: seeing beyond 6/6,” Optom. Vis. Sci 72, 186–191 (1995). [DOI] [PubMed] [Google Scholar]
- 61.Elliott D, “Contrast sensitivity decline with ageing: a neural or optical phenomenon?” Ophthalmic Physiol. Opt 7, 415–419 (1987). [PubMed] [Google Scholar]
- 62.Nameda N, Kawara T, and Ohzu H, “Human visual spatio-temporal frequency performance as a function of age,” Optom. Vis. Sci 66, 760–765 (1989). [DOI] [PubMed] [Google Scholar]
- 63.Dressler M and Rassow B, “Neural contrast sensitivity measurements with a laser interference system for clinical and screening application,” Invest. Ophthalmol. Visual. Sci 21, 737–744 (1981). [PubMed] [Google Scholar]
- 64.Burton K, Owsley C, and Sloane M, “Aging and neural spatial contrast sensitivity: photopic vision,” Vis. Res 33, 939–946 (1993). [DOI] [PubMed] [Google Scholar]
- 65.van den Berg TJTP, Franssen L, and Coppens JE, “Straylight in the human eye: testing objectivity and optical character of the psycho-physical measurement,” Ophthalmic Physiol. Opt 29, 345–350 (2009). [DOI] [PubMed] [Google Scholar]
- 66.van den Berg T, “The (lack of) relation between straylight and visual acuity. Two domains of the point-spread-function,” Ophthalmic Physiol. Opt 37, 333–341 (2017). [DOI] [PubMed] [Google Scholar]
- 67.Thibos L, Wheeler W, and Horner D, “Power vectors: an application of Fourier analysis to the description and statistical analysis of refractive error,” Optom. Vis. Sci 74, 367–375 (1997). [DOI] [PubMed] [Google Scholar]
- 68.Charman W, Jennings J, and Whitefoot H, “The refraction of the eye in the relation to spherical aberration and pupil size,” Br. J. Physiol. Opt 32, 78–93 (1978). [PubMed] [Google Scholar]
- 69.Ravikumar S, Thibos L, and Bradley A, “Calculation of retinal image quality for polychromatic light,” J. Opt. Soc. Am. A 25, 2395–2407 (2008). [DOI] [PubMed] [Google Scholar]


