Noninvasive Characterization of In Situ Forming Implant Diffusivity Using Diffusion-weighted MRI

Abstract

In situ forming implants (ISFIs) form a solid drug-eluting depot, releasing drug for an extended period of time after a minimally-invasive injection. Clinical use of ISFIs has been limited because many factors affect drug release kinetics. The aim of this study was to use diffusion-weighted MRI (DWI) to noninvasively quantify spatial-temporal changes in implant diffusivity in situ. ISFIs were formed using poly(lactic-co-glycolic) acid, with a molecular weight of either 15 kDa or 52 kDa, and fluorescein as the mock drug. Drug release, polymer erosion and degradation, and implant diffusivity were analyzed in vitro over 21 days. DWI was also performed in vivo over 5 days. Spatial diffusivity maps of the implant were generated using DWI data. Results showed constant diffusivity at the implant shell ((1.17±0.128)×10⁻³ mm²/s) and increasing diffusivity within the interior over time (from (0.268±0.0813)×10⁻³ mm²/s during day 1 to (1.88±0.0400)×10⁻³ mm²/s at 14 d), which correlated with increasing porosity of the implant microstructure. Implants formed in vivo followed the same diffusivity trend as those in vitro. This study validates the use of DWI to provide novel functional information about implant behavior through its ability to noninvasively characterize transport properties within the implant both in vitro and in vivo.

1. Introduction

Despite their popularity, traditional oral dosage forms, such as pills, suffer from problems with patient adherence. Frequent and consistent administration is required to maintain drug levels within the therapeutic window to achieve the proper balance between effectiveness and toxicity. However, many patients fail to adhere to their dosing regimens. The inconvenience of frequent and consistent dosing deters some patients. Others struggle with the complexity of multi-drug regimens, as each drug must be taken at a specific time. It can be difficult for patients, especially those of the elderly population, to remember to take their medication at these specific times or even at all. Lack of patient adherence results in fluctuating drug plasma levels that are not maintained in the therapeutic range, leading to greater risk for side effects, disease progression, and increased hospital visits. [1] [2] [3]

Novel drug delivery systems, such as injectable implants, have been developed with numerous advantages over traditional oral delivery platforms. One such class of injectable systems are in situ forming implants (ISFIs), first developed by Dunn et al. [4] ISFIs are a liquid solution of polymer and drug that can be injected via a small-gauge needle into the body. Once in the body, the solution solidifies into a solid drug-eluting implant that can release drug for an extended period of time. [4] Sustained release of drug from a single injection greatly reduces the frequency of administration, simplifying dosing regimens and improving patient adherence. [5] Drug release from the implant can be tuned to maintain drug plasma levels within the therapeutic window of the drug for prolonged periods of time. [6] Additionally, this type of parenteral administration is especially beneficial for drugs with a narrow therapeutic index or drugs with low oral bioavailability, like proteins and peptides. [7] Another advantage is the ability to localize therapy directly to a target site in order to reduce systemic involvement and reduce side effects. [8] [9] [10]

A key feature of ISFIs is their ability to solidify in situ, allowing relatively noninvasive administration as a low viscosity solution. For phase-sensitive ISFIs, solidification occurs as a result of polymer precipitation due to solvent/nonsolvent exchange. [11] [12] These implants consist of a biodegradable, hydrophobic polymer that is dissolved in a water-miscible, biocompatible organic solvent that can be mixed with a drug. When this polymeric solution comes into contact with an aqueous environment, the organic solvent diffuses out of the polymer solution while water simultaneously begins to diffuse into the mixture, causing the polymer to precipitate. The result of this phase inversion process is the formation of a solid drug-eluting depot that releases drug for an extended period of time. [13] [14] The drug release profile follows a characteristic three-phase pattern beginning with a period of burst release as the solvent initially diffuses out, followed by a period of diffusion-controlled release, which occurs before the polymer begins to degrade. Finally, as a consequence of polymer degradation, there is a period of enhanced degradation-facilitated release. [13] [15] The release profile of ISFIs can be tuned by altering the rate of solvent/nonsolvent exchange and polymer degradation. [13] These parameters control the implant microstructure, which impacts the diffusivity and corresponding drug release.

A number of techniques have been developed to characterize the phase transition of these polymers including optical, spectroscopic, and medical imaging based strategies. [16] [17] [18] Medical imaging provides a way to track changes in the implant in situ over time. [19] Medical imaging modalities include ultrasound, x-ray computed tomography (CT), and magnetic resonance imaging (MRI). Ultrasound has been used to study the effects of varying polymer molecular weight [20], drug properties [21], additives [22], and the injection site [23] [24] on polymer precipitation with the benefit of obtaining real-time images of implant shape and size [25]. Micro-CT has been used to measure implant porosity and pore size in vitro. [26] Finally, benchtop-MRI has been used to produce images of ISFIs in vivo over seven weeks to visualize solvent exchange and implant disappearance. [27] In addition to structural information, MRI also has great potential to provide novel functional information about ISFIs.

MRI uses a magnetic field and radiofrequency pulses to generate an image nondestructively and noninvasively, without the use of ionizing radiation. In addition to collecting anatomical information, MRI can be used to quantify the Brownian diffusion of water molecules within an imaging voxel using a technique called diffusion-weighted imaging (DWI). [28] Different rates of diffusion in free versus restricted mediums allow for image contrast. Diffusion gradients are used so that more mobile protons produce less signal than stationary protons. Changing the strength and timing of these gradients, via modification of the b-value, results in control over the amount of diffusion weighting. [28] The b-value is set by the operator, where a higher b-value increases the degree of diffusion weighting.

DWI can be used to create a spatial-temporal map of diffusivity. Not only are images obtained for the visualization of implant shape and size over time, but DWI provides additional functional information by allowing for quantification of the diffusivity in the implants over time. The goal of the current study was to use DWI to noninvasively and nondestructively quantify implant diffusivity over time both in vitro and in vivo, which can be used to give information about drug release behavior without removal and destruction of the implants. Drug release, polymer erosion, and polymer degradation studies were done to characterize ISFI behavior in vitro over 21 days. A lower molecular weight (15 kDa) as well as a higher molecular weight (52 kDa) poly(lactic-co-glycolic) acid (PLGA) were used to form the implants to provide a comparison between a faster-eroding (15 kDa) and a slower-eroding (52 kDa) implant. Fluorescein was chosen as the mock drug due to its similar size to small molecular weight drugs and the prior characterization of its release kinetics from ISFIs. A DWI protocol was developed to noninvasively quantify ISFI diffusivity in vitro over 21 days. Scanning electron microscopy (SEM) was performed to evaluate the microstructure through traditional destructive methods. Lastly, to demonstrate translational potential, DWI was performed in vivo over five days.

2. Materials and Methods

2.1. Materials

50:50 poly(lactic-co-glycolic) acid (PLGA) with an acid endcap and molecular weight of 10–15 kDa (2A) was obtained from Akina, Inc. 50:50 poly(lactic-co-glycolic) acid (PLGA) with an acid endcap and molecular weight of 52 kDa (4A) was obtained from Evonik Industries. N-methyl-2-pyrrolidone (NMP) was obtained from Fisher Scientific. Fluorescein disodium salt (MW 376.28) was obtained from Acros Organics. All supplies were used as received.

2.2. Preparation of Polymer Solutions

PLGA, NMP, and fluorescein were combined in a 39:60:1 mass ratio. Fluorescein was first dissolved in NMP, then PLGA was added and dissolved in the solvent/drug mixture by stirring overnight. Solutions were used within seven days of preparation.

2.3. Drug Release Studies

First, implants were formed by injecting 60 μL of the polymer solution into 10 mL of phosphate buffered saline (PBS) in a 20 mL scintillation vial. The implants had an average mass of 29 mg and were kept at 37°C on a shaker at 100 rpm. Samples were taken from the bath-side solution at 0.25, 0.5, 1, 2, 4, 6 h after implant formation and then again at 1, 2, 3, 4, 5, 6, 7, 10, 14, 17, and 21 d. To maintain sink conditions, the bath solution was completely replaced with fresh PBS at these time points. After 21 d, the implants were dissolved in 5 mL of 2M NaOH to determine residual drug mass. The fluorescence of each sample was quantified using a SpectraMax M5 microplate reader with an excitation wavelength of 485 nm and an emission wavelength of 525 nm, and results were compared to a standard curve to obtain the mass of fluorescein released.

To distinguish between the three characteristic phases of drug release from the implants, a one-way ANOVA with Tukey’s multiple comparisons test was performed. This test allowed for groups of timepoints to be distinguished from one another based on statistical significance at a confidence level of 95%. The groups were associated with the burst, diffusion, or degradation phase of release. The slope of the cumulative release curve over the corresponding set of timepoints was taken in order to quantify the percent released during each phase.

2.4. Erosion Study

The initial mass of each implant was recorded immediately after the 60 μL polymer solution was injected into the PBS bath. At each time point (1, 3, 7, 10, 14, 17, and 21 d after implant formation), the implants were removed from the bath solution, frozen at −80°C, and then lyophilized for four days. The final, dry weight was then recorded. To maintain sink conditions, the bath solution was replaced every 24 h for the first 7 d and then at each subsequent time point (at 10, 14, 17, and 21 d). The implant’s dry mass was divided by its initial mass to plot the erosion profile.

2.5. Degradation Study

To study changes in the polymer’s molecular weight over time, the lyophilized implants from the erosion study were used. After recording their dry weight for the erosion study, the implants were stored at −80°C until analysis using triple detector gel permeation chromatography (GPC-TD). The GPC-TD system consisted of an Agilent 1260 Infinity II HPLC connected to Dawn Heleos II (MALLS) coupled to Dynapro Nanostar DLS via optical cable, Optilab T-rEX (RI detector) and Viscostar III viscometer operated by Astra 7 software. GPC analysis was performed by injecting 50 μL of 2.5 mg/mL polymer solution. Separation was performed with a linear gradient column (Tosoh Bioscience LLC, TSKgel GMHHR-L, 7.8 mm × 30 cm) at 0.6 mL/min flow of acetone. The separation was performed in acetone due to its greater dn/dc for PLGA as compared to tetrahydrofuran, which is typically used for GPC analysis. In addition, individual dn/dc values were experimentally determined for PLGA based on the L:G ratio. This was performed utilizing a batch method measurement in Astra 7 software using Optilab T-rEX. The obtained dn/dc values used for Astra 7 software calculations allow greater accuracy in light scattering data used for molar mass determination. The number average molecular weight (Mn) over 21 d was normalized to the Mn of the implant at 1 d to plot the degradation profile.

2.6. Diffusion-weighted MRI (DWI)

Implants at each of the time points were placed in a 3D-printed insert designed to center the implants in the MRI scanner (Supplemental Figure 1). Prior to imaging, implants were kept at 37°C on a shaker at 100 rpm. DWI was conducted using a Bruker BioSpec 70/30 USR 7T Preclinical MRI system and Bruker RF RES 300 ¹H 075/040 QSN TR rat head/mouse body volume coil. A standard diffusion-weighted spin echo protocol was utilized (TE=17.5 ms, TR=2500 ms, FOV=35×35 mm², slice thickness=0.80 mm, b=0,1000 s/mm²). Implants were imaged at the following time points: 0.25, 1, 2, 4, 6, 24, 48, 72, 96, 120, 144, 168, 240, 336, 408, 504 h. The same implant was not imaged at each time point, rather a new implant was created specifically for each time point.

2.7. DWI Analysis

2.7.1. Creation of Apparent Diffusion Coefficient Maps

The raw diffusion data were used to create apparent diffusion coefficient (ADC) maps of the implants. The Stejskal-Tanner equation [Eq.1] quantifies the signal loss due to proton movement [29]:

$$S(b)=S_0{e}^{-bD}$$ [Eq.1]

where S(b) is the signal received at a certain b-value, S₀ is the signal without diffusion weighting (b=0 s/mm²), b is the b-value, and D is the diffusion coefficient. This equation can be rearranged to solve for the diffusion coefficient, referred to as the apparent diffusion coefficient (ADC) to indicate that it represents the reduction of multi-directional diffusivity in a volume element to a single average:

$$ADC=-\frac{1}{b}\ln (\frac{S_b}{S_0})$$ [Eq.2]

First, the Bruker FID files were read into Matlab as k-space data, which were reconstructed into DWI images via Inverse Fast Fourier Transform (IFFT). The ADC maps were then obtained via Eq.2, where b = 1000 s/mm², S_b are DWI images of b = 1000 s/mm², and S₀ are the baseline T₂-weighted images with b = 0 s/mm². The ADC maps had a resolution of 128×128 pixels with each pixel having a width of 0.273 mm. Only one diffusion direction was applied because the spherical polymer was assumed isotropic, and in a multi-directional DWI spin echo study, the diffusion coefficients in all directions appeared similar.

2.7.2. Calculation of Mean Diffusivity

From the ADC maps, the implant was selected as the region of interest (ROI) for calculating mean diffusivity (MD). MD was calculated as the average diffusion coefficient of the selected pixels. Two different methods were used to select the implant ROI from the surrounding water background. The first method was to manually select the ROIs using a custom Matlab code. Using the first method, pixels comprising the entire implant (shell and core) were included, resulting in a global MD measurement. The second method was to automatically segment the ROI by setting a threshold diffusivity value to eliminate background values. All pixels greater than or equal to the threshold value were automatically segmented out of the image so that the ROI remained while the free water (with a higher diffusivity) was eliminated. Automatic ROI segmentation is a much quicker process. However, threshold-based segmentation does not allow for a global measurement of the implant as any water within the implant would be eliminated with the background. Thus, segmentation only provides a measurement of the polymer-rich phase. Calculating the global MD of the entire implant and the MD of the polymer-rich domains provide insight into both the polymer-rich and polymer-lean domains.

2.7.3. Evaluating Spatial-Temporal Changes in Diffusivity

The ADC maps were also used to evaluate diffusivity as a function of implant radius. This method provided more spatial information as compared to just the single averaged MD value. A custom Matlab code was used for this analysis. The implant ROI was manually selected. The ROI was then eroded in layers from the outside inward. Each layer had a thickness of one pixel with the MD value then calculated for each layer of pixels produced. Since the implants varied in size, the pixel distances were normalized from 0 to 1 to allow for comparison between implants. The implant center was defined as 0, and the last row of pixels comprising the implant shell was defined as 1. An empirical relationship was developed to compare the spatial-temporal profiles of diffusivity. The data were fit to a four-parameter logistic curve using Matlab.

2.8. Scanning Electron Microscopy (SEM)

At selected time points after MRI scanning, implants were freeze-fractured using dry ice. The fractured implants were then lyophilized for 4–5 d prior to mounting on aluminum stubs and sputter-coating with platinum for 60 s using a Cressington 208 HR sputter coater for an estimated platinum coating thickness of 3–4 nm. Imaging was performed using a FEI NovaNanoSEM and a Quanta 3D FEG SEM with a spot size of 3, a voltage of 5.00 kV, and a working distance of approximately 5 mm.

2.9. SEM Image Analysis

ImageJ 1.52 (NIH, Maryland) was used to analyze the implant microstructure from SEM images. The shell thickness of the implant was measured using the straight-line measurement tool at various points around the shell and taking the average of the measurements. The interior pore size of the implants was measured by cropping out three different regions of the implant’s interior and using the straight-line measurement tool to measure the diameters of the pores within each region. Pore diameters from each of the three regions were averaged.

2.10. Ultrasound Imaging

Implants were formed by injecting 60 μL of the polymer solution into 10 mL of phosphate buffered saline (PBS) in a 20 mL scintillation vial. The implants were kept at 37°C on a shaker at 100 rpm. The bath solution was replaced every 24 h for the first 7 d and then at 10, 14, 17, and 21 d. At each time point (1, 4, 7, 10, 14, and 21 d after formation), the implants were removed from the bath solution and placed into a PBS-filled well in an agarose phantom (2% w/v in PBS). A Vevo 2100 Ultrasound Imaging System (FujiFilm VisualSonics Inc., Toronto Canada) with a 40 MHz transducer (MS550-D) was then used to obtain images of the implant. Images were taken in B-mode at a gain of 22 dB at the center of each implant. After each imaging time point, the implants were placed back into 10 mL of PBS in their corresponding scintillation vials until the next imaging session so that the same implants could be imaged over time.

2.11. In vivo Studies

2.11.1. ISFI Injection

All animal studies were performed following protocols approved by the Purdue Animal Care and Use Committee. Three 4-week old male C57BL/6 WT mice were bred from mice originally received from The Jackson Laboratory. Polymer solution was prepared as already described in Section 2.2 and used within three days. For the in vivo studies, only the 52 kDa PLGA was used. To perform the injection, the mice were anesthetized using 1.5% isoflurane with an oxygen flow rate of 2 L/min. Fur was trimmed with an electric shaver prior to application of a 10% Povidone-iodine solution and then wiped with a sterile alcohol prep pad. For each implant, approximately 100 μL of polymer solution was injected subcutaneously using a 23-gauge needle to form an implant of approximately 90 mg (range 64–121 mg). A larger volume of solution was injected in vivo as compared to the in vitro experiments to account for the loss of polymer solution in the dead space of the needle. Two implants were injected per mouse, one over each flank.

2.11.2. Imaging

At set time points (1h, 6h, 24h, 72h, and 120h after injection), DWI was performed on each mouse. The mice were anesthetized with 2.5% isoflurane with an oxygen flow rate of 250 mL/min prior to transfer into the Bruker BioSpec 70/30 USR 7T Preclinical MRI system. Ophthalmic ointment was applied, and a respiratory monitor was attached. The respiratory rate was continuously monitored using a Monitoring and Gating System from Small Animal Instrument, Inc. (SAII), and the percent of isoflurane in oxygen was adjusted to maintain a respiratory rate of about 60 respirations/min. A heater was placed in the MRI system to maintain the surrounding bore temperature at 26°C. The Bruker RF RES 300 1H 075/040 QSN TR rat head/mouse body volume coil was used with a standard diffusion-weighted spin echo protocol (TE=17.5 ms, TR=2500 ms, FOV=30×30 mm², slice thickness=0.80 mm, b=0,1000 s/mm²). A b-value of 1000 was chosen because high b-values minimize any effect of perfusion on the diffusion measurements. [30] In contrast to in vitro imaging, several slices were obtained through each implant instead of a single slice through the center. Additionally, a trigger was used to gate the imaging acquisition based on the respiratory rate. After imaging, mice were monitored continuously during recovery from anesthesia, placed on a 37°C heating pad, and injected with 0.5 mL warm saline to speed recovery. At the completion of the study, the mice were euthanized with CO₂ gas followed by cervical dislocation. Implants were then resected and stored at −80°C until analyzed using SEM imaging as described in Section 2.8.

2.11.3. Analysis

For analysis of in vivo DWI results, ADC maps were created as described in Section 2.7.1. An ADC map was created for each of the seven slices taken through each of the six implants at each of the five timepoints (Supplemental Figures 5–10). In order to calculate MD, the implant was selected as the ROI from the ADC map. Because the implant was more difficult to visualize in vivo, two researchers independently hand-selected ROIs in triplicate from each ADC map so that an average of the six MDs was used to represent the MD of that ROI. A custom Matlab code was used for the analysis, and MRI localizer images were used to guide ROI selection. Slices with no visible implant were not used in ROI analysis.

Both the MD and cross-sectional area varied depending on which slice was chosen for analysis. To determine an average MD value for each implant, the weighted average (by pixels) of MD was calculated from each slice taken throughout the implant excluding the topmost and bottommost slices due to poor visibility in those outermost slices. This was repeated for each of the six implants at all five timepoints. Then, the average MD at each timepoint was determined by averaging the MD values from each implant at that timepoint.

2.12. Statistical Analysis

Minitab 16.1.0 statistical software was used for all analyses. To test for statistical significance between different timepoints, a one-way ANOVA with Tukey’s multiple comparisons and confidence level of 95% was used. Tukey’s multiple comparisons allowed for the grouping of timepoints that were not statistically different from each other. To test for statistical significance between two values at the same timepoint, a 2-sample t-test at a confidence level of 95% was used. Resulting p-values less than 0.05 were considered significant. A sample size of n=5 was used in the drug release studies, a sample size of n=6 was used for the in vivo studies, and a sample size of n=3 was used in all other experiments. All values were reported as mean ± standard deviation.

3. Results

3.1. In vitro Drug Release

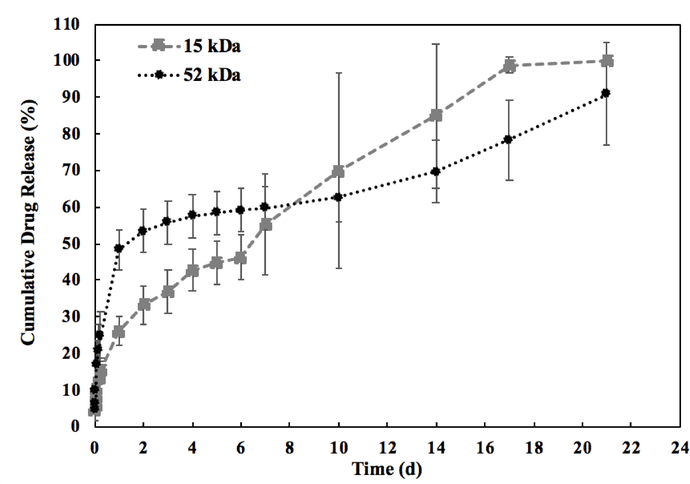
Figure 1 shows the cumulative drug release over 21 d for both 15 kDa and 52 kDa implants. For both implants, the burst release phase was completed during the first 24 h after implant formation. Within 24 h, the 52 kDa implant released 48.3 ± 5.31% of total drug, which was significantly greater than the 26.2 ± 3.75% of total drug released from the 15 kDa implants (p<0.05). Following the initial burst, a period of diffusion-facilitated release was observed. This phase lasted from 24 h to 10 d post-formation for the 52 kDa implants during which 1.39 ± 0.45% of drug was released per day. Comparatively, the 15 kDa implant had a shorter diffusion-facilitated release phase lasting from 24 h to 7 d post-formation, in which a significantly higher daily release was observed relative to the 52 kDa formulation at 4.33 ± 2.17% per day (p<0.05). Degradation-facilitated release began earlier for 15 kDa implants than for the 52 kDa implants (after 7 d and 10 d respectively). The degradation-facilitated release phase for the 15 kDa formulation occurred between 7 d and 14 d post-formation, releasing 4.21 ± 2.20% of drug per day. The higher molecular weight polymer degraded more slowly with degradation-facilitated release lasting from 10 d to 21 d post-formation for the 52 kDa implants. During this period, 2.60 ± 1.01% of drug was released per day. No statistical difference was observed during degradation-facilitated release between the 15 kDa and 52 kDa formulations. These values are summarized in Table 1.

Figure 1: Cumulative mass release of fluorescein from the implants.

Release measured over 21 d with black circles indicating the 52 kDa implant and gray squares indicating the 15 kDa implant (n = 5, error bars are mean ± SD).

Table 1:

Quantification of average fluorescein release during each release phase

Release	15 kDa	52 kDa
Burst (%)	26.2 ± 3.75*	48.3 ± 5.31*
Diffusion (%/d)	4.33 ± 2.17**	1.39 ± 0.446**
Degradation (%/d)	4.21 ± 2.20	2.60 ± 1.01

^*indicates significantly different burst release for 52 kDa vs. 15 kDa (p=0.0001)

^**indicates significantly different diffusion-facilitated release for 52 kDa vs. 15 kDa (p=0.041)

3.2. In vitro Implant Erosion and Degradation

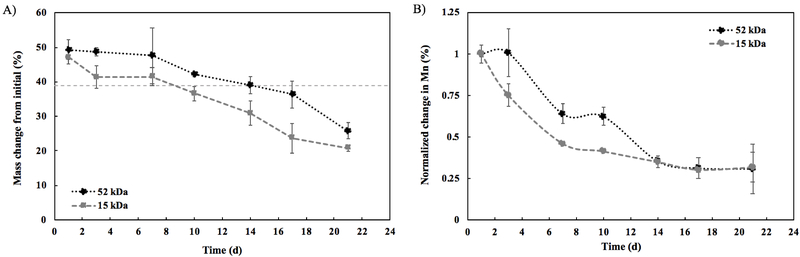
The polymer comprises 39% of the total implant mass initially. Thus, onset of erosion begins when the implant mass drops below the 39% polymer mass. A significant difference was observed for the onset of erosion between the two formulations. Erosion began between 14 d and 17 d post-formation for the 52 kDa implants, with an average residual mass of 39.1%±2.4% at 14 d dropping to 36.4%±4.0% at 17 d. For the 15 kDa implants, erosion began sooner, between 7 d and 10 d post-formation, with an average residual mass of 41.5%±2.6% at 7 d dropping to 36.6%±2.2% by 10 d (Figure 2A). Changes in the Mn of the polymer over time can be seen in the degradation profile in Figure 2B. The 15 kDa implant degraded more quickly due to its lower molecular weight. At 7 d, there was a statistically significant difference in Mn change between the two formulations. The Mn of the 15 kDa implant was reduced to 46.2%±0.50% of its initial value, while the Mn of the 52 kDa implant was still at 64.0%±6.0% of its initial value (p<0.05). The statistically significant difference continued at 10 d, but after 14 d there was no significant difference in Mn change between the two formulations. At 14 d, the Mn was 35.1%±3.3% (15 kDa) and 35.6%±1.0% (52 kDa) of its initial value.

Figure 2: Polymer erosion and degradation.

A) Polymer erosion over 21 d (n = 3, errors bars are mean ± SD); 39% line represents the theoretical mass of polymer in the implant. B) Polymer degradation over 21 d (n = 3, errors bars are mean ± SD). Change in molecular weight reported using number average molecular weight (Mn) and normalized to the Mn of the implant at day 1. For both, black circles represent the 52 kDa implant and gray squares represent the 15 kDa implant.

3.3. In vitro Diffusion-weighted Imaging (DWI)

3.3.1. Spatial Profile of Implant Diffusivity from ADC Maps

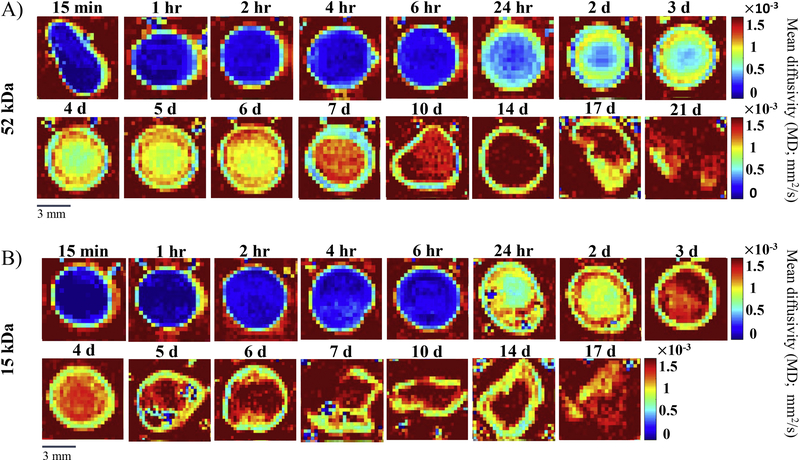
ADC maps were used to represent the scale of diffusivity values with each pixel corresponding to a diffusivity value at that specific position within the implant. Blue represented low diffusivity and red represented high diffusivity. ADC maps were obtained at 16 timepoints for the 52 kDa implants and at 15 timepoints for 15 kDa implants. Representative images for each timepoint are shown in Figure 3 with all other images presented in Supplemental Figure 2. The implants were imaged in an aqueous bath, which had a high diffusivity as evidenced by the red background in the ADC maps. Spatial-temporal changes within the implant were observed.

Figure 3: Apparent diffusion coefficient (ADC) maps of a representative implant at each time point.

A) ADC maps of the 52 kDa implant over 21 d. B) ADC maps of the 15 kDa implants over 17 d. Red represents high diffusivity, while blue represents low diffusivity. A different implant was imaged at each timepoint. The full set of ADC maps can be found in the supplemental material (Supplemental Figure 2).

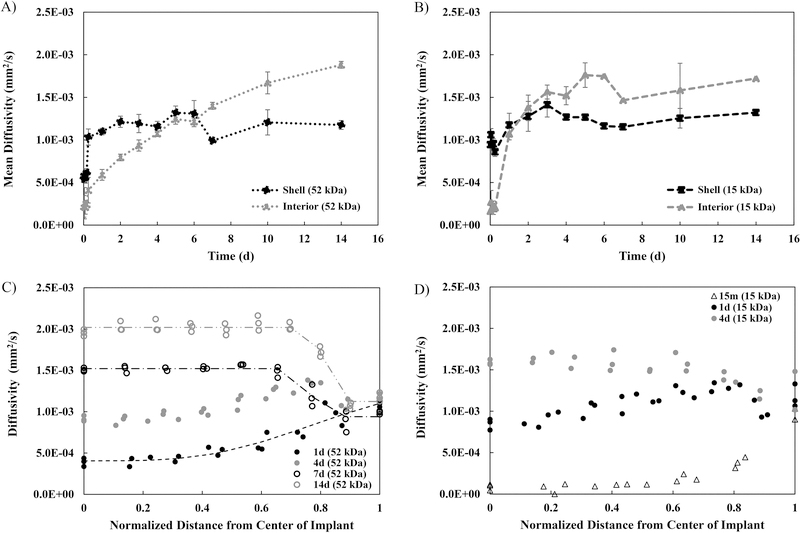
For the 52 kDa implant, we observed a distinct region of higher diffusivity around the implant interior that we interpret as the formation of a shell. The shell formation occurred within the first 15 min after exposure to an aqueous bath. After the first 4 h, this shell had a relatively constant diffusivity for the remainder of the 21 d study with an average shell diffusivity of (1.17 ± 0.128) × 10⁻³ mm²/s. No statistically significant differences in the shell diffusivity were observed after the 4 h timepoint. However, the implant interior showed marked changes in diffusivity over time (Figure 4A). Initially, during the first 6 h, low diffusivity was observed throughout the entire implant interior, averaging (0.268 ± 0.0813) × 10⁻³ mm²/s across the first five timepoints. No significant changes occurred within the first 6 h, but these initial timepoints did have significantly lower diffusivity than the diffusivity at any of the remaining timepoints. After 24 h, we observed the development of a diffusivity gradient in the implant’s interior (Figure 4C). At 24 h, there was an increase in the implant diffusivity from a minimum diffusivity value of (0.390 ± 0.0503) ×10⁻³ mm²/s at the center of the implant to a maximum diffusivity of (1.10 ± 0.0383) ×10⁻³ mm²/s at the shell. Interestingly, after 2 d, a high diffusivity region developed between the shell and the implant interior domain. This region can be qualitatively visualized in Figure 3A as a ring of higher diffusivity from 2 d to 6 d and quantitatively shown as the peak in diffusivity ((1.36 ± 0.0196) ×10⁻³ mm²/s for the 4 d implants) occurring at approximately 80% of the maximal implant radius before the slight decrease in diffusivity at the shell (Figure 4C). This region of high diffusivity was lost by day 7. At 7 d, the diffusivity of the entire implant interior increased to (1.40 ± 0.0409) ×10⁻³ mm²/s, which was significantly greater than that of the shell ((0.990 ± 0.0197) ×10⁻³ mm²/s, p<0.05). After 7 d, there was a significant increase in the diffusivity of the interior domain (averaging (1.78 ± 0.150) ×10⁻³ mm²/s from 10 d to 14 d, Figure 4A) with the interior of the implants having a diffusivity equal to the aqueous bath by 14 d. Spatially, at 14 d, the diffusivity of the interior remained relatively constant ((1.88 ± 0.0400) ×10⁻³ mm²/s) until a significant drop in diffusivity at the shell ((1.18 ± 0.0524) ×10⁻³ mm²/s, p<0.05, Figure 4C). At further timepoints (17 d and 21 d), the 52 kDa implants were too fragile to handle and image without damaging them, so the diffusivity as a function of position within the implant could not be accurately determined at these timepoints.

Figure 4: Spatial profiles of diffusivity from the ADC maps.

MD of the shell compared to the interior over 14 d for A) the 52 kDa implants and for B) the 15 kDa implants. Diffusivity as a function of distance from the center of the implant at selected timepoints for C) the 52 kDa implants and for D) the 15 kDa implants. For all, errors bars are mean ± SD. Sample size of n=3 except for the following implants due to implant degradation: 52 kDa 21d (n=1), 15 kDa 6d, 7d, 14d (n=2), and 15 kDa 17d (n=1).

The diffusivity maps were parameterized using a four-parameter logistic curve fit that was applied to data from the diffusivity versus distance from the center of the implant analysis at selected timepoints (Table 2). Parameter A represents the minimum value that can be obtained, while Parameter D represents the maximum value Parameter B is Hill’s slope, which is the steepness of the curve at the inflection point (Parameter C). These curves visualized the increase in diffusivity in the interior of the implant over time from (0.590 ± 0.0633) ×10⁻³ mm²/s at 1 d to (1.88 ± 0.0400) ×10⁻³ mm²/s at 14 d, and the concurrent constant diffusivity, averaging (1.17 ± 0.128) ×10⁻³ mm²/s, in the shell (Figure 4C). The peak in the 4 d curve representing the ring of higher diffusivity prevented this curve from being fit to a four-parameter logistic model. Parameter B, the slope at the inflection point of the curve, showed a significant increase in steepness from 1 d (−4.10 ±1.35) to 14 d (154.6 ± 2.00). At 1 d, the diffusivity gradually increased from the center to the shell. At 7 d, the diffusivity dropped from the interior to the shell, and by 14 d, this drop in diffusivity from the interior to the shell became more drastic as evidenced by larger slope.

Table 2:

Parameters from 4-parameter logistic fit of diffusivity as a function of distance for the 52 kDa implant

Parameter		1 d	7 d	14 d
A	maximum	0.174 ± 0.299	1.53E-03 ± 1.84E-05	2.02E-03 ± 5.82E-05
B	slope	−4.10 ± 1.35	54.5 ± 52.8	154.6 ± 2.00
C	inflection pt.	4.11 ± 5.85	0.763 ± 0.022	0.804 ± 0.0029
D	minimum	4.11E-04 ± 5.53E-05	9.35E-04 ± 6.79E-05	1.12E-03 ± 3.82E-05
	R2	0.989 ± 0.0043	0.976 ± 0.016	0.987 ± 0.0073

For the 15 kDa implant, similar trends were observed. However, the increase in diffusivity over time was more rapid. Again, the formation of a shell was clearly observed. Figure 4B shows the quantification of the shell versus interior diffusivity for the 15 kDa implant over time. There was no statistically significant change in the diffusivity of the 15 kDa implant shell over time, averaging (1.15 ± 0.168) ×10⁻³ mm²/s. No statistical difference was observed between the diffusivity of the 15 kDa implant shell and 52 kDa implant shell. During the first 6 h, the average diffusivity of the entire implant interior remained low at a value of (0.209 ± 0.0462) ×10⁻³ mm²/s. Spatially, at 15 min, we see a consistently low diffusivity in the interior ((0.165 ± 0.121) ×10⁻³ mm²/s) with a sharp increase in diffusivity occurring right at the shell ((0.945 ± 0.0763) ×10⁻³ mm²/s) (Figure 4D). Between 6 h and 24 h, there was a significant increase in the diffusivity of the implant interior. Just as with the 52 kDa implant, a region of high diffusivity developed between the shell and implant interior. This region can be seen in Figure 3B as a ring of higher diffusivity in the 1 d and 2 d implants and is observed as the peak in diffusivity ((1.31 ± 0.0348) ×10⁻³ mm²/s at 1 d) occurring at approximately 80% of the maximal implant radius before the slight decrease in diffusivity at the shell (Figure 4D). After only 3 d, this region of elevated diffusivity was lost as the entire implant interior increased to a more uniform diffusivity ((1.56 ± 0.0820) ×10⁻³ mm²/s, Figure 4D). In addition, after 3 d, there was no statistically significant change in the diffusivity of the interior as it remained high with an average of (1.62 ± 0.119) ×10⁻³ mm²/s from 3 d to 14 d (Figure 4B). By 6 d, the 15 kDa implant became fragile to handle and image without destruction. Indeed, the 17 d implant was imaged in pieces and the 21 d timepoint could not be obtained.

3.3.2. Mean Diffusivity of Implants from ADC Maps

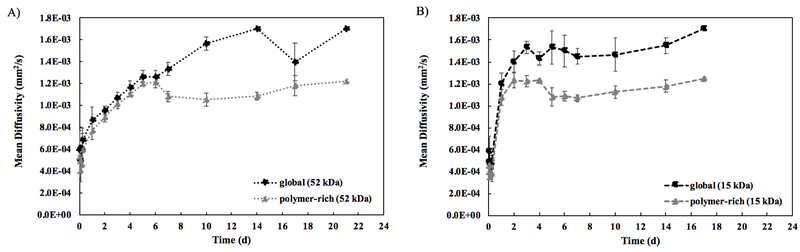
To quantify the diffusivity of an implant, the overall MD value was calculated for the complete implant at each timepoint. Diffusivity values were obtained for the entire implant (global, which includes the contribution from polymer-lean domains) and for only the polymer-rich regions of the implant (polymer-rich). Supplemental Figure 3 shows a schematic of the two different methods used to calculate these values. For the polymer-rich measurements, the polymer was isolated from the aqueous phase of the implants by automatically removing pixels at or above a threshold value matching the diffusivity value of the water background. For the 52 kDa implant, shown in Figure 5A, there was no statistically significant difference in MD calculated for the global versus polymer-rich portions through the first 6 d. Both show increasing diffusivity over time. At 6 d, the global MD average was (1.27 ± 0.0577) ×10⁻³ mm²/s, while the polymer-rich portion had an average MD of (1.22 ± 0.0556) ×10⁻³ mm²/s (p>0.05). However, at 7 d, the global MD value for the implant was significantly higher than the polymer-rich MD ((1.33 ± 0.0577) ×10⁻³ mm²/s compared to (1.08 ± 0.0512) ×10⁻³ mm²/s, p<0.05). The maximum difference was observed at 14 d, where the global MD value was (1.70 ± 0.00) ×10⁻³ mm²/s while the polymer-rich portion had a significantly lower MD of (1.08 ± 0.0351) ×10⁻³ mm²/s (p<0.05).

Figure 5: Mean diffusivity calculations comparing MD calculated from entire implant (global) to MD obtained from thresholding out the water, leaving only polymer-rich domains (polymer-rich).

A) MD over 21 d for the 52 kDa implants. B) MD over 17 d for the 15 kDa implants. For all, errors bars are mean ± SD. Sample size of n=3 except for the following implants due to implant degradation: 52 kDa 21d (n=1), 15 kDa 6d, 7d, 14d (n=2), and 15 kDa 17d (n=1).

The 15 kDa implants (Figure 5B) show a divergence between the global and polymer-rich MD values sooner than for the 52 kDa implants. By 3 d, the global MD value already was significantly higher than the polymer-rich MD value ((1.53 ± 0.0577) ×10⁻³ mm²/s compared to (1.23 ± 0.0503) ×10⁻³ mm²/s, p<0.05). The maximum difference was observed at 5 d with the global MD value at (1.53 ± 0.153) ×10⁻³ mm²/s, significantly higher than the polymer-rich MD at (1.08 ± 0.0834) ×10⁻³ mm²/s (p<0.05). From 6 d on, the difference between global and polymer-rich MD was no longer statistically significant due to low sample size, as some implants were too fragile to handle at later timepoints. Additionally, both measurements show a statistically significant jump in the MD between the 6 h and 1 d timepoints (averaging (0.430 ± 0.0832) ×10⁻³ mm²/s at 6 h compared to (1.14 ± 0.104) ×10⁻³ mm²/s at 1 d), rather than the slower, steadier increase in MD seen in the 52 kDa implants. For both the global and polymer-rich MD calculations, after the statistically significant increase in MD at 1 d, there is no statistically significant difference in MD across any of the remaining timepoints.

3.4. In vitro Implant Microstructure Analysis using Scanning Electron Microscopy (SEM)

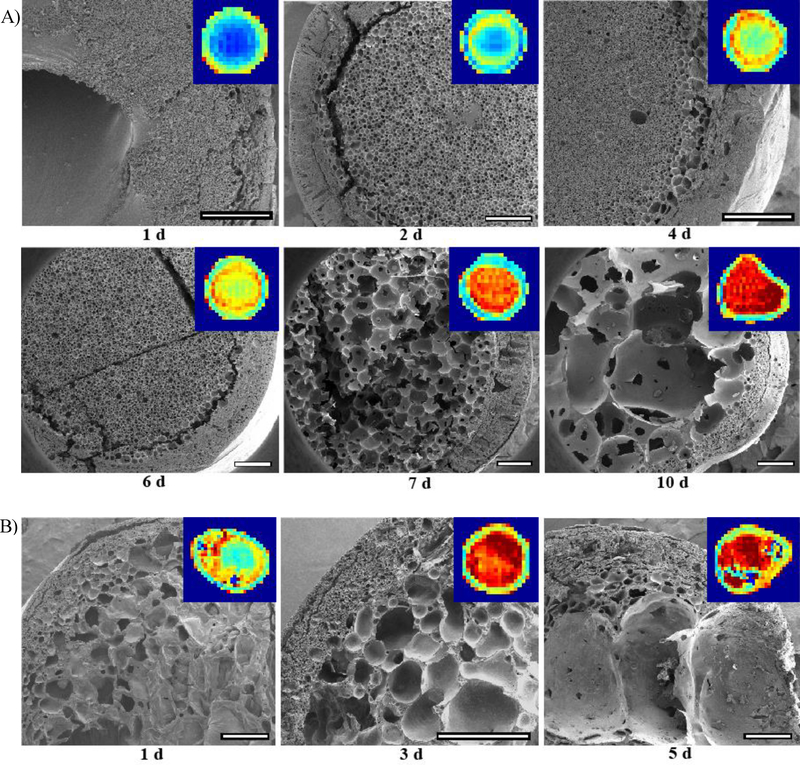
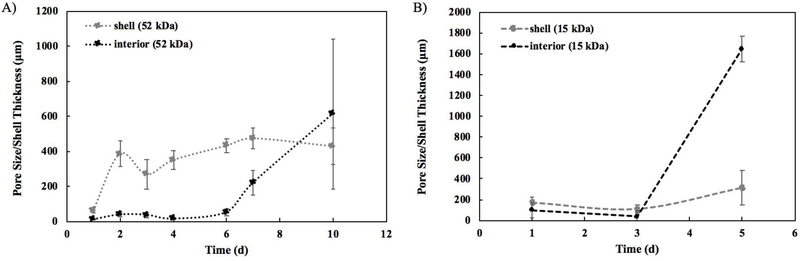
SEM images of implants were obtained from 1 d to 10 d post-formation for 52 kDa implants (Figure 6A) and from 1 d to 5 d post-formation for 15 kDa implants (Figure 6B). After the 10 d and 5 d timepoints, implants could not be processed for imaging without destroying the microstructure. SEM images for the 52 kDa implant at 1 d revealed the presence of a polymer-dense core with a poorly defined interconnected porous network and a small pore diameter, averaging 10.7 ±3.29 μm. The shell at 1 d was also significantly thinner than any later timepoints with a thickness of only 63.8±14.5 μm relative to an average thickness of 390.0±73.0 μm from 2 d −10 d (p<0.05) (Figure 7A). Over time, the solid polymer-dense core transitioned into an interconnected porous network, which was evident up to day 6. The average pore diameter from 2 d to 6 d was 35.7±15.4 μm. Additionally, the ring of higher diffusivity was visible in the ADC maps between the implant interior and shell from 2 d to 6 d. The pore diameter in this interface region was larger, though not significantly, than the interior at each timepoint from 2 d to 6 d with an average size of 57.9±14.2 μm. At 7 d, a marked change in microstructure was observed in the form of significantly larger pores (average diameter 216.1±71.3 μm), which continued to significantly increase in diameter at the 10 d timepoint (average diameter 612.7±428.2 μm). The shell, however, had a relatively constant thickness after 1 d, averaging 390.0±73.0 μm from 2 d to 10 d.

Figure 6: Comparison of ADC maps to implant microstructure.

SEM images inset with corresponding ADC map A) taken over 10 d for the 52 kDa implant and B) taken over 5 d for the 15 kDa implant. All scale bars are 500 μm.

Figure 7: Quantification of the pore diameter in the implant interior and quantification of shell thickness of the implants from the SEM images.

A) Analysis over 10 d for the 52 kDa implants. B) Analysis over 5 d for the 15 kDa implants. For all, errors bars are mean ± SD using samples taken from three separate regions of each image.

Larger pores were observed in the 15 kDa implant much sooner, from 3 d to 5 d, limiting the analysis to 5 d. Average pore diameter significantly increased from 91.8±70.2 μm at 1 d to 1649±122.3 μm at 5 d. The shell thickness also increased from an average of 140.9±57.4 μm from 1 d to 3 d to an average of 317.4±167.3 μm at 5 d (Figure 7B). For both 52 kDa implants and 15 kDa implants, ultrasound images were also obtained for further qualitative verification of implant structure (Supplemental Figure 4). For 52 kDa implants, erosion was observed at 7 d via ultrasound. By 14 d, the entire interior of the implant was hollow with only the shell remaining as visible on the ultrasound (Supplemental Figure 4). Evidence of erosion was already visible in the 15 kDa implants on the ultrasound by 4 d and progressed over the 21 days.

3.5. In vivo Validation

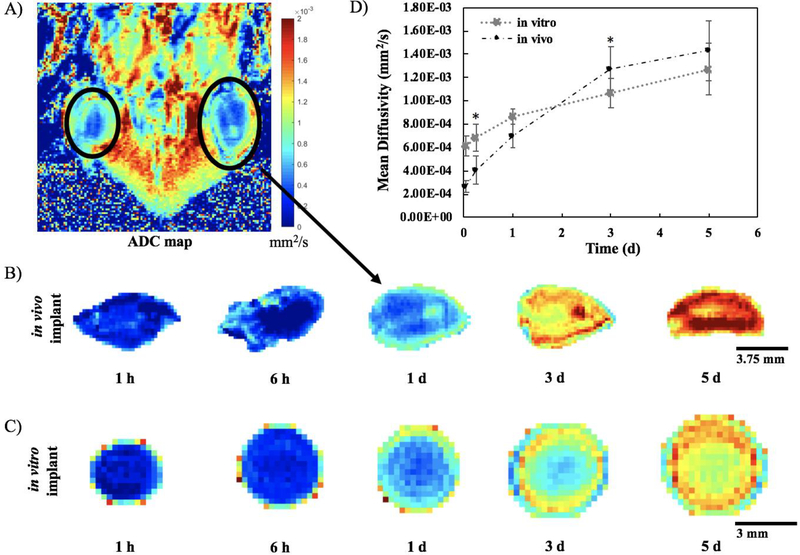
Three mice were imaged over five days after subcutaneous ISFI injection into both the right and left flanks. Only the 52 kDa implant was chosen to validate the technique due to its slower degradation rate. Figure 8A shows a representative ADC map from one slice through one mouse at the 1 d time point, while the complete set of in vivo ADC maps can be found in Supplemental Figures 5–10. Isolating a representative implant slice at each timepoint from one mouse demonstrates that a similar trend in implant diffusivity (Figure 8B) is observed relative to the in vitro ADC maps (Figure 3, with selected timepoints reproduced in Figure 8C). Both in vivo and in vitro implants were initially at a low diffusivity, evidenced by the dark blue on the ADC maps. In both implants, the diffusivity steadily increased over time as the ADC maps transitioned to orange and red, which was more noticeable in vivo. Correspondingly, quantifying the MD showed the same general trend in vitro versus in vivo (Figure 8D). Within the first day, the in vitro implants had a slightly higher MD than those formed in vivo (averaging (0.721 ± 0.132) ×10⁻³ mm²/s in vitro vs. (0.458 ± 0.0383) ×10⁻³ mm²/s in vivo), while the opposite is true at the 3 d and 5 d time points (averaging (1.17 ± 0.141) ×10⁻³ mm²/s in vitro vs. (1.35 ± 0.109) ×10⁻³ mm²/s in vivo). However, only the 6 h and 3 d timepoints had statistically significantly different MDs when comparing implants formed in vitro to those formed in vivo. At 6 h, the average MD for implants formed in vivo was (0.407 ± 0.125) ×10⁻³ mm²/s, which was significantly lower than the average MD for implants formed in vitro of (0.682 ± 0.114) ×10⁻³ mm²/s (p<0.05). By 5 d, the MD value had peaked to (1.43 ± 0.254) ×10⁻³ mm²/s in vivo and (1.27 ± 0.0577) ×10⁻³ mm²/s in vitro, but these values were not statistically different.

Figure 8: In vivo DWI analysis.

A) Representative ADC map from one slice through one mouse at 1 d. Top of the image is towards the head of the mouse and bottom of image is the tail. B) Representative in vivo implant isolated from the ADC maps at each timepoint. C) Representative in vitro implant isolated from the ADC maps at the same timepoints for comparison. D) Mean Diffusivity (MD) over 5 d comparing implants formed in vivo (n=6) versus those formed in vitro (n=3). (errors bars are mean ± SD). * indicates p < 0.05

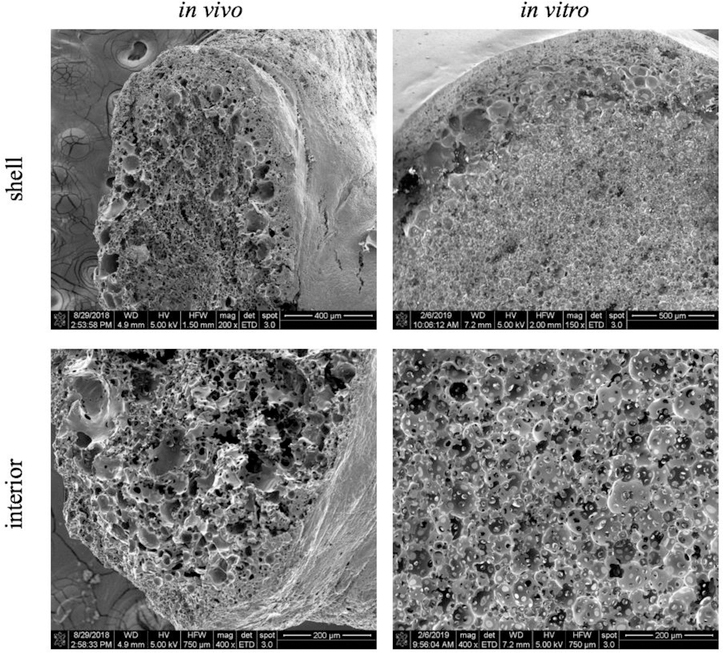
SEM images were taken after the completion of the in vivo study to investigate the microstructure of implants after 5 d in vivo. Comparison of implant geometry between implants formed in vitro and those formed in vivo shows that the spherical geometry observed in vitro is lost (Figure 9). Instead, implants have a more planar geometry when formed in vivo due to the constraints of the subcutaneous space. The shell and interconnected porous network that are easily visible in vitro are not nearly as developed in vivo. The in vitro implant shows relatively uniform circular pores in the interior surrounded by the implant shell. However, in vivo, pores are still present, but they are not as uniform or as interconnected as observed in vitro. The shell in vivo is also more variable in thickness.

Figure 9: Comparison of implant microstructure in vivo versus in vitro.

SEM images taken of the implant after the final 5d timepoint in vivo compared to an in vitro 5 d timepoint.

4. Discussion

In situ forming implants (ISFIs) provide sustained release of a drug after a minimally-invasive injection, which improves patient adherence, allows for delivery of drugs that cannot be administered orally, and facilitates local physical targeting to the site of action. Clinical use of ISFIs has been limited as many factors such as the drug properties and the injection site can affect drug release kinetics. MRI provides a noninvasive and nondestructive method by which functional properties of the implant can be characterized in situ. The focus of this study was to use DWI to characterize changes in the characteristic mass transport properties of the implants in situ over time by tracking spatial-temporal changes in diffusivity within the implant both in vitro and in vivo.

Our DWI results, visualized through ADC maps and quantified using MD, correlate well with the results from drug release studies and with images of the implant microstructure shown using SEM. During the first 24 h, both implants displayed the characteristic burst release phase. This burst occurs because initially, as the implant is forming, solvent rushes out into the aqueous environment taking the water-soluble mock drug fluorescein with it. Immediately after injection into an aqueous environment, a thin region of polymer precipitates, forming a shell that acts as a diffusion barrier to the aqueous environment and is the site of the initial solvent exchange process. Interestingly, the shell is initially observed as a ring of higher diffusivity around the implant interior. The high diffusivity of the shell is likely due to the exchange of solvent and water occurring at this barrier, resulting in polymer-lean pockets that have a higher diffusivity than the polymer-rich interior. Within the interior of the implants, the diffusivity is relatively constant at a low value immediately after injection into the aqueous environment, as seen on the ADC maps (Figure 3A) and quantified with MD (Figure 4A). The low diffusivity inside the implant can be attributed to the viscous nature of the unsolidified polymer/solvent solution, as water has not yet penetrated the core. Indeed, SEM images could not be obtained for these initial timepoints as the interior of the implant had not solidified enough to successfully freeze-fracture and mount for imaging. During burst release, we observed that that the 5 kDa implant’s cumulative drug release was significantly lower than that of the 52 kDa implant. We attribute the difference in burst to the greater affinity that the 15 kDa PLGA has for the solvent relative to the 52 kDa PLGA, which results in a decrease in the transport of drug with the solvent during shell formation for the 15 kDa implant. [13] Additionally, the higher molecular weight of the 52 kDa implant should accelerate the phase inversion process. The rapid phase transition would drive two distinct phenomena. First the rapid loss of solvent would help drive transport of drug out of the implant. Second, the formation of a more interconnected network of polymer-leans domains would allow for more rapid drug release compared to the lower molecular weight implant [15] [16].

Dramatic changes occurred in both drug release and implant diffusivity by 24 h. In terms of drug release, both implants entered into diffusion-facilitated release, measurable by a significant reduction in the amount of drug released per day. While 48.3% ± 5.31% (52 kDa) and 26.1% ± 3.75% (15 kDa) of the drug was released in the first 24 h, now only 1.39% ± 0.446% (52 kDa) and 4.33% ± 2.17% (15 kDa) of drug is released per day. This reduction occurs because the drug must now diffuse through the polymer network and is no longer transported with the solvent as during the initial phase transition process. The result is a slower and steadier release of drug from 1 d to 10 d (52 kDa) or 1 d to 7 d (15 kDa). The 15 kDa implant did release significantly more drug per day during this diffusion period, likely due to the high diffusivity of the 15 kDa implants relative to the 52 kDa implants. Additionally, within the 15 kDa implants, the degradation and erosion processes are more rapid than the 52 kDa implants (Figure 2B), which would also contribute to the increasing MD of the implant.

Correspondingly, the ADC maps also showed a dramatic difference starting at 24 h with an increase in diffusivity throughout the entire 15 kDa implant and not just at the shell. While the shell is still visible as a diffusion barrier, the increased interior diffusivity indicates an increase in the number of polymer-lean/water-rich pores within the surrounding polymer-rich phase of the implant. We hypothesize that due to the high critical water concentration required to drive polymer precipitation for the 15 kDa polymer implants [30], there is a delay in phase transition that allows for the polymer-lean droplets to aggregate. The resultant droplet aggregation results in a network of large interconnected pores, which ultimately leads to the increase in diffusivity of 15 kDa implants relative to implants made with 52 kDa PLGA. Furthermore, after 24 h, both the 15 kDa PLGA implants and the 52 kDa implants retain approximately 10% of the initial solvent mass (Figure 2A). However, the 15 kDa PLGA implants lose an additional 6% of their initial mass within 48 h after formation, which we hypothesize to be primarily solvent. The formation of an interconnected network of large pores would allow for the rapid solvent loss observed in the erosion study (Figure 2A) and would ultimately lead to polymer-lean domains that have a viscosity that approaches water. Thus, the polymer-lean domains would have a higher diffusivity than the more solid polymer-rich domains. By day 6, implants fabricated with 15 kDa PLGA started to break apart when handled. Thus, measurements could not be obtained in triplicate for many of the timepoints after 6 d. For the 15 kDa implants, SEM images at 5 d already showed the development of large pores matching the large regions of high diffusivity shown on the 5 d ADC maps. Based on our studies, DWI studies using low molecular weight polymers would benefit from higher sampling rates over the course of the first 24 h.

For the 52 kDa implants, during the diffusion-controlled drug release phase, there is a steady increase in MD over time. From the SEM images, we see a highly porous microstructure, although there is no statistically significant change in pore size during this 1 d to 6 d period. We hypothesize that the observed diffusivity map is the result of the difference in the critical water concentration for the 52 kDa PLGA implants. [31] Similar to the 15 kDa implants, approximately 50% of the solvent mass is lost within the first 24 h after introduction of the implant to the non-solvent (Figure 2A). However, the 52 kDa implants have a significantly lower critical water concentration than the 15 kDa implants, which we hypothesize drives a more rapid rate of polymer precipitation and ultimately leads to stabilization of smaller pores, which would lower the MD relative to the 15 kDa implants. No significant change in mass is observed for the 52 kDa implants until after 7 d (Figure 2A), which indicates that solvent is being retained within the polymer network. Interestingly, there is not a significant change in pore size throughout the implant volume, however we do observe a diffusivity gradient (Figure 6 and 7). We hypothesize that the diffusivity gradient develops as a result of the residual solvent. After the initial phase inversion, the concentration of solvent would be highest at the center of the implant. The elevated solvent concentration would lead to polymer-lean domains that have a higher polymer content and viscosity. The higher viscosity would ultimately decrease the diffusivity of the polymer-lean domains at the center of the implant. Over time, the solvent would diffuse from the center of the implant and would be more uniformly distributed throughout the implant. As a consequence, the viscosity of the polymer-lean domains would decrease, resulting in the observed increase in the MD of the implant over time.

An additional feature visualized on the ADC maps between 2 d to 6 d post-formation is the development of a ring of elevated diffusivity between the implant interior and shell. Measuring the diffusivity as a function of radius reveals the corresponding peak in diffusivity at approximately 80% of the maximum implant radius, as measured from the center of the implant to the shell. Likely this region represents a transition zone in the implant microstructure. Water has reached a critical concentration in the solvent/polymer mixture so that phase separation is more complete in this region resulting in a larger number of polymer-lean pores with a greater amount of water as compared to solvent. The shell remains at a lower diffusivity as it is the barrier to diffusion, while the interior core has had less exposure to the surrounding water. Indeed, at 2 d, the SEM image did show a central core of nonporous polymer still remaining. We hypothesize that an additional feature creating this transition zone is an accumulation of H⁺ ions at the shell/interior interface as H⁺ ions from degradation products in the interior of the implant hit the diffusion barrier of the solidified shell. The resultant accumulation of H⁺ ions would lead to enhanced autocatalytic degradation, causing this region to have larger pores than the interior of the implant and thus an increased diffusivity.

Following this period, the 52 kDa implants all showed a marked change at day 7, visible both in the ADC maps and in the SEM images. The ADC maps showed the interior of the implant as red, indicating high diffusivity. The 7 d timepoint is the first timepoint where the diffusivity within the implant interior is higher than the diffusivity of the shell, remaining relatively constant as a function of distance from the center of the implant until dropping off at the shell. Consistent with these results, the SEM image shows a sudden increase in the diameter of the pores, significantly larger than at 6 d, as it is clear the implant has started to degrade by day 7. Lastly, 7 d marks the divergence of the implant’s global MD value from the MD value associated with the polymer-rich phase. The global MD is continually increasing as the diffusivity within the implant is increasing to that of the water bath outside the implant. However, the MD of the polymer-rich portion has decreased from the maximum value observed at 6 d because now only the shell is where most of the solid polymer remains. The divergence between the global and polymer-rich MD values indicates that a significant amount of the implant interior has degraded, resulting in a large free volume within the implant interior. Thus, mass transport occurs more freely because of the larger pores that result. These changes that occurred at 7 d continue to intensify through 14 d as the implant continues to degrade and the diffusivity of the interior continues to increase. At 10 d, the MD within the implant is even higher, correlating with significantly larger pores visualized with SEM. At 14 d, the interior of the implant on the ADC map visibly appears to have the same diffusivity as the water bath background. Only the lower diffusivity of the shell allows the implant to be visualized. Indeed, the 14 d implant was hollow when freeze-fractured so that it could not be successfully prepared for SEM imaging, and ultrasound imaging also revealed a hollow interior. By 17 d and 21 d, the 52 kDa implant, well into degradation-facilitated release by this point, would easily break into pieces, limiting the information that could be obtained from DWI.

To ensure that the DWI technique could translate in vivo, where it has the most potential as a noninvasive visualization and quantitative technique, we evaluated implants in a murine model. While it was fairly straightforward to detect the implant when scanning in the MRI, it was much more difficult to delineate the boundaries of the implant after the data was reconstructed into the ADC maps. Of course, this was as expected since the implant was no longer in a freely diffusing water bath with high diffusivity. Rather, variable diffusivity values were observed throughout the mouse. Still, we were able to demonstrate that DWI could be performed successfully, as the implant could still be visualized and selected as the ROI for MD calculations. One imaging slice was taken through the center of the implants in vitro, but because the center was less apparent in vivo, several slices were taken throughout the implant volume. Diffusivity did vary, at least slightly, throughout the volume of the implant, so a weighted average of MD by number of pixels in each slice was used for the purposes of comparison to in vitro data. After 5 d in vivo, an increase in diffusivity was observed that corresponded well with the in vitro data. While the in vivo and in vitro implants had fairly similar diffusivities, a difference could be seen in the microstructure of the implants (Figure 9). The in vitro implants have a more defined and interconnected porous network, while the in vivo implants are more heterogeneous in their porosity and structure. A probable reason for this difference is a lack of water surrounding the implants formed in the subcutaneous space as compared to the in vitro implants formed in a PBS bath. As water is a vital part of the solvent exchange process, a difference in the amount of water present in vivo versus in vitro would certainly have an impact on the dynamics of the phase inversion process. Having similar diffusivity values in the in vivo versus in vitro implants despite the difference in microstructure show that microstructure and pore size are not the only factors affecting diffusivity within the implant. The viscosity within the pores, for example, would also play a major role in dictating the release of drug from the implants.

5. Conclusion

Diffusion-weighted imaging has been shown to add valuable functional information to characterize the in situ behavior of ISFIs. These diffusivity measurements provide noninvasive insight into transport within the microstructure of the implant. Future work involves combining this functional information with more detailed structural information, such as porosity measurements obtained from μ-CT imaging or ultrasound, to provide an even greater degree of characterization. The end goal of characterization is to help expedite clinical translation of ISFIs by providing a more thorough and quantitative understanding of how tuning parameters of the implant will affect drug release and reproducibility. Additionally, DWI itself has potential to provide more information, such as an analysis of changes in diffusivity throughout the volume of the implant rather than just a single slice. One limitation of the DWI analysis done in this study was the eight-minute scan time required for each diffusion-weighted spin echo sequence. Additional efforts to optimize the DWI sequence used or even to exploit the versatility of MRI to gain other novel information about ISFIs provide future avenues to investigate. Despite these limitations, DWI has the potential to inform models to drive the rational design of implants. DWI also has the potential to assess the performance of ISFIs after injection in humans, by monitoring the device noninvasively to ensure it is performing optimally based on the stage of degradation of the implant.

Highlights.

• In situ forming implants (ISFIs) are injectable, long-acting drug release depots

• Diffusion-weighted MRI was used as a novel modality to noninvasively analyze ISFIs

• DWI can quantify spatial-temporal changes in diffusivity within ISFIs in situ

• DWI gives insight into transport properties within ISFIs both in vitro and in vivo