EEGSourceSim: A framework for realistic simulation of EEG scalp data using MRI-based forward models and biologically plausible signals and noise

Abstract

Background

Electroencephalography (EEG) is widely used to investigate human brain function. Simulation studies are essential for assessing the validity of EEG analysis methods and the interpretability of results.

New Method

Here, we present a simulation environment for generating EEG data by embedding biologically plausible signal and noise into MRI-based forward models that incorporate individual-subject variability in structure and function.

Results

The package includes pipelines for the evaluation and validation of EEG analysis tools for source estimation, functional connectivity, and spatial filtering. EEG dynamics can be simulated using realistic noise and signal models with user specifiable signal-to-noise ratio (SNR). We also provide a set of quantitative metrics tailored to source estimation, connectivity and spatial filtering applications.

Comparison with Existing Method(s)

We provide a larger set of forward solutions for individual MRI-based head models than has been available previously. These head models are surface-based and include two sets of regions-of-interest (ROIs) that have been brought into registration with the brain of each individual using surface-based alignment - one from a whole brain and the other from a visual cortex atlas. We derive a realistic model of noise by fitting different model components to measured resting state EEG. We also provide a set of quantitative metrics for evaluating source-localization, functional connectivity and spatial filtering methods.

Conclusions

The inclusion of a larger number of individual head-models, combined with surface-atlas based labeling of ROIs and plausible models of signal and noise, allows for simulation of EEG data with greater realism than previous packages.

1. Introduction

Electroencephalography (EEG) provides non-invasive access to the electrical activity of the brain with millisecond precision. EEG measurements have been widely used in clinical and research settings, and a remarkable number of analytical approaches have been developed for their analysis and interpretation. However, EEG measures volume-conducted brain electrical activity at the scalp and therefore the ground truth underlying the EEG signal, i.e. its cortical sources, is generally not known. The direct measurement of these cortical sources requires invasive intracranial or intracerebral recordings, which are difficult to obtain in human. Consequently, simulation studies have played a major role in providing ground truth data for the development and validation of EEG-based analysis techniques.

Among the most common EEG analysis approaches are source estimation which is used to determine the likely location of the cortical generators of scalp activity (Michel et al., 2004; Grech et al., 2008), functional connectivity analysis which is used to measure synchronization of neuronal activity between different brain areas (Sakkalis, 2011; He et al., 2019), and spatial filtering, which is used to provide a low dimensional representation of multi-electrode data with improved interpretability and/or signal to noise ratio (Cohen, 2017). Simulations have historically played a major role in the development of each of these methods.

Determining the underlying cortical sources of scalp EEG – the inverse problem – is an ill-posed problem because there are an infinite number of possible source distributions that can generate a specific scalp distribution and only a small number of measurements. To overcome this ill-posed problem and specify a unique solution, regularization is usually used (Groetsch and Groetsch, 1993; Hansen, 2005). Based on regularization parameters, inverse solution models introduce assumptions such as smoothness (de Peralta Menendez et al., 2001; Pascual-Marqui et al., 2002), or sparsity (Gorodnitsky and Rao, 1997; Lim et al., 2017). Based on each of these assumptions, the results of source estimation can be significantly different (Michel et al., 2004; Grech et al., 2008). Besides these assumptions, other factors can drastically affect EEG source estimation such as the choice of head model, forward solution, source location and orientation (Henson et al., 2009; Ahlfors et al., 2010b; Acar and Makeig, 2013). In order to assess the effect of these factors on source estimation, simulation studies have been widely used. However, the ultimate validity of source estimation methods, in terms of real data applications, depends critically on the realism of the EEG simulation. The realism of EEG simulations for source estimation has varied widely, ranging from placement of current dipoles in a spherical head model (Mosher et al., 1999) to more extended sources in more realistic head models (Grech et al., 2008; Ahlfors et al., 2010b, 2010a; Stenroos and Hauk, 2013). Published implementations use a wide variety of models and parameters, but the source code and details of the parameters used are typically not available. This makes it difficult to reproduce these implementations and thus to compare the results obtained from different implementations. Simulation toolboxes for application of source estimation are included within some EEG analysis toolboxes, like Fieldtrip or Brainstorm. These simulations are usually implemented as assessment tools for specific methods implemented within that toolbox, rather than a general multi-purpose simulation environment.

Functional connectivity (FC) estimation is a particularly challenging approach and is usually implemented in conjunction with EEG source estimation. The challenge lies in the fact that FC approaches are affected by both errors in the source estimation process and errors specific to the FC measures themselves (Schoffelen and Gross, 2009; Palva and Palva, 2012; Bastos and Schoffelen, 2016; Barzegaran and Knyazeva, 2017). Simulation studies for evaluating this class of methods incur the burden of simulating the intrinsic signal dynamics and connectivity pattern of the brain itself, as well as the background and measurement noises. The ground truth of these dynamics and their effect on FC estimation is not known with any great precision in EEG applications. Beyond toy examples for assessment of FC analyses (Schoffelen and Gross, 2009; Palva and Palva, 2012; Cho et al., 2015; Barzegaran and Knyazeva, 2017), a number of simulation toolboxes have been developed for FC analysis. Haufe et al. (Haufe and Ewald, 2016) have developed an open source simulation framework which uses realistic head models and noise modelling at both the source and sensor levels. The EEG simulations of this framework are limited to models with two interconnected sources that can be placed coarsely in one of the brain quadrants. Implementation of more complex sources is not yet available in this toolbox. Another simulation toolbox for connectivity analysis is Source Information Flow Toolbox (SIFT) (Delorme et al., 2011). This toolbox was developed to be used in parallel with EEGLAB and for estimation of FCs based on real EEG data, but it is not a stand-alone simulation toolbox, being dependent on EEGLAB.

Another widely used EEG analysis approach, is spatial filtering. Spatial filtering is a popular tool for separating signal and noise subspaces, resulting in dimensionality reduction, denoising and potentially interpretable scalp topographies. The linear filters are typically found by optimizing weightings of the contribution of each electrode with regard to some assumed signal property, e.g. orthogonality (PCA) or independence (ICA) of the underlying sources, inter-trial similarity (RCA) or disjoint spectral power distributions of signal and noise components (SSD). However, it is not always clear which filtering method is best suited for a specific application and simulation studies can provide guidelines for selecting the appropriate spatial filtering method. In a simulation study, Cohen (Cohen, 2017) has compared the performance of a number of linear spatial filters in terms of accuracy, SNR and interpretability of the filters. However, this paper does not supply the simulation implementations as a toolbox or software package. To our knowledge, there are no realistic EEG simulation environment that allows systematic evaluation of spatial filtering methods. SimBCI (Lindgren et al., 2018) is a recent simulation framework, designed specifically for brain computer interface (BCI) applications. However, this toolbox only allows a limited options of source location and signal types and uses average head models rather than individually-defined head models.

The aforementioned toolboxes have been developed for the assessment of specific EEG analysis approaches. They consider a specific type of signal dynamics, or noise model that satisfies the assumptions of the targeted analysis approach. To our knowledge, only a few generic multi-purpose EEG simulation toolboxes are available. Among them is SEREEGA (Krol et al., 2018), a simulation framework designed for generating ERP data, using five distinct average head models, some template signals and different components of noise. Human Neocortical Neurosolver (https://hnn.brown.edu/), is a toolbox that incorporates more complex computational models to brain circuits to simulate brain responses and some spontaneous EEG activity (like beta and gamma rhythms) (Lee and Jones, 2013; Sherman et al., 2016). However, this toolbox is mostly developed to test the hypotheses of the circuit mechanisms underlying EEG signal rather than a simulation environment for testing of the EEG analysis approaches in presence of individual variabilities, i.e. individual head models and ROI definition, and different models of signal and noise.

Here, we introduce a simulation framework (EEGSourceSim) that increases realism relative to previous simulation environments by incorporating a large data set of individual head models, realistic source geometry modeling based on functionally and anatomically defined ROIs rather than arbitrary vertices and more realistic models of signal and noise. This open-source framework can be utilized to interpret the results of different approaches to source estimation, spatial filtering and functional connectivity analysis and to compare them on a set of quantitative evaluation metrics.

2. Methods

2.1. Code and data set availability

EEGSourceSim is an open source toolbox, implemented using MATLAB. This toolbox can be run on any operation system and requires MATLAB version R2016b or newer. In addition to the simulation software and metrics for assessing each method, we provide 23 individual-participant Boundary Element Method forward matrixes computed by MNE Suite with corresponding cortical surface meshes (the source space). For each individual, we have labelled the cortical surface with ROIs from a visual area atlas (Wang et al., 2014). We also provide labels for a set of ROIs covering all of cerebral cortex, from a multimodal parcellation based on both anatomical and functional properties of cortex (Glasser et al., 2016). The toolbox and the data set are available at https://osf.io/fmuae (DOI 10.17605/OSF.IO/FMUAE). The details about the execution time of this toolbox are available at https://osf.io/fmuae/wiki/Execution%20time.

2.2. Anatomical data

2.2.1. Data acquisition

Functional and structural MRI data were collected on a General Electric Discovery 750 (General Electric Healthcare) equipped with a 32-channel head coil (Nova Medical) at the Center for Cognitive and Neurobiological Imaging at Stanford University. For each of our 23 participants, we acquired two whole-brain T1-weighted structural datasets (1.0 × 1.0 × 1.0 mm resolution, TE=2.5 ms, TR=6.6 ms, flip angle=12, FOV=256 × 256) and one single whole-brain T2-weighted structural dataset (1.0 × 1.0 × 1.0 mm resolution, TE=75 ms, TR=2500 ms, flip angle=90, FOV=256 × 256). These three scans were used for the tissue segmentation procedure necessary to create individual forward models. For each participant, we also used a Polhemus FASTRAK system to digitize the locations of electrodes in 128-channel EGI Sensor Net arrays.

2.2.2. Individual forward models

In order to generate individual forward models, we first extracted cortical surfaces using FreeSurfer’s recon-all function (http://surfer.nmr.mgh.harvard.edu). Gray matter, white matter, and CSF boundaries were extracted with two T1-weighted (T1w) images and the T2-weighted (T2w) image as inputs to recon-all function. Using the T2w image in addition to the T1w images in recon-all function reduces the segmentation error. We then generated a smooth cortical surface with equal curvature for gyri and sulci by defining a mid-gray surface halfway between the gray and white matter boundaries, using Freesurfer’s mris_expand function. This function expands the white matter outwards by a fraction of the cortical thickness (here 0.5), while maintaining self-intersection and smoothness constraints. We then down-sampled this surface to 20,484 uniformly spaced vertices and placed current dipoles on each of the vertices orientated orthogonally to the surface. Because of the smooth curvature of the mid-grey surface, i.e. it has no sharp curvature at gyri or sulci, the orientation of the current dipoles changes smoothly over its surface, which results in more realistic forward and inverse solutions.

We then used FSL’s betsurf tool (http://www.fmrib.ox.ac.uk/fsl/) to define brain/skull (inner skull surface), skull/scalp (outer skull surface) and scalp/air (scalp surface) boundaries. We ran betsurf once with both T1w and T2w (for T1w here we used the nu file from the output of recon-all function) images and once only with T2w image. The two sets of extracted surfaces were visually inspected for accuracy, and the best surfaces were selected for further steps. The segmentation was done only with betsurf function and no manual editing was applied.

The electrode locations of the 128-channel EGI Sensor Net arrays were then co-registered to the high-resolution scalp surfaces extracted from T1-weighted MRIs (using FreeSurfer), using a set of fiducials and a warping algorithm, using in-house Matlab code distributed in the mrC toolbox (https://github.com/svndl/mrC).

We then estimated individual forward models using Boundary Element Method (BEM), implemented in MNE Suite toolbox (http://www.nmr.mgh.harvard.edu/martinos/userInfo/data/sofMNE.php). The forward models were estimated based on the three surfaces (brain/skull, skull/scalp and scalp/air), cortical source meshes, and co-registered electrodes locations. The forward model linearly links the current dipoles located on the 20,484 vertices of the cortical meshes to the EEG signal recorded at the 128 electrodes on the scalp. As a result, the forward solution can be written in a form of a transformation matrix with source number X sensor number dimensions. For more details of our forward modeling approach refer to (Cottereau et al., 2012, 2015).

2.2.3. ROI definitions

We make two sets of functionally and anatomically realistic regions-of-interest (ROIs) available in our simulation package. The first consists of a set of 25 topographically organized visual ROIs derived from a probabilistic atlas (Wang et al., 2014). This atlas was generated by using retinotopic mapping procedures to define 25 topographically organized ROIs covering 22 bilateral visual field maps in ~50 individual participants. Each participant’s cortical surface was standardized using icosahedral tessellation and projection (Argall et al., 2006), followed by an assessment of the likelihood across participants of any particular vector on the standardized surface belonging to a particular ROI (Wang et al., 2014). The atlas was defined using a maximum probability approach, which considers a given vector as part of the set of ROIs if it is more often found within the set, than outside the set, across participants. If this is the case, the vector was assigned the value of the most likely ROI, and if not, it was considered to be outside the set of ROIs. The maximum probability approach captures much of the overall structure of ROIs defined for individual participants and generalizes well to novel participants who did not contribute to the atlas generation (Wang et al., 2014). The atlas is publicly available at http://scholar.princeton.edu/sites/default/files/napl/files/probatlas_v4.zip. We converted the ROIs from standardized surface space to an individual surface space for each of our participants using nearest-node interpolation implemented in the AFNI’s SurfToSurf function (https://afni.nimh.nih.gov/). This function interpolates two surfaces assuming the surfaces have similar shape but different meshes. This interpolation is done by projecting each node (N1) and its normal from the first surface to the other surface, finding the triangle on the second surface that is intersected by this projection. The node in this triangle that is closest to the node N1 is the output of interpolation. We then used surface-based clustering to eliminate vertices more than 1 edge removed from the main cluster of each ROI, to ensure that all ROIs consisted exclusively of contiguous vertices. This step eliminated small speckles, while having minimal effect on the overall structure and extent of the ROIs. Finally, the ROIs were down-sampled to match the 20,484-vertex surface mesh used for source generation/localization.

The second set of ROIs consisted of 180 ROIs that together constitute a parcellation of the entire cerebral cortex, thus offering the user the ability to simulate activity outside of visual cortex using a set of ROIs that have a more realistic basis than parcellations made arbitrarily or based purely on cortical anatomy. The ROIs were defined using a multi-modal machine-learning approach that identified sharp changes in cortical architecture, function, connectivity, and/or topography across a group of 210 healthy young adults from the Human Connectome Project (Glasser et al., 2016). The parcellation is publicly available at https://figshare.com/articles/HCP-MMP1_0_projected_on_fsaverage/3498446/2. We used a version of the parcellation that had been projected onto Freesurfer’s fsaverage standard surface and then used Freesurfer’s mri_annotation2label and mri_surf2surf functions to convert the annotation files to files in which integer values at each surface vertex indicated ROI membership, converting the resulting files to the native space of each participant. The resulting .mgz files were finally converted to gifti format using Freesurfer’s mris_convert function, which were then down-sampled to match the 20,484-vertex surface mesh used for source generation/localization.

2.3. Simulation of brain signals and scalp EEG recordings

Brain activity is modeled as the linear superposition of task- or stimulation-related signal activity s(t) and task- or stimulation-unrelated background activity s_n(t). s(t) and s_n(t) are projected from source space to channel space by the subject-specific forward model A. At the channel level, extra-cranial noise is added as a further noise component. The details of signal and noise models are presented in the following.

2.3.1. Signal modeling

In the current version of the framework two different types of signal are implemented: narrow-band steady state evoked potentials (SSEP) and multivariate autoregressive model (MAR) used to model the activity of two or more linearly interacting ROIs. Signals can be assigned uniformly to either all source vertices (indexed by k ∈ {k}_ROI) in a desired region of interest, or to a subset of vertices located in the center of that ROI, where the size of ROI can be defined by the user (as the number of vertices or the surface area). The signal can also be placed with a spatial normal distribution centered at the centroid of the ROI with the standard deviation equal to maximum distance of vertices within ROI from the centroid.

SSEP modeling

Steady state evoked potentials are modeled as the superposition of sinusoidal waves corresponding to the first H harmonics h of the fundamental frequency f (h = 1) as

$$s^k(t)=\sum _{h=1}^H{a}_h^k\cos \left(2\pi hft+{\phi }_h^k\right)$$ (1).

Each harmonic component is defined per ROI by its amplitude $a_h^k$ and phase ${\phi }_h^k$.

MAR modeling of interacting ROIs

Auto regressive models are widely used to generate EEG data in simulation studies of functional connectivity analysis methods (Pascual-Marqui et al., 2014; Stokes and Purdon, 2017). Multivariate AR models (MAR) support simulation of an ROI’s internal dynamics and linear interactions between ROIs. This makes MAR a first-order approximation model for the dynamics of brain functional networks. Previous simulation studies usually provide one specific example for this class of signal models, while here we provide a more flexible framework where the user can define the number of interacting nodes (ROIs), external input signals, their internal dynamics and interactions between them. The general form of MAR model can be defined as

$$\begin{gathered} \left[\begin{array}{c}{s}^1(t)\\ ⋮\\ s^K(t)\end{array}\right]=\left[\begin{array}{ccc}{a}^{1,1}(1)& a^{2,1}(1)& \ddots \\ a^{1,2}(1)& \ddots & a^{K,K-1}(1)\\ \ddots & a^{K-1,K}(1)& a^{K,K}(1)\end{array}\right]\left[\begin{array}{c}{s}^1(t-1)\\ ⋮\\ s^K(t-1)\end{array}\right]+\cdots \\ +\left[\begin{array}{ccc}{a}^{1,1}(T)& a^{2,1}(T)& \ddots \\ a^{1,2}(T)& \ddots & a^{K,K-1}(T)\\ \ddots & a^{K-1,K}(T)& a^{K,K}(T)\end{array}\right]\left[\begin{array}{c}{s}^1(t-T)\\ ⋮\\ s^K(t-T)\end{array}\right]+\left[\begin{array}{c}{w}^1(t)\\ ⋮\\ w^K(t)\end{array}\right] \end{gathered}$$ (2)

Where K indicates the number of the nodes within the network, T is the order of the MAR model and A is a KxKxT matrix indicating the AR coefficients of the system and w^k(t) is the additive noise of the system. s^k(t) is the realization of the activity of node k at time t.

MAR model parameter estimation

The matrix A, i.e. the coefficients of MAR model, needs to be estimated based on the desired behavior of the system. The diagonal of matrix A indicates the internal dynamics of the nodes, for example for node k the vector [a^k,k(1) … a^k,k(T)] indicates its behavior. To generate oscillatory activity for a node, the roots of VAR(1) (or state space) model of this vector need to be complex conjugate (Stokes and Purdon, 2017). In our implementation, one or two oscillatory activities for each node are allowed. The off-diagonal coefficients of matrix A, indicate the interaction between the nodes. In our implementation, we allow different kinds of linear interactions implemented by FIR filters: high-, low-, band-pass and band-stop. The user can indicate the type of filter, the cut-off frequency(ies) and filter order and gain. The off-diagonal of coefficients of the matrix are then estimated using the MATLAB signal processing toolbox.

For the model to be stable, we only allow feed-forward networks. If feedback dynamics were allowed it might lead to divergence of the system and some non-linearity like normalization is required (Tsai et al., 2012). To simulate feedforward networks, only the upper or lower triangle of matrix A needs to be estimated and the other should be set to zero.

An example of this type of signal, with three interconnected nodes is presented in the section 3.3.

2.3.2. Noise modeling

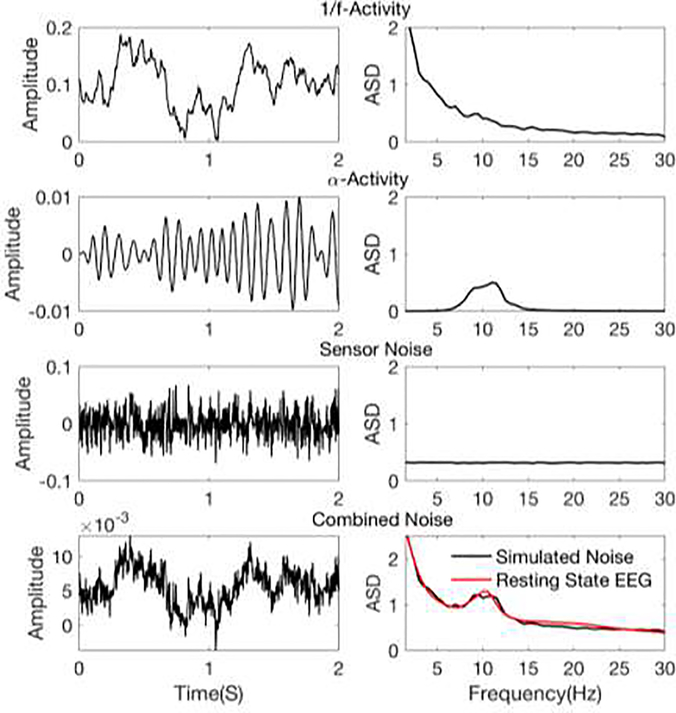
In the current version of the framework, we have modeled the background activity of the brain using 1/f-activity (or pink noise) and α-activity. Sensor noise is modeled at the channel level as an additive white Gaussian noise. Examples of the simulated activity are presented in Figure 1.

Figure 1.

Example realizations of different noise processes. Left column: Time course of EEG noise signal from an occipital electrode (electrode 29 of EGI system). Right column: Amplitude spectral density of EEG noise signal, calculated over 30 seconds of simulated noise and averaged over all electrodes. The 1/f and α activities are projected onto channel level using the forward solution.

1/f-activity

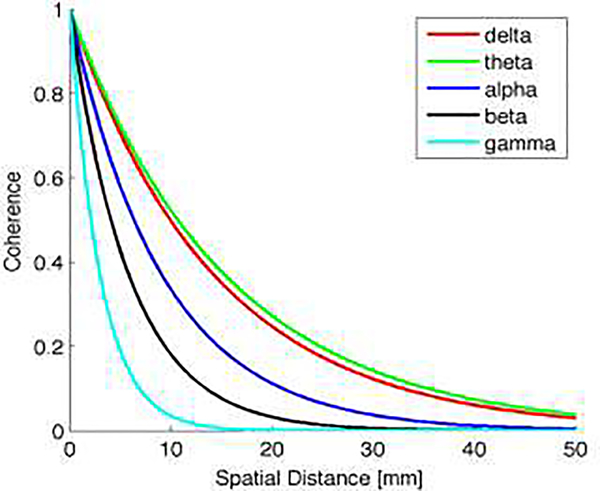
Spectrally pink components of neural background activity are modeled for all source nodes by spatially coherent 1/f noise. For this, temporally and spatially uncorrelated white Gaussian noise is filtered to have power spectral density of 1/f. Spatial coherence is imposed per frequency band (delta, theta, alpha, beta and gamma) to the resulting signal s_1/f(t). To obtain a realistic model of spatial coherence, the decay with spatial distance is modeled using the spatial coherence measured by intracranial recordings (Kellis et al., 2016) per frequency band. The coherence dependence on spatial distance is presented in Figure 2 for each frequency band.

Figure 2.

Decay of spatial coherence in dependence of spatial distance for different frequency bands.

α-activity

To simulate activity in the α-band, a white Gaussian noise signal is filtered using a 3^rd-order Butterworth filter with a lower cutoff frequency of 8Hz and a higher cutoff frequency of 12Hz. The resulting signal s_α(t) is assigned to the source vertices of all visual ROIs of Wang atlas in a spatially uniform fashion. These ROIs includes primary visual cortex, dorsal, ventral and lateral streams (In sum 25 ROIs in each hemisphere).

Sensor noise

At the channel level, sensor noise ε(t) is modeled as spatially and temporally uncorrelated white Gaussian noise.

The noise activities are combined at the channel level. For this, activities that are defined at the source level (1/f-activity s_1/f(t) and alpha-activity s_α(t)) are projected to channel space using the subject-wise forward model A with

$${\mathit{x}}_{\mathit{\alpha }}(t)=\mathit{A}{\mathit{s}}_{\mathit{\alpha }}(t)$$ (3)

and

$${\mathit{x}}_{\frac{\mathbf{1}}{\mathit{f}}}(t)=\mathit{A}{\mathit{s}}_{\frac{\mathbf{1}}{\mathit{f}}}(t)$$ (4)

leading to the channel space representation of 1/f-activity x_1/f(t) and α-activity x_α(t). The total noise activity at channel level is calculated as the sum of the three noise components, weighted by the noise parameters α, β, γ.

$$\begin{gathered} {\mathit{x}}_n(t)=\frac{\alpha }{\sqrt{{\alpha }^2+{\beta }^2+{\gamma }^2}}\frac{{\mathit{x}}_{\alpha }(t)}{{\Vert {\mathit{x}}_{\alpha }(t)\Vert }_F}+\frac{\beta }{\sqrt{{\alpha }^2+{\beta }^2+{\gamma }^2}}\frac{{\mathit{x}}_{\frac{1}{f}}(t)}{{\Vert {\mathit{x}}_{\frac{1}{f}}(t)\Vert }_F} \\ +\frac{\gamma }{\sqrt{{\alpha }^2+{\beta }^2+{\gamma }^2}}\frac{\mathit{\epsilon }(t)}{\Vert \mathit{\epsilon }(t){\Vert }_F} \end{gathered}$$ (5)

where ∥·∥_F denotes the Frobenius norm over all channels. In order to have realistic noise-power ratios, the noise parameters are estimated using empirical data as described in the following section.

Noise parameter estimation

To set the parameters α, β, γ in formula 5, we used a large resting state EEG dataset. The dataset consisted of EEGs of 60 participants, from 20 to 81 years of age (45.9 ± 16.2, mean ± standard deviation, and 33 females ) recorded during approximately 8 minutes of resting state with eyes closed (REC) and 8 minutes of resting state with eyes open (REO), using an ANT 64 channel EEG system (ANT Neuro b.v., Enschede, The Netherlands), for more details of the dataset see (Knyazeva et al., 2018).

The EEG spectrum of the REC and REO conditions (X_REC (f), and X_RE0 (f)) were calculated for each electrode using Fourier transformation and was averaged over all electrodes. The same Fourier transformation was applied to simulated noise components in electrode space (X_α(f), ${\mathit{X}}_{\frac{1}{f}}(f)$, and X_ε(f)). The noise parameters can be then estimated by minimization of the mean squared error as follows

$$\alpha ,\beta ,\gamma =\underset{\alpha ,\beta ,\gamma }{\mathrm{argmin}}\left(\sum _{n,i}\Vert {\mathit{X}}_n(f)-{\mathit{X}}_{RECorREO}(f){\Vert }^2\right)$$ (6)

where X_n (f) can be calculated with the same as formula (5), where x_α (t), ${\mathit{x}}_{\frac{1}{f}}(t)$, and x_ε (t) are replaced by X_α (f), ${\mathit{X}}_{\frac{1}{f}}(f)$, and X_ε (f) accordingly. After finding the optimal noise parameters, the final noise is calculated from formula (5).

The simulation framework allows users to select the REC condition of formula (6), to simulate background activity with high alpha amplitude, the REO condition, to simulate background activity with low alpha amplitude, or define the noise parameters (α, β, γ) manually.

2.3.3. Combining signal and noise components

To combine signal and noise activities at the channel level, source signal activity s(t) is projected to channel signal activity x_s(t) with

$${\mathit{x}}_{\mathit{s}}\left(t\right)=\mathit{A}\mathit{s}\left(t\right).$$ (7)

The simulated noise EEG recording with a chosen signal-to-noise ratio λ is then calculated as

$$\mathit{x}(t)=\sqrt{\frac{\lambda }{\lambda +1}}\frac{{\mathit{x}}_{\mathit{s}}(t)}{{\Vert {\mathit{x}}_{\mathit{s}}(t)\Vert }_{\mathit{F}}}+\frac{1}{\sqrt{\lambda +1}}\frac{{\mathit{x}}_{\mathit{n}}(t)}{{\Vert {\mathit{x}}_{\mathit{n}}(t)\Vert }_{\mathit{F}}}.$$ (8)

2.3.4. Multiple epochs and variability

Real EEG recordings are characterized by a high degree of variability given identical stimulation. This variability may occur on trial-level or on subject-level. In the simulation framework presented here, trial-wise variation of the EEG-signal is modeled by the trial-wise redraw of the random processes underlying the three noise components described in Section 2.3.2. Subject-specific forward models capture variability at the subject-level by considering individual head anatomies. The noise parameters α, β, γ and λ allows for variability to be introduced at any level between the trial- and subject-level, because they can be adjusted per subject or over the course of trials, e.g. based on a pre-defined rule.

2.3.5. Summary of the simulation pipeline and its parameters

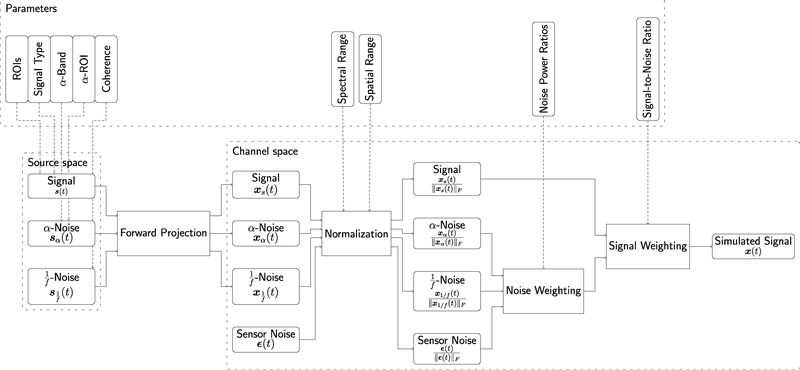
The previous subsections detailed the signal, noise and processing models underlying the proposed simulation framework. A summarizing overview over the full signal flow leading to the simulated signal x(t) is presented in Figure 3. The flow diagram also outlines the parameters that can be set by the user and that influence the behaviour of the different modules of the simulation pipeline. A summary of the main parameters with suggested values as used in our application examples can be found in Table 1. However, with regard to most parameters, e.g. the signal type, the proposed framework is easily extendable. More details on parameters and implementation can be found in https://osf.io/fmuae/wiki/.

Figure 3. EEGSourceSim pipeline overview.

The lower row of the figure indicates the main modules of the pipeline in source and channel space. The upper row of the figure indicates the parameters that the user needs to provide for each module of the pipeline.

Table 1.

Summary of the input parameters, and the suggested values for each.

Parameter	Description	Suggested values
Signal Type	Description of signal time course	SSEP or MAR (see Sec. 3)
SignalSF	Sampling frequency of the simulation	100 Hz
ROIs	A list of ROIs to be used as nodes with active signal	Two sets of example-specific ROIs (see Sec. 3)
Subject list	A list of subject IDs to be used in simulation	All available 23 subjects
α-Band	Frequency band of α-activity	8Hz to 12 Hz
α-ROI	Set of indices of alpha active nodes	All visual ROIs of Wang atlas
Spectral Range	Set of frequencies bin indices to normalize over	Normalization over [0 SignalSF/2]; Normalization of signal frequency bins (Sec. 3.3)
Spatial Range	Normalize in source space over all ROIs, or active ROIs, or in channel space over all channels	Normalization over all channels (Sec. 3.3)
Noise Power Ratio	A structure with power ratio between different noise sources (α, β, γ) in formula (5)	Calculate based on real resting state EEG data
Signal-to-Noise Ratio	Real number, λ in formula (8)	$\frac{1}{2\times \mathit{SignalSF}}$, appropriate for SSEP signal

3. Examples of simulation framework applications

3.1. Source estimation

Here, we illustrate using EEGSourceSim to compare the performance of EEG inverse solutions, using the minimum norm solution (MN) with and without functional area constrained estimator (MN-FACE) (Cottereau et al., 2012) as test cases.

3.1.1. Simulation setup and inverse solutions

Forward models of ten subjects from our dataset were selected, and their MN and MN-FACE inverse solutions were calculated based on a simulated Steady State Visual Evoked (SSVEP) potential data. MN is a standard approach to solving the EEG source reconstruction problem. In order to solve the ill-posed inverse solution, MN uses Tikhonov regularization to produce a spatially smooth source current density solution with minimum power (Tikhonov and Arsenin, 1977; Grech et al., 2008). The MN-FACE, introduced by (Cottereau et al., 2012), improves reconstruction accuracy of MN by adding functional area constrains. To evaluate the accuracy of the two inverse solutions, we first calculated resolution matrices for each inverse solution and each subject. A resolution matrix is calculated by multiplying forward matrix by inverse matrix, and it captures the relationship between the true and estimated source current densities. If an inverse solution is ideal, resolution matrix should be an identity matrix, and if the inverse solution has high error, the non-diagonal elements of resolution matrix are non-zero (Pascual-Marqui et al., 2002).

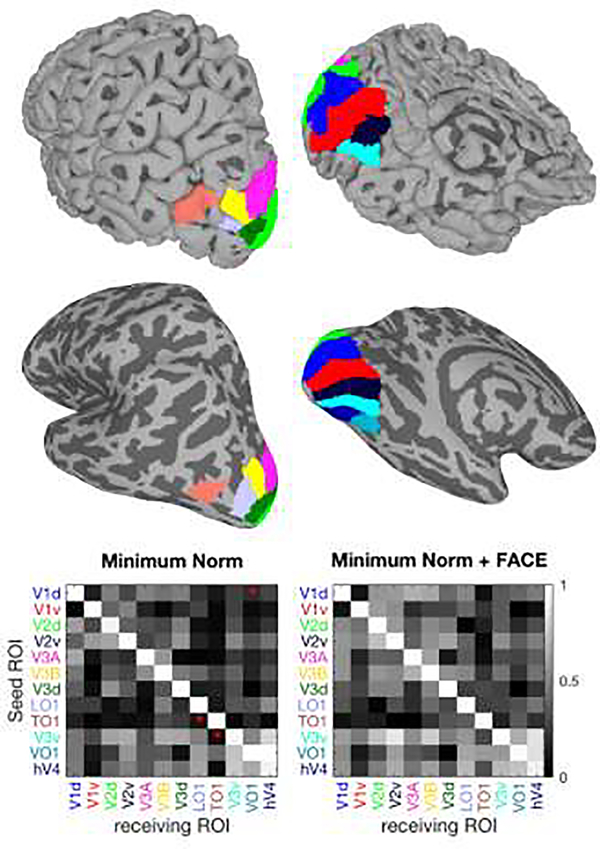
We then selected a number of visual ROIs from the Wang atlas, including dorsal (V1d, V2d, V3d, V3A, V3B, TO1, LO1) and ventral (V1v, V2v, V3v, VO1, hV4) visual areas (Figure 4). Simulated EEG signal (at one time point) were generated for each of these ROIs, one at a time, by assigning ones to the current source densities within that ROI, while keeping the rest of current source densities at zero. These current densities were then multiplied by the resolution matrices to estimate the reconstructed source current densities.

Figure 4. Source estimation example.

The eight selected ROIs are presented in the upper two rows on uninflated (upper) and inflated (lower) left hemisphere cortical surfaces with dorsolateral (left) and ventromedial views (right). Note that the inflated surface representation was not used for simulation, but is included in order to show the full extent of all ROIs. The bottom row presents the cross-talk matrices for two inverse solutions. The ROI names are color coded according to the surface maps. The red asterisks on each of cross-talk matrices, indicate which solution has significantly lower cross-talk compared to the other inverse solution (paired t-test, p < 0.01).

3.1.2. Evaluation metrics

We provide several metrics for evaluating the quality of inverse solutions:

• A cross-talk matrix is estimated as the reconstructed current density of ROIs (receiver ROIs), when only a specific ROI (seed ROI) is active in original current source density. A perfect reconstruction will result in a diagonal cross-talk matrix, with one on the diagonal and zeros of the diagonal.

• A Relative Energy metric indicates the ratio of energy in the sources of the activated ROI to the energy in all sources. This value can vary between zero (totally false reconstruction) and one (perfect reconstruction).

• An Area Under Curve (AUC) metric is calculated using the Precision Recall curve (PR). When the data is imbalanced, that is the number of actual negatives is much higher than the actual positives, PR is a more informative assessment curve than other alternative receiver operating characteristics (Saito and Rehmsmeier, 2015). Precision or positive predictive value (PPV) is calculated as the ratio of true positives to all detected positives i.e. what ratio of detected positive are actually correct. Recall or true positive rate (TPR) is the ratio of true positives to actual number of positives, i.e. what proportion of actual positives was detected. In the context of source estimation, PR is calculated by thresholding the estimated normalized source energies and indicates what proportion of detected active sources are actual active sources. If the reconstruction is ideal, AUCPR is one.

• A Focalization Error metric calculated as the normalized reconstruction error of the active ROI current, calculated by mean squared error.

The implementation of the cross-talk, relative energy and Focalization Error metrics is detailed in (Cottereau et al., 2012, 2015).

3.1.3. Example Results for Source Estimation

Results of source estimations using MN and MN-FACE solutions averaged over 10 subjects are shown in Figures 4 and 5. Figure 4, top shows the eight visual ROIs used in the simulation on uninflated and inflated cortical surfaces. The uninflated surface accurately presents the cortical anatomy and 3D geometry of the ROIs, while the inflated surface makes it easier to visualize each ROI’s continuous coverage of the cortical surface. The cross-talk matrices for the MN and MN-FACE methods are shown at the bottom of Figure 4. To compare the cross-talk matrices of pairs of inverse solutions over subjects, we applied a paired t-test to each element of the matrices.

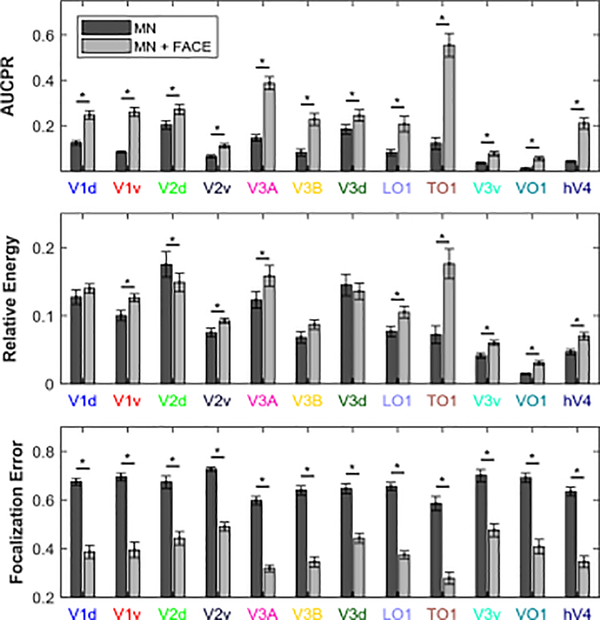
Figure 5. AUCPR, relative energy, and focalization error of MN and MN-Face inverse solutions.

ROIs are color coded according to Figure 4. Asterisks indicate significant differences between MN and MN-FACE results (paired t-test p < 0.01).

Here, the MN inverse solution showed lower cross-talk in many elements of the matrix. These differences are caused by FACE constraint imposed on the MN solution. We note that this apparently weaker performance is likely due to the fact that applying the FACE constraint results in more signal power being attributed to visual areas, which in turn increases the likelihood of cross-talk between them. To compare the performance of the two inverse solutions more accurately, we should thus also consider the source estimation errors over whole cortex.

On all of the three other metrics, which capture errors across the whole cortex, the MN-FACE solution outperformed the MN solution, as can be seen in Figure 5. Paired t-test were used to compare the AUCPRs, relative energy and focalization error of MN and MN-FACE solutions for each ROI simulation. In this example, the AUCPR estimated with MN-FACE was significantly higher in all ROIs (p < 0.001) compared to MN. The Relative Energy estimated with MN-FACE was higher in most of the ROIs (p < 0.05), except for some dorsal ROIs (V1d, V2d, V3A and V3B). The Focalization Error was significantly lower for MN-FACE than for MN in all ROIs (p < 0.001).

The simplified example presented here considers only two inverse models and a small number of simulated sources. However, the simulation framework can be used to compare any inverse solution using the set of evaluation metrics provided. We simulated one ROI at a time in this example, but users can also study cancellation or mixing effects by placing active sources in multiple ROIs at the same time. The 20-participant dataset can also be used to evaluate the effects of individual variability and ROI variability on source estimation such as the effects of depth, orientation, source extent, etc). Finally, it is important to emphasize that the simulation presented here used a static model, i.e. only considering a single time point. The static approach does not consider signal dynamics, and is indifferent to noise, but a more realistic evaluation of source estimation can be achieved using the dynamic modelling of signal and noise provided by our framework.

3.2. Functional connectivity analysis

In this section we demonstrate how to assess different approaches to functional connectivity analyses using the EEGSourceSim framework. For this purpose, we use a comparison of two commonly used functional connectivity measures, weighted phase-locking index and imaginary coherence methods under different SNR levels.

3.2.1. Simulation setup

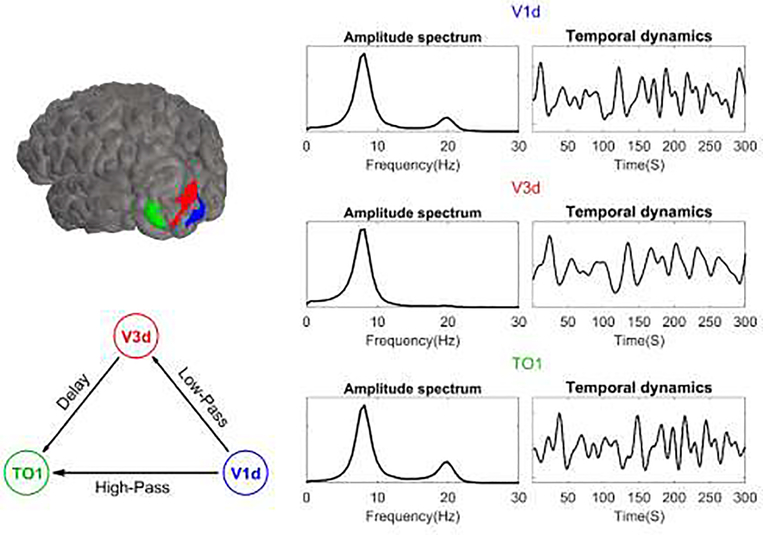
Spontaneous EEG data was simulated at a 300 Hz sampling frequency and 2 second epoch length. The source signals were generated using an MAR model. The model consisted of three interconnected ROIs: dorsal V1, dorsal V3, and TO1 each located in the left hemisphere. The location of these ROIs is shown in the top left part of Figure 6, and the connectivity graph used for the simulation is shown in the bottom left part. We selected these ROIs because they had low source estimation errors and cross-talk values in the previous example (see Figure 5).

Figure 6. Network model and the resulting MAR signals used for a functional connectivity analysis simulation.

In the upper left, the three left hemisphere ROIs are shown on an example brain. In the lower left, the network structure, which created the MAR input is presented with the nodes color-coded as in the ROIs. On the right, the amplitude spectral densities of the ROI signals are presented.

The signal that was placed in V1d had internal dynamics comprised of lower (8Hz) and higher frequency (20 Hz) broadband oscillatory activity. These oscillations were propagated to other ROIs through two paths. The first path was simulated as a high pass FIR filter (cut-off frequency of 13 Hz) from V1d to TO1 where only the 20 Hz oscillation was transferred through it. The other path consisted of a connection from V1d to V3d via a low-pass FIR filter (cut-off frequency of 13 Hz), where only the 8Hz oscillation was passed through, followed by a connection from V3d to TO1 after a delay. The result was that the low frequency oscillation was transferred through an indirect path from V1d to TO1. This network configuration reflects known properties of the visual pathway (Ponce et al., 2008).

Ten subjects were selected for this simulation and EEG signals were generated at different SNR levels (λ ∈ {0.003, 0.01, 0.0316, 0.1, 0.3162, 1.0, 3.1623, 10.0}, which resulted in SNRs ranging from −25 to 10 dB in 5 dB steps). SNR was defined at the single trial level based on the broad band frequency range (5 to 25 Hz). For each SNR level and subject, 15 two-second epochs of EEG signal were generated.

3.2.2. Functional connectivity measures

To estimate source functional connectivity, we first estimated the source signal using an inverse solution and then computed the functional connectivity between the different ROIs. This approach of EEG source functional connectivity analysis has been widely used by researchers (Astolfi et al., 2004; Babiloni et al., 2005; Barzegaran et al., 2016), for review see (Schoffelen and Gross, 2009; Barzegaran and Knyazeva, 2017). To minimize source estimation errors, the source signal was estimated by the MN-FACE inverse solution. Two commonly used functional connectivity measures, (1) the imaginary part of coherence, ICoh (Nolte et al., 2004) and (2) the Weighted Phase Lagged Index, WPLI (Vinck et al., 2011) (implemented in the Fieldtrip toolbox (Oostenveld et al., 2011), were applied to estimate the connectivity between the ROIs. ICoh is calculated as the imaginary part of the cross-spectrum of the two signals, and is shown to be unaffected by volume conductance of independent sources. WPLI is estimated based on the distribution of relative phase of the two signals. If one signal leads or lags the other, the WPLI index will be high. WPLI weights the contribution of the phases by the magnitude of imaginary component of cross spectrum to decrease the sensitivity to noise and volume conductance. These two measures are minimally affected by volume conductance and outperform many other FC measures such as coherence or PLV (Gordon et al., 2013; Van Diessen et al., 2015). The values of ICoh and WPLI both vary between zero and one, where one implies maximum synchronization and zero means no synchronization.

3.2.3. Evaluation metrics

We compared the source functional connectivity estimates of ICoh and WPLI at different SNR levels. The metrics for evaluation of functional connectivity analysis were defined according to (Palva and Palva, 2012)

• To visualize the detected network, we generated an ROI connectivity matrix that determines the strength of estimated functional connectivity between ROIs.

• To determine the proportion of detected connections that are actual functional connection, we calculated AUC using the Precision-Recall curve (AUCPR) as in the source localization example, but here based on thresholded ICoh and WPLI connectivity matrices, rather than normalized source energies.

3.2.4. Example Results for Functional Connectivity estimation

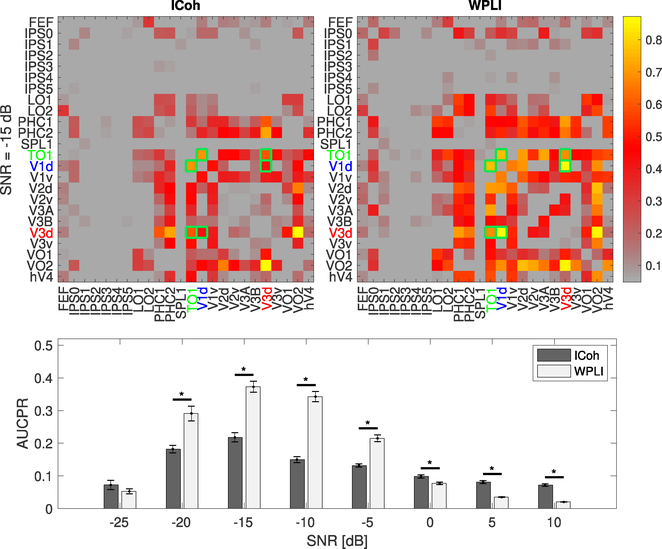
Connectivity matrices for ICoh and WPLI are shown in Figure 7 top left and top right, respectively. The three active ROIs are indicated by the color codes. As can be seen, there is substantial spurious connectivity outside of the simulated ROI for both measures. To allow reliable statistical comparison of WPLI and ICoh, we estimated standard errors of the AUROC for each connectivity measure by Monte Carlo simulation over the simulated EEG data (80 draws for each SNR level, where for each draw we selected 75 trials over all subjects). The AUROC results, shown at the bottom of Figure 7 indicate that overall, WPLI performed better than ICoh in the detection of true positives. As SNR increases from very low values (from −25 to −10 dB), the performance of both measures improves. However, after −10 dB, as the SNR level increases, the performance of the two connectivity measures deteriorates, and they detect a large number of false positives. (Palva et al., 2018) has shown that false positive or ghost FCs are detected even with methods that are resilient to direct effects of volume conduction, such as WPLI. This happens due to field spread in the vicinity of true interactions. In our simulation, as the SNR level increases, cross-talk has a stronger effect on the propagation of signals into the other ROIs which results in higher false positive rates and therefore worse performance. A similar effect has been observed previously (Barzegaran and Knyazeva, 2017).

Figure 7. Connectivity matrices (top) and AUCPR estimates (bottom) for ICoh and WPLI at 8Hz and at different SNR levels.

The upper row shows the connectivity matrices for ICoh and WPLI at SNR= −15 dB. The colorbar indicates the normalized estimated connectivity strength. The matrix elements marked with green frames indicate the gold standard FC elements. The simulated FC at this frequency was present between V1d and V3d, and V3d and TO1. The lower row plots the mean AUCPR of Icoh and WPLI, with standard error of mean presented as error bars. The stars indicate significant differences between ICoh and WPLI results (paired t-test p < 0.01)

In this section, we have presented a simple example simulation of functional connectivity analysis based on source-level EEG with three linearly interacting sources. However, the framework can also be used to study more complex network structures, including whole brain networks using the Glasser et al (Glasser et al., 2016) atlas and more complex MAR model or nonlinear models. More complex signal modeling can be incorporated within the simulation framework by modifying the signal of interest that is input to the framework. As the framework generates simulation data at both source and sensor levels, it can be used to compare functional connectivity and other estimates of connectivity at both levels.

3.3. Spatial filters

In our third example we show how EEGSourceSim can be used to evaluate linear spatial filters, and compare three different methods: Principal Component Analysis (PCA), Spatio-Spectral Decomposition (SSD) (Nikulin et al., 2011), and Reliable Component Analysis (RCA) (Dmochowski et al., 2015). We show how a plausible simulation of steady-state evoked responses at different levels of SNR can guide method selection.

3.3.1. Spatial filter simulation setup

We illustrate the evaluation of spatial filters with a simple example that modeled two SSVEP source signals located at distinct visual ROIs. Each source signal comprised of two sinusoids at 2Hz (the nominal first harmonic of the SSVEP signal) and 6 Hz (the third harmonic of the SSVEP signal). For the first source (S1) amplitudes were constant over trials ($a_1^{S1}=2$, $a_3^{S1}=1.5$, where $a_1^{S1}$ indicates the amplitude of the first harmonic in source S1 and $a_3^{S1}$ is the amplitude of the third harmonic) with no phase shift (${\phi }_1^{S1}={\phi }_3^{S1}=0$, where ${\phi }_1^{S1}$ indicates the phase of the first harmonic in source S1 and ${\phi }_3^{S1}$ is the phase of the third harmonics). The S1 signal was placed at source-mesh vertices corresponding to the dorsal sub-division of visual area V2 in the right hemisphere (V2d-R). The second source signal (S2) was set in quadrature to the first source signal $\left({\phi }_1^{S2}={\phi }_3^{S2}=\pi /2\right)$ with its amplitudes being sampled per trial from a standard uniform distribution ($a_1^{S2}=a_3^{S2}=a$ with a ~ U (0,1)). The S2 signal was placed at source-mesh vertices corresponding to the dorsal-lateral area LO1 in the left hemisphere (LO1-L). The SSVEP signals were simulated over a range of SNRs (λ ∈ {0.01, 0.0316, 0.1, 0.3162, 1.0, 3.1623, 10.0}, corresponding to SNR values in the range from −25 to 10 dB in 5 dB steps) for the same subset of ten subjects used in previous examples. These SNR values were calculated in sensor space, i.e. the source and noise signals were first projected into sensor space separately by multiplying their source-space signal by the forward matrix (see Eq. 8). The SNR is then defined as the ratio of average source-signal power in the first and third harmonic frequency bins to the average noise power in the respective side-bins of the first and third harmonics over all electrodes. For each subject and SNR level, we simulated the SSVEP signal with 200 2-second trails and sampling frequency of 100Hz.

3.3.2. Spatial decomposition methods

PCA is a classical technique to decompose a multidimensional signal into decorrelated components. The decomposition transform is found under the constraint of maximal energy (or variance) compactness of the signal and results in an orthogonal basis set. RCA decomposes the signal into its components based on the assumption of trial-to-trial reproducibility (Dmochowski et al., 2015). This leads to a generalized eigenvalue problem and, as such, to potentially non-orthogonal components. SSD assumes the signal to be of spectrally disjoint signal and noise components, as for the RCA, leading to a generalized eigenvalue problem (Nikulin et al., 2011).

3.3.3. Example Results for Spatial Filtering

The simulation framework provides ground truth information for the SSVEP signals that would be recorded in a hypothetical noise-free situation. By adding noise to the signal, we can quantitatively evaluate how effective different decomposition techniques are in recovering the neural source signal and the lead fields (scalp topographies) of the known sources.

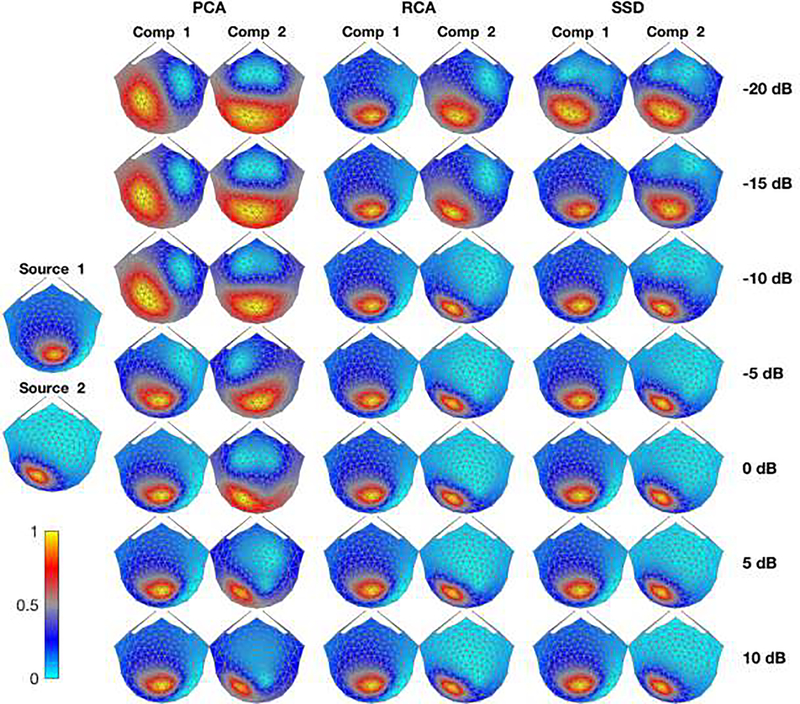
The lead fields of the two visual ROIs used in this simulation are shown in the leftmost column of Figure 8. S1 was located in the V2d-R and had constant amplitude. This source generates an approximately ellipsoidal horizontal topography located roughly over O2. S2, located in LO1-L was amplitude-varying and exhibits an ellipsoid topography rotated by about 45 degrees, centered approximately between P3, P7 and O1. The recovered scalp topographies are shown in Figure 8 for the first two components derived from the PCA, RCA and SSD approaches over the range of varied SNR. At low SNRs (−20dB, −15dB, −10dB), PCA is unable to recover a topography resembling any of the lead fields of the two sources. As SNR increases (−5dB and higher), the amplitude-constant source (S1) starts to emerge in the first PCA component. However, it only detects the S2 source at SNRs higher than 5 dB. Contrary to PCA, RCA can successfully detect S1 in their first component under all SNR values and SSD detects it with SNRs higher than −20dB. The second source S2 emerges in the second component of RCA and SSD as the SNR value increases (−5dB for RCA and −10dB for SSD).

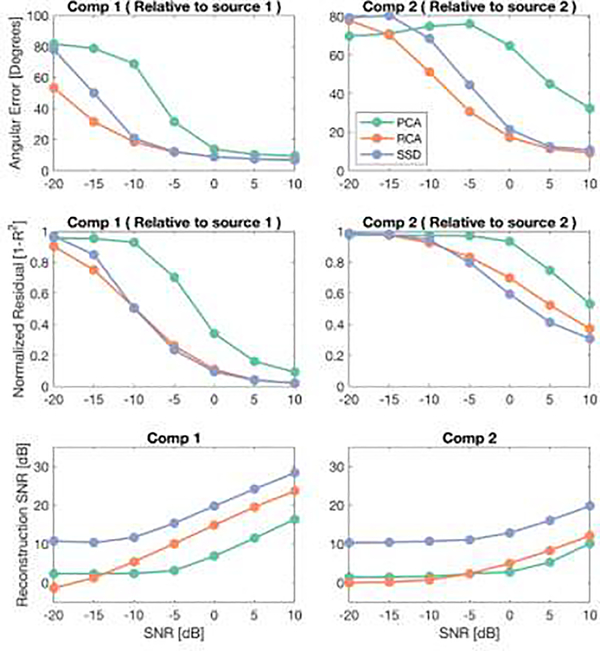
Figure 8. Spatial filter topography maps of three decomposition techniques.

The left most column presents the lead fields corresponding to source 1 (V2d-R) and source 2 (LO1-L) averaged over 10 subjects (Normalized to have values between 0 and 1). The normalized topographic maps of each filter for their first and second component are presented (averaged over 10 subjects and trials) over different SNR values (each SNR value is presented in one row) are shown in the second to sixth columns.

To quantitatively assess the performance of the three spatial filters, we employ three evaluation metrics previously used to asses spatial filters (Cohen, 2017).

• Angular Error indicates how much the spatial filter topography resembles the lead field (scalp topography) of the activated source. It is calculated as

$$\mathit{Angular}\mathit{error}={\cos }^{-1}(|r|)$$

Where r is the correlation coefficient between the filter topography and the source lead field. Its value ranges from 90° (maximum topography difference) to 0° degrees (equal topographies).

• Normalized Residual shows how well the filtered signal matches the original signals put in the ROIs (signal fitting). It is calculated as one minus the square of correlation coefficient (1 – R²) of the component signal and the original signal. Its value varies from 0 (maximum fit) to 1 (no signal fitting).

• Reconstruction SNR is calculated as the SNR of the filtered signal at the frequency of the SSVEP harmonics. This metric indicates how successful the spatial filters are in increasing the SNR of EEG. Here, we calculated it with the same approach as the input SNR and converted it to dB (10log10).

In order to have reliable estimation of the evaluation metrics, we used a Monte Carlo simulation, where for each subject we drew 40 samples each consisting of 20 trials selected randomly (with replacement) from the original set of 200 simulation trials. The spatial filters and evaluation metrics were calculated separately for each sample and then averaged over 40 samples.

Figure 9, top row shows the Angular Error calculated between the topographic maps of the first two components of each spatial filtering method and the lead field of the two source lead fields that were presented in Figure 8. For each spatial filter, the first component had the lowest angular error with the first source (S1) lead field, and the second component had the lowest angular error with the second source (S2) lead field. Therefore, to simplify the figure, we only present the Angular Error of the first component relative to S1 and Angular Error of the second component relative to S2. Among the three spatial filters, PCA has the highest angular error over all SNR values and for both components. Even though RCA and SSD have much lower error than PCA and perform closely in terms of angular error, RCA has lower error than SSD at small SNR values.

Figure 9. Angular Error, Normalized Residuals and Reconstruction SNRs of three spatial filters.

The first columns represent the results of the first components of PCA, RCA and SSD, averaged over subjects and trials. The same results for the second components are presented in the second column.

In terms of Normalized Residuals and for the first component, RCA and SSD perform equally, while PCA has higher residual values. For the second component, the performance of the RCA and SSD does not differ significantly from each other, and PCA has slightly worse performance than the others. For the three methods, residuals of the second components are each worse compared to their respective residuals of the first component.

Finally, the reconstruction SNR of SSD and PCA show similarly shaped functions of SNR, with the SSD curve being shifted upwards by about 15 dB. The RCA reconstruction SNR, by contrast is a linear function of input SNR. For the second component the reconstruction SNR functions increased slower with increasing input SNR and were higher than 0 dB for PCA and RCA only for the input SNRs higher than 0 dB. SSD appears to have a bias that can be seen at low SNR that is not shared by the other methods.

In this section, we presented a simulation example for assessing three spatial filtering methods. We evaluated the ability of these spatial filters to decompose two SSVEP signals placed in different visual ROIs, under different SNR values. Beyond this simple demonstration example, EEGSourceSim can be used to assess and validate spatial filters under different assumptions such as the magnitude of trial-to-trial variability, individual variability or in presence of outliers or various artifacts. By varying the number and locations of SSVEP sources, a more generalized assessment of the filters could also be obtained or filters for particular known sources could be evaluated.

4. Discussion

Here we introduce EEGSourceSim, a realistic EEG simulation framework that incorporates individually-defined forward models, functionally meaningful regions of interest and realistic models of signal and noise. These features of our framework provide greater realism for simulation of scalp EEG signals compared to existing toolboxes. In addition, we provide a general framework that can be used for the evaluation and validation of a wide range of methods used in EEG analysis. As potential applications, we presented examples for source estimation, functional connectivity analysis, and spatial filtering evaluation. A major advantage of our framework is the fact that it can be used to evaluate different analysis pipelines instead of focusing on one specific analysis technique/pipeline. This level of integration is important because some pipeline elements – source estimation and functional connectivity being a key example – are often used in conjunction.

An important feature of our simulation framework is the incorporation of a large data set of individually-defined forward models. Existing simulation toolboxes/studies have relied on average head models (Haufe and Ewald, 2016; Krol et al., 2018) or a single or small number of individual head models (Ahlfors et al., 2010b) for estimating the EEG forward model. Using individual forward models for simulating EEG data is beneficial for a number of reasons. Several studies have indicated higher accuracy of individual head models compared to average head models. For example, Henson et al. (Mattout et al., 2007; Henson et al., 2009) have shown that BEM forward models calculated based on individual head models have higher accuracy than those of calculated using template brains and spherical head models. It is important to note that BEM can be used to improve the accuracy of template-based forward models, as demonstrated by (Darvas et al., 2006; Valdes-Hernandez et al., 2009) who used a template calculated by non-linear averaging MRIs from 152 adult humans (ICBM152) (Fonov et al., 2011). More recently, Huang et al (Huang et al., 2016), used another approach, the Finite Element Method (FEM) to create a forward model based on ICBM152. They showed that the FEM model performs better on source localization and transcranial electric stimulation (tES) targeting than a BEM model based on the same ICBM152 template. However, the BEM and FEM forward models of template brains fall behind the forward models calculated based on the individual brains, in terms of source localization and tES targeting (Huang et al., 2016).

In addition, substantial individual differences in cortical geometry, skull thickness, and the shape of the volume conductor can drastically affect EEG forward and inverse modeling (Von Ellenrieder et al., 2009; Ahlfors et al., 2010b, 2010b). The result is that activity in a specific brain region may result in different scalp topographies and signals across individuals. Accounting for these individual variabilities is essential for evaluation of EEG analysis methods such as source estimation and spatial filtering and this cannot be achieved using average head models. Our large dataset of forward models thus provides more realistic EEG simulations at the individual level and also allows researchers to evaluate methods in the presence of individual variability.

In studies of brain function, a basic assumption is that specific regions of the brain are active and accordingly, simulations should be based on functional ROIs, rather than arbitrary dipoles or parcellations. Because of this, we provide functionally and anatomically defined ROIs for each individual that can be used for designing more realistic source distributions that are functionally meaningful and that can be tailored to the user’s research question. Our approach thus contrasts to those of previous simulation toolboxes that generate synthetic EEG by placing dipoles on the cortical surface or in the gray matter volume with arbitrary location and extents. For example, Haufe et al. (Haufe and Ewald, 2016) divided the brain into eight octants and placed their signal as dipoles located randomly within two of these octants. Even though this simulation can satisfy assumptions needed for some methodological assessments, it does not resemble realistic brain activity and therefore the generalization of the assessments to real EEG data might not be valid. In other simulation studies (Sohrabpour et al., 2016; Barzegaran and Knyazeva, 2017; Krol et al., 2018), the signal was placed manually or in randomly selected dipoles with specific size without taking to account the underlying functional ROIs.

In addition to the unique anatomical dataset (individual forward models, cortical meshes and ROIs), we provide a realistic approach to implementing the dynamics of the EEG signal. Our noise model consists of various elements, each of them simulate noise generated by biological or measurement sources. Coherent pink noise is a biologically plausible model for simulating the brain’s background activity which we fitted on the basis of human intracranial recordings (Kellis et al., 2016). In previous simulation studies, the brain’s background activity is usually simulated either using incoherent white noise (Pascual-Marqui et al., 2014; Barzegaran et al., 2016) or incoherent pink noise (Haufe and Ewald, 2016; Krol et al., 2018). Even though these models of noise replicate the brain’s background activity to some extent, they do not fully conform to direct measurements of cortical activity, i.e they do not take into account the spatial coherence of the pink noise and its frequency dependency. This is of importance specifically in simulation studies of functional connectivity analysis, where these frequency-dependent coherences might result in frequency-dependent biases in estimation of FC. Moreover, previous studies usually do not include an alpha noise component which is one of the most prominent signals that can be recorded from visual cortex using EEG. Therefore, it is essential to be considered in EEG simulation studies of visual cortex.

In addition, in contrast to previous simulation studies, EEGSourceSim estimates the noise parameters, the ratio of pink noise, alpha activity and sensor-level white noise, based on a resting state EEG data set. This provides users with two sets of noise parameters, that corresponds to EEG collected under high and low alpha conditions, that they can choose between according to their interest. Besides the two standard sets of parameters, users also have the option to extend the model by manually selecting parameters that capture the noise environment expected in their paradigms.

EEGSourceSim provides two main approaches for signal modeling: deterministic sinewaves and MAR signal models. The deterministic sinewaves can be used to realistically simulate any sensory SSEP modality by appropriately selecting ROIs. On the other hand, MAR can model the activity of one or a network of interconnected ROIs. Based on the input and the internal dynamics of the ROIs, MAR can generate spontaneous and/or rhythmic brain activities, such as theta or beta like activity, or SSEP or ERP activities. In addition to these two signal models, EEGSourceSim can take an external source signal input, such as an ERP model based on experimental data or any other signal generated by computational models.

Future directions and possible extensions

In the current version of the framework, only BEM forward models are available to the users. Due to identification issues, we are not able to provide original MRI scans of individuals and the defaced MRI scans cannot be used for head modeling (Because of the electrodes located on the face). Therefore, there is a limitation to modify the head models and add additional atlases by the users based on current MRI dataset. However, in the future versions of the framework, more advanced forward modeling approaches such as the Finite Element Method (FEM) can be implemented to increase the realism of EEGSourceSim.

As a feature of this open source toolbox, the other modules of this framework (Figure 3) can be easily accessed and modified to meet the user’s requirements. In terms of signal dynamics, there is a large scope for more realistic signal modeling. More intricate models to simulate complex functional interactions like cross-frequency coupling can be added to the signal model. In addition, more detailed computational models of EEG signal generation such as that provided by the Human Neocortical Neurosolver (https://hnn.brown.edu) could be used instead of the relatively simple signals in the present version. Because the signal modeling is a separate module in this framework, users can use different signal models than the available models and input the generated signal to the framework. In addition, for noise modeling, users can modify the noise parameters or add other models of noise to the source space or sensor space signal according to their requirements.

Conclusion

Given the unknown ground truth (underlying cortical sources) of EEG signals, it is critical to evaluate EEG analysis methods using simulations before applying them to real EEG data. EEGSourceSim provides a highly realistic simulation environment for evaluating a wide range of EEG analysis methods. It provides a powerful assessment tool by taking individual variation into account through the use of individual forward models, ROIs based on cortical anatomy and function, and realistic models of signal and noise.

Highlights.

• We present a highly realistic framework for EEG simulation

• The toolbox includes a large dataset of individual surface-based forward models

• This dataset includes regions-of-interest from visual and whole atlases

• We implement highly realistic models of noise fit to real resting state EEG

• We provide application examples with a set of quantitative evaluation metrics

Abbreviations

AUCPR

Area Under Curve of Precision Recall

BEM

Boundary Element Method

EEG

Electroencephalography

FC

Functional Connectivity

ICoh

Imaginary part of Coherence

MAR

Multivariate Auto Regressive model

MN

Minimum Norm solution

MN-FACE

Minimum Norm solution with Functional Area Constrained Estimator

MRI

Magnetic Resonance Imaging

PCA

Principle Component Analysis

RCA

Reliable Component Analysis

ROI

Region of Interest

SNR

Signal-to-Noise Ratio

SSD

Spatio-Spectral Decomposition

SSEP

Steady State Evoked Potentials

SSVEP

Steady State Visual Evoked Potentials

WPLI

Weighted Phase Lagged Index