Closed-loop vasopressor control: in-silico study of robustness against pharmacodynamic variability

Abstract

Initial feasibility of a novel closed-loop controller created by our group for closed-loop control of vasopressor infusions has been previously described. In clinical practice, vasopressor potency may be affected by a variety of factors including other pharmacologic agents, organ dysfunction, and vasoplegic states. The purpose of this study was therefore to evaluate the effectiveness of our controller in the face of large variations in drug potency, where ‘effective’ was defined as convergence on target pressure over time. We hypothesized that the controller would remain effective in the face up to a tenfold variability in drug response. To perform the robustness study, our physiologic simulator was used to create randomized simulated septic patients. 250 simulated patients were managed by the closed-loop in each of 7 norepinephrine responsiveness conditions: 0.1 ×, 0.2 ×, 0.5 ×, 1 ×, 2 ×, 5 ×, and 10 × expected population response to drug dose. Controller performance was evaluated for each level of norepinephrine response using Varvel’s criteria as well as time-out-of-target. Median performance error and median absolute performance error were less than 5% in all response levels. Wobble was below 3% and divergence remained negative (i.e. the controller tended to converge towards the target over time) in all norepinephrine response levels, but at the highest response level of 10 × the value approached zero, suggesting the controller may be approaching instability. Response levels of 0.1 × and 0.2 × exhibited significantly higher time-out-of-target in the lower ranges (p < 0.001) compared to the 1 × response level as the controller was slower to correct the initial hypotension. In this simulation study, the closed-loop vasopressor controller remained effective in simulated patients exhibiting 0.1 to 10 × the expected population drug response.

1. Introduction

The critical importance of mean arterial pressure (MAP) control in sepsis has been well-established [1–3]. In the operating room, cumulative hypotension has been shown to contribute to increased stroke risk [4], acute kidney injury [5], myocardial injury [6], and overall mortality [7]. Even short periods of hypotension, however, may be sufficient to increase morbidity [8, 9], and two large studies have recently confirmed that even mild hypotension still increases overall mortality risk in this population [10, 11].

When MAP targets in strictly-defined clinical protocol studies are compared to the observed results of those studies, providers often systematically overshoot the target by as much as 20 mmHg [12–18]. The original Rivers’ protocol targeted a MAP of 65 mmHg and even included specific instruction to initiate a vasodilator if MAP exceeded 90 mmHg, but pressures in the study routinely were recorded in the mid 1990s, more than 30 points above target [17]. Other studies have shown that higher targets (above 90 mmHg, for example), are routinely undershot in the results by 10–15 mmHg [1, 18]. More recent studies have confirmed these biases and error rates [19]. These are protocols being followed in the best of conditions, under close observation in studies, and are probably not representative of the variation that occurs outside of study conditions, which is likely larger. The reasons for these errors in hitting targets are obviously thought to be multifactorial, but definitely include provider workflow problems and human biases [1, 20].

Thus, regardless of why it is initiated, once the decision to put a patient on a vasopressor infusion is made, the published evidence shows quite clearly that there is poor accuracy and precision in keeping that target. Titration of vasopressor to achieve a specific target is a task a computer controller can perform well and for which it is ideally suited. Our group has previously brought a closed-loop infusion system for goal-directed fluid therapy from bench testing to clinical use, and have now turned our focus to vasopressor control.

Initial feasibility of a novel closed-loop controller created by our group for closed-loop control of vasopressor infusions has been previously described [21]. The controller has been shown to function acceptably in the fact of varying degrees of infusion line delay [21] and pharmacokinetics (altered drug metabolism speed) [21]. Another major source of potential clinical variability would be pharmacodynamic variability. In clinical settings (and especially in critically ill patients in whom vasopressor therapy may be indicated), vasopressor potency may be affected by a variety of factors including other pharmacologic agents, organ dysfunction, and vasoplegic states. Thus, robustness to this potential variability must be established as a safety prerequisite before clinical testing would be appropriate. The purpose of this study was therefore to evaluate the performance of our controller in the face of large variations in drug potency. Our hypothesis was that the system would tolerate a tenfold variability in simulated patient response (drug potency) to a given dose of vasopressor while still remaining effective. “Effective” in this context was defined as convergence on MAP target over time.

2. Methods

The present study did not involve human subjects and was performed entirely in-silico, and was therefore IRB exempt.

2.1. Closed-loop vasopressor controller

The vasopressor infusion controller has been described previously [21]. Briefly, the controller was developed in Microsoft Visual C (Microsoft Corp, Redmond WA) and has three main layers which calculate output. In effect, these three layers represent a diagnostic layer (collecting and processing the incoming data), a prescriptive layer (whereby the processed data is converted into an error signal), and a treatment layer (where the error signal prescription is converted into a treatment dose).

The first layer is a data collection and management layer that collects incoming vital signs data and current controller output, filters the data for obvious error, stores the values, and calculates additional real-time derived values like a moving-average infusion rate and a time-delayed infusion rate. In the present study, blood pressure data was sampled from the simulator once a second. Since the previous publication [21], the derived measure of ‘mean MAP over time’ in the data module has been replaced with ‘filtered MAP’. This measure is MAP run through an infinite-impulse response low-pass filter (IIRLPF) using the same methodology as Görges and colleagues in their report of an online system identification methodology [22]. Compared to mean MAP, the IIRLPF value remains robust to noise in the input data, but more rapidly trends change in MAP value compared to a straight time-averaged value.

The second controller layer is a proportional-integral-derivative (PID) control layer which uses the IIRLPF MAP as input, compares this to the user-defined MAP target, and outputs an adjustment control value. The proportional and derivative errors are dampened in a run-time user-configurable region above and below the target MAP referred to as ‘tolerance zones’ in which blood pressure error is corrected less aggressively. These regions are designed to allow the user to designate the preferred direction of error from target. Since MAP error in vasopressor treatment is usually preferred to be over-target instead of under-target, the default tolerance zones are 2 mmHg below target and 5 mmHg above.

The PID calculated adjustment value is then passed to the final layer of the controller, a rules-based component that takes the adjustment control value and converts it into a drug dose change specific to the vasopressor being infused. The rules component also includes run-time configurable infusion rate limits (upper and lower) to restrict the range of dose the controller may titrate within, and dose-changes-per-minute limits (to accommodate infusion pump capability limits where needed, as well as input sources that do time-averaging of output vital signs).

2.2. Simulation environment

To perform the robustness study, our physiologic simulator was used to create randomized simulated patients. The simulator was built in Microsoft Visual C++ and the design has been described extensively in previous publications [23, 24], includes a core model based on Guyton and work by other authors [25, 26] and has recently been upgraded to include a detailed right heart and pulmonary circulation model [23].

In preparation for the current study, generic vasopressor drug responses were replaced with an explicit drug model for norepinephrine. The drug characteristics were drawn from available sources [12, 27–29]. Administration was not immediate, but rather delayed by a configurable time-span of seconds. For this study the delay value was fixed at 12 s (short delay). Robustness against longer infusion delays has been previously evaluated [21]. After the injection delay, the new dose is added to the plasma and the plasma concentration (including any existing drug concentration) is recalculated. Finally, the plasma drug concentration was used to determine the physiologic effect of the drug. Elimination from the plasma was then modeled as a first-order process directly dependent on drug plasma concentration for this study.

The concentration-response curve for norepinephrine in the model approximates a logarithmic curve in shape—rapid rise with small plasma concentrations with decreasing returns for progressively larger dosing. The actual formula for the effect is in the form:

$$\text{Alpha\_effect = }\left[\mathrm{1 }- (\text{MD50}/(\text{MD50}+\text{Norepi\_Plasma\_Concentration}))\right]\times 100$$

where MD50 is the value for the dose of norepinephrine that produces half of the maximum possible patient response and Alpha_effect is a number from 0 to 100 that is factored into the vascular tone of both the arterial and venous trees. For variation of the patient response levels tested in the protocol (detailed below), the MD50 value was varied.

2.3. Robustness testing

In order to test robustness against patient-based variability in potency, two sets of Monte-Carlo simulations were run using the closed-loop vasopressor (“CLV”) controller to manage a vasopressor infusion in simulated patients. The patient simulator was run on one PC, and the CLV controller run on a second networked PC. The simulator transferred packets that contained a time-stamp along with blood pressure (systolic, diastolic, and mean arterial pressure; SBP, DBP, and MAP respectively), heart rate (HR), and the ‘last received’ infusion rate as a communication confirmation to the CLV controller. The CLV controller in turn transferred back to the simulator timestamped packets that contained a drug name and an infusion rate in micrograms per minute.

The first set of simulated patients were otherwise ‘healthy’ cardiovascular patient models with weights from 60 to 120 kg and a fixed amount of septic shock added to the model. “Shock Factor” in the simulator is a dimensionless number that ranges from 0 to 10 and determines how much pathologic dilation is applied to the systemic arteries and veins. In practice, numbers below 2 have little effect, and above 8 are usually “fatal” (meaning the simulator pressure and flow falls to zero). The shock factor was randomized to a starting value of 4–6 which resulted in a starting MAP of mid-40’s to mid-50’s (though interactions with the randomized patient weights and core inter-patient cardiovascular system difference sometimes resulted in small baseline aberrations outside of this range). In this series of simulations, the shock factor was kept constant in order to evaluate the performance and stability of the controller in the face of patient pharmacodynamic variability on an otherwise stable system (the “Stable” group).

The second set of simulated patients were set up at baseline identically to the first set of patients, but during the simulation run the shock factor would wander at random time to new random values in a wider range (3.5–7; the “Dynamic” group). The process worked as follows: each second, the simulator had a 1/900 chance of choosing a new shock factor target in the range of 3.5–7.0. This should result in approximately 1 change of shock factor every 15 min on average. When a new target is chosen, the shock factor then moves toward the new target at one of three rates chosen at random: 0.1 per 3s, 4s, or 5s. This created a more challenging scenario for the CLV controller to manage in order to assess the impact of patient pharmacodynamic variability on general performance characteristics of the controller.

In both simulation groups norepinephrine was used as the vasopressor for CLV control. The controller was configured to target a MAP of 70, with no limits on minimum or maximum drug dose. The expected mean population response to a given dose of norepinephrine (established from the drug characteristic references noted above) was a priori set as the “standard” response, or 1 × magnitude response. Based on that standard, individual simulated patients in both groups were randomly configured to respond to a dose of norepinephrine at factors of 0.1 ×, 0.2 ×, 0.5 ×, 1 ×, 2 ×, 5 ×, or 10 × compared to the standard (“patient norepinephrine response levels”). The closed-loop system was blind to the patient response factor; it received only blood pressure and heart rate data over the network as noted above. All simulation scenarios ran for 1 h of simulated time. In each group (Stable and Dynamic), each norepinephrine response level was run 250 times, an arbitrary number expected to provide an adequate sample for analysis.

2.4. Analysis

In the Stable scenarios, controller performance was evaluated for each level of norepinephrine response using Varvel’s criteria [30] (median performance error (“MDPE”), median absolute performance error (“MDAPE”), wobble, and divergence), as well as quantification of total time out of target in specific ranges (± 0–5 mmHg, ± 5–10 mmHg, and ± > 10 mmHg) and graphically via spaghetti plots. Acceptable safety performance for a given norepinephrine response level was a priori defined as negative divergence (i.e., convergence on target pressure over time). In the Dynamic scenarios, Varvel’s criteria would be inappropriate given the changing sepsis background (terms like divergence and wobble are not directly accessible when the background shock factor is changing since the controller performance is being affected by outside forces), so performance was evaluated with time-out-of-target criteria and graphically.

Results are reported as percentages, or as mean ± standard deviation. Analysis was performed using Microsoft Excel and R (https://www.r-project.org).

3. Results

A total of 3500 simulated patients were run in a 60-min CLV management scenario: 250 patients in each of 7 norepinephrine response levels in the Stable simulations group, and 250 in each of 7 norepinephrine response levels in the Dynamic simulations group. There were no controller software or network communication errors encountered during the simulations.

In the Stable simulations group, CLV controller performance measures for each norepinephrine response level are shown in Table 1. MDEP was less than 4% in all response conditions, was lowest (< 1%) in the 0.5, 1, and 2 × response levels, and increased more rapidly in the higher response levels than the lower levels. Similar trends were seen in MDAEP (all values < 4.1%, lowest values in 0.5, 1, and 2 × response levels) and wobble (all values < 2.7%, lowest values in 0.5, 1, and 2 × response levels). Divergence remained negative (i.e. the controller tended to converge towards the target over time) in all norepinephrine response levels, but at the higher response level of 10 × the value approached zero, suggesting the controller may be approaching instability. As predicted by the divergence measure, oscillation measurement and graphing reveals that the 10 × response level did indeed begin exhibiting oscillations. The amplitude and frequency of the oscillations was 4 mmHg at 18–22 cycles per hour. The oscillations were persistent but remained stable and did not increase in amplitude.

Table 1.

Performance criteria for closed-loop vasopressor controller in stable sepsis simulation scenarios with differing norepinephrine pharmacodynamics

Norepinephrine response level	MDPE (%)	MDAPE (%)	Wobble (%)	Divergence (%) m−1	Oscillation (cycles h−1)	Oscillation amplitude (mmHg)
0.1 ×	1.0	1.2	0.5	− 7.1	-	-
0.2 ×	0.9	1	0.6	− 4.6	-	-
0.5 ×	0.7	0.8	0.4	− 2.3	-	-
1 ×	0.7	0.7	0.3	− 1.2	-	-
2 ×	0.6	0.7	0.4	− 1	-	-
5 ×	0.7	0.7	0.4	− 0.3	-	-
10 ×	1.2	1.2	1.0	− 0.1	18–22	4

MDPE median performance error, MDAPE median absolute performance error; definitions (including wobble and divergence) found in Varvel et al. [30]

Oscillation and Oscillation Amplitude—the frequency of cycling of the MAP around the target, and the total pressure change (maximum–minimum) during a cycle

Measurement of the time-out-of-target for the different response levels in both the Stable and Dynamic scenarios are shown in Table 2. Response levels of 0.1 × and 0.2 × exhibited significantly higher time-out-of-target in the lower ranges (p < 0.001) compared the 1 × response level as the controller was slower to correct the initial hypotension. In the Dynamic scenarios, the majority of the timeout-of-target was within 5 mmHg of the target, the exception being the 0.1 and 0.2 × response levels which showed significant lag in initial correction.

Table 2.

Heat map of percentage of time outside of target range by norepinephrine response factor

	Stable Sepsis						Dynamic Sepsis
Norepinephrine Response Level	Under Target			Over Target			Under Target			Over Target
	>10 mmHg	5–10 mmHg	0–5 mmHg	0–5 mmHg	5–10 mmHg	>10 mmHg	>10 mmHg	5–10 mmHg	0–5 mmHg	0–5 mmHg	5–10 mmHg	>10 mmHg
0.1 ×	8.5	4.8	8.4	0.0	0.0	0.0	8.4	7.3	13.6	5.1	2.6	1.2
0.2 ×	5.3	2.8	4.1	0.0	0.0	0.0	4.3	4.0	12.8	5.5	1.4	0.1
0.5 ×	2.7	1.4	1.9	0.0	0.0	0.0	2.8	2.1	8.7	5.1	1.0	0.1
1 ×	1.7	0.8	1.0	0.0	0.0	0.0	1.6	0.9	5.4	2.6	0.1	0.0
2 ×	0.9	0.4	2.2	0.0	0.0	0.0	0.9	0.4	5.4	1.2	0.0	0.0
5 ×	0.6	0.9	0.8	0.0	0.0	0.0	0.6	1.0	4.3	0.9	0.0	0.0
10 ×	0.5	0.7	0.8	0.3	0.0	0.0	0.6	1.3	2.8	1.1	0.0	0.0

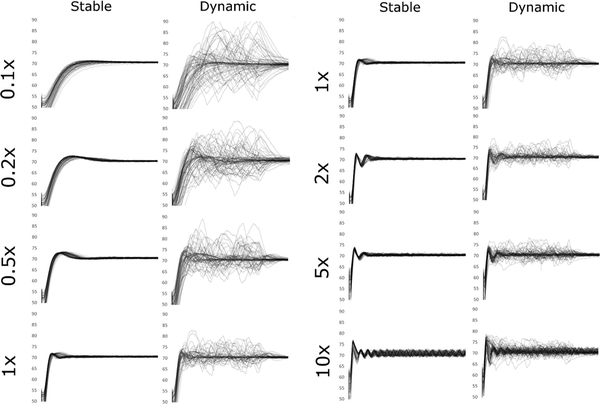
Spaghetti plots of the MAP for each individual run in both scenarios are shown in Fig. 1. These confirmed visually what the measured performance values showed numerically. First, in the Stable Sepsis simulations, both speed of correction and overshoot increase as norepinephrine response level increases, but on the high side oscillations begin to appear at the 10 × level. These oscillations persist but appear to remain stable over time. In the Dynamic Sepsis simulations, the lower response levels show very slow correction of perturbations of MAP.

Fig. 1.

Mean arterial pressure plots from each study condition. Each individual 60-min simulation run is represented by a single line in the graph for each condition. In the Stable conditions the simulated patient has a constant degree of vasodilation applied. In the Dynamic conditions, the background vasodilation ‘wanders’ at random to new values, creating a more challenging management condition for the controller. Moreover, the rate of change of the background vasodilation was allowed to occur very quickly to challenge the controller. 0.1 ×, 0.2 ×, and so on refer to the simulated patient norepinephrine response relative to the standard “1 ×” response patient

4. Discussion

In the present in-silico study, we have shown that the CLV controller is robust to variability in simulated patient pharmacodynamics—specifically the inter-patient variability in vasopressor potency. At extremes on the low end of responsiveness (0.1 × and 0.2 × expected response) the controller is slower to correct disturbances relative to normal response ranges. While correction speed becomes sub-optimal and the patient therefore spends more time out of target than ideal, the controller remains safe from the standpoint of making the correct adjustments in response to changes in blood pressure. At extremes on the high end of responsiveness (10 × expected response), the controller begins to oscillate (the blood pressure swings back and forth across the target without settling) because the controller cannot make a small enough change to avoid overshooting back and forth. Alternately, in the higher responsiveness ranges corrections to disturbances are very fast (Fig. 1), demonstrating the inevitable trade-off between speed and stability that all controllers must weigh. Based on the observed results, if properly tuned to the typical population pharmacodynamic response for a drug, the present controller should remain stable so long as specific patient pharmacodynamics remain within an order of magnitude (either 10 × greater or lesser) of expected.

In comparison to published results, time out of target for all tested patient response levels were still excellent. Lamontagne et al., in studying a population with a reported target of MAP 65–70 for non-neurologic vasopressor treatment, report 6% of management time 5 mmHg or more below target, and 37% management time 10 mmHg or more above target. The average MAP in that study was 72 with a standard deviation of 10 mm Hg. Comparison data collected by the authors from their own institutions from routine clinical use showed similar patterns (~ 10% time significantly below target, 30% or more time significantly above target) [31]. In the present study, by comparison, once the system has had a chance to begin treatment the steady group patients across all patient response levels spent 1.3% of management time 5 mmHg or more below and 0% of management time 10 mmHg or more above target, with a standard deviation of 1.3 mmHg. In the dynamic group across all patient response levels, once the system began treatment patients spent 3.5% of management time 5 mmHg or more below target and 5.6% of management time 10 mmHg or more above target, with a standard deviation of 3.0. Thus, the results obtained in the present study would represent a significant reduction in the variability seen in standard practice if they hold in in-vivo practice.

Additional improvements to the controller may make it more effective. First, a relatively straightforward enhancement would be allowing the supervising healthcare provider some ability to adjust the controller in response to observed performance. Even three basic settings (like ‘low’, ‘normal’, and ‘high’ gain) would permit the user to increase speed of response in patients who were sluggish responders and to decrease response in patients who were showing evidence of oscillation during treatment. Moreover, oscillation detection is something that can be done by the software itself [32], and a recommendation made to the user or even automatic adjustment to the controller made by the software itself. Finally, the oscillation observed in the highly norepinephrine-responsive patients may result in part from the intrinsic time-delay of the system; in this set of simulations drip adjustments were delayed by 12 s of simulated time to represent lag in the infusion line, and an additional 5–10 s for the drug to be ‘circulated’ in the patient model and reach receptor sites. In clinical practice it is obviously impossible to remove these delays between rate changes and effect-site concentration changes, and they may well be longer than 17–22 s. While we have shown the controller is stable with longer delays (up to 60 s) [21], it may be possible to identify the specific delay and patient responsiveness during operation and adjust therapy accordingly [22].

Unlike more traditional engineering fields like manufacturing, controllers dealing with biologic systems must more often deal with input-to-effect time delays that are longer, and the effect of a steady input may result in varying effect from one moment to the next as other elements of the underlying physiology change (time-dependent intra-patient variability). These differences in general mean that biologic systems require a slower and more incremental control model than applications like manufacturing (where exact weights, accelerations, and so on can be consistently and precisely calculated) allow. On the other hand, even very slow but constant titration of vasopressors will likely represent a significant improvement over the hand-titration which is the current standard of care.

Like any controller, physiologic closed-loops must also deal with unpredictable outside disturbances. Interventions like changes in anesthetic depths, administration of other medications, changes in surgical stimulation or blood volume, and more may all affect the underlying relationships between vascular tone, arterial blood volume, and cardiac output that determine blood pressure. The random disturbances in the present work were implemented as changes in the underlying physiologic vascular tone, so would most closely mimic clinical disturbances acting the same way (changes in the degree of vasoplegia from shock, changes in anesthetics, etc.). Clinical disturbances like blood loss will need to be assessed independently with regards to interactions with this type of closed-loop control.

Moreover, there will be additional clinical considerations that will require careful safety planning and oversight during use. The quality of the arterial waveform, for example, will be important; dampening of the signal or mis-placement of the transducer relative to the patient’s heart will lead to erroneous input. Clinical developments like hemorrhage will need treatment independent of vasopressor, and in fact vasopressor titration by a closed-loop may actually mask symptoms of hemorrhage if the supervisor is unaware of the increasing dose requirements as the hemorrhage progresses. Ideally, integration with additional inputs like depth of anesthesia would help the system obtain a holistic view of the patient under management. Obviously, significant clinical evaluation will be required to ensure acceptable operation and supervisor awareness of the system state.

4.1. Limitations

The present study has examined drug response ranges from 0.1 to 10 times the expected population response. It is possible that individual patients may nevertheless have responses which fall outside of this range. On the low end this would likely represent futile treatment (titration of a drug that is having virtually no effect on blood pressure), and on the high end this could result in dangerous oscillation of the blood pressure and outright control instability. Before clinical use, both of these possibilities must be accounted for with safety protocols and detection routines in the controller. Additionally, while we have looked independently at infusion line lag times of up to 60 s and delayed metabolism of drug mass in our previous work, the variability in pharmacodynamics examined in the present study have not been examined in detail in combination with the above factors. Finally, as with any simulation study, the results obtained herein compared to clinical use will depend on how closely the patient model reflects reality. As all models are simplifications of the modeled system, careful observation is warranted in an in-vivo model in order to detect differences in behavior in clinical use.

5. Conclusion

In this Monte Carlo simulation study, the closed-loop vasopressor controller remained effective in simulated patients exhibiting 0.1–10 × the expected population drug response.