3D-T_1ρ Prepared Zero Echo Time-Based PETRA Sequence for In Vivo Biexponential Relaxation Mapping of Semisolid Short-T₂ Tissues at 3 T

Abstract

Background:

In addition to the articular cartilage, osteoarthritis (OA) affects several other tissues such as tendons, ligaments, and subchondral bone. T_1ρ relaxation study of these short T₂ tissues may provide a more comprehensive evaluation of OA.

Purpose:

To develop a 3D spin-lattice relaxation in the rotating frame (T_1ρ) prepared zero echo time (ZTE)-based pointwise encoding time reduction with radial acquisition (3D-T_1ρ-PETRA) sequence for relaxation mapping of semisolid short-T₂ tissues on a clinical 3 T scanner.

Study Type:

Prospective.

Population:

Phantom, two bovine whole knee joint and Achilles tendon specimens, 10 healthy volunteers with no known inflammation, trauma or pain in the knee or ankle.

Field Strength/Sequence:

A customized PETRA sequence to acquire fat-suppressed 3D T_1ρ-weighted images tissues with semisolid short ${\text{T}}_2/{\text{T}}_2^{*}$ relaxation times in the knee and ankle joints at 3 T.

Assessment:

Mono- and biexponential T_1ρ relaxation components were assessed in the patellar tendon (PT), anterior cruciate ligament (ACL), posterior cruciate ligament (PCL), and Achilles tendon (AT).

Statistical Tests:

Kruskal–Wallis with post-hoc Dunn’s test for multiple pairwise comparisons.

Results:

Phantom and ex vivo studies showed the feasibility of T_1ρ relaxation mapping using the proposed 3D-T_1ρ-PETRA sequence. The in vivo study demonstrated an averaged mono-T_1ρ relaxation of (median [IQR]) 15.9 [14.5] msec, 23.6 [9.4] msec, 17.4 [7.4] msec, and 5.8 [10.2] msec in the PT, ACL, PCL, and AT, respectively. The bicomponent analysis showed the short and long components (with their relative fractions) of 0.65 [1.0] msec (46.9 [15.3]%) and 37.3 [18.4] msec (53.1 [15.3]%) for PT, 1.7 [2.1] msec (42.5 [12.5]%) and 43.7 [17.8] msec (57.5 [12.5]%) for ACL, and 1.2 [1.9] msec (42.6 [14.0]%) and 27.7 [14.7] msec (57.3 [14.0]%) for PCL and 0.4 [0.02] msec (58.8 [13.3]%/) and 31.3 [10.8] msec (41.2 [13.3]%) for AT. Statistically significant (P≤ 0.05) differences were observed in the mono- and biexponential relaxation between several regions.

Data Conclusion:

The 3D-T_1ρ-PETRA sequence allows volumetric, isotropic (0.78 × 0.78 × 0.78 mm), biexponential T_1ρ assessment with corresponding fractions of the tissues with semisolid short ${\text{T}}_2/{\text{T}}_2^{*}$.

SPIN-LATTICE RELAXATION in the rotating frame (T_1ρ) has been proposed for different musculoskeletal applications such as detecting early-stage osteoarthritis (OA).¹ The T_1ρ relaxation time can quantify the biochemical changes associated with proteoglycans (PG), water content, and disruption of collagen and anisotropy.¹

In addition to hyaline articular cartilage, OA affects several other tissues such as the deep meniscus, tendon, ligament, radial and calcified layers of cartilage, and subchondral bone. Hence, T_1ρ and T₂ relaxation study of these tissues may provide a better evaluation of OA.^2,3 However, these highly organized anisotropic tissues have very short T₂ values and as a result are not visible in the images acquired by standard sequences (GRE or FSE) with echo times (TEs) in the range of few milliseconds. Ultrashort echo time (UTE)⁴ and zero echo time (ZTE)-based pulse sequences⁵ employ specialized acquisition and reconstruction techniques to visualize semisolid short-T₂ tissues in vivo.

In UTE pulse sequences, the data acquisition starts as soon as possible after application of the RF pulses. The readout gradient is turned on at the same time, and the data are acquired on a center-out k-space trajectory such as radial,⁴ spirals,⁶ cones,⁷ or twisted projections⁸ in 2D or 3D mode.

Similar to UTE techniques, in ZTE pulse sequences the data acquisition starts with minimum delay after RF excitation. However, unlike UTE, the readout gradients are turned on before application of the RF pulse,⁵ and hence, the center of k-space is traversed at the echo time of zero. Due to a mandatory delay for switching the hardware from transmitting to receive mode, the center of k-space is not sampled, and data acquisition begins at some minimum k-space radius. Several strategies are proposed in the literature to fill in the center of k-space such as algebraic reconstruction,⁹ single-point imaging (SPI),¹⁰ and water- and fat-suppressed proton projection (WASPI).¹¹

The comparison of ZTE and UTE sequences in qualitative knee imaging has been discussed in previous studies.^12,13 Lee et al¹² showed that both UTE and ZTE pointwise encoding time reduction with radial acquisition (PETRA)¹⁰ sequences could visualize the short T₂ tissues and the signal intensity in the images from both sequences was significantly lower in the patients with a meniscal tear in comparison with the normal group. The PETRA images also showed significant differences between the normal group and patients with degenerated menisci. In another study, Larson et al¹³ reported similar contrast and signal-to-noise ratio (SNR) efficiency between ZTE and UTE pulse sequences for volumetric imaging of ultrashort T₂ components at 7 T. The UTE images suffer from fidelity artifacts, while shading artifact was observed in ZTE images. However, methods of correction for both of these artifacts exist.¹³ Radial UTE MRI sequences can also suffer from image blurring because of off-resonance and fast ${\text{T}}_2^{*}$ signal decay. Kobayashi et al¹⁴ proposed a gradient-modulated technique to reduce the blurring for the PETRA sequence.

For quantitative imaging of fast-relaxing tissues, different techniques such as the 3D-UTE,^7,15 the 2D-UTE,^16–18 and the stack of spirals (AWSOS),¹⁹ have been proposed. Du et al proposed a UTE-T_1ρ sequence for imaging the meniscus and Achilles tendon.²⁰ Other studies have investigated the suitability of quantitative ${\text{T}}_2^{*}$ mapping in the Achilles tendon.^21,22 Moreover, Williams et al²³ proposed measuring ${\text{T}}_2^{*}$ as a marker for subclinical changes in menisci after an anterior cruciate ligament tear.

Different water compartments in the tissues have different T_1ρ or T₂ relaxation components. For example, in most of the knee joint structures, including patellar tendon (PT), posterior cruciate ligament (PCL), and anterior cruciate ligaments (ACL), have both dominant bound/restricted water compartment associated with collagen and/or proteoglycans, and minor less restricted / free water compartment associated with macromolecules. Several studies showed the short component sensitivity to pathology by comparing the short ${\text{T}}_2^{*}$ component between healthy and patient groups.^24,25 In this article we propose a technique based on PETRA¹⁰ sequence for biexponential T_1ρ relaxation mapping in the semisolid short ${\text{T}}_2/{\text{T}}_2^{*}$ relaxing tissues such as tendons and ligaments.

Materials and Methods

3D-T_1ρ-PETRA Pulse Sequence

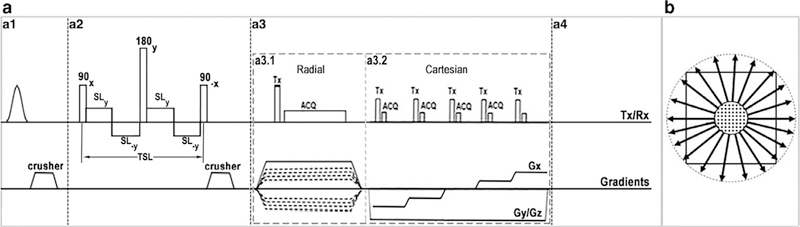
Figure 1 illustrates the pulse sequence diagram and k-space trajectory of the 3D T_1ρ-PETRA sequence. The PETRA sequence¹⁰ was modified to integrate the T1_ρ preparation module with the capability of varying the spin-lock pulse duration. The sequence consists of an optional chemical shift-based fat suppression module (Fig. 1.a1), self-compensated paired T_1ρ preparation module (Fig. 1.a2), PETRA hybrid readouts (Fig. 1.a3), and a delay for longitudinal magnetization recovery for reducing T₁ contamination (Fig. 1.a4).

FIGURE 1:

3D-T_1ρ-PETRA (a) pulse sequence diagram and (b) k-space trajectory. (a1) Fat suppression module. (a2) self-compensated paired T_1ρ preparation module. (a3) PETRA acquisition: (a3.1) radial and (a3.2) Cartesian SPI parts. (a4) Longitudinal magnetization restoration delay. (b) k-space trajectory. The k-space center is filled with Cartesian SPI while the rest is filled using the radial acquisition.

The T_1ρ preparation module starts with a 90 excitation pulse along the x-axis followed by a low-power spin lock pulse along the y-axis and a −90 pulse in the x-axis to tip the magnetization back to its initial direction along the z-axis. A 180 refocusing pulse was applied along the y-axis in the middle of the module to compensate for the B₀ inhomogeneity effect. Moreover, the spin-lock pulse was divided into four segments with altering phase to compensate the B₁ inhomogeneities.²⁶

The PETRA imaging sequence consists of two readouts (radial, and a Cartesian single point imaging [SPI]) acquisition part and has been described previously.¹⁰ The high spatial frequency data are acquired using radial spokes evenly distributed over a sphere in the k-space (Fig. 1.a3.1) while the center of k-space is acquired in the Cartesian part, which results in a low-resolution image.¹⁰ In this method, the gradients are turned on first, and after the gradient ramp up, a hard low flip angle pulse is applied followed immediately by readout after a necessary delay time for T/R switching. The gradients have constant amplitude during the excitation and readout. The center of k-space was not sampled in the radial part since it is located at the center of the excitation pulse before the mandatory delay of 70 μs for hardware switching. These essential missing central k-space points are acquired in the Cartesian part of the sequence, one by one, with a stepwise variation of the gradient amplitude (Fig. 1.a3.2).¹⁰ The overall acquisition scheme is segmented in the sense of adding one T_1ρ preparation module before each segment of n consecutive PETRA acquisitions and one delay time after each segment. The contrast-relevant inner Cartesian part of k-space is reordered according to the distance to the center of k-space such that the amount of T_1ρ weighting is strongest for the points closest to the center of k-space.

Fat suppression was achieved by adding a fat suppression pulse¹⁰ in front of the T_1ρ preparation module for each segment.

Quantitative measurement of T_1ρ was achieved by acquiring 3D-T_1ρ-PETRA scans at a series of spin-lock times (T_sl).

The implementation of the reconstruction is based on the Grodzki et al method,¹⁰ which provides clinical image quality. The weight of the radial sampling points is scaled inversely to the sampling density and adapted to the density of the Cartesian grid at the center of k-space to ensure a smooth transition between radial and Cartesian sampling.

T_1ρ Relaxation Mapping

The monoexponential relaxation times were calculated voxel-by-voxel by fitting the signal intensity decay over time to:

$$S\left(T_{sl}\right)=f_m\exp \left(-\frac{{\text{T}}_{\text{sl}}}{{\text{T}}_{1\text{ρ},\text{m}}}\right)+{\text{s}}_0$$ (1)

Where f_m is the amplitude of the exponential term, T_1ρ,m is the monoexponential relaxation time, T_sl is the spin-lock pulse duration, and s₀ is a constant considering the residual noise.

Subsequently, the biexponential relaxation components were calculated in the same manner by fitting the data to:

$$S\left(T_{st}\right)=f_s\exp \left(-\frac{{\text{T}}_{\text{sl}}}{{\text{T}}_{1\text{ρ},\text{s}}}\right)+f_l\exp \left(-\frac{{\text{T}}_{\text{sl}}}{{\text{T}}_{1\rho ,\text{l}}}\right)+s_0$$ (2)

Where T_1ρ,s and T_1ρ,l corresponds to the short and long relaxation time components, respectively. 0 ≤ f_s ≤ 1 and f_l = 1 – f_s are the fractions of the short the long components, respectively.

In the final biexponential fitting map, the pixels that did not satisfy the following conditions were excluded from the map:

$$\left(f_s>{\alpha }_s\right)\&\left(f_l>{\alpha }_l\right)\&\left(F_{\text{ratio}}>{\alpha }_F\right)$$ (3)

where α_s and α_l are the minimum short and long fractions as was set to 10%²⁷ and α_F = 4.32 are the threshold based on the P = 0.1 F-distribution table for p₁ = 2 and p₂ = 4 degree of freedom in the mono- and biexponential models, respectively. The F_ratio is calculated as:

$$F_{ratio}=\frac{\frac{SS{E}_m-SS{E}_b}{p_2-p_1}}{\frac{SS{E}_b}{L-p_2}}$$ (4)

where SSE_m and SSE_b are the sum of square error for the mono- and biexponential models, respectively. L is the number of T_sl timepoints acquired for fitting.²⁷

Monte Carlo Simulations

The sensitivity of the biexponential fitting procedure to SNR, number of acquired T_sl, as well as the fitting error for tissues with different relaxation values was explored with Monte Carlo simulations. A set of signals was generated with a different set of T_sl, SNR, and T_1ρ relaxation times. A random complex noise with normal distribution N(0, σ) with σ = 1/^SNR was added to the signal. The magnitude of the complex signal is then used as a signal with Rician noise. The relaxation components were then estimated by fitting the biexponential model to the noisy signal. The process was repeated for 1000 independent noise trails, and the median of normalized absolute deviation (MNAD) was calculated for each parameter as:

$$\mathit{M}\mathit{N}\mathit{A}\mathit{D}=\mathit{m}\mathit{e}\mathit{d}\mathit{i}\mathit{a}\mathit{n}\mathbf{\left(}\frac{\left|{\mathit{y}}_{\mathit{e}}-{\mathit{y}}_{\mathit{a}}\right|}{\left({\mathit{y}}_{\mathit{e}}+{\mathit{y}}_{\mathit{a}}\right)/\mathbf{2}}\mathbf{\right)},$$ (5)

where y_a and y_e are the actual and estimated values, respectively.

Phantom Study

The 3D T_1ρ-PETRA techniques were applied to a phantom consisting of a tube of 3% agarose (simulating biological tissue or cartilage),²⁸ a tube of vegetable oil (simulating fat), and a piece of a rubber eraser, simulating the tissue with semisolid short T₂ relaxation times. T_1ρ-weighted scans were acquired with spin-lock frequency (F_sl) = 500 Hz at different T_sl including 0 msec, 0.5 msec, 1 msec, 2 msec, 3.5 msec, 5 msec, 10 msec, 20 msec, and 30 msec. The fat suppression and T_1ρ preparation modules were applied at every 26 readouts to minimize the image acquisition time, resulting in a segment size of 26. The imaging parameters were repetition time / echo time (TR/TE): 5/0.07 msec, field of view (FOV): 200 × 200 mm, flip angle: 6, slice thickness: 0.78 mm, matrix size = 256 × 256 × 256, nominal voxel size: 0.78 × 0.78 × 0.78 mm, receiver bandwidth = 399 Hz/px, T₁ recovery delay = 500 msec, number of radial spokes = 8000, number of segments = 350, number of readouts in each segment = 26, and number of Cartesian sample points = 1419. The total scan time was 33:45 minutes. To avoid any slice selectivity of the pulse, a short RF excitation pulse (60 μs), was used to enable higher excitation bandwidths; however, the flip angle is limited due to maximum available B₁ and specific absorption rate (SAR) constraint.¹⁰

Ex Vivo Bovine Study

Fresh bovine whole knee joint and Achilles tendon specimens (n = 2) were obtained from a slaughterhouse (Max Insel Cohen, Livingston, NJ). The tissue was covered with Parafilm to avoid dehydration during the MRI scans. The tissues were at MRI room temperature before starting the scans. T_1ρ-weighted images were acquired from the specimens. The scans were performed in the sagittal plane with F_sl = 500 Hz at nine different T_sl including 0 msec, 0.5 msec, 1 msec, 2 msec, 3.5 msec, 5 msec, 10 msec, 20 msec, and 30 msec. To examine the T₁ effect on the T_1ρ estimation, the ex vivo bovine specimen experiments were repeated with a 2-sec T₁ restoration delay. The rest of the parameters were kept the same. The total scan time was increased to 112:57 minutes. The actual T₁ value of the ex vivo bovine specimens were also measured by acquiring T₁-weighted scans with 13 different inversion recovery times (TI) including 100 msec, 200 msec, 300 msec, 400 msec, 500 msec, 600 msec, 700 msec, 800 msec, 900 msec, 1000 msec, 1200 msec, 1500 msec, and 2000 msec using the same PETRA readout.

In Vivo Study

Ten healthy volunteers without any clinical symptoms of OA or other knee injuries were recruited for knee and ankle study (five volunteers for each study) with a mean age of 30 ± 4 years, mean weight of 63 ± 15 kg, and mean height of 169 ± 12 cm. The study was approved by the Institutional Review Board (IRB), and all the volunteers provided written informed consent prior to the MRI scan. All the scans were performed on a 3 T whole-body clinical MRI scanner (Magnetom Prisma, Siemens Healthcare, Erlangen, Germany) with a 15-channel Tx/Rx knee coil (QED, Cleveland, OH) and 16-channel foot/ankle coil (Siemens Healthcare).

Fat-suppressed T_1ρ-weighted scans were acquired using the 3D-T_1ρ-PETRA sequence with F_sl = 500 Hz at 9 T_sl durations including 0 msec, 0.5 msec, 1 msec, 2 msec, 3.5 msec, 5 msec, 10 msec, 20 msec, and 30 msec. The rubber was taped to the joint as a reference. A fat suppression module was applied to eliminate any blurring and chemical artifacts and to increase the dynamic range of tendons and ligaments signal.^29,30 The sequence acquisition parameters were identical to the phantom study with the total scan time of 33:45 minutes. The T_1ρ-weighted images were also acquired using a customized turbo fast low angle shot (TFL) sequence^31,32 for comparison. The result is presented in the Supporting Material (Fig. S1).

Data Analysis

Monoexponential and biexponential models were fitted to the signal decay over time using the trust-region algorithm. The T_1ρ components were calculated pixel-by-pixel over five consecutive slices for each volunteer in four regions of interest (ROIs) including the knee PT, ACL, PCL, and ankle Achilles tendon (AT). The AT was divided further into five segments: intramuscular tendon (IMT), free proximal (FPT), free mid-tendon (FMT), free distal tendon (FDT), and calcaneal tendon (CT).³³

All the scripts were written in MatLab (R2017b, MathWorks, Natick, MA). ROIs were manually drawn in ITK-Snap and exported to MatLab for relaxation analysis.

Statistical Analysis

Statistical analysis was performed using MatLab. A pairwise nonparametric Kruskal–Wallis test was performed to assess differences in T_1ρ values measured using the monoexponential and biexponential models among the nine different ROIs in ankle and knee. The post-hoc Dunn’s test with the significant level of α = 0.05 was performed for multiple comparisons.

Results

Monte Carlo Simulations

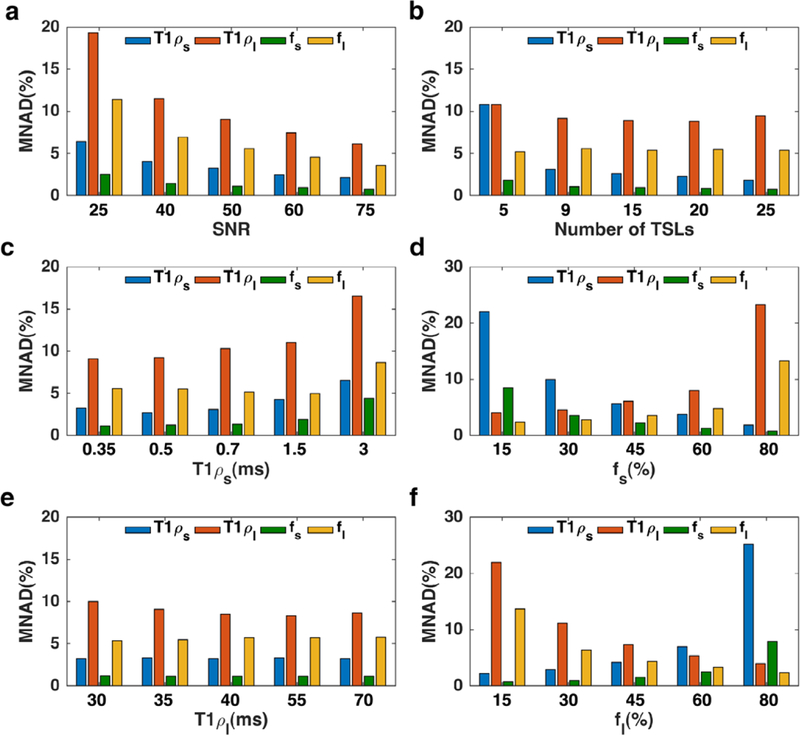
The Monte Carlo simulation results are shown in Fig. 2. The simulation showed (Fig. 2a) less than 10% error in the measurement of all components with SNR >50. Under the given SNR, acquiring scans with a fewer number of T_sl is desired to shorten the total scan time. As shown in Fig. 2b, there is less than 2% error difference between 15 and 9 T_sl. The improvement is negligible considering the cost of more than 50% increase in the scan time; hence, 9 T_sl were acquired in in vivo studies. Figure 2c,d shows the fitting error for different short and long components, respectively, while Fig. 2e,f demonstrated the effect of fractions. The component with a higher fraction has less estimation error.

FIGURE 2:

Monte Carlo simulations. (a) The effect of SNR on biexponential estimation (b) Acquiring scan at more T_sl timepoints reduces the estimation error. (c) The smaller short component (T_1ρ,s) has less estimation error, (d) higher short fraction leads to a smaller error in estimating short component. (e) The shorter long component has more estimation error. (f) Higher long fraction leads to a smaller error in estimating long component.

Phantom and Ex Vivo Bovine Study

Figure 3a shows a representative slice at different T_sl. The phantom signal decay over time and the rubber eraser signal disappeared at longer T_sl due to its very short T₂. Figure 3b shows the signal decay and the exponential fit at a representative voxel. The phantom experiments demonstrated an average T_1ρ of 0.86±0.37 msec for the rubber eraser.

FIGURE 3:

The phantom consists of a tube of 3% agarose (simulating biological tissue or cartilage), a tube of vegetable oil (simulating fat) and a piece of a rubber eraser, simulating the tissue with semisolid short T₂ relaxation times. The oil signal is reduced due to the application of FatSat pulse. The fast T_1ρ relaxation decay can be observed in the rubber eraser.

Table 1 shows the results of the ex vivo study on the bovine knee joint and AT. The relaxation maps from a representative slice are demonstrated in Fig. 4.

TABLE 1.

Summary of ex vivo Bovine and in vivo Knee and Ankle Study

ROIs	T1ρm (msec) median (IQR)	T1ρs (msec) median (IQR)	T1ρl (msec) median (IQR)	Fractions (%) median (IQR))	Fractionl (%) median (IQR)
Bovine PT	26.62 (6.15)	0.42 (0.04)	41.85 (6.95)	38.04 (9.07)	61.96 (9.07)
Bovine ACL	18.16 (2.38)	0.75 (0.23)	25.87 (1.84)	26.37 (5.66)	73.63 (5.66)
Bovine PCL	12.91 (2.53)	0.64 (0.13)	27.29 (2.96)	43.89 (7.37)	57.11 (7.37)
Bovine AT	5.42 (1.68)	0.43 (0.07)	22.55 (4.99)	55.63 (5.57)	44.37 (5.57)
Knee PT	15.92 (14.49)	0.65 (1.01)	37.32 (18.36)	46.87 (15.35)	53.13 (15.35)
Knee ACL	23.61 (9.44)	1.66 (2.12)	43.69 (17.83)	42.47 (12.51)	57.53 (12.51)
Knee PCL	17.42 (7.37)	1.16 (1.86)	27.66 (14.68)	42.64 (14.03)	57.36 (14.03)
Achilles IMT	2.88 (2.20)	0.36 (0.07)	42.79 (12.67)	68.24 (7.43)	31.76 (7.43)
Achilles FPT	3.06 (1.64)	0.40 (0.33)	37.83 (9.01)	68.92 (6.69)	31.08 (6.69)
Achilles FMT	3.80 (6.07)	0.37 (0.38)	36.07 (7.64)	64.61 (5.44)	35.39 (5.44)
Achilles FDT	6.89 (6.46)	0.37 (0.04)	30.28 (9.03)	58.81 (2.67)	41.19 (2.67)
Achilles CT	3.91 (5.35)	0.38 (0.28)	35.14 (6.75)	64.05 (5.50)	35.95 (5.50)
Achilles tendon	5.78 (10.25)	0.39 (0.02)	31.34 (10.82)	58.82 (13.32)	41.18 (13.32)

Medians and interquartile range (IQR) of multicomponent T_1ρ relaxation times and corresponding fractions in ligaments and tendons (PT, ACL, PCL, and AT).

PT: Patellar Tendon; ACL: Anterior Cruciate Ligament; PCL: Posterior Cruciate Ligament; AT: Achilles Tendon; IMT: Intramuscular Tendon FPT: Free Proximal Tendon; FMT: Free Mid Tendon; FDT: Free Distal Tendon; CT: Calcaneal Tendon

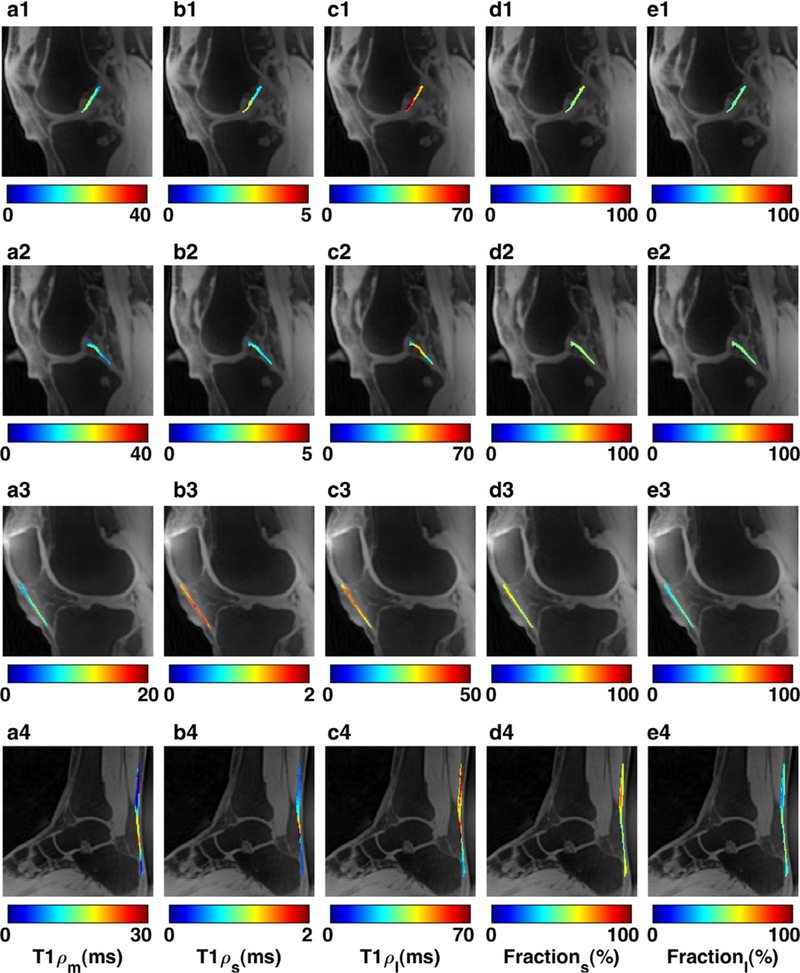
FIGURE 4:

Representative T_1ρ maps from ex vivo bovine scans in four ROIs including (a1) Anterior and posterior cruciate ligaments, (a2) patellar tendon, and (a3) Achilles tendon. (b1–3) The binary map is showing the location of pixels included in the biexponential estimation. (c1–3) mono relaxation time, (d1–3) short T_1ρ relaxation time, (e1–3) long T_1ρ relaxation time, (f1–3) short T_1ρ fraction, and (g1–3) long T_1ρ fraction maps.

The comparison between the experiment with 500 msec and 2000 msec T₁ restoration delay showed a 2% difference in estimating the monoexponential relaxation. The T₁ median and interquartile range (IQR) were 623.36(57.38) ms, 570.08 (47.68) ms, and 349.16(70.14) ms in ACL, PCL, and AT, respectively. The representative T₁ and T_1ρ relaxation maps and fits are shown in Supporting Information Figs. S2 and S3, respectively.

In Vivo Study

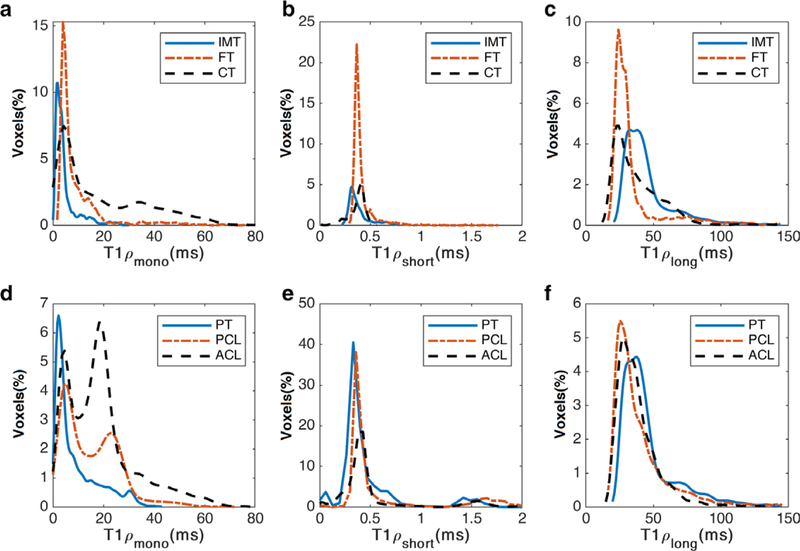
The T_1ρ descriptive statistics from the in vivo study are summarized in Table 1. The SNRs (mean ± SD) were 46 ± 8.9 and 32.7 ± 5.5 in the ankle and knee study, respectively. The representative relaxation maps in different ROIs in knee and ankle joints are demonstrated in Fig. 5. Based on the F_ratio criterion in Eq. [3], 79 ± 37% of the voxels in AT, 85 ± 6% of the voxels in PT, 64 ± 41% of the voxels in ACL, and 76 ± 30% of the voxels in PCL were included in the biexponential maps. The histogram distribution of relaxation components in each ROI are shown in Fig. 6.

FIGURE 5:

Representative T_1ρ maps of in vivo knee and ankle study. (a1–4) mono T_1ρ relaxation time, (b1–4) short T_1ρ relaxation time, (c1–4) long T_1ρ relaxation time, (d1–4) short T_1ρ fraction, and (e1–3) long T_1ρ fraction maps.

FIGURE 6:

The histogram distribution over different ROIs (a–c) ankle and (d–f) knee study for (a,d) mono (b,e) short and (c,f) long component. The y-axis shows the relative frequency for 100 bins.

Figure S4 shows axial reformatted slices from fat-suppressed T_1ρ-weighted PETRA images of a volunteer. Slices at five different positions along the Achilles tendon including the 1) intramuscular tendon, 2) free proximal tendon, 3) free mid-tendon, 4) free distal tendon, and 5) calcaneal tendon are presented. The ability to evaluate the relaxation maps from different views is shown in Fig. 7.

FIGURE 7:

Reformatted (a1–d1) axial and (a2–d2) coronal monoexponential maps from sagittal (a3–d3) plane in (a1–a3) patellar tendon (b1–b3) ACL, (c1–c3) PCL, and (d1–d3) Achilles tendon. The positions of reformatted slices are denoted on the corresponding maps.

The comparison of fit residuals of the mono- and biexponential models (Fig. S5) showed that the biexponential model better represented the T_1ρ relaxation decay than the monoexponential model. The Kruskal–Wallis followed by post-hoc Dunn’s tests for each component revealed significant differences between relaxation components in several ROIs. The results of pairwise comparisons is shown in Table 2.

TABLE 2.

Dunn’s Post-Hoc Pairwise Comparison Between Different ROIs for Mono- and Biexponential Components

ROI1	ROI2	T1ρm	T1ρs	Fractions	T1ρl	Fractionl
ACL	CT	0.97	1.00	0.70	0.99	1.000
ACL	FDT	0.61	0.92	0.31	1.00	0.97
ACL*	FMT	0.040	0.68	0.019	1.00	0.37
ACL*	FPT	0.006	0.79	0.003	1.00	0.100
ACL*	IMT	0.004	0.44	0.002	1.00	0.072
ACL	PCL	1.00	1.00	1.00	1.00	1.00
ACL	PT	1.00	1.00	1.00	1.00	1.00
CT	FDT	1.00	1.00	1.00	1.00	1.00
CT	FMT	0.98	1.00	0.99	1.00	0.99
CT	FPT	0.69	1.00	0.91	0.99	0.91
CT	IMT	0.62	1.00	0.85	0.89	0.85
CT	PCL	1.00	0.74	0.95	0.99	0.95
CT	PT	1.00	1.00	0.99	1.00	0.99
FDT	FMT	1.00	1.00	1.00	1.00	1.00
FDT	FPT	0.98	1.00	0.99	1.00	0.99
FDT	IMT	0.97	1.00	0.99	0.96	0.99
FDT	PCL	0.98	0.26	0.67	1.00	0.68
FDT	PT	0.98	0.91	0.89	1.00	0.89
FMT	FPT	1.00	1.00	1.00	1.00	1.00
FMT	IMT	1.00	1.00	1.00	1.00	1.00
FMT	PCL	0.35	0.10	0.09	1.00	0.09
FMT	PT	0.33	0.66	0.20	1.00	0.21
FPT	IMT	1.00	1.00	1.00	1.00	1.00
fpt*	PCL	0.07	0.15	0.014	1.00	0.014
fpt*	PT	0.06	0.78	0.036	1.00	0.036
IMT*	PCL	0.043	0.036	0.010	1.00	0.010
IMT*	PT	0.040	0.42	0.026	1.00	0.026
PCL	PT	1.00	1.00	1.00	1.00	1.00

The regions with a statistically significant difference (P < 0.05) are shown in bold and with asterisk.

PT: Patellar Tendon; ACL: Anterior Cruciate Ligament; PCL: Posterior Cruciate Ligament; AT: Achilles Tendon; IMT: Intramuscular Tendon FPT: Free Proximal Tendon; FMT: Free Mid Tendon; FDT: Free Distal Tendon; CT: Calcaneal Tendon.

Discussion

In this article we present a ZTE MRI technique based on a PETRA sequence for in vivo, bicomponent T_1ρ relaxation mapping of semisolid short-T₂ tissues such as ligaments and tendons on a 3 T scanner. To the best of our knowledge, this is the first work proposing a ZTE sequence for bicomponent T_1ρ analysis of semisolid tissues with very short T₂ values. ROIs were defined in the PT, ACL, and PCL of the knee joints and AT of the ankle joint, and mono- and biexponential T_1ρ relaxation components were measured in each ROI. The results showed that biexponential fitting might better distinguish the short relaxation time associated with the restricted water in the macromolecules. The isotropic spatial resolution allowed the multiplanar reformatting of the scans and evaluation of the relaxation, in any plane, and hence the complete coverage of the surface of the tendons and ligaments.

The higher bandwidth required for 3D excitation was achieved using a very short hard RF excitation pulse. This allows for limited flip angles due to available maximum B₁ amplitude and limited pulse duration. Li et al³⁴ proposed a variable flip angle method using a quadratic phase-modulated RF excitation pulse to achieve maximal transverse magnetization and equal amplitude of the short-T₂ signal. However, the method cannot be used for relaxation mapping since the signal amplitude becomes dependent on the flip angles in addition to the T_1ρ decay.

The 8000 radial spokes acquired in this experiment covers about 4% of full Nyquist sampling (256 × 256 × π = 205,887), which results in image blurring. As shown in Supporting Information Fig. S6, increasing the number of spokes from 8000 to 24,000 will reduce the blurring at the cost of increasing the scan time.

The bandwidth of the fat sat (FS) pulse was 220 Hz (half of the chemical shift w.r.t. water) and its duration was 5120 μs. The fat suppression was less effective in longer TSLs. However, it is not possible to put the fat suppression module after T_1ρ preparation, due the long duration of the FS pulse.

The results of the ex vivo study are in agreement with the in vivo measurement. Our T_1ρ,m of 6.50 ± 3.37 msec in AT is in agreement with the Du et al²⁰ study (4.95 ± 0.23 msec). The reported values for T_1ρ,m for ACL and PCL in the Ma et al³⁵ study (ACL: 34.9 ± 2.8 msec, PCL: 21.6 ± 1.4 msec) are higher than T_1ρ,m of 21.8 ± 6.3 msec and 16.2 ± 4.1 msec in our study for ACL and PCL, respectively. The reason could be due to the T_1ρ dispersion effect as a result of using adiabatic spin-locking pulses in the Ma et al study.

The bicomponent T_1ρ analysis of bound and free water in various knee joint tissues and the muscle was reported previously^31,32,36 employing conventional readouts (TFL). Juras et al²⁵ reported the bicomponent ${\text{T}}_2^{*}$ analysis of AT using a variable-echo-time (vTE) technique and showed the significant difference for short component between healthy and diseased AT. The longer TEs >800 μs used in that study in comparison with our study (TE = 70 μs) makes the technique more sensitive to the long component than the short component.

The proposed sequence supported using chemical shift-based fat suppression pulses for contrast generation. However, our results showed it is less effective at longer T_sl. One possible reason could be the segmented structure of the sequence. The fat suppression pulse was applied once prior to the T_1ρ preparation module followed by a set of excitation pulses. It cannot be applied before each excitation due to the time constraints. The short T₁ of the fat leads to its partial signal recovery between two consecutive FS pulses.

The application of a long continuous wave spin-lock pulse makes the sequence SAR-intensive. In our proposed technique, the 500 msec delay used for T₁ recovery also eliminates the SAR constraint. Real-time SAR monitoring during the in vivo scans confirmed that it was always below the US Food and Drug Administration (FDA) limit (<50%).

We have only demonstrated the technical feasibility of the 3D T1_ρ-PETRA sequence in providing volumetric bicomponent analysis of semisolid tissues with very short T₂ in a rubber eraser phantom, ex vivo bovine knee joint, and in vivo knee joint applications. No patients were recruited for this study and the study group was fairly small. Further repeatability and reproducibility experiments are also warranted to validate the proposed technique. Second, the magic angle effect can influence the T_1ρ value due to the dipolar interactions of fiber orientation with respect to B₀. While the PT and AT are parallel to B₀ and the PCL is orthogonal to B₀, the orientation degree of the tibial part of the ACL to B₀ is close to the magic angle.³⁷ Application of the higher spin-lock frequency (1–2 KHz) to diminish the magic angle effect is not feasible for in vivo studies due to the SAR constraints. Moreover, as shown by Wang and Xia,³⁸ only the single relaxation behavior is observed at a higher spin-lock field. Hence, a 500 Hz spin-lock frequency was selected in this study as a good trade-off between reducing the magic angle effect and observing the biexponential behavior.

There is large uncertainty of the fitted parameters due to the nature of the biexponential model for relaxation decay, and in the presence of noise several equally well-fitted combinations of parameters can be found.³⁹ Several investigators proposed methods to improve the fitting of multicomponent signals, including using a priori information to stabilize the fitting process and optimizing the acquisition parameters.⁴⁰ Recently, Anastasiou and Hall⁴¹ used Cramer–Rao theory and simulations to show that the T₂ fit errors were minimized by maximizing the SNR of the images acquired, as well the number of points used in the fitting procedure and by using a biexponential system with a high T₂₂/T₂₁ ratio. However, acquiring more timepoints and increasing the SNR requires a longer scan time. In our study, the total scan time of ~34 minutes needed to acquire 9 T_sl is too long for clinical use. We will plan on using compressed sensing and deep learning reconstruction techniques to further reduce the acquisition time in our future study. The technique can be potentially applied to other applications such as studies of calcified cartilage layer, cortical bone, and myelin in addition to studying ligaments and tendon disorders.

In conclusion, the 3D T_1ρ-PETRA technique provides a robust volumetric bicomponent T_1ρ mapping of semisolid short T₂ tissues such as ACL, PCL, and PT in the knee joint and AT in the ankle joint.