Abstract
Introduction
Circulating tumor cells (CTCs) in microcirculation undergo significant deformation and frictional interactions within microcapillaries. To understand the physical parameters governing their flow-induced transport, we studied the pressure-driven flow of cancer cells in a microfluidic model of a capillary network.
Methods
Our microfluidic device contains an array of parallel constrictions separated by regions where cells can repetitively deform and relax. To characterize the transport behavior, we measured the entry time, transit time, and shape deformation of tumor cells as they squeeze through the network.
Results
We found that entry and transit times of cells are much lower after repetitive deformation as their elongated shape enables easy transport in subsequent constrictions. Furthermore, upon repetitive deformation, the cells were able to relieve only 25% of their 40% imposed compressional strain, suggesting that tumor cells might have undergone plastic deformation or fatigue. To investigate the influence of surface friction, we characterized the transport behavior in the absence and presence of bovine serum albumin (BSA) coating on the constriction walls. We observed that BSA coating reduces the entry and transit time significantly. Finally, using two breast tumor cell lines, we investigated the effect of metastatic potential on transport properties. We found that the cell lines could be distinguished only upon surface treatment with BSA, thus surface-induced friction is an indicator of metastatic potential.
Conclusions
Our results suggest that pre-deformation can enhance the transport of CTCs in microcirculation and that frictional interactions with capillary walls can play an important role in influencing the transport of metastatic CTCs.
Electronic supplementary material
The online version of this article (doi:10.1007/s12195-017-0499-2) contains supplementary material, which is available to authorized users.
Keywords: Tumor cells, Microfluidics, Capillary, Friction, Repeated deformation
Introduction
Circulating tumor cells (CTCs) play an important role in cancer metastasis.4,11,26,31,36 Cells from the primary tumor detach, intravasate into blood vessels, and are transported by blood flow to distant sites. These CTCs can pass through, become physically trapped in microcapillaries or adhere to the endothelium lining the blood vessels. These arrested CTCs can extravasate, enter neighboring tissues and produce secondary tumors. Thus, flow-induced transport of CTCs to distant organs is an essential event in the multistep process of cancer metastasis.33,51
Two important physical properties regulate flow-induced CTC transport—tumor cell deformability3,14,24,35,54 and friction with capillary walls.3,13,24,38 When the size of tumor cells is larger than the microcapillary diameter, they deform and squeeze through the capillaries due to a combination of fluid stresses and cell deformability. Depending on the cell confinement and deformability, significant normal stresses can be exerted on the capillary walls, resisting their motion. In addition to normal stresses, tangential stresses due to friction between the cell and capillary walls can also impede their motion. Here, the friction force may arise from several factors including viscous dissipation in the lubricating layers between the capillary wall and cell membrane, wall roughness, and intermolecular interactions due to receptor–ligand binding interactions.1,3,13
Studying the influence of cell deformability and friction on CTC transport is difficult with in vivo models, due to the inability to precisely control fluid stresses, capillary diameter, and network architecture. Recently, microfluidic devices have emerged as powerful tools addressing the limitations of in vivo models and mimicking in vitro the different processes involved in cancer metastasis.8,22,32,37,47,55 In fact, several studies have used constricted microchannels to mimic the flow-induced deformation and squeezing of cancer cells through tight spaces.1,3,21,24,25,29,53
The majority of studies on flow-induced deformation of tumor cells have been conducted in the simplest microfluidic configuration possible—a single constricted microchannel whose hydraulic diameter is smaller than the tumor cell.3,21,24,25 In this case, individual tumor cells sequentially flow through the constriction, deform at the entrance of the constriction, and the deformed cell passes through the microchannel. The time taken for a cell to cross the entrance of the constriction—the entry time; and the time taken to traverse the length of the microchannel—the transit time (sometimes also referred to as passage time24) have been used as metrics of deformability.3,21,34 A recent study by Byun et al. 3 showed that the entry time can be more sensitive to the deformability of a tumor cell, while transit time can be dominated by friction. In addition, these parameters were shown to correlate with differences in metastatic potential of tumor cells.
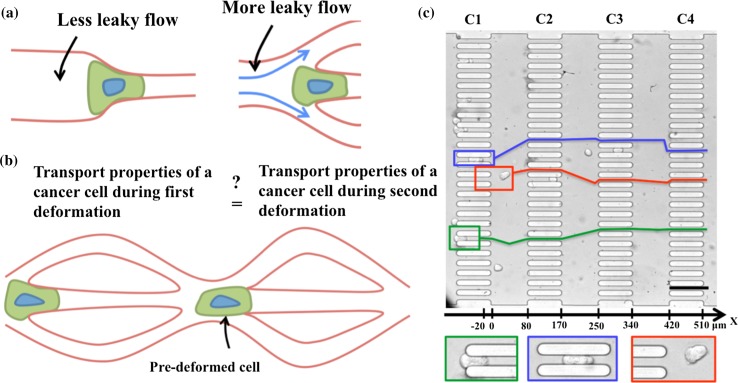
Investigations in the simple constricted microchannel geometry provide essential information on tumor cell transport although they do not capture other flow and geometrical features that are inevitably present when CTCs flow through the complex networks in vivo such as bifurcations in organ capillaries and trifurcations in vasculatures from angiogenesis.5,9,30 For example, as shown in Fig. 1a, the pressure force on a cell due to fluid flow is stronger in a single constriction than in a network of capillaries, since flow can bypass around the cell—potentially leading to differences in entry times. In addition, while a tumor cell experiences deformation only once in a single constriction, in a capillary network repeated deformation of the same cell can occur (Fig. 1b).
Figure 1.
A microfluidic capillary network for probing flow induced squeezing and friction of tumor cells. (a) A schematic of the cell passing through a single constricted capillary (left) vs. in a network of capillaries (right). The surrounding fluid can bypass at capillary junctions; (b) a schematic showing repeated tumor cell deformation; (c) a bright field image of the microfluidic device (top) containing 4 columns (C1–C4) and 27 rows of constricted channels with W × L × H = 11.8 μm × 91.8 μm × 15 μm. Three cells (MCF-7) have been identified in red, blue and green boxes, and their corresponding trajectories are shown as lines in the same color. The x-axis shows marked gradations on a linear scale highlighting areas where cells undergo compressional strain and relaxation. Scale bar is 100 μm. The bottom row shows the three cells enlarged.
It is thus evident that the dynamics of flow-induced tumor cell transport in microcapillary networks is rather different from that in a single constricted capillary. Currently, it is unknown how entry and transit times vary when tumor cells are transported through capillary networks, and how repeated deformation alters these parameters that are indicative of tumor cell deformability and friction. Moreover, if tumor cells are pre-deformed in one capillary, is it easier for them to pass through other capillaries? And are metastatic cells more easily transported after pre-deformation than non-metastatic cells? Such questions are beginning to be addressed using microfluidic devices.29,39 It is important to address these questions comprehensively to understand what physical factors ultimately regulate CTC transport and cancer metastasis.
In this study, we designed a microfluidic capillary network, which has parallel arrays of constriction channels that allow trafficking and repeated deformation of cancer cells. In vivo, during metastasis cancer cells are transported through both systemic and pulmonary microcirculation. The systemic circulation consists of tubule-like capillaries. The complex pulmonary circulation was conceptualized using a sheet-and-post model (i.e., analogous to a parking garage with intervening posts) by Sobin et al.44 However, Guntheroth et al. 16 showed that the pulmonary circulation does not conform to the sheet-and-post model, but is tubule-like. The constricted channels used in our device are tubule-like and therefore mimic an important feature of the microcirculation in vivo.
Here, we use the microcapillary network device and characterize the transport behavior in terms of cell entry time, transit time, and shape deformation. To investigate the influence of friction, we compared the transport behavior in the presence and absence of bovine serum albumin (BSA) coating of the constriction channel walls. Finally, we sought to distinguish breast cancer cell lines with different metastatic potential based on their frictional behavior and assessed the effect of metastatic potential on the transport of pre-deformed cancer cells.
Materials and Methods
Microfluidic Device Design and Fabrication
The microfluidic capillary network devices were made using soft lithography.52 The layout of the microfluidic capillary network was designed to induce repeated deformation of tumor cells as well as visualize the entire process within the field of view of the camera. In vivo, microcapillaries have a diameter of 4–9 μm and a length of 600 μm.
The capillary network consists of a total of 108 constriction channels laid out in the form of 27 rows and 4 columns (C1, C2, C3 and C4), as shown in Fig. 1c. Each constriction channel has a length (L) of 91.8 ± 4.3 μm, a width (W) of 11.8 ± 0.7 μm. All the features in the device have a uniform depth (H) of 15 ± 0.4 μm. This design allows the tumor cells to be deformed in the constrictions, and relax in the space between the columns. The length of these relaxation chambers (see Fig. 1c) is 82 ± 0.7 μm, which corresponds to approximately six cell diameters, considering the mean diameter of tumor cells used in the study is ≈18 μm. We note that in these relaxation chambers the tumor cells are free to relax in the horizontal plane of the chamber, and not in the depth-wise direction since the chamber depth is smaller than the mean cell diameter.
To investigate the effect of surface-dependent friction, a solution of 4 wt% BSA (Sigma Aldrich, MO, USA) in phosphate buffered saline (PBS) (Thermo Fisher Scientific, MA, USA) was pipetted into the device and incubated for 1 h, followed by a PBS rinse. In parallel, untreated devices were filled with PBS and stored at room temperature for 1 h before experiments were performed.
The microfluidic capillary network design shown in Fig. 1c does not fully mimic the geometric features of capillaries in vivo, but captures essential features. Our constriction widths are ≈2× larger, while lengths are ≈6× shorter than most systemic microcirculation capillaries.23,42 If we had chosen a channel width of 4 μm, the compressive strain on the cells would have been 350% instead of the 40% imposed in our study. Such large strains would have required much longer relaxation chambers—making it difficult to study the influence of repeated deformation—which is a main goal of this study. In addition, using longer and narrower channels would reduce device throughput. Thus, our microfluidic device design is a minimal model of systemic microcirculation. We further note that the BSA channel wall coating does not mimic in vivo conditions, however, BSA is frequently used in microfluidic devices to prevent non-specific cell adhesion1,21,24 and thus investigating its influence on tumor cell–channel wall interactions is worthwhile.
Cell Culture
The breast cancer cells lines—MDA-MB-231 and MCF-7—were grown in the DMEM media supplemented by 10% FBS, 1% penicillin–streptomycin and 1 nM sodium pyruvate (MDA-MB-231 were purchased from ATCC, Manassas, VA and MCF-7 cells were provided by Dr. Lauren Gollahon’s Lab at Texas Tech University). To harvest the cells, 5 mL trypsin/EDTA solution were added to the cells after removing the media, incubated for 2–3 min and neutralized by 500–550 μL FBS. During the experiment, we added Trypan blue to the cell media, to identify only viable cells with a volumetric ratio of 2:1. In this mixture, final concentration of cells was 1–3 × 105 cells/mL, which was used to conduct the microfluidic experiments. All materials for cell culture were purchased from Thermo Fisher Scientific, MA.
Experimental Set-Up and Data Analysis
To inject the cells into the microfluidic device we used a constant pressure source (MFC8-FLEX4C, Fluigent, Inc.) and imposed a fixed pressure drop of 4 kPa, in the same range as the capillary blood pressure (1.3–4.6 kPa),50 across the whole device. The pressure gradient provides a shear stress of 2.2–3.7 Pa, depending on the number of channels blocked by cells, which is also in the same range of shear stress as in the blood capillaries (0.1–3 Pa).33,46,48,49
We visualized the flow of tumor cells into the device with an inverted microscope (IX70, Olympus, Inc.) using 20× magnification and in bright field mode. Images were recorded with a high-speed camera (Phantom V310, Vision Research, Inc., NJ, USA) at a frame rate of 1000 fps. The spatial resolution in the images was 0.915 μm/pixel. All the images were analyzed manually using ImageJ (1.47v) to obtain cell size, entry time, transit time, and deformation index. Kolmogorov–Smirnov test was used for statistical analysis of the data.
Metrics Used to Quantify Cancer Cell Transport and Shape Deformation
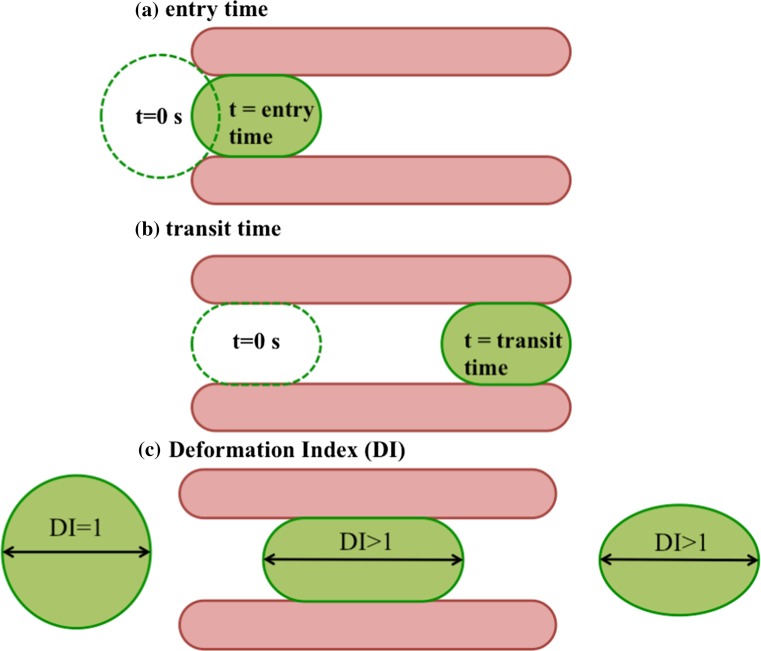
To characterize tumor cell transport in the capillary network, we measure the cells’ entry and transit times. The entry time represents the time that a cell takes to fully enter the constriction channel upon its first encounter (Fig. 2a) and the transit time is the time needed for a cell to reach the channel exit from the moment it fully enters (Fig. 2b).
Figure 2.
Metrics used to characterize tumor cell transport in the microfluidic capillary network. (a) The entry time is the time that a cell takes to fully enter the constriction channel upon its first encounter with the constriction walls; (b) the transit time is the time elapsed between when a cell has fully entered the constriction and prior to its exit; (c) the deformation index (DI) is the ratio of the major axis of the cell at each location in the device to the major axis prior to deformation in the constriction.
As a cell passes through the microcapillary network, it experiences repeated compressional deformation and relaxation. To quantify the compression and relaxation behavior of the tumor cells, we define a deformation index (DI).45 As illustrated in Fig. 2c, DI is defined as D x/D o, where D x is the major axis of the cell at any x location (see Fig. 1c) in the device and D o is the major axis of the initial cell shape prior to any deformation in the constriction channels. Given that we can measure the major axis of the cell to within one pixel error, the measurement error in DI is 5% based on the mean cell size.
Results
Dynamics of Cancer Cells in the Microfluidic Capillary Network
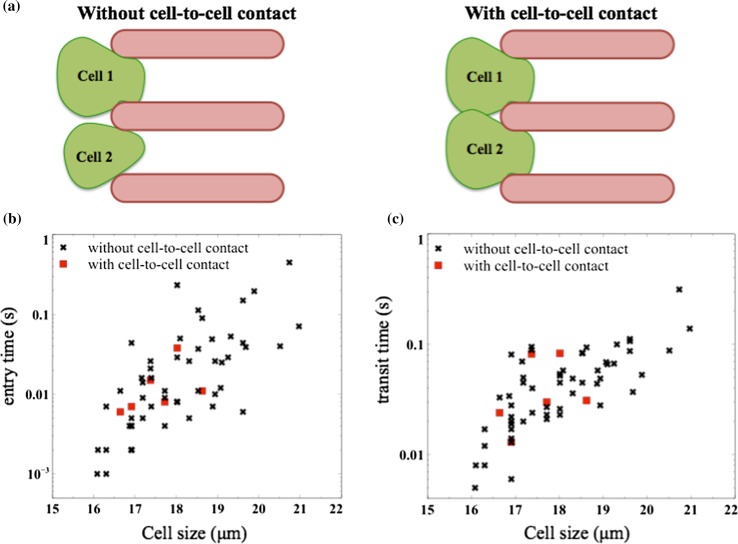
In our experiments we injected a population of tumor cells into the microfluidic capillary network at a fixed pressure drop. Although the dynamics of the collection of tumor cells in the network was complex, we made the following qualitative observations of their transport behavior. (i) due to the parallel arrangement of constrictions, we observed that as one tumor cell was trying to squeeze through the constriction, other tumor cells entered into the neighboring constrictions and tended to squeeze through because of the sustained pressure drop across the device. This behavior was shown in Fig. 1c. (ii) The cells undergoing compression in the constrictions tended to relax in the space between the columns C1 and C4, which we call relaxation chambers. (iii) The deformed cells exiting a constriction sometimes deviated from their original trajectory as they passed through subsequent constrictions (see trajectory lines in Fig. 1c). This drift could be due to the presence of lateral flow when some of the constrictions were occluded by cells and possibly due to the rotational motion of the deformed cells. (iv) Usually we observed the deformed cells to enter into the constriction with their major axis aligned, however, rarely (2–3 cells out of 50) were observed to arrive on the broadside. These cells that end up on the broadside have 22–37% higher entry time than the population, but do not affect the mean transport metrics of the population. (v) Cell-to-cell contact during squeezing through constrictions (see Fig. 3a) was infrequently observed due to the low cell concentrations used in the study.
Figure 3.
Influence of cell size and occlusion events on transport metrics. (a) Schematic illustrating the absence and presence of cell-to-cell contact before entering the constriction channels; (b) entry time as a function of cell size, in the presence and absence of cell-to-cell contacts; (c) transit time as a function of cell size. The legend is the same as (b). The data here is shown for MCF-7 cells.
To quantify the transport behavior of tumor cells, we measured the entry and transit time for a collection of MCF-7 cells passing through the first parallel array of constrictions. We found that the transport metrics depend on cell size; the larger cells took more time to enter and transit the channels. Due to the large variability in entry and transit times of isolated tumor cells, we found that entry and transit times of cells undergoing cell-to-cell contact were not drastically affected (Figs. 3b and 3c).
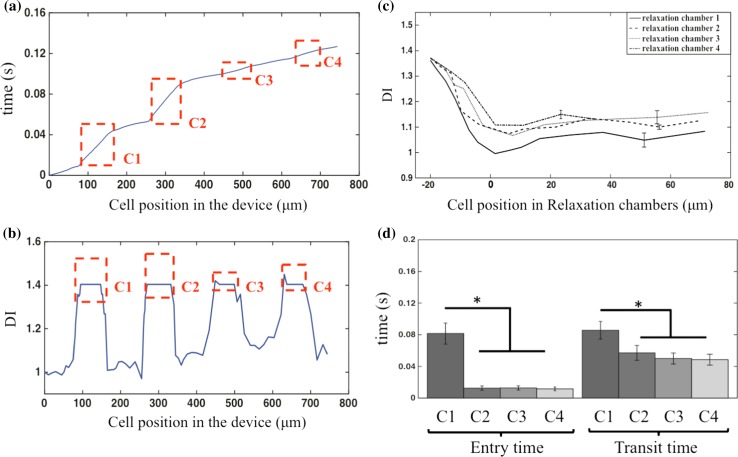
Next, to understand the response of an individual tumor cell when exposed to repeated compressional strain and relaxation in the microcapillary network, we followed the same tumor cell as it passed through each of the columns present in the network. A representative trajectory is shown in Fig. 4a. We found that the C1 and C2 entry and transit times were similar but the C3 and C4 entry and transit times were much shorter. This trend could be discerned from the four times higher slope (≈4 × 10−4 s/μm) in the trajectory when it crossed the first two arrays compared to the last two arrays, indicating its trafficking was slower in the first two columns. In addition, the slope of the trajectory in the last two constriction arrays (≈1 × 10−4 s/μm) was almost the same as the slope of the trajectory in the relaxation chambers (Fig. 4a), suggesting that the velocity of the cancer cells was similar in C3 and C4 to the velocity of the cells in the intervening relaxation chambers.
Figure 4.
Transport dynamics of cancer cells passing through the microfluidic capillary network. (a) A representative trajectory of a tumor cell in the microfluidic capillary network. Highlighted (in red) are the constriction zones C1–C4; (b) variation of the deformation index (DI) for the same cell shown in (a); (c) the average DI of five cells with very similar size while relaxing in the relaxation chambers after each constriction array. The DI values of C2–C4 are significantly different from C1, p value <0.05; (d) average entry and transit time ± SEM for the same five cells, shown in (c). The data here is shown for MCF-7 cells. *p-value <0.05. All the data shown was obtained in BSA-coated channels.
To explain the observations found from the trajectory analysis, we plot the DI for the same cell vs. its location inside the device (Fig. 4b). Before entering the constrictions, the cell remained intact and was barely deformed with a DI ≈ 1. Entering the constriction channels the cell accumulates a strain of 40%, since DI ≈ 1.4. When the cell exited the first constriction array, and entered in the relaxation chamber, it relaxed to almost its initial shape. However, when the cell experienced the same 40% strain repeatedly in each of the subsequent constrictions, its relaxation declined starting from the second relaxation chamber, i.e., the cell lost its ability to recover its original shape in subsequent deformation events. This ability of the tumor cell to remain deformed while it passed through the constrictions in the last two columns was responsible for its fast passage through the later constriction arrays.
We confirmed the above key findings by analyzing four more tumor cells of similar size (19.5 ± 0.2 μm) and averaging the DI of all five cells in each relaxation chamber, as shown in Fig. 4c. We found that tumor cells almost regained their original shape in the first relaxation chamber with DI ≈ 1.05 ± 0.06. However, in subsequent relaxation chambers, the deformed cells did not fully recover their original shape as reflected in the higher DI of ≈1.15 ± 0.04. These elongated cells transited through constrictions more easily, evident from the reduced entry and transit times measured in the latter constriction arrays (see Fig. 4d).
The results from the repetitive deformation of cells in the microfluidic network provide important insights into the rheology of breast tumor cells. For a purely elastic material, the strain would instantaneously recover after cessation of stress. After the first constriction array, it took a finite time (≈12 ms) for the cells to fully relieve their compressional strain. This suggests that these cells, as expected, are viscoelastic materials. Interestingly, after the third deformation, the cells were able to relieve only 25% of their 40% compressional strain during the ≈9 ms of experimental observation time. This suggests that due to repeated compressional strain, the cytoskeleton had undergone plastic deformation, so that the deformation was irreversible and the original cell shape cannot be recovered fully during passage between the arrays. It is possible that the cytoskeleton had undergone fatigue where each deformation episode induced microscopic faults, preventing full shape recovery. We note that cell fatigue has been recently reported for red blood cells after 500–900 repetitive deformation events.41 For tumor cells, we anticipate that fewer repetitive deformation events may be needed to induce fatigue, as they are less extensible.
Characterizing Surface-Dependent Friction of Cancer Cells
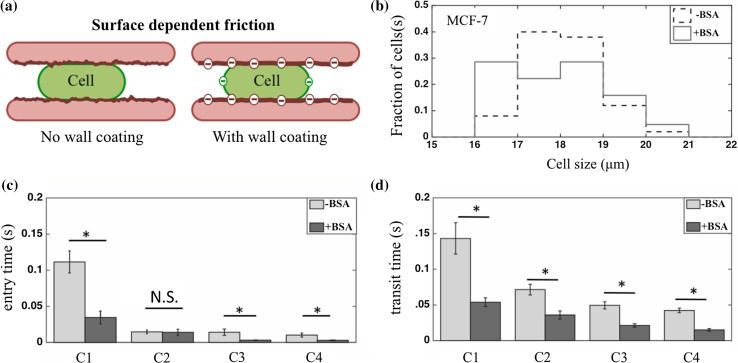
When cancer cells passed through constricted channels, they were inevitably in contact with the channel walls. As a result, depending on the surface properties of the channels, there could be significant frictional forces resisting cell motion. As shown in Fig. 5a, this surface-dependent friction of tumor cells could be due to wall roughness and the properties of the material coating. To investigate the effect of surface-dependent friction, we coated the channel walls with BSA—a biocompatible protein with a net negative charge.7,10 It had been reported to increase the mean roughness of PDMS surface by ~4 nm.43 In addition to changes in wall roughness due to BSA treatment, its negative charge could also impact the electrostatic interactions with cell membrane since it was effective at preventing non-specific adhesive interactions between cells and microfluidic substrates.21,25,29
Figure 5.
Influence of BSA coating on tumor cell transport. (a) A schematic showing that surface-dependent friction of tumor cells can be influenced by factors such as wall roughness, coating and electrostatic interactions; (b) the size distribution of MCF-7 cells used in the experiments with uncoated and BSA-coated constriction arrays. Fraction of cells is the ratio of cells in each size range to the total number of cells; (c) entry time ± SEM of MCF-7 cells in the presence (n = 61) and absence (n = 50) of BSA coating, shown for cells passing through the constriction arrays; (d) transit time ± SEM of MCF-7 cells in the presence and absence of BSA coating, shown for cells passing through the construction arrays. *p-value <0.05, N.S. not significant.
Since cell size influenced the transport metrics (c.f., Fig. 3), we collected data from the same range of cell diameters (16–21 μm) with and without BSA treatment (Fig. 5b). We observed that coating the channels with BSA caused a significant decrease of both entry and transit times of MCF-7 cells through the first (C1) set of constriction arrays. Thus, BSA coating reduced the surface friction and enabled MCF-7 cells to squeeze faster through the constriction arrays.
We also analyzed the effect of BSA on cell squeezing through the remaining constriction arrays: C2–C4 (Figs. 5c and 5d). Except for C2, we found that both entry and transit times are reduced in the presence of BSA coating in all the arrays. This might be because of the gradual reduction of entry time in BSA coated constriction arrays, whereas in uncoated channels the reduction is steep and abrupt from the first deformation. In other words, since the cells in the first channel of BSA coated devices passed faster and experienced strain for a shorter time, they tended to relax back more and passed in a slightly lower time in second deformation (this is also observed for the five cells shown in Fig. 4d).
Distinguishing Tumor Cell Lines of Different Metastatic Potential Based on Their Frictional Behavior
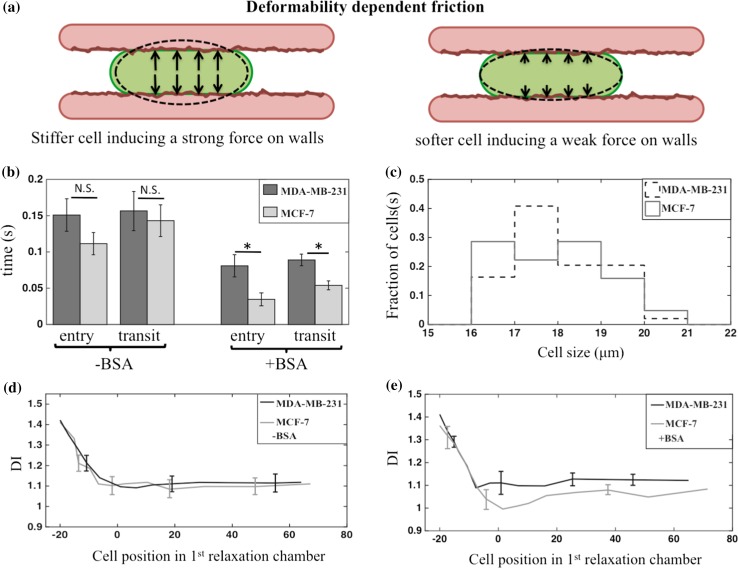
Metastasis involves the transport of cancer cells from the primary tumor to distant organs. The cells that succeed in this journey are expected to possess distinct biophysical properties.51 For example, studies suggest that the deformability of highly metastatic cells is different from weakly metastatic or normal cells.3,15 Changes in cell deformability can arise due to variations in their mechanical properties including elastic modulus, viscosity, or membrane tension.24 As shown in Fig. 6a, a less deformable (stiffer) cell can exert greater normal forces on the walls when passing through a constricted capillary than a more deformable (softer) cell, increasing the frictional resistance to motion. This deformability-dependent friction is distinct from surface-dependent friction; however, experimentally it is difficult to decouple the two contributions from metrics such as entry and transit times. Here, we compared the overall frictional behavior of highly metastatic MDA-MB-231 with that of weakly metastatic MCF-7 breast tumor cells12,15 in the microfluidic capillary network with the aim of distinguishing them based on entry and transit times.
Figure 6.
Deformability dependent friction and its relation to tumor cell metastatic potential. (a) A stiff cell (left) exerts strong normal force on the channel walls whereas a soft cell (right) exerts a weak force on channel walls; (b) entry and transit times ± SEM of breast tumor cells from their first deformation in BSA-coated and uncoated devices. The MDA-MB-231 and MCF-7 cells only differ in BSA coated devices. For BSA-coated devices, n = 61 and 49 for MCF-7 and MDA-MB-231 cells, respectively. For uncoated channels, n = 50 and 24 for MCF-7 and MDA-MB-231 cells, respectively; (c) the size distribution of MDA-MB-231 and MCF-7 cells used in obtaining the data for BSA coated channels; (d) the relaxation behavior (DI ± SEM) of MDA-MB-231 and MCF-7 cells in uncoated devices. The data shown is the mean obtained from n = 5 cells of nearly the same size; (e) the same as (d), except the data is obtained from BSA-coated devices. In both (d) and (e) there is no statistical difference between the two cell types. *p-value <0.05, N.S. not significant.
Tracking only cells passing through C1, Fig. 6b shows that entry and transit times of MDA-MB-231 cells were statistically similar to MCF-7 cells, for the same sampled size distribution, in the PDMS device without BSA coating (Fig. 6c). However, in devices with BSA coating, we found that the entry and transit time of MDA-MB-231 cells were higher than MCF-7 cells by ~57 and ~39%, respectively.
The reason that the two cell lines did not show any difference in transport properties in the absence of BSA coating could be that the PDMS surfaces are highly hydrophilic2,20 (due to air plasma treatment during device manufacturing52). These hydrophilic surfaces may make cells adhere to channel walls, since the cell membrane lipid layer also contains hydrophilic heads.19,28 As a result, the differences in cell surface properties might not be elicited due to the adhesive character of hydrophilic PDMS walls. However, when the channels were coated with BSA, a negatively charged protein, highly metastatic cells responded less to BSA treatment to pass through constricted capillaries. It has been reported that MCF-7 cells have a higher surface charge density (−0.02 C/m2) than MDA-MB-231 cells (−0.015 C/m2) at the pH (=7.1) of culture media.10 Thus, it is possible that the negatively charged BSA repelled MDA-MB-231 less than MCF-7 due to its weaker negative charge. In other words, differences in the cell frictional properties due to surface charge may be more important in dictating the cell response to BSA.
We also considered if any differences existed in the two cell types based on how their shape relaxed with time after exiting the first constriction array. The premise here is that more deformable cells when compressed would relax to a greater extent than less deformable cells. We analyzed five cells each of MDA-MB-231 and MCF-7, with almost the same size, and plot in Figs. 6d and 6e, the mean DI vs. their location in the first relaxation chamber. Both in the absence and presence of BSA, the data overlapped in the initial 20 μm, when the cells were departing the channel; and in the relaxation chamber (0–80 μm). A small difference appeared to exist between the relaxation behavior of MDA-MB-231 and MCF-7 in BSA-coated devices (c.f., Fig. 6e), but they were within the margin of error. We also determined the DI values of the cell population, which has different cell sizes and found that DI after the first deformation was unable to distinguish these two metastatic cell lines (see Supplementary Fig. S1). Therefore, under such large compressional strain, we did not detect any difference in their shape relaxation behavior. Thus, frictional behavior rather than relaxation behavior was better at differentiating the two cell lines of different metastatic potential.
Effect of Metastatic Potential on the Transport of Pre-Deformed Cancer Cells
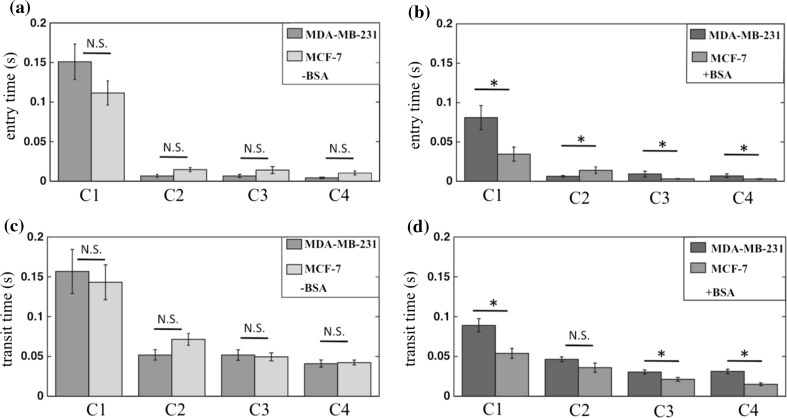
So far we discussed the results for the two cell lines based on their transport through the first set of constriction arrays. We now address whether the differences observed in entry/transit times due to deformation in C1 arrays still persist during passage through C2–C4 constriction arrays.
Figure 7 shows the entry/transit time results for the two cell lines, in the absence and presence of BSA. We observed that in the absence of BSA treatment, similar to C1 arrays, the entry and transit times did not vary significantly between the two cell lines, after passing through constriction arrays C2–C4. However, the entry and transit times for the cell lines vary when treated with BSA. These results suggest highly metastatic cells (MDA-MB-231) can be distinguished from weakly metastatic cells (MCF-7) even after pre-deformation.
Figure 7.
The relation between repeated deformation and metastatic potential of tumor cells. The entry time ± SEM of highly (MDA-MB-231) and weakly (MCF-7) metastatic breast cells in (a) uncoated (b) BSA-coated constriction arrays. The transit time ± SEM of highly (MDA-MB-231) and weakly (MCF-7) metastatic breast cells in (c) uncoated (d) BSA-coated constriction arrays. In untreated constrictions, the cells did not show difference in entry and transit times, whereas in BSA-coated constrictions, both entry and transit time showed a significant difference in all arrays, except for transit times of array C2. For BSA-coated devices, n = 61 and 49 for MCF-7 and MDA-MB-231 cells, respectively. For uncoated channels, n = 50 and 24 for MCF-7 and MDA-MB-231 cells, respectively. *p-value <0.05, N.S. not significant.
Literature studies12,15 show that the deformability of MCF-7 cells are different from that of MDA-MB-231. However, under our experimental conditions and the metrics we used, we are unable to distinguish the two cell lines based on deformability-dependent friction since the difference between the cell lines was elicited only with BSA treatment. Thus, the surface-dependent friction was better at distinguishing these highly metastatic from weakly metastatic cancer cells.
In this study, we considered the case where the constrictions were of the same diameter in C1–C4 arrays. However, if the pre-deformed cells were to enter an even narrower constriction (and therefore experience larger strain), it is possible that the two cell types can again be differentiated based on deformability-induced friction. In fact, in microcirculatory networks, microcapillaries of diameters ranging from 4 to 9 μm18 are known to exist, suggesting that the deformability dependent frictional differences between highly and weakly metastatic cells might persist even after pre-deformation.
Discussion
In this study, we used a microfluidic capillary network and investigated the transport properties of tumor cells with an emphasis on their frictional behavior. We examined the role of repeated deformation and metastatic potential on the transport behavior. In this section, we contrast the results from our work with investigations in a single constricted channel, and also the few studies that explored the effect of repeated cellular deformation.
Entry and Transit Time as Measures of Cell Deformability and Friction
Using a single constriction channel (see Table 1), Byun et al. 3 claimed that entry and transit time as dominant measures of cell deformability and friction, respectively. This result was arrived by inhibiting actin polymerization (using Latrunculin B) on mouse lymphoblastic leukemia cells (H1975). They observed that depolymerization of actin networks led to a significant change (~70%) in entry time whereas the transit time was affected less (~30%). They observed similar results by treating mouse embryonic fibroblasts with a microtubule inhibitor drug, Nocodazole. In addition, they treated the constriction with poly-l-lysine that imparted positive charge to the channel walls, and found a stronger effect on transit time of H1975 cells than entry time (~80 vs. ~40%, respectively). These systematic experiments allowed them to conclude that entry time reflected strongly the influence of cell deformability while transit time reflected the effect of cell surface friction. Lange et al.’s investigation27 also showed that entry time is sensitive to cytoskeletal interventions.
Table 1.
Summary of studies using constriction channels to study cell deformability and friction.
| Studies | Constriction types | Cell lines | Wall treatment | Max. strain** (%) | Constriction geometry (μm) | Duration of strain (s)*** |
|---|---|---|---|---|---|---|
| Byun et al. 3 | Single | Embryonic fibroblasts (MEFs), mouse and human lung cancer cells (T Met, T nonMet, and T Met-Nkx2-1), a mouse lymphoblastic leukemia (H1975, H1650 and HCC827) | PEG and PLL(20)-g[3.5]-PEG(2), poly-l-lysine | 195 | W = 6, H = 15, L = 50 | 0.001–1 |
| Hou et al. 21 | Single | Breast tumor cell (MCF-7) and breast normal cell (MCF-10A) | BSA (4 wt%) | 60 | W = 10, H = 10, L = 150 | 0.5–3 |
| Khan et al. 24 | Single | Leukemia cells (CCRF-CEM), prostate cancer cells (LNCaP, CL-1 and CL-2), astrocytoma (1321N1), glioblastoma (A172), and benign glial cells (L0329, L0367) | BSA (4% wt%) | 40 | W = 9–12, H = 8–15, L = 190–350 | 0.03–0.08 |
| Gabriele et al. 13 | Single | Monocytic THP-1 cells | Pluronic (1 wt%) | 120 | W = 4, H = 16, L = NA | 1–1000 |
| Adamo et al.1 | Single | Cervical tumor cells (HeLa) | BSA (3 wt%) + pluronic (1 wt%) | 90 | W = 7, H = 15, L = 15 | 0.0005–0.0035 |
| Chen et al.6 | Single | Osteoblast (MC-3T3) and osteocyte (MLO-Y4), murine breast cancer cells (EMT6) and its drug resistant (EMT6/AR1.0) | No surface treatment | 160 | W = 6 and 8, H = 6 and 8, L = 200 | 0.01–20 |
| Guofeng et al. 17 | Single | Breast tumor cell (MCF-7) and breast normal cell (MCF-10A) | No surface treatment | Not known | D = 6–16, L ≈ 115 | 0.001–3 |
| Lange et al. 27 | Single | Leukemia cells (K562), breast (MDA-MB-231), human bone osteosarcoma (U2OS), human embryonic kidney cells (HEK293T) | Pluronic (1 wt%) | 70 | W = 5, H = 9, L ≈ 10 | 0.005–1 |
| Mak and Erickson29 | Multiple | Breast cancer cells (MDA-MB-231) | No surface treatment | 160 | W = 3.3, H = 10, L = 10 and 60 | 50–550 |
| Ren et al. 39 | Multiple | Highly metastatic tumor (MDA-MB-231) and normal (MCF-10A) breast cells | No surface treatment | 136 | W = 10, H = 8, L = 50 | 0.01–0.05 |
| This work | Multiple | Highly- (MDA-MB-231) and weakly- (MCF-7) metastatic breast tumor cells | With and without BSA (4 wt%) | 40 | W = 11.8, H = 12.4, L = 80 | 0.001–0.2 |
** Most works reported either the strain or deformation index from which strain could be measured.21,27,29 However to measure the cell strain in some other works,1,3,6,39 we supposed the cells have the same volume as their initial volume, and measured the cell deformed size from its initial volume that occupies channels with fixed width. The cell size or volume range reported in their figures has been used to measure the cell volume. The strain is then measured by: strain = (D deformed − D initial)/D initial, where D is cell diameter. *** To measure the duration of applied strain, we assumed cells have a fixed velocity (V) along the channel. The duration of applied strain is then estimated as: t = L/V, where L is the channel length
In our study, we found that for MCF-7 entry and transit times were reduced by 69 and 62%, respectively upon BSA treatment. Likewise, for MDA-MB-231 cells, entry and transit times were reduced by 46 and 43%, respectively in the presence of BSA coating. Thus, unlike Byun et al.,3 our choice of surface coating led to appreciable changes in both entry and transit time. This can be due to differences in the cell lines and surface coatings used. It is also possible that the large compression strain of up to 195% imposed by Byun et al.,3 compared to 40% (maximum) strain in our study, might have caused cell deformability and friction to dominate entry time and transit time, respectively—since the cell has to deform more to enter a narrower constriction, and the higher compression increases the cell membrane contact with channel walls.
In addition to the work of Byun et al., and this study, there are several other works1,6,13,17,21,24,27,29,39 that investigated cell passage through a single constriction channel. However, as shown in Table 1, none of them reported how transport metrics change with and without channel surface treatment,1,3,13,21,25,27 nor did they use any wall coating.6,17,29,39
Role of Repeated Deformation
Unlike the single-constriction studies, only a few studies investigated the influence of repeated deformation using multi-constriction devices (see Table 1). In our study, we found that cancer cells can readily pass through constrictions after pre-deformation due to their inability to recover their shape fully after the compression strain was induced on them in the constrictions. A similar finding was made by Mak and Erickson,29 where they fabricated five constrictions connected in series and imposed a much larger compressional strain of up to 160% on MDA-MB-231 cells. However, this study did not compare cell lines of different metastatic potential. A more recent study by Ren et al.,39 did compare metastatic (MDA-MB-231) with normal breast cells (MCF-10A) in a similar multi-constriction device without surface treatment and showed that the ratio of entry velocities of deformed cells were able to better differentiate the two cell types. In our case, we found that only with surface treatment, we were able to elicit the differences in the transport properties of the highly metastatic MDA-MB-231 and weakly metastatic MCF-7 breast tumor cells. A possible explanation for this is that the compressional strain of up to 136% imposed by Ren et al.,39 that was much larger than ours.
A key finding of this work is that we could only distinguish MCF-7 and MDA-MB-231 cells with BSA treatment, and the underlying mechanism remains elusive. It is apparent that friction is important, which may arise due to interactions between the cell membrane, lubricating fluid layer, and channel wall. However, the manner in which these interactions are manifested in these two cell lines is not fully clear. In general, when the lubricating layer thickness δ is <O(10) nm, friction is dominated by surface and intermolecular interactions. However, when δ is >100 nm, friction due to the hydrodynamic shear force in the lubricating layer dominates.24,40 Preira et al. 38 measured δ ≈ 70 nm for cell velocities of 0.1–1 mm/s, which are comparable to our conditions, suggesting that BSA might be altering the surface (e.g., roughness) and intermolecular (e.g., electrostatic) forces in a way that differences between the two cell lines are elicited.
Conclusions
During the transport in the microcirculation, CTCs experience friction with the capillary walls and multiple deformation events in capillaries. Inspired by this, we fabricated a microfluidic capillary network containing arrays of constrictions separated by relaxation chambers where tumor cells repeatedly undergo compression and relaxation, as well as frictional contact with the constriction walls. Using this microfluidic model, our investigation reveals important insights into the transport behavior of CTCs in microcirculation as summarized below.
-
(i)
We found that tumor cells pass through the initial arrays of constriction channels with low velocity, but in the later arrays their velocity is higher due to the deformation-induced elongated shape. Thus, pre-deformation can enhance the transport of CTCs in the microcirculation.
-
(ii)
Upon repeated deformation we find that the tumor cells are unable to recover their original shape fully, suggesting that plastic deformation or cell fatigue can occur under microcirculatory conditions.
-
(iii)
We found that the two cell lines tested cannot be distinguished based on relaxation behavior. Instead, cell surface-induced friction was correlated with their metastatic potential. Thus, frictional interactions with capillary walls can play an important role in influencing the transport of metastatic CTCs in microvasculature.
The approach we presented here can be further extended to study the influence of cytoskeletal drugs and membrane inhibitors to understand the molecular determinants of cell-surface friction and identify structural elements in the cell that are most sensitive to repetitive deformation.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Acknowledgments
We acknowledge support from the Cancer Prevention and Research Institute of Texas (Grant No. RP 140298).
Conflicts of interest
Nabiollah Kamyabi, Zeina S. Khan and Siva A. Vanapalli declare that they have no conflicts of interest.
Ethical Standards
No human studies or animal studies were carried out by the authors for this article.
References
- 1.Adamo A, et al. Microfluidics-based assessment of cell deformability. Anal. Chem. 2012;84:6438–6443. doi: 10.1021/ac300264v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Bhattacharya S, Datta A, Berg JM, Gangopadhyay S. Studies on surface wettability of poly(dimethyl) siloxane (PDMS) and glass under oxygen-plasma treatment and correlation with bond strength. J. Microelectromech. Syst. 2005;14:590–597. doi: 10.1109/JMEMS.2005.844746. [DOI] [Google Scholar]
- 3.Byun S, et al. Characterizing deformability and surface friction of cancer cells. Proc. Natl Acad. Sci. USA. 2013;110:7580–7585. doi: 10.1073/pnas.1218806110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Chambers AF, Groom AC, MacDonald IC. Dissemination and growth of cancer cells in metastatic sites. Nat. Rev. Cancer. 2002;2:563–572. doi: 10.1038/nrc865. [DOI] [PubMed] [Google Scholar]
- 5.Chang YS, et al. Mosaic blood vessels in tumors: frequency of cancer cells in contact with flowing blood. Proc. Natl Acad. Sci. USA. 2000;97:14608–14613. doi: 10.1073/pnas.97.26.14608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Chen J, et al. Classification of cell types using a microfluidic device for mechanical and electrical measurement on single cells. Lab Chip. 2011;11:3174–3181. doi: 10.1039/c1lc20473d. [DOI] [PubMed] [Google Scholar]
- 7.Cheng YL, Darst SA, Robertson CR. Bovine serum albumin adsorption and desorption rates on solid surfaces with varying surface properties. J. Colloid Interface Sci. 1987;118:212–223. doi: 10.1016/0021-9797(87)90450-4. [DOI] [Google Scholar]
- 8.Das T, Chakraborty S. Perspective: flicking with flow: can microfluidics revolutionize the cancer research? Biomicrofluidics. 2013;7:11811. doi: 10.1063/1.4789750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.di Tomaso E, et al. Mosaic tumor vessels: cellular basis and ultrastructure of focal regions lacking endothelial cell markers. Cancer Res. 2005;65:5740–5749. doi: 10.1158/0008-5472.CAN-04-4552. [DOI] [PubMed] [Google Scholar]
- 10.Dobrzynska I, Skrzydlewska E, Figaszewski ZA. Changes in electric properties of human breast cancer cells. J. Membr. Biol. 2013;246:161–166. doi: 10.1007/s00232-012-9516-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Friedl P, Wolf K. Tumour-cell invasion and migration: diversity and escape mechanisms. Nat. Rev. Cancer. 2003;3:362–374. doi: 10.1038/nrc1075. [DOI] [PubMed] [Google Scholar]
- 12.Fu Y, Chin LK, Bourouina T, Liu AQ, VanDongen AM. Nuclear deformation during breast cancer cell transmigration. Lab Chip. 2012;12:3774–3778. doi: 10.1039/c2lc40477j. [DOI] [PubMed] [Google Scholar]
- 13.Gabriele S, Benoliel AM, Bongrand P, Theodoly O. Microfluidic investigation reveals distinct roles for actin cytoskeleton and myosin II activity in capillary leukocyte trafficking. Biophys. J. 2009;96:4308–4318. doi: 10.1016/j.bpj.2009.02.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gossett DR, et al. Hydrodynamic stretching of single cells for large population mechanical phenotyping. Proc. Natl Acad. Sci. USA. 2012;109:7630–7635. doi: 10.1073/pnas.1200107109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Guck J, et al. Optical deformability as an inherent cell marker for testing malignant transformation and metastatic competence. Biophys. J. 2005;88:3689–3698. doi: 10.1529/biophysj.104.045476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Guntheroth WG, Luchtel DL, Kawabori I. Pulmonary microcirculation: tubules rather than sheet and post. J. Appl. Physiol. 1982;53:510–515. doi: 10.1152/jappl.1982.53.2.510. [DOI] [PubMed] [Google Scholar]
- 17.Guofeng G, et al. Real-time control of a microfluidic channel for size-independent deformability cytometry. J. Micromech. Microeng. 2012;22:105037. doi: 10.1088/0960-1317/22/10/105037. [DOI] [Google Scholar]
- 18.Guyton AC, Hall JE. Textbook of Medical Physiology. 11. Philadelphia: Elsevier Saunders; 2006. pp. 161–194. [Google Scholar]
- 19.Halldorsson S, Lucumi E, Gomez-Sjoberg R, Fleming RM. Advantages and challenges of microfluidic cell culture in polydimethylsiloxane devices. Biosens. Bioelectron. 2015;63:218–231. doi: 10.1016/j.bios.2014.07.029. [DOI] [PubMed] [Google Scholar]
- 20.Hillborg H, et al. Crosslinked polydimethylsiloxane exposed to oxygen plasma studied by neutron reflectometry and other surface specific techniques. Polymer. 2000;41:6851–6863. doi: 10.1016/S0032-3861(00)00039-2. [DOI] [Google Scholar]
- 21.Hou HW, et al. Deformability study of breast cancer cells using microfluidics. Biomed. Microdevices. 2009;11:557–564. doi: 10.1007/s10544-008-9262-8. [DOI] [PubMed] [Google Scholar]
- 22.Kamyabi N, Vanapalli SA. Microfluidic cell fragmentation for mechanical phenotyping of cancer cells. Biomicrofluidics. 2016;10:021102. doi: 10.1063/1.4944057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Kaneko N, Matsuda R, Toda M, Shimamoto K. Three-dimensional reconstruction of the human capillary network and the intramyocardial micronecrosis. Am. J. Physiol. Heart Circ. Physiol. 2011;300:H754–H761. doi: 10.1152/ajpheart.00486.2010. [DOI] [PubMed] [Google Scholar]
- 24.Khan ZS, Kamyabi N, Hussain F, Vanapalli SA. Passage times and friction due to flow of confined cancer cells, drops, and deformable particles in a microfluidic channel. Converg. Sci. Phys. Oncol. 2017;3:024001. doi: 10.1088/2057-1739/aa5f60. [DOI] [Google Scholar]
- 25.Khan ZS, Vanapalli SA. Probing the mechanical properties of brain cancer cells using a microfluidic cell squeezer device. Biomicrofluidics. 2013;7:11806. doi: 10.1063/1.4774310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Krebs MG, et al. Molecular analysis of circulating tumour cells—biology and biomarkers. Nat. Rev. Clin. Oncol. 2014;11:129–144. doi: 10.1038/nrclinonc.2013.253. [DOI] [PubMed] [Google Scholar]
- 27.Lange JR, et al. Microconstriction arrays for high-throughput quantitative measurements of cell mechanical properties. Biophys. J. 2015;109:26–34. doi: 10.1016/j.bpj.2015.05.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lee JN, Jiang X, Ryan D, Whitesides GM. Compatibility of mammalian cells on surfaces of poly(dimethylsiloxane) Langmuir. 2004;20:11684–11691. doi: 10.1021/la048562+. [DOI] [PubMed] [Google Scholar]
- 29.Mak M, Erickson D. A serial micropipette microfluidic device with applications to cancer cell repeated deformation studies. Integr. Biol. (Camb.) 2013;5:1374–1384. doi: 10.1039/c3ib40128f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.McDonald DM, Choyke PL. Imaging of angiogenesis: from microscope to clinic. Nat. Med. 2003;9:713–725. doi: 10.1038/nm0603-713. [DOI] [PubMed] [Google Scholar]
- 31.Miyamoto DT, Sequist LV, Lee RJ. Circulating tumour cells—monitoring treatment response in prostate cancer. Nat. Rev. Clin. Oncol. 2014;11:401–412. doi: 10.1038/nrclinonc.2014.82. [DOI] [PubMed] [Google Scholar]
- 32.Ng J, Shin Y, Chung S. Microfluidic platforms for the study of cancer metastasis. Biomed. Eng. Lett. 2012;2:72–77. doi: 10.1007/s13534-012-0055-x. [DOI] [Google Scholar]
- 33.Nguyen DX, Bos PD, Massague J. Metastasis: from dissemination to organ-specific colonization. Nat. Rev. Cancer. 2009;9:274–284. doi: 10.1038/nrc2622. [DOI] [PubMed] [Google Scholar]
- 34.Nyberg KD, et al. The physical origins of transit time measurements for rapid, single cell mechanotyping. Lab Chip. 2016;16:3330–3339. doi: 10.1039/C6LC00169F. [DOI] [PubMed] [Google Scholar]
- 35.Otto O, et al. Real-time deformability cytometry: on-the-fly cell mechanical phenotyping. Nat. Methods. 2015;12:199–202. doi: 10.1038/nmeth.3281. [DOI] [PubMed] [Google Scholar]
- 36.Pantel K, Speicher MR. The biology of circulating tumor cells. Oncogene. 2015 doi: 10.1038/onc.2015.192. [DOI] [PubMed] [Google Scholar]
- 37.Polacheck WJ, Li R, Uzel SGM, Kamm RD. Microfluidic platforms for mechanobiology. Lab Chip. 2013;13:2252–2267. doi: 10.1039/c3lc41393d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Preira P, Valignat M-P, Bico J, Théodoly O. Single cell rheometry with a microfluidic constriction: quantitative control of friction and fluid leaks between cell and channel walls. Biomicrofluidics. 2013;7:024111. doi: 10.1063/1.4802272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Ren X, Ghassemi P, Babahosseini H, Strobl J, Agah M. Single-cell mechanical characteristics analyzed by multi-constriction microfluidic channels. ACS Sens. 2017 doi: 10.1021/acssensors.6b00823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Ruths M, Berman AD, Israelachvili JN. In: Nanotribology and Nanomechanics: An Introduction. Bhushan B, editor. Berlin: Springer; 2005. pp. 389–481. [Google Scholar]
- 41.Sakuma S, et al. Red blood cell fatigue evaluation based on the close-encountering point between extensibility and recoverability. Lab Chip. 2014;14:1135–1141. doi: 10.1039/c3lc51003d. [DOI] [PubMed] [Google Scholar]
- 42.Schmidt RF, Thews G, editors. Human Physiology. 2. Berlin: Springer; 1989. [Google Scholar]
- 43.Schrott W, et al. Study on surface properties of PDMS microfluidic chips treated with albumin. Biomicrofluidics. 2009;3:44101. doi: 10.1063/1.3243913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Sobin SS, Tremer HM, Fung YC. Morphometric basis of the sheet-flow concept of the pulmonary alveolar microcirculation in the cat. Circ. Res. 1970;26:397–414. doi: 10.1161/01.RES.26.3.397. [DOI] [PubMed] [Google Scholar]
- 45.Tomaiuolo G, et al. Microfluidics analysis of red blood cell membrane viscoelasticity. Lab Chip. 2011;11:449–454. doi: 10.1039/C0LC00348D. [DOI] [PubMed] [Google Scholar]
- 46.Turitto VT. Blood viscosity, mass transport, and thrombogenesis. Prog. Hemost. Thromb. 1982;6:139–177. [PubMed] [Google Scholar]
- 47.Vanapalli SA, Duits MH, Mugele F. Microfluidics as a functional tool for cell mechanics. Biomicrofluidics. 2009;3:12006. doi: 10.1063/1.3067820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Weinbaum S, Cowin SC, Zeng Y. A model for the excitation of osteocytes by mechanical loading-induced bone fluid shear stresses. J. Biomech. 1994;27:339–360. doi: 10.1016/0021-9290(94)90010-8. [DOI] [PubMed] [Google Scholar]
- 49.Weinbaum S, Duan Y, Satlin LM, Wang T, Weinstein AM. Mechanotransduction in the renal tubule. Am. J. Physiol. Renal Physiol. 2010;299:F1220–F1236. doi: 10.1152/ajprenal.00453.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Williams SA, et al. Dynamic measurement of human capillary blood pressure. Clin. Sci. (Lond.) 1988;74:507–512. doi: 10.1042/cs0740507. [DOI] [PubMed] [Google Scholar]
- 51.Wirtz D, Konstantopoulos K, Searson PC. The physics of cancer: the role of physical interactions and mechanical forces in metastasis. Nat. Rev. Cancer. 2011;11:512–522. doi: 10.1038/nrc3080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Xia Y, Whitesides GM. Soft lithography. Annu. Rev. Mater. Sci. 1998;28:153–184. doi: 10.1146/annurev.matsci.28.1.153. [DOI] [Google Scholar]
- 53.Xue C, et al. Constriction channel based single-cell mechanical property characterization. Micromachines. 2015;6:1457. [Google Scholar]
- 54.Yamauchi K, et al. Real-time in vivo dual-color imaging of intracapillary cancer cell and nucleus deformation and migration. Cancer Res. 2005;65:4246–4252. doi: 10.1158/0008-5472.CAN-05-0069. [DOI] [PubMed] [Google Scholar]
- 55.Zhang Z, Nagrath S. Microfluidics and cancer: are we there yet? Biomed. Microdevices. 2013;15:595–609. doi: 10.1007/s10544-012-9734-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.