Cell Sequence and Mitosis Affect Fibroblast Directional Decision-Making During Chemotaxis in Microfluidic Mazes

Abstract

Introduction

Directed fibroblast migration is central to highly proliferative processes in regenerative medicine and developmental biology. However, the mechanisms by which single fibroblasts affect each other’s directional decisions, while chemotaxing in microscopic pores, are not well understood.

Methods

We explored effects of cell sequence and mitosis on fibroblast platelet-derived growth factor-BB (PDGF-BB)-induced migration in microfluidic mazes with two possible through paths: short and long. Additionally, image-based modeling of the chemoattractant’s diffusion, consumption and decay, was used to explain the experimental observations.

Results

It both cases, the cells displayed behavior that is contradictory to expectation based on the global chemoattractant gradient pre-established in the maze. In case of the sequence, the cells tend to alternate when faced with a bifurcation: if a leading cell takes the shorter (steeper gradient) path, the cell following it chooses the longer (weaker gradient) path, and vice versa. Image-based modeling of the process showed that the local PDGF-BB consumption by the individual fibroblasts may be responsible for this phenomenon. Additionally, it was found that when a mother cell divides, its two daughters go in opposite directions (even if it means migrating against the chemoattractant gradient and overcoming on-going cell traffic).

Conclusions

It is apparent that micro-confined fibroblasts modify each other’s directional decisions in a manner that is counter-intuitive to what is expected from classical chemotaxis theory. Consequently, accounting for these effects could lead to a better understanding of tissue generation in vivo, and result in more advanced engineered tissue products in vitro.

Electronic supplementary material

The online version of this article (10.1007/s12195-018-0551-x) contains supplementary material, which is available to authorized users.

Introduction

Directional decision-making during cell migration is important for regenerative medicine (e.g. tissue engineering, wound healing)47 and developmental biology20,43 since tissue development depends on how the cells distribute themselves within the complex pores of the extra-cellular matrix (ECM).15,20,34 However, current single cell studies are not representative of the scenarios in which multiple cells enter the pores simultaneously and influence each other’s decisions. At the same time, “collective” migration investigations mainly focus on cells that form stable adhesions between each other during movement (e.g., epithelial cells).14,33,37 Yet, fibroblasts, which are more relevant to synthesizing collagen and ECM, tend to migrate as individual cells when squeezing through the microscopic tissue pores.44 Previous studies on how social interactions influence fibroblasts’ migration behaviors mainly focused on random migration, while we could not find published examples of such influences on chemotaxis.1,2,5,21,25,28,46 As a result, the processes by which single fibroblasts affect each other’s directional decision-making while chemotaxing in tissues are not well understood. Given the lack of knowledge, this manuscript set out to investigate two unexplored aspects of fibroblast migration that are particularly relevant to proliferative environments commonly encountered in regenerative medicine: effects of cell sequence and mitosis on chemotaxis in micro-sized pores.

In case of the former, we hypothesized that the order in which the cells enter the pores will affect their directional choices at bifurcations. Fibroblast migration in tissue is primarily regulated via attraction to chemical substances originating from the hematopoietic and blood system, or from products of the ECM. However, other cell types have been known to self-generate/modify existing chemical gradients when confined in microscopic spaces.13,38 Moreover, fibroblasts are known to deposit integrin-containing “migration tracks” that affect the motility of their neighbors.5,17 Therefore, it is logical to conclude that the localized fibroblast sequence effects will compete with the global chemotactic gradient in the microscopic pores.

Secondly, since tissue generation is a highly proliferative process, we aimed to explore the effects that cell division has on the fibroblast decision-making during chemotactic migration. Mitosis has been found to affect migration in both fibroblasts5,6,28 and other cell types.11,26,48 However, these experiments were conducted in the absence of a chemotactic gradient and/or micro-confinement, which is more representative of geometric features of tissue microenvironments.29 Therefore, we wanted to see whether the cell division effects on fibroblast hold true under chemotaxis and in the spatial confinement.

To that end, we chose the most appropriate migration platform from currently available sources7,26,30–32,38—a microfluidic maze, which contains confinement features that offer multiple directional choices.7,38 Specifically, the maze consists of a long path, a short path, and dead ends. In order to emulate chemotaxis in tissue-like environments and induce the fibroblast migration across the maze, we selected platelet derived growth factor—BB (PDGF-BB), a fibroblasts “mitoattractant” (i.e., both a chemoattractant40–42 and a mitogen4,12,22,23 at the same time).

To our surprise, we found that in both, the cell sequence and the mitosis cases, the cell–cell interactions cause the fibroblasts to display behavior that is contradictory to what would be classically expected from the chemoattractant gradient established in the maze. Namely, we found that the fibroblasts path choices alternate depending on each predecessor’s decision, and that cell division occurring during the chemotaxis yields daughter cells with directional bias distinctive from that of their siblings. Therefore, the presented results carry practical implications for both engineered tissue design, and for understanding the fibroblast biology in their native micro-constricted environments.

Materials and Methods

Materials

Polydimethylsiloxane (PDMS) Sylgard 184 was purchased from Dow Corning (Midland, MI). Negative photoresist SU-8 was purchased from Microchem (Newton, MA). Bovine collagen Type I 3 mg ml⁻¹ solution (PureCol) was purchased from Advanced Biomatrix (San Diego, CA). Recombinant rat platelet-derived growth factor-BB (PDGF-BB) was purchased from R&D Systems (Minneapolis, MN). Culture media was prepared from Minimum Essential Medium (MEM) (Sigma, MO) supplemented with 10% (v/v) fetal bovine serum (FBS) (VWR, Radnor, PA), and 1% (v/v) penicillin–streptomycin (10,000 U mL⁻¹) (Thermofisher, Waltham, MA). Basal media was composed of MEM supplemented with 1% (v/v) penicillin–streptomycin. For incubation in 5% CO₂ atmosphere, media was buffered by 26 mM sodium bicarbonate (Sigma, MO). CO₂-independent media buffered by 20 mM HEPES (Sigma, MO) was used for the microscope stage-top experiment.

Device Description

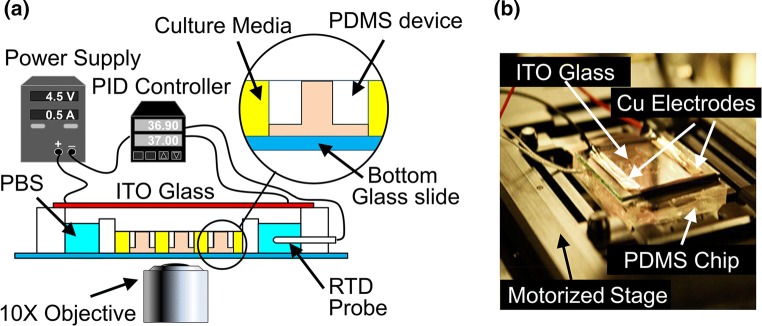
The microfluidic platform used in this work consists of micron-sized mazes (adapted from a cancer migration study by Scherber et al.).38 The maze is a network of bifurcations consisting of two through paths, one short (1300 µm) and one long (1700 µm), and several dead ends. Its channels were chosen to have a rectangular profile 24 µm wide by 17 µm high (see Figs. 1a and 1d), in order to limit the number of cells entering the maze to 1–3 at a time. Each maze had a single entrance and exit, shown at the bottom and top of those figures, respectively. Twenty mazes of identical design were replicated per a single microfluidics device (see Figs. 1b and 1e). The device connected a large cell seeding area, with zero initial concentration of the chemoattractant, to a central reservoir of chemoattractant-rich media, via the mazes. In this manner, a stable chemoattractant gradient was established between the cell compartment and the central reservoir, in order to prescribe direction to the cell migration. Finally, multiple identical devices were placed inside of a PDMS enclosure for high-throughput experimentation (see Figs. 1c and 1f). The enclosure also isolated the whole setup from the external environment, in order to prevent contamination.

Figure 1.

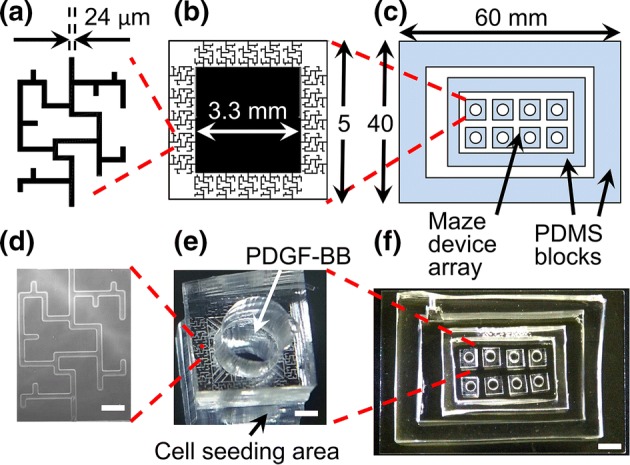
(a, b, c) Schematics showing dimensions of a single maze, a single microfluidic device, and an array of the devices inside of a stage-top custom incubation chamber, respectively. (d) Phase contrast microscopy image of a single maze network. Scale bar is 100 µm. (e) Photograph of a single microfluidic device, consisting of 20 maze networks that share a central chemoattractant reservoir. A circular 3 mm diameter hole was punched in the center of each device in order to deposit the PDGF-BB into the reservoir. Cells were seeded outside of the devices. Scale bar is 1 mm. (f) An array of microfluidic devices placed inside a stage-top custom incubation chamber, consisting of two PDMS blocks bonded to the top of a glass slide. Scale bar is 5 mm.

Custom Incubation Chamber for Culturing on the Microscope Stage

PDMS with a base-to-crosslinking agent ratio of 10:1 was poured into two 100 mm petri dishes to different thicknesses: 8 and 10 mm. After heating at 65°C overnight, the resulting solid PDMS blocks were removed from the petri dishes and cut in rectangular shapes: one smaller and one larger. A 2-mm hole was punched on one side of the larger block for mounting a temperature sensor. The two blocks were then treated with air plasma using a plasma cleaner (PDC-001, Harrick Plasma, Ithaca, NY), and bonded on to a pre-cleaned 50 × 75 × 1 mm glass slide (Ted Pella, Redding, CA), one inside the other (see Fig. 1c and 1f). The larger and thicker block served as the periphery of the incubation chamber, while the smaller block formed an enclosure for the microfluidic devices array, in order to prevent contamination from the temperature sensor opening. Phosphate buffer saline (PBS) was added to the space between the two PDMS blocks in order to humidify the incubation chamber.

Device Fabrication

The mold for the device was fabricated using SU-8. First, the microscale pattern was sketched using AutoCAD (Autodesk, Mill Valey, CA) and printed at 16,525 dpi on a transparency (Fineline Imaging, Colorado Springs, CO) to generate a high-resolution photomask. SU-8 was spin coated, exposed to UV light, and developed on a 4-in silicon wafer (University Wafer, Boston, MA) following the manufacturer‘s protocol to generate 17-µm high microfluidic channels. Microfluidic devices were fabricated using a single-layer soft lithography method. Typically, PDMS with a base-to-agent ratio of 10:1 was poured over the photo-patterned mold, degassed, and cured at 65 °C overnight. The cast PDMS was carefully peeled off from the master, and a 3-mm biopsy punch was used to create a central hole in each device for PDGF-BB delivery to the chemoattractant reservoir. Individual devices were cut using a thin razor blade, rinsed with 70% isopropyl alcohol and left dried in an oven. Then 6–8 devices were treated with air plasma for 30 s at medium radio-frequency power, before they were bonded inside of the culture chamber. The assembly was then heated to 65 °C on a hot plate for 5 min to improve the bonding.

Surface Treatment

Right after bonding, the device was placed under a 200-mTorr vacuum for 2 min to remove air inside the micro channels. Immediately after being released from vacuum, about 150 µg ml⁻¹ collagen type I solution was added to completely coat the micro channels and the cell seeding area. The coated device was then sterilized by UV light inside a biohood for 1 h, and washed several times with PBS before use.

Cell Preparation

Mouse embryo NIH/3T3 (ATCC^® CRL-1658TM) fibroblasts were purchased from ATCC (Manassas, VA). Prior to being transferred to the microfluidic device for the migration experiments, the cells were incubated in the culture media inside of T75 flasks. The flasks were kept at 37 °C and in a humidified atmosphere of 5% CO₂ in air. The culture media was changed every 2 days to ensure normal cell growth. Prior to the migration experiments, the cells were trypsinized from the T75 flasks and loaded into the chip, with a seeding density of about 50,000 cells cm⁻². The chip was incubated at 37 °C under 5% CO₂ for 6 h to allow cell attachment. Then the cells were cultured in serum-starved media (MEM supplemented with 1% penicillin–streptomycin) for 6 h.

Cell Migration Experiments and Image Acquisition

At the start of the experiment, cell culture media in the chip was replaced with CO₂-independent basal media buffered by HEPES. 20 µL of basal media supplemented with 25–50 ng mL⁻¹ PDGF-BB was then added into the central reservoir of each device. The concentration of PDGF-BB at the exit was chosen to be higher than that typically used to induce migration and mitosis,12 keeping in mind that it would be lower at the maze’s entrance. A negative control experiment was performed to make sure that the behavior of this cell line is indeed unique to situations were a chemotactic gradient is present (see Supplemental Video 1).

The experimental setup used a custom incubation system, which is illustrated in Fig. 2. A resistance temperature detector (RTD) sensor (Auberin, Alpharetta, GA) was mounted to the mounting hole on the larger PDMS block. The chip was covered by a 15 Ω cm⁻² Indium Tin Oxide (ITO)-coated glass slide (Adafruit, NY) and mounted on a motorized microscope stage (Ludl Electronic, Hawthorne, NY). Electrodes on the ITO glass slide were connected to a bench top power supply (MPJA, FL) to supply a heating power of 1.5 W. The RTD sensor was connected to a PID controller (Auberin, Alpharetta, GA) which helped to maintain a constant temperature of 37 ± 0.2 °C. Time-lapse phase-contrast imaging of the fibroblast migration was performed using a fully automated Olympus IX83 microscope fitted with a 10X phase-contrast objective (Olympus, Japan), a CMOS camera (Orca Flash 4.0 V2, Hamamatsu, Japan), and an autofocus module (ZDC, Olympus, Japan). Time-lapse images were automatically captured at 5–15 min intervals for duration of 20 h. For each device at each time step, 36 tile images were acquired at different locations, stitched, and stabilized using an in-house Matlab^® 2016b code (The MathWorks, Inc., Natick, MA). The cells were labeled manually.

Figure 2.

(a) Experiment setup schematic, showing the custom incubation chamber used for culturing on the automated microscope’s stage. The setup consisted of a benchtop variable power supply, which provided a current of 0.5 A to an ITO glass that was placed on top of the PDMS chamber. Heat generated by the glass warmed up the media inside of the chamber. Temperature was measured using a RTD sensor coupled to a PID controller, which modulated the power supply in order to maintain a constant temperature of 37 °C. (b) Photograph of the incubation chamber in operation. Electric current was fed to the resistive layer of the ITO glass through a pair of copper electrodes. This led to heat generation underneath of the PDMS chamber. The incubation chamber was placed on top of a XY motorized stage, controlled by the computer, for imaging.

Data Analysis

Migratory cells were tracked using the Manual Tracking plug-in for ImageJ software (National Institutes of Health).39 The directional decision chosen by each individual cell at the long-short bifurcation was determined via manual observation. Quantitative data of cell sequence was generated using an in-house Matlab^® 2016b code (The MathWorks, Inc., Natick, MA). Cells that underwent division were not included in the sequential cell migration statistics. Instead, the directional decisions of the mitotic cells were counted separately. Significance level was determined by the non-parametric binomial test. Statistical significance was set as p < 0.05.

Global PDGF-BB Gradient Simulation Within a Maze Without Cells

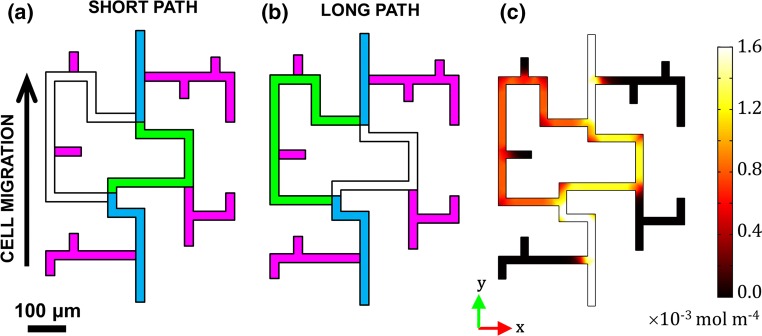
The PDGF-BB concentration gradient formed between the two ends of the maze was simulated numerically using COMSOL 5.3a Multiphysics (COMSOL, Burlington, MA). Specifically, steady state two dimensional transport of diluted species was modelled inside of 24-µm wide by 17-µm high channels, resembling the real maze geometry (see Fig. 3). The chemoattractant reservoir and the cell seeding area were treated as infinite sources and sinks, respectively. Constant concentration boundary conditions, corresponding to the experiment, were set to C_P,exit = 50 ng mL⁻¹ PDGF-BB at the source (i.e., maze exit), and to zero at the sink (i.e., maze entrance). A diffusion coefficient of D_P,maze = 1 × 10⁻¹⁰ m²/s was used to represent the PDGF-BB (MW = 25 kDa) in an aqueous solution.3 Chemoattractant gradient values at every point in the maze were calculated from the vector magnitude of two components, x-axis (horizontal) and y-axis (vertical), both of which increased towards the higher concentration of PDGF-BB (see Fig. 3c). The presence of the cells in the maze was not taken into account by the calculation.

Figure 3.

Illustration of possible path choices available to the cells in the microfluidic maze. Blue = common paths; Pink = dead ends. (a) Short path labelled in Green; (b) Long path labelled in Green; (c) PDGF-BB gradient magnitude calculated from COMSOL. The maze entrance is at the bottom, and its exit is at the top.

Model Validation via Fluorescent Dextran Tracking Experiments

Fluorescein isothiocyanate (FITC)-labeled dextran with an average molecular weights of 20 kDa (FD20S, Sigma, St. Louis, MO) was dissolved to 3 mg/ml in water. Three milliliter of the solution was dialyzed using a Slide-A-Lyzer^® 20,000 molecular weight cut-off dialysis cassette (66003, Thermofisher, Waltham, MA) to remove low-molecular weight contaminants. A FITC-dextran concentration of 200 µg/ml for testing the gradient evolution dynamics inside of the microfluidic maze.

Results

To better understand how single fibroblasts affect each other’s directional decision-making under chemotaxis in microscopic tissue-like environments, we studied their motility in spatially confined maze channels. The mazes contained two possible through paths and multiple dead-ends. The cells entered the mazes through a common path, and would eventually reach a bifurcation where they had a choice of either a shorter through path (see Fig. 3a), or one that was approximately 1.3 times longer (see Fig. 3b). Eventually, they exited the maze through another common path (assuming that they did not get stuck in a dead-end).

Since the fibroblasts migrated in response to a concentration gradient of PDGF-BB established inside of the maze, we characterized the relative difference in the chemotactic driving forces between the two paths via a COMSOL simulation (see Fig. 3c). The chemoattractant concentration in the maze increased from the zero boundary condition at its entrance (where the cell seeding area was) to 50 ng mL⁻¹ at its exit, in order to match the experiment. The resulting global gradient, shown in Fig. 3c, was about 1.5 times higher in the short path than the long path, mainly due to the length difference between them. Therefore, it would be logical to expect that the cells would be more likely to select the shorter path, in order to ascend the steepest gradient possible.

To test whether the above prediction is valid, the cells were allowed to migrate across the maze in response to two different PDGF-BB concentrations at the exit: 25 and 50 ng mL⁻¹. Manual tracking was used to collect statistics on their positions in the maze, throughout the duration of each experiment (e.g., Videos 1 and 2). Moreover, we also recorded the sequence in which the cells entered the maze and made their directional decisions once inside.

Experimentally-Observed Effects of Cell Sequence on the Fibroblasts Directional Decision-Making

Overall, we found no statistically significant differences between the two PDGF-BB tested concentrations; and the shorter path was indeed preferred over the longer path for the leading cells that were the first to arrive at the bifurcation (see Fig. 4a). Specifically, we used a binomial test to gauge the directional bias of the cells towards the short or the long path. Consequently, we were able to reject the null hypothesis that the cells were not biased towards the short path, with a 95% level of confidence. In other words, the first cells to enter the maze preferred the short path; and the distribution between the short and the long paths was approximately 60–40%, when only these cells were considered. However, surprisingly, if all the cells entering the maze were accounted for (regardless of their order), the directional bias disappeared, and the prediction was no longer valid (see Fig. 4b). In this case, we were not able to reject the null hypothesis with the same level of confidence; and this signified a lesser bias towards the short path.

Figure 4.

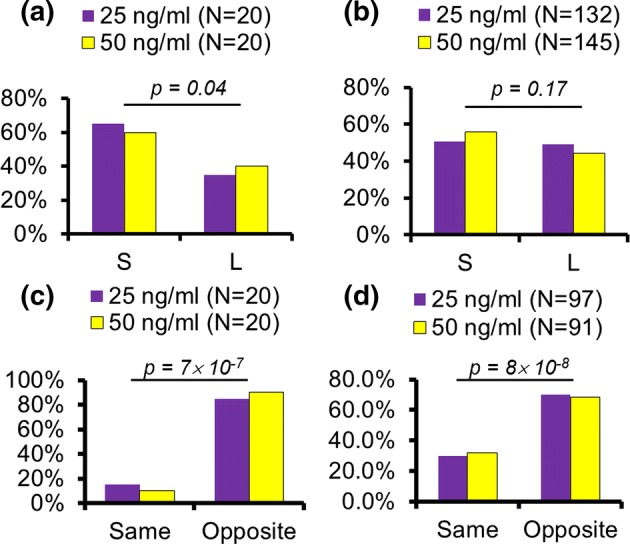
(a) Directional choices of the first cells to reach the maze bifurcation (S = short path, L = long path). (b) Directional choices of all cells reaching the maze bifurcation, regardless of order. (c) Directional choices of the first two cells reaching the maze bifurcation, when the cell sequence is taken into account. (d) Directional choices of any two consecutive cells to reach the maze bifurcation. N indicates the number of cells (a, b) and sequences (c&d) being counted. N is low in case of (a) and (c) since only first and second cells were considered. N is high in case of (b) and (d) since all cell orders were taken into account. p values are calculated using the Binomial Test.

In order to investigate this curious phenomenon further, we considered the sequence in which the cells arrived at the bifurcation. This type of analysis showed that the cells alternate their directional choices between the short and the long paths (Video 1 and Video 2, respectively). Hence, we defined a binary variable for either ‘opposite’ or ‘same’ choices made by the leading-following cell pairs, and used the binomial test to quantify their bias. Figure 4c shows that most of the cell pairs chose an opposite path relative to each other, when only the first two cells that entered the maze were considered. Likewise, Fig. 4d shows that the trend remained the same when the choices of any two consecutive cells were considered. In fact, the statistical analysis showed that in both cases the cells were biased towards the opposite choice with a > 99% confidence.

Specifically, Supplementary Fig. 1A shows that there was a slight bias (~ 50% of the occurrences) towards the Short-Long decision, possibly because the first cells to enter the maze were likelier to choose the short path (as was shown in Fig. 4a). The second likeliest case was Long-Short; followed by Short–Short, accounting for less than 10% of the occurrences. Finally, the Long–Long case happened with a negligible probability. Similarly, the alternation of the directional choice persisted even with the subsequent cells: Supplementary Fig. 1B shows the probabilities of fibroblast directional decisions when the choices of any two consecutive cells are considered. Here, ‘same’ choice decisions were slightly more frequent, but the overall trend remained the same, and the cells were more likely to choose the paths opposite to that of their predecessors’. Hence, we hypothesized that the observed alternation of the directional decisions was caused by a localized consumption of the chemoattractant by the individual cells. So, we performed image-based simulations in order to test this hypothesis.

Image-Based Simulation of Localized PDGF-BB Consumption by the Cells in the Maze

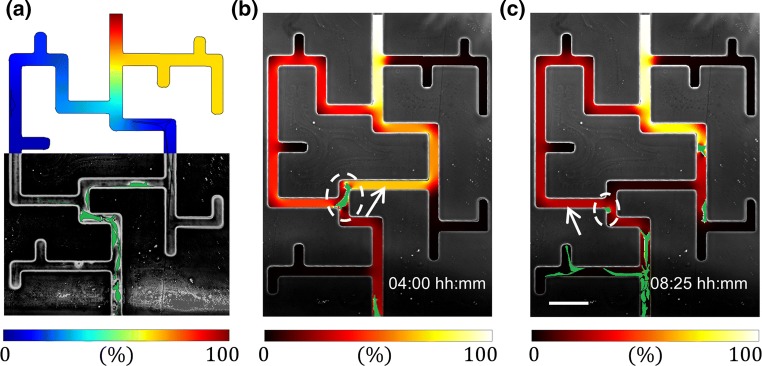
In order to visualize how the individual fibroblasts modify the PDGF-BB localized concentration gradient established in the maze, phase microscopy time-lapse images were used to incorporate the effects of the presence of the cells into the COMSOL diffusion simulations. While the maze geometry remains static, the cell shapes and locations are obtained via image processing and are passed into the diffusion solver. The boundary conditions remain the same as in the steady state “no cell” model described in the Methods section, while the cell migration is updated at intervals of ∆t = 15 min (corresponding to the experimental image acquisition times). The main difference here is that the PDGF-BB is depleted over time via a natural decay and via endocytosis by the fibroblast cells. Following Menon et al. and Haugh, these effects are represented by adding the following consumption terms to the COMSOL model: − k_decay C_P everywhere in the maze, and − k_endocytosisC_fC_P to the cells domains.16,27 Here, k represents reaction rate constants, C_P is the local concentration of PDGF-BB and C_f is the fibroblast “density”—an analogue of a chemical species concentration in a continuum representation of the cells. However, since our model has discrete cells, we assume that C_f = C_f,max (corresponding to $\overline{f}$ in Menon et al.), which is derived based on the carrying capacity of the fibroblast cells. Moreover, the diffusivity of the PDGF inside of the cells D_P,cell was arbitrarily set to two orders of magnitude slower than in the channels, in order to simulate the effect of the chemoattractant diffusion being slowed down within the cells. The physical values of the relevant model inputs are summarized in Table 1, and the idea behind the approach is shown in Fig. 5a. Additionally, we verified that the simulated PDGF diffusion kinetics matches those of experimental fluorescent dextran with a similar molecular weight (see Supplemental Video 2); and that the presence of the individual cells in the maze’s channels do not block the diffusion of the dextran (see Supplemental Video 3).

Table 1.

Simulation parameters used in the image-based model of PDGF-BB consumption by individual fibroblasts.

Parameter	Description	Value
C P,exit	PDGF-BB concentration at the exit of the maze	2 × 10−6 mol/m3
C P,entrance	PDGF-BB concentration at the maze entrance	0 mol/m3
DP,maze	Diffusivity of PDGF-BB in the channels	1 × 10−10 m2/s
DP,cell	Diffusivity of PDGF-BB in the cells	1 × 10−12 m2/s
C f,max	Maximum Fibroblast “density”	0.1 g/cm3
k decay	PDGF-BB decay constant	2.78 × 10−5 s−1
k endocytosis	PDGF-BB degradation constant	0.555 cm3 g−1 s−1

Figure 5.

Image-based modeling of localized fibroblast effects on the PDGF-BB distribution within the maze. (a) Demonstration of the image-based concept. Upper half corresponds to the COMSOL simulation, with the PDGF-BB concentration scaled by the exit boundary condition concentration; while the lower half is the phase microscopy image of the fibroblasts (labeled in green) chemotaxing through the maze. (b) and (c) Simulation results of real-time modifications to the PDGF-BB gradient overlaid on the experimental microscopy images, showing the first and second cells’ directional decisions at the maze bifurcation, respectively. Note that although the gradient is scaled between 0 and 100%, the actual value corresponding to the latter is chosen differently between the two timeframes in order to enhance visibility (for actual gradient values see Video 4). Dashed white circle highlights the decision-making cell, while white arrow points to the higher chemoattractant gradient path chosen by the cell.

The model showed that each fibroblast consumed the PDGF-BB in its locality (see Video 3), and thereby affected the distribution of the chemoattractant’s concentration gradient significantly (see Video 4). This analysis also showed that the “leading” cell’s choice is motivated by the steeper gradient in the shorter path, as is expected (see Fig. 5b). Conversely, the “trailing” cell senses a steeper gradient in the longer path, because the “leading” cell in front of it has consumed the chemoattractant in the short path (see Fig. 5c). This finding supports the hypothesis that the presence of the individual cells can overcome the external chemotactic cues via self-generation of local gradients. However, given that tissue generation is a highly-proliferative process, we also wanted to explore the effects of cell mitosis on fibroblast migration.

Experimentally-Observed Effects of Mitosis on the Fibroblasts Directional Decision-Making

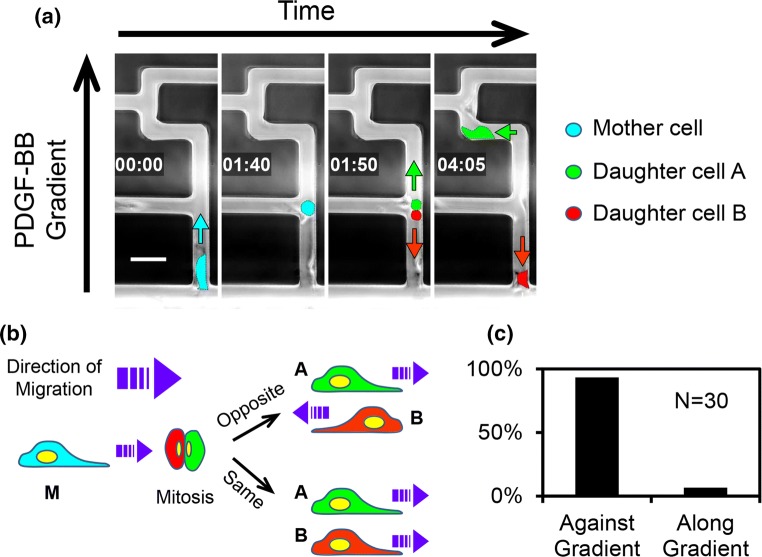
In the past, mitosis has been found to affect fibroblast migration under non-chemotactic conditions,5,6,28 while here we explored its effect on the cells’ directional decision-making in the presence of PDGF-BB. To do that, the fibroblasts undergoing division were manually tracked and analyzed. Figure 6a shows a time montage of such an event occurring, while the mother cell was navigating the maze’s common path from the entrance. This figure shows that after the division, one of the daughter cells continued along the positive PDGF-BB gradient path, while the second daughter went against it (in the opposite direction).

Figure 6.

(a) Time-lapsed montage of cells undergoing mitosis when migrating in the maze. The cells were false-colored for visual recognition. Cyan, red, and green arrows show the direction of migration of the mother and the two daughter cells, respectively. The time is displayed as hh:mm. The scale bar is 50 µm. (b) Diagram showing two directional scenarios encountered by the two daughter cells. (c) Frequency of occurrence of the two directional scenarios shown in panel (b).

Overall, we observed two modes of the daughter cells’ migration: either both went along the gradient (though often taking different paths through the maze, as in the cell sequence case), or one went along the gradient and the other against it (see Fig. 6b). However, the probabilities of each mode differed significantly: only < 10% of occurrences for the former (Fig. 6c, Video 5), vs. > 90% for the latter (Video 6). Furthermore, it was especially surprising to see that some of the daughter cells that went against the gradient did so despite the oncoming traffic of other migrating cells; and ultimately were able to exit the maze entirely, through the entrance (Video 6). Therefore, it is apparent that the mitosis-driven repulsion between the daughter fibroblasts is so great that it is able to overcome both the chemotactic forces and the “inertia” of the other cells migrating along the gradient. That is, in many instances the daughter cell has to squeeze past heavy oncoming traffic of densely-packed cells entering the maze.

Finally, we observed that the mitosis happened more frequently at regions in the maze that are closer to the entrance, and less frequently near its exit (see Supplemental Fig. 2A). This is likely because the threshold12 at which fibroblast proliferation is induced corresponds to the lower PDGF-BB concentrations that are experienced by the cells near the maze entrance. Although cell mitosis has been found to be affected by micro-confinement,45 we do not believe that this the case here; because, according to Supplemental Fig. 2B, the highest proportion of cell divisions per maze segment visits occurred in a dead-end (and not at the maze entrance, where the confinement was first encountered).

Discussion

This manuscript investigated fibroblast chemotaxis in tissue-mimicking microarchitectures, in order to understand how these cells influence each other’s directional decision-making under microscopic confinement. Understanding these mechanisms is important to developmental biology, multiple tissue pathologies,8,9,18,19,24,36 and regenerative medicine,47 because fibroblasts are the primary cell type responsible for normal tissue homeostatic processes. For example, they are involved in collagen synthesis, the build-up of connective tissues (e.g., cartilage, bone), and wound healing in response to injury.35,43 Therefore, characterizing their migratory behavior in microscopic pores can lead to improved tissue patterning and product uniformity. Subsequently, since tissue generation is a highly dynamic and proliferative process, we hypothesized that cell–cell interactions and cell division should affect fibroblasts’ decisions.

To test the hypothesis, we induced fibroblast chemotaxis in microfluidic mazes, and collected migration statistics as a function of the sequence at which the cells arrived at the path bifurcations. Unexpectedly, we found that consecutive cells alternate their decisions in order to avoid following each other, even if that means choosing the longer path through the maze (i.e., a weaker chemoattractant gradient). This seems to be contradictory to studies performed in similar mazes, but with cancer cells and immune cells.7,38 However, a major difference is that those were single cell studies, while ours were multi-cell. Therefore, one possible explanation is that the leading cell alters the local chemoattractant concentration by consuming the PDGF-BB (at a rate higher than it is replenished via diffusion). Subsequently, choosing an alternate path may in fact result in a steeper local gradient for the subsequent cells. Another possible explanation is the integrin migration tracks that fibroblasts have been known to leave behind them.5,17 However, this is less likely, as those findings report cells following each other’s migration tracks, not avoiding them. Moreover, fibroblasts are known to attract each other via fibroblast growth factor and ECM degradation proteinase release.4 Therefore, it is surprising to see them avoiding each other to such a great extent that they would contradict the optimal route expected from the PDGF-BB gradient.

Nonetheless, our simple image-based model is able to explain the experimental observations by using published reaction kinetic parameters (shown in Table 1),16,27 and two simplifying assumptions. Namely, the first assumption is that the endocytosis of PDGF occurs as a pseudo-first order reaction: − k_effectiveC_P, where the effective reaction rate constant k_effective = 0.0555/s is a product of two other constants, k_endocytosis and C_f,max. This simplification is necessitated by the fact that the published PDGF endocytosis models treat the fibroblasts as a continuous species with a concentration, while our model has discrete cells (which makes it unobvious what value to use for C_f). However, it does yield a reasonable value for an estimated maximum receptor-mediated endocytosis uptake rate per cell of ~ 1 × 10² molecules/min/cell. Moreover, a parameter sensitivity analysis of the model showed robustness in its predictions (see Online Appendix).

The second key assumption in our model is that the PDGF diffusion occurs much faster than does the cell migration. This is necessary, because the cell geometries are updated at the frequency at which the images are captured by the microscope, once every ∆t_microscope = 15 min; while the time resolution in the diffusion solver is chosen to be ∆t_simulation = 1 min (based on the observation that a finer time step did not improve the results). The assumption is valid, because fibroblast cells in our maze have an average speed of 2–4 μm/min (or 0.03–0.06 μm/s); whereas, the diffusion coefficient used to represent the PDGF-BB (MW = 25 kDa) in an aqueous solution was D_P,maze = 1 × 10⁻¹⁰ m²/s.3 A rough estimate of the PDGF-BB diffusion speed can be calculated by dividing D_P,maze by a characteristic length scale, which can be taken as the width of the maze channel. Furthermore, the result is multiplied by a factor of 4, to account for two-dimensional diffusion. This yields ~ 16.7 μm/s. Hence, the PDGF-BB diffusion is about 2 orders of magnitude faster than the cell migration.

Additionally, we demonstrated that the division of the parental fibroblasts was highly asymmetric in terms of the migration choices of their descendants. This was evidenced by one of the daughters being more likely to move against the chemoattractant gradient, often disregarding the oncoming traffic created by the other cells in the maze. The finding is consistent with previous reports of fibroblast daughter cells creating tracks that are mirror images of each other,6 when migrating on a gold particle-coated substrate5; and also, migrating in opposite directions on a collagen matrix.28 However, in the latter work, the daughters separated only temporarily when the cells divided on fibrin (instead of on collagen), and eventually came back together along the same path (which was not the case in our study). Therefore, the effect appears to be substrate-dependent. Moreover, these experiments were conducted in the absence of a chemotactic gradient and without micro-confinement, so they are not a one-to-one comparison with our work.

Such heterogeneity between sibling cells is typically attributed to differences in the relative expressions of chemoattractant receptors on their surfaces. The case of the fibroblast PDGF-BB-driven chemotaxis is also a receptor-mediated process.4,10 Therefore, it is possible that there were differences in PDGF receptor expression levels between the sibling cells. Similar asymmetric receptor distributions have been observed in migrating cells before.13 Hence, it would be interesting to image the PDGF-BB receptor distribution in the fibroblasts membranes at the time of mitosis. However, immunofluorescent labelling of the PDGF receptors would also block the receptors sites, subsequently hindering the chemotaxis. Therefore, non-blocking fluorescent tags are needed.

In summary, our study provides insight into how individual fibroblasts affect each other’s decision-making processes during chemotaxis in spatially confined microarchitectures. A limitation of this work is that the pore sizes are much larger, and the substrate (poly-d-lysine coated glass) is much stiffer, in the maze compared to a typical extracellular matrix. Therefore, the results presented here are not a one-to-one comparison with the extracellular space of in vivo tissue. Nonetheless, they still carry practical implications for both understanding the biology of chemotactically driven morphogenesis processes in vivo, as well as for artificial tissue design in vitro. For example, scaffold architectures could be optimized for achieving desired cell distributions by taking into account how the fibroblasts alternate the paths they take at bifurcations. Furthermore, our model could help to select cells with a higher migration potential by selectively isolating the cells that choose the shorter path through the maze. Finally, this study raises some critical questions about what is behind the discovered effects that compete with the chemotaxis. For example, the reason why the mitotic cells display highly distinctive directional choices may be either due to a difference in receptor expression in the daughter cells, or due to the migration tracks left by their parent. Therefore, these effects, and other possibilities, need to be investigated further.

Conclusions

In conclusion, we conducted a study of fibroblast interactions during chemotaxis in a microfluidic maze made to resemble in vivo tissue pores. Through this study, we have demonstrated that the directional decisions of these cells are influenced by the sequence in which they arrive at path bifurcations, and that their path choices alternate depending on each predecessor’s decision. Also, we showed that cell division occurring during the chemotaxis yields daughter cells with directional bias distinctive from that of their siblings. Furthermore, in both cases, the fibroblast–fibroblast influence appeared to overcome the directional guiding of the chemoattractant gradient established within the maze. We presented a hypothesis the that sequence effect is likely due to a localized chemoattractant consumption by the leading cells, while the mitotic effect could be caused by an asymmetric PDGF-BB receptor inheritance by the two daughters. Moreover, we confirmed the former via image-based modeling of PDGF-BB consumption by the individual fibroblasts; however, further investigations are needed to validate the latter. Nonetheless, the presented results carry practical implications for developmental biology, multiple pathologies, and tissue engineering.

Electronic supplementary material

Below is the link to the electronic supplementary material.