Synesthetes perseverate in implicit learning: Evidence from a non-stationary statistical learning task

Abstract

Synesthetes automatically and consistently experience additional sensory or cognitive perceptions in response to particular environmental stimuli. Recent evidence suggests that the propensity to develop synesthesia is genetic while the particular associations experienced by a given synesthete are influenced by learning. Despite the potential role of implicit learning in the formation of synesthetic associations, there has been minimal investigation of synesthetes’ implicit learning abilities. In this study, we examine linguistic-colour synesthetes’ ability to implicitly learn from and adjust to non-stationary statistics in a domain unrelated to their particular form of synesthesia. Engaging participants in a computer game Whack-the-mole, we utilise the online measure of reaction time to assess the time course of learning. Participants are exposed to “worlds” of probabilities that, unbeknownst to them, undergo unannounced changes, creating unpredictable statistical shifts devoid of accompanying cues. The same small set of probability worlds are repeated throughout the experiment to investigate participants’ ability to retain and learn from this repetitive probabilistic information. The reaction time data provide evidence that synesthetes require more information than nonsynesthetes to benefit from the non-stationary probability distributions. These findings demonstrate that linguistic-colour synesthetes’ implicit learning abilities—in a domain far from their synesthetic experiences—differ from those of nonsynesthetes.

Introduction

Synesthetes automatically and consistently experience additional sensory or cognitive perceptions in response to particular environmental stimuli. For example, a grapheme-colour synesthete might experience the colour plum when perceiving the letter q. Although this phenomenon with its hallmark conscious, automatic, and stable associations has been documented for over a century (Calkins, 1893; Claparède, 1903), its cause has remained largely undetermined. While there is evidence supporting the hypothesis that the propensity to develop synesthesia is genetic (e.g., Asher et al., 2009; Barnett et al., 2008), other evidence is consistent with the hypothesis that particular synesthetic associations are influenced by learning (e.g., Bankieris & Aslin, 2016, 2017; Witthoft and Winawer, 2013; Witthoft, Winawer, & Eagleman, 2015).

Early synesthesia theories proposed a critical role for learning in the formation of synesthetic associations (Calkins, 1893; Claparède, 1903), and this idea has been revitalised by recent findings. Witthoft and Winawer (2013) conducted a small-scale study of 11 grapheme-colour synesthetes and reported that the grapheme-colour pairings of these adult synesthetes largely overlapped with the colours of toy letters and numbers to which they were exposed as children. This finding suggests that the grapheme-colour pairings the synesthetes experienced as young children influenced the formation of their synesthetic associations. This same research group later corroborated this finding with a large-scale study investigating the influence of such coloured toys on 6,588 grapheme-colour synesthetes’ associations (Witthoft et al., 2015). By examining the grapheme-colour associations present in a particular toy set and tracking the availability of this toy set to consumers, they found evidence supporting the influence of early environmental exposure on the formation of synesthetic associations. Specifically, none of the synesthetes born before the toy set was publicly available had a large number of synesthetic associations overlapping with the coloured toys, while nearly 15% of participants born in the decade following the availability of this specific toy set had a significant overlap with the associations present in the coloured toys. These findings suggest that exposure to a particular set of environmental stimuli can influence the formation of synesthetic associations and that learning in early childhood plays a role in synesthesia. As synesthesia is neither taught to nor intentionally acquired by children, implicit learning in particular is a likely candidate for impacting the development of synesthetic associations.

Despite the potential role of implicit learning in synesthesia, only two studies to date have investigated differences in implicit learning abilities between synesthetes and nonsynesthetes. By embedding probabilistic shape-colour associations within a detection task, we recently found that linguistic-colour synesthetes implicitly learned associations more quickly, had increased long-term retention of these associations, and had decreased ability to learn shuffled associations (Bankieris & Aslin, 2017). These findings demonstrate that synesthetic experiences become quickly entrenched once acquired from environmental associations, suggesting that synesthetes’ implicit learning abilities differ from those of nonsynesthetes. Given that the shape-colour associations learned by our grapheme-colour synesthetes in this study were in the same domain as their synesthetic associations, it is possible that these differences in implicit learning are restricted to a synesthetes’ experienced domain. Examining synesthetes’ implicit learning abilities in a more general sense, Rothen et al. (2013) tested grapheme-colour synesthetes, sequence-space synesthetes, and nonsynesthetes in an artificial grammar learning study. In this study, participants were exposed to two different grammars within the training phase of the experiment—one with symbols and one with letters. At test, participants made grammaticality judgements on strings from the grammars they were exposed to during learning. Grapheme-colour synesthetes performed more accurately than controls on letter strings but not symbol strings, suggesting that their increased accuracy was related to their synesthetic colour experiences triggered by the letter strings. Supporting this interpretation of the results, sequence-space synesthetes—whose synesthesia occurs in a domain outside of the materials used in this study—did not perform more accurately than controls on either grammar. Accordingly, neither of these studies support the hypothesis that synesthetes have extraordinary implicit learning abilities in domains beyond their synesthesia, but rather exhibit superior learning because of the benefit provided by their synesthetic experience. In this study, we investigate synesthetes’ implicit learning abilities in a domain unrelated to their particular form of synesthesia (specifically, statistical learning of probabilistic distributions) and utilise the online measurement of reaction time (RT) to examine the time course of learning.

To mimic the real world in which synesthetes acquire their associations, we examine their ability to learn non-stationary probabilistic associations. That is, a given synesthetic child does not experience 100% yellow m’s while growing up, but rather sees m’s in a variety of colours. If these statistics were generated from a stationary world, she would only need to discount the variability inherent in probabilistic processes as noise to successfully learn about her environment. The real world, however, is non-stationary adding a layer of difficulty to this learning task. The learner in this non-stationary environment must determine if observed variability is indeed noise generated by a probabilistic process, or instead is a new signal resulting from a change of the underlying statistics themselves. Applied to our synesthetic child example, she may see a high proportion of yellow m’s while she is reading a children’s book, but then encounter no yellow m’s while looking at her mother’s calendar. The child must decipher whether this lack of yellow m’s is noise, or meaningful signal.

Given the aforementioned studies and the fact that synesthetes acquire additional associations while living in the same environment as nonsynesthetes, their implicit learning of statistics from probability distributions could differ from that of the nonsynesthetic population. Perhaps synesthetes are quicker to learn the underlying distribution of environmental statistics, tuning out or modelling noise more easily than nonsynesthetes. Another possibility (in addition to or in place of the previous suggestion) is that synesthetes are resistant to changes in probability distributions. The consistency of synesthetes’ associations suggests that once the underlying probability distribution has been determined, synesthetes might need more evidence than nonsynesthetes to conclude that a statistical shift has occurred. Finally, considering that synesthetes’ associations remain stable for decades (e.g., Simner & Logie, 2007), synesthetes may remember previously encountered probability distributions better than nonsynesthetes. Our broad hypothesis is that synesthetic associations are manifestations of synesthetes’ implicit learning abilities. While synesthetic grapheme-colour associations appear throughout adolescence (Simner & Bain, 2013) likely because this is when detailed knowledge of linguistic stimuli are acquired, we posit that any implicit learning differences between synesthetes and nonsynesthetes exist in adulthood as well as childhood. In this study, we tested synesthetes’ sensitivity to non-stationary probabilistic structures in a computerised game Whack-the-mole created by Qian and colleagues (Qian, Jaeger, & Aslin, 2016). Participants tapped a touch-screen location where a mole was depicted as surfacing from one of four holes as fast as they could. By altering the underlying statistics of the mole’s appearance, we investigated participants’ ability to learn, retain, and adjust to non-stationary probability distributions. This experimental design allows us to examine the time course of synesethetes’ implicit statistical learning in a domain outside of their particular synesthetic associations.

Methods

Participants

Nine linguistic-colour synesthetes (mean age = 24.1, SD = 8.63, males = 4) experiencing colour in response to graphemes, days of the week, and/or months of the year and nine nonsynesthetes (mean age = 19.7, SD = 1.7, males = 1, see Table 1 for further age details) participated in this experiment. An additional two nonsynesthetes who completed the experiment were excluded from analyses due to a failure to display general task learning during the experiment (i.e., no RT decrease from first trial to final trial). Nonsynesthetes were recruited from the Rochester area and synesthetes were recruited from our existing database of Rochester area synesthetes. All participants were compensated US$10/hr for their participation. Ethical approval was obtained from the University of Rochester Research Subjects Review Board.

Table 1.

Participant ages (years) by group.

Controls	Synesthetes
18	18
18	18
18	19
20	20
20	21
20	21
20	27
22	28
22	45

Synesthetes’ self-reported experiences were confirmed with a consistency test administered via the online testing site, synesthete.org (see Eagleman, Kagan, Nelson, Sagaram, & Sarma, 2007, for methods). This test identifies synesthetes based on replicated findings that synesthetes are significantly more consistent when repeatedly choosing synesthetic colours for the stimuli eliciting them (e.g., letters) compared to nonsynesthetes. Our synesthetes experienced colours in response to graphemes (n = 6), days of the week (n = 5), and/or months of the year (n = 4) as confirmed by mean standardised scores of .47 (SD = .12), .57 (SD = .16), and .45 (SD = .08), respectively, where a score below 1.0 confirms synesthesia (see Eagleman et al., 2007, for details). Two synesthetes experienced colours for graphemes, days of the week, and months of the year; one had synesthetic colours for only days of the week and months of the year; five were solely grapheme-colour synesthetes; one synesthete experienced colours for only days of the week. Nonsynesthetes completed a synesthesia questionnaire (see synesthete.org), indicated no synesthetic experiences, and were further verbally questioned to ensure a complete lack of such experiences.

Apparatus

Subjects played the Whack-the-mole game on a Windows Surface 3 with a 10.75-inch touch screen and 1,920 by 1,280 pixel screen resolution. The game window occupied the entirety of the screen.

Procedure

Whack-the-mole

Participants were simply told to watch for the mole and touch it as soon as possible, using only one finger from their dominant hand throughout the experiment (see Figure 1). Trials continued until the participant made a correct response or 2 s elapsed. A correct response to the appearance of the mole consisted of a touch to a predefined area surrounding the hole out of which the mole popped. We used RT in milliseconds (ms) as our dependent measure and defined it as the duration between the moment the mole was just visible on the screen and the moment it was touched. Participants were neither informed of nor instructed to learn about the probability of the mole appearing in any given hole. Thus, any learning regarding the underlying statistical regularities in our experiment was implicit, in the sense of being uninstructed by task feedback. Note that the background animals were consistent in number (4 hippos, 2 dinosaurs, 2 snails), with positions randomly reshuffled on each trial. These background animals added an overall level of difficulty (via distraction) to the task, but did not serve as a contextual cue that would inform the observer about the currently assigned world. The landscape (e.g., tree, clouds, position of holes) was consistent across all trials.

Figure 1.

Whack-the-mole screen shot. On each trial, the mole emerged from one of the four holes. The positions of the other animals were randomly reshuffled on each trial.

The game presented participants with four different “worlds” of probability distributions. Each world had a probability distribution of 1 / 2, 1 / 6, 1 / 6, and 1 / 6 across the four holes. What differed between the worlds was the assignment of each probability to the four holes (see Table 2). That is, each world had a different dominant hole out of which the mole was most likely to pop (1 / 2 of the trials), and all other holes shared the remaining probability equally (1 / 6 of the trials each). The game was split into three identical blocks with 2-min breaks in between. Each block presented the four worlds in a pseudorandom order so that each world appeared three times and followed every other world once (with the constraint that a given world was never repeated in immediate succession). This design yields 12 “bundles” (i.e., consecutive trials of the experiment that abide by the same probability distribution) per block and nine presentations of each world throughout the entire experiment (see Table 3). Each bundle occurred for 36, 42, or 48 trials to prevent subjects from learning when a shift from one world to the next would occur, while maintaining precise probability distributions. The ordering of these bundle lengths was pseudorandomly generated so that each world appeared at each length once per block.

Table 2.

Probability distributions for each of the four worlds used in the experiment.

	Hole 1	Hole 2	Hole 3	Hole 4
World 1	1/ 2	1/ 6	1/ 6	1/ 6
World 2	1/ 6	1/ 2	1/ 6	1/ 6
World 3	1/ 6	1/ 6	1/ 2	1/ 6
World 4	1/ 6	1/ 6	1/ 6	1/ 2

Table 3.

Experimental structure for block 1.

World	A	B	C	A	D	B	D	C	B	A	C	D
World frequency	1	1	1	2	1	2	2	2	3	3	3	3
Bundle	1	2	3	4	5	6	7	8	9	10	11	12
Length	36	42	48	42	36	36	48	36	48	48	42	42

Participants completed three identical blocks with 2-min breaks in between.

Rather than generating hole appearances in a truly probabilistic manner, we sampled hole appearances without replacement from a vector strictly following the desired probabilities. For example, for a 36-trial-long bundle following the probability distribution of World B, hole appearances would be sampled without replacement from a vector containing 18 twos, 6 ones, 6 threes, and 6 fours. These fixed probabilities ensure that participants are receiving the intended statistics, removing unnecessary noise that would be created by implementing true probability in our finite bundle lengths. Finally, we encouraged participants to make quick responses by displaying a score in the top-right corner of the game window. Each trial rewarded the participant points based solely on a linear function of their RT, providing no information about the underlying structure of the experiment.

N-back

After completing the Whack-the-mole task, participants additionally completed a control task to ensure that synesthetes and nonsynesthetes did not differ in general motivation or working memory (Gheri, Chopping, & Morgan, 2008). This control task was a custom n-back task which presented white symbols in the centre of a grey screen one at a time. Stimuli were eight familiar punctuation and mathematical symbols that did not elicit synesthetic colours: %, #, &, *, =, ?, {, and ¡. Participants monitored the presented symbols and indicated the repetition of a symbol from 2 or 3 screens ago (depending on the block) by pressing the space bar. Each trial began with the presentation of a fixation dot in the centre of the screen for 500 ms. This fixation dot was then replaced by one of the eight symbols for 500 ms followed by a 2000 ms interstimulus interval (ISI) during which the screen was blank. Participants completed 20 two-back and 20 three-back practice trials to ensure that the task was understood before beginning the experimental trials. Then, participants completed six 48 trial blocks—three blocks of two-back and three blocks of three-back, interleaved—with mandatory 60-s breaks in between blocks. Stimulus presentation was randomised within blocks with the constraint that each block contained 33% targets and 67% foils. We displayed the type of block (two-back or three-back) at the top of the screen to ensure that participants did not get confused regarding the task. In addition, we displayed participants’ accuracy at the end of each trial to encourage their continued effort. Importantly, our synesthetes did not experience synesthetic colours for any of the eight symbols used.

Data analysis

All analyses were conducted using the statistical software package R version 3.2.4. We excluded any trial that lasted for 2 s without a correct response and removed outliers on a subject-by-subject basis by excluding trials on which a participant’s RT was more than 2.5 standard deviations away from their mean RT (1549/27,215 = 5%). We then performed a mixed-effects linear regression on the subset of trials in which the mole popped out of the “promoted” location or the “demoted” location. For a given bundle, we defined the promoted hole as the hole with the highest probability assigned to it. As a world was never repeated back to back and all four of our worlds had the same individual probabilities, this hole always changed from a 1 / 6 probability to a 1 / 2 probability. Likewise, we defined the demoted hole as the hole that was the most likely in the previous bundle. This demoted hole always changed from a probability of 1 / 2 to a probability of 1 / 6. We exclude the holes that do not change from one bundle to the next from our analysis because these holes do not provide information for subjects to learn. We also exclude the very first bundle of the experiment from these analyses as there is neither a promoted nor demoted hole before any statistics have been observed, yielding a total of 16,776 analysed trials.

Results

First, we confirm that the nonsynesthete control participants did learn about the probability distributions present in the game. This was necessary to ensure that the general properties of the task were learnable given the four probability worlds chosen and the three different bundle lengths. Next, we investigate whether synesthetes and nonsynesthetes exhibit differences in learning as a function of world frequency (i.e., how many times they have encountered a given world). In our analyses, a decrease in RT indicates learning about the probability distributions because a stronger expectation for the mole to pop out of a particular hole will likely lead to a reduced RT if the mole does appear in that expected location.

We conducted a mixed-effects linear regression predicting log RT from world frequency (1–9), log bundle trial (i.e., the trial number within a bundle; 1–48 on a linear scale), hole type (promoted as 0, demoted as 1), group (nonsynesthete as 0, synesthete as 1), and all interactions. We also modelled hole identity (1–4 as a factor) and log experiment trial (1–1,532 on a linear scale) as fixed effects to control for random behaviour differences across hole locations and a general practice and/or fatigue effect, respectively. Finally, we included random intercepts and slopes (world frequency, log bundle trial, and hole type) by participant. Log RT was used as the dependent variable due to the skewed distribution of RTs; taking the log of RT creates a more Gaussian distribution suitable for our analyses. All numerical predictors were centred. We note that this design and analysis includes a correlation of .92 between log experiment trial and world frequency and further discuss ways to disentangle this correlation in the “Discussion” section. Additional analyses including age as a predictor were conducted and all main findings reported below remained unchanged.

General learning in nonsynesthete controls

Before examining group differences in learning across repetitions of statistics (i.e., worlds), we confirmed that non-synesthetic participants exhibited signs of general learning in our experiment. Specifically, participants should exhibit RT differences between promoted holes and demoted holes on average. Because promoted holes always have a probability of 1 / 2 associated with them and demoted holes always have a probability of 1 / 6 associated with them, participants should have slower RTs to demoted hole trials compared to promoted hole trials regardless of what they are learning about repeated probability distributions (i.e., worlds). With nonsynesthetes coded as the reference group (i.e., 0), the coefficients (excluding group, and group interactions) indicate how the relevant variable affects nonsynesthetes’ RTs. Indeed, our results confirm that nonsynesthetes were sensitive to this probabilistic distinction between promoted and demoted holes, with slower RTs to demoted holes than to promoted holes, B = 0.048, SE = .008, p < .001. Moreover, even if non-synesthetes were only tracking local statistics and were unaware of the repeating probability distributions underlying the game, their RTs to moles surfacing from the promoted hole should decrease throughout a bundle while their RTs to moles appearing in the demoted hole should increase throughout a bundle. The results from our regression detailed in Table 4 and displayed in Figure 2 indicate that nonsynesthetes did learn from the presented statistics, with RTs to promoted holes decreasing as a bundle progressed (B = −0.025, SE = .002, p < .001) and a significant interaction of trial within bundle and hole type indicating that RTs increased within a bundle for the demoted hole; B = 0.043, SE = .004, p < .001. Together, these findings demonstrate that nonsynesthetes learned from the basic, local probabilities presented in the experiment.

Table 4.

Detailed regression results for reaction time behaviour.

	B	SE		χ2 (df)
Intercept	6.225	(0.021)			***
World frequency	−0.006	(0.002)		4.21(1)	*
Log bundle trial	−0.025	(0.002)		40.19(1)	***
Hole type	0.048	(0.008)		22.29(1)	***
Group	−0.021	(0.029)		0.51(1)
Hole 2	−0.048	(0.003)
Hole 3	−0.049	(0.003)		335.33(3)	***
Hole 4	−0.034	(0.003)
Log experiment trial	−0.030	(0.003)		93.5(1)	***
World frequency: log bundle trial	−0.001	(0.001)		0.53(1)
World frequency: hole type	0.001	(0.001)		0.91(1)
Log bundle trial: hole type	0.043	(0.004)		114.22(1)	***
World frequency: group	0.005	(0.003)		2.94(1)
Log bundle trial: group	0.000	(0.003)		1.00(1)
Hole type: group	−0.010	(0.011)		0.92(1)
World frequency: log bundle trial: hole type	−0.002	(0.002)		0.93(1)
World frequency: log bundle trial: group	0.000	(0.001)		0.02(1)
World frequency: hole type: group	0.005	(0.002)		8.01(1)	**
Log bundle trial: hole type: group	0.006	(0.006)		0.94(1)
World frequency: log bundle trial: hole type: group	0.002	(0.002)		1.26(1)

SE: standard error of the estimate.

Hole type is dummy coded such that promoted hole = 0 and demoted hole = 1. Group is also dummy coded with control = 0 and synesthete = 1. All continuous predictors are centred. Significance values are generated via model comparison and results are annotated with asterisks.

^*p < .05

^**p < .01

^***p < .001.

Figure 2.

Learning within a bundle: differential effect of bundle trial for demoted and promoted holes. Means and standard errors are plotted. Lines are linear regression fits generated for visualisation only. Datapoints are jittered on the x-axis to reduce overlap.

Group differences in learning

Next, we investigated whether synesthetes and controls differed in what they learned about the shifting probability distributions present in the Whack-the-mole game. Specifically, we ask (1) whether synesthetes are faster implicit learners by looking at RT patterns within a bundle and (2) if synesthetes have better memory representations of the probability worlds by looking at the effect of repeating probability distributions on RT.

Differences within a bundle.

If synesthetes are faster at implicitly detecting that a shift in the underlying probability distributions has occurred, we would expect their RTs to the promoted hole to decrease more rapidly than controls’ RTs within a bundle. Likewise, their RTs to the demoted hole should increase more rapidly than controls’ RTs throughout a bundle. Our analysis does not provide support for this possibility as there is neither a significant group by bundle trial nor group by bundle trial by hole type interaction (see Table 4). These results do not indicate that synesthetes and controls learn different amounts of information, or learn at different rates, from trial to trial within a bundle.

Differences across repetition of worlds.

Finally, we investigated whether synesthetes and controls differed in their sensitivity to repeating worlds. By repeating probability distributions throughout the experiment, we could determine whether synesthetes’ memory for previously encountered worlds was better than that of controls. If the memory for repeated probability worlds differed between synesthetes and controls, we would expect to see a significant interaction including world frequency and group. Our analysis revealed a significant interaction among world frequency, hole type and group, with synesthetes’ RT to demoted holes decreasing more slowly than controls’ RT to demoted holes as a given world reappears; B = 0.005, SE = .002, p < .01 (see Figure 3). Furthermore, the lack of a significant hole type by world frequency interaction fails to provide evidence that the rate of RT decrease for controls differs by hole type (see Table 4). Interestingly, a comparison of group RT for the very first world frequency suggests that this effect is driven by synesthetes’ failure to distinguish promoted and demoted holes in early presentations (t = 0.73 ns), whereas controls’ RT to demoted and promoted holes differed from the first presentation onward, t = 6.72, p < .001.

Figure 3.

Learning across world frequency: visualisation of group by world frequency by hole type interaction. Means and standard errors are plotted. Lines are linear regression fits generated for visualisation only. Datapoints are jittered on the x-axis to reduce overlap. Note that there is a difference in slope between the two lines for synesthetes whereas these lines are parallel for controls.

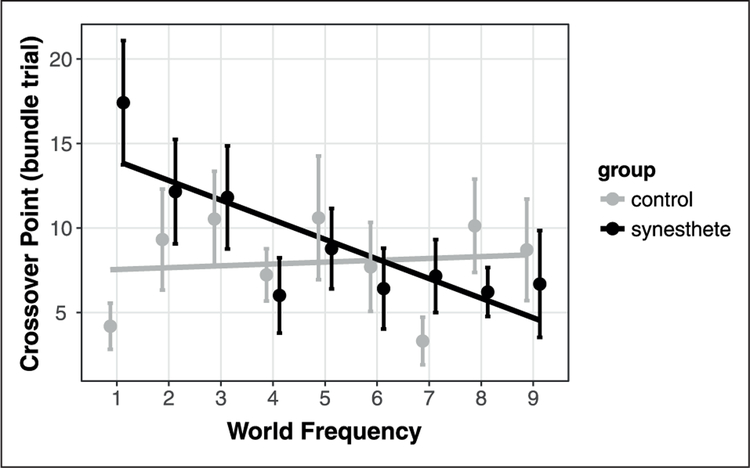
To further investigate this finding, we examined the “crossover point,” or the trial within a bundle where RTs to promoted holes became faster than RTs to demoted holes, across world frequency for each group of participants. To calculate crossover point, we fit linear models predicting log RT with log bundle trial for each combination of participant, world frequency, and hole type (promoted or demoted). For each participant and world frequency, the crossover point was then selected as the first trial for which the predicted log RT for promoted holes was less than demoted holes. Using this calculated crossover point, we conducted a mixed-effects linear regression predicting crossover point from the interaction of group and world frequency as well as varying intercepts by participant and varying slopes by participant and world frequency. As seen in Figure 4, this crossover point for nonsynesthetes was early in the bundle and remained stable as worlds were encountered again and again during the game. In contrast, the crossover point for synesthetes occurred later within a bundle compared to controls for low world frequencies, and as the experiment progressed it shifted earlier in the bundle, becoming indistinguishable from that of controls. Thus, the effect of world frequency on crossover point differs for synesthetes and nonsynesthetes, as confirmed by the significant group by world frequency interaction B = −1.29, SE = .49, p < .01. This analysis suggests that synesthetes are resistant to changing statistics in the beginning of the experiment, but come to expect these shifts as they experience more of them. In contrast, nonsynesthetes more readily adapt to shifts in probability worlds and maintain that flexibility throughout the game.

Figure 4.

Crossover point by group and world frequency. Means and standard errors are plotted. Lines are linear regression fits generated for visualisation only. Datapoints are jittered on the x-axis to reduce overlap.

N-back results

Data from an n-back task were collected to ensure that group differences during the Whack-the-mole task were not due to motivational or general working memory differences. We removed practice trials (defined as the first 88 trials) as well as the first two or three trials per block (depending on whether it was a 2-back or 3-back block because these trials have no correct answer) before analysing the data. We then constructed a mixed-effects logistic regression model fitting participants’ accuracy by group (control as –.5, synesthete as .5) and block type (2-back as –.5, 3-back as .5), the group by block type interaction, block number (as a factor) as well as intercept and slopes by participant. Our results indicated a significant effect of block type, with lower accuracy for 3-back blocks than 2-back blocks, B = −1.58, SE = .19, p < .001. Crucially, we found neither an effect of group (M _S = .89, M_C = .86) nor an interaction between group and block type. These results fail to provide evidence that synesthetes and controls performed differently overall and or differ in general working memory capabilities.

Discussion

Linguistic-colour synesthetes and nonsynesthetes in this study were tested for their sensitivity to non-stationary statistics by playing a computerised Whack-the-mole game. Participants simply tapped a surfacing mole as quickly as possible, without knowing that the mole did not emerge from a hole randomly, but rather emerged as determined by one of four possible probability distributions. These probability worlds were reintroduced throughout the experiment, allowing us to observe the effect of repeating probabilistic structures on participants’ behaviour. We examined RT as an index of participants’ ability to implicitly learn the structure underlying this task.

The structure of our Whack-the-mole task presents the opportunity to evaluate learning of the game’s statistics at two levels. First, we can examine participants’ behaviour on a trial-by-trial basis within a bundle to investigate quick learning of local statistics. We did not find that synesthetes and nonsynesthetes differed at this level of learning, with both groups demonstrating decreased RTs to promoted holes and increased RTs to demoted holes within a bundle. These results suggest that synesthetes and nonsynesthetes did not differ in what they learned about our task within a single bundle.

Second, as we repeated the same four probability distributions multiple times throughout the experiment, we can additionally look at what participants learned from seeing the same statistics repeatedly. At this level of learning, we found that synesthetes and nonsynesthetes differed. Specifically, synesthetes seemed unable to benefit from the presented statistics initially, requiring a greater accumulation of information before discriminating promoted and demoted holes. In addition, synesthetes experienced difficulty adjusting to the shifting statistics during early phases of this experiment (as demonstrated by their late crossover points) but adapted to the non-stationary task after multiple shifts of the probability worlds. In contrast, nonsynesthetes’ RTs for demoted holes were slower than those for promoted holes during the very first presentation of the probability distributions. This suggests that nonsynesthetes were adapting to the shifting statistics more readily than synesthetes in the beginning of the experiment. In addition, nonsynesthetes’ RT difference between demoted and promoted holes remained stable across repetitions. Thus, we did not find evidence indicating that nonsynesthetes gained any information from the repetition of probability distributions.

These results point to specific ways in which synesthetes’ implicit learning differs from nonsynesthetes’. Interestingly, our findings suggest that synesthetes may be cautious learners, requiring more evidence to uncover the non-stationary probability distribution, in line with our previous findings demonstrating that synesthetes struggle to learn shuffled associations (Bankieris & Aslin, 2016, 2017). However, that earlier study used an implicit learning task whose stimuli fell within the domain of their synesthesia (i.e., colour-shape). Taken together, our findings suggest that synesthetes may be more committed to originally experienced statistics (either those presented within an experiment or experienced in their environment) than nonsynesthetes, consistent with their general superiority for retaining key statistics (e.g., colour-grapheme pairs) in their environment. It is possible that synesthetes’ sensitivity to repeated probability distributions may lead to the acquisition of synesthetic associations in childhood. As our study examined the online implicit learning of probabilistic distributions, these results suggest that synesthetes’ altered implicit learning abilities extend beyond the domain of their particular synesthetic experiences. We hypothesise that synesthetic associations may be an obvious manifestation of more general implicit learning abilities present in adult and child synesthetes.

Regarding the nonsynesthetes performance on our task, previous work (Qian et al., 2016) has demonstrated that nonsynesthetes are sensitive to the repetition of probability distributions in a variation of this Whack-the-mole task which contains a more complex set of probabilities and shifts. We did not find such an improvement for nonsynesthetes in this study, perhaps because the cost of storing and retrieving simpler representations (i.e., only four probability worlds) outweighed the benefit. That is, using the local statistics may have provided the controls in our task with nearly the same benefit as recognising probability worlds per se, but with fewer cognitive demands.

Another difference from our earlier work was the absence of contextual cues that could serve to highlight the transitions from one probability world to another, as well as which world was active (i.e., knowing which hole was promoted). In this study, we chose to introduce shifts in probability distributions without any contextual cues. Future studies could use correlated cues to further investigate whether synesthetes are “slow learners,” unaware of the local statistics at first presentation, or “conservative learners,” aware of the local statistics but hesitant to adjust their behaviour. With the addition of 100% correlated cues (e.g., only bunnies as the distractor animals with probability world 1 in our Whack-the-mole setup), participants should have less of a reason to be conservative. Thus, if synesthetes’ RTs to demoted and promoted hole types still diverged slowly with predictive cues, that would provide evidence against synesthetes being “conservative learners.” Another way to further understand the differential repetition effect across groups would be to create a more complex set and presentation order of probability worlds. Creating probability worlds with entirely different probability distributions (instead of the same probabilities shifted across holes) would increase the benefit of tracking the repetition of probability worlds. Our current experimental design may be too simple for non-synesthetes to expend the necessary resources required to store and retrieve probability distributions. In addition, a more complex design could introduce novel probability worlds later in the experiment, reducing the high correlation between repetition and experimental trial present in this study. Future research investigating synesthetes’ sensitivity to non-stationary environmental statistics will further clarify the potential role of implicit learning in the formation of synesthetic associations.