Unusual physiological properties of two ganglion cell types in primate retina

Summary

The functions of the diverse retinal ganglion cell types in primates, and the parallel visual pathways they initiate, remain poorly understood. Here, unusual physiological and computational properties of the ON and OFF smooth monostratified ganglion cells are explored. Large-scale multi-electrode recordings from 48 macaque retinas revealed that these cells exhibit irregular receptive field structure composed of spatially segregated hotspots, quite different from the classical center-surround model of retinal receptive fields. Surprisingly, visual stimulation of different hotspots in the same cell produced spikes with subtly different spatiotemporal voltage signatures, consistent with a dendritic contribution to hotspot structure. Targeted visual stimulation and computational inference demonstrated strong nonlinear subunit properties associated with each hotspot, supporting a model in which the hotspots apply nonlinearities at a larger spatial scale than bipolar cells. These findings reveal a previously unreported nonlinear mechanism in the output of the primate retina that contributes to signaling spatial information.

eTOC Blurb

Rhoades et al. find the smooth monostratified retinal ganglion cells in the primate retina have unusual receptive fields consisting of multiple hotspots. This differs from classical center-surround receptive field models and suggests a role in nonlinear visual computation.

Introduction

A diverse collection of retinal ganglion cell (RGC) types extracts features of the visual scene and transmits the results to various targets in the brain. Each RGC type exhibits characteristic light responses, connects to specific retinal interneuron types, and covers the entire visual field, forming a distinct channel of information. Work in mice and other species has begun to reveal the diverse computations performed by the various RGC types, and their relationship to visual behaviors (Gollisch and Meister, 2010; Masland, 2001; Rodieck, 1998; Wässle, 2004).

However, in the primate retina, despite a nearly complete anatomical catalog of roughly 20 RGC types, understanding of their distinct visual computations and underlying cellular and circuit properties remains limited (Dacey et al., 2003; Masri et al., 2019; Yamada et al., 2005). Most physiological studies have been performed on the five numerically dominant RGC types: ON and OFF midget (Dacey, 1993), ON and OFF parasol (Chichilnisky and Kalmar, 2002), and small bistratified (Field et al., 2007). These cells are usually characterized as exhibiting classical Gaussian center-surround receptive field (RF) structure, with relatively little evidence for specialized functional properties such as those found in mouse RGCs (Crook et al., 2008; Enroth-Cugell and Robson, 1966; Kuffler, 1953; Rodieck, 1998; but see Manookin et al., 2018). The function of visual signaling in the remaining low-density RGC types remains largely unknown (Puller et al., 2015), and the anatomical homology of RGC types between rodents and primates is far from clear (Roska and Meister 2014; Peng et al., 2019). Thus, it is uncertain whether the low-density RGC types in primates could serve distinctive roles in vision based on unique physiological mechanisms, as is the case in other species.

A primary reason for this limited understanding is the technical challenge of recording from low-density RGC types in primate, each of which constitute only a few percent of the total population (Dacey et al., 2003; Yamada et al., 2005). Here we combine large-scale multi-electrode recording with single-cell patch recording to explore the properties of two low-density RGC types: the ON and OFF smooth monostratified (SM) cells (Crook et al., 2008). These two cell types exhibited unusually irregular RFs with multiple distinct hotspots of light sensitivity. An unexpected spike generation mechanism produced distinct spatio-temporal spike voltage signatures in a given RGC. Closed-loop visual stimulation and computational inference revealed that the hotspots behave as nonlinear subunits that are larger and more spatially segregated than those found in other cell types, potentially allowing selectivity for different spatial features than the well-known bipolar cell subunits.

Results

Receptive field properties of simultaneously recorded retinal ganglion cell types

To explore the properties of low-density RGC types, large-scale multi-electrode recordings were used to simultaneously record the light responses of hundreds of RGCs (Chichilnisky and Kalmar, 2002; Field et al., 2010; Frechette et al., 2005; Litke et al., 2004). The spatial, temporal, and chromatic response properties of each recorded RGC were examined by computing the reverse correlation between its spike train and a spatiotemporal noise stimulus. The resulting spike-triggered average (STA) stimulus captures the spatial RF, time course, and chromatic properties of each cell analyzed (Fig. 1; Chichilnisky, 2001). To distinguish cell types, the RF area and first principal component of the STA time course were examined (Fig. 1A). As previously demonstrated (Field et al., 2007), the five major high-density cell type can be readily identified based on these properties (Fig. 1D–H). In addition, in a given recording, a collection of RGCs was identified that had RF sizes and other functional properties clearly distinct from the five major types (Fig. 1B–C). Often, one or more subsets of these RGCs appeared to comprise a single functional type, based on their homogeneous RF size, response time course, and spike train autocorrelation properties, as well as non-overlapping RFs consistent with the mosaic organization known for most RGC types (Chichilnisky and Kalmar, 2002; Dacey, 1993; Devries and Baylor, 1997; Field et al., 2007; Frechette et al., 2005; Peichl, 1991; Wassle et al., 1981). Below, evidence is provided that two of the low-density RGC types frequently observed were ON and OFF SM cells.

Figure 1: Receptive field properties of simultaneously recorded retinal ganglion cell types.

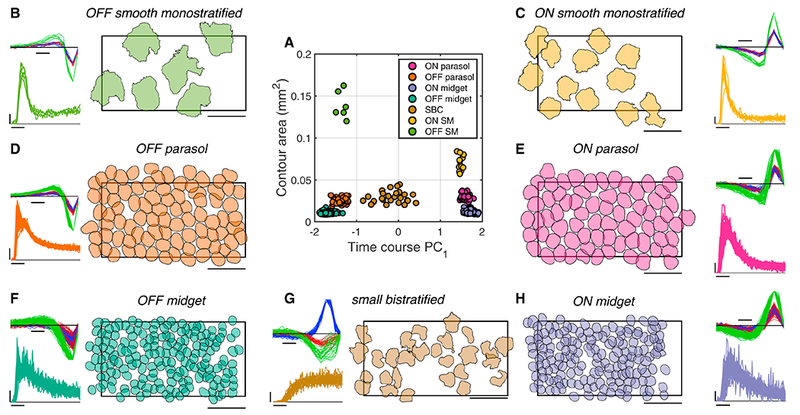
A: RF contour area and first principal component of time course for each RGC in a single recording form distinct clusters revealing seven distinct cell classes. Temporal equivalent eccentricity: 7 mm (31.4 degrees) (Dacey and Petersen, 1992; Perry and Cowey, 1985).

B: Properties of a single cell class, identified as OFF smooth monostratified (see Fig. 2). Right: contours outline the normalized RF (threshold: 0.18) and are shrunk 30% around their centers for visualization (see Methods). Contours thus should not be interpreted as capturing the RF spatial extent, but as summarizing the relative sizes of RFs of different RGC types. Rectangle indicates the outline of the MEA (1800 μm x 900 μm). Scale bar: 500 μm. Top left: STA time courses for red, green, and blue display phosphors, normalized to the peak for each cell. Scale bar: 50 ms. Bottom left: Autocorrelation function, indicating the probability of a cell spike (scale bar: 0.01) as a function of time (scale bar: 10 ms) relative to the occurrence of the previous spike.

C-H: As in B, for the other cell classes recorded simultaneously.

Classification of low-density cell types across recordings

Identification of SM cells required a different logic from that used to identify the five high-density RGC types. The high-density RGC types can be easily classified across recordings because of their unique density and spatial, temporal, and chromatic light response properties (Chichilnisky and Kalmar, 2002; Dacey, 1993; Field et al., 2007). However, many of the anatomically identified low-density RGC types have similar dendritic field size and density to one another, and other physiological properties of these cell types are largely unknown, making reliable classification difficult (Dacey et al., 2003), particularly in the presence of variability across recordings.

To aid in classification across recordings, analysis was performed on 53 recordings from 40 monkeys, each of which contained multiple ON and/or OFF low-density cell types. First, within each recording, the collection of low-density RGC types was segregated into several distinct groups of cells, based on differences in their time courses and autocorrelation function (see Fig. 1). Second, separately for the ON and OFF low-density RGCs in each recording, the group of cells with the fastest time course, as measured by the time of zero crossing of the STA time course, was labeled as Group 1 (G1), while the remaining low-density cells were combined and labeled Group 2 (G2) (Fig. 2A, C). Third, the time of zero crossing and the biphasic index (Fig. 2A) of all the low-density cells were normalized by those of the simultaneously recorded parasol cells. The G1 group of cells, across many recordings, had homogeneous times of zero crossing and biphasic index: the average distance from an ON (OFF) G1 cell to the center of the G1 cluster was 0.13 (0.21) (Fig. 2B, D). This value was substantially lower than that for the unambiguously defined ON (OFF) midget RGCs, which exhibited average distances of 0.51 (0.78). The tight clustering of G1 was interpreted as evidence that it represents a single cell type identified across recordings. A support vector machine classifier was used to conservatively define a boundary around the G1 cells. The G2 cluster exhibited greater variability and based on RF overlap between cells in this group, probably consisted of multiple RGC types. G2 cells were not analyzed further.

Figure 2: Classification of low-density cell types across recordings.

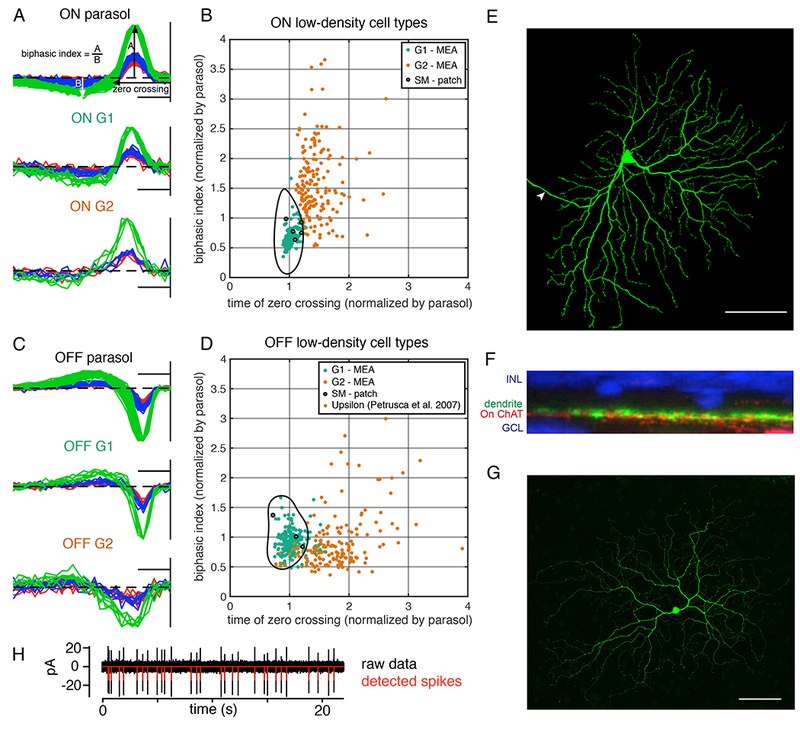
A: STA time courses, normalized to peak, of On parasol cells and ON low-density cell types from one preparation. Measurement of zero crossing and biphasic index are indicated. Vertical line at the right indicates the time of the spike. Scale bar: 50 ms.

B: Each point indicates the time of zero crossing and biphasic index of an ON low-density cell, normalized by the average respective properties of the ON parasol cells in the same recording. The fastest low-density cells in each recording (G1; teal) cluster tightly (384 cells from 31 recordings), compared to the other low-density cells (G2; orange) recorded in the same preparations. Within the black boundary, a support vector machine predicts a classification of G1 with greater than 95% probability. Only cells within the black boundary are analyzed further. Outlined black dots correspond to anatomically identified ON SM cells.

C: As in A, for OFF parasol and OFF low-density cells.

D: As in B, but for 346 cells from 27 recordings containing multiple types of OFF low-density cells. The 23 brown points correspond to upsilon cells recorded on a MEA (Petrusca et al., 2007).

E: ON SM cell in the peripheral retina injected with biocytin during whole-cell patch clamp recording (eccentricity: ~8 mm, ~40 degrees). The maximum-intensity projection of a confocal image stack is shown. Arrow indicates the axon. Scale bar: 100 μm.

F: Cross section showing the dendrites of the cell in E (green). Vertical dimension indicates depth within the retinal neuropil. Stratification is shown relative to the starburst amacrine cell dendrites (red; ChAT label) and the ganglion cell and inner nuclear layers (blue; DAPI label). The cell stratified slightly scleral to the ON starburst amacrine cell dendrites, as is typical of ON SM cells.

G: As in E, for an OFF SM cell (eccentricity: ~8 mm, ~40 degrees). Scale bar: 100 μm.

H: Raw recorded voltage (black) and detected spikes (red) from a patch clamp recording.

The ON and OFF G1 clusters were hypothesized to correspond to the ON and OFF SM cells, for several reasons. First, the ON and OFF G1 cells had very similar properties to one another, other than response polarity, suggesting that they are paired cell types (Ravi et al., 2018; Watanabe and Rodieck, 1989). Among the known low-density primate RGC types, other than ipRGCs and cells that receive strong input from S cones (Dacey, 2004; Dacey et al., 2005; Liao et al., 2016), only two are unambiguously paired: SM and narrow thorny. Second, the response kinetics of the ON and OFF G1 cells were very similar to those of parasol cells, with normalized biphasic index and zero crossing values close to 1 (Fig. 2B, D). SM cell dendrites, unlike those of narrow thorny cells, co-stratify with the parasol cell dendrites in the inner plexiform layer. Thus SM cells presumably receive similar bipolar cell input to parasol cells; this input would be expected to produce similarly transient kinetic response properties (Crook et al., 2008). Third, the RF diameters of G1 cells match the previously reported RF sizes of SM cells – approximately 2-3 times that of parasol cells (Crook et al., 2008; Petrusca et al., 2007). For these reasons, ON and OFF G1 cells were tentatively identified as ON and OFF SM cells, respectively.

To confirm this hypothesized anatomical identity, the same time course measurements were performed on morphologically identified ON and OFF SM RGCs and ON and OFF parasol RGCs with single-cell patch clamp recordings. To directly determine the morphological type, cells were filled with biocytin (0.5%) and imaged (Fig. 2E and 2G). SM cells were identified by their large dendritic trees, relatively sparse branching, limited dendritic overlap, and an overall smooth appearance with prominent swellings at branch points, all of which are typical of SM cells (Crook et al., 2008). The dendrites of filled SM cells stratified in the expected position relative to the starburst amacrine cell dendrites (Fig. 2F). An example of the spikes recorded from an SM cell with patch recordings demonstrates sufficient signal for reliable spike detection (Fig. 2H).

All five ON and three OFF morphologically identified SM cells, normalized and plotted in the same manner as low-density cells from MEA recordings, fell within the conservatively computed G1 classification boundary (Fig. 2B, 2D: black outlined cells). This finding further supports the hypothesis developed above that the G1 cells from MEA recordings are in fact SM cells. In the remainder of this paper, G1 cells will be referred to as SM cells. Note that the response properties of 21 out of 23 of previously reported “upsilon” cells, hypothesized to be OFF SM cells (Petrusca et al., 2007), also fall within the G1 classification boundary (Fig. 2D: brown cells).

Receptive field structure of ON and OFF smooth monostratified cells

Surprisingly, SM cells displayed irregular, patchy RF structure not observed in other simultaneously recorded RGC types. RF structure was examined using coarse spatiotemporal noise stimuli, because finer stimuli elicited weak responses in SM cells. However, to avoid lattice artifacts introduced by large stimulus pixels (84.8 x 84.8 μm), the stimulus was jittered on a finer underlying lattice (5.3 x 5.3 μm), enabling STA computation at a finer resolution. The resulting RFs were irregularly shaped, with distinct hotspots separated by regions of low sensitivity (Fig. 3B). Similar hotspots were observed in RFs of anatomically identified SM cells recorded with patch clamp (Fig. 3B; bottom left).

Figure 3: Receptive field structure of ON and OFF smooth monostratified cells.

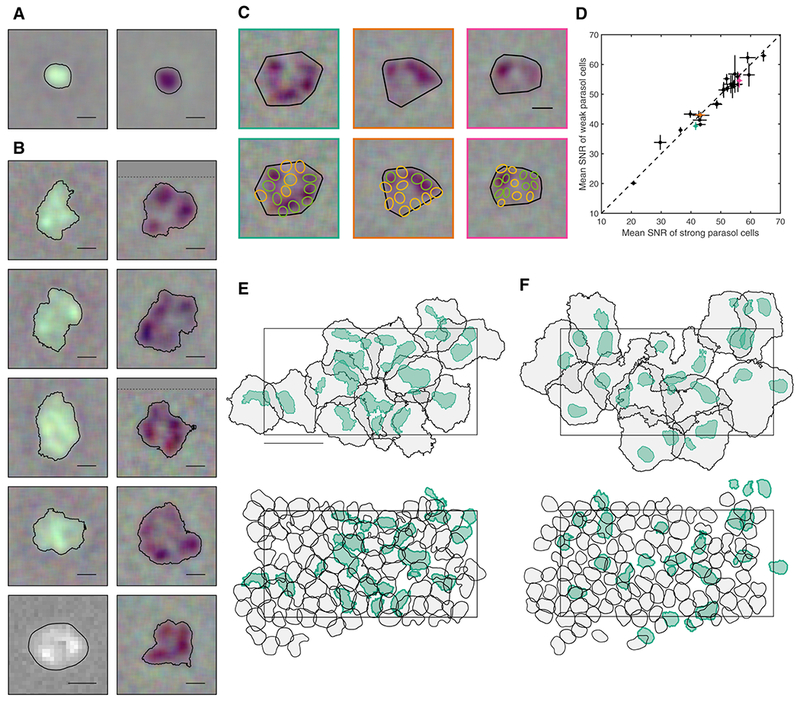
A: ON (left) and OFF (right) parasol cells RFs, with typical regular, radially symmetric structure. Contour threshold: 0.15. Scale bar: 200 μm.

B: ON (left) and OFF (right) SM cell RFs, exhibiting distinctive hotspots. The bottom left ON SM cell was recorded with patch clamp; the remaining cells were recorded on a MEA. The dotted line in some RFs indicates the end of the visual stimulus (the remainder of the STA was filled in with grey). Contour threshold: 0.15. Scale bar: 200 μm.

C: RF alignment of three OFF SM cells (top) with the simultaneously recorded OFF parasol cells (bottom; green/yellow). The RFs of parasol cells indicated in green and yellow overlie hotspots and gaps in the SM cell RF, respectively. Scale bar: 200 μm.

D: The SNR of parasol cell RFs lying between SM cell hotspots (C, green) is shown as a function of the SNR of parasol cell RFs overlying hotspots (C, yellow). Mean ± SEM across parasol cells is shown for 26 SM cells from three recordings. Three examples highlighted in teal, orange, and pink correspond to the three SM cells shown in C.

E: The RFs of a population of ON SM cells (black; contour threshold: 0.1) and the hotspot(s) within each RF (teal; variable threshold to match parasol size). Below, the same hotspots are shown (teal) with the simultaneously recorded ON parasol cells (contour threshold: 0.5). Rectangle indicates the outline of the electrode array. Temporal equivalent eccentricity: 12 mm. Scale bar: 500 μm.

F: As in E, for OFF SM and OFF parasol cells.

The unusual SM cell RF structure was quantified by an inhomogeneity index, given by the mean squared deviation from a 2D Gaussian fit to the RF (after normalizing the RF and subtracting the variance of the background from the deviation metric). The SM cell RFs exhibited an inhomogeneity index (0.047 ± 0.028; mean ± SD; 97 SM cells from 6 recordings) substantially higher than that of parasol cell RFs (0.012 ± 0.011; 830 parasol cells from 3 recordings) (Wilcoxon rank sum test p = 1.66e-39). The inhomogeneity index in OFF SM cells (0.065 ± 0.027) was also higher than that in ON SM cells (0.033 ± 0.020), consistent with the more distinct appearance of hotspots in OFF SM cell RFs (see Fig. 3B; Wilcoxon rank sum test p = 6.99e-8 in 55 ON cells and 42 OFF cells from 6 recordings). The hotspot size in ON SM cells (median 0.025 mm², 136 cells) was larger than that in OFF SM cells (median 0.017 mm², 156 cells). This difference was statistically significant across the population (one-tailed t test, p = 0.00043).

A possible artifactual explanation for the observed hotspots would be damaged photoreceptors between hotspots. This possibility was tested by examining simultaneously recorded parasol cells with RFs overlying the RFs of SM cells. For each SM cell, the OFF parasol cells with RFs intersecting the SM cell RF were identified. The parasol cells were then divided into two groups: those overlying a strong region in the SM cell RF (i.e. in a hotspot), and those overlying a weak region (i.e. between hotspots). If the SM cell hotspots were the result of photoreceptor damage, then the parasol cell RFs overlying hotspots (Fig. 3C; green) would be expected to have higher signal to noise ratio (SNR) than the parasol cell RFs overlying gaps between hotspots (Fig. 3C; yellow), because the same photoreceptors provide input to both cell types. Contrary to this prediction, no systematic difference was observed in the SNR of the parasol cell RFs over the strong and weak areas of the SM cell RF (Fig. 3D).

Another possibility, given the size of the hotspots, is that SM cells represent collections of parasol cells erroneously grouped together during spike sorting. This was tested by direct comparison of the hotspot locations to the parasol cell RFs. While some hotspots overlapped with parasol cells (as would be expected by chance), many did not (Fig. 3E–F). If the hotspots aligned with the parasol cells, then the distance between the centroid of each hotspot and the nearest parasol cell would be small. Instead, the distances covered a range from 0 to the ON (OFF) median parasol neighbor distance of 124.8 μm (117.8 μm) with a mean ± SD value of 49.7 ± 28.9μm (57.7 ± 28.3).

Coordination of fine RF structure

In midget and parasol cells, fine scale interdigitation produces complete tiling of visual space more uniform than would be expected from a lattice of independently formed RFs (Gauthier et al., 2009). To test whether the ON and OFF SM cell RFs similarly interdigitate, RFs coverage of visual space (Fig. 4A) was compared to a null distribution obtained by rotating the RFs randomly around their centers (Fig. 4B; Gauthier et al., 2009). A uniformity index (UI – the fraction of pixels within the convex hull of the mosaic that were covered by the RF contour of exactly one cell) was computed for each mosaic. The UI of the data was in general at the high end of the null distribution; e.g. above the 98th percentile in 9/10 preparations (Fig. 4D), confirming that the ON and OFF SM cell types interdigitated to a degree higher than expected by chance.

Figure 4: Coordination of fine RF structure.

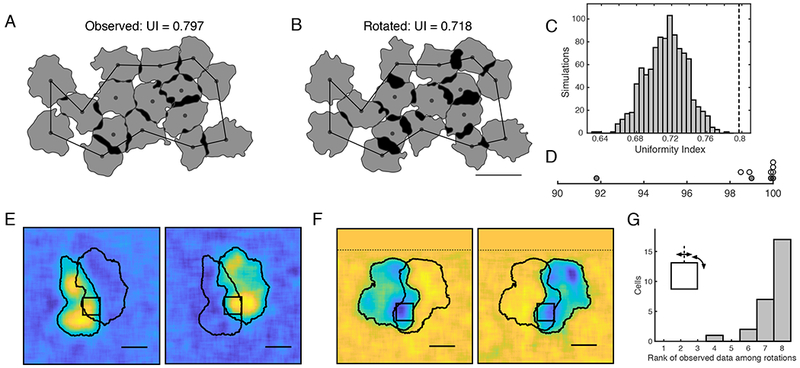
A: A mosaic of SM cell RFs in which white regions are covered by no cells, gray by one cell, and black by multiple cells. The UI was computed within the black boundary (see Methods). Contour threshold: 0.13.

B: The RF of each cell was rotated at a random angle around its center point and the contour threshold was recomputed to maximize the UI. Scale bar: 500 μm.

C: UI of the data (black dashed line) and the null distribution produced by 1,000 simulations of randomly rotated cells

D: Percentile of the UI of the data compared to the null distribution, for 6 ON SM cell mosaics (white) and 4 OFF SM cell mosaics (grey).

E: The RFs of two ON SM cells sharing a hotspot are shown (RFs contour threshold: 0.2). Black square: 132.5 x 132.5 μm region used for rotation/reflection analysis. Scale bar: 200 μm.

F: Same as E, for two OFF SM cells.

G: The rank of the correlation between RFs in the region of overlap, among the correlation obtained from seven rotations of the overlap region (27 cell pairs from 15 recordings).

Each hotspot in the irregular RF structure could represent the input of a single presynaptic neuron, such as a bipolar or amacrine cell. Two observations argue against an origin of hotspots in individual bipolar cells. First, the hotspots are large compared to RFs expected from known primate bipolar types (Boycott and Wassle, 1991; Tsukamoto and Omi, 2015, 2016; but see Dacey et al., 2000 and Discussion). Second, SM cells exhibited significant frequency-doubled responses to contrast-reversing gratings with spatial periods (~50-100 μm; Crook et al., 2008; Petrusca et al., 2007) smaller than the diameter of the hotspots (~150 μm). Thus, each hotspot is likely composed of multiple bipolar cells that contribute to nonlinear responses.

Note, however, that multiple bipolar inputs could in principle be conveyed to a SM cell by a single amacrine cell. This possibility was examined by observing that, if each hotspot were produced by the input of a single cell, then RFs of neighboring SM cells should either share entire hotspots, or not overlap at all. Most SM cell RFs did not overlap at all (Fig. 3E, F) and a small subset of SM cells exhibited significant overlap with a neighbor (Fig. 4E, F). In the latter cases, to test whether the shared hotspot contribution to the RF of both cells was the same, a 132.5 μm x 132.5 μm region (black square) was centered on the pixel with the maximum intensity product in the RFs of the two cells (i.e. peak of the shared input region). If each hotspot were produced by input from a single cell, the hotspot would be expected to have the same spatial structure in the RFs of both cells. Therefore, the correlation of the RFs within the region of overlap would in general be reduced by rotations and reflections. Contrary to this prediction, rotations and reflections around the midpoint of the region of overlap usually increased the correlation (Fig. 4G). This finding supports the idea that the hotspots were not formed by the input of individual presynaptic cells, but instead by multiple inputs sampled differently by neighboring SM cells.

Potential mechanism of RF hotspots

Another mechanism that could contribute to hotspots is active conductances or other electrical properties of SM cell dendrites. In particular, dendritic spiking has previously been observed in mammalian RGCs (Oesch et al., 2005; Velte and Masland, 1999). The possibility of dendritic spiking in SM cells is suggested by a surprising observation: visual stimulation of each hotspot generated a slightly different spatiotemporal voltage signature associated with spikes in the SM cell.

Specifically, in the process of segregating spikes from different RGCs based on their distinct signatures (i.e. voltage waveforms recorded on multiple electrodes, Fig. 5E; see Methods), several slightly different spike signatures were often observed for a single SM cell (Fig. 5A, G). These examples of distinct signatures were confirmed statistically with k-means clustering (Fig. 5A, G). Moreover, when the STA was computed using reverse correlation with just the spikes in one sub-cluster, a single hotspot from the SM cell RF emerged, rather than the entire RF (Fig. 5B).

Figure 5: Potential mechanism of receptive field hotspots.

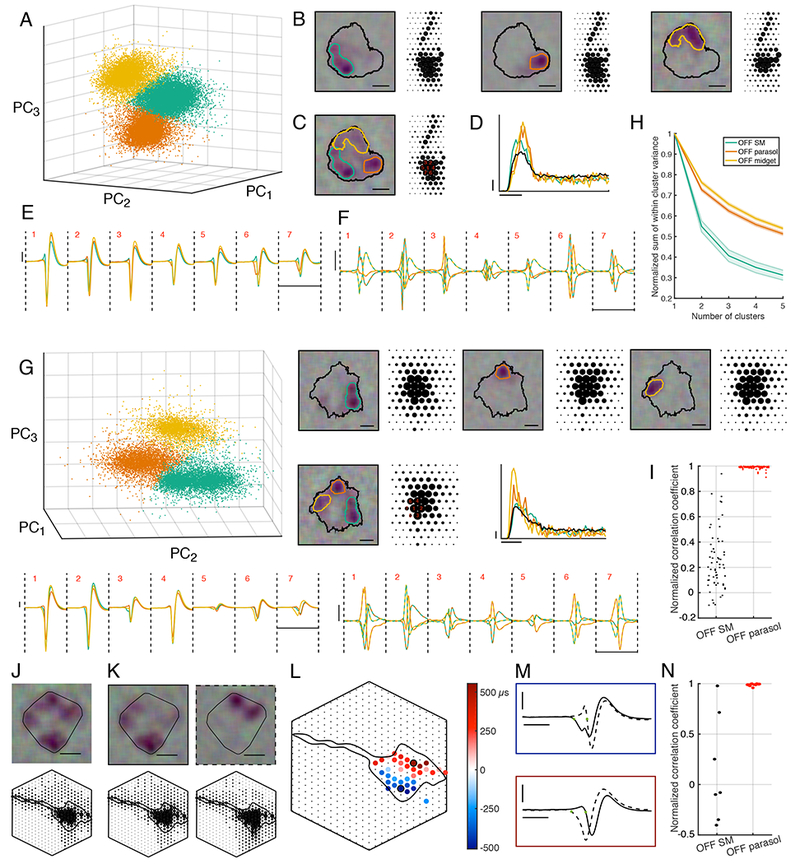
A: First three principal components of the spike signatures from one OFF SM cell. The k-means algorithm identified three clusters, indicated by different colors.

B: RFs and EIs computed from each subcluster of spikes. The black contour was fitted on the full RF (threshold: 0.15), and the colored contours were fitted to subcluster RFs (threshold: 0.3). Scale bar: 200 μm. Electrode spacing: 60 μm.

C: As in B, but with the RF and EI computed from all the SM cell spikes. Red numbers indicate electrodes examined in E, F.

D: Autocorrelation function of the SM cell (black), and of each subcluster (orange, teal, and yellow). Probability of spiking (scale bar: 0.01) is shown as a function of time relative to the previous spike (scale bar: 10 ms).

E: Mean voltage signatures of SM cell spike subclusters, across the seven electrodes used in spike sorting, numbered in red in panel C. Voltage (scale bar: 50 μV) is shown as a function of time (scale bar: 5 ms). Colors correspond to subclusters shown in A.

F: Difference between mean signatures in different sub-clusters from E is shown on an expanded scale. Each line is colored with the two colors representing the subtracted signatures. Scale bars as in E.

G: Same as A-F, for a different OFF SM cell.

H: Sum of within cluster variance divided by total variance in k-means clustering, as a function of the number of clusters (mean ± SEM for 19 SM cells from 11 recordings, 66 parasol cells from 2 recordings, 252 midget cells from 2 recordings).

I: Normalized subcluster EI pairwise correlation coefficients for each cell are shown. Left column: 19 SM cells from 11 recordings. Right column: 34 OFF parasol cells from 2 recordings.

J: The RF and maximum projection of the EI of an OFF SM cell. The convex hull of the contour (threshold: 0.25) is shown. Scale bar: 200 μm. Electrode spacing: 30 μm. Hexagon indicates the outline of the electrode array.

K: The RF and maximum projection of the EI computed from sub-clusters, which together constitute all the spikes from the SM cell indicated in J. Each signature was associated with a different region of the RF, yet the spatial structure of the EI is similar. Scale bar: 200 μm. Electrode spacing: 30 μm.

L: Timing difference between the onset of electrical activity (determined by a threshold) in the two spike subclusters, shown over a collection of electrodes. Red indicates the onset for the second cluster (panel K, dotted border) is earlier than that for the first cluster (K, solid border); blue indicates the reverse. The RFs produced by spikes with different signatures (K) aligns with the locations of earlier onset (see also movie S1).

M: Spike signatures on two electrodes with maximal timing differences (black in L). The blue (red) panel shows the electrical signal originating from the first (second) cluster. Timing differences in L were measured as the difference between the times indicated by the green points. Horizontal scale bar: 1 ms. Vertical scale bar: 50 μV.

N: As in I, for 7 SM cells and 14 parasol cells recorded on an electrode array with 30μm spacing.

The multiple distinct spike signatures observed in SM cells are not a ubiquitous feature of primate RGCs: visual inspection of the signatures of midget and parasol cells failed to reveal any subclusters of the kind seen in SM cells. To quantify this observation, the sum of within-cluster variance normalized by the total variance was computed for different numbers of clusters used in k-means clustering. The metric is expected to decrease with an increasing number of clusters for all cell types because the spike signatures do not form a perfect Gaussian distribution, but the metric declines to a greater degree for SM cells, consistent with a more multi-modal spike signature distribution in these cells (Fig. 5H).

To test if the distinct spike signature clusters are associated with distinct hotspots in the RF, the k-means algorithm was run on each cell to determine 3 subclusters of spikes. For each of the three pairs formed from these three subclusters, the correlation between the RFs associated with those spikes was measured. To account for variability in the signal to noise ratio of different cell types, these correlations were normalized by the mean of the null distribution of correlations between the RF from all the spikes and the RF from a randomly selected subset of spikes. This procedure was applied to both SM cells and parasol cells. The normalized correlations between subcluster RFs was low for SM cells, while for parasol cells, they were close to 1 (Fig. 5I). Thus, while a clustering algorithm can divide any collection of spikes into three groups, those groups are associated with different parts of the RF only in SM cells.

The concern that these sub-clusters could reflect spikes from multiple RGCs incorrectly identified as arising from a single SM cell was excluded for several reasons. First, if this were the case, then the collection of spikes in the larger cluster identified as a SM cell should exhibit refractory period violations, as is generally true when midget and parasol cell spikes are erroneously combined (not shown). The autocorrelation function of the resulting SM cell spike train (Fig. 5D) showed no spikes within 1.7 ms of each other. Second, the form of this autocorrelation was consistent across SM cells within a recording (Fig. 1), which would not occur if each SM cell cluster were composed of various erroneous mixtures of spikes from different cells of different types in the vicinity. Third, the electrical image (EI), or average spatial electrical footprint observed on the array during a spike, reveals the location of the soma, dendrites, and axons of the recorded cell and was nearly identical for all sub-clusters (Fig. 5B; Greschner et al., 2014; Litke et al., 2004; Petrusca et al., 2007). Fourth, given that the hotspots were roughly the size of parasol cell RFs (Fig. 3), it seems possible that the subclusters were in fact parasol cell spikes. However, the observed hotspots did not align to the RFs of simultaneously recorded parasol cells (Fig. 3E–F), and there are no other RGC types in the primate retina that are expected to have RFs the same size as those of parasol cells (Dacey, 2004). Fifth, the possibility that SM cells represent mixtures of erroneously combined spikes from spiking amacrine cells was excluded both because their EIs are very different (Greschner et al., 2014; Litke et al., 2004; Petrusca et al., 2007), and because in cases when amacrine cells were recorded, the hotspots did not align with the amacrine cell RFs (not shown). Finally, the distinct spike signatures were also not obviously attributable to the different states of the ion channels that would cause spikes closely spaced in time to produce different voltage fluctuations during a spike: removal of all spikes within 500 ms of preceding spikes produced similar results (not shown). Thus, the existence of multiple distinct spike signatures in a single cell appear to be an unusual feature of SM cells.

To investigate the relationship between the RF hotspots and the dendritic origin of multiple distinct spike signatures in each SM cell, EIs of SM cells were examined on an electrode array with 30 μm spacing (rather than 60 μm), providing a higher spatial resolution view of the extracellular voltage signal (Fig. 5J). To estimate the time of initial activity in the dendrites, the time when the recorded voltage first fell below a threshold on each electrode was measured for each spike cluster separately (Fig. 5M, green points), Electrodes in which the differences between the time of initial activity of different clusters was small (including electrodes over the axon where the signatures are nearly identical) were not colored (Fig. 5L). Comparing this time for each cluster revealed spatial segregation in the appearance of the earliest voltage deflections (Fig. 5L). For the spike cluster associated with RF hotspots in the bottom left (Fig 5K: solid outline), the electrical activity appeared first on the electrodes in the bottom left (Fig. 5L; blue electrodes). For the spike cluster associated with RF hotspots in the top right (Fig 5K: dotted outline), the electrical activity appeared first on the electrodes in the top right (Fig. 5L; red electrodes; see Movie S1 to observe the electrical activity over time). To summarize this finding across cells, normalized correlation coefficients between EIs from different sub-clusters were computed. The correlation coefficient was less than 0.75 for 6 out of 7 SM cells, while it was near one for all 14 parasol cells tested (Fig. 5N), indicating that the EIs of SM cell sub-clusters are usually distinct.

Nonlinearity of hotspots

What role do RF hotspots play in visual computation? Nonlinear spatial RF subunits are critical to generating complex computations in RGCs, and bipolar cells are the only known mechanism (Demb et al., 1999, 2001; Hochstein and Shapley, 1976; Shapley and Victor, 1979; Victor and Shapley, 1979). Given the large size of and separation between SM cell hotspots, and their unusual electrical properties, it is possible that each hotspot behaves as a nonlinear computational subunit formed by a distinct mechanism, and operating at a larger spatial scale, than has been seen in previous studies.

To test this possibility, a closed loop experiment was performed targeting the distinct spots independently. First, the RF of the SM cell was identified (Fig 6A). Then, circular stimulus regions were placed over two hotspots, with their sizes adjusted to match the total weight of the SM cell RF in each region. These two regions were then used to create a targeted visual stimulus, in which intensity of the stimulus in each of the two regions was modulated independently, thus probing the summation between hotspots. The temporally integrated contrast on each region and the resulting firing rate of the SM cell were binned and fitted with a predicted surface determined by either a linear model or a nonlinear model (Fig. 6C, D). In the linear model, visual inputs from the distinct regions are summed before a rectifying nonlinearity; in the nonlinear model, the input from each region is rectified before summation. For example, if one region was stimulated with a strong negative stimulus while the other region was stimulated with a strong positive stimulus, the linear model would predict a low firing rate, while the nonlinear model would predict a high firing rate. For each cell, the observed data (Fig. 6B) was compared to both fitted models. The nonlinear model resulted in lower mean squared error for 27 out of 30 cells from six retinas, suggesting that nonlinear mechanisms acting before the summation of signals across hotspots are the major determinant of SM cell responses (Fig. 6E). Thus, hotspots behave as nonlinear computational subunits within the RF, potentially as a result of aggregating bipolar cell inputs or other mechanisms (see below and Discussion).

Figure 6: Nonlinearity of hotspots.

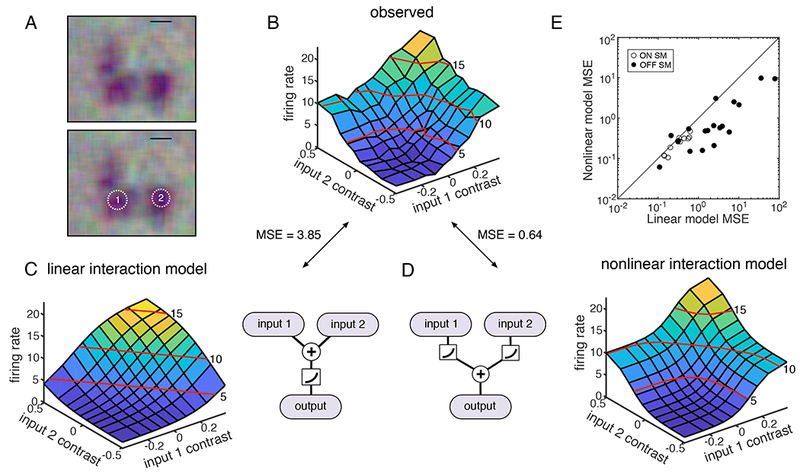
A: The RF of an OFF SM cell is shown at top, and again at bottom with two regions targeted for stimulation with equal weight in the RF. Scale bar: 200 μm.

B: Average firing rate of the SM cell as a function of instantaneous contrast on each input region. Red lines indicate contour at 5, 10, and 15 Hz.

C: The predicted firing rate of a linear model is shown as a function of the instantaneous contrast on each input region; schematic shows signals from different input regions summing before rectification.

D: As in C, but for a nonlinear response model, in which signals from different input regions sum after rectification.

E: Mean square error in predicted firing rate from the nonlinear model fits is shown as a function of the error in the linear model fits, for 30 OFF SM cells from 6 recordings.

Examination of subunits using spike-triggered stimulus clustering

The closed loop experiment above identified nonlinear summation between pairs of hotspots. Can a single model quantitatively capture the dominant nonlinear interactions between all the hotspots observed in each SM cell RF? To answer this question, a computational procedure was used to automatically extract the spatial structure of nonlinear subunits and summarize their contributions to firing (Shah et al., 2018; see also Liu et al., 2017).

The model consisted of two linear-nonlinear (LN) stages (Fig. 7A). In the first stage, the spatial stimulus was projected linearly onto a collection of fitted spatial subunits, and the output of each subunit was subjected to an exponential nonlinearity. In the second stage, the outputs from each subunit were weighted and summed, and the results was subjected to a final nonlinearity. To reduce the dimensionality of the data, the subunits were assumed to be spatio-temporally separable and to each have the same temporal filter, which was estimated from the STA. The spatial stimulus associated with each spike was thus computed by convolving the SM cell response time course with the stimulus. Model fitting was performed on 80% of the data in two alternating stages: first the subunits were estimated by clustering the spike triggered stimuli, and second, the subunit weights and parameters of the output nonlinearity were estimated. This procedure yielded multiple estimated spatial subunits, determined by two hyperparameters: the number of subunits and a regularization value that emphasized spatial locality.

Figure 7: Examination of subunits using spike-triggered stimulus clustering.

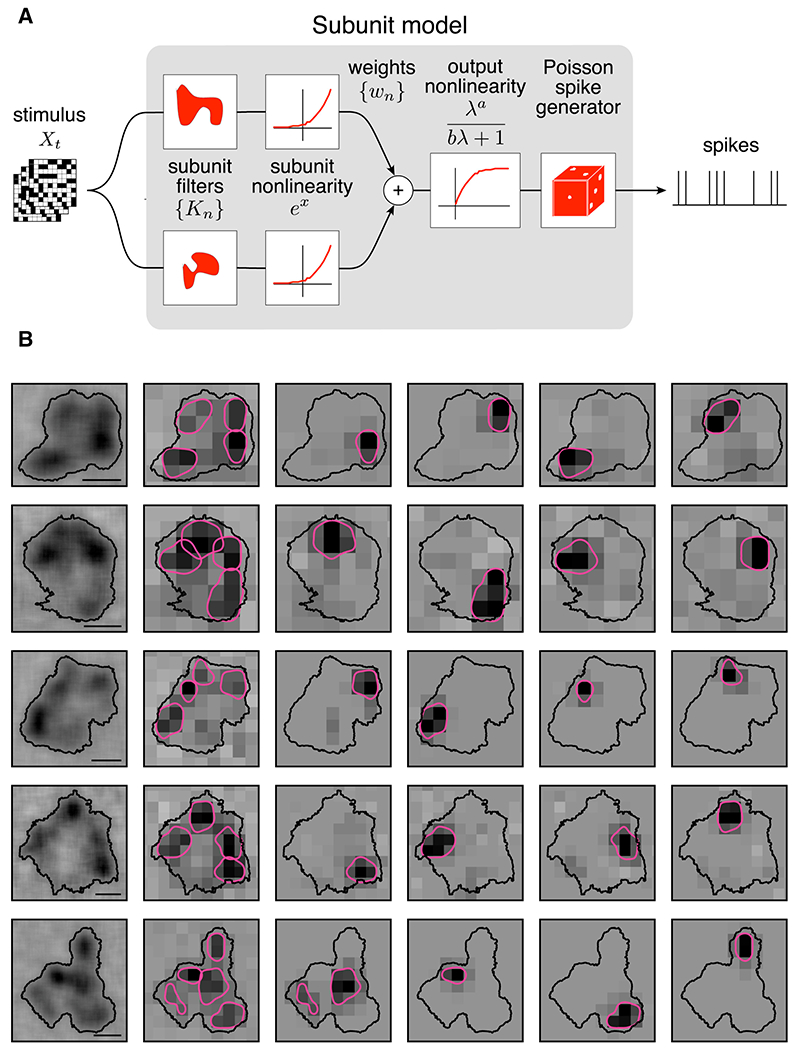
A: The subunit model is constructed as a cascade of two LN stages. In the first stage, subunit activation values are computed by linearly filtering the stimulus (X_t) with subunit kernels (K_n), followed by an exponential nonlinearity. In the second stage, a sum of subunit activation values, multiplied by weights (w_n), is passed through a saturating nonlinearity to drive Poisson spike generation.

B: Five OFF SM cell RFs are shown with subunits fitted using the model. Left: RF of the SM cell, measured with a jittering pixel lattice, revealing hotspots. Contour threshold: 0.15. Second from left: the RF, measured with a fixed pixel lattice for model fitting, and the fitted subunit filters. The subunit filters were blurred, normalized, and summarized with contours (threshold: = 0.4). Last four columns: subunit filters shown separately. Scale bars: 200 μm.

The model was fitted to SM cell data to identify computational subunits and compare them to the observed hotspots. The number of subunits was fixed at four for simplicity, and to focus on the major nonlinearities that drive firing. The regularization parameter was selected to maximize log-likelihood on a 10% validation data set. The subunits resulting from the fit were then compared with the hotspots identified in the same cell. In cells that exhibited clear and distinct RF hotspots, and for which model fits produced spatially localized subunit filters, a close alignment was frequently observed (Fig. 7B). This indicates that RF hotspots represent the primary sources of nonlinear computation in SM cells.

Computational subunits align with regions associated with distinct spike signatures

The previous results suggest a simple picture of SM cell visual computation: hotspots in the RF, formed by electrical compartments (Fig. 5), dominate SM cell nonlinear computations over space (Figs. 6 and 7). A final test of consistency of this picture is to examine directly whether hotspots producing different spike signatures align with the locations of computational subunits. A four-subunit model was fitted to the RF, and then compared to four compartments estimated from spike signature clustering (Fig. 5B). For cells exhibiting four cleanly separated subclusters, the computationally estimated subunits largely aligned with the regions identified by different spike signatures, confirming their correspondence (Fig. 8A, B).

Figure 8: Computational subunits align with regions associated with distinct spike signatures.

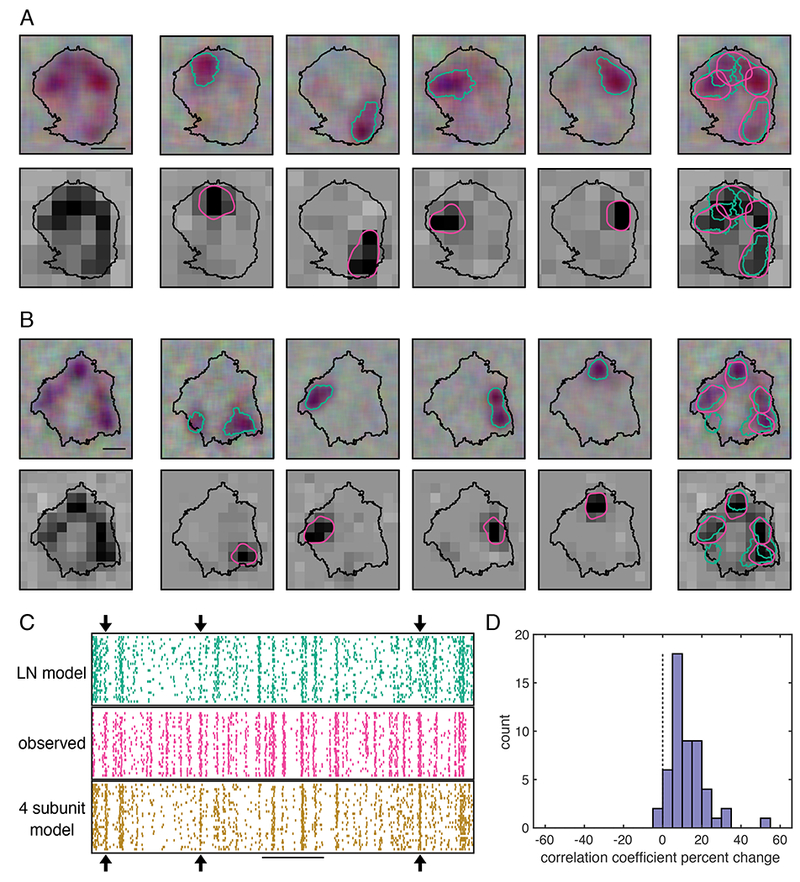
A: Left column: The RF of an OFF SM measured with a jittered pixel lattice (top) or fixed lattice (bottom). Contour threshold: 0.15. Scale bar: 200 μm. Top middle four panels: The RFs associated with four spike signature sub-clusters (contour threshold: 0.25), identified as above (Fig. 5). Bottom middle four panels: the four subunit model filters, blurred and shown as contours (threshold: 0.45). Right column: hotspots determined by spike signatures (teal), and model subunits (pink).

B: Same as A, for an OFF SM cell from a different recording.

C: Middle: Raster shows observed OFF SM cell firing over time in response to a white noise stimulus (pixel size: 84.8 x 84.8 μm). Top: LN model prediction of the SM cell response. Bottom: Subunit model prediction. Arrows indicate events captured by the subunit model but not the LN model. Scale bar: 1 s.

D: Histogram of the percent change in the correlation coefficient of the firing rate of the subunit model with the observed firing rate, relative to that of the LN model, for held out validation data (10%). 52 OFF SM cells from 10 recordings.

To test if the subunit model resulted in more accurate predictions of SM cell responses than the commonly used LN model, predicted responses to repeated presentations of a white noise stimulus were computed for each model. The LN model consisted of a single spatial filter, and a nonlinearity composed of the two nonlinearities used in the subunit model; in other words, it was equivalent to the subunit model with a single subunit. At specific points during stimulus presentation, observed spikes were more accurately captured by the subunit model than by the LN model (Fig 8C, arrows). Note, however, that many periods of firing were not accurately captured by either model. Therefore, while the subunit model resulted in more accurate predictions, more improvements to the model are necessary for a full understanding of SM cell function.

To compare the performance of the subunit model to a LN model across many cells and recordings, the correlation coefficient between predicted and measured firing rates was computed on 10% held-out data for the subunit and LN model. The correlation coefficient was systematically larger for the subunit model than the LN model (12.6 ± 9.4%, mean ± SD for 52 cells; Fig. 8D). Thus, in addition to capturing the dominant sources of spatial nonlinearity, the subunit model provided a more accurate account of light response. Because predictions were cross validated, this finding reflects a more accurate model structure rather than merely a larger number of parameters fitted to the data.

Discussion

The physiological properties of the ON and OFF SM cells were investigated using large-scale multielectrode recordings, supplemented with patch clamp recordings to verify cell type identity. These two cell types exhibited complete mosaic coverage with precise interdigitation, as seen in the high-density RGC types. However, unlike the high-density RGC types, SM cells exhibited irregular RFs composed of several large hotspots. Visual stimulation of each hotspot produced slightly different spike signatures in a given SM cell. A subunit computational model fitted to the data also identified these hotspots as the primary regions of nonlinear computation. This evidence is consistent with dendritic mechanisms producing nonlinear spatial summation in SM cells, at a larger scale than can be produced by known bipolar cell nonlinearities.

Unusual receptive field structure

The characteristic distinct hotspots observed in SM cell RFs have not been observed in other primate RGCs. Previously, canonical models such as the center-surround difference of Gaussian model of the RF (Enroth-Cugell and Robson, 1966; Rodieck and Stone, 1965), combined with the LN model of neural responses, have been used to describe RGCs (Chichilnisky, 2001). These models fail to adequately describe the structure (Fig. 3B) and responses (Fig. 8C, D) of SM cells.

First, the distinct hotspots in the RF depart strikingly from circularly symmetric center-surround models. Hotspots may not have been observed in the two previous studies of SM cells, for two reasons. In one study, RFs were measured with 90 μm pixels (Petrusca et al., 2007), a resolution at which the hotspots would have been difficult to distinguish. In a second study, direct measurements of SM cell RFs were not made (Crook et al., 2008); instead, the approximate size of the RF was measured using gratings of different spatial frequencies with the assumption that RFs conform to a Gaussian center-surround model. The stimulus used in this study (large pixels on an underlying jittering lattice) permitted computation of the RF at high resolution, resulting in a clearer picture of RF structure.

Second, the hotspots combine nonlinearly to drive firing, resulting in more predictive power from a computational model incorporating subunits than from an LN model. The nonlinearity could be produced entirely by bipolar cell rectification, as observed in other RGCs (Demb et al., 1999, 2001). However, alignment of the spike signature differences and the main computational nonlinearities with hotspots (Fig. 8A) suggest a different subunit mechanism in SM cells: nonlinear combination of visual signals across subunits resulting from dendritic spiking.

Identification of SM cells

Light responses of low-density primate RGC types have been examined relatively little, due to the experimental challenges of recording spikes from rare cells. Large-scale MEA technology enabled recording complete populations of SM cells within a region of the retina (852 cells from 74 recordings of 48 macaque monkeys). However, variability across recordings, potentially arising from differences in species, age, gender, health, and eccentricity, in addition to experimental considerations such as dissection technique and recording temperature, makes it difficult to identify SM cells reliably across preparations.

Normalizing time course properties by those of the easily identified, simultaneously recorded parasol cells revealed consistent physiological properties of identified SM cells despite this variability (Fig. 2). The narrow range of kinetic properties of putative SM cells corresponded closely with those of anatomically identified SM cells (Fig. 2B, D). This method relied on the assumption that among the low-density RGCs recorded using the MEA, the recorded type with the fastest light response kinetics was usually the SM cells. This assumption is supported by the relatively large spike amplitude and size of SM cell somas compared to those of other low-density cell types (Crook et al., 2008), making the SM cell spikes easier to detect and segregate on the MEA. Potential failures of the approach are discussed further in Methods.

Mechanism for spike signature differences

The difference in extracellularly recorded spike signatures elicited by stimulation of distinct hotspots supports the hypothesis that each hotspot has a distinct role in spike generation, and in particular suggests different action potential initiation sites in SM cell dendrites.

The number of distinct hotspots observed in SM cells is approximately equal to the number of primary dendrites observed with anatomical measurements (Crook et al., 2008; Fig 2E, G), suggesting that each hotspot corresponds to signals from a different primary dendrite. SM cell dendritic arbors differ from those of midget and parasol cells in at least two ways (Crook et al., 2008; Watanabe and Rodieck, 1989): 1) the SM cell primary dendrites leave the area near the soma uncovered and 2) distal dendrites are sparser (Dacey and Brace, 1992). These features could produce low sensitivity regions between dendritic branches, giving rise to hotspots in the RF, but would not necessarily explain different spike signatures from each hotspot. The cellular mechanisms that cause these distinct spike signatures are not clear and would likely require extensive intracellular recordings, pharmacology, and/or optical imaging to explore further.

Computational model of hotspot nonlinearity

Nonlinearities are fundamental to RGC computation and enable RGCs to produce responses to spatial patterns finer than the RF (Freeman et al., 2015; Hochstein and Shapley, 1976; Victor and Shapley, 1979). To date, the only known mechanism of nonlinear subunits in RGCs is bipolar cells (Demb et al., 2001). In hippocampal and cortical pyramidal cells, nonlinear subunits are created within single cells by dendritic spiking (Schwindt and Crill, 1997; Turner et al., 1991), a mechanism which could increase the computational power of each neuron (Poirazi et al., 2003; Polsky et al., 2004). The SM cell hotspots associated with spikes that have different spatiotemporal voltage signatures are suggestive of a nonlinear computation in SM cells related to dendritic spiking.

Much is still unknown about the connectivity and nonlinearities in the SM cell circuit. For example, it is not clear exactly how the hotspots relate to bipolar cells: bipolar cell locations are not easily measured, but the known sizes of the bipolar cells presynaptic to the SM cells suggests that each hotspot would probably be composed of several bipolar cells, possibly of multiple types (Boycott and Wassle, 1991; Crook et al., 2008; Dacey et al., 2000; Jacoby et al., 2000; Tsukamoto and Omi, 2015, 2016). Several findings argued against each hotspot being composed of single bipolar cell: shared hotspots in neighboring SM cells did not originate from a single presynaptic neuron (Fig. 4E–G), diffuse bipolar cells are smaller than the hotspots, and nonlinear summation was also observed within the hotspots, at the right spatial scale for bipolar cells. Note, however, that the ON “giant bipolar” cell type (Tsukamoto and Omi, 2016) is approximately in the same size range as some of the hotspots. The connectivity of this bipolar type to the SM cells is unknown, and it is not clear whether there is an OFF correlate.

Taken together, the results suggest there are multiples layers of nonlinearities in SM cells, at the scale of bipolar cells as well as at the scale of the hotspots. The subunit model identified the hotspots as the primary source of nonlinearities in the circuit.

The role of SM cells in vision

In rodents, rabbits, and cats, specialized functions such as direction selectivity (Barlow et al., 1964), object motion selectivity (Olveczky et al., 2003; Zhang et al., 2012), local edge detection (Levick, 1967), looming detection (Münch et al., 2009), anticipation of motion (Berry et al., 1999), motion reversal (Chen et al., 2014), latency encoding (Gollisch and Meister, 2008) and suppression by motion (Tien et al., 2015) likely play unique roles in vision and visually-guided behavior. In SM cells, the irregularity of hotspot structure would lend itself to a spatial computation, potentially related to motion detection (Borst and Euler, 2011; Gollisch and Meister, 2010), in which the spatial separation of the hotspots enables sensitivity that would not be obtained from a Gaussian RF. The possibility that these unusual features of SM cells produce a specialized visual function will require further investigation.

STAR Methods

Contact for Reagent and Resource Sharing

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Colleen Rhoades (crhoades227@gmail.com).

Experimental Model and Subject Details

Eyes were removed from terminally anesthetized macaque monkeys (Macaca mulatta, Macaca fascicularis) euthanized by other laboratories in the course of their experiments, in accordance with the Institutional Animal Care and Use Committee guidelines. Prior to enucleation, the animals underwent various procedures including SIV infections, rabies injections, and chronic cortical recording implantation. Some animals suffered from health problems including diabetes, arthritis, dementia, seizures, or hepatic amyloidosis, but no visual impairments were known.

Method Details

Tissue preparation and electrophysiology

Large-scale multi-electrode array (MEA) recordings were performed from retinas of macaque monkeys, as described previously (Chichilnisky and Baylor, 1999; Field et al., 2007). Following enucleation, the anterior portion of the eye and vitreous were removed. The eye was stored in a dark container in oxygenated Ames’ solution (Sigma, St. Louis, MO) at 33°C, pH 7.4. Under infrared illumination, a small piece of retina approximately 3x3 mm, from a retinal region with eccentricity between 4.5-17 mm (4.0-17 mm temporal equivalent eccentricity; Chichilnisky and Kalmar, 2002) or 20-82.6 degrees (Dacey and Petersen, 1992; Perry and Cowey, 1985) was dissected and placed ganglion cell side down on the MEA for recording. In some preparations, the RPE remained attached during the recording; in others the RPE was removed. For the RPE-attached recordings, the choroid was removed up to Bruch’s membrane to improve oxygenation and maintain even retinal thickness. During the entire recording, the retina was perfused with oxygenated Ames’ solution. RPE-attached recordings were performed at 30-32°C and isolated retina recordings at 32-37°C. The duration of recording spanned 30 minutes to 18.5 hours. No changes in recording quality were observed over the course of long recordings. Unless specifically noted below, methods described apply to MEA recordings.

Several types of custom planar large-scale multielectrode arrays were used. The array either had a rectangular outline with 16 x 32 electrodes at 60 μm pitch, or a hexagonal outline with 519 electrodes at 120 μm or 30 μm pitch (Field et al., 2010; Litke et al., 2004). Recorded voltages were bandpass filtered, amplified, and digitized at 20 kHz using custom electronics (Litke et al., 2004). Recordings were analyzed to isolate spikes produced by different cells, a process called spike sorting, summarized here (Field et al., 2007). To detect spikes on each electrode, a threshold of four times the standard deviation of the voltage over time was used. Voltage waveforms surrounding the time of the spike (−0.5 to 0.75 ms) on that electrode and the surrounding six electrodes were extracted and concatenated into a vector. This vector is called the spike signature. Principal component analysis, typically followed by noise whitening, and unsupervised clustering using a mixtures of Gaussian model on the first five principal components of the vector signatures was performed (Duda et al., 2001). Clusters consisting of more than 100 spikes were identified as neurons if a 1 ms refractory period was observed among the spikes in that cluster. Duplicate copies of neurons detected on multiple center electrodes were identified by temporal cross-correlation and were removed. SM cell spikes were more difficult to accurately cluster than those of other RGC types because of the lower firing rate and the smaller spike amplitude. In addition to the automated clustering described above, the clusters on every electrode where an SM cell was identified were manually verified. If necessary, clusters were merged or split if incorrectly identified by automated clustering.

For the patch clamp experiments, recordings were performed from an RPE-attached retinal preparation at temporal equivalent eccentricities of 4-8 mm (18-36 degrees) in macaque retinas with conditions closely matched to MEA recordings. Recordings were performed using borosilicate glass pipettes containing Ames’ medium during extracellular (loose patch) recordings. Cells were filled with biocytin (0.5%; EZ-Link hydrazide, ThermoFisher) during whole-cell, voltage-clamp recordings with an intracellular solution containing (in mM): 105 CsCH3SO3, 10 TEA-Cl, 20 HEPES, 10 EGTA, 2 QX-314, 5 Mg-ATP, and 0.5 Tris-GTP, pH ~7.3 with CsOH, ~280 mOsm. (Manookin et al., 2015). The retina was superfused with Ames solution at 32-35°0. Cells were filled with biocyti n (0.5%; EZ-Link, ThermoFisher) for later anatomical imaging. Following recording, tissue was immersion fixed in a solution containing 4% PFA for 30-45 min and washed with 1X PBS. Tissue was counterstained with Streptavidin-conjugated Alexa 488 to visualize filled cells. Cell nuclei were stained with DAPI and starburst amacrine cells were stained with antibodies against choline acetyltransferase (ChAT). These stains allowed for accurate identification of dendritic stratification in the inner nuclear layer (Manookin et al., 2008). Images of filled cells were acquired using a SP8 confocal microscope (Leica) and used for anatomical verification. Tissue quality was assessed by recording contrast responses from parasol ganglion cells neighboring the targeted SM cell. In sensitive tissue, parasol ganglion cells were expected to increase their spike rate by at least 20 spikes/s to a 5% contrast spot presented over the receptive field at a photopic mean luminance (Fred Rieke, personal communication). Cells recorded in retinal regions that did not meet this selection criterion were excluded from the manuscript. Spike responses in SM cells were recorded with binary white noise stimuli refreshing at 60 Hz (pixel size, 20-25 μm on a side) for at least 35 min, and spatiotemporal receptive fields were recovered by cross-correlating the stimulus sequence with the cell’s spike output.

Visual stimulation

The image from a gamma-corrected CRT monitor (Sony Trinitron Multiscan E100; Sony, Tokyo, Japan) refreshing at 120 Hz was optically reduced and projected onto the retina. In RPE-attached recordings, the visual stimulus was delivered through the mostly transparent electrode array. In isolated retina recordings, the visual stimulus was delivered from the photoreceptor side. For all experiments except those in Fig. 2, low photopic light levels were used (rates of 800-2200, 800-2200, and 400-900 photoisomerizations per second for the L, M and S cones respectively; see Field et al., 2009, 2010). For Fig. 2, the light levels spanned the photopic and scotopic ranges.

A white noise stimulus consisting of a lattice of pixels flickering independently at 15-120Hz was used to characterize the spatial, temporal, and chromatic response properties of the recorded RGCs (Chichilnisky, 2001). Different experiments utilized different pixel sizes, ranging from 21.2 to 106 μm on a side. On each refresh, the intensity of each display primary at each pixel location was assigned a value randomly selected from a binary distribution. The pixel contrast (standard deviation of the difference from the mean pixel intensity) was 96% for each display primary. In some experiments, 84.8 μm X 84.8 μm pixels were displayed on an underlying lattice jittering on a 5.3 μm grid. The duration of each recording with white noise stimulation was 15-300 min.

Light response characterization

The spike triggered average (STA) stimulus for each neuron was computed from the response to the white noise stimulus (Chichilnisky, 2001), to reveal spatial, temporal, and chromatic properties of the light response.

Previously, 2D Gaussian fits have been used to characterize the RF size of RGCs (Enroth-Cugell and Robson, 1966; Enroth-Cugell et al., 1983; Rodieck and Stone, 1965). However, the RFs of the SM cells have distinct hotspots (Fig. 3B) and thus are not accurately summarized with such a fit (Brown et al., 2000; Gauthier et al., 2009; Rowe and Cox, 1993; Rowe and Palmer, 1995; Schwartz et al., 2012; Soo et al., 2011; Soodak et al., 1991). For each SM cell, a contour was used to summarize the RF. The threshold of the contour, after normalizing the RF to a maximum amplitude of 1, varied due to differences in SNR among the SM cell recordings and varying degrees of separation of the hotspots. The threshold used in each figure panel is reported in the caption. For Fig. 5J–K, the convex hull of the contour was shown due to the separation of the hotspots.

In Fig. 1, to visualize the mosaic coverage typically reported using difference of Gaussians fitting (Devries and Baylor, 1997), the contours were shrunk by 30% around the center. The shrinkage was applied because the white noise stimulus was displayed on an underlying jittering lattice that resulted in spatial correlations that artificially extended the size of the RF contour. A higher contour threshold was not used because it failed to capture the complete RF of the SM cells with strong hotspot structure. The contours in Fig. 1 should not be interpreted as the actual RF sizes, but rather the relative sizes of the RFs of different RGC types.

The response time course (Fig. 1, 2) was obtained by averaging the values of the significant pixels in the STA across time. Significant pixels were defined as those with an absolute maximum value more than 4.5 times the robust standard deviation (Freeman et al., 2015) of all the pixels in the STA. The RF was visualized as the frame of the STA corresponding to the peak of the response time course. The autocorrelation functions (e.g. Fig. 1) were normalized to unit area. To measure the size of the hotspots, a collection of a contours with a fixed threshold of 0.6 were fitted on 136 ON SM cells and 156 OFF SM cells recorded with the same white noise stimulus consisting of 84.4 μm pixels on a 5.5 μm jittering lattice.

Cell type classification

Cell type classification within a recording was performed by identifying distinct clusters in the response properties of all cells recorded with white noise stimulation (Fig. 1; Field et al., 2007). In Fig. 1, the area of the RF contour for each cell and the first principal component of the STA time courses were examined for classification. In other recordings, the second principal component of the time course and the principal components of the autocorrelation functions were also used (not shown). Neurons with evidence of contamination of spikes from another cell, low spike counts, or low SNR were not analyzed. The similarities of autocorrelation functions within a cell type and the differences across cell types also confirmed cell type classification (Fig. 1; Devries and Baylor, 1997). In each recording, the correspondence between functionally recorded RGC types and anatomically identified types for ON parasol, OFF parasol, ON midget, OFF midget, and small bistratified cells were inferred from cell densities and light response properties (Chichilnisky and Kalmar, 2002; Field et al., 2007; Dacey 2004). All other RGCs were identified as low-density cells. Recorded spiking amacrine cells were identified by their distinctive spatio-temporal spike waveforms (Greschner et al., 2014) and not analyzed further.

To classify the distinct types of low-density RGCs, a collection of 53 recordings, each containing multiple ON and/or multiple OFF low-density cells were examined. For each recording, cell type classification was performed (Fig. 1) based on RF size, time course, autocorrelation function, and mosaic overlap. The low-density cell type with the fastest kinetics in the recording, measured by the time of zero crossing (Fig. 2A) was labeled G1, and the other low-density cell types were combined and labeled G2.

To determine if G1 cells had reproducible kinetic properties across recordings, the time of zero crossing and biphasic index were computed with the following procedure: 1) the time course was averaged from the significant pixels and smoothed with a moving average of span two. 2) The time of zero crossing was linearly interpolated from the measurements around zero. 3) The biphasic index was measured as the maximum absolute amplitude of the signal in the peak lobe divided by the maximum absolute amplitude of the signal in the trough lobe. 4) The time of zero crossing and biphasic index of ON (OFF) low-density cells were normalized by the average value obtained from the simultaneously recorded ON (OFF) parasol cells.

The G1 and G2 cells were distinct based on these two normalized metrics. To determine the boundary between the G1 and G2 cell clusters, a support vector machine was fit with a radial kernel (Boser et al., 1992). The classification boundary was selected to contain all points that the support vector machine classified as G1 with greater than 95% probability.

To confirm the anatomical identity of the G1 cells, the same parameters were computed on morphologically identified SM and parasol cells with single cell patch clamp (Fig. 2B, D). SM cells were filled with biocytin (0.5%) during patch-clamp recording. Anatomical identity of the SM cells was confirmed based on the appearance of the dendrites and the dendritic stratification. Cell types in the retina extend their dendrites into stereotyped regions of the neuropil to make specific connections with presynaptic neurons. The stratification depth of recorded cells was determined by counterstaining the tissue with DAPI—a dye that stains nuclei and marks the location of the cell body layers. The tissue was also stained with antibodies against choline acetyltransferase (ChAT) that specifically identify starburst amacrine cells, which are used as a more precise marker of dendritic depth (Manookin et al., 2008). Both the stratification and dendritic appearance were as expected for SM cells (Crook et al., 2008).

The success of the SM cell classification in MEA recordings is supported by considering what would happen under two potential failure modes: 1) no SM cells were recorded and 2) the classification boundary included multiple cell types. They will be addressed in turn:

1) If SM cells were not recorded in a preparation, but multiple other types of low-density cells were recorded, the cells labeled G1 would not be SM cells, and would have time course properties diverging from the majority of the G1 cluster. These cells would presumably appear as outliers from the tightly clustered G1 points. If most recordings did contain SM cells, the conservatively defined classification boundary would likely not be affected greatly by these outliers. Indeed, some recordings contained no cells within the classification boundary.

2) If there were two or more low-density cell types with similar kinetic properties, then across 53 recordings it is likely that two or more of those cell types would be recorded in the same retina, revealing failures of mosaic organization. In this case, certain G1 and G2 cells would have similar kinetic properties. Instead, however, in no cases did both G1 and G2 cells appear within the SM cell classification boundary. This observation suggests that the boundary is restrictive enough to exclude other RGC types.

Recordings were included in the analysis if (a) at least 3 SM cells were recorded, apparently forming a small mosaic with their RFs, (b) SM cells exhibited similar spatial, temporal, and chromatic properties, (c) the spike sorting procedure could clearly separate the spikes of the SM from the other cells recorded on that electrode, and (d) the time course parameters fell within the boundary defined in Figure 2.

Photoreceptor control analysis

For each OFF SM cell, the contour fit at a threshold of 0.15 on the RF (normalized to a peak of 1) was computed. The OFF parasol cells with RF centers (defined by a 2D Gaussian fit) that fell within the convex hull of the contour fit of the SM cell were selected for analysis. The SNR of each parasol cell was computed by dividing the peak value of the Gaussian fit by the standard deviation of a 10x10 background pixel region (each pixel is 42.8 x 42.8 μm). If the average of the SM cell RF within the parasol cell RF, defined by 1 SD parameter of a spatial Gaussian fit, was less than a threshold, then the parasol cell was classified as “strong”; otherwise, the parasol cell was classified as “weak”. The mean ± SEM of the SNR for the strong and the weak parasol cells in each recording were shown (Fig. 3D). OFF SM cells were used for this control because the OFF SM cells exhibited more separated and distinct hotspots than the ON SM cells (see Fig. 3B).

Interdigitation analysis

For analysis of interdigitation (Fig. 4A–D), mosaics of five or more neighboring ON or OFF SM cells recorded with white noise (pixel size 21.2 - 53.0 μm) were examined. The RF was blurred with a Gaussian (SD = 21.2 μm) before fitting a contour to the spatial RF. For each cell type in each recording, the same contour threshold was applied to all cells. The optimal contour threshold was defined as the value that maximized the UI: the number of pixels covered by the contour of exactly one cell, divided by all the pixels within the bounded region. The boundary of the region was determined by performing the procedure outlined previously (Gauthier et al., 2009). Briefly, a Delaunay triangulation of the centers of the contour fits of all cells was computed. The area within a triangle was included in the overall boundary if the cells at its vertices were closer than 1.9 times the median nearest neighbor spacing of all the cells in the mosaic, indicating no apparent gap in the mosaic. The UI was computed within the boundary. The UI was also computed on 1000 simulated mosaics obtained by random rotations of the measured RFs around the centers of their contour fits. The contour threshold was then recomputed, maximizing the UI. The distribution of UI values produced by the 1000 perturbations (Fig. 4C) was treated as the null distribution for statistical testing.

Shared input

To determine which cell pairs had overlapping hotspots, strong pixels (with an intensity greater than 50% of the maximum value) were identified for each cell. If the two cells shared strong pixels, then the cell pair was identified as sharing a hotspot. A square was identified, centered at the pixel with the maximum intensity product in the two RFs. The correlation coefficient between the pixel intensities in the two cells within the square was computed for the observed data, as well as for 7 manipulations in which the data from one cell was rotated by 0, 90, 180, or 270 degrees, and/or flipped horizontally around the center point. The coefficients were ranked in descending order and the rank of the observed data compared to the various manipulations was reported, where rank 1 indicated highest correlation. If the hotspots in the two cells had identical sensitivity profiles, then the observed data would have a rank of 1.

Spike signature splitting

In the spike sorting procedure (see above), sub-clusters were sometimes observed within the cluster corresponding to a single SM cell. An automated procedure was developed to identify such sub-clusters. For each electrode, the standard spike sorting approach as described previously was applied. Then 50 iterations of k-means clustering with random initial conditions were performed on the first five principal components of the spike signatures from the SM cell with the number of clusters equal to the number of visible hotspots in the RF. The iteration with the smallest total sum of distances was used. The RFs of each cluster were then computed, fitted with contours, and compared to the RF computed from all the SM cell spikes. The threshold for the contour of the SM cells and the hotspots in this analysis was 0.2.

The EI for each cluster on the electrode was computed as well as the EI for the subclusters. For every RGC spike, the voltage waveform 2.5 ms before to 2.5 ms after the time of peak spike amplitude was averaged for every electrode on the array. By averaging across all the spikes from a cell and taking the maximum projection across time, the EI revealed the unique somatic, dendritic, and axonal signatures of each neuron. The outline of the maximum projection of the EI (Fig. 5J, K), was the boundary around the electrodes in the combined cluster where the voltage fell below −30 μV.

To observe the spatial separation in the origin of the electrical signal, the automated signature clustering analysis was performed on SM cells recorded on an array with 30 μm spacing. The time preceding the spike at which the signature first fell below a threshold of 5.5 μV was recorded for each electrode and each cluster. The threshold was chosen to be robust to noise (Fig. 5M, green points). This measured time on each electrode for the second cluster (Fig. 5K, dotted line) was subtracted from the time for the first cluster (Fig. 5K, solid line). Red electrodes in Fig. 5L were those for which the first cluster was faster than the second cluster, and vice versa for blue electrodes. Electrodes for which the difference was less than 50 μV were not shown.

Closed loop white noise stimulus

For closed loop visual stimulation (Fig. 6), the STA was computed following spike sorting while the recording was taking place. Two circular stimulation spots were placed to overlap with the hotspots observed in the RF. The spot size was adjusted so that both encompassed approximately the same integrated weight of the STA. Each spot was independently stimulated with binary white noise for 15-30 minutes. The temporally integrated contrast on each spot was determined by convolving the stimulus with the time course of the STA. The firing rate was determined by counting spikes in 8.33 ms bins corresponding to stimulus display frames. The effective contrast values on both spots, as well as the firing rate, were collected into 10x10x10 bins of variable size such that each bin contained the same number of samples. The linear model is described by:

$$f=\frac{a_1}{1+e^{(-a_2(a_3{x}_1+x_2-a_4\left)\right)}}+a_5$$

The nonlinear model is described by:

$$f=\frac{a_1}{1+e^{(-a_2(a_3{x}_1-a_4\left)\right)}}+\frac{a_1}{1+e^{(-a_2(x_2-a_4\left)\right)}}+a_5$$

where x₁ and x₂ are the binned input contrast values, and a₁, a₂, a₃, a₄, and a₅ are the five fit parameters. The models were fitted for each cell minimizing the mean squared error between f and the recorded binned firing rate.

Spiking response model fitting

The subunit model construction and fitting approach were described previously (Shah et al., 2018). Briefly, the model was fitted using an alternating cascade of two linear-nonlinear stages, with Poisson spike generation. In the model, the visual stimulus was convolved with the average time course of the neuron to produce the instantaneous stimulus (X_t). The inner product of the stimulus with each of the model linear subunit filters (K_n) was computed (where the total number of desired subunits was fixed) and followed by an exponential nonlinearity. Then, the subunit outputs were multiplied by non-negative weights (W_n), summed, and passed through a final output nonlinearity of the form $g(x)=\frac{x^a}{bx+1}$, resulting in the firing rate: g(Σw_ne^K_n·X_t). Spikes were predicted from this rate with a Poisson spike generator. A locally normalized L1 regularizer was used which penalizes large weights if all the neighboring weights are small. The model was fitted on 80% of the data. A range of regularization values was searched for each cell, and the value that maximized log likelihood on a 10% test data set were used.

The LN model, used for comparison to the performance of the subunit model (Fig. 8), was fitted using the same method previously described for the subunit model, except the number of subunits was fixed at one. The reported percentage improvement in correlation coefficient was measured as the difference between the correlation coefficient of the four-subunit model and the LN model divided by the correlation coefficient of the LN model. The correlation coefficient was measured on 10% of the white noise data, which was not used in either the fitting or model selection process.

For simplicity, the number of subunit filters was fixed at four in order to approximately correspond to the number of visible hotspots and directly test if the strongest nonlinear summations were between the hotspots. When the number of subunit filters was increased up to 8, the performance of the model in spike prediction improved with each additional subunit filter, but saturated. With four subunit filters, 81% of the performance was captured and with 6 subunit filters, 99% was captured. Although 6 subunits captured the population data more accurately, in any given cell it was more difficult to determine the optimal number. Therefore, the number of filters was chosen to err on the side of underfitting rather than overfitting the model.

Quantification and Statistical Analyses

Statistical analyses were performed in MATLAB (R2015+, Mathworks) or Python. Final figures were created in MATLAB, Python, Igor Pro, Adobe Illustrator, and/or Intaglio. The details of the statistical analysis for each result can be found in the Results section and in the captions. The definition of the measurement (mean, median, SD, SEM) is listed next to the reported numbers throughout the text. The number of cells and number of recordings used in each experiment is described in the text.

Inclusion criteria for MEA recordings is listed in the last paragraph of the method section “Cell type classification”. Inclusion criteria for patch clamp recordings is listed in the last paragraph of the methods section “Tissue preparation and electrophysiology”.

Data and Software Availability

Visual stimulation (http://stage-vss.github.io, http://gru.stanford.edu/doku.php/mgl/overview) and data acquisition (http://symphony-das.github.io) software are freely available. Analysis software is available upon request.

Supplementary Material

1

Supplemental Movie 1: Dendritic origin of spike signature differences, Related to Figure 5 The electrical image over time of the two distinct SM cell signature clusters shown in Fig. 5K. The electrical signal corresponding to different hotspots in the RF originates from different spatial locations, as shown at approximately −250 μs (and summarized in Fig. 5L). Each black dot is an electrode on the 519 hexagonal multi-electrode array. Yellow indicates negative voltage deflection while purple indicates positive voltage deflection. The size indicates the magnitude of the voltage deflection. At 0 μs, the spike occurs. The red dots mark the electrode with maximal overall deflection (approximately the soma location).

Highlights.

• Smooth monostratified ganglion cells have hotspots in their receptive fields

• Each hotspot does not originate from an individual presynaptic input

• Stimulation of distinct hotspots produces subtly different spike waveforms

• The hotspots form nonlinear computational subunits larger than bipolar cells