Abstract
The goal of this study is to estimate micro-architectural parameters of cortical porosity such as pore diameter (ϕ), pore density (ρ) and porosity (ν) of cortical bone from ultrasound frequency dependent attenuation using an artificial neural network (ANN). First, heterogeneous structures with controlled pore diameters and pore densities (mono-disperse) were generated, to mimic simplified structure of cortical bone. Then, more realistic structures were obtained from high resolution CT scans of human cortical bone. 2-D dimensional finite-difference time-domain simulations were conducted to calculate the frequency-dependent attenuation in the 1–8MHz range. An ANN was then trained with the ultrasonic attenuation at different frequencies as the input feature vectors while the output was set as the micro-architectural parameters (pore diameter, pore density and porosity). The ANN is composed of three fully connected dense layers with 24, 12 and 6 neurons, connected to the output layer. The dataset was trained over 6000 epochs with a batch size of 16. The trained ANN exhibits the ability to predict the micro-architectural parameters with high accuracy and low losses. ANN approaches could potentially be used as a tool to help inform physics-based modelling of ultrasound propagation in complex media such as cortical bone. This will lead to the solution of inverse-problems to retrieve bone micro-architectural parameters from ultrasound measurements for the non-invasive diagnosis and monitoring osteoporosis.
Keywords: Quantitative Ultrasound, Multiple Scattering, Cortical Bone, Osteoporosis, Neural Networks
I. INTRODUCTION
Osteoporosis is the most common metabolic bone disorder. It affects both cortical and trabecular bone. It is characterized by low bone mass, tissue degradation, deteriorated macroscopic mechanical properties and altered micro-architecture [1]–[4]. Loss in bone mass leads to frequent fracturing, higher mortality and reduction in life expectancy by 1.8 years[5]–[7]. For these reasons, early diagnosis and monitoring of osteoporosis is crucial. Several imaging modalities provide semi-quantitative to qualitative analysis of the bone. DXA (Dual X-Ray Absorption) correlates well bone mineral density (BMD). High resolution peripheral quantitative computed tomography (HR-pQCT) and magnetic resonance imaging (MRI) based techniques are also used for the characterization of bone. However all these methods have short comings. MRI lacks resolution[8], and CT based methods are associated with radiation doses making it unsuitable for frequent use, screening and monitoring [9]–[11]. MRI and CT are also associated with high costs and low portability. DXA is less ionizing but BMD measured with DXA insufficiently correlates with fracture risk[12]. DXA assessments suffer from high variability from person to person[13].
Traditional ultrasound imaging is based on the concept of echolocation. However, in highly heterogeneous media such as bone or the lung, traditional imaging methods fail. This is due to the high heterogeneity and large impedance changes within the propagating media. The presence of fluid-filled pores introduces multiple scattering and aberrations, making bone elusive to ultrasound imaging for osteoporosis and osteopenia diagnosis[14]–[16]. Quantitative ultrasound (QUS) techniques are better suited for such applications. The backscattered signals from propagation in such complex media can be characterized using quantitative methods[17], [18], [27]–[34], [19]–[26]. As the ultrasonic wave travels through a complex heterogeneous medium, its propagation is affected by the micro- and macroscopic changes. Correlating changes in trabecular micro-architecture to ultrasonic parameters such as frequency dependent attenuation, phase velocity or backscattering coefficient[35]–[38] have provided insights into quantifying microstructural parameters. QUS can also be used to extract macroscopic changes such as elasticity by measuring the axial speed of sound, which is recognized to be a significant parameter in overall bone quality[39]–[44]. The fact that ultrasound is a mechanical wave makes it sensitive to macro-mechanical changes of bone[45], [46]. A multitude of research studies have been performed to investigate the dependence of ultrasonic parameters on the micro-architectural properties of trabecular bone but not enough on the cortical bone. Analysis of parameters such as frequency dependent attenuation, wave velocity, backscatter coefficient and diffusion constant has shown promise [18], [26], [28], [47]–[49]. Various QUS methods have been developed to study cortical bone thickness and the wave speed, which can then be associated to its macro-mechanical properties [39], [50]–[56]. Zheng et al. applied a spectral ratio method to estimate the broadband ultrasound attenuation (BUA) in cortical bone[57]. Similar work was done by Xia et al., wherein they calculated the normalised BUA (nBUA) to characterize cortical bone[58]. Guided waves incorporating the lamb wave theory and dispersion curves have also been adopted to characterize cortical bone[59]–[64]. Recent work by Yousefian et al.[65]–[67] showed that a phenomenological power law model of the frequency dependent attenuation could potentially be used to characterize the micro-architectural properties of complex porous structures, giving access to pore diameter (ϕ), pore density (ρ) and porosity (ν). There is a number of ultrasonic parameters, including phase velocity, backscattering coefficient, diffusion constant etc. that are associated with the micro-structural change in random media. However, previous studies by the authors[65], [67] and other groups show the sensitivity of attenuation to micro-structural changes in cortical bone in the MHz , mainly because among all the other US parameters, attenuation is associated with scattering. With osteoporosis, porosity parameters, including pore size and density, change, [2]–[4] which affects ultrasonic scattering. Because of this, we limited our study to attenuation to predict micro-structural properties.
Data-driven predictions combined with machine learning enable us to generate prediction outcomes and is currently being extensively used for clinical applications[68]–[71]. Clinical level classification accuracies of skin cancer and breast cancer are now achievable using Convolutional Neural Networks (CNN)[72]. Neural networks have the ability to identify patterns and relationships from complex data sets[73], [74]. In supervised learning, a labelled training data set is used to map the input to the output. Here, we propose to use neural networks to map ultrasonic data (the frequency-dependent attenuation) to microstructural features of cortical bone (pore diameter, pore density and porosity).
The purpose of this paper is not only to attempt to develop a potential inverse problem solving method using machine learning, but also to use machine learning to explore the dependence of ultrasonic attenuation to these micro-architectural properties. We envision that neural networks will inform physics-based modelling efforts by putting the spotlight on the specific features that are the most relevant to the relationship between ultrasound parameters and microstructural parameters. We could then potentially draw on information obtained from machine learning to refine models of ultrasound propagation in cortical bone.
In this study, finite difference time domain (FDTD) simulations were conducted to calculate the frequency dependent attenuation (1MHz-8MHz) in 2-D geometries resembling simplified cortical bone structures (mono-disperse). Pore diameter and pore densities were modified to obtain attenuation data for a wide range of micro-structural features. In addition, realistic cortical bone structures (poly-disperse) were obtained from high resolution CT scans of human cortical bone and using image processing techniques, from which micro-architectural parameters were extracted. Frequency-dependent attenuation values were mapped to the corresponding micro-architectural parameters and used as the data set. An artificial neural network (ANN) was then trained over the simulated data set to predict micro-architectural parameters. In section II, we discuss the data collection methodology for both mono and poly-disperse cases. Section III presents how the ANN model was formulated followed by the results and conclusion in sections IV and V.
II. DATA COLLECTION AND METHODOLOGY
A. FDTD Simulation
All simulations of ultrasound propagation through structures mimicking cortical bone were carried out using SimSonic, an open source simulation software based on FDTD numerical methods[39], [75]. The simulated media were solid slabs with fluid filled pores resembling bone tissue (marrow inside cortical bone). The solid phase was given the properties of pure bone whereas the fluid filled pores were given properties of water. Absorption coefficients were attributed to both the solid and fluid phases. For the cortical bone matrix, the absorption coefficient was set to 10dB/cm/MHz which is arbitrary. This was chosen because to the best of our knowledge there hasn’t been any research on the absorption coefficient in the tibia cortical bone. Attenuation from both scattering and absorption (visco-elasticity) was therefore accounted for [76]. The material properties of the solid and fluid phases are summarized in Table 1. Simulations were carried out in the structures in the 1–8MHz range with 1MHz frequency intervals. The transmitted wave was a Gaussian ultrasonic pulse with a −6 dB, 20% bandwidth. Shown in Figure 1 is an example of the transmitted signal in the time and frequency domains for a 1, 5 and 8MHz pulse.
Table 1:
Material properties for FDTD simulations[39]
| Solid Properties | Value | Fluid Properties | Value |
|---|---|---|---|
| Wave Speed Cb (mm/μs) | 4 | Wave Speed Cw (mm/μs) | 1.54 |
| Density ρb(g/ml) | 1.85 | Density ρw(g/ml) | 1.00 |
| Absorption Coeff αb (dB/cm/MHz) | 10 | Absorption Coeff αw (dB/cm/MHz) | 0.1 |
Figure 1:
Signal in time and frequency domain
With a highest simulated frequency of 8MHz, the smallest wavelength is equal to 500 μm. All simulations were carried out in 2-D with a grid step size of = =10μm (50 points per wavelength at 8 MHz). Perfectly Matching Layer (PML) boundary conditions were applied at both ends of the simulation domain in the direction of wave propagation to minimize the effect of boundary reflections. Symmetry boundary conditions were applied in the direction perpendicular to wave propagation to simulate a plane wave and to eliminate effects of diffraction. In order to satisfy the CFL (Courant-Friedrich Levy) condition, the CFL number was set to 0.99 [77] and the sampling time step was chosen as
| (1) |
Where is the maximum speed of sound in the simulation domain and d is the dimension of the space (d=2 for 2D). On average each set of 2D simulation for the given grid step at each frequency takes between 2 to 3 minutes. Lower frequencies simulations take more time because of the greater PML thickness surrounding the structure
B. Mono-Disperse Geometry
Simple mono-disperse structures resembling cortical bone were generated using a Monte Carlo method for each combination of ϕ and ρ. For each pore with the given diameter, the center coordinates (Xc,Yc) are chosen randomly with a uniform distribution between the boundaries of the structure Xc∈[Xl,Xu] and Yc∈[Yl,Yu] such that P(Xc) = 1/(Xu-Xl) and P(Yc) = 1/(Yu-Yl). Applying a constraint to make sure that there will not be any overlap between the boundaries of neighboring pores, pores are distributed in the solid bone matrix until the required pore density is reached.
The ϕ and ρ ranged from 20–120 μm (discrete steps of 10 μm) and 3–16 pores/mm2 (3,5,6,7,8,10,12,14,15,16) respectively. The porosity was derived from pore diameter and pore density based on Equation 2.
| (2) |
From Equation 2, it can be determined that the porosity ranged from 0.001 to 0.18 (zero being no fluid and one fluid only). The generated structures had a dimension of 10mm by 10mm (1000 pixels by 1000 pixels). Shown in Figure 2 are examples of two mono-disperse structures generated for FDTD simulations. 110 unique combinations of pore diameter and pore density were generated and FDTD simulations were carried out. For each combination, three different realisations were generated to form 330 simulations in total (3 (realisations) x 110 (cases)).
Figure 2:
Mono-disperse bone schematic geometry, A: ϕ =50 μm, ρ = 3 pores/mm2, B: ϕ =120 μm, ρ =16 pores/mm2
C. Poly-Disperse Structures
The structure presented in the previous section is a simplified representation of bone micro-architecture. In order to obtain more realistic cortical bone simulation domains, 2-D images were obtained from high resolution CT scans of a human cortical bone. 3-D CT scans of resolution 6.5 μm were obtained, as described in [78], [79] and 2-D planar cross sections were randomly taken for FDTD simulations. The CT scans were normalized and binarized based on a threshold which demarcated the bone matrix and the fluid filled pores. Due to high spatial resolution and contrast of SR CT images, a wide range of threshold levels would have resulted in the same binarized image and segmentation was straightforward and a global threshold was used for all specimen[80].
The porosity of the images was obtained by dividing the number of pixels associated with the liquid phase to the total number of pixels in the cross-section. To measure the average pore diameter and pore density, every single closed surface within the segmented bone cross-section was labelled. The number of labels indicated the total number of pores, and the ratio between pore number and the entire bone area provided the pore density in pores / mm2. To estimate the mean pore diameter, pores were assumed to have a circular shape. The area of each pore was equated to the area of a circle and diameter of each pore was calculated. By measuring the area of each pore and averaging the calculated diameters, the mean pore diameter and its standard deviation was obtained. FDTD simulations were carried out on 964 cross sectional structures with the ϕ, ρ, ν and standard deviation (SD) of the pore diameter ranging from 27-115 μm, 9-22 pores/mm2, 0.01 – 0.2 and 16-82 μm respectively. Shown in figure 3 are examples of poly-disperse structures obtained from CT scans after image processing.
Figure 3:
Poly-disperse bone schematic geometry, A: ϕ =50 μm, ρ = 16.85 pores/mm2, ν=0.047, SD=33 μm, B: ϕ =71 μm, ρ =14.3 pores/mm2, ν=0.081, SD = 47 μm
D. Attenuation Measurement: Time-distance matrix approach (TDMA)
Plane waves were transmitted through the structures (mono and poly-disperse) using FDTD simulations. Receivers were placed at 30 consecutive longitudinal positions along the structure in the direction of wave propagation, separated by the same distance, (0.3mm for mono-disperse and 0.09mm for poly-disperse). The emitter and receiver size was the same as the simulation domain size (10 mm for mono-disperse and 3.7 mm for poly-disperse) hence covering the whole height of the slab. Time domain signals were recorded by each receiver in a time-distance matrix , which was then converted into the frequency domain . The received time signals for the 100 μm ϕ, and 7 pore/mm2 ρ are shown in Figure 4.
Figure 4:
Received Signals at different receivers for 100 μm ϕ, and 7 pore/mm2 ρ at 4MHz.
In the time domain, the wave amplitude was assumed to have an exponential decay (Shown in Figure 4) over time. Doing a fast Fourier transform (FFT) of all the time signals allowed us to obtain the frequency domain data. The attenuation-dependent frequency was then calculated based on Equation 3[47].
| (3) |
Hence, for each frequency, if was plotted versus x, the absolute value for the slope of the linear fit to the data represents the attenuation coefficient, . Using a frequency sweep from 1 to 8 MHz, the attenuation coefficient was calculated, details of which can be found in the work by Yousefian et al [65]. Shown in Figures 5 and 6 are frequency dependent attenuation plots for the mono-disperse and poly-disperse cases.
Figure 5:
Frequency dependent attenuation for mono-disperse FDTD simulation
Figure 6:
Frequency dependent attenuation for poly-disperse FDTD simulation
It can be clearly seen that with an increase in pore diameter, the attenuation at a given frequency increases. This is attributed to additional losses in the ultrasonic wave due to stronger scattering. Similarly, with an increase in pore density, the attenuation increases, due to an increased number of scatterers, accentuating the attenuation.
III. NEURAL NETWORK MODEL
Data from FDTD simulations was used to train an ANN. The ANN model built for supervised training consisted of five fully connected layers, as shown in Figure 7. It should be noted that Figure 7 is not an accurate representation of the number of neurons in each layer, but rather is a pictorial representation of how the neurons in each layer are connected. In supervised learning, a labelled set of data is used to map the input data to the desired output. In a regression problem, the output is not a classification but discrete output values, which are mapped to the input feature vector. The ANN was trained based on backpropagation, with the input layer having 8 neurons and the output layer having 3 or 4 neurons depending on whether standard deviation of the pores (in the poly-disperse structures) has been considered as an output or not. The number of neurons in the hidden layers have been set as 24, 12 and 6. We deliberately kept the number of neurons low in this problem statement to avoid over-fitting. The at frequencies 1–8MHz was used as the input feature vector , whereas the output layer gave the predicted ϕ, ρ and ν. Hence, is an 8-dimensional space where as is a 3 or 4-dimensional space (for mono- and poly-disperse structures respectively). All the ANN modelling was done in the Python API of TensorFlow.
Figure 7:
Schematic of the ANN structure. The arrows depict connection between neurons of 2 layers
Once all the data was acquired, the total data set was split into training and test data (test size=0.2). The training data (Both and ) was scaled using the StandardScaler transformation in Python. While training and compiling the ANN model, we used the Adam optimizer. Furthermore, the training data was then split into training and validation sets (cross validation size=0.2) and the validation loss (mean squared error) was monitored for convergence or fine-tuning of the hyper-parameters. The batch size while training was set to 16 samples and the ANN was trained over 6000 epochs. The validation loss was calculated based on the equation shown below
| (4) |
Where is the actual output, is the prediction from the model and n is the total number of data sets over which the loss is being calculated. The performance of the ANN model was evaluated based on the validation loss.
For this study, we built three separate ANNs. The first ANN only took into account the mono-disperse structures. The second ANN only considered the poly-disperse structures. Finally, a unified ANN model was trained using all mono and poly-disperse cases. For the mono-disperse case, the output parameters were set as pore diameter, pore density and porosity. We acquired 330 (110 × 3 (realisations)) sets of data. For a given realisation, 110 sets were acquired by varying the ϕ and ρ in ranges of 20–120 μm (11 discrete steps) and 3–16 (10 discrete steps) pores/mm2 respectively. Synthetic data was then generated from these 110 sets of data using spline interpolation. 110 sets of data were interpolated to 1130 sets of data with steps in pore diameter and pore density set to 2 μm and 0.23 pores/mm2. This was considered a reasonable assumption since at a given frequency, the attenuation increased monotonously with an increase in pore diameter and pore density as shown in Figure 8.
Figure 8:
Attenuation trends at Frequency =8MHz, A: Fixed pore diameter, B: Fixed pore density
Figure 8 depicts the trend in attenuation at a central frequency of 8 MHz. For a fixed ϕ, the attenuation increases with increasing ρ. Similarly, for a fixed ρ, the attenuation increases with increasing ϕ. The reason for this interpolation to generate synthetic data was to have enough data sets for training. For the poly-disperse cases, enough data sets were readily available via the CT slices and no such interpolation was conducted. The output variables were set as ϕ, ρ, ν and SD. For the third unified neural network, which combines both the data sets, the output vector had four variables (ϕ, ρ, ν and SD). Shown in table 2 are the details of all the neural networks. The difference in the number of trainable parameters arises from the difference in output variables.
Table 2:
Details of three ANN Models
| DNN Model | Dimesion of Input Feature Vector |
Output Variables |
Trainable Parameters |
Total Data Sets |
|---|---|---|---|---|
| Mono-Disperse | 8 | 3 | 615 | 3390 |
| Poly-Disperse | 8 | 4 | 622 | 964 |
| Combined | 8 | 4 | 622 | 1294 |
IV. RESULTS
The convergence of the ANN for the mono-disperse model over 6000 epochs is shown in Figure 9. Even though the training losses are 0.07, the validation loss was determined to be 0.13. Shown in Figure 9 are the results obtained from the ANN on the mono-disperse structures, comparing the estimated values of pore density, pore diameter and porosity to the true values.
Figure 9:
ANN Results for Mono-Disperse data only
The x-axis depicts the true values whereas the y-axis depicts the values predicted by the ANN post training. The normalized root mean square deviation (NRMSD) for the test data was calculated based on equations (5) and (6).
| (5) |
| (6) |
Where, y is the true value, N is the total number of readings and is the mean of the actual values. NRMSD was found to be 0.06, 0.18 and 0.065 and R2 were found to be 0.98, 0.81 and 0.99 for pore diameter, pore density and porosity respectively.
Shown in Figure 10 are the results obtained using the ANN on the poly-disperse structures. Normalized root mean square deviation (NRMSD) for the test data was found to be 0.069, 0.071, 0.043 and 0.055 for porosity, pore diameter, pore density and standard deviation respectively. For the poly-disperse case, the porosity (R2=0.99) and the pore density (R2=0.94) are both predicted accurately and independent of each other.
Figure 10:
ANN Results for Poly-Disperse data only
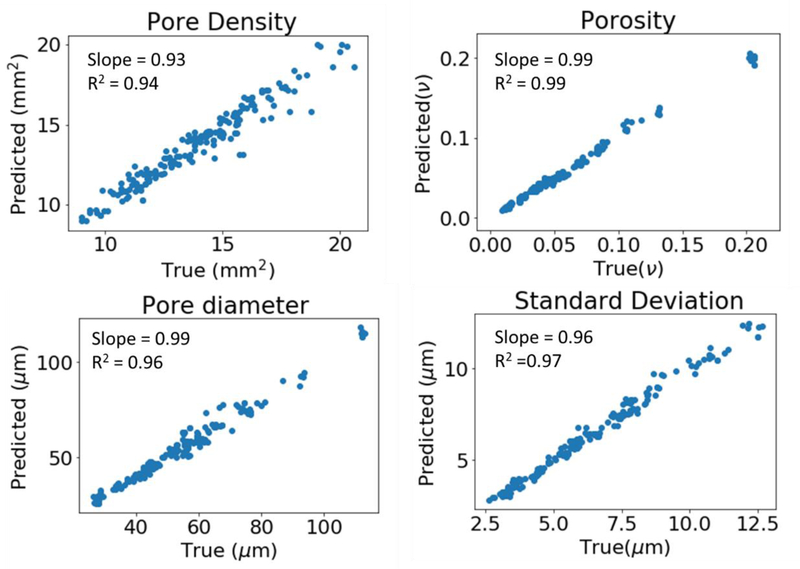
Figure 11 shows the results obtained from an ANN with input data as the data obtained from both mono-disperse and poly-disperse simulations. The loss and validation loss for the combined ANN was 0.05 and 0.15 respectively. The results showcased in Figure 11 exhibit high accuracy in predicting porosity, pore diameter and SD with R2 values of 0.97, 0.94 and 0.98 respectively. NRMSD for the test data was found to be 0.09, 0.10, 0.21 and 0.11 for ν, ϕ, ρ and SD respectively.
Figure 11:
ANN Results for Mono and Poly-disperse combined data (Unified Model)
V. DISCUSSION
One of the limitations of the present study is the need to interpolate the data set for the monodisperse structures. Because the Monte Carlo method necessary to create the monodisperse structures is computationally heavy, no more than 110 simulations could be conducted. This data set was not large enough to allow the training of the neural network. However, the relationship between frequency-dependent attenuation on one hand, and pore diameter and pore density on the other hand, is monotonous (Fig.8), so this interpolation can be assumed reliable. Using more than 1130 data sets did not improve the accuracy of the results significantly, but increased computation times significantly. This is why an interpolation to 1130 was chosen.
A validation loss of 0.13 was found. The number of neurons chosen for the ANN was based on two major factors: computational time and overfitting. By increasing the number of neurons, the validation loss is bound to get lower; however, over-fitting might occur if too many neurons are used in the hidden layer. Also, given the relative simplicity of the problem, large number of neurons were unnecessary.
It can clearly be seen that for prediction of ρ, the ANN does not perform as well as it does for the other two parameters. At low pore diameter, with change in pore density, the frequency dependent attenuation does not change much. It is hypothesized that at low pore diameter, scattering is weaker and attenuation is dominated by absorption. However, at higher pore diameters, the attenuation changes more significantly with changes in pore density. In this stronger scattering regime, the porosity affects attenuation more significantly. This is illustrated in Figure 12. It is interesting to note that pore density is the controlled variable along with pore diameter. The porosity is obtained from equation 2 and is derived from pore diameter and pore density. The ANN is capable of predicting porosity with high accuracies, however it is not as accurate with pore density. This could be attributed to the fact that porosity has a dependence of ϕ2 and hence the determining factor for porosity becomes the pore diameter and the effect of pore density is reduced.
Figure 12:
Attenuation plots for varying pore diameters and pore sizes.
The fact that the ANN predicts the SD (the standard deviation of the pore diameter distribution obtained from image processing of CT scans) shows its potential to be sensitive to the kind of pore distribution that exist in real cortical bone. Indeed, for the poly-disperse case, porosity is not derived from pore diameter and pore density and is obtained from image processing as detailed in section II.
One can clearly see in Figure 11, the pore density predictions are less accurate in the low range of ρ values between 3 and 9 pores/mm2 which mostly correspond to the mono-disperse case; however, for mid-range and higher pore densities, the ANN is sensitive and can predict ρ more accurately. Note here that for true SD values of zero (mono-disperse), the ANN predicts SD values between 0–3 μm. This demonstrates that the ANN has the potential to identify the type of distribution and even predict the standard deviation of the distribution of scatterers in the cortical bone with high fidelity.
It should be noted that the purpose of our study was mainly to determine the independent effect of the parameters of the cortical microstructure on ultrasonic attenuation. Controlling pore diameter and pore density independently would have been difficult to do experimentally, where changing one parameter while keeping the other one constant (as we did for the mono-disperse case) would have been impossible. Moreover, having access to large enough numbers of bone samples to train the ANN could be challenging, and out of scope of this proof of concept.
A limitation of the ANN model was its lower R2 values and higher NRMSD for predicting pore density. From the unified ANN, it can be said that the ANN is sensitive to the range of pore diameter. At lower pore diameters, the attenuation may not be sensitive enough to pore density, which can be seen in Figure 12. However these are for only mono-disperse cases. On the other hand, for the poly-disperse case, the data is more spread out and the additional training parameter SD allows for better discrimination between pore densities with higher accuracies.
The current state of the art in predicting the micro-architectural parameters of bone using ultrasound involves simple phenomenological observations of correlations between ultrasound parameters and bone microstructure, as well as more advanced physics-based modeling approaches. In trabecular bone. several studies have compared ultrasonic predictions to trabecular microstructural parameters obtained from high resolution micro-CT. Relatively high correlations have been observed between porosity, trabecular thickness, frequency dependent attenuation and speed of sound [81,82]. In cortical bone, Laugier et al. used a guided wave approach to predict cortical thickness (R2=0.89, p<10−5) and porosity (R2=0.63, p<10−5)[83,84]. Similar work done by Schneider et al. [85] has further confirmed guided wave parameters to be correlated with porosity and thickness. In terms of physics-based modelling of ultrasound propagation, Yousefian et al [67] have demonstrated the potential of scattering models to predict cortical porosity from ultrasound data, and Karbalaeisadegh et al have demonstrated that average pore diameter and porosity were associated to the diffusivity of ultrasound [86]. Based on these models and observations, various approaches have been attempted to solve the inverse problem. Some inverse problems were based on the Biot model in trabecular bone [87–89]. Several inverse solutions have also been proposed to predict backscatter coefficient, nBUA, cortical bone thickness, elastic velocities, and cortical porosity [29], [90–93]. Although these approaches are highly interesting, the solutions to these inverse problems are unfortunately often not unique. Exploring data-driven inverse problems using machine learning such as the one proposed here is therefore highly relevant, as it holds potential for the non-invasive, quantitative assessment of bone using ultrasound. A pilot study was recently conducted by Vogl et al [94], in which low frequency ultrasound data was used to train a support vector machine, with velocity of guided waves in the tibia at different frequencies at an input. This study showed a good agreement between the predictions of the model and DXA values at the lumbar spine. The frequencies used in this pilot study suggest that the algorithm was mostly sensitive to tibial cortical thickness. However, to our knowledge, no previous effort was conducted to leverage an ANN to predict the micro-architectural parameters of cortical porosity. In the present study, we also chose a mixed approach, that combine physics-based insights (the knowledge that frequency dependent attenuation is related to cortical porosity) and data driven insights. We therefore propose to characterize cortical porosity in terms of averaged statistical properties. This ANN method has shown the ability to predict a variety of parameters such as pore diameter (R2=0.94), pore density (R2=0.62), porosity (R2=0.98) and pore distribution (R2=0.98). Applications of machine learning to bone characterization are still at an early stage, but they hold tremendous promise, and the diversity of potential future approaches is high.
VI. CONCLUSION AND FUTURE WORK
An ANN was trained on FDTD simulated data of ultrasound propagation in cortical bone mimicking structures with controlled porosity, pore diameter and pore density. An ANN was trained for mono-disperse (created using a Monte Carlo approach) and poly-disperse (obtained from human femur CT scans) structures. The two structures were then combined and a unified ANN was established. The trained model, taking the ultrasonic attenuation data as the input feature vector, predicted the micro-architectural properties. The agreement between the predicted values and true values ranges from good to excellent. The ANN consistently predicted porosity and pore diameter with R2 values greater than 0.9 and slopes of magnitude 1. The ANN showed potential in solving the inverse-problem by accurately predicting the porosity, pore diameter and standard deviation (SD). The lack of sensitivity towards ρ does indicates that, in the near future, one could shift towards only looking at porosity and pore diameter in the ANN model for predicting the onset of osteoporosis and characterizing the cortical bone. The unified ANN, was able to differentiate between the mono-disperse and poly-disperse cases, exhibiting its ability to predict the type of pore distribution in the micro-architecture. Many studies suggest significant correlations between ultrasound parameters and bone parameters. It is now necessary to develop inverse problems in order to retrieve these bone parameters from ultrasound measurements. However, phenomenological models and relationships based on observation are sub-optimal for the development of solving of inverse problems. It will therefore be necessary to develop physics-based models. We propose to use data driven predictions to inform the development of these physics-based models, due to their ability to point out the relevant parameters that need to be focused on.
In the near future, the ANN can be trained with the ultrasonic attenuation data to predict more traditional micro-structural parameters such as bone mineral density (BMD) and bone volume/ Total Volume (BV/TV). This in combination with porosity, pore diameter and pore density could help us establish a holistic prediction model for the cortical bone.
VII. ACKNOWLEDGEMENTS
This work was partially supported by National Institutes of Health grant no. R03EB022743. The authors also acknowledge Dr Maciej A. Mazurowski, Duke Radiology Dept., for his assistance in developing the ANN model.
VIII. REFERENCES
- [1].Chen H, Zhou X, Fujita H, Onozuka M, and Kubo KY, “Age-related changes in trabecular and cortical bone microstructure,” International Journal of Endocrinology. 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Yerramshetty J. and Akkus O, “Changes in Cortical Bone Mineral and Microstructure with Aging and Osteoporosis,” in Skeletal Aging and Osteoporosis, 2013, pp. 115–131. [Google Scholar]
- [3].McCalden RW, McGlough JA, Barker MB, and Court-Brown CM, “Age-related changes in the tensile properties of cortical bone. The relative importance of changes in porosity, mineralization and microstructure,” J. Bone Jt. Surg. - Ser. A, vol. 75, no. 8, pp. 1193–1205, 1993. [DOI] [PubMed] [Google Scholar]
- [4].Schaffler MB and Burr DB, “STIFFNESS OF COMPACT BONE : EFFECTS OF POROSITY AND DENSITY,” vol. 21, no. I, pp. 13–16, 1988. [DOI] [PubMed] [Google Scholar]
- [5].Sornay-Rendu E, Munoz F, Duboeuf F, and Delmas PD, “Rate of forearm bone loss is associated with an increased risk of fracture independently of bone mass in postmenopausal women: The OFELY study,” J. Bone Miner. Res, 2005. [DOI] [PubMed] [Google Scholar]
- [6].Braithwaite RS, Col NF, and Wong JB, “Estimating Hip Fracture Morbidity, Mortality and Costs,” pp. 364–370, 2003. [DOI] [PubMed] [Google Scholar]
- [7].Schuit SCE, Van Der Klift M, Weel AEAM, De Laet CEDH, Burger H, Seeman E, Hofman A, Uitterlinden AG, Van Leeuwen JPTM, and Pols HAP, “Fracture incidence and association with bone mineral density in elderly men and women: The Rotterdam Study,” Bone, 2004. [DOI] [PubMed] [Google Scholar]
- [8].Krug R, Burghardt AJ, Majumdar S, and Link TM, “High-Resolution Imaging Techniques for the Assessment of Osteoporosis,” Radiologic Clinics of North America. 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Boutroy S, Bouxsein ML, Munoz F, and Delmas PD, “In Vivo Assessment of Trabecular Bone Microarchitecture by High-Resolution Peripheral Quantitative Computed Tomography,” vol. 90, no. 12, pp. 6508–6515, 2005. [DOI] [PubMed] [Google Scholar]
- [10].Wehrli FW, Song HK, Saha PK, and Wright AC, “Quantitative MRI for the assessment of bone structure and function y,” pp. 731–764, 2006. [DOI] [PubMed] [Google Scholar]
- [11].Link TM, “Osteoporosis Imaging : State of the Art and Advanced,” vol. 263, no. 1, pp. 3–17, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Bolotin HH, “DXA in vivo BMD methodology: An erroneous and misleading research and clinical gauge of bone mineral status, bone fragility, and bone remodelling,” Bone, vol. 41, no. 1, pp. 138–154, 2007. [DOI] [PubMed] [Google Scholar]
- [13].Garg M. and Kharb S, “Dual energy X-ray absorptiometry: Pitfalls in measurement and interpretation of bone mineral density,” Indian J. Endocrinol. Metab, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Haïat G, Lhémery A, Renaud F, Padilla F, Laugier P, and Naili S, “Velocity dispersion in trabecular bone : Influence of multiple scattering and of absorption Velocity dispersion in trabecular bone : Influence of multiple,” vol. 4047, no. 2008, 2017. [DOI] [PubMed] [Google Scholar]
- [15].Conoir J, “Multiple scattering in a trabecular bone : Influence of the marrow viscosity on the effective properties Multiple scattering in a trabecular bone : Influence of the marrow viscosity on the effective properties,” no. June, pp. 1–5, 2003. [DOI] [PubMed] [Google Scholar]
- [16].Litniewski J, Wojcik J, and Nowicki A, “Contribution of multiple scattering to the trabecular bone backscatter - dependence on porosity and frequency,” 2012 IEEE Int. Ultrason. Symp., pp. 1–4, 2012. [Google Scholar]
- [17].Mohanty K, Blackwell J, Egan T, and Muller M, “Characterization of the Lung Parenchyma Using Ultrasound Multiple Scattering,” Ultrasound Med. Biol, vol. 43, no. 5, pp. 993–1003, May 2017. [DOI] [PubMed] [Google Scholar]
- [18].Du H, Mohanty K, and Muller M, “Microstructural characterization of trabecular bone using ultrasonic backscattering and diffusion parameters,” J. Acoust. Soc. Am, vol. 141, no. 5, pp. EL445-EL451, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Yamamoto K, Yaoi Y, Yamato Y, Yanagitan T, Matsukawa M, and Yamazaki K, “Ultrasonic Wave Properties in Bone Axis Direction of Bovine Cortical Bone,” Jpn. J. Appl. Phys, vol. 47, no. 5, pp. 4096–4100, May 2008. [Google Scholar]
- [20].Wear KA and Garra BS, “Assessment of bone density using ultrasonic backscatter,” Ultrasound Med. Biol, vol. 24, no. 5, pp. 689–695, June 1998. [DOI] [PubMed] [Google Scholar]
- [21].Wear KA, “Frequency dependence of ultrasonic backscatter from human trabecular bone: Theory and experiment,” J. Acoust. Soc. Am, vol. 106, no. 6, pp. 3659–3664, December 1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Wear KA, “The effects of frequency-dependent attenuation and dispersion on sound speed measurements: applications in human trabecular bone,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control, vol. 47, no. 1, pp. 265–273, 2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Wear KA, “A stratified model to predict dispersion in trabecular bone,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control, vol. 48, no. 4, pp. 1079–1083, July 2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Wear KA, “Characterization of trabecular bone using the backscattered spectral centroid shift,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control, vol. 50, no. 4, pp. 402–407, April 2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Wear KA, “The dependencies of phase velocity and dispersion on trabecular thickness and spacing in trabecular bone-mimicking phantoms,” J. Acoust. Soc. Am, vol. 118, no. 2, pp. 1186–1192, August 2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Wear KA, Nagaraja S, Dreher ML, Gibson SL, Wear KA, Nagaraja S, and Dreher ML, “Relationships of quantitative ultrasound parameters with cancellous bone microstructure in human calcaneus in vitro,” vol. 1605, no. 2012, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Padilla F. and Wear K, “Scattering by Trabecular Bone,” in Bone Quantitative Ultrasound, Dordrecht: Springer Netherlands, 2011, pp. 123–145. [Google Scholar]
- [28].Padilla F. and Laugier P, “Recent Developments in Trabecular Bone Characterization Using Ultrasound,” 2005. [DOI] [PubMed] [Google Scholar]
- [29].Bréban S, Padilla F, Fujisawa Y, Mano I, Matsukawa M, Benhamou CL, Otani T, Laugier P, and Chappard C, “Trabecular and cortical bone separately assessed at radius with a new ultrasound device, in a young adult population with various physical activities,” Bone, vol. 46, no. 6, pp. 1620–1625, Jun. 2010. [DOI] [PubMed] [Google Scholar]
- [30].Sasso M, Haïat G, Yamato Y, Naili S, and Matsukawa M, “Dependence of ultrasonic attenuation on bone mass and microstructure in bovine cortical bone,” J. Biomech, vol. 41, no. 2, pp. 347–355, January 2008. [DOI] [PubMed] [Google Scholar]
- [31].Mizuno K, Matsukawa M, Otani T, Takada M, Mano Isao, and Tsujimoto T, “Effects of structural anisotropy of cancellous bone on speed of ultrasonic fast waves in the bovine femur,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control, vol. 55, no. 7, pp. 1480–1487, July 2008. [DOI] [PubMed] [Google Scholar]
- [32].Haïat G, Sasso M, Naili S, and Matsukawa M, “Ultrasonic velocity dispersion in bovine cortical bone: An experimental study,” J. Acoust. Soc. Am, vol. 124, no. 3, pp. 1811–1821, September 2008. [DOI] [PubMed] [Google Scholar]
- [33].Grimal Q, Grondin J, Gué S, Barkmann R, Engelke K, Glü C-C, and Laugier P, “Quantitative Ultrasound of Cortical Bone in the Femoral Neck Predicts Femur Strength: Results of a Pilot Study.” [DOI] [PubMed] [Google Scholar]
- [34].Pinton G, Aubry J-F, Bossy E, Muller M, Pernot M, and Tanter M, “Attenuation, scattering, and absorption of ultrasound in the skull bone,” Med. Phys, vol. 39, no. 1, pp. 299–307, December 2011. [DOI] [PubMed] [Google Scholar]
- [35].Wear KA, Nagaraja S, Dreher ML, and Gibson SL, “Relationships of quantitative ultrasound parameters with cancellous bone microstructure in human calcaneus in vitro,” J. Acoust. Soc. Am, vol. 131, no. 2, pp. 1605–1612, Feb. 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Droin P, Berger G, and Laugier P, “Velocity dispersion of acoustic waves in cancellous bone,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control, vol. 45, no. 3, pp. 581–592, May 1998. [DOI] [PubMed] [Google Scholar]
- [37].Nicholson PHF, Lowet G, Langton CM, Dequeker J, and Van der Perre G, “A comparison of time-domain and frequency-domain approaches to ultrasonic velocity measurement in trabecular bone,” Phys. Med. Biol, vol. 41, no. 11, pp. 2421–2435, November 1996. [DOI] [PubMed] [Google Scholar]
- [38].Hakulinen MA, Töyräs J, Saarakkala S, Hirvonen J, Kröger H, and Jurvelin JS, “Ability of ultrasound backscattering to predict mechanical properties of bovine trabecular bone,” Ultrasound Med. Biol, vol. 30, no. 7, pp. 919–927, July 2004. [DOI] [PubMed] [Google Scholar]
- [39].Bossy E, Talmant M, and Laugier P, “Three-dimensional simulations of ultrasonic axial transmission velocity measurement on cortical bone models.,” J. Acoust. Soc. Am, vol. 115, no. 5 Pt 1, pp. 2314–2324, 2004. [DOI] [PubMed] [Google Scholar]
- [40].Bossy E, Talmant M, and Laugier P, “Effect of bone cortical thickness on velocity measurements using ultrasonic axial transmission: A 2D simulation study,” J. Acoust. Soc. Am, vol. 112, no. 1, pp. 297–307, July 2002. [DOI] [PubMed] [Google Scholar]
- [41].Muller M, Moilanen P, Bossy E, Nicholson P, Kilappa V, Timonen J, Talmant M, Cheng S, and Laugier P, “Comparison of three ultrasonic axial transmission methods for bone assessment,” Ultrasound Med. Biol, vol. 31, no. 5, pp. 633–642, May 2005. [DOI] [PubMed] [Google Scholar]
- [42].Raum K, Leguerney I, Chandelier F, Bossy E, Talmant M, Saïed A, Peyrin F, and Laugier P, “Bone microstructure and elastic tissue properties are reflected in QUS axial transmission measurements,” Ultrasound Med. Biol, vol. 31, no. 9, pp. 1225–1235, September 2005. [DOI] [PubMed] [Google Scholar]
- [43].Haïat G, Naili S, Grimal Q, Talmant M, Desceliers C, and Soize C, “Influence of a gradient of material properties on ultrasonic wave propagation in cortical bone: Application to axial transmission,” J. Acoust. Soc. Am, vol. 125, no. 6, pp. 4043–4052, Jun. 2009. [DOI] [PubMed] [Google Scholar]
- [44].Naili S, Vu M-B, Grimal Q, Talmant M, Desceliers C, Soize C, and Haïat G, “Influence of viscoelastic and viscous absorption on ultrasonic wave propagation in cortical bone: Application to axial transmission,” J. Acoust. Soc. Am, vol. 127, no. 4, pp. 2622–2634, April 2010. [DOI] [PubMed] [Google Scholar]
- [45].Kaufman JJ and Einhorn TA, “Perspectives: Ultrasound assessment of bone,” J. Bone Miner. Res, vol. 8, no. 5, pp. 517–525, December 2009. [DOI] [PubMed] [Google Scholar]
- [46].Seeman E. and Delmas PD, “Bone Quality — The Material and Structural Basis of Bone Strength and Fragility,” N. Engl. J. Med, vol. 354, no. 21, pp. 2250–2261, May 2006. [DOI] [PubMed] [Google Scholar]
- [47].Mézière F, Muller M, Bossy E, and Derode A, “Measurements of ultrasound velocity and attenuation in numerical anisotropic porous media compared to Biot’s and multiple scattering models,” Ultrasonics, vol. 54, no. 5, pp. 1146–1154, 2014. [DOI] [PubMed] [Google Scholar]
- [48].Anderson CC, Bauer AQ, Holland MR, Pakula M, Laugier P, and Bretthorst GL, “Inverse problems in cancellous bone : Estimation of the ultrasonic properties of fast and slow waves using Bayesian probability theory,” 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Grimal Q. and Laugier P, “Quantitative Ultrasound Assessment of Cortical Bone Properties: Beyond Bone Mineral Density,” IRBM, vol. In Press, no. In Press, 2019. [Google Scholar]
- [50].Moilanen P, Bousson V, Laugier P, Cheng S, Nicholson PHF, Timonen J, and Talmant M, “ Ultrasonically determined thickness of long cortical bones: Two-dimensional simulations of in vitro experiments,” J. Acoust. Soc. Am, 2007. [DOI] [PubMed] [Google Scholar]
- [51].Nicholson PHF, Moilanen P, Laugier P, Timonen J, Cheng S, and Talmant M, “ Ultrasonically determined thickness of long cortical bones: Three-dimensional simulations of in vitro experiments,” J. Acoust. Soc. Am, 2007. [DOI] [PubMed] [Google Scholar]
- [52].Foiret J, Minonzio JG, Chappard C, Talmant M, and Laugier P, “Combined estimation of thickness and velocities using ultrasound guided waves: A pioneering study on in vitro cortical bone samples,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control, vol. 61, no. 9, pp. 1478–1488, 2014. [DOI] [PubMed] [Google Scholar]
- [53].Mandarano-Filho LG, Bezuti MT, Mazzer N, and Barbieri CH, “Influence of cortical bone thickness on the ultrasound velocity.,” Acta Ortop. Bras, vol. 20, no. 3, pp. 184–90, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Rose EC, Hagenmüller M, Jonas IE, and Rahn BA, “Validation of speed of sound for the assessment of cortical bone maturity,” vol. 27, pp. 190–195, 2005. [DOI] [PubMed] [Google Scholar]
- [55].Sievänen H, Cheng S, Ollikainen S, and Uusi-Rasi K, “Ultrasound velocity and cortical bone characteristics in vivo,” Osteoporos. Int, 2001. [DOI] [PubMed] [Google Scholar]
- [56].Eneh CTM, Jurvelin JS, Töyräs J, Malo MKH, and Afara IO, “Porosity predicted from ultrasound backscatter using multivariate analysis can improve accuracy of cortical bone thickness assessment,” J. Acoust. Soc. Am, 2017. [DOI] [PubMed] [Google Scholar]
- [57].Zheng R, Le LH, Sacchi MD, Ta D, and Lou E, “Spectral ratio method to estimate broadband ultrasound attenuation of cortical bones in vitro using multiple reflections,” Phys. Med. Biol, 2007. [DOI] [PubMed] [Google Scholar]
- [58].Xia Y, Lin W, and Qin Y, “The influence of cortical end-plate on broadband ultrasound attenuation measurements at the human calcaneus using scanning confocal ultrasound,” J. Acoust. Soc. Am, vol. 118, no. 3, pp. 1801–1807, September 2005. [DOI] [PubMed] [Google Scholar]
- [59].Moilanen P, Nicholson PHF, Kilappa V, Cheng S, and Timonen J, “Assessment of the cortical bone thickness using ultrasonic guided waves: Modelling and in vitro study,” Ultrasound Med. Biol, vol. 33, no. 2, pp. 254–262, February 2007. [DOI] [PubMed] [Google Scholar]
- [60].Moilanen P, “Ultrasonic guided waves in bone,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control, vol. 55, no. 6, pp. 1277–1286, Jun. 2008. [DOI] [PubMed] [Google Scholar]
- [61].Nicholson PHF, Moilanen P, Kärkkäinen T, Timonen J, and Cheng S, “Guided ultrasonic waves in long bones: modelling, experiment and in vivo application.,” Physiol. Meas, vol. 23, no. 4, pp. 755–68, November 2002. [DOI] [PubMed] [Google Scholar]
- [62].Protopappas VC, Fotiadis DI, and Malizos KN, “Guided ultrasound wave propagation in intact and healing long bones,” Ultrasound Med. Biol, vol. 32, no. 5, pp. 693–708, May 2006. [DOI] [PubMed] [Google Scholar]
- [63].Foiret J, Minonzio J-G, Chappard C, Talmant M, and Laugier P, “Combined estimation of thickness and velocities using ultrasound guided waves: a pioneering study on in vitro cortical bone samples,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control, vol. 61, no. 9, pp. 1478–1488, September 2014. [DOI] [PubMed] [Google Scholar]
- [64].Xu K, Minonzio J-G, Ta D, Hu B, Wang W, and Laugier P, “Sparse SVD Method for High-Resolution Extraction of the Dispersion Curves of Ultrasonic Guided Waves,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control, vol. 63, no. 10, pp. 1514–1524, October 2016. [DOI] [PubMed] [Google Scholar]
- [65].Yousefian O, Karbalaeisadegh Y, Banks HT, White RD, and Muller M, “The effect of pore size and density on ultrasonic attenuation in porous structures with mono-disperse random pore distribution: A two-dimensional in-silico study,” J. Acoust. Soc. Am, vol. 144, no. 2, pp. 709–719, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [66].Yousefian O, White R, Banks HT, and Muller M, “Ultrasonic attenuation spectroscopy and dispersion characteristics in cortical bone,” in IEEE International Ultrasonics Symposium, IUS, 2017. [Google Scholar]
- [67].Yousefian O, Karbalaeisadegh Y, and Muller M, “Modeling ultrasound attenuation in porous structures with mono-disperse random pore distributions using the independent scattering approximation: A 2D simulation study,” Phys. Med. Biol, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [68].Geras KJ, Wolfson S, Shen Y, Wu N, Kim SG, Kim E, Heacock L, Parikh U, Moy L, and Cho K, “High-Resolution Breast Cancer Screening with Multi-View Deep Convolutional Neural Networks,” pp. 1–9. [Google Scholar]
- [69].Ribli D, Horváth A, Unger Z, Pollner P, and Csabai I, “Detecting and classifying lesions in mammograms with Deep Learning,” pp. 1–7, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [70].Kourou K, Exarchos TP, Exarchos KP, V Karamouzis M, and Fotiadis DI, “Machine learning applications in cancer prognosis and prediction,” CSBJ, vol. 13, pp. 8–17, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [71].Chen JH and Asch SM, “Machine Learning and Prediction in Medicine — Beyond the Peak of Inflated Expectations,” N. Engl. J. Med, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [72].Esteva A, Kuprel B, Novoa RA, Ko J, Swetter SM, Blau HM, and Thrun S, “Dermatologist-level classification of skin cancer with deep neural networks,” Nature, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [73].Zhou B. and Zhang X, “Lung mass density analysis using deep neural network and lung ultrasound surface wave elastography,” Ultrasonics, vol. 89, no. May, pp. 173–177, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [74].Steele AJ, Denaxas SC, Shah AD, and Hemingway H, “Machine learning models in electronic health records can outperform conventional survival models for predicting patient mortality in coronary artery disease,” pp. 1–20, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [75].Bossy E. and Grimal Q, “Numerical methods for ultrasonic bone characterization,” in Bone Quantitative Ultrasound, 2011, pp. 181–228. [Google Scholar]
- [76].Sasso M, Haïat G, Yamato Y, Naili S, and Matsukawa M, “Frequency Dependence of Ultrasonic Attenuation in Bovine Cortical Bone: An In Vitro Study,” Ultrasound Med. Biol, vol. 33, no. 12, pp. 1933–1942, 2007. [DOI] [PubMed] [Google Scholar]
- [77].Virieux J, “P-SV wave propagation in heterogeneous media: Velocity‐stress finite‐difference method,” GEOPHYSICS, vol. 51, no. 4, pp. 889–901, April 1986. [Google Scholar]
- [78].Cai X, Peralta L, Gouttenoire P-J, Olivier C, Peyrin F, Laugier P, and Grimal Q, “Quantification of stiffness measurement errors in resonant ultrasound spectroscopy of human cortical bone,” J. Acoust. Soc. Am, 2017. [DOI] [PubMed] [Google Scholar]
- [79].Cai X, Brenner R, Peralta L, Olivier C, Gouttenoire PJ, Chappard C, Peyrin F, Cassereau D, Laugier P, and Grimal Q, “Homogenization of cortical bone reveals that the organization and shape of pores marginally affect elasticity,” J. R. Soc. Interface, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [80].Nuzzo S, Peyrin F, Cloetens P, Baruchel J, and Boivin G, “Quantification of the degree of mineralization of bone in three dimensions using synchrotron radiation microtomography,” Med. Phys, vol. 29, no. 11, pp. 2672–2681, October 2002. [DOI] [PubMed] [Google Scholar]
- [81].Padilla F. and Laugier P, “Recent developments in trabecular bone characterization using ultrasound,” Curr. Osteoporos. Rep, vol. 3, no. 2, pp. 64–69, June 2005. [DOI] [PubMed] [Google Scholar]
- [82].Ulrich D, van Rietbergen B, Laib A, and uegsegger P, “The ability of three-dimensional structural indices to reflect mechanical aspects of trabecular bone,” Bone, vol. 25, no. 1, pp. 55–60, July 1999. [DOI] [PubMed] [Google Scholar]
- [83].Minonzio J-G, Bochud N, Vallet Q, Bala Y, Ramiandrisoa D, Follet H, Mitton D, and Laugier P, “Bone cortical thickness and porosity assessment using ultrasound guided waves: An ex vivo validation study,” Bone, vol. 116, pp. 111–119, November 2018. [DOI] [PubMed] [Google Scholar]
- [84].Bochud N, Vallet Q, Minonzio J-G, and Laugier P, “Predicting bone strength with ultrasonic guided waves,” Sci. Rep, vol. 7, no. 1, p. 43628, May 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [85].Schneider J, Ramiandrisoa D, Armbrecht G, Ritter Z, Felsenberg D, Raum K, and Minonzio J-G, “In Vivo Measurements of Cortical Thickness and Porosity at the Proximal Third of the Tibia Using Guided Waves: Comparison with Site-Matched Peripheral Quantitative Computed Tomography and Distal High-Resolution Peripheral Quantitative Computed Tomography,” Ultrasound Med. Biol, vol. 45, no. 5, pp. 1234–1242, May 2019. [DOI] [PubMed] [Google Scholar]
- [86].Karbalaeisadegh Y, Yousefian O, Iori G, Raum K, & Muller M. (2019). Acoustic diffusion constant of cortical bone: Numerical simulation study of the effect of pore size and pore density on multiple scattering. The Journal of the Acoustical Society of America, 146(2), 1015–1023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [87].Fellah ZEA, Sebaa N, Fellah M, Mitri FG, Ogam E, Lauriks W, and Depollier C, “Application of the biot model to ultrasound in bone: Direct problem,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control, vol. 55, no. 7, pp. 1508–1515, 2008. [DOI] [PubMed] [Google Scholar]
- [88].M. a. Biot, “Generalized Theory of Acoustic Propagation in Porous Dissipative Media,” J. Acoust. Soc. Am, vol. 34, no. 9A, p. 1254, 1962. [Google Scholar]
- [89].Bochud N, Vallet Q, Bala Y, Follet H, Minonzio J-G, and Laugier P, “Genetic algorithms-based inversion of multimode guided waves for cortical bone characterization,” Phys. Med. Biol, vol. 61, no. 19, pp. 6953–6974, October 2016. [DOI] [PubMed] [Google Scholar]
- [90].Jenson Frédéric, Padilla F. rédéri, and Laugier P, “Prediction of frequency-dependent ultrasonic backscatter in cancellous bone using statistical weak scattering model,” Ultrasound Med. Biol, vol. 29, no. 3, pp. 455–464, March 2003. [DOI] [PubMed] [Google Scholar]
- [91].Tran TNHT, Sacchi MD, Ta D, Nguyen V-H, Lou E, and Le LH, “Nonlinear Inversion of Ultrasonic Dispersion Curves for Cortical Bone Thickness and Elastic Velocities,” Ann. Biomed. Eng, June 2019. [DOI] [PubMed] [Google Scholar]
- [92].Sebaa N, Fellah ZEA, Fellah M, Ogam E, Mitri FG, Depollier C, and Lauriks W, “Application of the Biot model to ultrasound in bone: Inverse problem,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control, vol. 55, no. 7, pp. 1516–1523, July 2008. [DOI] [PubMed] [Google Scholar]
- [93].White RD, Yousefian O, Banks HT, & Muller M. (2018, October). Inferring porosity from frequency dependent attenuation in cortical bone mimicking porous media. In 2018 IEEE International Ultrasonics Symposium (IUS) (pp. 1–4). IEEE. [Google Scholar]
- [94].Vogl F, Friesenbichler B, Hüsken L, Kramers-de Quervain IA, & Taylor WR (2019). Can low-frequency guided waves at the tibia paired with machine learning differentiate between healthy and osteopenic/osteoporotic subjects? A pilot study. Ultrasonics, 94, 109–116. [DOI] [PubMed] [Google Scholar]